Ultra-Wideband Differential Line-to-Balanced Line Transitions for Super-High-Speed Digital Transmission
Abstract
:1. Introduction
2. Differential Line and Balanced Lines for Digital Signaling
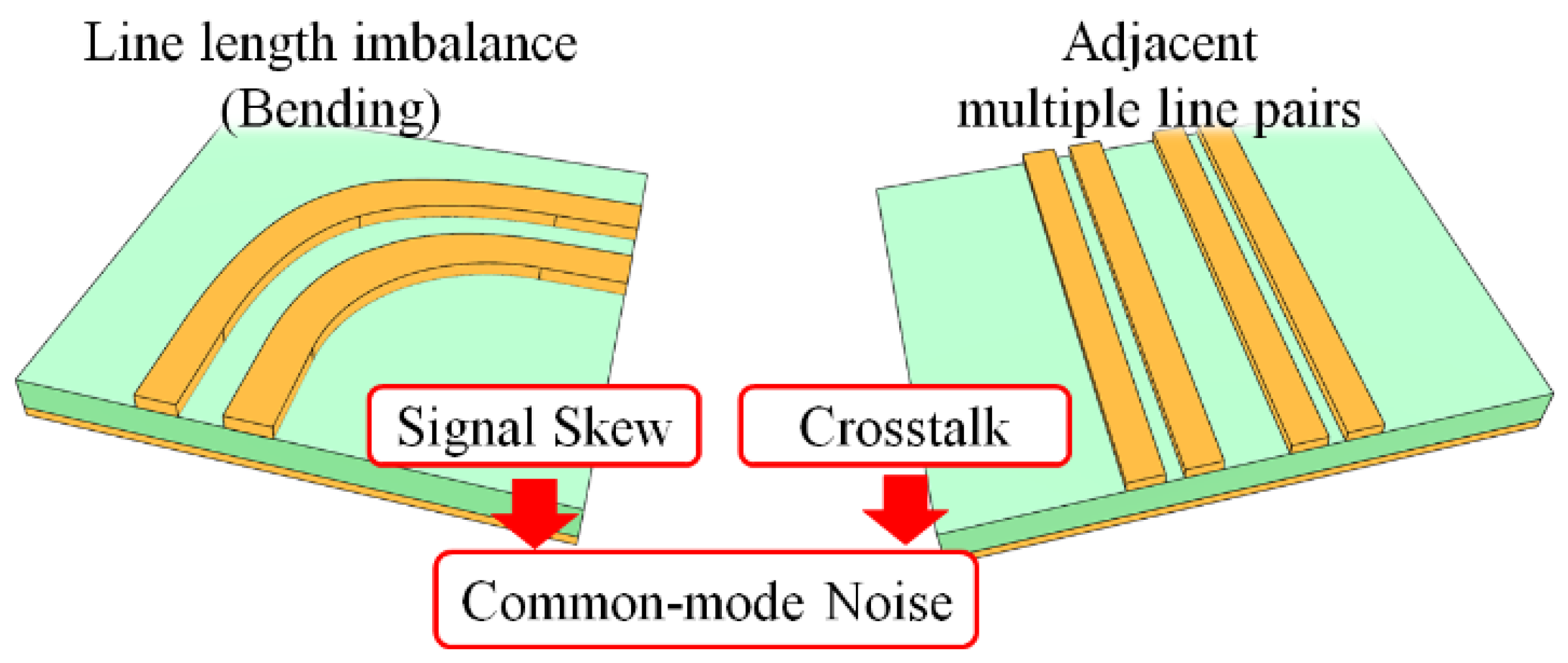
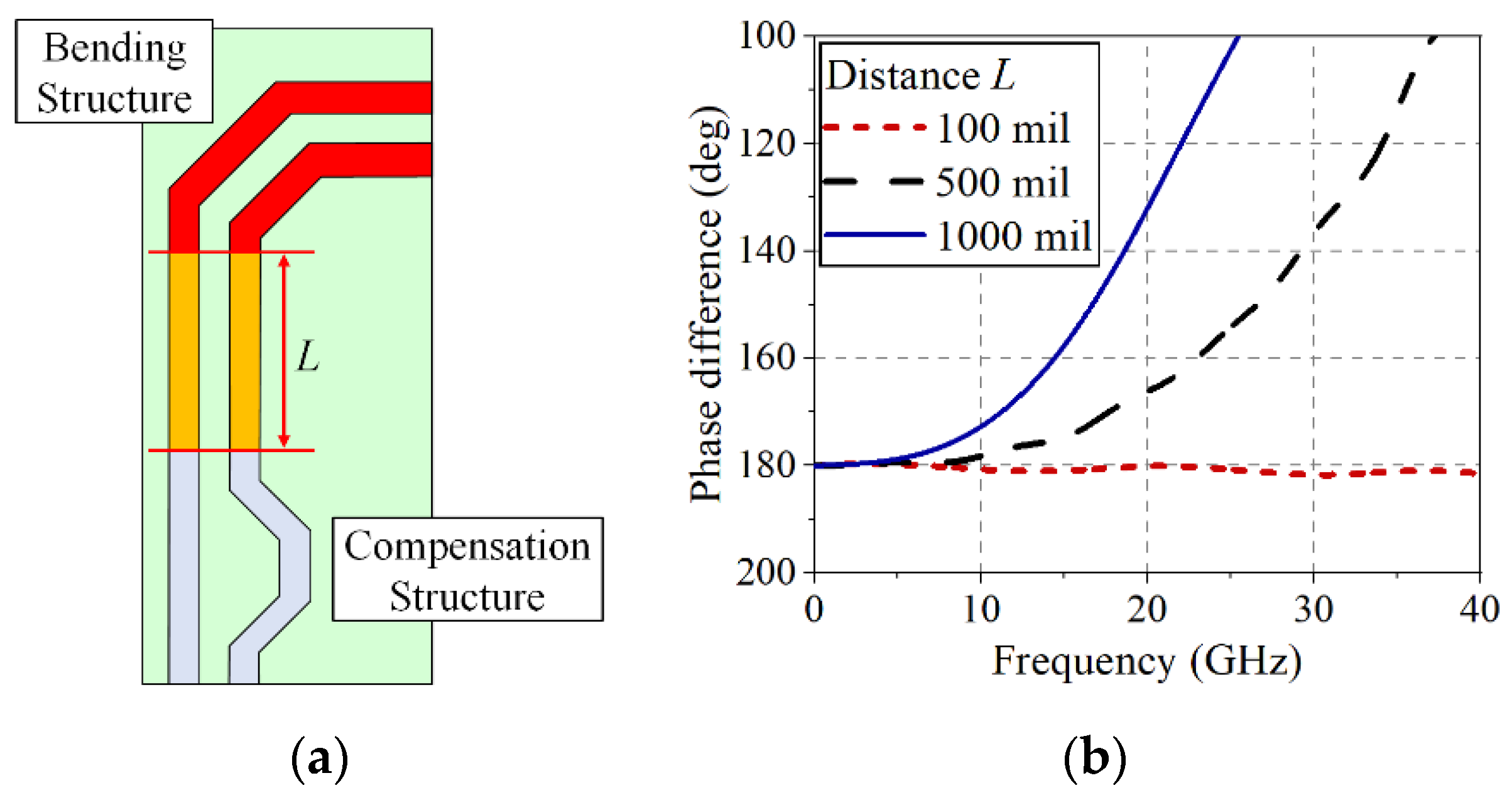
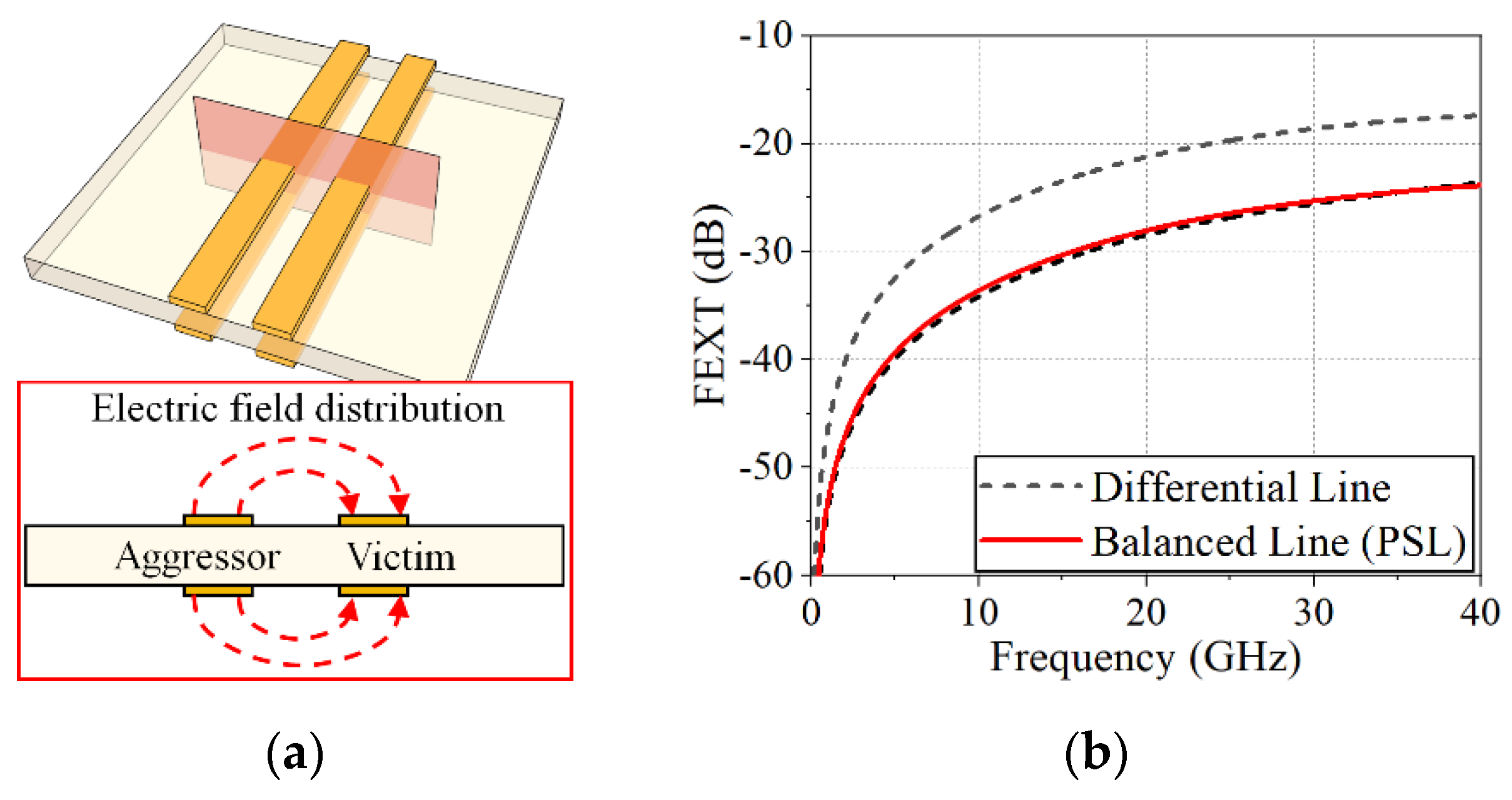
2.1. Differential Line and Its Issues
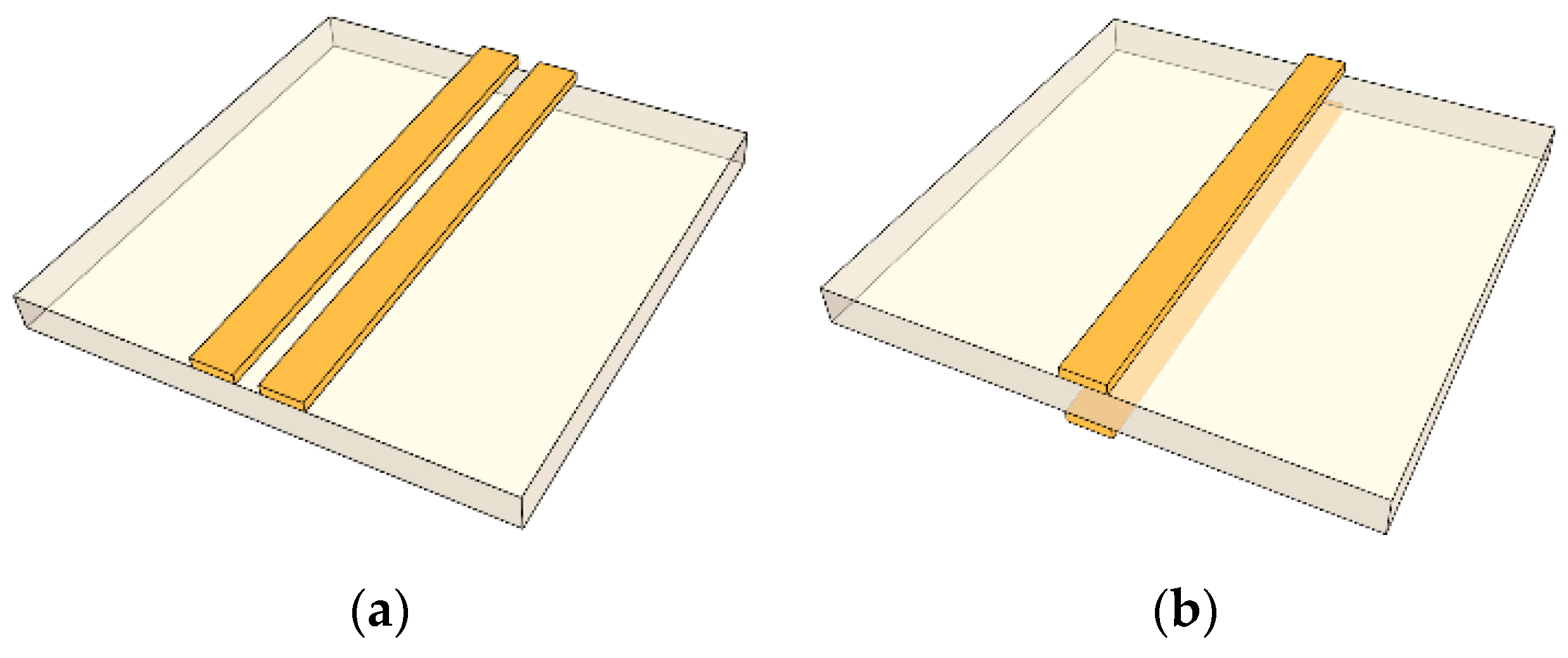
2.2. Balanced Lines: CPS and PSL
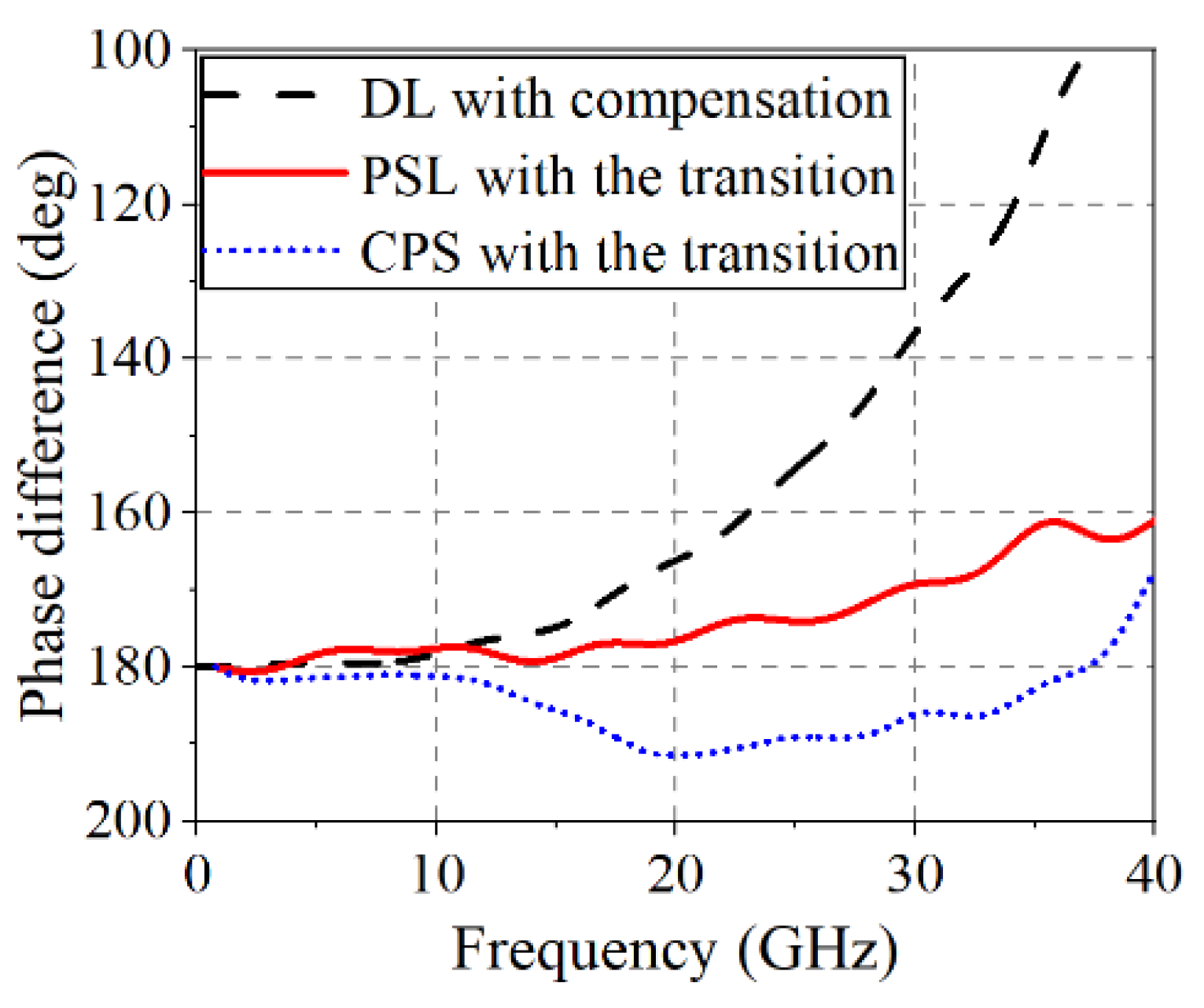
3. Proposed DL-to-BL Transitions
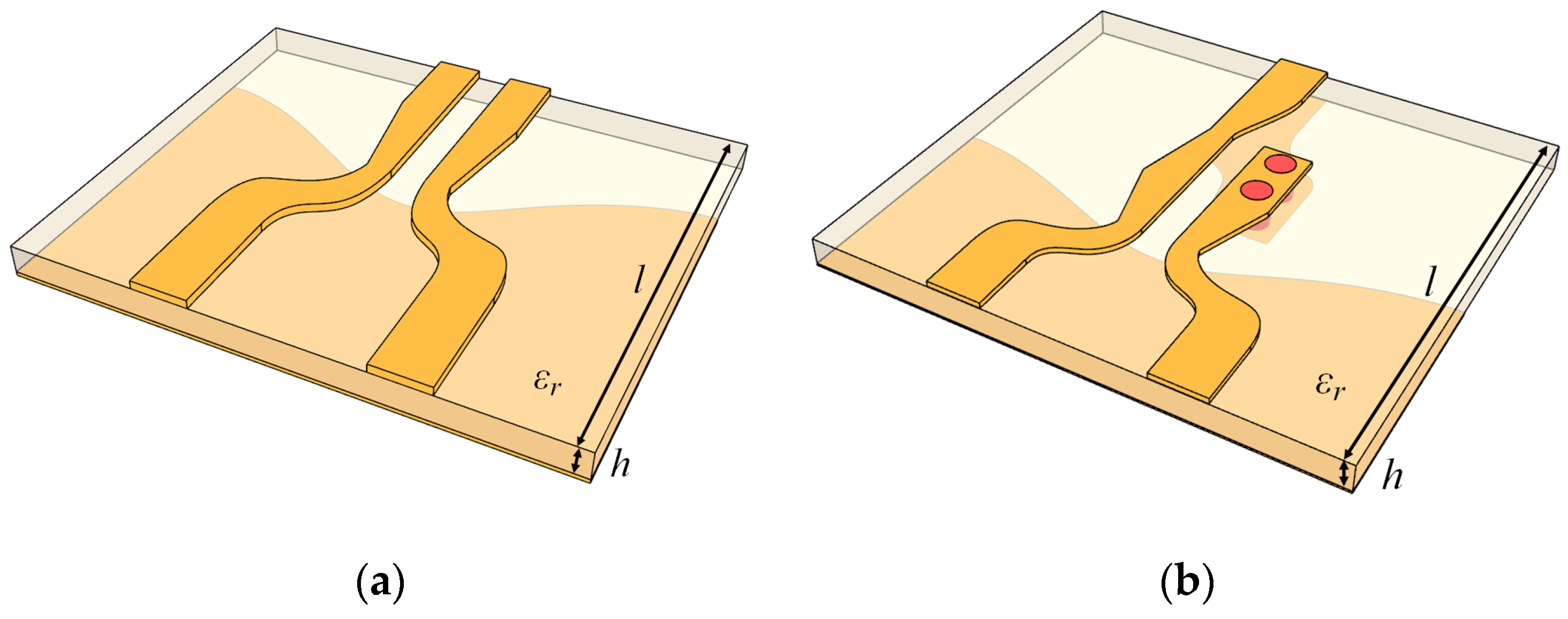
4. Design of the DL-to-CPS Transition
4.1. Design
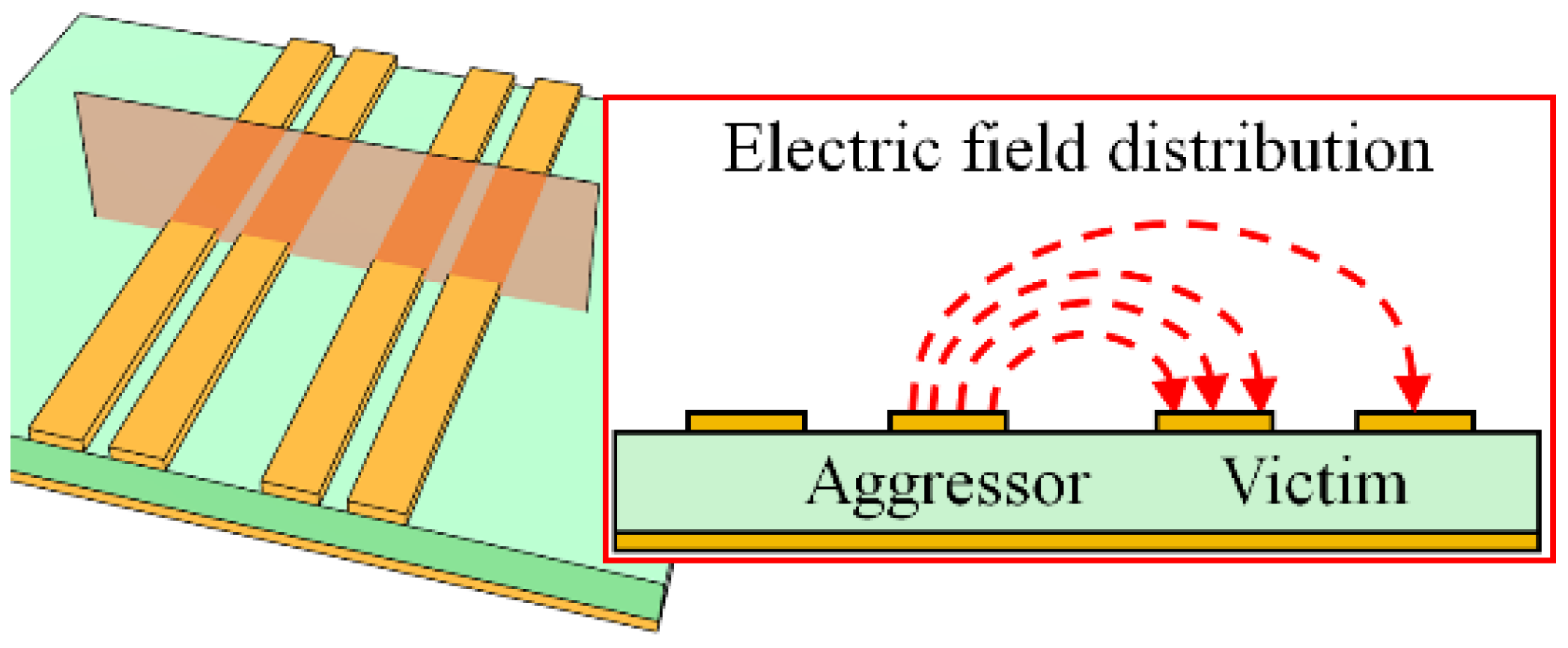
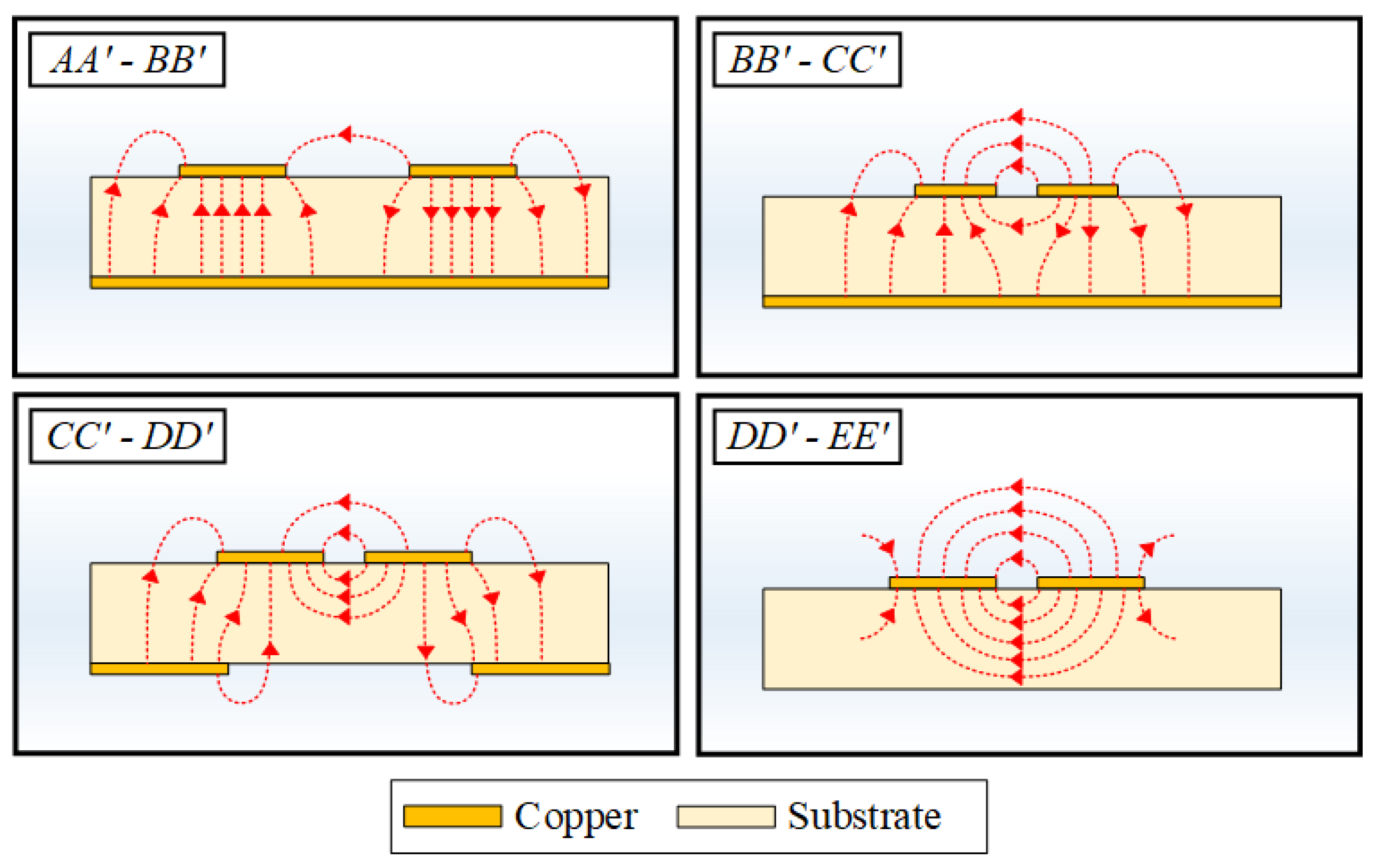
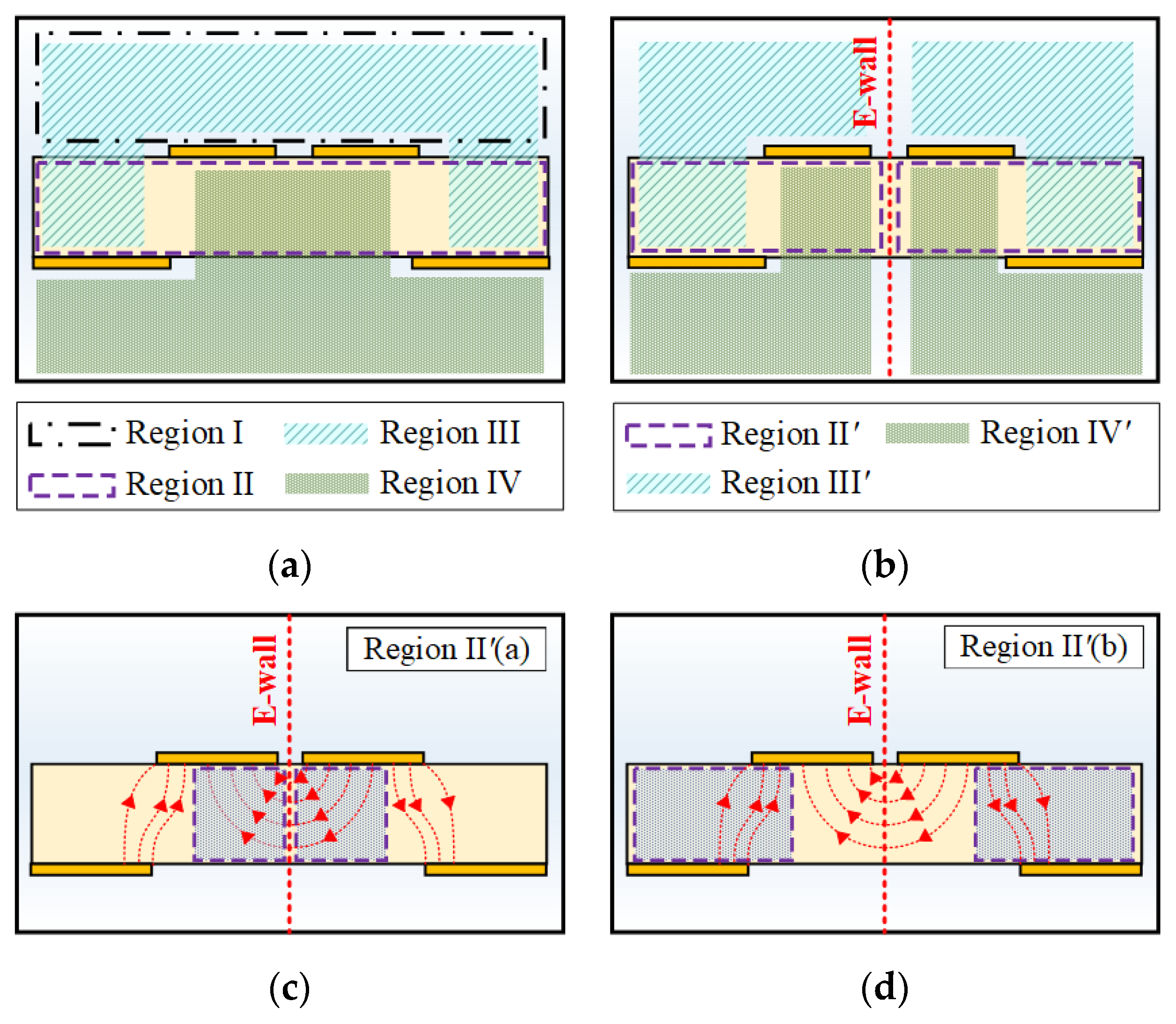
4.2. Electric Field Distribution
4.3. Cross-Sectional Model and Analytical Formulas
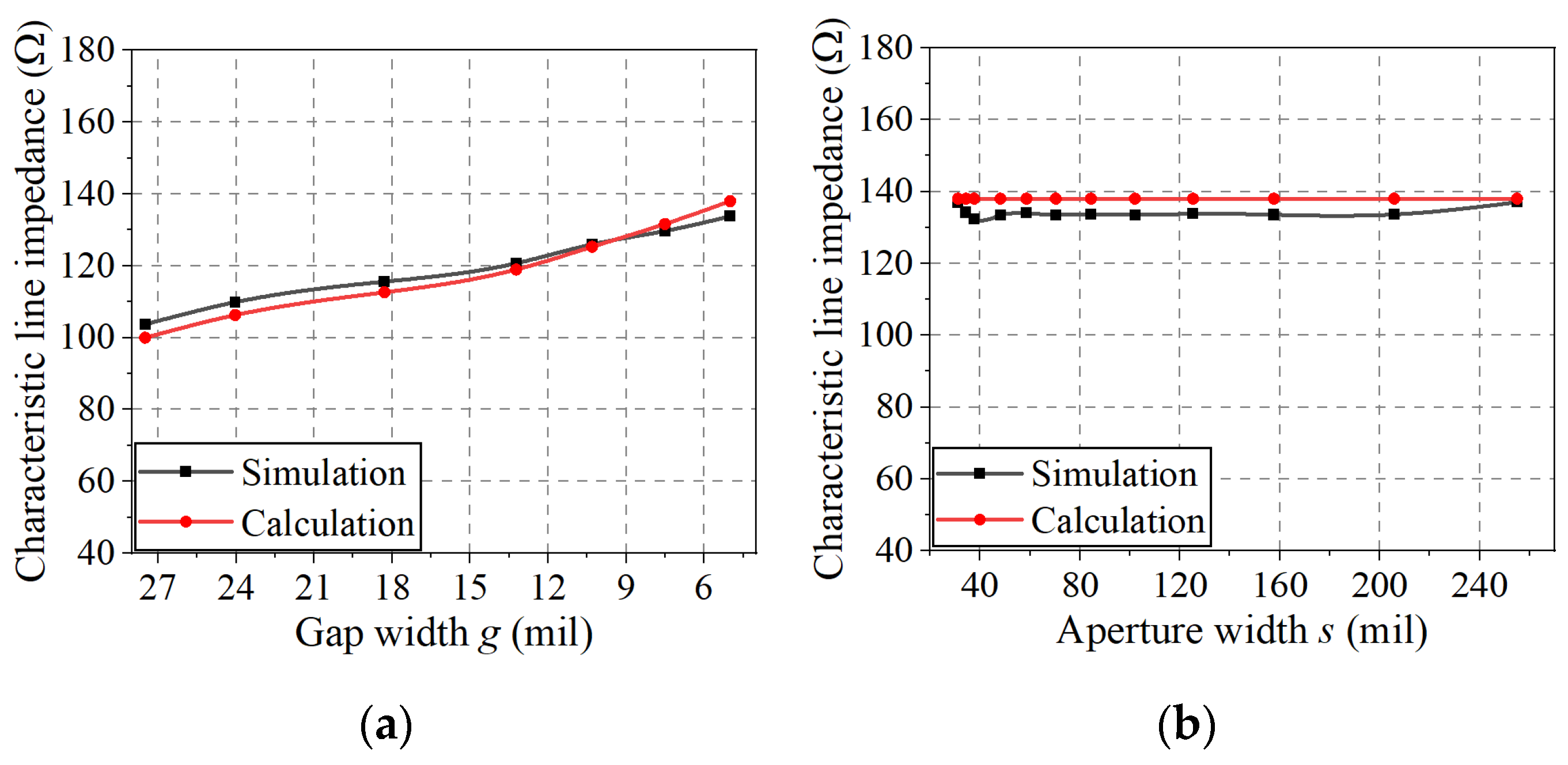
4.4. Calculation of Characteristic Line Impedance
5. Design of the DL-to-PSL Transition
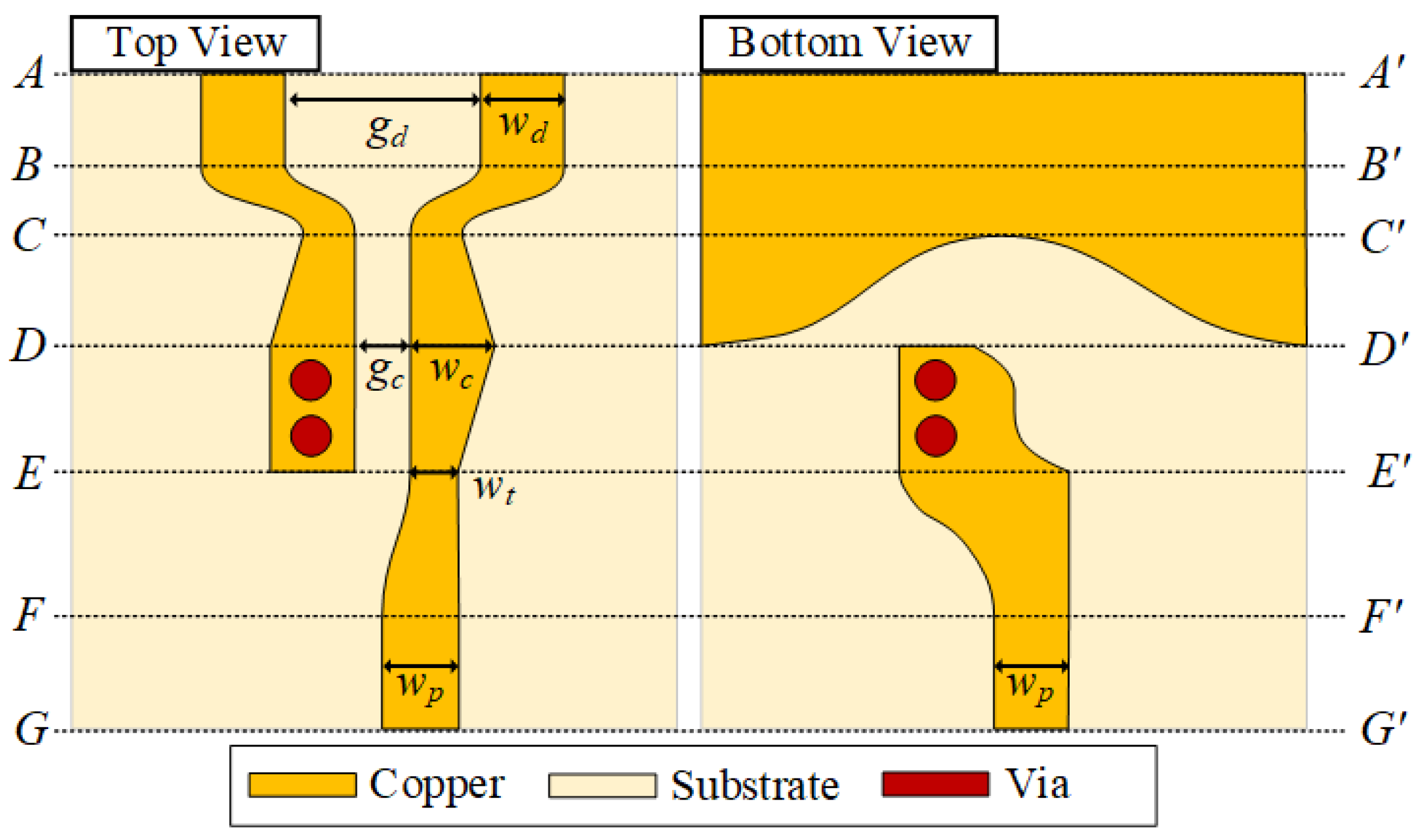
5.1. Design
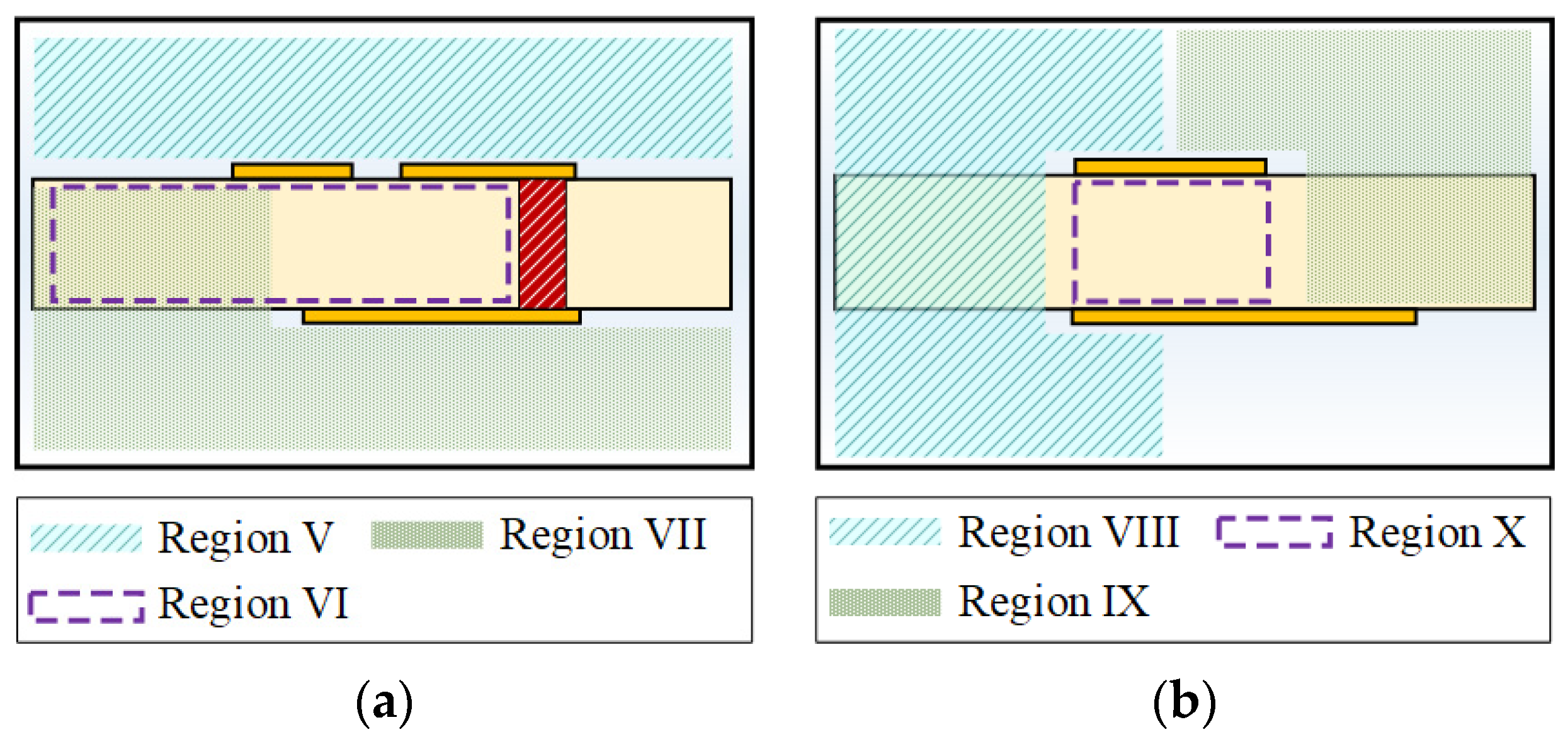
5.2. Electric Field Distribution
5.3. Cross-Sectional Model and Analytical Formulas
5.4. Calculation of Characteristic Line Impedance
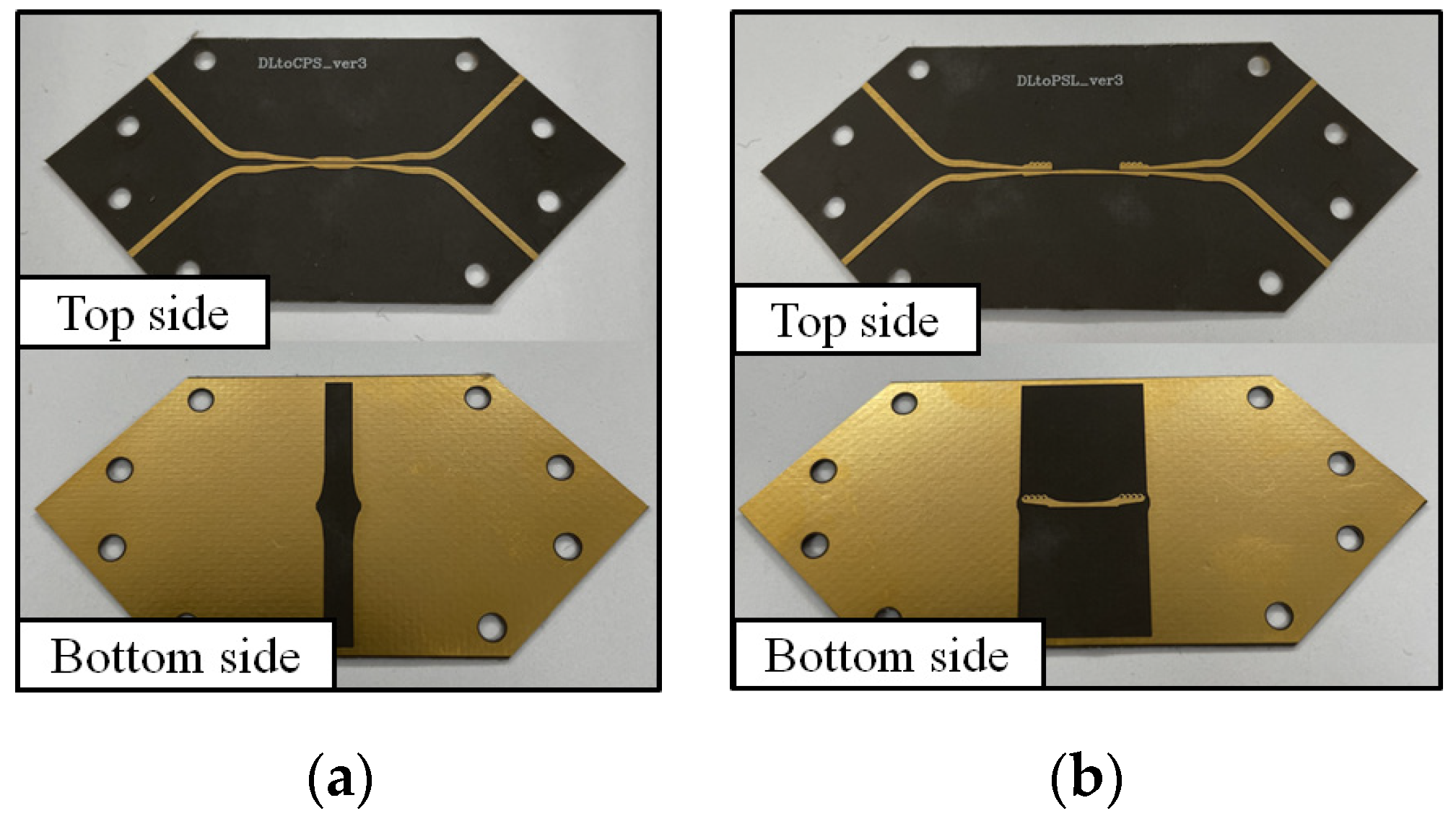
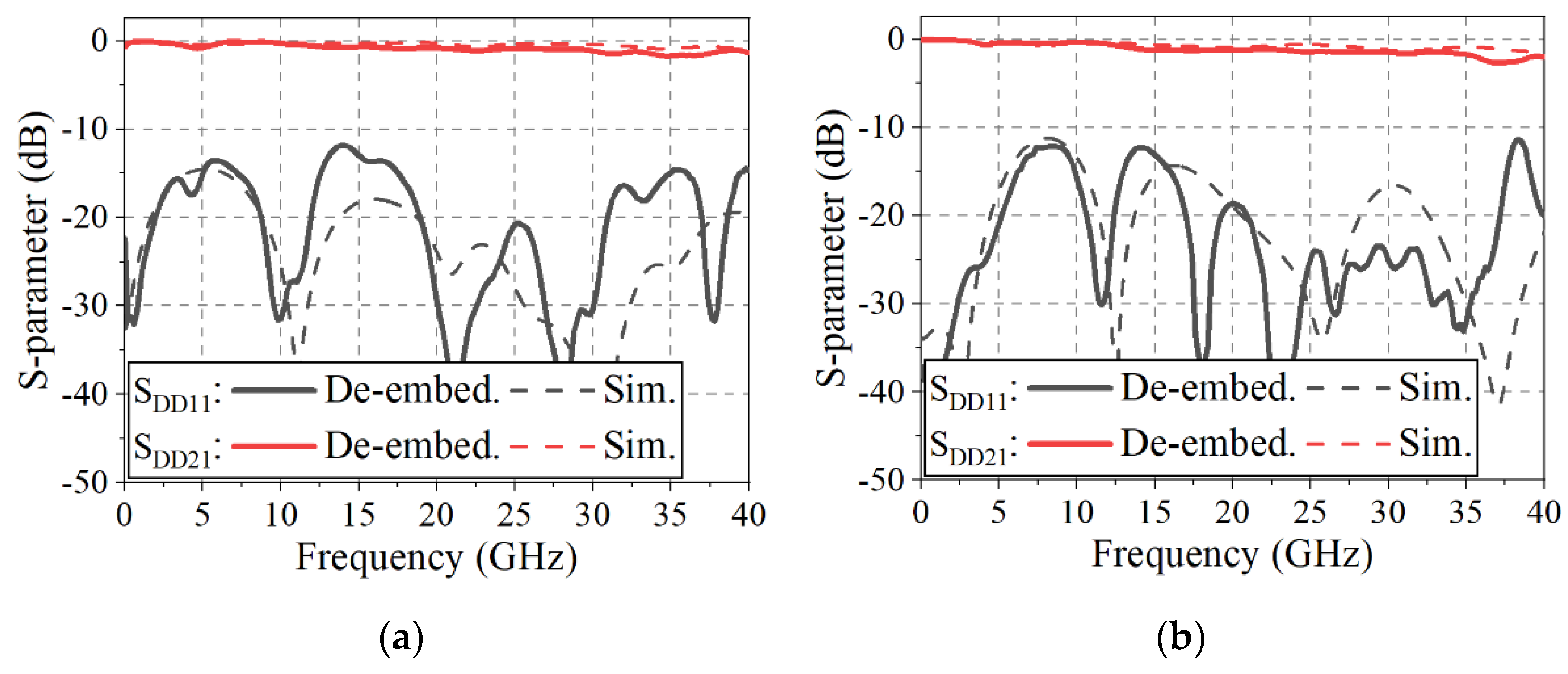
6. Fabrication and Measurements
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Kang, K.; Huang, Y.; Shafi, M.; Molisch, A.F. Millimeter and THz wave for 5G and beyond. China Commun. 2019, 16, iii–vi. [Google Scholar]
- Bogatin, E. Signal and Power Integrity—Simplified, 3rd ed.; Pearson Education: Boston, MA, USA, 2018; pp. 725–731. [Google Scholar]
- Hall, S.H.; Heck, H.L. Advanced Signal Integrity for High-Speed Digital Design; John Wiley & Sons: New York, NY, USA, 2009; pp. 297–314. [Google Scholar]
- Wu, T.; Buesink, F.; Canavero, F. Overview of Signal Integrity and EMC Design Technologies on PCB: Fundamentals and Latest Progress. IEEE Trans. Electromagn. Compat. 2013, 55, 624–638. [Google Scholar]
- Wang, J.; Xu, C.; Zhong, S.; Bai, S.; Lee, J.; Kim, D. Differential via Designs for Crosstalk Reduction in High-Speed PCBs. In Proceedings of the 2020 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Reno, NV, USA, 28 July–28 August 2020; pp. 145–149. [Google Scholar] [CrossRef]
- Lee, S.; Lim, J.; Oh, S.; Kim, Y.; Oh, D.; Lee, J. Differential-to-Common-Mode Conversion Suppression Using Mushroom Structure on Bent Differential Transmission Lines. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 702–711. [Google Scholar] [CrossRef]
- Shiue, G.-H.; Guo, W.-D.; Lin, C.-M.; Wu, R.-B. Noise reduction using compensation capacitance for bend discontinuities of differential transmission lines. IEEE Trans. Adv. Packag. 2006, 29, 560–569. [Google Scholar] [CrossRef]
- Chang, C.; Fang, R.; Wang, C. Bended Differential Transmission Line Using Compensation Inductance for Common-Mode Noise Suppression. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1518–1525. [Google Scholar] [CrossRef]
- Signal Integrity Journal eBook. 2019, pp. 4–7. Available online: https://www.signalintegrityjournal.com/ext/resources/eBooks/2019/ANRITSU-FEB-2019-EBOOK-v7.pdf (accessed on 7 June 2022).
- Kim, Y.; Kim, I.; Woo, D.; Choi, M.; Cho, Y.; Kim, K.W. Ultra-Wideband Components Using a Microstrip-to-CPS Balun. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Korea, 21–25 September 2009; pp. 1–2. [Google Scholar] [CrossRef]
- Woo, D.; Kim, Y.; Kim, I.; Cho, Y.; Kim, K.W. Broadband Antennas Using a Planar Ultra-Wideband Balun. In Proceedings of the 2008 11th IEEE International Conference on Communication Technology, Hangzhou, China, 10–12 November 2008; pp. 305–308. [Google Scholar] [CrossRef]
- Woo, D.; Kim, Y.; Cho, Y.; Kim, K.W. Ultra-Wideband Fermi Antenna Using Microstrip-to-CPS Balun. IEICE Trans. Commun. 2010, E93.B, 2219–2222. [Google Scholar] [CrossRef]
- Wu, X.; Bao, Z.-H.; Shi, J.; Wang, J.; Chen, J.-X.; Cao, Q.-H.; Chu, H.; Tang, H. A Compact Differential Band-Notched Dipole Antenna. In Proceedings of the 2014 3rd Asia-Pacific Conference on Antennas and Propagation, Harbin, China, 26–29 July 2014; pp. 410–411. [Google Scholar] [CrossRef]
- Kim, S.; Chang, K. Ultrawide-band transitions and new microwave components using double-sided parallel-strip lines. IEEE Trans. Microw. Theory Tech. 2004, 52, 2148–2152. [Google Scholar] [CrossRef]
- Chen, J.; Chin, C.K.; Xue, Q. Double-Sided Parallel-Strip Line with an Inserted Conductor Plane and Its Applications. IEEE Trans. Microw. Theory Tech. 2007, 55, 1899–1904. [Google Scholar] [CrossRef]
- Armstrong, K. PCB Design Techniques: For the SI and EMC of Gigabit/Second Differential Transmission Lines Intertek UK. 2010. Available online: https://www.semanticscholar.org/paper/PCB-Design-Techniques-%3A-For-the-SI-and-EMC-of-%2F-Smieee/60b0606d9faea7ea8df3ff567279a6011e05fd40 (accessed on 31 August 2022).
- Zhang, H.; Li, X.; Mao, J. A New Structure for Broadband Transition Between Differential Stripline and Differential GCPW. In Proceedings of the 2020 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shanghai, China, 20–23 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Dong, Y.; Johansen, T.K.; Zhurbenko, V.; Hanberg, P.J. Coplanar Transitions Based on Aluminum Nitride Interposer Substrate for Terabit Transceivers. In Proceedings of the 2017 47th European Microwave Conference (EuMC), Nuremberg, Germany, 10–12 October 2017; pp. 620–623. [Google Scholar] [CrossRef]
- Lee, G.H.; Kim, D.H.; Mohyuddin, W.; Kumar, S.; Choi, H.C.; Kim, K.W. Design of an ultra-wideband coplanar strip-to-parallel stripline transition using an analytical model based on conformal mapping. Microw. Opt. Technol. Lett. 2021, 63, 1054–1060. [Google Scholar] [CrossRef]
- Lee, G.H.; Mohyuddin, W.; Choi, H.C.; Kim, K.W. Asymmetric Ultra-Wideband Microstrip-to-Coplanar Stripline Transition. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 386–388. [Google Scholar] [CrossRef]
- Lee, G.H.; Kim, K.W.; Choi, H.C. Development of the Ultra-Wideband Microstrip-to-Parallel Stripline Transition Based on Conformal Mapping. J. Korean Inst. Electromagn. Eng. Sci. 2020, 31, 216–224. [Google Scholar] [CrossRef]
- Abu Khater, M. High-Speed Printed Circuit Boards: A Tutorial. IEEE Circuits Syst. Mag. 2020, 20, 34–45. [Google Scholar] [CrossRef]
- Intel. High-Speed Board Layout Guidelines. Available online: https://www.intel.com/content/www/us/en/support/programmable/support-resources/quality/brd-index.html (accessed on 11 May 2022).
- Texas Instruments. High-Speed Layout Guidelines (Rev.A). Available online: https://www.ti.com/lit/pdf/scaa082 (accessed on 24 February 2022).
- Brooks, D. Differential Signals, Rules to Live by UltraCAD Design Inc. USA. May 2001. Available online: https://www.ultracad.com/article_outline.html (accessed on 24 February 2022).
- Johnson, H. High-Speed Digital Design. IEEE Microw. Mag. 2011, 12, 42–50. [Google Scholar] [CrossRef]
- Intel. AN 672: Transceiver Link Design Guidelines for High-Gbps Data Rate Transmission. Available online: https://www.intel.com/content/www/us/en/docs/programmable/683624/current/an-672-transceiver-link-design-guidelines.html (accessed on 11 May 2022).
- Peterson, Z. Differential Crosstalk and Spacing between Differential Pairs Altium Limited. USA. September 2020. Available online: https://resources.altium.com/p/differential-crosstalk-and-spacing-between-differential-pairs-0 (accessed on 24 May 2022).
- Kam, D.G.; Lee, H.; Kim, J. Twisted differential line structure on high-speed printed circuit boards to reduce crosstalk and radiated emission. IEEE Trans. Adv. Packag. 2004, 27, 590–596. [Google Scholar] [CrossRef]
- Balan, T.S.; Devadas, B.; Srivastava, G.K. Suppression of Common and Differential Component of Crosstalk Coupling onto the Differential Line and Field Analysis of the Crosstalk. In Proceedings of the 2018 IEEE Symposium on Electromagnetic Compatibility, Signal Integrity and Power Integrity (EMC, SI & PI), Long Beach, CA, USA, 30 July–3 August 2018; pp. 260–264. [Google Scholar] [CrossRef]
- Olney, B. Differential Pair Routing In-Circuit Design Pty. Ltd. Australia. June 2015. Available online: https://www.icd.com.au/articles/Differential_Pair_Routing_PCB-Oct2011.pdf (accessed on 9 May 2022).
- De Paulis, F.; Raimondo, L.; Connor, S.; Archambeault, B.; Orlandi, A. Compact Configuration for Common Mode Filter Design based on Planar Electromagnetic Bandgap Structures. IEEE Trans. Electromagn. Compat. 2012, 54, 646–654. [Google Scholar] [CrossRef]
- Feng, L.-P.; Zhu, L.; Zhang, S.; Zhang, X. Compact Chebyshev Differential-Mode Bandpass Filter on λ/4 CPS Resonator with Intrinsic Common-Mode Rejection. IEEE Trans. Microw. Theory Tech. 2018, 66, 4047–4056. [Google Scholar] [CrossRef]
- Ouyang, Z.-A.; Zhu, L.; Qiu, L.-L. Wideband Balanced Filters with Intrinsic Common-Mode Suppression Using Coplanar Strip Double-Sided Shunt-Stub Structures. IEEE Trans. Microw. Theory Tech. 2021, 69, 3770–3782. [Google Scholar] [CrossRef]
- Peik, S.; Langner, F. New Differential PSL Coupled Resonator Filters. In Proceedings of the 2008 IEEE MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 15–20 June 2008; pp. 447–450. [Google Scholar] [CrossRef]
- Feng, L.-P.; Zhu, L.; Zhang, S. Differential-Mode Low-Pass Filter Using Hybrid CPS and G-CPS with Intrinsic Common-Mode Rejection. IEEE Trans. Microw. Theory Tech. 2021, 67, 1836–1843. [Google Scholar] [CrossRef]
- Feng, W.; Pan, B.; Zhu, H.; Zhou, X.Y.; Che, W.; Xue, Q. High Performance Balanced Bandpass Filters with Wideband Common Mode Suppression. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1897–1901. [Google Scholar] [CrossRef]
- Wu, M.; Qiu, K.; Zhang, G. 112 Gbps Serial Transmission over Copper-PAM4 vs. PAM8 Signaling. In Proceedings of the DesignCon 2017-Signal Integrity Journal, Santa Clara, CA, USA, 31 January 2017–2 February 2017. [Google Scholar]
- Gupta, K.C.; Garg, R.; Bahl, I.J.; Bhartia, P. Microstrip Lines and Slotlines, 3rd ed.; Artech House: Boston, MA, USA, 1996; pp. 381–393. [Google Scholar]
- Simons, R.N. Coplanar Waveguide Circuits, Components, and Systems; John Wiley & Sons: New York, NY, USA, 2001; pp. 152–170. [Google Scholar]
- Lee, G.H.; Kumar, S.; Mohyuddin, W.; Choi, H.C.; Kim, K.W. Generalized Design Technique of Ultra-Wideband Transitions for Quasi-TEM Planar Transmission Lines Based on Analytical Models. IEEE Access 2021, 9, 52619–52633. [Google Scholar] [CrossRef]
- Bockelman, D.E.; Eisenstadt, W.R. Pure-mode network analyzer for on-wafer measurements of mixed-mode S-parameters of differential circuits. IEEE Trans. Microw. Theory Tech. 1997, 45, 1071–1077. [Google Scholar] [CrossRef]
- Engen, G.F.; Hoer, C.A. Thru-Reflect-Line: An Improved Technique for Calibrating the Dual Six-Port Automatic Network Analyzer. Microw. Theory Tech. IEEE Trans. 1979, 27, 987–993. [Google Scholar] [CrossRef]
- Cho, H.; Burk, D.E. A three-step method for the de-embedding of high-frequency S-parameter measurements. IEEE Trans. Electron Devices 1991, 38, 1371–1375. [Google Scholar] [CrossRef]
- Vaitkus, R.L. Wide-band de-embedding with a short, an open, and a through line. Proc. IEEE 1986, 74, 71–74. [Google Scholar] [CrossRef]
- Chen, B.; Ye, X.; Samaras, B.; Fan, J. A novel de-embedding method suitable for transmission-line measurement. In Proceedings of the Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC), Taipei, Taiwan, 25–29 May 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, B.; He, J.; Guo, Y.; Pan, S.; Ye, X.; Fan, J. Multi-Ports (2n) 2×-Thru De-Embedding: Theory, Validation, and Mode Conversion Characterization. IEEE Trans. Electromagn. Compat. 2019, 61, 1261–1270. [Google Scholar] [CrossRef]
- Chen, B. 2X-Thru, 1X-Reflection, and Thru-Line de-Embedding: Theory, Sensitivity Analysis, and Error Corrections. Ph.D. Dissertation, Department Electrical and Computer Engineering, Missouri University of Science and Technology, Rolla, MO, USA, 2019. [Google Scholar]
- Wu, C.; Chen, B.; Mikheil, T.; Fan, J.; Ye, X. Error Bounds Analysis of De-Embedded Results in 2x Thru De-Embedding Methods. In Proceedings of the 2017 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Washington, DC, USA, 7–11 August 2017; pp. 532–536. [Google Scholar] [CrossRef]
- Hall, S.H.; Heck, H.L. Appendix B: FourPort Conversions between T and S Parameters. In Advanced Signal Integrity for High-Speed Digital Designs; IEEE: New York, NY, USA, 2009; pp. 641–643. [Google Scholar] [CrossRef]
- Chen, Y. De-Embedding Method Comparisons and Physics Based Circuit Model for High Frequency D-Probe. Master’s Thesis, Department Electrical and Computer Engineering, Missouri University of Science and Technology, Rolla, MO, USA, 2018. [Google Scholar]
- Liu, C. 224 Gb/s Per Lane: Options and Challenges. March 2021. Signal Integrity Journal. Available online: https://www.signalintegrityjournal.com/articles/2018-gbs-per-lane-options-and-challenges (accessed on 25 May 2022).






| Ref. | Structure | Characteristic Line Impedance [Ω] | Operating Bandwidth [GHz] |
|---|---|---|---|
| [19] | CPS-to-PSL | 147/50, 120/50 | 6.4–40 |
| [20] | CPS-to-MSL | 147/50 | 6–40 |
| [21] | PSL-to-MSL | 50/50 | DC-40 |
| Parameters | wd | wc | wm | gd | gc | l |
|---|---|---|---|---|---|---|
| Size in mil (mm) | 26.8 (0.68) | 20 (0.51) | 9.78 (0.25) | 27.5 (0.70) | 5 (0.13) | 230 (5.84) |
| Parameters | wd | wc | wt | wp | gd | gc | l |
|---|---|---|---|---|---|---|---|
| Size in mil (mm) | 26.8 (0.68) | 20 (0.51) | 11 (0.28) | 15. 9(0.40) | 27.5 (0.70) | 5 (0.13) | 410 (5.84) |
| Transition | Size [mil (mm)] * |
|---|---|
| DL-to-CPS | 660 × 1000 × 11.4 (16.8 × 25.4 × 0.29) |
| DL-to-PSL | 970 × 1000 × 11.4 (24.6 × 25.4 × 0.29) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, B.C.; Lee, G.H.; Lee, J.S.; Nashuha, S.H.; Choi, H.C.; Kim, K.W. Ultra-Wideband Differential Line-to-Balanced Line Transitions for Super-High-Speed Digital Transmission. Sensors 2022, 22, 6873. https://doi.org/10.3390/s22186873
Min BC, Lee GH, Lee JS, Nashuha SH, Choi HC, Kim KW. Ultra-Wideband Differential Line-to-Balanced Line Transitions for Super-High-Speed Digital Transmission. Sensors. 2022; 22(18):6873. https://doi.org/10.3390/s22186873
Chicago/Turabian StyleMin, Byung Cheol, Gwan Hui Lee, Jung Seok Lee, Syifa Haunan Nashuha, Hyun Chul Choi, and Kang Wook Kim. 2022. "Ultra-Wideband Differential Line-to-Balanced Line Transitions for Super-High-Speed Digital Transmission" Sensors 22, no. 18: 6873. https://doi.org/10.3390/s22186873
APA StyleMin, B. C., Lee, G. H., Lee, J. S., Nashuha, S. H., Choi, H. C., & Kim, K. W. (2022). Ultra-Wideband Differential Line-to-Balanced Line Transitions for Super-High-Speed Digital Transmission. Sensors, 22(18), 6873. https://doi.org/10.3390/s22186873






