Stability Analysis of Two Power Converters Control Algorithms Connected to Micro-Grids with Wide Frequency Variation
Abstract
:1. Introduction
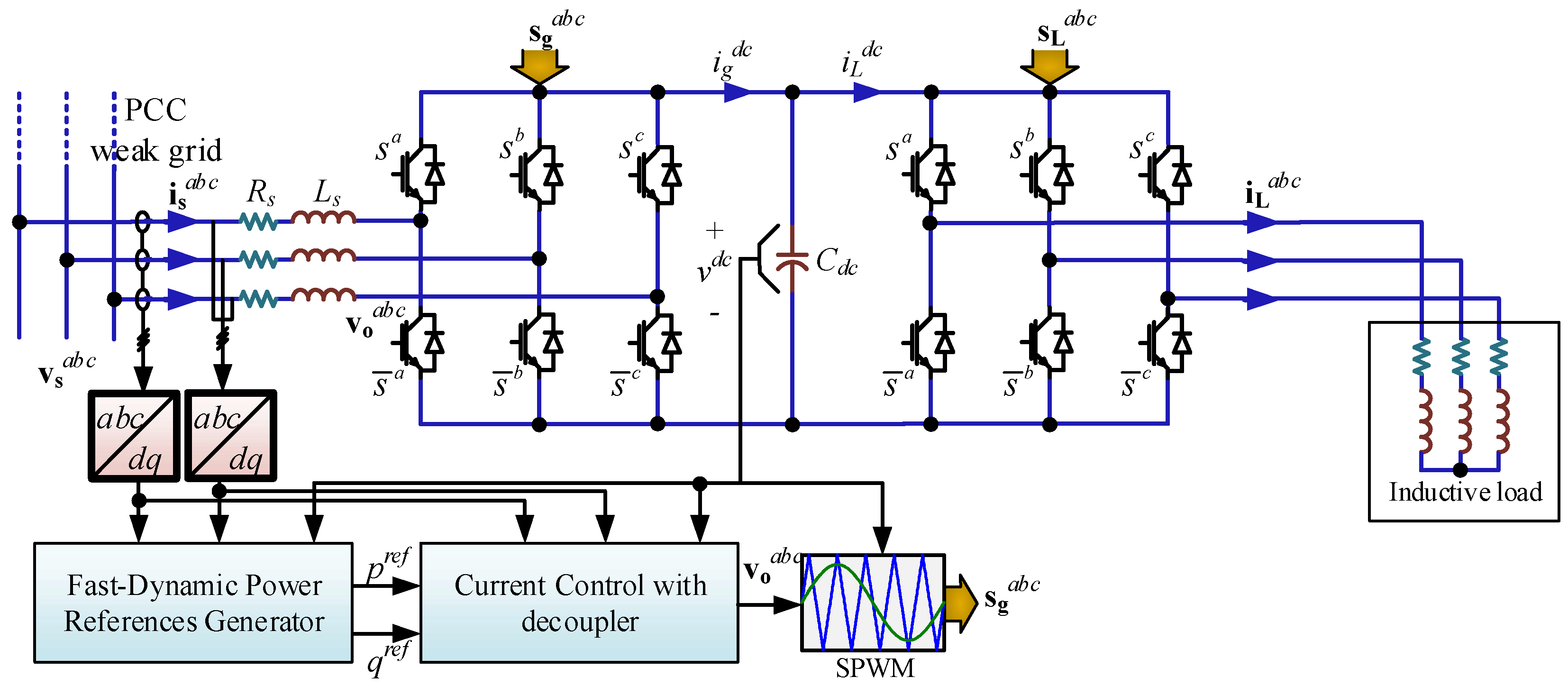
2. Modeling of Power Converters under Variable Grid Frequency
3. Control of Power Converters under Variable Grid Frequency
3.1. Control Goals
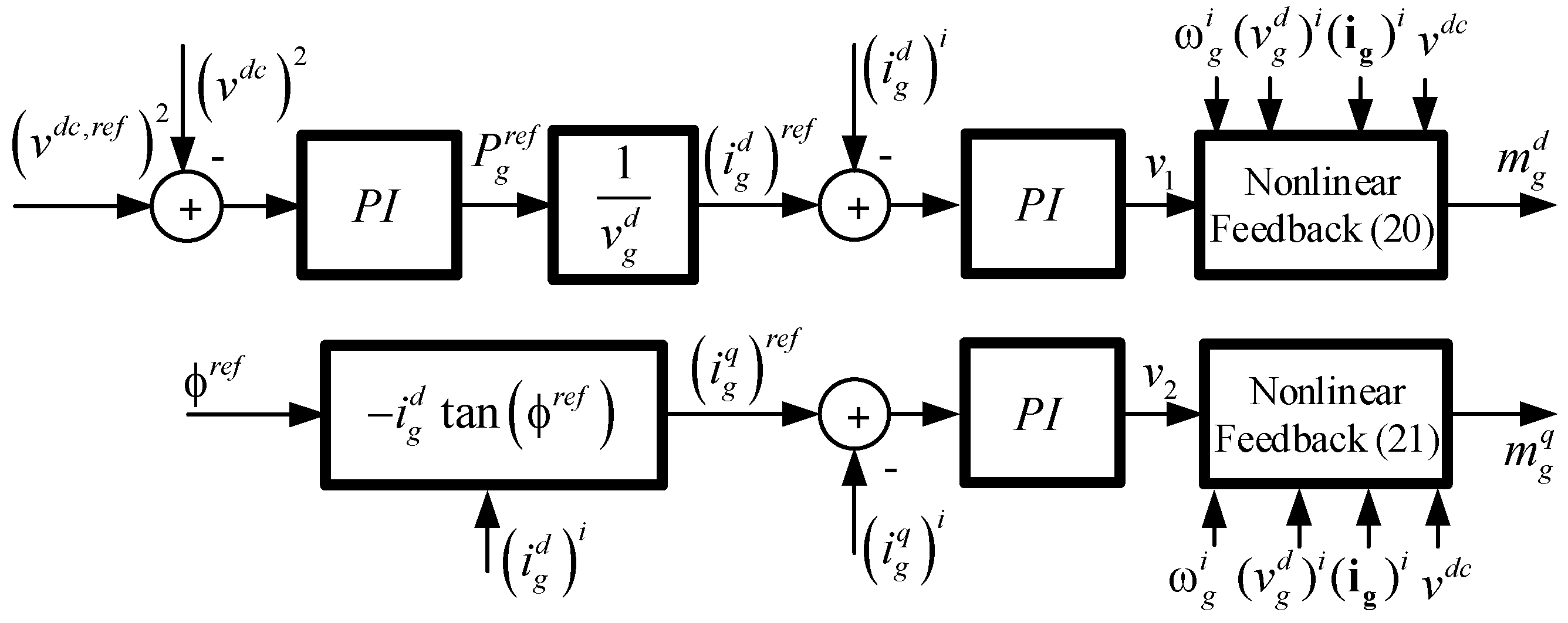
3.2. Linear Control with Static Decoupler
3.3. Linear Control with Dynamic Decoupler
4. Stability Analysis Procedure
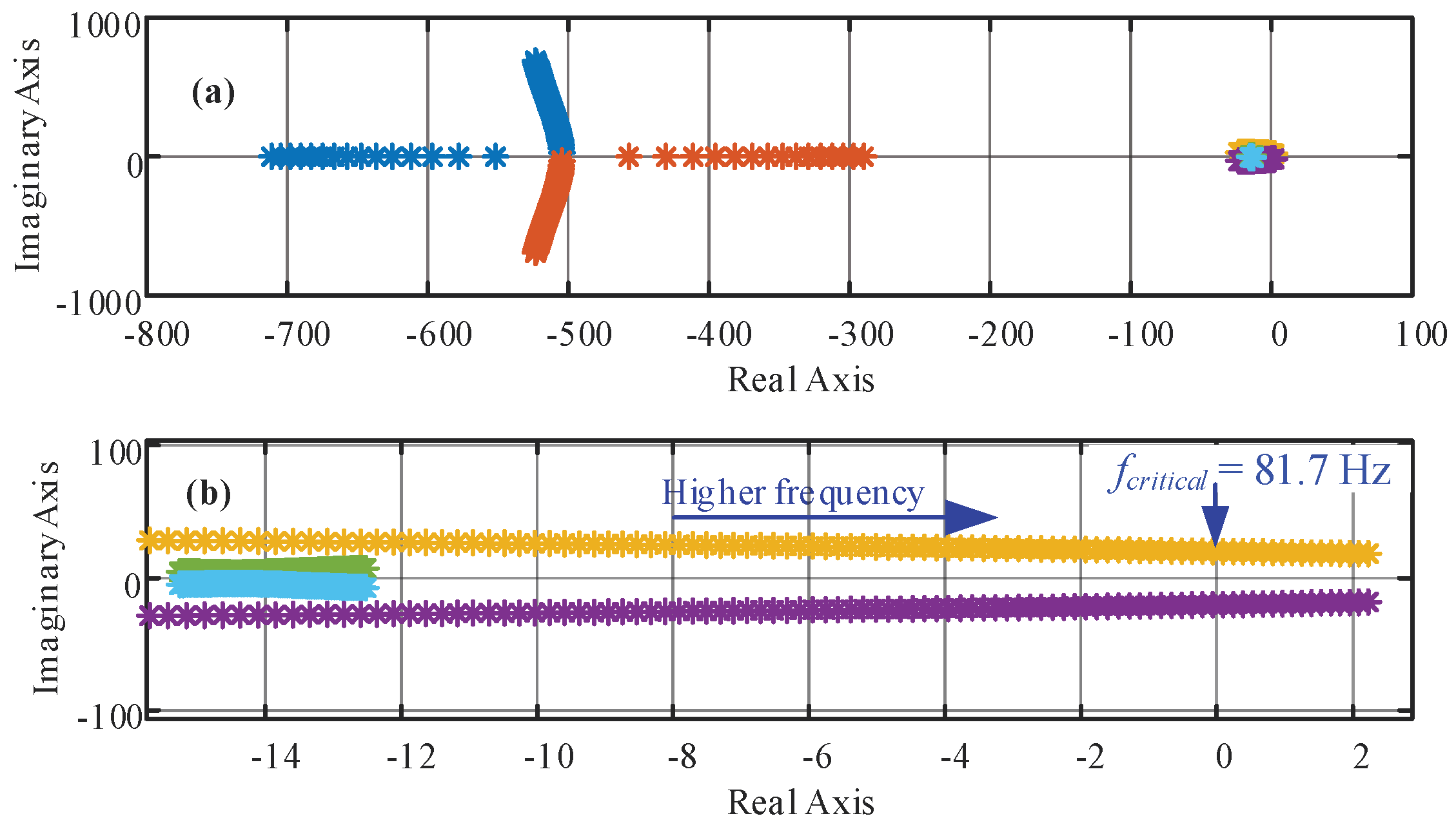
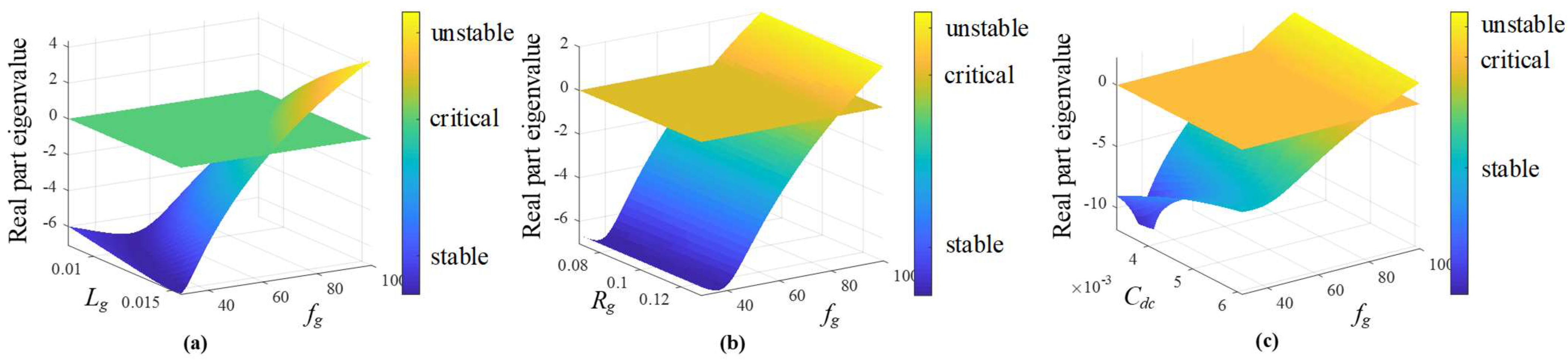
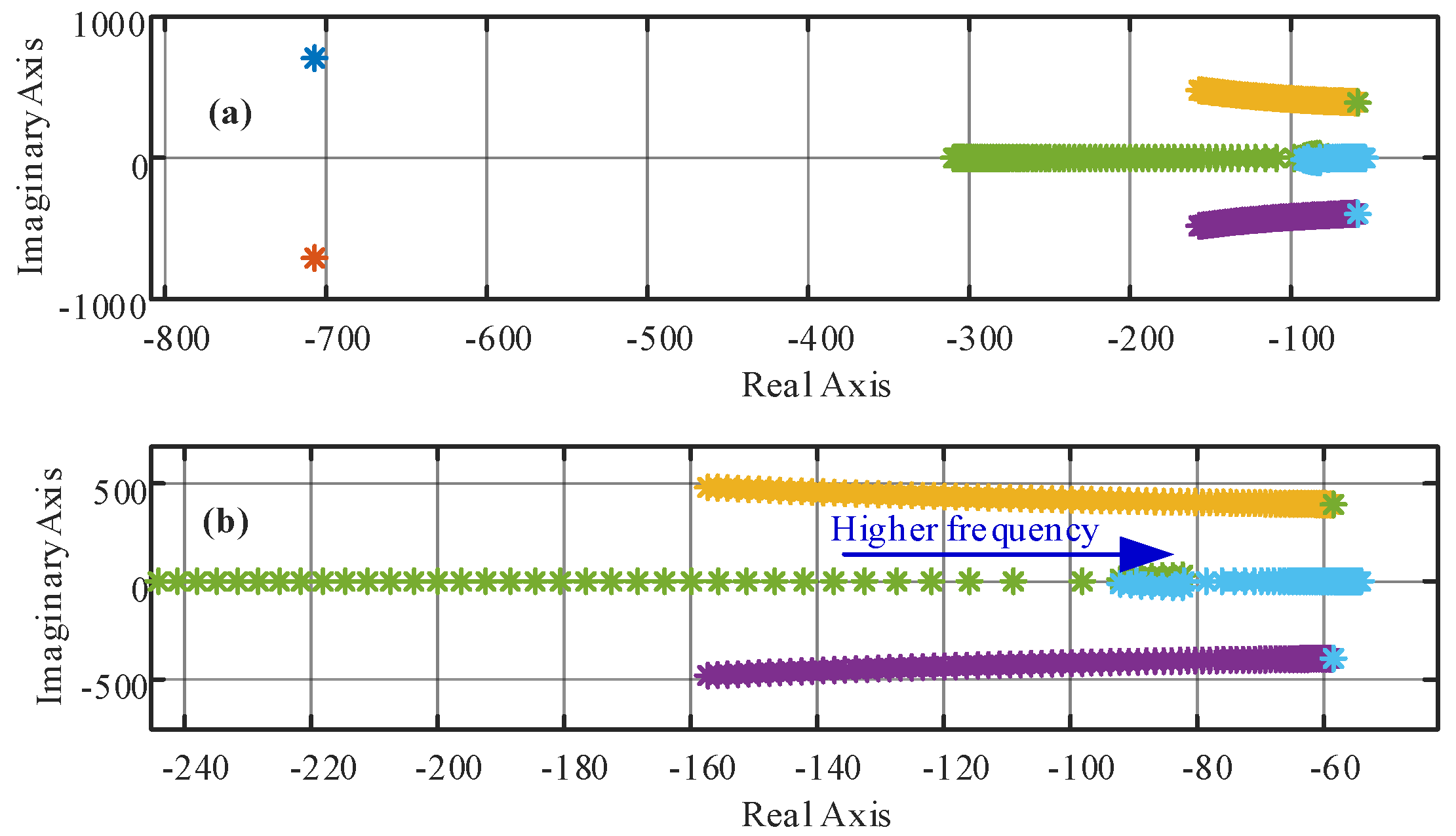
4.1. Stability Analysis of Static Decoupler Control
4.2. Stability Analysis of Dynamic Decoupler Control
5. Simulated Results
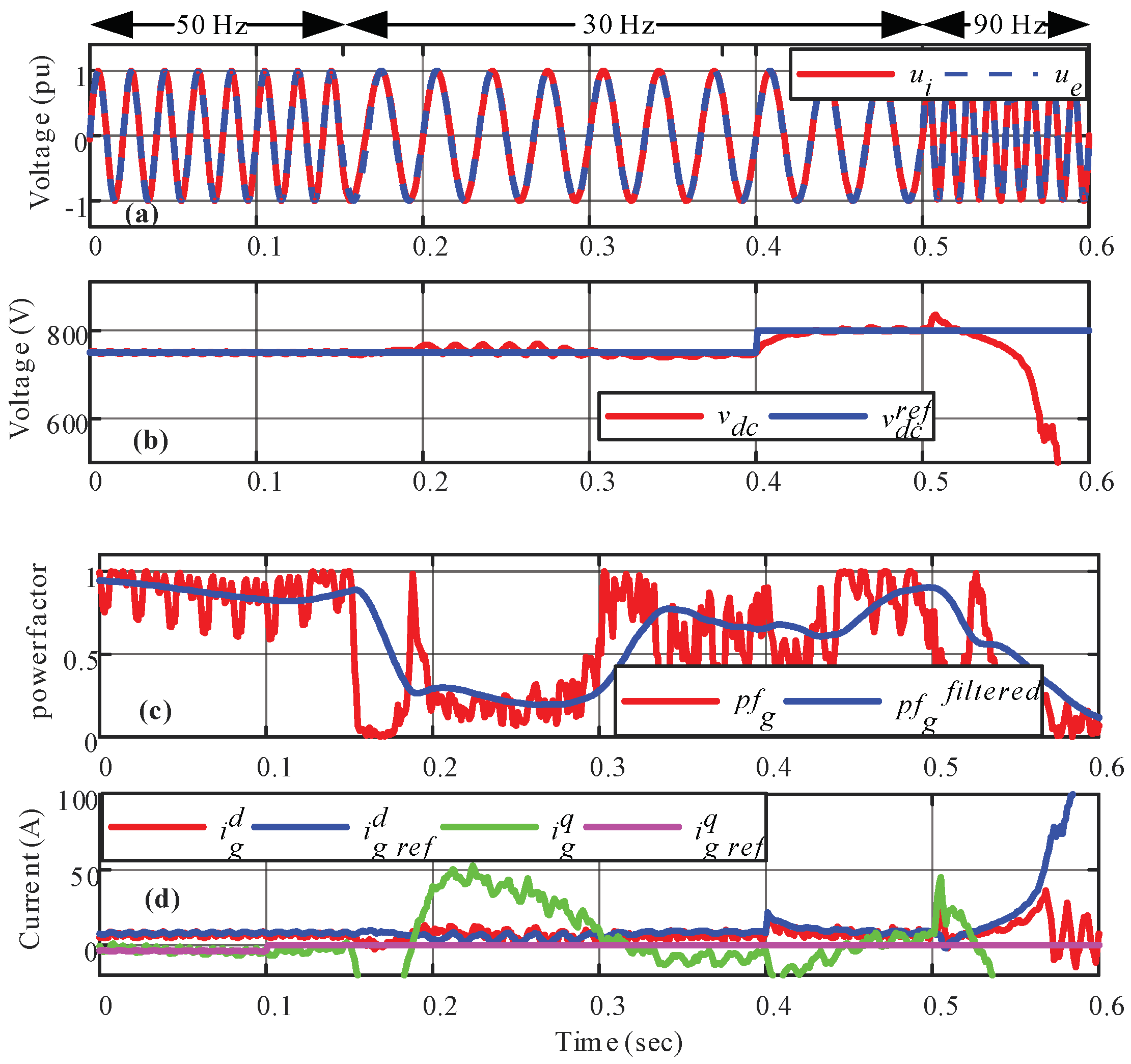
5.1. Static Control Response
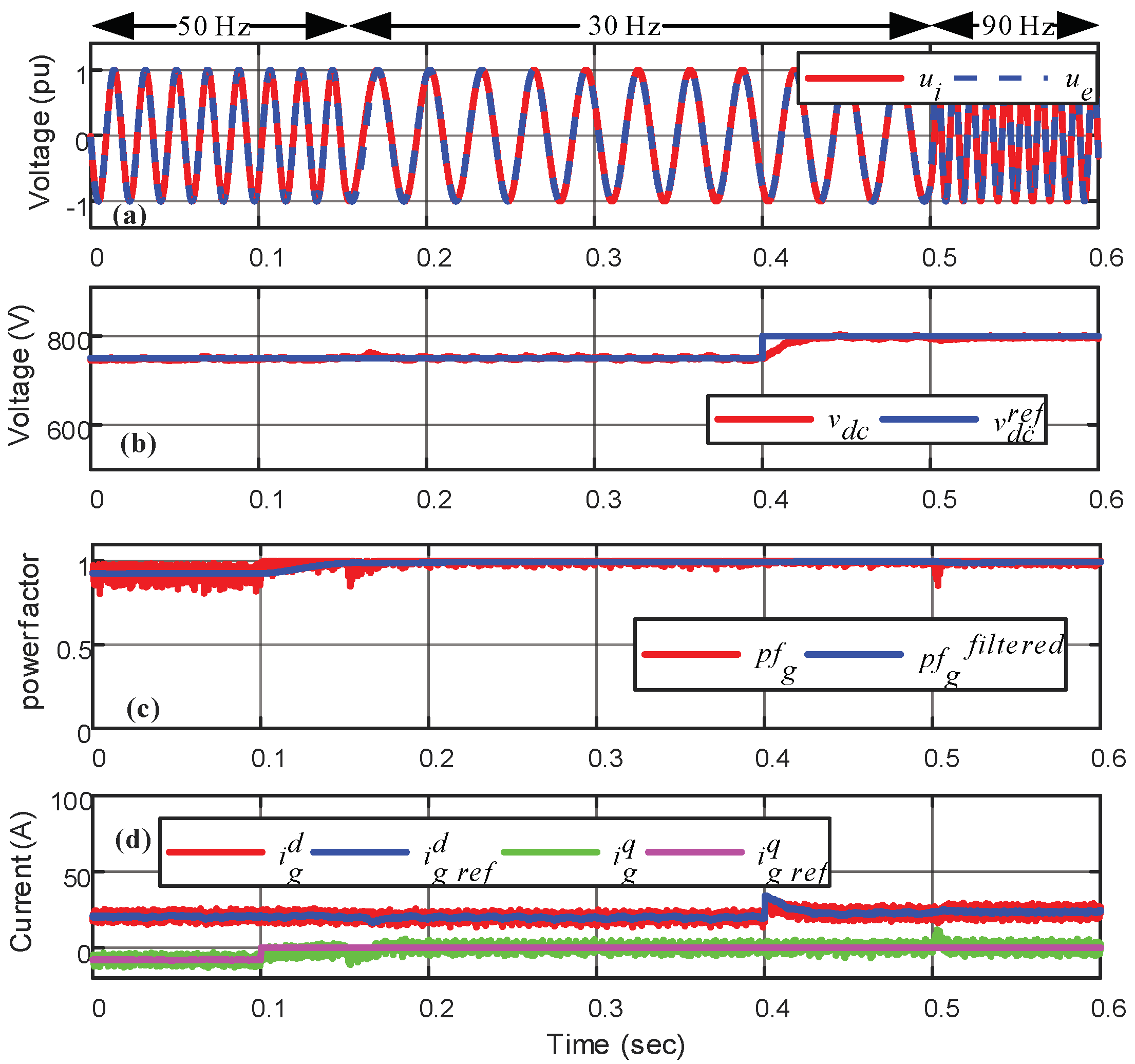
5.2. Dynamic Control Response
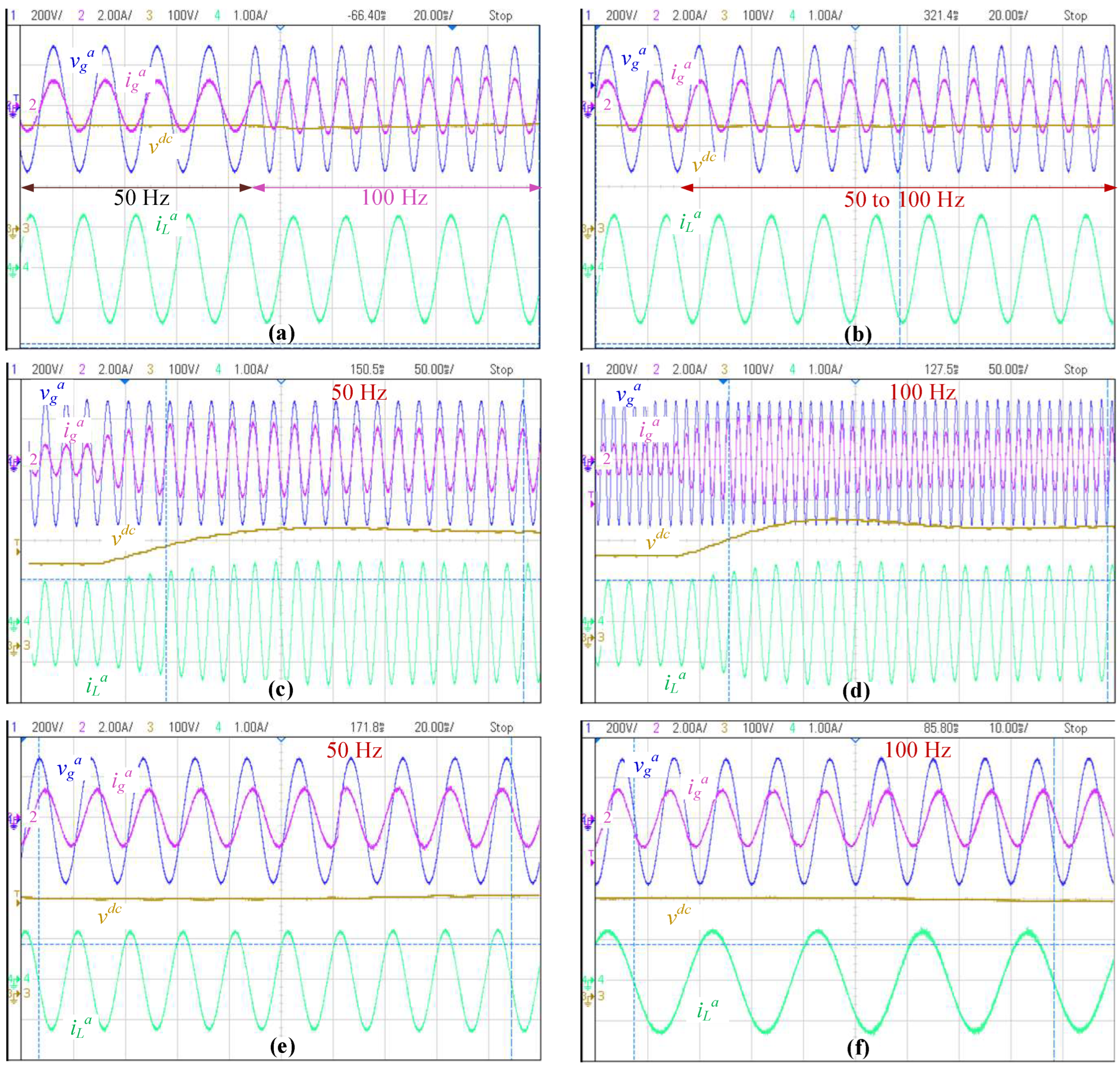
6. Experimental Results
7. Discussion
- ➢ Define the model in the variable state representation;
- ➢ Define the controllers in the variable state representation;
- ➢ Build the representation of the whole system, including all the dynamics in the power converters, as currents, voltages, PLL internal dynamics, controllers, etc.;
- ➢ Determine the Jacobian as a function of the rest of the variables;
- ➢ Find the eigenvalues as a function of the variables of interest such as frequency, parameters and operating points where the system would work.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Young, K.; Dougal, R.A. SRF-PLL with Dynamic Center Frequency for Improved Phase Detection. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 212–216. [Google Scholar]
- Zhang, Z.; Liu, Y.; Li, J. A HESM-Based Variable Frequency AC Starter-Generator System for Aircraft Applications. IEEE Trans. Energy Convers. 2018, 33, 1998–2006. [Google Scholar] [CrossRef]
- Zanchetta, P.; Degano, M.; Liu, J.; Mattavelli, P. Iterative Learning Control With Variable Sampling Frequency for Current Control of Grid-Connected Converters in Aircraft Power Systems. IEEE Trans. Ind. Appl. 2013, 49, 1548–1555. [Google Scholar] [CrossRef]
- Rohten, J.A.; Espinoza, J.R.; Munoz, J.A.; Sbarbaro, D.G.; Perez, M.A.; Melin, P.E.; Silva, J.J.; Espinosa, E.E. Enhanced Predictive Control for a Wide Time-Variant Frequency Environment. IEEE Trans. Ind. Electron. 2016, 63, 5827–5837. [Google Scholar] [CrossRef]
- Rohten, J.A.; Silva, J.J.; Munoz, J.A.; Villarroel, F.A.; Dewar, D.N.; Rivera, M.E.; Espinoza, J.R. A Simple Self-Tuning Resonant Control Approach for Power Converters Connected to Micro-Grids With Distorted Voltage Conditions. IEEE Access 2020, 8, 216018–216028. [Google Scholar] [CrossRef]
- Ntomalis, S.; Iliadis, P.; Atsonios, K.; Nesiadis, A.; Nikolopoulos, N.; Grammelis, P. Dynamic Modeling and Simulation of Non-Interconnected Systems under High-RES Penetration: The Madeira Island Case. Energies 2020, 13, 5786. [Google Scholar] [CrossRef]
- Azizipanah-Abarghooee, R.; Malekpour, M.; Dragicevic, T.; Blaabjerg, F.; Terzija, V. A Linear Inertial Response Emulation for Variable Speed Wind Turbines. IEEE Trans. Power Syst. 2020, 35, 1198–1208. [Google Scholar] [CrossRef]
- Areerak, K.-N.; Wu, T.; Bozhko, S.V.; Asher, G.M.; Thomas, D.W.P. Aircraft Power System Stability Study Including Effect of Voltage Control and Actuators Dynamic. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2574–2589. [Google Scholar] [CrossRef]
- Etxegarai, A.; Eguia, P.; Torres, E.; Iturregi, A.; Valverde, V. Review of Grid Connection Requirements for Generation Assets in Weak Power Grids. Renew. Sustain. Energy Rev. 2015, 41, 1501–1514. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Wojcik, J.; Wang, J.; Li, D.; Draganescu, M.; Li, Y.; Miao, S. Review of Voltage and Frequency Grid Code Specifications for Electrical Energy Storage Applications. Energies 2018, 11, 1070. [Google Scholar] [CrossRef]
- Herrejón-Pintor, G.A.; Melgoza-Vázquez, E.; Chávez, J.D.J. A Modified SOGI-PLL with Adjustable Refiltering for Improved Stability and Reduced Response Time. Energies 2022, 15, 4253. [Google Scholar] [CrossRef]
- Aldbaiat, B.; Nour, M.; Radwan, E.; Awada, E. Grid-Connected PV System with Reactive Power Management and an Optimized SRF-PLL Using Genetic Algorithm. Energies 2022, 15, 2177. [Google Scholar] [CrossRef]
- Liu, B.; An, M.; Wang, H.; Chen, Y.; Zhang, Z.; Xu, C.; Song, S.; Lv, Z. A Simple Approach to Reject DC Offset for Single-Phase Synchronous Reference Frame PLL in Grid-Tied Converters. IEEE Access 2020, 8, 112297–112308. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, D. Effect of Control-Loops Interactions on Power Stability Limits of VSC Integrated to AC System. IEEE Trans. Power Deliv. 2018, 33, 301–310. [Google Scholar] [CrossRef]
- Liu, R.; Wang, S.; Liu, G.; Wen, S.; Zhang, J.; Ma, Y. An Improved Virtual Inertia Control Strategy for Low Voltage AC Microgrids with Hybrid Energy Storage Systems. Energies 2022, 15, 442. [Google Scholar] [CrossRef]
- Bimarta, R.; Tran, T.V.; Kim, K.-H. Frequency-Adaptive Current Controller Design Based on LQR State Feedback Control for a Grid-Connected Inverter under Distorted Grid. Energies 2018, 11, 2674. [Google Scholar] [CrossRef]
- Panda, R.K.; Mohapatra, A.; Srivastava, S.C. Enhancing Inertia of Solar Photovoltaic-based Microgrid through Notch Filter-based PLL in SRF Control. IET Gener. Transm. Distrib. 2020, 14, 379–388. [Google Scholar] [CrossRef]
- Xia, T.; Zhang, X.; Tan, G.; Liu, Y. All-Pass-Filter-Based PLL for Single-Phase Grid-Connected Converters Under Distorted Grid Conditions. IEEE Access 2020, 8, 106226–106233. [Google Scholar] [CrossRef]
- Xu, J.; Qian, Q.; Zhang, B.; Xie, S. Harmonics and Stability Analysis of Single-Phase Grid-Connected Inverters in Distributed Power Generation Systems Considering Phase-Locked Loop Impact. IEEE Trans. Sustain. Energy 2019, 10, 1470–1480. [Google Scholar] [CrossRef]
- Luo, W.; Wei, D. A Frequency-Adaptive Improved Moving-Average-Filter-Based Quasi-Type-1 PLL for Adverse Grid Conditions. IEEE Access 2020, 8, 54145–54153. [Google Scholar] [CrossRef]
- Yogarathinam, A.; Kaur, J.; Chaudhuri, N.R. Impact of Inertia and Effective Short Circuit Ratio on Control of Frequency in Weak Grids Interfacing LCC-HVDC and DFIG-Based Wind Farms. IEEE Trans. Power Deliv. 2017, 32, 2040–2051. [Google Scholar] [CrossRef]
- Rohten, J.A.; Espinoza, J.R.; Munoz, J.A.; Perez, M.A.; Melin, P.E.; Silva, J.J.; Espinosa, E.E.; Rivera, M.E. Model Predictive Control for Power Converters in a Distorted Three-Phase Power Supply. IEEE Trans. Ind. Electron. 2016, 63, 5838–5848. [Google Scholar] [CrossRef]
- Zuniga-Reyes, M.-A.; Robles-Ocampo, J.-B.; Sevilla-Camacho, P.-Y.; Rodriguez-Resendiz, J.; Lastres-Danguillecourt, O.; Conde-Diaz, J.-E. Photovoltaic Failure Detection Based on String-Inverter Voltage and Current Signals. IEEE Access 2021, 9, 39939–39954. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; Alvarez-Diazcomas, A.; Rodríguez-Reséndiz, J. Transformerless Multilevel Voltage-Source Inverter Topology Comparative Study for PV Systems. Energies 2020, 13, 3261. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; Alvarez-Diazcomas, A.; Macias-Bobadilla, G.; Rodríguez-Reséndiz, J. Leakage Current Reduction in Single-Phase Grid-Connected Inverters—A Review. Appl. Sci. 2020, 10, 2384. [Google Scholar] [CrossRef]
- Alvarez-Diazcomas, A.; López, H.; Carrillo-Serrano, R.V.; Rodríguez-Reséndiz, J.; Vázquez, N.; Herrera-Ruiz, G. A Novel Integrated Topology to Interface Electric Vehicles and Renewable Energies with the Grid. Energies 2019, 12, 4091. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; López Tapia, H.J.C.; Carrillo-Serrano, R.V.; Rodríguez-Reséndiz, J.; Vázquez Nava, N. A New Predictive Control Strategy for Multilevel Current-Source Inverter Grid-Connected. Electronics 2019, 8, 902. [Google Scholar] [CrossRef]
- Lopez, H.; Rodriguez Resendiz, J.; Guo, X.; Vazquez, N.; Carrillo-Serrano, R.V. Transformerless Common-Mode Current-Source Inverter Grid-Connected for PV Applications. IEEE Access 2018, 6, 62944–62953. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Wang, Y.; Zha, X.; Yue, S.; Cheng, X.; Gao, L. Deloading Power Coordinated Distribution Method for Frequency Regulation by Wind Farms Considering Wind Speed Differences. IEEE Access 2019, 7, 122573–122582. [Google Scholar] [CrossRef]
- Mujcinagic, A.; Kusljugic, M.; Nukic, E. Wind Inertial Response Based on the Center of Inertia Frequency of a Control Area. Energies 2020, 13, 6177. [Google Scholar] [CrossRef]
- Li, T.; Li, Y.; Yang, J.; Ge, W.; Hu, B. A Modified DSC-Based Grid Synchronization Method for a High Renewable Penetrated Power System Under Distorted Voltage Conditions. Energies 2019, 12, 4040. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Wang, X.; Qiao, J.; Wang, L. Improved Current Decoupling Method for Robustness Improvement of LCL-Type STATCOM Based on Active Disturbance Rejection Control. IEEE Access 2019, 7, 121781–121792. [Google Scholar] [CrossRef]
- Munoz, J.A.; Espinoza, J.R.; Moran, L.A.; Baier, C.R. Design of a Modular UPQC Configuration Integrating a Components Economical Analysis. IEEE Trans. Power Deliv. 2009, 24, 1763–1772. [Google Scholar] [CrossRef]
- Rohten, J.A.; Espinoza, J.R.; Munoz, J.A.; Melin, P.E.; Espinosa, E.E. Discrete Nonlinear Control Based on a Double Dq Transform of a Multi-Cell UPQC. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 4134–4139. [Google Scholar]
- Housseini, B.; Okou, A.F.; Beguenane, R. Robust Nonlinear Controller Design for On-Grid/Off-Grid Wind Energy Battery-Storage System. IEEE Trans. Smart Grid 2018, 9, 5588–5598. [Google Scholar] [CrossRef]
- Aliaga, R.; Rivera, M.; Wheeler, P.; Munoz, J.; Rohten, J.; Sebaaly, F.; Villalon, A.; Trentin, A. Implementation of Exact Linearization Technique for Modeling and Control of DC/DC Converters in Rural PV Microgrid Application. IEEE Access 2022, 10, 56925–56936. [Google Scholar] [CrossRef]
- Ma, W.; Ouyang, S.; Zhang, J.; Xu, W. Control Strategy Based on $\text{H}\infty$ Repetitive Controller With Active Damping for Islanded Microgrid. IEEE Access 2019, 7, 162157–162168. [Google Scholar] [CrossRef]
- Rohten, J.; Espinoza, J.; Villarroel, F.; Perez, M.; Munoz, J.; Melin, P.; Espinosa, E. Static Power Converter Synchronization and Control under Varying Frequency Conditions. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 786–791. [Google Scholar]
- Munoz, J.; Baier, C.; Espinoza, J.; Rivera, M.; Guzman, J.; Rohten, J. Switching Losses Analysis of an Asymmetric Multilevel Shunt Active Power Filter. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 8534–8539. [Google Scholar]
- Munoz, J.A.; Reyes, J.R.; Espinoza, J.R.; Rubilar, I.A.; Moran, L.A. A Novel Multi-Level Three-Phase UPQC Topology Based on Full-Bridge Single-Phase Cells. In Proceedings of the IECON 2007—33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 1787–1792. [Google Scholar]
- Dewar, D.; Rohten, J.; Formentini, A.; Zanchetta, P. Decentralised Optimal Controller Design of Variable Frequency Three-Phase Power Electronic Networks Accounting for Sub-System Interactions. IEEE Open J. Ind. Appl. 2020, 1, 270–282. [Google Scholar] [CrossRef]


| Parameters | Value | P.U. |
|---|---|---|
| vg | 220 V, rms | 1 |
| vdc | 750 V | 3.4 |
| ZL (50 Hz) | 8.8 Ω | 1 |
| RL (50 Hz) | 7 Ω | 0.80 |
| LL (50 Hz) | 17 mH | 0.61 |
| Rg (50 Hz) | 0.1 Ω | 0.011 |
| Lg (50 Hz) | 12 mH | 0.43 |
| Cdc (50 Hz) | 4.7 mF | 0.36 |
| fg | 50 Hz | 1 |
| fsw | 1.05 kHz | 21 |
| N | 204 | -- |
| kc (current) | 1.0 | -- |
| Ti (current) | 20 m | -- |
| kc (dc voltage) | 0.070 | -- |
| Ti (dc voltage) | 0.10 | -- |
| Parameters | Value | Critical Frequency |
|---|---|---|
| Lg | 70% | Over 100 Hz |
| nominal | 81.7 Hz | |
| 130% | 62.4 Hz | |
| Rg | 70% | 81.2 Hz |
| nominal | 81.7 Hz | |
| 130% | 82.2 Hz | |
| Cdc | 70% | 82.4 Hz |
| nominal | 81.7 Hz | |
| 130% | 81.1 Hz |
| Controller Algorithm | Robustness to Frequency Variation | Computational Burden | Dynamic Performance | Maintains Tuned Characteristics | Uses Frequency Value |
|---|---|---|---|---|---|
| Static decoupler based | Med | Low | Low | No | No |
| Dynamic decoupler based | High | Med | High | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rohten, J.; Villarroel, F.; Pulido, E.; Muñoz, J.; Silva, J.; Perez, M. Stability Analysis of Two Power Converters Control Algorithms Connected to Micro-Grids with Wide Frequency Variation. Sensors 2022, 22, 7078. https://doi.org/10.3390/s22187078
Rohten J, Villarroel F, Pulido E, Muñoz J, Silva J, Perez M. Stability Analysis of Two Power Converters Control Algorithms Connected to Micro-Grids with Wide Frequency Variation. Sensors. 2022; 22(18):7078. https://doi.org/10.3390/s22187078
Chicago/Turabian StyleRohten, Jaime, Felipe Villarroel, Esteban Pulido, Javier Muñoz, José Silva, and Marcelo Perez. 2022. "Stability Analysis of Two Power Converters Control Algorithms Connected to Micro-Grids with Wide Frequency Variation" Sensors 22, no. 18: 7078. https://doi.org/10.3390/s22187078
APA StyleRohten, J., Villarroel, F., Pulido, E., Muñoz, J., Silva, J., & Perez, M. (2022). Stability Analysis of Two Power Converters Control Algorithms Connected to Micro-Grids with Wide Frequency Variation. Sensors, 22(18), 7078. https://doi.org/10.3390/s22187078











