High-Acceleration Vibration Calibration System Based on Phase-Locked Resonance Control
Abstract
:1. Introduction
2. Materials and Methods
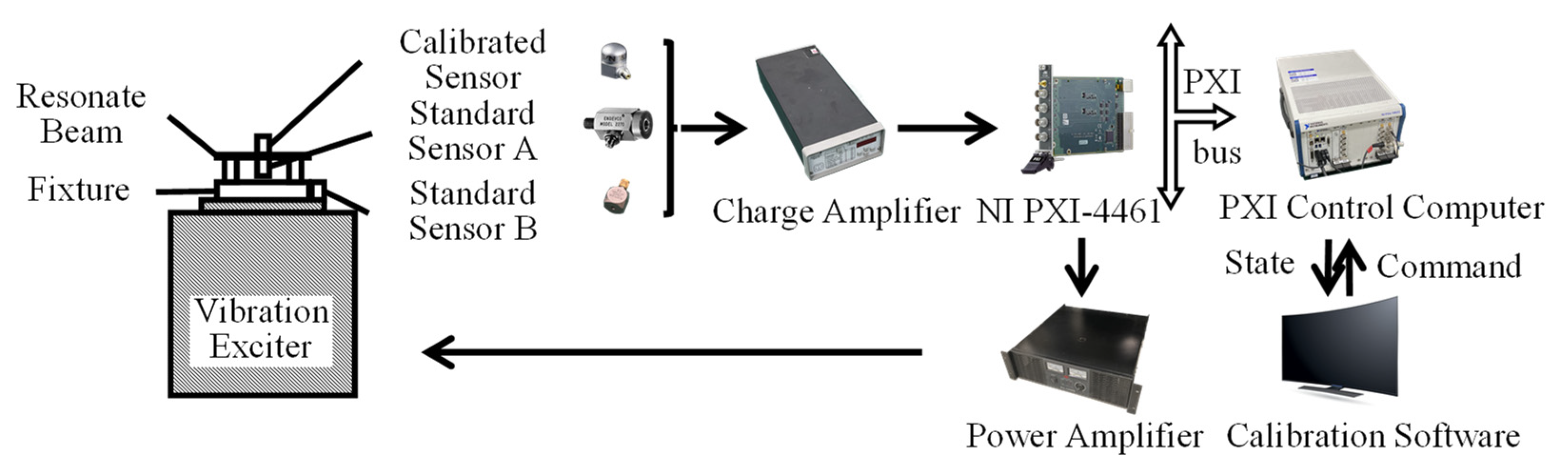
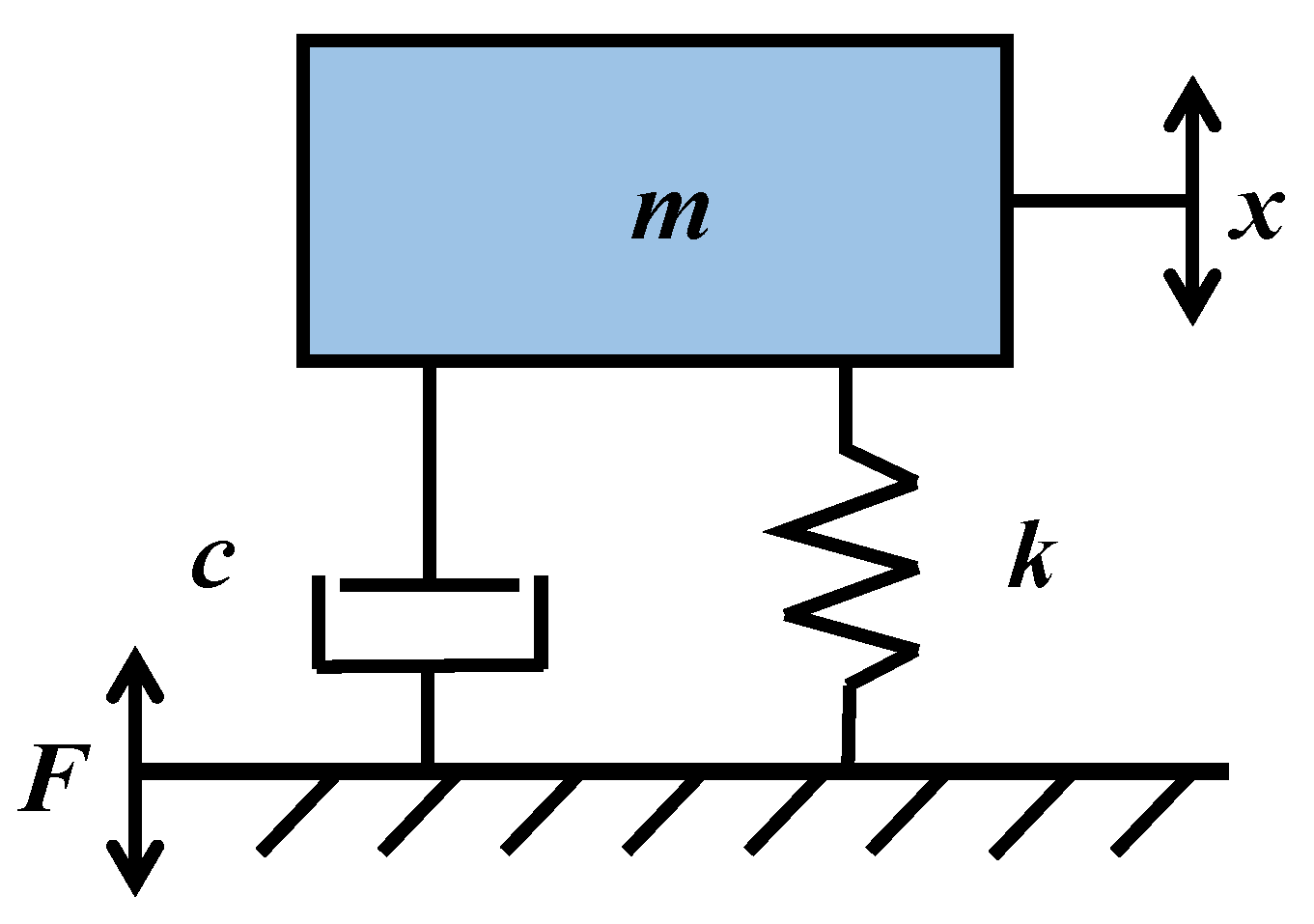
2.1. Resonance Calibration Device
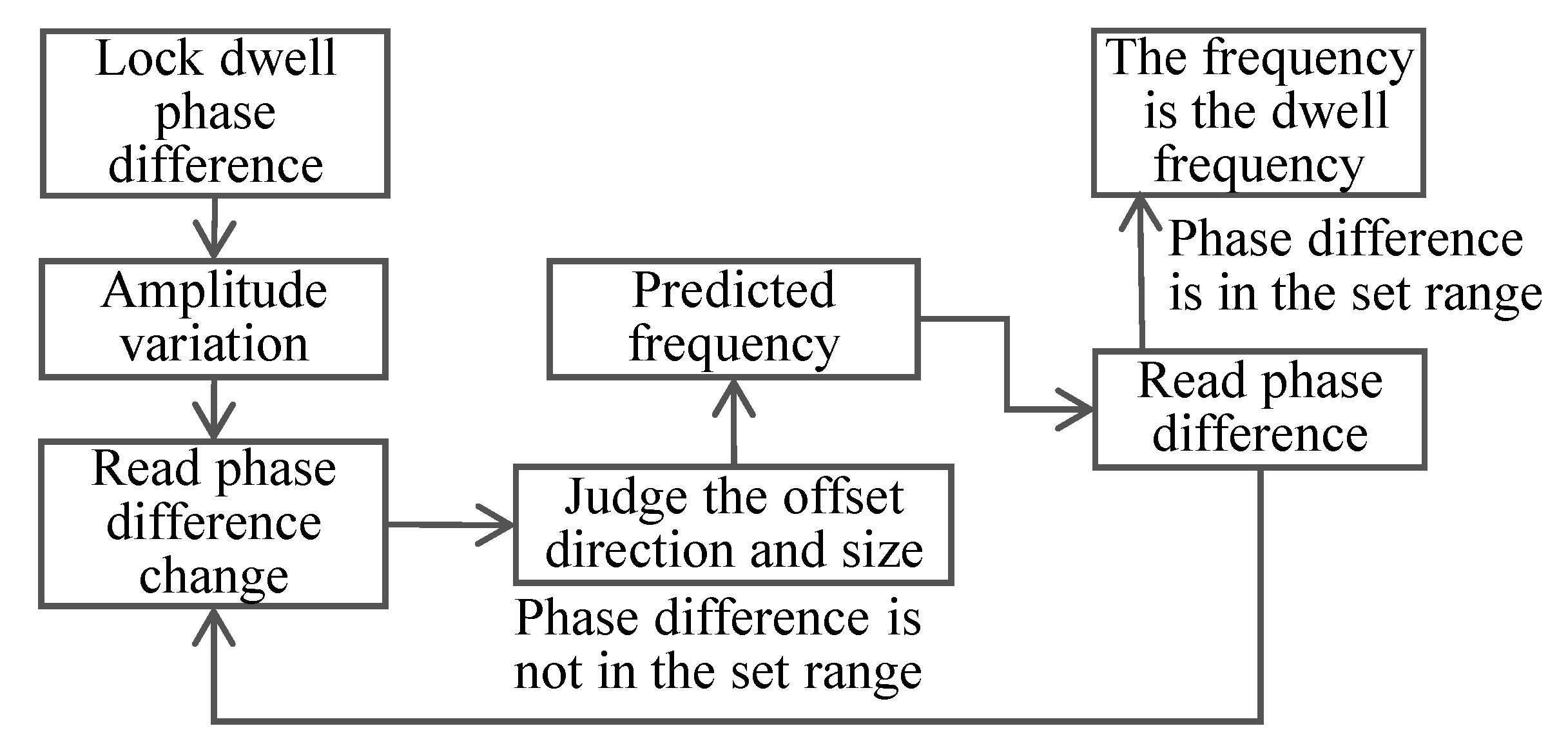
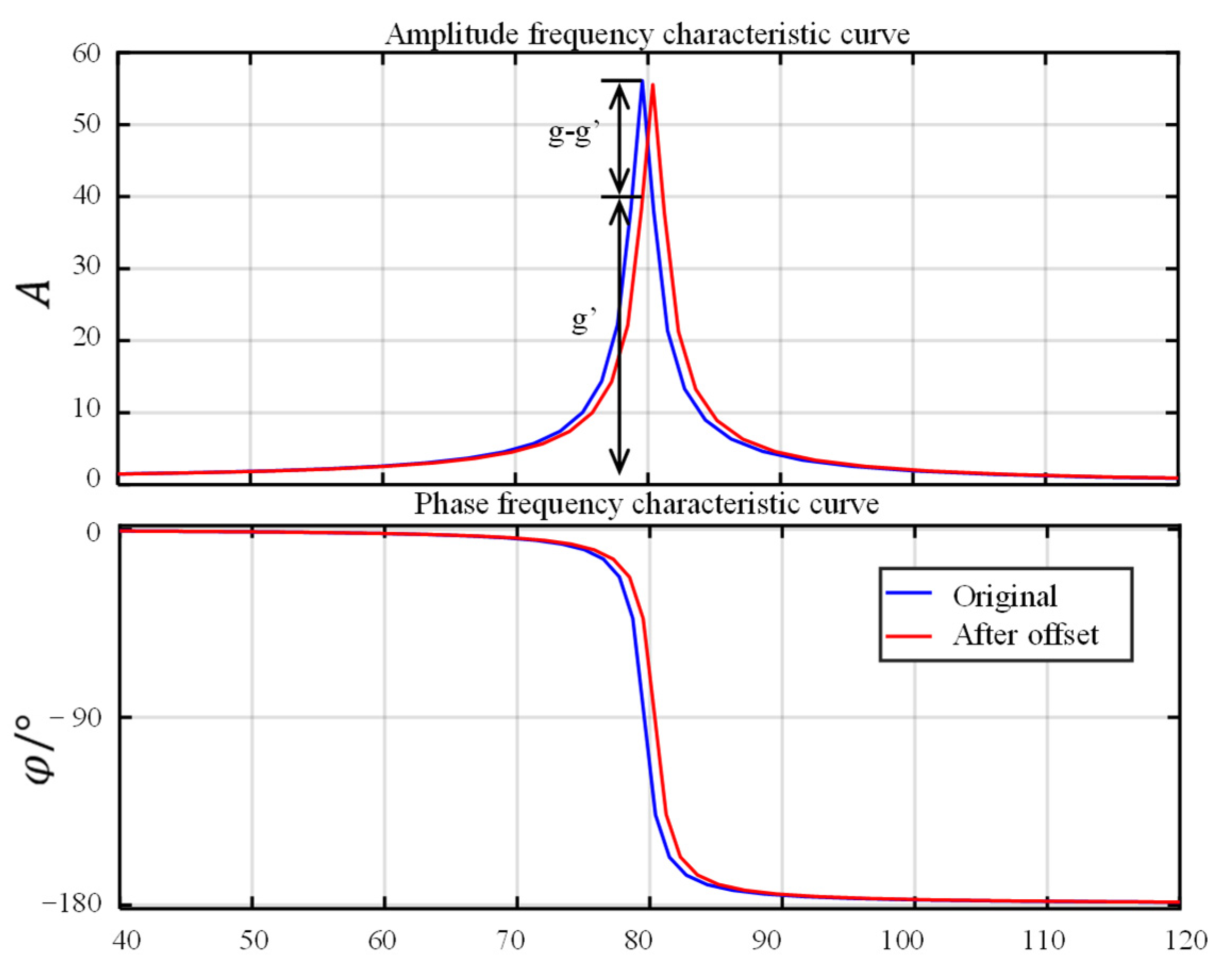
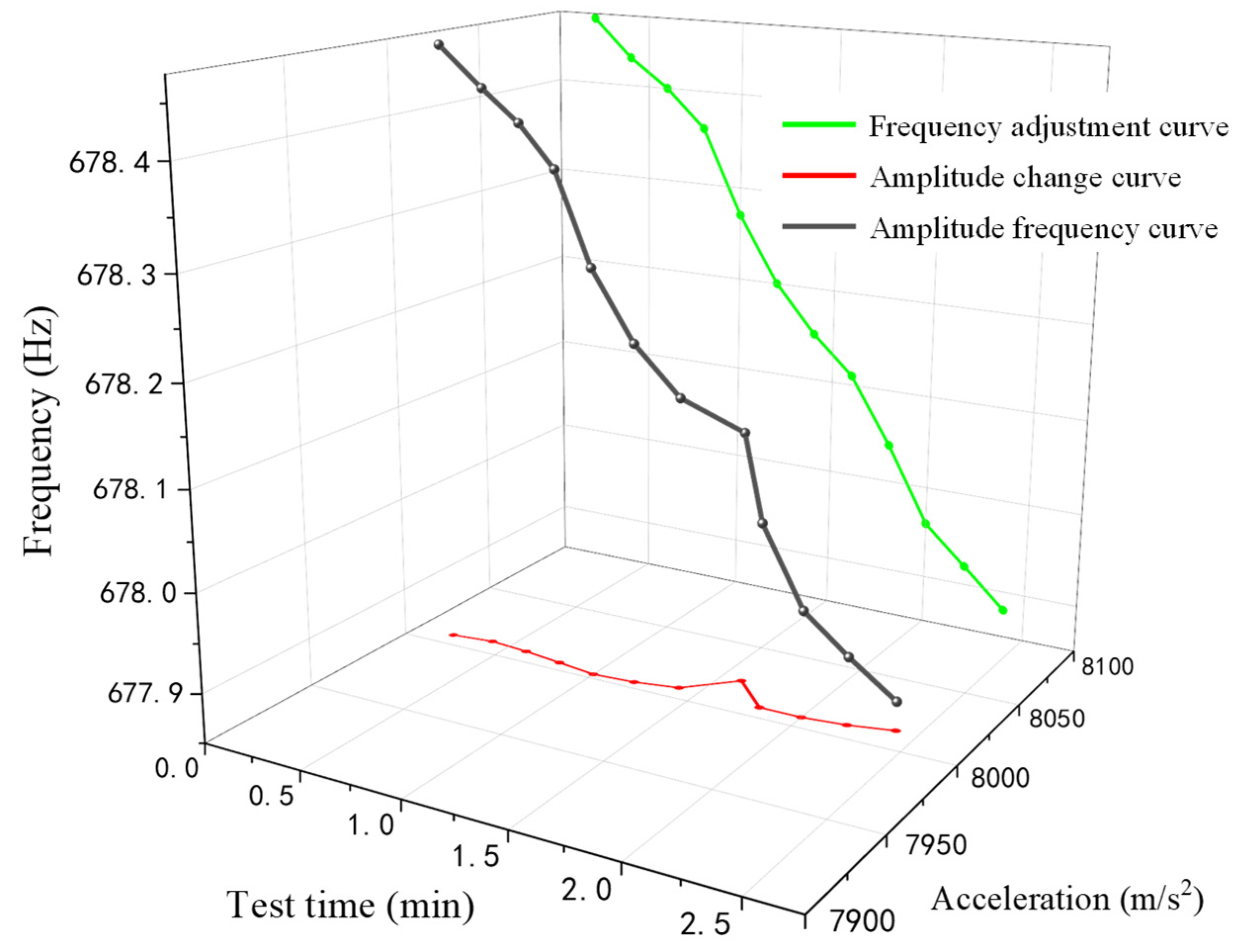
2.2. Phase-Locked Tracking Control
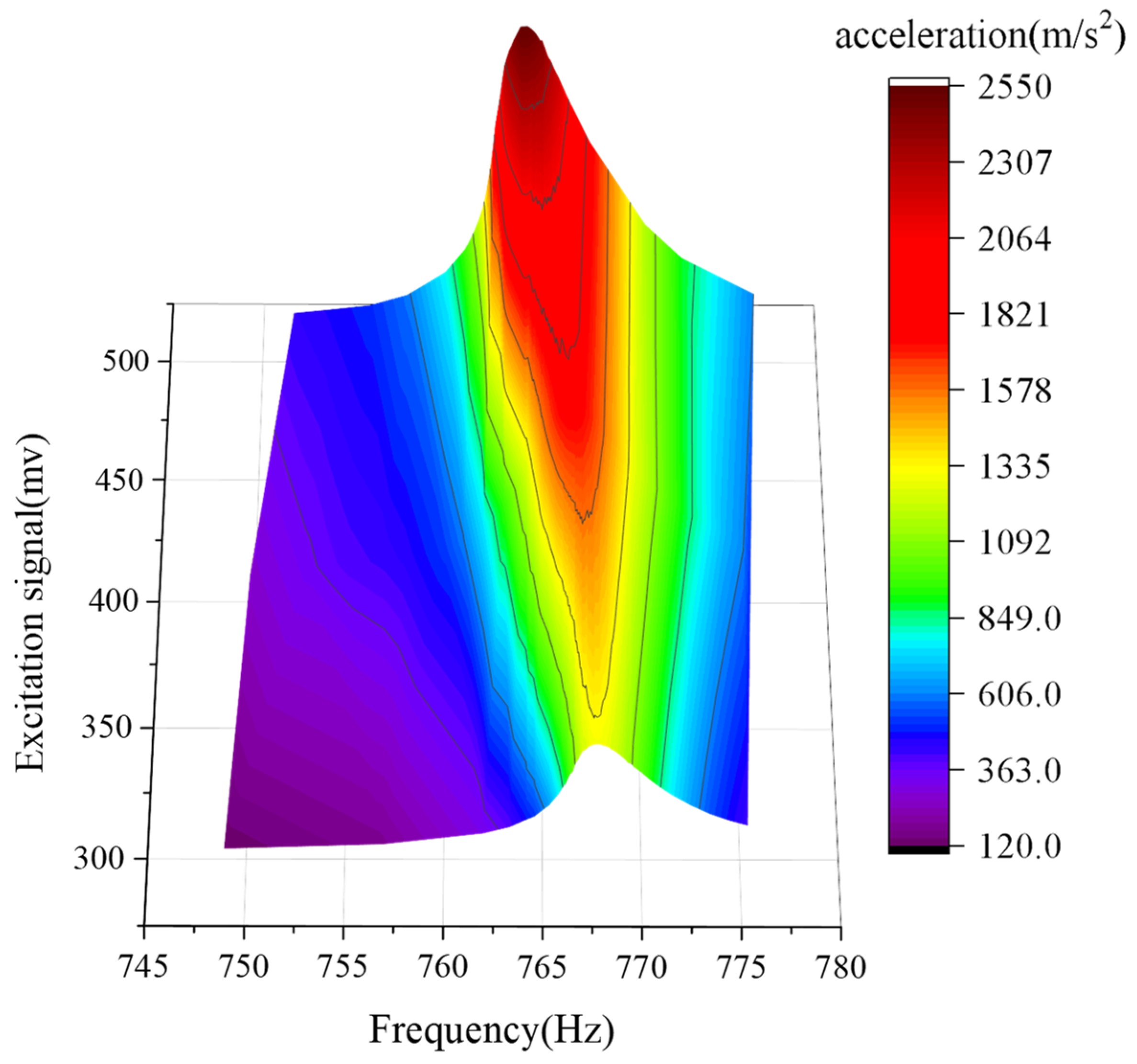
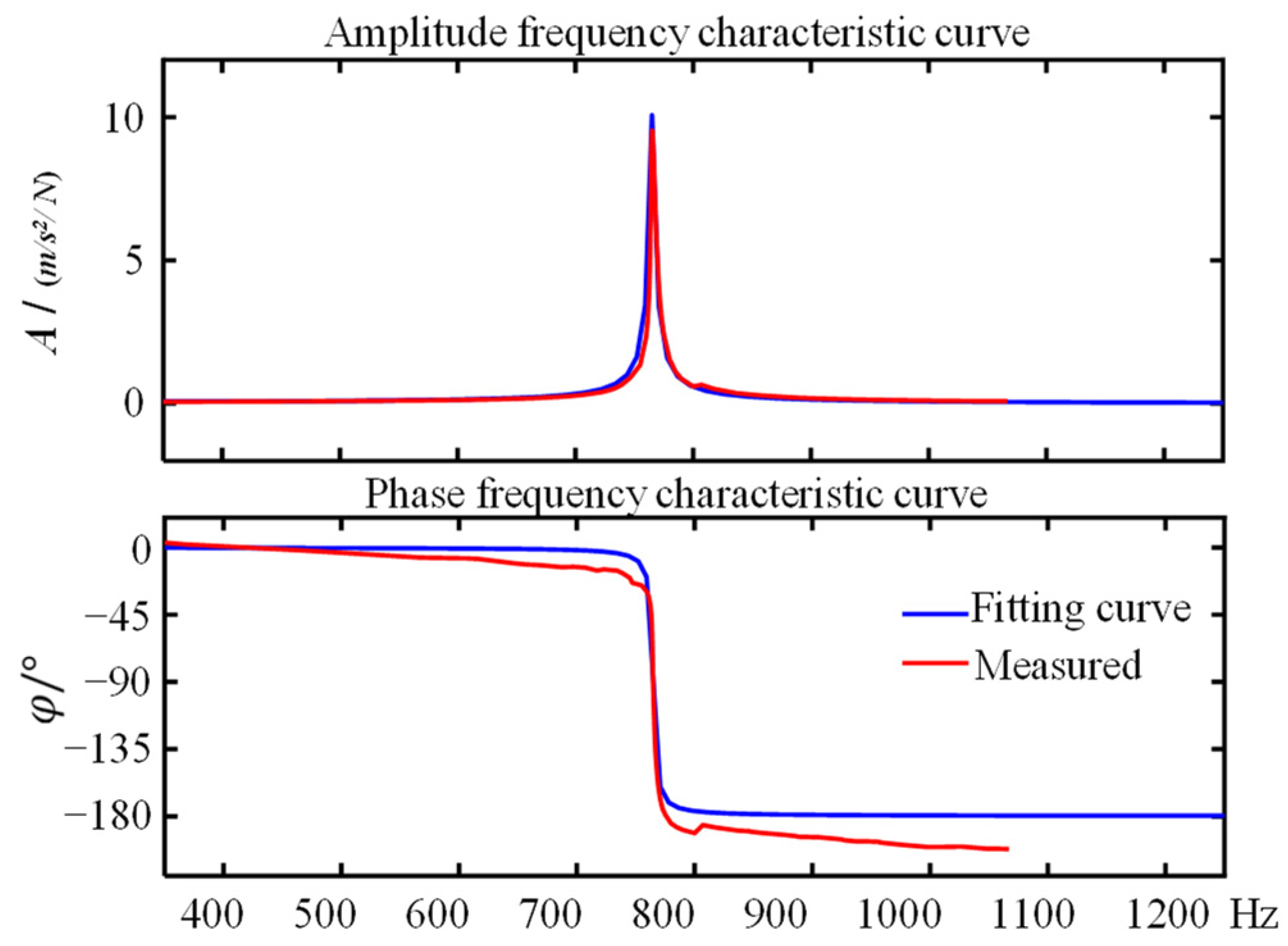
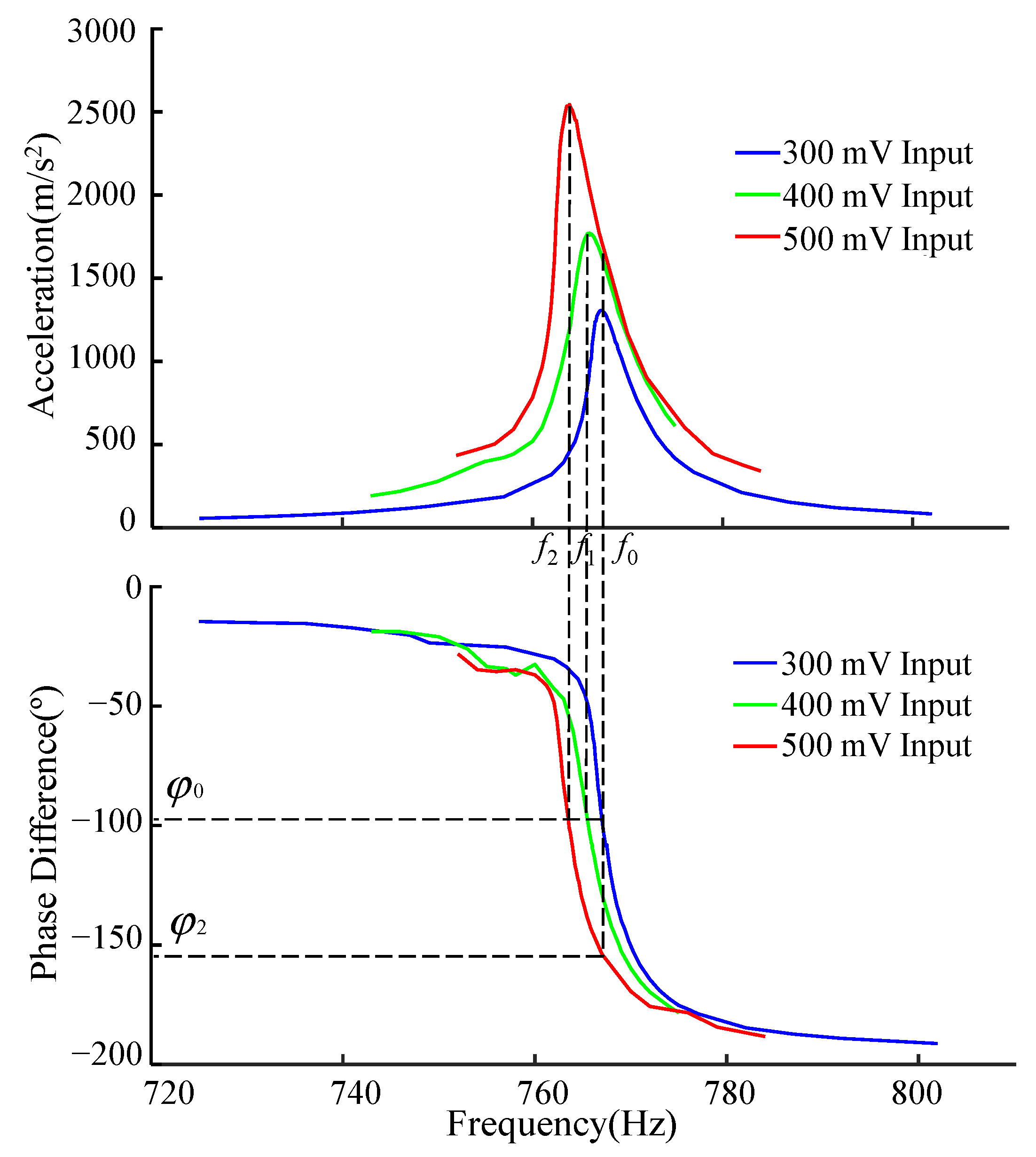
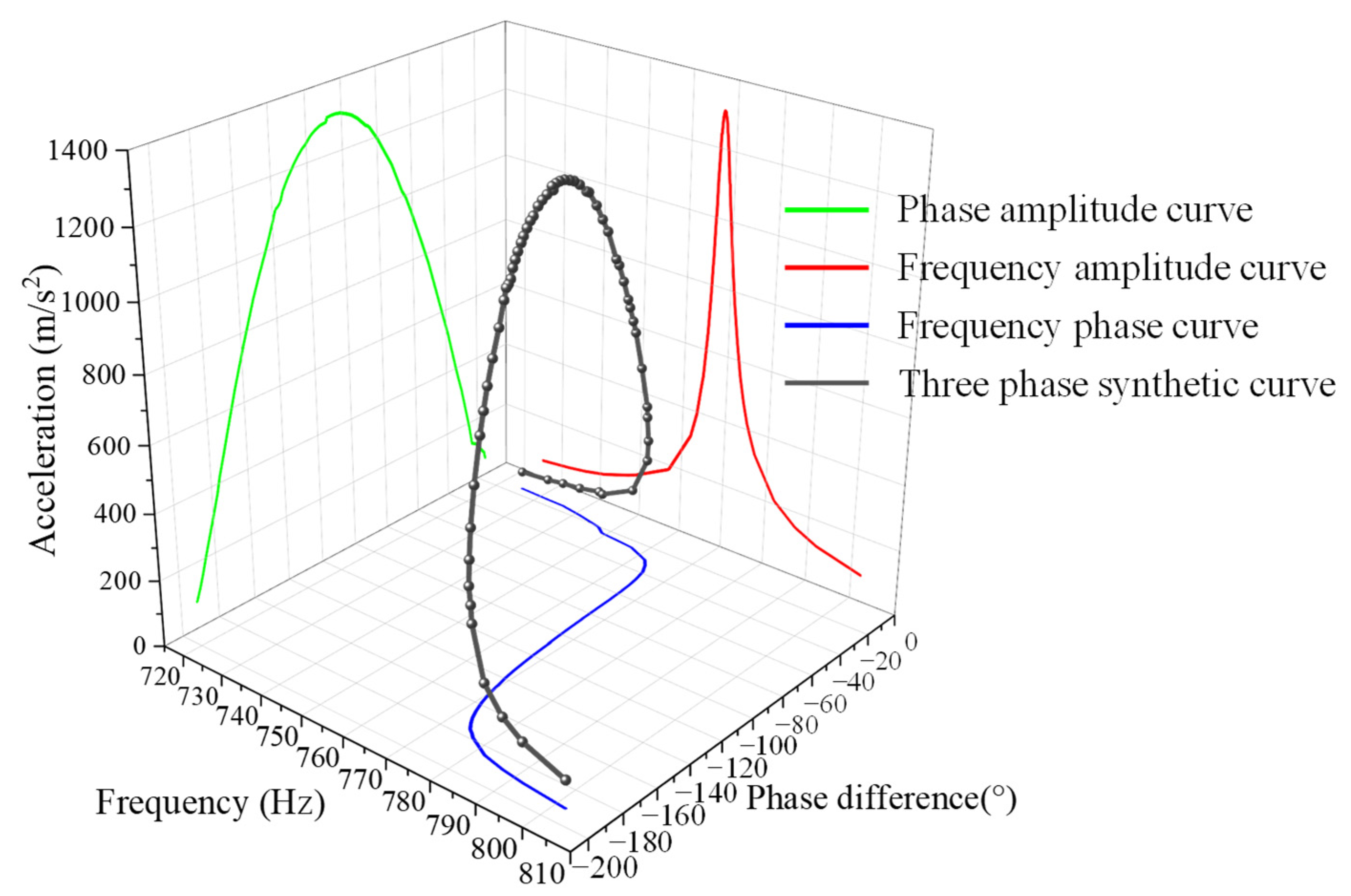
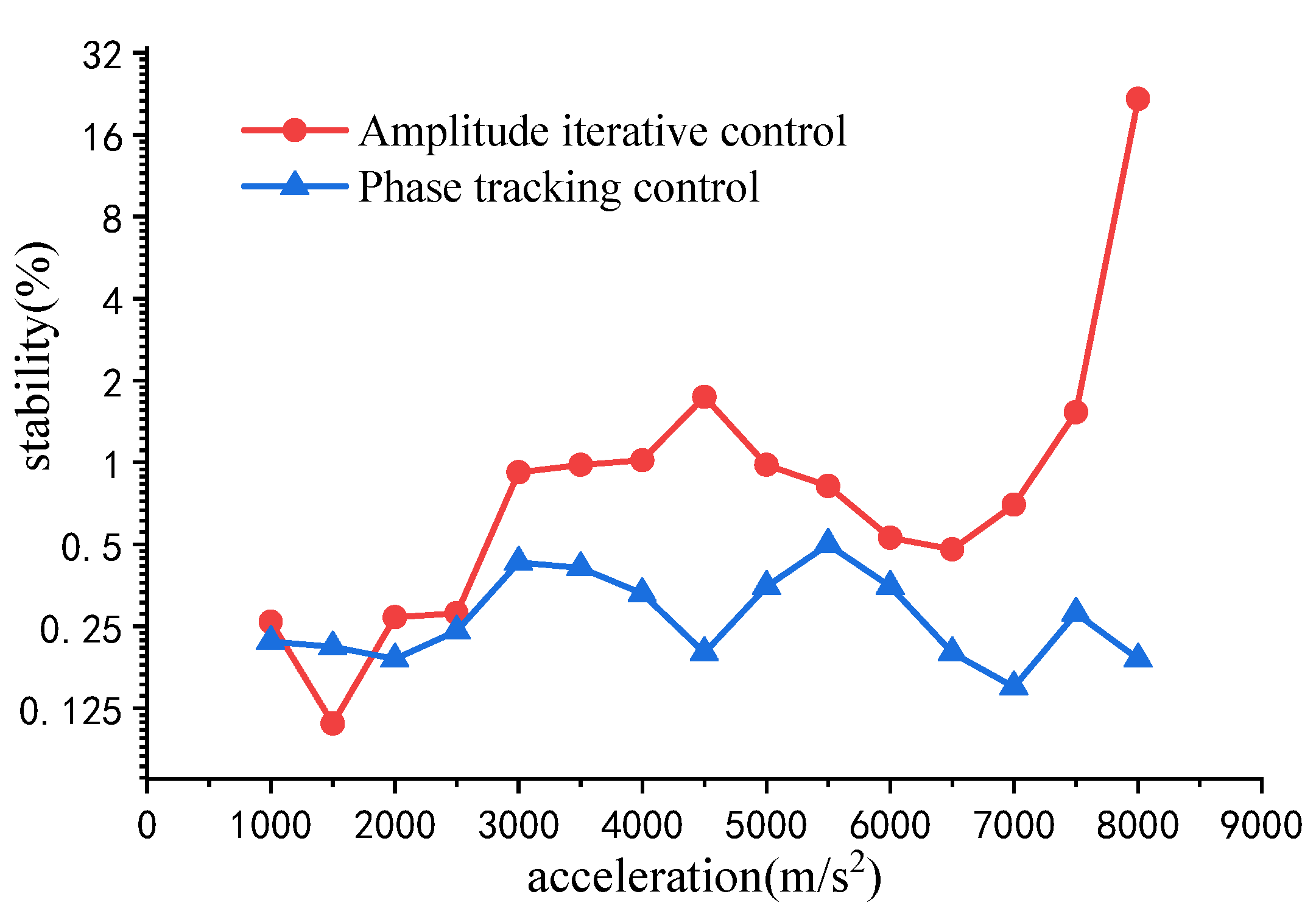
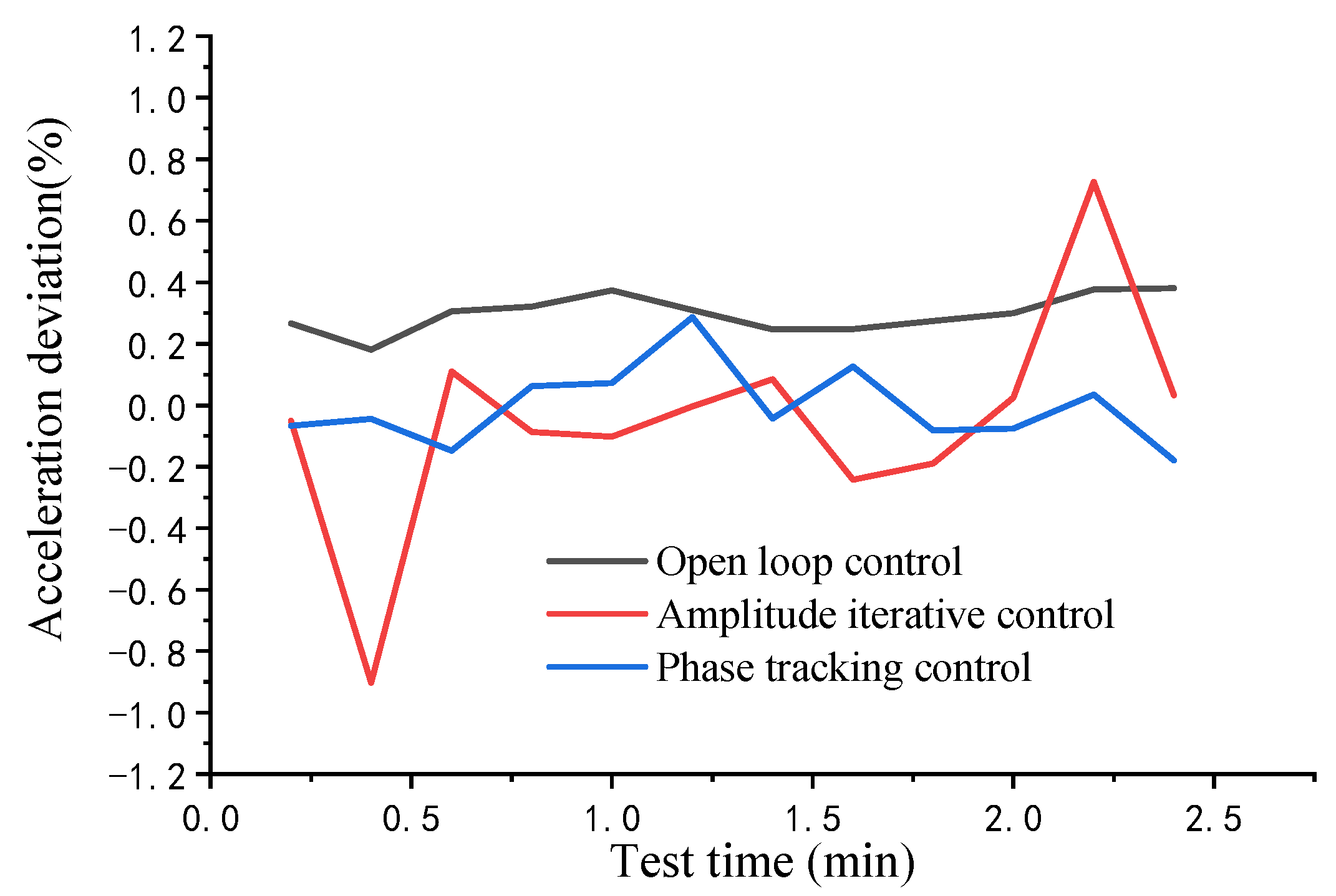
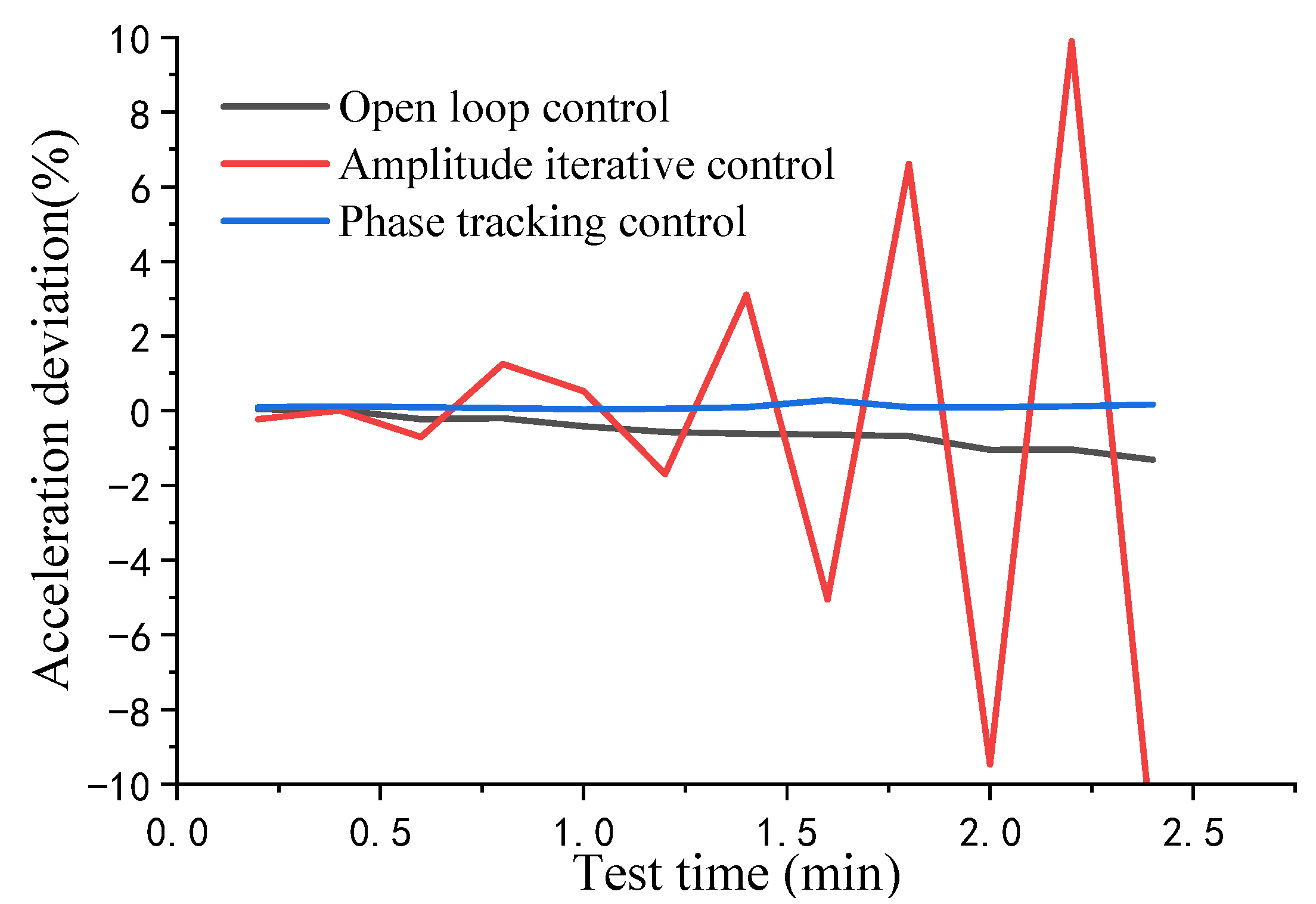
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, D.; Park, C.; Park, N.; Park, Y. Vibration Analysis of Bracket for Vehicle Components; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V001T09A001. [Google Scholar]
- Ansari, M.Z.; Cho, C.; Kim, J.; Bang, B. Comparison between Deflection and Vibration Characteristics of Rectangular and Trapezoidal profile Microcantilevers. Sensors 2009, 9, 2706–2718. [Google Scholar] [CrossRef]
- Lu, Y.; Xiang, P.; Dong, P.; Zhang, X.; Zeng, J. Analysis of the effects of vibration modes on fatigue damage in high-speed train bogie frames. Eng. Fail. Anal. 2018, 89, 222–241. [Google Scholar] [CrossRef]
- Mei, R.; Li, J.; Lin, G.; Pan, R.; Zhu, X. Evaluation of the vibration response of third generation nuclear power plants with isolation technology under large commercial aircraft impact. Prog. Nucl. Energy 2020, 120, 103230. [Google Scholar] [CrossRef]
- Yan, Y.; Chai, M. Sealing failure and fretting fatigue behavior of fittings induced by pipeline vibration. Int. J. Fatigue 2020, 136, 105602. [Google Scholar] [CrossRef]
- Ahirrao, N.; Bhosle, S.; Nehete, D. Dynamics and Vibration Measurements in Engines. Procedia Manuf. 2018, 20, 434–439. [Google Scholar] [CrossRef]
- Ripper, G.P.; Dias, R.S.; Garcia, G.A. Primary accelerometer calibration problems due to vibration exciters. Measurement 2009, 42, 1363–1369. [Google Scholar] [CrossRef]
- Sprecher, D.; Hof, C. Primary accelerometer calibration by scanning laser Doppler vibrometry. Meas. Sci. Technol. 2020, 31, 065006. [Google Scholar] [CrossRef]
- Yang, M.; Zhu, H.; Cai, C.; Wang, Y.; Liu, Z.; Zhou, S. Monocular Vision-Based Earth’s Graviation Method Used for Low-Frequency Vibration Calibration. IEEE Access 2020, 8, 129087–129093. [Google Scholar] [CrossRef]
- Lang, G.F.; Snyder, D. Understanding the physics of electrodynamic shaker performance. J. Sound Vib. 2001, 35, 24–33. [Google Scholar]
- Enokida, R.; Kajiwara, K.; Nagae, T.; Nakashi, M. Pounding shaking table test techniques to realize high frequency input over the redroducible frequency of tables. J. Struct. Constr. Eng. 2010, 75, 1975–1982. [Google Scholar] [CrossRef]
- Sakai, M.; Kanazawa, K.; Ohtori, Y. Development of High Acceleration Shaking Table System Using Resonance Vibration; American Society of Mechanical Engineers: New York, NY, USA, 2016; p. V008T08A009. [Google Scholar]
- Krenk, S.; Høgsberg, J. Equal modal damping design for a family of resonant vibration control formats. J. Vib. Control 2012, 19, 1294–1315. [Google Scholar] [CrossRef]
- Gillich, N.; Tufisi, C.; Sacarea, C.; Rusu, C.V.; Gillich, G.-R.; Praisach, Z.-I.; Ardeljan, M. Beam Damage Assessment Using Natural Frequency Shift and Machine Learning. Sensors 2022, 22, 1118. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ying, J.; Liu, J.; Shu, F.; Lang, T.; Jing, X.; Hong, Z. Resonant transparency of a planar anapole metamaterial at terahertz frequencies. Photon. Res. 2021, 9, 125. [Google Scholar] [CrossRef]
- Silalahi, H.M.; Chen, Y.-P.; Shih, Y.-H.; Chen, Y.-S.; Lin, X.-Y.; Liu, J.-H.; Huang, C.-Y. Floating terahertz metamaterials with extremely large refractive index sensitivities. Photon. Res. 2021, 9, 1970. [Google Scholar] [CrossRef]
- Xu, R.; Xu, X.; Yang, B.-R.; Gui, X.; Qin, Z.; Lin, Y.-S. Actively logical modulation of MEMS-based terahertz metamaterial. Photon. Res. 2021, 9, 1409. [Google Scholar] [CrossRef]
- Wu, W.; Chen, Y.; Lee, B.; He, J.; Peng, Y. Tunable Resonant Frequency Power Harvesting Devices; SPIE: Bellingham, WA, USA, 2006; pp. 55–62. [Google Scholar]
- Béliveau, A.; Spencer, G.; Thomas, K.; Roberson, S. Evaluation of MEMS capacitive accelerometers. IEEE Des. Test Comput. 1999, 16, 48–56. [Google Scholar] [CrossRef]
- Yan, R.; Li, X.; Chen, Z.; Xu, Q.; Chen, X. Improving calibration accuracy of a vibration sensor through a closed loop measurement system. IEEE Instrum. Meas. Mag. 2016, 19, 42–46. [Google Scholar] [CrossRef]
- Chen, W.; Jin, M.; Song, H. Optimal configuration of shakers for phase resonance testing using modal parameters. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5676–5690. [Google Scholar] [CrossRef]
- Moheimani, S.R.; Vautier, B.J. Resonant control of structural vibration using charge-driven piezoelectric actuators. IEEE Trans. Control. Syst. Technol. 2005, 13, 1021–1035. [Google Scholar] [CrossRef]
- Svensson, J.L.; Andersson, P.B.; Kropp, W. On the design of structural junctions for the purpose of hybrid passive–active vibration control. J. Sound Vib. 2010, 329, 1274–1288. [Google Scholar] [CrossRef]
- Qiu, Z.-C.; Meng, F.-K.; Han, J.-D.; Liu, J.-G. Acceleration Sensor-based First Resonance Vibration Suppression of a Double-clamped Piezoelectric Beam. Int. J. Acoust. Vib. 2016, 21, 11–23. [Google Scholar] [CrossRef]
- Mondal, J.; Chatterjee, S. Controlling self-excited vibration of a nonlinear beam by nonlinear resonant velocity feedback with time-delay. Int. J. Non-linear Mech. 2021, 131, 103684. [Google Scholar] [CrossRef]
- Sorokin, S.V.; Ershova, O.A.; Grishina, S.V. The active control of vibrations of composite beams by parametric stiffness modulation. Eur. J. Mech.-A/Solids 2000, 19, 873–890. [Google Scholar] [CrossRef]
- Latham, J.; McIntyre, M.L.; Mohebbi, M. Sensorless Resonance Tracking and Stroke Control of a Linear Vapor Compressor Via Nonlinear Observers. IEEE Trans. Ind. Electron. 2017, 65, 3720–3729. [Google Scholar] [CrossRef]
- Ávila, H.E.; Sousa, F.R.; Pagano, D.J. Resonant cavity water cut meter with automatic resonance tracking system. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Zhai, G.; Yang, X.; Lv, Q. A calibration system of resonant high-acceleration and metrological traceability. Meas. Sci. Technol. 2021, 32, 125904. [Google Scholar] [CrossRef]
- ISO 16063-21:2003; Methods for the Calibration of Vibration and Shock Transducers—Part 21: Vibration Calibration by Comparison to a Reference Transducer. International Organization for Standardization: Geneva, Swizterland, 2003.
- Cornel, M.I.; Gillich, G.R.; Maia, N.M.M. A method for an accurate estimation of natural frequencies using swept-sine acoustic excitation. Mech. Syst. Signal Process. 2019, 116, 693–709. [Google Scholar] [CrossRef]
- Davis, S.; Bucher, I. Automatic vibration mode selection and excitation; combining modal filtering with autoresonance. Mech. Syst. Signal Process. 2018, 101, 140–155. [Google Scholar] [CrossRef]
- Hayashi, S. On the tracking of resonance and antiresonance of a piezoelectric resonator. II. Accurate models of the phase locked loop. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1992, 39, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.Z.; Xu, W.; Li, X.; Liu, Y.; IEEE. A Novel Resonant Frequency Estimation Method Based on Recursive Least Squares Algorithm for Linear Compressor. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 1992–1997. [Google Scholar]



| Material | Elastic Modulus E/GPa | Poisson’s Ratio μ | Density ρ/kg·m−3 | Yield Strength σb /MPa |
|---|---|---|---|---|
| Q235 | 210 | 0.28 | 7800 | 220 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, R.; Liu, Z.; Zhai, G.; Lv, Q.; Yang, M.; Cai, C. High-Acceleration Vibration Calibration System Based on Phase-Locked Resonance Control. Sensors 2022, 22, 7208. https://doi.org/10.3390/s22197208
Cheng R, Liu Z, Zhai G, Lv Q, Yang M, Cai C. High-Acceleration Vibration Calibration System Based on Phase-Locked Resonance Control. Sensors. 2022; 22(19):7208. https://doi.org/10.3390/s22197208
Chicago/Turabian StyleCheng, Ran, Zhihua Liu, Guodong Zhai, Qi Lv, Ming Yang, and Chenguang Cai. 2022. "High-Acceleration Vibration Calibration System Based on Phase-Locked Resonance Control" Sensors 22, no. 19: 7208. https://doi.org/10.3390/s22197208
APA StyleCheng, R., Liu, Z., Zhai, G., Lv, Q., Yang, M., & Cai, C. (2022). High-Acceleration Vibration Calibration System Based on Phase-Locked Resonance Control. Sensors, 22(19), 7208. https://doi.org/10.3390/s22197208





