A Spatiotemporal Calibration Algorithm for IMU–LiDAR Navigation System Based on Similarity of Motion Trajectories
Abstract
:1. Introduction
2. Navigation System Calibration Problem Description
2.1. Inertial Measurement Unit Model
2.2. 3D LiDAR Ranging System Model
2.3. Geometric Model of Robot Motion Trajectory
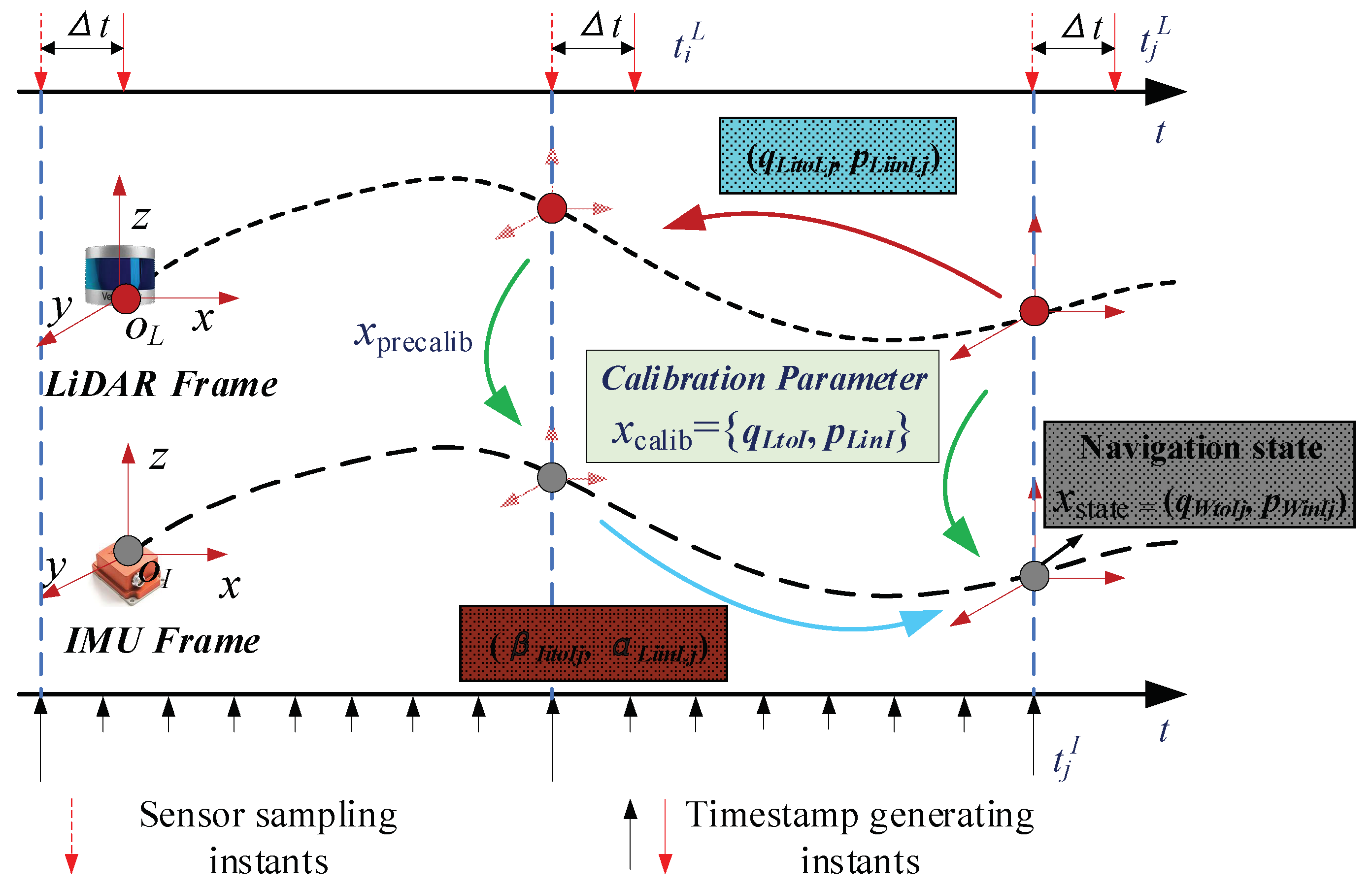
3. Spatiotemporal Calibration of Multisensor Navigation System
3.1. Initial Multisensor Calibration Value Based on Local Trajectory Similarity
3.2. Multisensor Spatiotemporal Parameter Calibration Nonlinear Optimization
3.2.1. IMU Preintegration Factor
3.2.2. LiDAR Odometry Prior Factor
3.2.3. LiDAR Odometry Factor
- Point Cloud Feature Extraction;
- 2.
- LiDAR Factor;
3.2.4. Objective Function of Nonlinear Optimization
| Algorithm1: LiDAR/IMU spatiotemporal calibration. |
| Input: IMU set I [1], point cloud set P {P1, …, PN} Output: External spatial parameter Til, temporal parameter Δt while (True) do Modeling Gyro measurement data set Ii with B-splines Solving the motion between lidar frames by NDT algorithm Solving external parameters Til0 using hand–eye calibration Time offset Δt0 solving to minimize the Hausdorff distance Preintegration using IMU measurement for i = 1, …, K do Distortion correction of point cloud by initial calibration Construct IMU preintegration factor, lidar prior factor and lidar factor Perform nonlinear optimization on the data in the window to solve the state xi end end |
4. Simulation Analysis
5. Experiment
5.1. Sensor Spatiotemporal Unified Parameter Calibration Experiment
5.2. Sensor Fusion Localization and Mapping Test Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Guanbei, W.; Guirong, Z. LIDAR/IMU Calibration Based on Ego-Motion Estimation. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-Sam: Tightly-Coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021. [Google Scholar]
- Wisth, D.; Camurri, M.; Das, S.; Fallon, M. Unified multi-modal landmark tracking for tightly coupled lidar-visual-inertial odometry. IEEE Robot. Autom. Lett. 2021, 6, 1004–1011. [Google Scholar] [CrossRef]
- Lobo, J.; Dias, J.M. Relative pose calibration between visual and inertial sensors. Int. J. Robot. Res. 2007, 26, 561–575. [Google Scholar] [CrossRef]
- Alves, J.; Lobo, J.; Dias, J. Camera-inertial sensor modelling and alignment for visual navigation. Mach. Intell. Robot. Control 2003, 5, 103–112. [Google Scholar]
- Kang, J.; Doh, N.L. Full-DOF calibration of a rotating 2-D LIDAR with a simple plane measurement. IEEE Trans. Robot. 2016, 32, 1245–1263. [Google Scholar] [CrossRef]
- Pereira, M.; Santos, V.; Dias, P. Automatic Calibration of Multiple LIDAR Sensors Using a Moving Sphere as Target. In Robot 2015: Second Iberian Robotics Conference; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Liu, W.; Li, Z.; Malekian, R.; Sotelo, M.A.; Ma, Z.; Li, W. A novel multifeature based on-site calibration method for LiDAR-IMU system. IEEE Trans. Ind. Electron. 2019, 67, 9851–9861. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The kitti dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef] [Green Version]
- Fleps, M.; Mair, E.; Ruepp, O.; Suppa, M.; Burschka, D. Optimization Based IMU Camera Calibration. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Le Gentil, C.; Vidal-Calleja, T.; Huang, S. 3d Lidar-IMU Calibration Based on Upsampled Preintegrated Measurements for Motion Distortion Correction. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Furgale, P.; Rehder, J.; Siegwart, R. Unified Temporal and Spatial Calibration for Multi-Sensor Systems. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Rehder, J.; Beardsley, P.; Siegwart, R.; Furgale, P. Spatio-Temporal Laser to Visual/Inertial Calibration with Applications to Hand-Held, Large Scale Scanning. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Lv, J.; Xu, J.; Hu, K.; Liu, Y.; Zuo, X. Targetless Calibration of Lidar-Imu System Based on Continuous-Time Batch Estimation. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021. [Google Scholar]
- Van Nam, D.; Kim, G.-W. Online Self-Calibration of Multiple 2D LiDARs Using Line Features with Fuzzy Adaptive Covariance. IEEE Sens. J. 2021, 21, 13714–13726. [Google Scholar]
- Ao, Y.; Chen, L.; Tschopp, F.; Breyer, M.; Siegwart, R.; Cramariuc, A. Unified Data Collection for Visual-Inertial Calibration via Deep Reinforcement Learning. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar]
- Mair, E.; Fleps, M.; Suppa, M.; Burschka, D. Spatio-Temporal Initialization for IMU to Camera Registration. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011. [Google Scholar]
- Kelly, J.; Sukhatme, G.S. A General Framework for Temporal Calibration of Multiple Proprioceptive and Exteroceptive Sensors. In Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Li, M.; Mourikis, A.I. 3-D Motion Estimation and Online Temporal Calibration for Camera-IMU Systems. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Li, M.; Mourikis, A.I. Online temporal calibration for camera–IMU systems: Theory and algorithms. Int. J. Robot. Res. 2014, 33, 947–964. [Google Scholar] [CrossRef]
- Qin, T.; Shen, S. Online Temporal Calibration for Monocular Visual-Inertial Systems. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Liu, Y.; Meng, Z. Online temporal calibration based on modified projection model for visual-inertial odometry. IEEE Trans. Instrum. Meas. 2019, 69, 5197–5207. [Google Scholar] [CrossRef]
- Trawny, N.; Roumeliotis, S. Indirect Kalman Filter for 3D Attitude Estimation; Technical Report Number 2005-002; Department of Computer Science and Technology, University of Minnesota: Minneapolis, MN, USA, March 2005. [Google Scholar]
- Muhammad, N.; Lacroix, S. Calibration of a Rotating Multi-Beam Lidar. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Sommer, C.; Usenko, V.; Schubert, D.; Demmel, N.; Cremers, D. Efficient Derivative Computation for Cumulative B-Splines on Lie Groups. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Kim, M.-J.; Kim, M.-S.; Shin, S.Y. A General Construction Scheme for Unit Quaternion Curves with Simple High Order Derivatives. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 15 September 1995. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual--Inertial Odometry. IEEE Trans. Robo. 2016, 33, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Maas, H.-G.; Vosselman, G. Two algorithms for extracting building models from raw laser altimetry data. ISPRS J. Photogramm. Remote Sens. 1999, 54, 153–163. [Google Scholar] [CrossRef]
- Jutzi, B.; Gross, H. Normalization of LiDAR intensity data based on range and surface incidence angle. Environ. Sci. 2009, 38, 213–218. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-Time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and Slam; 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 21 June 2019).












| Num | x/m | y/m | z/m | roll/° | pitch/° | yaw/° |
|---|---|---|---|---|---|---|
| 0 | 0.305 | 3.810 | 0.610 | 0 | −180 | 0 |
| 1 | 3.810 | 3.810 | 1.219 | 0 | −188 | 8 |
| 2 | 7.010 | 5.669 | 1.524 | 0 | −174 | 95 |
| 3 | 7.224 | 11.582 | 0.610 | 0 | −176 | 25 |
| 4 | 13.472 | 10.668 | 0.914 | 0 | −185 | −55 |
| 5 | 13.259 | 4.145 | 1.219 | 0 | −180 | −150 |
| 6 | 7.772 | 3.810 | 0.914 | 0 | −180 | −180 |
| 7 | 2.438 | 1.067 | 1.219 | 0 | −188 | −100 |
| Num. | 5 ms | 10 ms | 15 ms | 20 ms | 30 ms |
|---|---|---|---|---|---|
| Kalibr | 4.87 | 9.84 | 15.22 | 19.84 | 29.88 |
| Linear * | 5.19 | 10.21 | 14.81 | 20.18 | 30.15 |
| Proposed | 5.34 | 10.19 | 14.83 | 19.85 | 29.91 |
| Method | Mean | Median | Std. Dev. | RMS |
|---|---|---|---|---|
| Linear * | 0.5993 | 0.6088 | 0.2340 | 0.6420 |
| Proposed | 0.2442 | 0.2484 | 0.1040 | 0.2647 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, S.; Xiu, X.; Miao, Z. A Spatiotemporal Calibration Algorithm for IMU–LiDAR Navigation System Based on Similarity of Motion Trajectories. Sensors 2022, 22, 7637. https://doi.org/10.3390/s22197637
Li Y, Yang S, Xiu X, Miao Z. A Spatiotemporal Calibration Algorithm for IMU–LiDAR Navigation System Based on Similarity of Motion Trajectories. Sensors. 2022; 22(19):7637. https://doi.org/10.3390/s22197637
Chicago/Turabian StyleLi, Yunhui, Shize Yang, Xianchao Xiu, and Zhonghua Miao. 2022. "A Spatiotemporal Calibration Algorithm for IMU–LiDAR Navigation System Based on Similarity of Motion Trajectories" Sensors 22, no. 19: 7637. https://doi.org/10.3390/s22197637
APA StyleLi, Y., Yang, S., Xiu, X., & Miao, Z. (2022). A Spatiotemporal Calibration Algorithm for IMU–LiDAR Navigation System Based on Similarity of Motion Trajectories. Sensors, 22(19), 7637. https://doi.org/10.3390/s22197637









