Quality Factor Enhancement of Piezoelectric MEMS Resonator Using a Small Cross-Section Connection Phononic Crystal
Abstract
1. Introduction
2. Materials and Methods
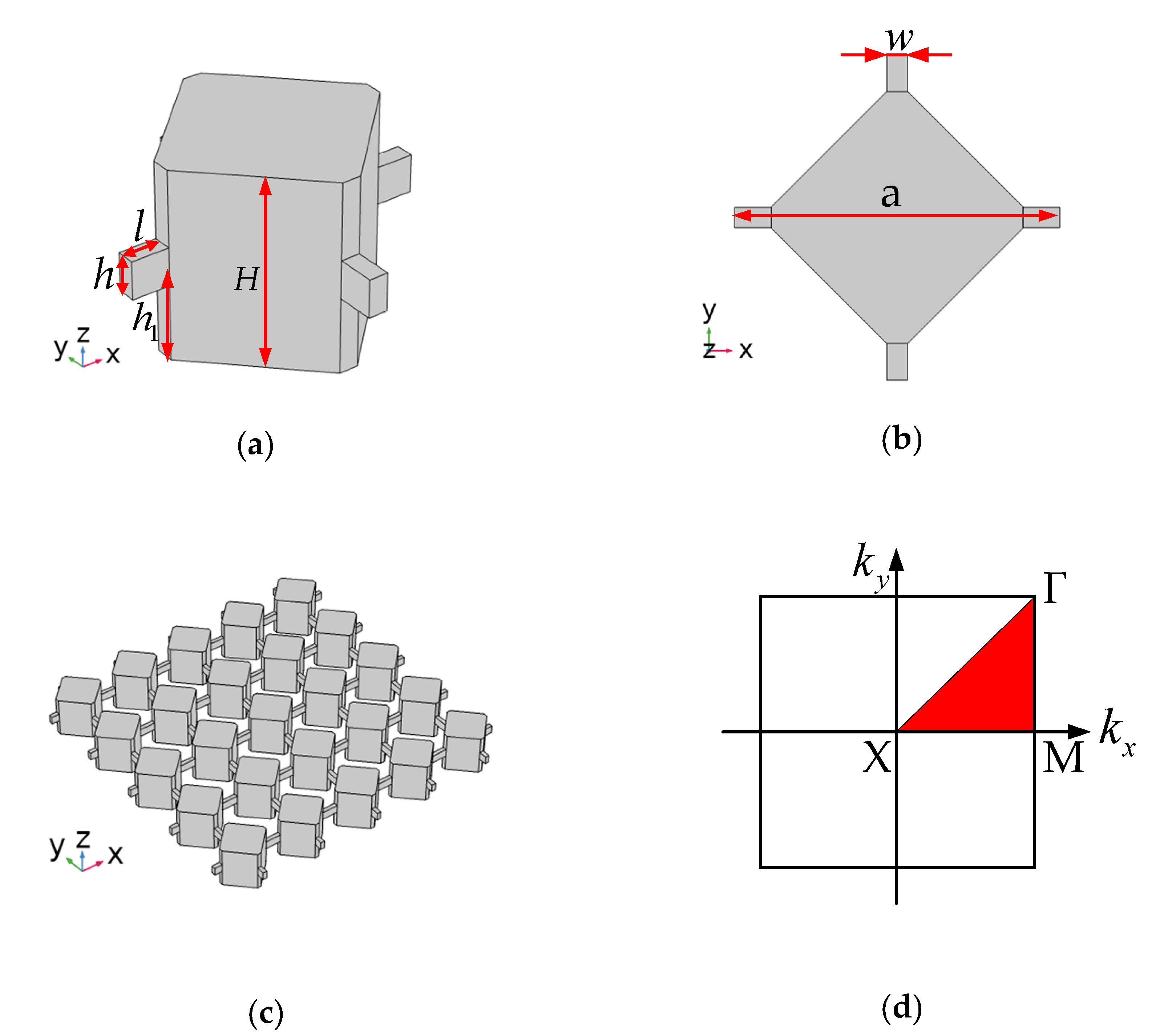
2.1. Phononic Crystals Structure
2.2. Phononic Crystals Band Gaps
2.3. Effect of the Structural Parameters on the Band Gap Range
2.4. Power Transmission Characteristics
3. MEMS Resonator Design and Finite Element Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bhugra, H.; Piazza, G. Piezoelectric Mems Resonators; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Diamond, B.M.; Neumann, J.J.; Gabriel, K.J. Digital sound reconstruction using arrays of CMOS-MEMS microspeakers. In Proceedings of the Fifteenth IEEE International Conference on Micro Electro Mechanical Systems IEEE, Boston, MA, USA, 8–12 June 2003. [Google Scholar]
- Acar, C.; Schofield, A.R.; Trusov, A.A.; Costlow, L.E.; Shkel, A.M. Environmentally Robust MEMS Vibratory Gyroscopes for Automotive Applications. IEEE Sens. J. 2009, 9, 1895–1906. [Google Scholar] [CrossRef]
- Berman, D.; Walker, M.J.; Krim, J. Contact voltage-induced softening of RF microelectromechanical system gold-on-gold contacts at cryogenic temperatures. J. Appl. Phys. 2010, 108, 044307. [Google Scholar] [CrossRef]
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.-Y.; Nabki, F. Micromachined Resonators: A Review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef] [PubMed]
- Brand, O.; Dufour, I.; Heinrich, S.; Josse, F.; Fedder, G.K.; Hierold, C.; Korvink, J.G.; Tabata, O. Resonant MEMS: Fundamentals, Implementation, and Application; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Segovia-Fernandez, J.; Cremonesi, M.; Cassella, C.; Frangi, A.; Piazza, G. Experimental Study on the Impact of Anchor Losses on the Quality Factor of Contour Mode AlN Resonators. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems, Barcelona, Spain, 16–20 June 2013; pp. 2473–2476. [Google Scholar]
- Frangi, A.; Cremonesi, M.; Jaakkola, A.; Pensala, T. Analysis of anchor and interface losses in piezoelectric MEMS resonators. Sens. Actuators A Phys. 2013, 190, 127–135. [Google Scholar] [CrossRef]
- Zou, J.; Lin, C.-M.; Tang, G.; Pisano, A.P. High-Q butterfly-shaped AlN lamb wave resonators. IEEE Electron Dev. Lett. 2017, 38, 1739–1742. [Google Scholar] [CrossRef]
- Tu, C.; Lee, J.E.-Y. Enhancing quality factor by etch holes in piezoelectric-on-silicon lateral mode resonators. Sens. Actuators A Phys. 2017, 259, 144–151. [Google Scholar] [CrossRef]
- Siddiqi, M.W.U.; Tu, C.; Lee, J.E.-Y. Effect of mode order, resonator length, curvature, and electrode coverage on enhancing the performance of biconvex resonators. J. Micromech. Microeng. 2018, 28, 094002. [Google Scholar] [CrossRef]
- Liu, J.; Workie, T.B.; Wu, Z.; Tang, P.; Hashimoto, K.Y. Acoustic Reflectors for Anchor Loss Reduction of Thin Film Piezoelectric on Substrate Resonators. In Proceedings of the 2021 IEEE MTT-S International Wireless Symposium (IWS), Nanjing, China, 23–26 May 2021. [Google Scholar]
- Liu, J.; Workie, T.B.; Wu, Z.; Tang, P.; Bao, J.-F.; Hashimoto, K.-Y. Q-Factor Enhancement of Thin-Film Piezoelectric-on-Silicon MEMS Resonator by Phononic Crystal-Reflector Composite Structure. Micromachines 2020, 11, 1130. [Google Scholar] [CrossRef]
- Khelif, A.; Adibi, A. Phononic Crystals: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Deymier, P.A. One-Dimensional Phononic Crystals. In Acoustic Metamaterials and Phononic Crystals; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 3; Volume 173, pp. 45–93. [Google Scholar] [CrossRef]
- Zhu, H.; Lee, J.E.-Y. AlN Piezoelectric on Silicon MEMS Resonator with Boosted Q using Planar Patterned Phononic Crystals on Anchors. In Proceedings of the 28th IEEE International Conference on Micro Electro Mechanical Systems IEEE, Estoril, Portugal, 18–22 January 2015. [Google Scholar]
- Khan, M.A.; Bao, J.F.; Bao, F.H.; Zhou, X. Concentric Split Alµminµm with Silicon-Alµminµm Nitride Annular Rings Resonators. Micromachines 2019, 10, 296. [Google Scholar] [CrossRef]
- Workie, T.B.; Wu, T.; Bao, J.F.; Hashimoto, K.Y. Design for high-quality factor of piezoelectric-on-silicon MEMS resonators using resonant plate shape and phononic crystals. Jpn. J. Appl. Phys. 2021, 60, SDDA03. [Google Scholar] [CrossRef]
- Bao, F.-H.; Wu, X.-Q.; Zhou, X.; Wu, Q.-D.; Zhang, X.-S.; Bao, J.-F. Spider web-like phononic crystals for piezoelectric MEMS resonators to reduce acoustic energy dissipation. Micromachines 2019, 10, 626. [Google Scholar] [CrossRef]
- Ha, T.D. Boosted anchor quality factor of a thin-film alµminµm nitride-on-silicon length extensional mode MEMS resonator using phononic crystal strip. Appl. Phys. A 2021, 127, 1–9. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromech. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Jiang, S.; Hu, H.; Laude, V. Low-frequency band gap in cross-like holey phononic crystal strip. J. Phys. D Appl. Phys. 2018, 51, 045601. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Kushwaha, M.; Halevi, P.; Martínez, G.; Dobrzynski, L.; Djafari-Rouhani, B. Theory of acoustic band structure of periodic elastic composites. Phys. Rev. B 1994, 49, 2313–2322. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Garcia, N. Theoretical study of three dimensional elastic band gaps with the finite-difference time-domain method. Appl. Phys. 2000, 87, 3120–3122. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P.; Goertzen, A.L.; Page, J.H. Elastic wave scattering by periodic structures of spherical objects: Theory and experiment. Phys. Rev. B 2000, 62, 2446–2457. [Google Scholar] [CrossRef]
- Siddiqi, M.; Lee, J.E.-Y. Wide Acoustic Bandgap Solid Disk-Shaped Phononic Crystal Anchoring Boundaries for Enhancing Quality Factor in AlN-on-Si MEMS Resonators. Micromachines 2018, 9, 413. [Google Scholar] [CrossRef]
- Tu, C.; Lee, J.E.-Y. VHF-band biconvex AlN-on-silicon micromechanical resonators with enhanced quality factor and suppressed spurious modes. J. Micromech. Microeng. 2016, 26, 065012. [Google Scholar] [CrossRef]
- Rawat, U.; Nair, D.R.; DasGupta, A. Piezoelectric-on-silicon array resonators with asymmetric phononic crystal tethering. Microelectromech. Syst. 2017, 26, 773–781. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, H.; Zhang, D.; Duan, X.; Zhang, H.; Pang, W. Design and fabrication of alµminµm nitride Lamb wave res-onators towards high figure of merit for intermediate frequency filter applications. Micromech. Microeng. 2015, 25, 035016. [Google Scholar] [CrossRef]











| Material | Parameters | Values |
|---|---|---|
| Silicon (Si) | Mass Density (kg/m3) | 2330 |
| Young’s Modulus (GPa) | = 169 | |
| = 169 | ||
| = 130 | ||
| shearing’s Modulus (GPa) | = 79.6 | |
| = 79.6 | ||
| = 50.9 | ||
| Poisson’s ratio (ν) | = 0.36 | |
| = 0.28 | ||
| = 0.064 | ||
| Alµminµm (Al) | Mass Density (kg/m3) | 2700 |
| Young’s Modulus (GPa) | 70 | |
| Poisson’s ratio (ν) | 0.35 | |
| Electrical conductivity (σ) | 33.5 × 106 | |
| Coefficient of thermal expansion (α) | 23.1 × 10−6 | |
| Heat capacity (Cp) | 904 | |
| Thermal conductivity (κ) | 237 | |
| Alµminµm Nitride (AIN) | Mass Density (kg/m3) | 3300 |
| Young’s Modulus (GPa) | 320 | |
| Poisson’s ratio (ν) | 0.24 | |
| Relative permittivity (ε) | 9 |
| PnC Shape | Dimensions (µm) | Range (MHz) | fc (MHz) | BG% |
|---|---|---|---|---|
| Air-Hole [16] | 22 | 136–147 | 141.5 | 7.7 |
| DTP [18] | 16 | 105–240 | 173 | 78 |
| Solid-Disk [27] | 22 | 93–175 | 134 | 61.1 |
| SCC (This work) | 16 | 56.6–269.6 | 163 | 130.6 |
| Parameters | Values (Unit) |
|---|---|
| Simulated resonant frequency (f0) | 149.66 (MHz) |
| Wave length (λ) | 56.6 (µm) |
| Inter digitated transducer (IDT) finger (n) | 5 |
| Tethers Width (Wt) | 18 (µm) |
| Tethers Length (Lt) | 56.6 (µm) |
| electrode gap (Ge) | 4 (µm) |
| Resonator width (Wr) | 141.5 (µm) |
| Resonator length (Lr) | 424.5 (µm) |
| Thickness of Al (TAl) | 0.1 (µm) |
| Thickness of AlN (TAlN) | 0.1 (µm) |
| Height of silicon substrate (HS) | 10 (µm) |
| Parameters | Mode 3 | Mode 3 (with PnC) | Mode 5 | Mode 5 (with PnC) | Mode 7 | Mode 7 (with PnC) |
|---|---|---|---|---|---|---|
| Resonant frequency (fr), MHz | 90.25 | 90.25 | 149.66 | 149.65 | 207.16 | 207.16 |
| Insertion Loss (IL), dB | 10.54 | 1.02 | 4.18 | 1.87 | 15.13 | 3.28 |
| Motional resistance (Rm), Ω | 235.29 | 3.39 | 18.18 | 4.29 | 156.25 | 48.31 |
| Coupling coefficient (Keff2), % | 0.006 | 0.006 | 0.02 | 0.02 | 0.006 | 0.006 |
| Simulated Qanchor | 35,039 | 58,012,627 | 61,207 | 124,051,263 | 28,026 | 462,009 |
| Loaded Quaity factor (Ql) | 25,068 | 85,948 | 16,629 | 21,079 | 26,513 | 103,585 |
| Unloaded Quality factor (Qu) | 35,659 | 79,0326 | 43,531 | 108,823 | 32,137 | 329,259 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhu, C.; Liu, H.; Li, Y.; Wang, Q.; Su, K. Quality Factor Enhancement of Piezoelectric MEMS Resonator Using a Small Cross-Section Connection Phononic Crystal. Sensors 2022, 22, 7751. https://doi.org/10.3390/s22207751
Li L, Zhu C, Liu H, Li Y, Wang Q, Su K. Quality Factor Enhancement of Piezoelectric MEMS Resonator Using a Small Cross-Section Connection Phononic Crystal. Sensors. 2022; 22(20):7751. https://doi.org/10.3390/s22207751
Chicago/Turabian StyleLi, Lixia, Chuang Zhu, Haixia Liu, Yan Li, Qi Wang, and Kun Su. 2022. "Quality Factor Enhancement of Piezoelectric MEMS Resonator Using a Small Cross-Section Connection Phononic Crystal" Sensors 22, no. 20: 7751. https://doi.org/10.3390/s22207751
APA StyleLi, L., Zhu, C., Liu, H., Li, Y., Wang, Q., & Su, K. (2022). Quality Factor Enhancement of Piezoelectric MEMS Resonator Using a Small Cross-Section Connection Phononic Crystal. Sensors, 22(20), 7751. https://doi.org/10.3390/s22207751





