Self-Pulsations in Terahertz Quantum Cascade Lasers under Strong Optical Feedback: The Effect of Multiple Reflections in the External Cavity
Abstract
:1. Introduction
2. Theoretical Model
3. Results
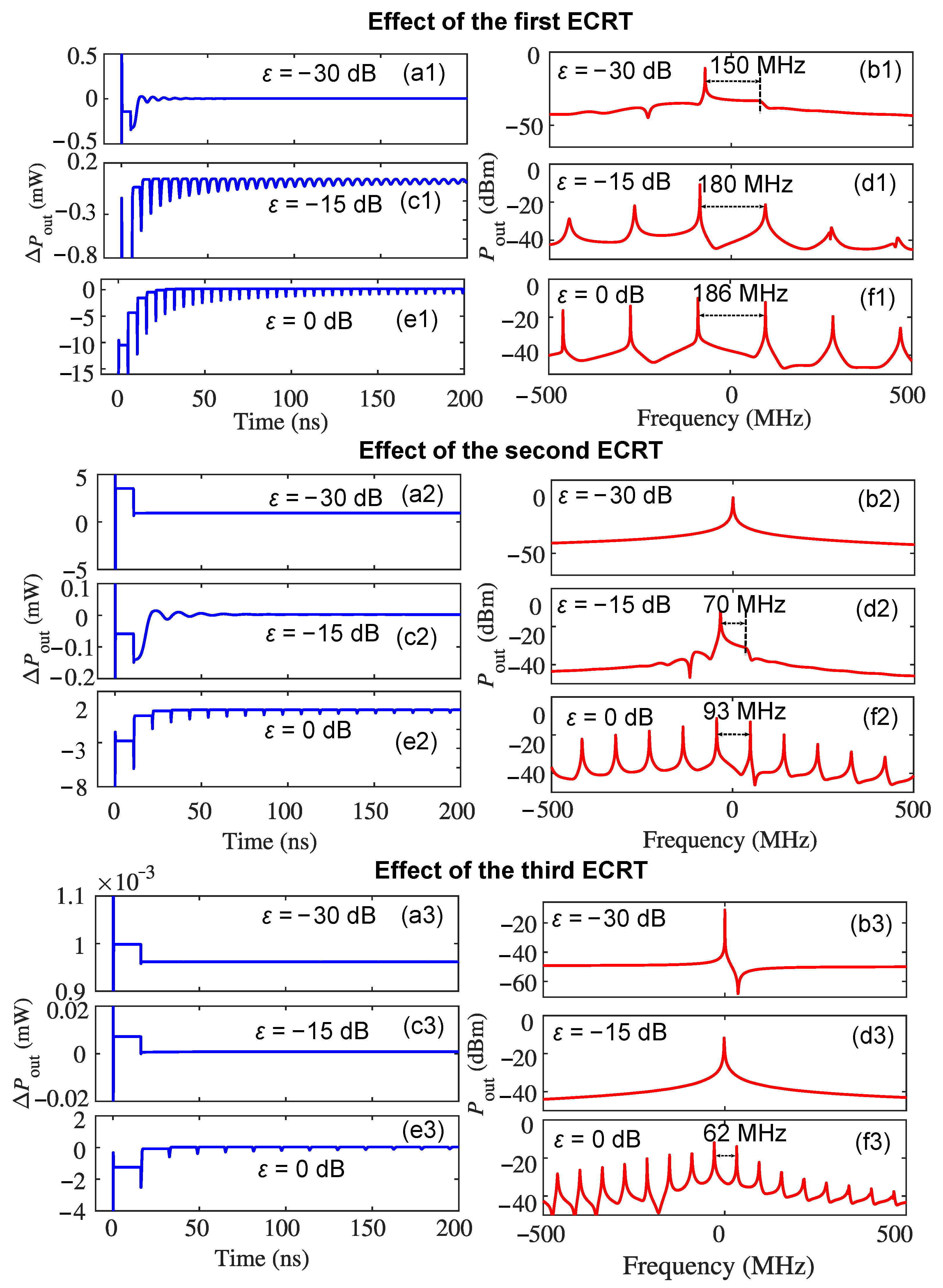
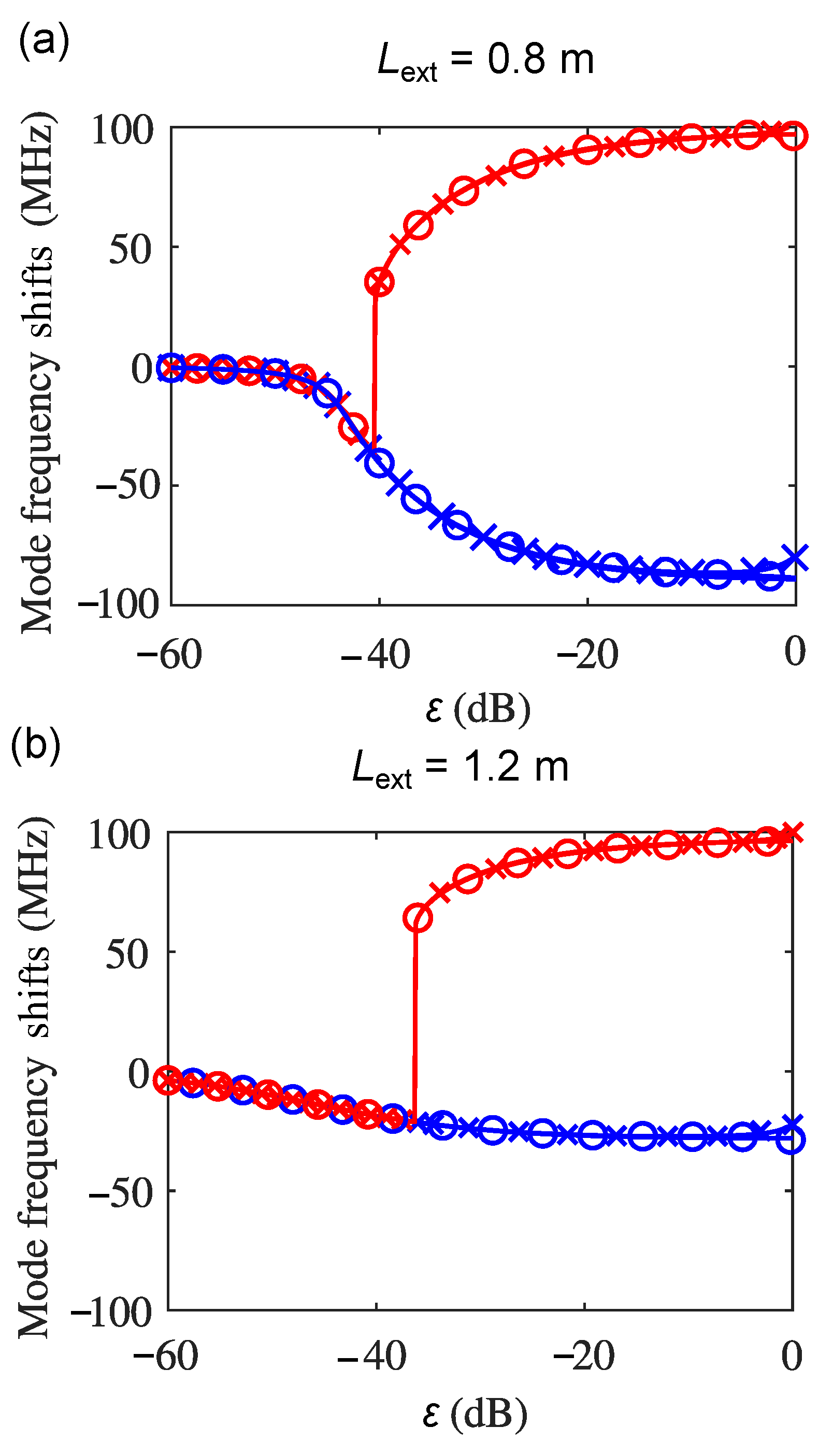
3.1. Effects of Each External Cavity Round Trip on Self-Pulsations Separately
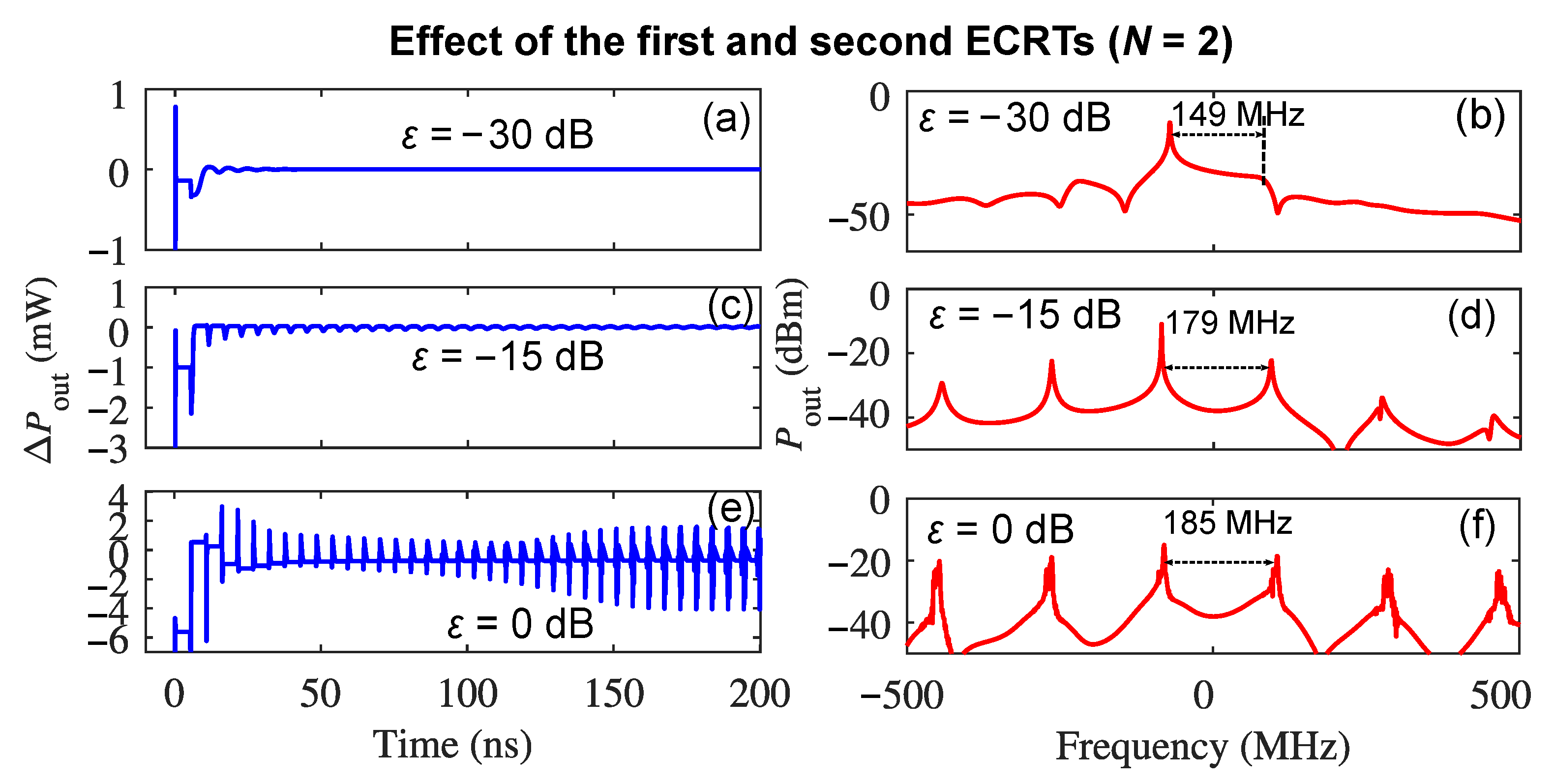
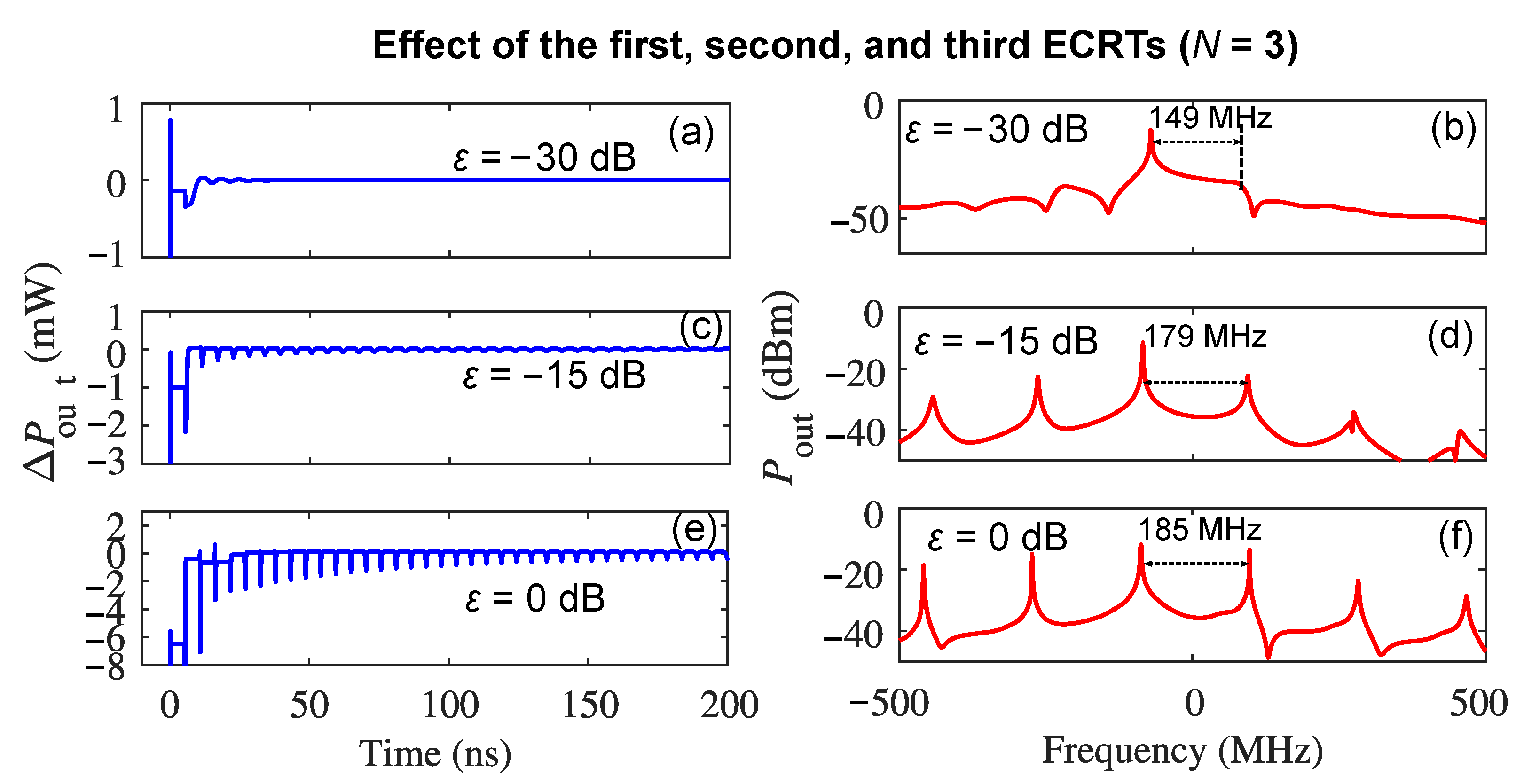
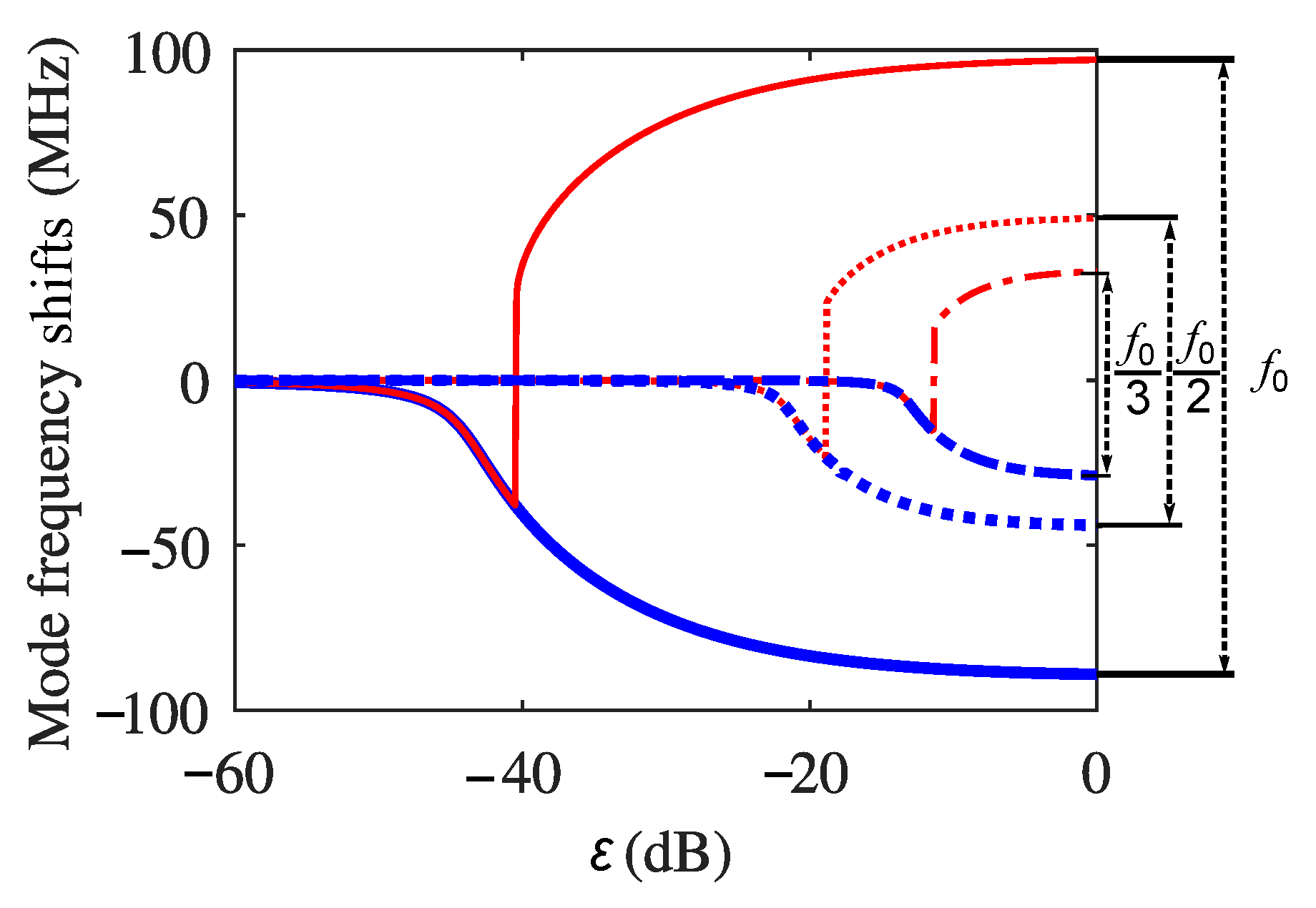
3.2. Effects of Multiple External Cavity Round Trips on Self-Pulsations Simultaneously
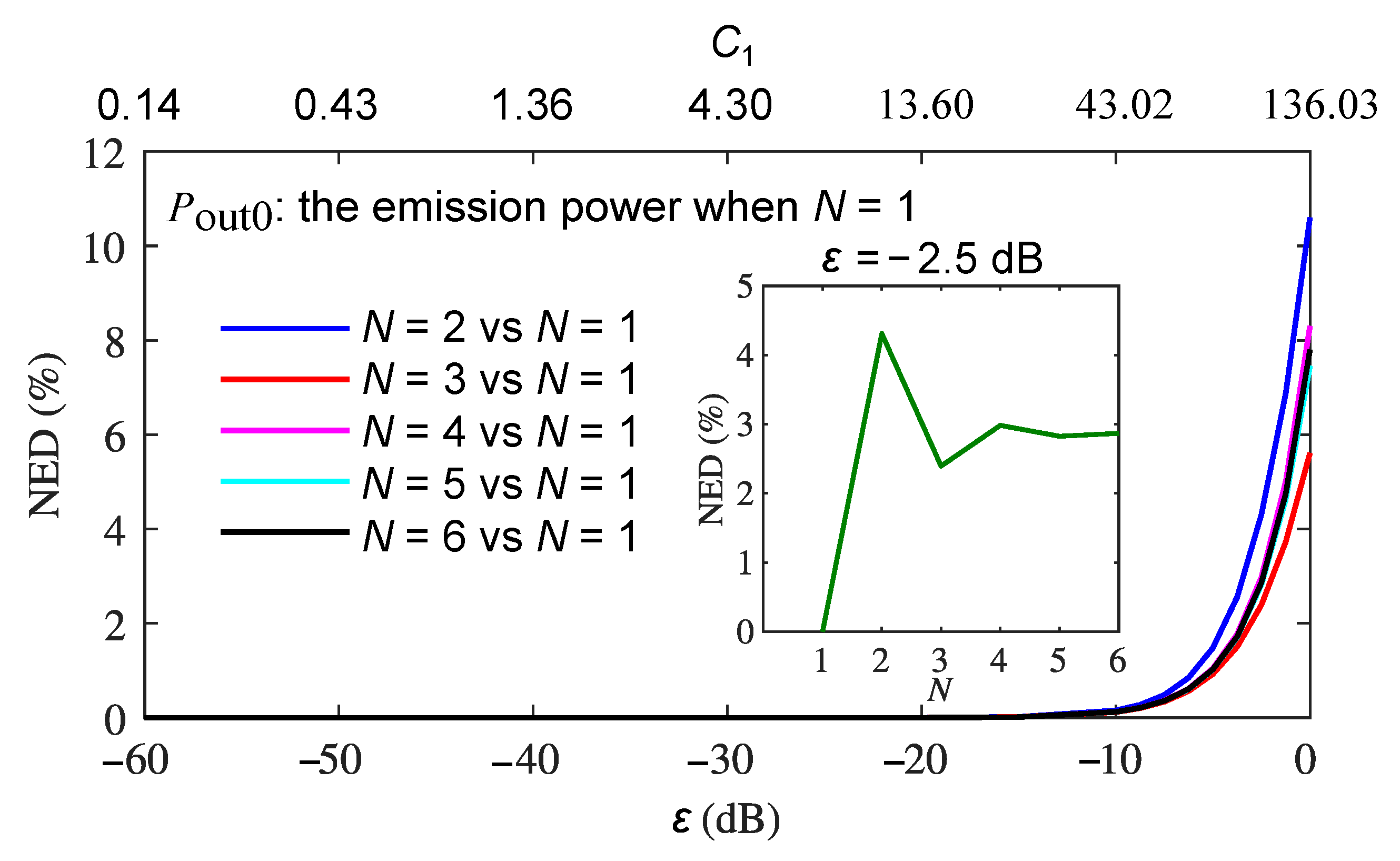
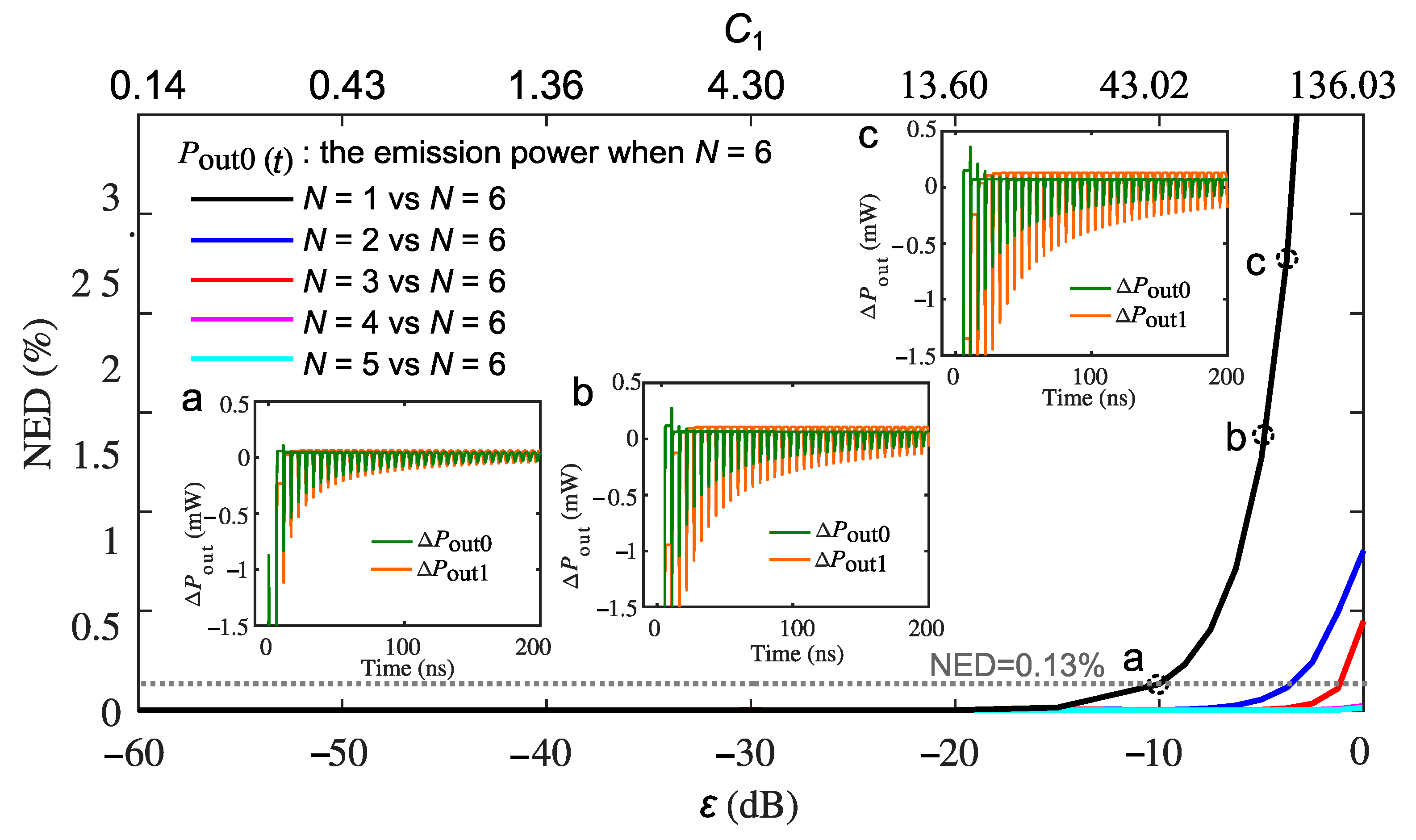
3.3. Normalized Energy Deviation with a Varying Feedback Level
4. Excess-Phase Equation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Köhler, R.; Tredicucci, A.; Beltram, F.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Ritchie, D.A.; Iotti, R.C.; Rossi, F. Terahertz semiconductor-heterostructure laser. Nature 2002, 417, 156–159. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Chen, L.; Freeman, J.; Salih, M.; Dean, P.; Davies, A.; Linfield, E. Multi-Watt high-power THz frequency quantum cascade lasers. Electron. Lett. 2017, 53, 799–800. [Google Scholar] [CrossRef] [Green Version]
- Ravaro, M.; Barbieri, S.; Santarelli, G.; Jagtap, V.; Manquest, C.; Sirtori, C.; Khanna, S.; Linfield, E. Measurement of the intrinsic linewidth of terahertz quantum cascade lasers using a near-infrared frequency comb. Opt. Express 2012, 20, 25654–25661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rösch, M.; Scalari, G.; Beck, M.; Faist, J. Octave-spanning semiconductor laser. Nat. Photonics 2015, 9, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Piccardo, M.; Capasso, F. Laser Frequency Combs with Fast Gain Recovery: Physics and Applications. Laser Photonics Rev. 2021, 16, 2100403. [Google Scholar] [CrossRef]
- Khalatpour, A.; Paulsen, A.K.; Deimert, C.; Wasilewski, Z.R.; Hu, Q. High-power portable terahertz laser systems. Nat. Photonics 2021, 15, 16. [Google Scholar] [CrossRef]
- Mezzapesa, F.P.; Columbo, L.L.; Brambilla, M.; Dabbicco, M.; Borri, S.; Vitiello, M.S.; Beere, H.E.; Ritchie, D.A.; Scamarcio, G. Intrinsic stability of quantum cascade lasers against optical feedback. Opt. Express 2013, 21, 13748–13757. [Google Scholar] [CrossRef]
- Columbo, L.L.; Brambilla, M. Multimode regimes in quantum cascade lasers with optical feedback. Opt. Express 2014, 22, 10105–10118. [Google Scholar] [CrossRef]
- Qi, X.; Bertling, K.; Taimre, T.; Agnew, G.; Lim, Y.L.; Gillespie, T.; Robinson, A.; Brünig, M.; Demić, A.; Dean, P.; et al. Observation of optical feedback dynamics in single-mode terahertz quantum cascade lasers: Transient instabilities. Phys. Rev. A 2021, 103, 033504. [Google Scholar] [CrossRef]
- Qi, X.; Bertling, K.; Taimre, T.; Lim, Y.L.; Gillespie, T.; Dean, P.; Li, L.H.; Linfield, E.H.; Davies, A.G.; Indjin, D.; et al. Terahertz imaging with self-pulsations in quantum cascade lasers under optical feedback. APL Photonics 2021, 6, 091301. [Google Scholar] [CrossRef]
- Qi, X.; Bertling, K.; Taimre, T.; Agnew, G.; Lim, Y.L.; Gillespie, T.; Demić, A.; Dean, P.; Li, L.H.; Linfield, E.H.; et al. Terahertz quantum cascade laser under optical feedback: Effects of laser self-pulsations on self-mixing signals. Opt. Express 2021, 29, 39885–39895. [Google Scholar] [CrossRef] [PubMed]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Tkach, R.; Chraplyvy, A.R. Regimes of feedback effects in 1.5-μm distributed feedback lasers. J. Light. Technol. 1986, 4, 1655–1661. [Google Scholar] [CrossRef]
- Donati, S.; Horng, R.H. The diagram of feedback regimes revisited. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1500309. [Google Scholar] [CrossRef]
- Heil, T.; Fischer, I.; Elsäßer, W.; Gavrielides, A. Dynamics of semiconductor lasers subject to delayed optical feedback: The short cavity regime. Phys. Rev. Lett. 2001, 87, 243901. [Google Scholar] [CrossRef] [PubMed]
- Soriano, M.C.; García-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers. Rev. Mod. Phys. 2013, 85, 421. [Google Scholar] [CrossRef] [Green Version]
- Jumpertz, L.; Schires, K.; Carras, M.; Sciamanna, M.; Grillot, F. Chaotic light at mid-infrared wavelength. Light. Sci. Appl. 2016, 5, e16088. [Google Scholar] [CrossRef] [Green Version]
- Rakić, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Indjin, D.; Ikonić, Z.; Harrison, P.; Valavanis, A.; Khanna, S.P.; et al. Swept-frequency feedback interferometry using terahertz frequency QCLs: A method for imaging and materials analysis. Opt. Express 2013, 21, 22194–22205. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.; Kundu, I.; Dean, P.; Agnew, G.; Taimre, T.; Valavanis, A.; Grier, A.T.; Linfield, E.H.; Davies, A.G.; Indjin, D.; et al. Mode selection and tuning mechanisms in coupled-cavity terahertz quantum cascade lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–12. [Google Scholar] [CrossRef]
- Kliese, R.; Taimre, T.; Bakar, A.A.A.; Lim, Y.L.; Bertling, K.; Nikolić, M.; Perchoux, J.; Bosch, T.; Rakić, A.D. Solving self-mixing equations for arbitrary feedback levels: A concise algorithm. Appl. Opt. 2014, 53, 3723–3736. [Google Scholar] [CrossRef]
- Agnew, G.; Grier, A.; Taimre, T.; Lim, Y.L.; Bertling, K.; Ikonić, Z.; Valavanis, A.; Dean, P.; Cooper, J.; Khanna, S.P.; et al. Model for a pulsed terahertz quantum cascade laser under optical feedback. Opt. Express 2016, 24, 20554–20570. [Google Scholar] [CrossRef] [PubMed]
- Dean, P.; Lim, Y.L.; Valavanis, A.; Kliese, R.; Nikolić, M.; Khanna, S.P.; Lachab, M.; Indjin, D.; Ikonić, Z.; Harrison, P.; et al. Terahertz imaging through self-mixing in a quantum cascade laser. Opt. Lett. 2011, 36, 2587–2589. [Google Scholar] [CrossRef] [Green Version]
- Lim, Y.L.; Dean, P.; Nikolić, M.; Kliese, R.; Khanna, S.P.; Lachab, M.; Valavanis, A.; Indjin, D.; Ikonić, Z.; Harrison, P.; et al. Demonstration of a self-mixing displacement sensor based on terahertz quantum cascade lasers. Appl. Phys. Lett. 2011, 99, 081108. [Google Scholar]
- Lim, Y.L.; Taimre, T.; Bertling, K.; Dean, P.; Indjin, D.; Valavanis, A.; Khanna, S.P.; Lachab, M.; Schaider, H.; Prow, T.W.; et al. High-contrast coherent terahertz imaging of porcine tissue via swept-frequency feedback interferometry. Biomed. Opt. Express 2014, 5, 3981–3989. [Google Scholar] [CrossRef] [Green Version]
- Mezzapesa, F.; Columbo, L.; Dabbicco, M.; Brambilla, M.; Scamarcio, G. QCL-based nonlinear sensing of independent targets dynamics. Opt. Express 2014, 22, 5867–5874. [Google Scholar] [CrossRef] [PubMed]
- Lim, Y.L.; Bertling, K.; Taimre, T.; Gillespie, T.; Glenn, C.; Robinson, A.; Indjin, D.; Han, Y.; Li, L.; Linfield, E.H.; et al. Coherent imaging using laser feedback interferometry with pulsed-mode terahertz quantum cascade lasers. Opt. Express 2019, 27, 10221–10233. [Google Scholar] [CrossRef] [PubMed]
- Rakić, A.; Taimre, T.; Bertling, K.; Lim, Y.; Dean, P.; Valavanis, A.; Indjin, D. Sensing and imaging using laser feedback interferometry with quantum cascade lasers. Appl. Phys. Rev. 2019, 6, 021320. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.; Agnew, G.; Taimre, T.; Han, S.; Lim, Y.L.; Bertling, K.; Demić, A.; Dean, P.; Indjin, D.; Rakić, A.D. Laser feedback interferometry in multi-mode terahertz quantum cascade lasers. Opt. Express 2020, 28, 14246–14262. [Google Scholar] [CrossRef]
- Fenner, D.B.; Hensley, J.M.; Allen, M.G.; Xu, J.; Tredicucci, A. Antireflection coating for external-cavity quantum cascade laser near 5 THz. MRS Online Proc. Libr. (OPL) 2007, 1016, 703. [Google Scholar] [CrossRef] [Green Version]
- Hugi, A.; Terazzi, R.; Bonetti, Y.; Wittmann, A.; Fischer, M.; Beck, M.; Faist, J.; Gini, E. External cavity quantum cascade laser tunable from 7.6 to 11.4 μm. Appl. Phys. Lett. 2009, 95, 061103. [Google Scholar] [CrossRef]
- Almond, N.W.; Qi, X.; Degl’Innocenti, R.; Kindness, S.J.; Michailow, W.; Wei, B.; Braeuninger-Weimer, P.; Hofmann, S.; Dean, P.; Indjin, D.; et al. External cavity terahertz quantum cascade laser with a metamaterial/graphene optoelectronic mirror. Appl. Phys. Lett. 2020, 117, 041105. [Google Scholar] [CrossRef]
- Chen, C.; Jia, Z.; Lv, Y.; Li, P.; Xu, B.; Wang, Y. Broadband laser chaos generation using a quantum cascade laser with optical feedback. Opt. Lett. 2021, 46, 5039–5042. [Google Scholar] [CrossRef] [PubMed]
- Green, R.P.; Xu, J.H.; Mahler, L.; Tredicucci, A.; Beltram, F.; Giuliani, G.; Beere, H.E.; Ritchie, D.A. Linewidth enhancement factor of terahertz quantum cascade lasers. Appl. Phys. Lett. 2008, 92, 071106. [Google Scholar] [CrossRef] [Green Version]
- Vitiello, M.S.; Consolino, L.; Bartalini, S.; Taschin, A.; Tredicucci, A.; Inguscio, M.; De Natale, P. Quantum-limited frequency fluctuations in a terahertz laser. Nat. Photonics 2012, 6, 525–528. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| —Injection efficiency into ULL | 54.41% |
| —Injection efficiency into LLL | 1.65% |
| I—Drive current | 1.2 A |
| —Total carrier lifetime in ULL | |
| —Non-radiative relaxation time from ULL to LLL | |
| —Total carrier lifetime in LLL | |
| —Spontaneous emission lifetime | |
| —Photon lifetime | |
| G—Gain factor | |
| M—Number of periods in active cavity | 90 |
| —Spontaneous emission factor | |
| —Emission frequency with no optical feedback | |
| —External cavity length | 0.8 m |
| —Refractive index of external cavity | 1.00 |
| —Round-trip time of the external cavity, | |
| —Laser cavity length | 2 mm |
| —Refractive index of active region | 3.3 |
| —Round-trip time of laser cavity, | 4.403 |
| —Feedback coupling coefficient of the s-th ECRT, | Varies |
| —Reinjection coupling factor | Varies |
| R—Reflection coefficient of external target | 0.7 |
| , —Reflection coefficient of laser facets | 0.2861 |
| —Linewidth enhancement factor | −0.1 [23] |
| —Feedback parameter of the s-th ECRT, | Varies |
| q—Elementary charge | 1.602 |
| c—Speed of light in vacuum | 299,792,458 m s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, X.; Loh, H.Y.; Taimre, T.; Bertling, K.; Indjin, D.; Rakić, A.D. Self-Pulsations in Terahertz Quantum Cascade Lasers under Strong Optical Feedback: The Effect of Multiple Reflections in the External Cavity. Sensors 2022, 22, 8501. https://doi.org/10.3390/s22218501
Qi X, Loh HY, Taimre T, Bertling K, Indjin D, Rakić AD. Self-Pulsations in Terahertz Quantum Cascade Lasers under Strong Optical Feedback: The Effect of Multiple Reflections in the External Cavity. Sensors. 2022; 22(21):8501. https://doi.org/10.3390/s22218501
Chicago/Turabian StyleQi, Xiaoqiong, Hui Yi Loh, Thomas Taimre, Karl Bertling, Dragan Indjin, and Aleksandar D. Rakić. 2022. "Self-Pulsations in Terahertz Quantum Cascade Lasers under Strong Optical Feedback: The Effect of Multiple Reflections in the External Cavity" Sensors 22, no. 21: 8501. https://doi.org/10.3390/s22218501
APA StyleQi, X., Loh, H. Y., Taimre, T., Bertling, K., Indjin, D., & Rakić, A. D. (2022). Self-Pulsations in Terahertz Quantum Cascade Lasers under Strong Optical Feedback: The Effect of Multiple Reflections in the External Cavity. Sensors, 22(21), 8501. https://doi.org/10.3390/s22218501








