Learning Optimal Time-Frequency-Spatial Features by the CiSSA-CSP Method for Motor Imagery EEG Classification
Abstract
:1. Introduction
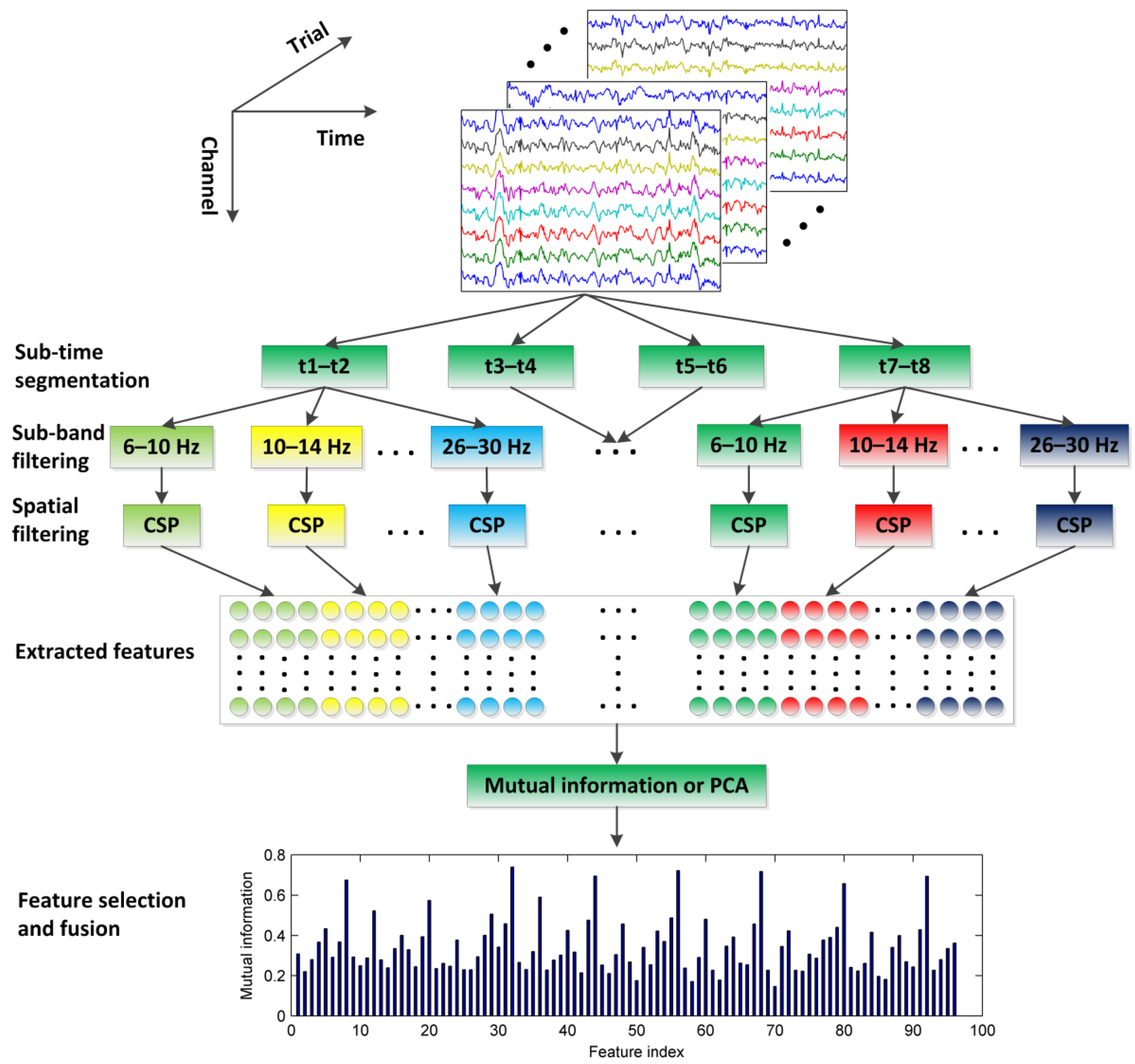
2. Methods
2.1. Time Segmentation of EEG Signal
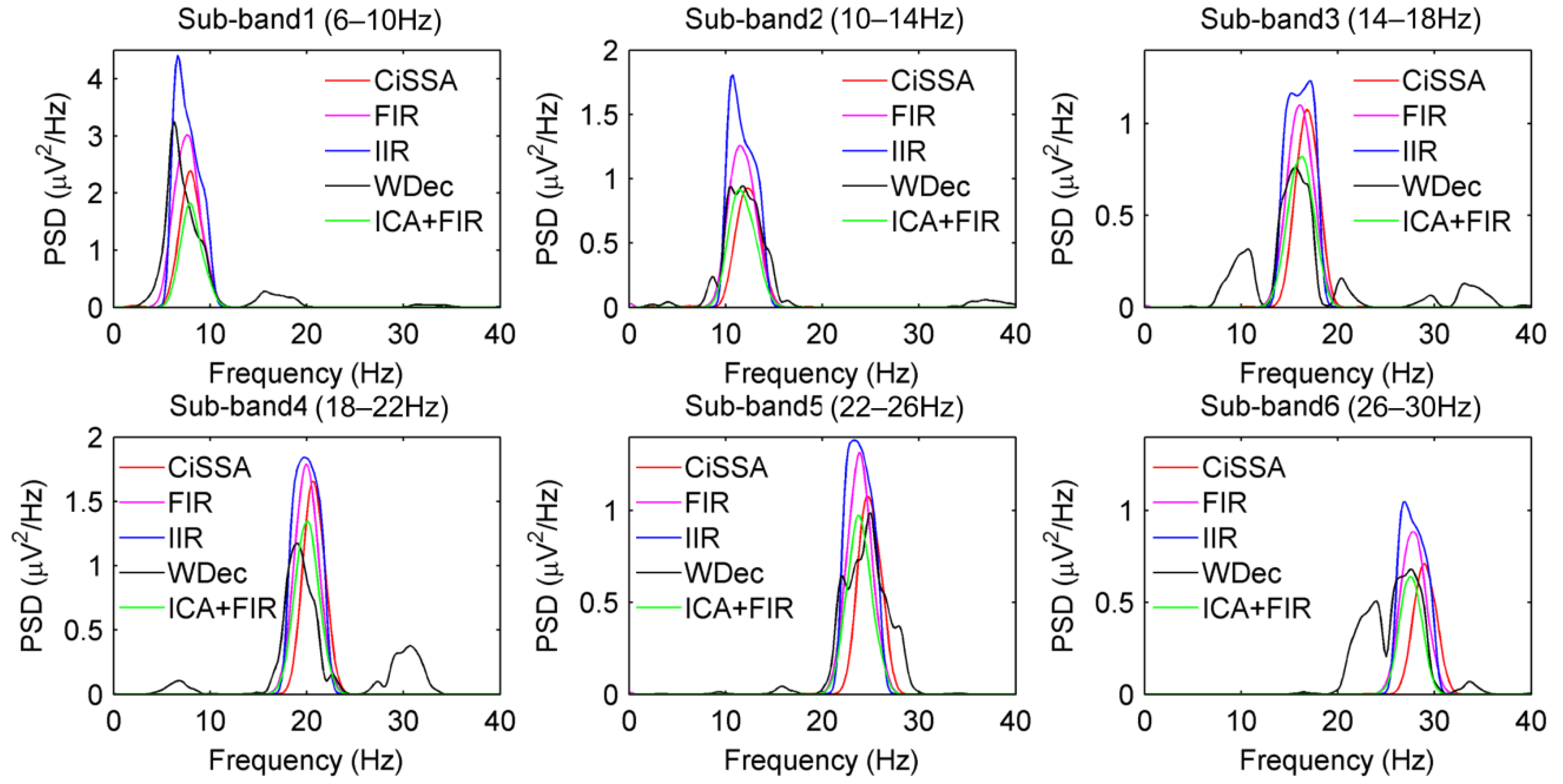
2.2. Sub-Band Filtering Using CiSSA
2.3. Feature Extraction Using Common Spatial Patterns
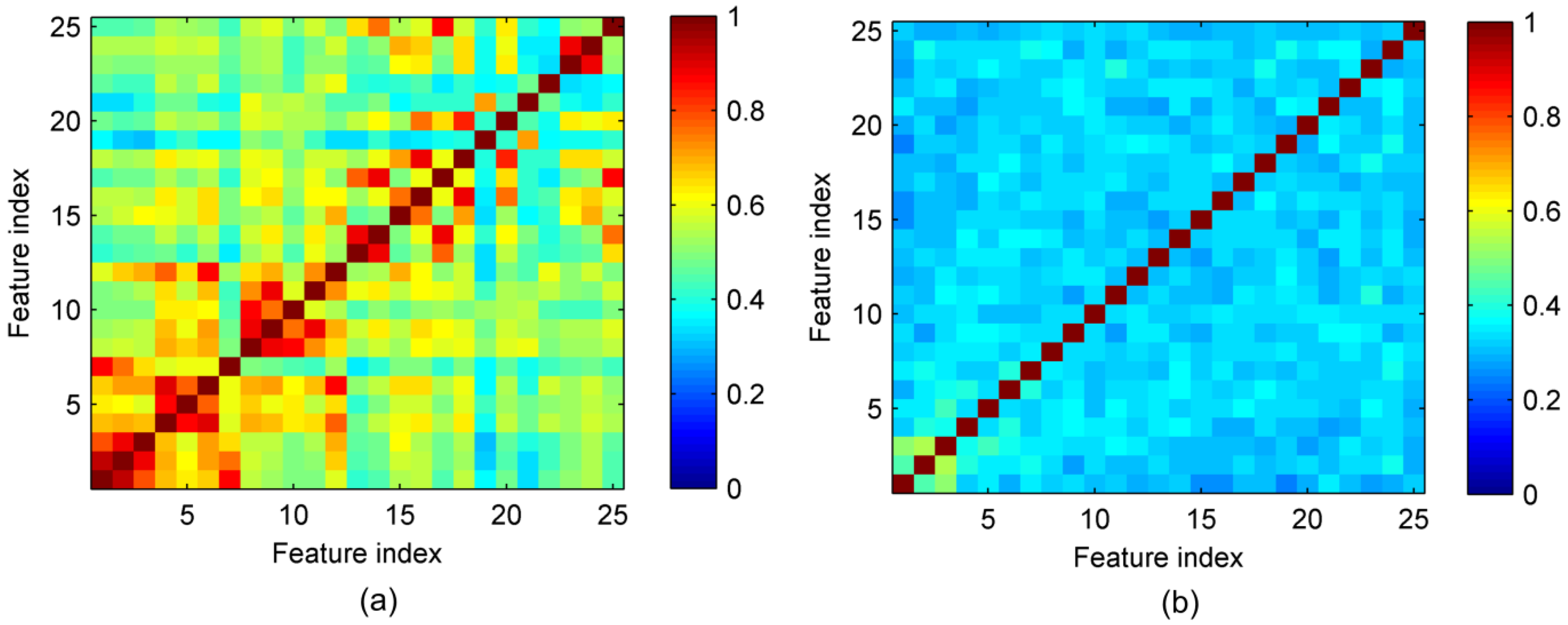
2.4. Feature Fusion
2.4.1. Mutual Information
2.4.2. PCA
3. Data and Experiment
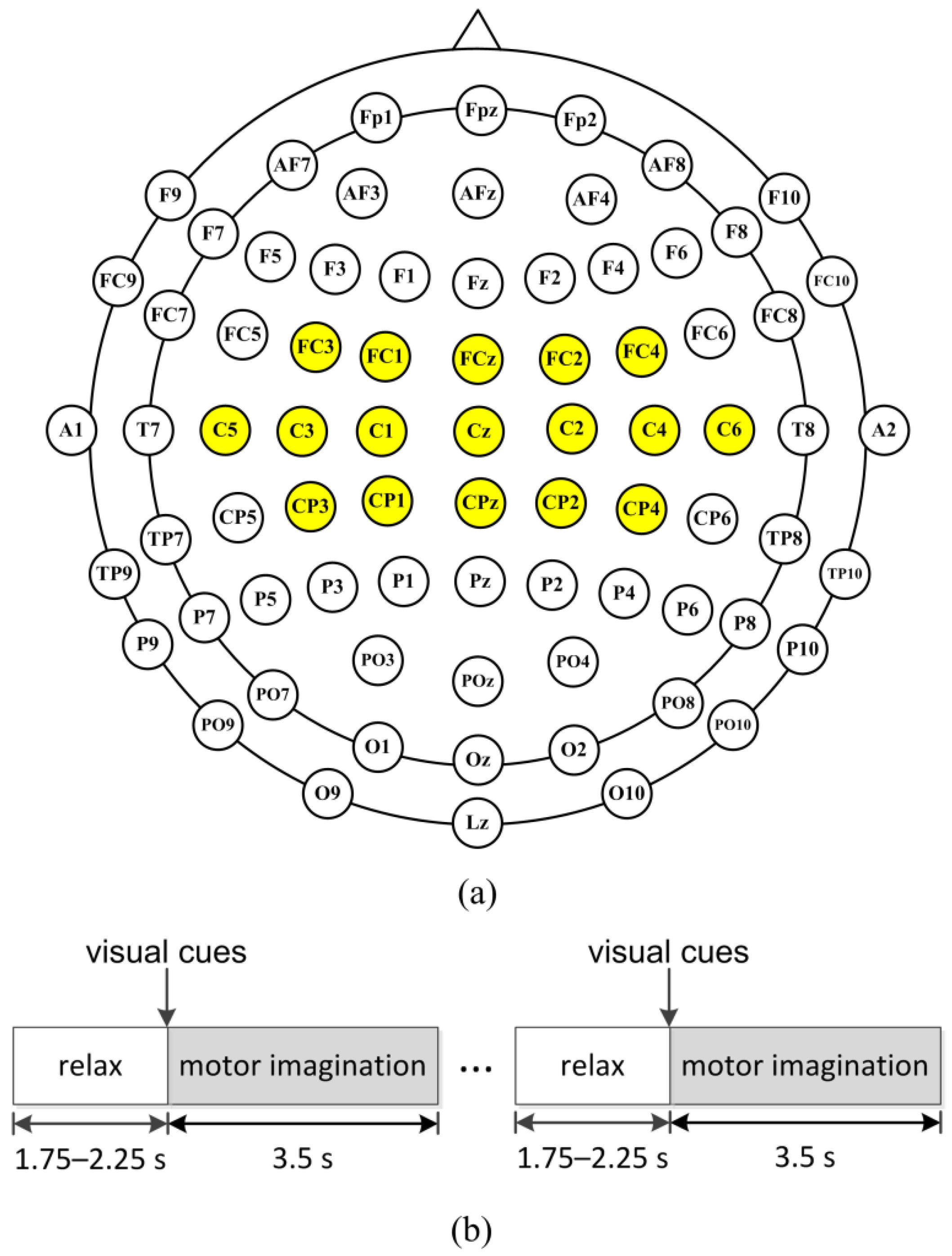
3.1. Public EEG Dataset
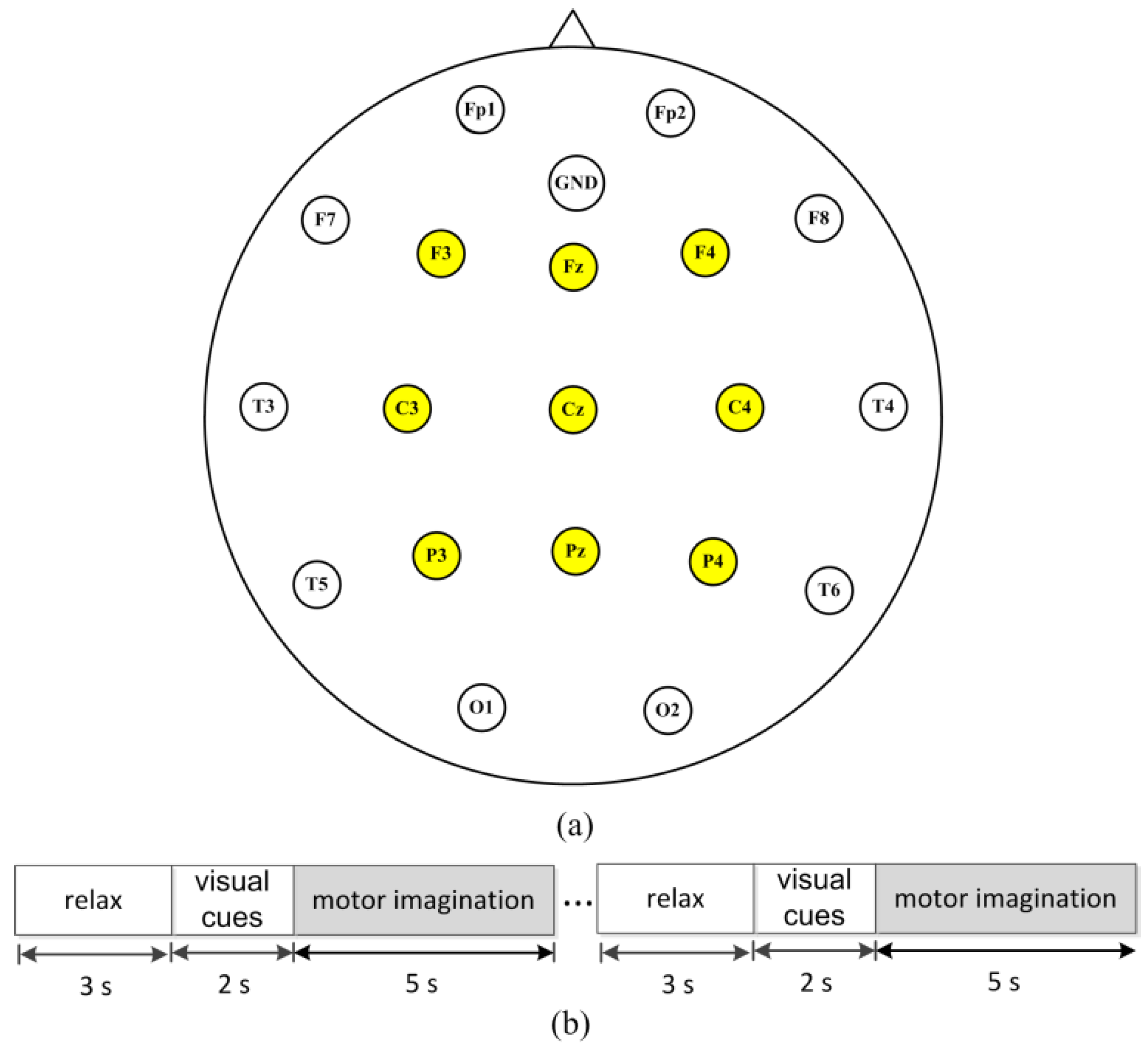
3.2. Experimental EEG Dataset
4. Results and Discussion
4.1. Results and Discussion of Public EEG Dataset
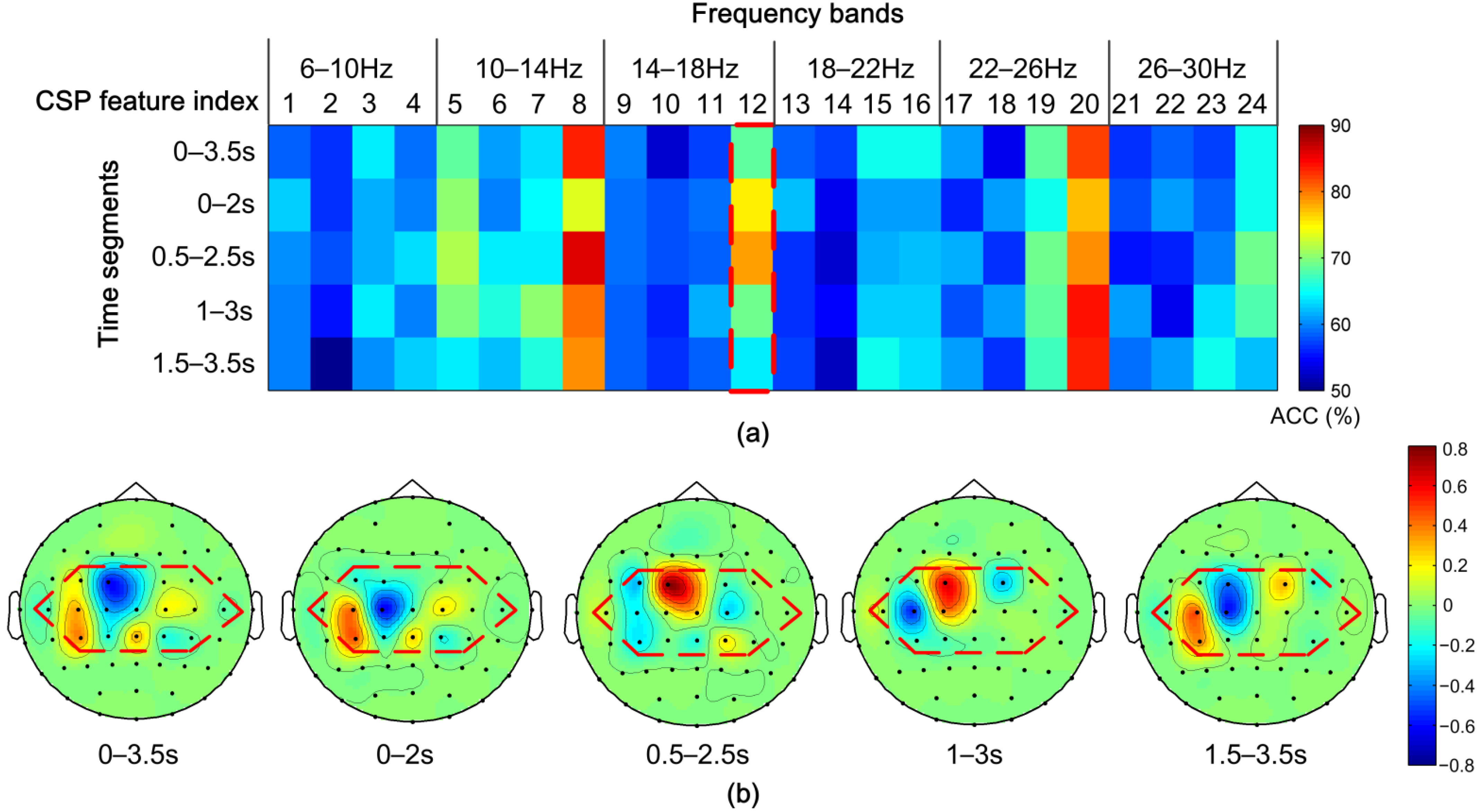
4.1.1. Discriminative Frequency Sub-Band Features
4.1.2. The Performance of Time Segmentation
4.1.3. The Effect of Feature Selection by MIBIF
4.1.4. The Effect of Dimensionality Reduction by PCA
4.1.5. Comparison with Other Competing Techniques
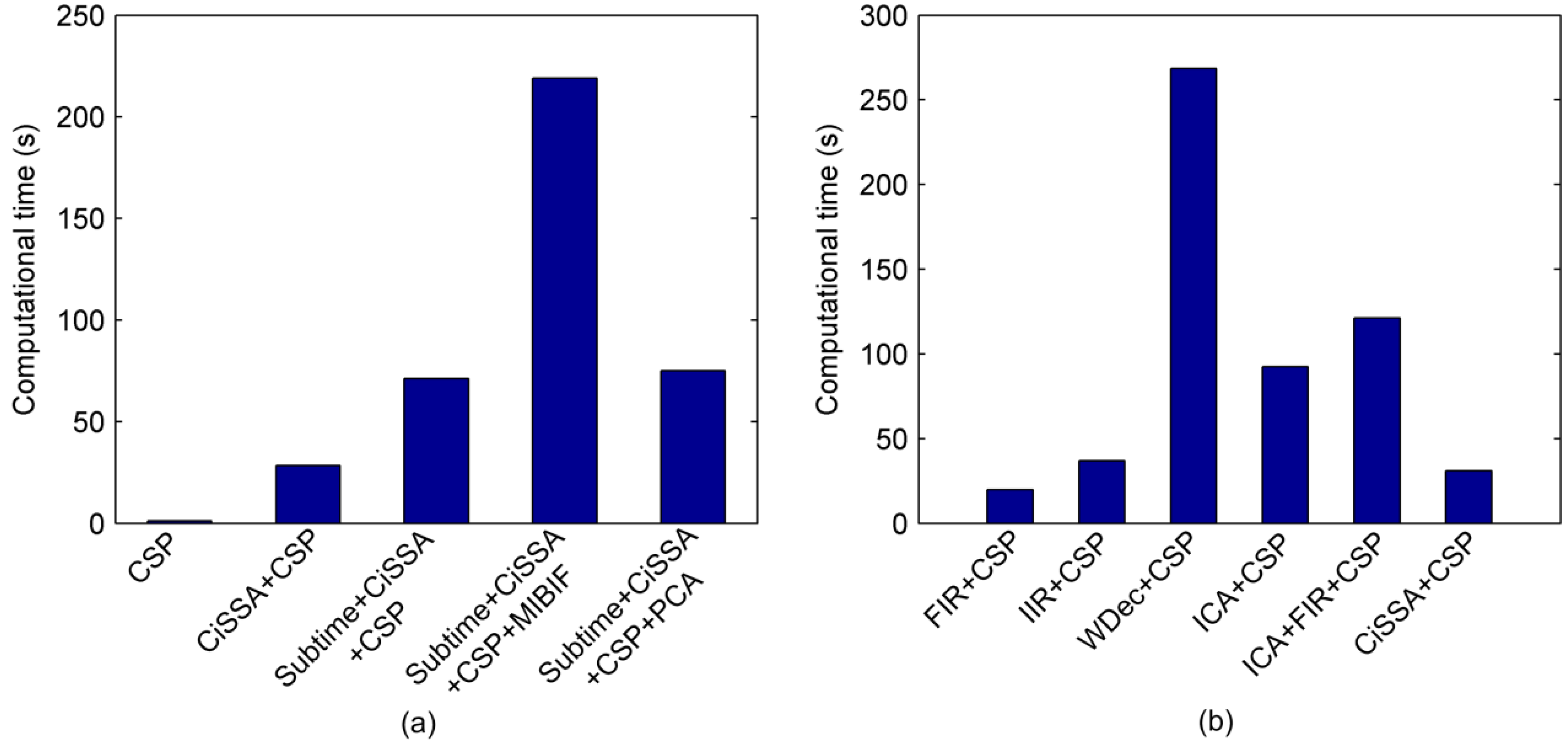
4.1.6. Computational Complexity
4.2. Results and Discussion of Experimental EEG Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Olivas-Padilla, B.E.; Chacon-Murguia, M.I. Classification of multiple motor imagery using deep convolutional neural networks and spatial filters. Appl. Soft Comput. 2019, 75, 461–472. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, Y.; Yin, E.; Jiang, J.; Zhou, Z.; Hu, D. An asynchronous hybrid spelling approach based on EEG–EOG signals for Chinese character input. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1292–1302. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Zhou, Z.; Yin, E.; Jiang, J.; Tang, J.; Liu, Y.; Hu, D. Toward brain-actuated car applications: Self-paced control with a motor imagery-based brain-computer interface. Comput. Biol. Med. 2016, 77, 148–155. [Google Scholar] [CrossRef]
- Chai, R.; Naik, G.R.; Nguyen, T.N.; Ling, S.H.; Tran, Y.; Craig, A.; Nguyen, H.T. Driver fatigue classification with independent component by entropy rate bound minimization analysis in an EEG-based system. IEEE J. Biomed. Health Inform. 2016, 21, 715–724. [Google Scholar] [CrossRef]
- Scherer, R.; Schloegl, A.; Lee, F.; Bischof, H.; Janša, J.; Pfurtscheller, G. The self-paced graz brain-computer interface: Methods and applications. Comput. Intell. Neurosci. 2007, 2007, 79826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miao, Y.; Jin, J.; Daly, I.; Zuo, C.; Wang, X.; Cichocki, A.; Jung, T.-P. Learning common time-frequency-spatial patterns for motor imagery classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 699–707. [Google Scholar] [CrossRef]
- Clerc, M. Brain Computer Interfaces, Principles and Practise. Biomed. Eng. Online 2013, 12, 1–4. [Google Scholar]
- Yang, Y.; Chevallier, S.; Wiart, J.; Bloch, I. Subject-specific time-frequency selection for multi-class motor imagery-based BCIs using few Laplacian EEG channels. Biomed. Signal Process. Control. 2017, 38, 302–311. [Google Scholar] [CrossRef]
- Ramoser, H.; Muller-Gerking, J.; Pfurtscheller, G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabil. Eng. 2000, 8, 441–446. [Google Scholar] [CrossRef] [Green Version]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Mutual information-based selection of optimal spatial–temporal patterns for single-trial EEG-based BCIs. Pattern Recognit. 2012, 45, 2137–2144. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Jin, J.; Wang, X. Sparse Bayesian learning for obtaining sparsity of EEG frequency bands based feature vectors in motor imagery classification. Int. J. Neural Syst. 2017, 27, 1650032. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Nam, C.S.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Temporally constrained sparse group spatial patterns for motor imagery BCI. IEEE Trans. Cybern. 2018, 49, 3322–3332. [Google Scholar] [CrossRef] [PubMed]
- Novi, Q.; Guan, C.; Dat, T.H.; Xue, P. Sub-Band Common Spatial Pattern (SBCSP) for Brain-Computer Interface. In Proceedings of the 2007 3rd International IEEE/EMBS Conference on Neural Engineering, Kohala Coast, HI, USA, 2–5 May 2007; pp. 204–207. [Google Scholar]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter Bank Common Spatial Pattern (FBCSP) in Brain-Computer Interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 2390–2397. [Google Scholar]
- Thomas, K.P.; Guan, C.; Tong, L.C.; Vinod, A.P. Discriminative FilterBank Selection and EEG Information Fusion for Brain Computer Interface. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 1469–1472. [Google Scholar]
- Zhang, Y.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Optimizing spatial patterns with sparse filter bands for motor-imagery based brain–computer interface. J. Neurosci. Methods 2015, 255, 85–91. [Google Scholar] [CrossRef]
- Hu, H.; Guo, S.; Liu, R.; Wang, P. An adaptive singular spectrum analysis method for extracting brain rhythms of electroencephalography. PeerJ 2017, 5, e3474. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.; Xiao, R.; Daly, I.; Miao, Y.; Wang, X.; Cichocki, A. Internal feature selection method of CSP based on L1-norm and Dempster–Shafer theory. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4814–4825. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Zhang, H.; Khan, M.S.; Mi, F. A self-adaptive frequency selection common spatial pattern and least squares twin support vector machine for motor imagery electroencephalography recognition. Biomed. Signal Process. Control. 2018, 41, 222–232. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, A. A new parameter tuning approach for enhanced motor imagery EEG signal classification. Med. Biol. Eng. Comput. 2018, 56, 1861–1874. [Google Scholar] [CrossRef] [Green Version]
- Malan, N.; Sharma, S. Motor imagery EEG spectral-spatial feature optimization using dual-tree complex wavelet and neighbourhood component analysis. IRBM 2022, 43, 198–209. [Google Scholar] [CrossRef]
- Higashi, H.; Tanaka, T. Common spatio-time-frequency patterns for motor imagery-based brain machine interfaces. Comput. Intell. Neurosci. 2013, 2013, 537218. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Feng, Z.; Ren, X.; Lu, N.; Luo, J.; Sun, L. Feature subset and time segment selection for the classification of EEG data based motor imagery. Biomed. Signal Process. Control. 2020, 61, 102026. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, J.; Xu, R.; Miao, Y.; Liu, C.; Cichocki, A. Multi-view optimization of time-frequency common spatial patterns for brain-computer interfaces. J. Neurosci. Methods 2022, 365, 109378. [Google Scholar] [CrossRef] [PubMed]
- Kirar, J.S.; Agrawal, R. Relevant feature selection from a combination of spectral-temporal and spatial features for classification of motor imagery EEG. J. Med. Syst. 2018, 42, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Wang, Z.; Xu, R.; Liu, C.; Wang, X.; Cichocki, A. Robust similarity measurement based on a novel time filter for SSVEPs detection. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Pei, Y.; Sheng, T.; Luo, Z.; Xie, L.; Li, W.; Yan, Y.; Yin, E. A Tensor-Based Frequency Features Combination Method for Brain–Computer Interfaces. In International Conference on Cognitive Systems and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 511–526. [Google Scholar]
- Kumar, S.; Sharma, A.; Tsunoda, T. An improved discriminative filter bank selection approach for motor imagery EEG signal classification using mutual information. BMC Bioinform. 2017, 18, 125–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, D.A.A.G.; Leavline, E.J. Dimensionality Reduction for Classification and Clustering. Int. J. Intell. Syst. Appl. 2019, 11, 61–68. [Google Scholar]
- Bógalo, J.; Poncela, P.; Senra, E. Circulant Singular Spectrum Analysis: A new automated procedure for signal extraction. Signal Process. 2021, 179, 107824. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and Circulant Matrices: A review. Found. Trends Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Physica D 1992, 158, 95–126. [Google Scholar] [CrossRef]
- Xu, S.; Hu, H.; Ji, L.; Peng, W. Embedding Dimension Selection for Adaptive Singular Spectrum Analysis of EEG Signal. Sensors 2018, 18, 697. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-H.; Lee, D.; Lee, S.-G. Filter bank regularized common spatial pattern ensemble for small sample motor imagery classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 26, 498–505. [Google Scholar] [CrossRef]
- Ince, N.F.; Goksu, F.; Tewfik, A.H.; Arica, S. Adapting subject specific motor imagery EEG patterns in space–time–frequency for a brain computer interface. Biomed. Signal Process. Control. 2009, 4, 236–246. [Google Scholar] [CrossRef]
- Park, S.-H.; Lee, S.-G. Small sample setting and frequency band selection problem solving using subband regularized common spatial pattern. IEEE Sens. J. 2017, 17, 2977–2983. [Google Scholar] [CrossRef]
- Li, Y.; Wen, P.P. Modified CC-LR algorithm with three diverse feature sets for motor imagery tasks classification in EEG based brain–computer interface. Comput. Methods Programs Biomed. 2014, 113, 767–780. [Google Scholar]
- Ke, L.; Shen, J. Classification of EEG signals by ICA and OVR-CSP. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 2980–2984. [Google Scholar]
- Miao, M.; Zeng, H.; Wang, A.; Zhao, C.; Liu, F. Discriminative spatial-frequency-temporal feature extraction and classification of motor imagery EEG: A sparse regression and Weighted Naïve Bayesian Classifier-based approach. J. Neurosci. Methods 2017, 278, 13–24. [Google Scholar] [CrossRef]
- Higashi, H.; Tanaka, T. Simultaneous design of FIR filter banks and spatial patterns for EEG signal classification. IEEE Trans. Biomed. Eng. 2012, 60, 1100. [Google Scholar] [CrossRef]
- Wu, W.; Gao, X.; Hong, B.; Gao, S. Classifying single-trial EEG during motor imagery by iterative spatio-spectral patterns learning (ISSPL). IEEE Trans. Biomed. Eng. 2008, 55, 1733–1743. [Google Scholar] [CrossRef]


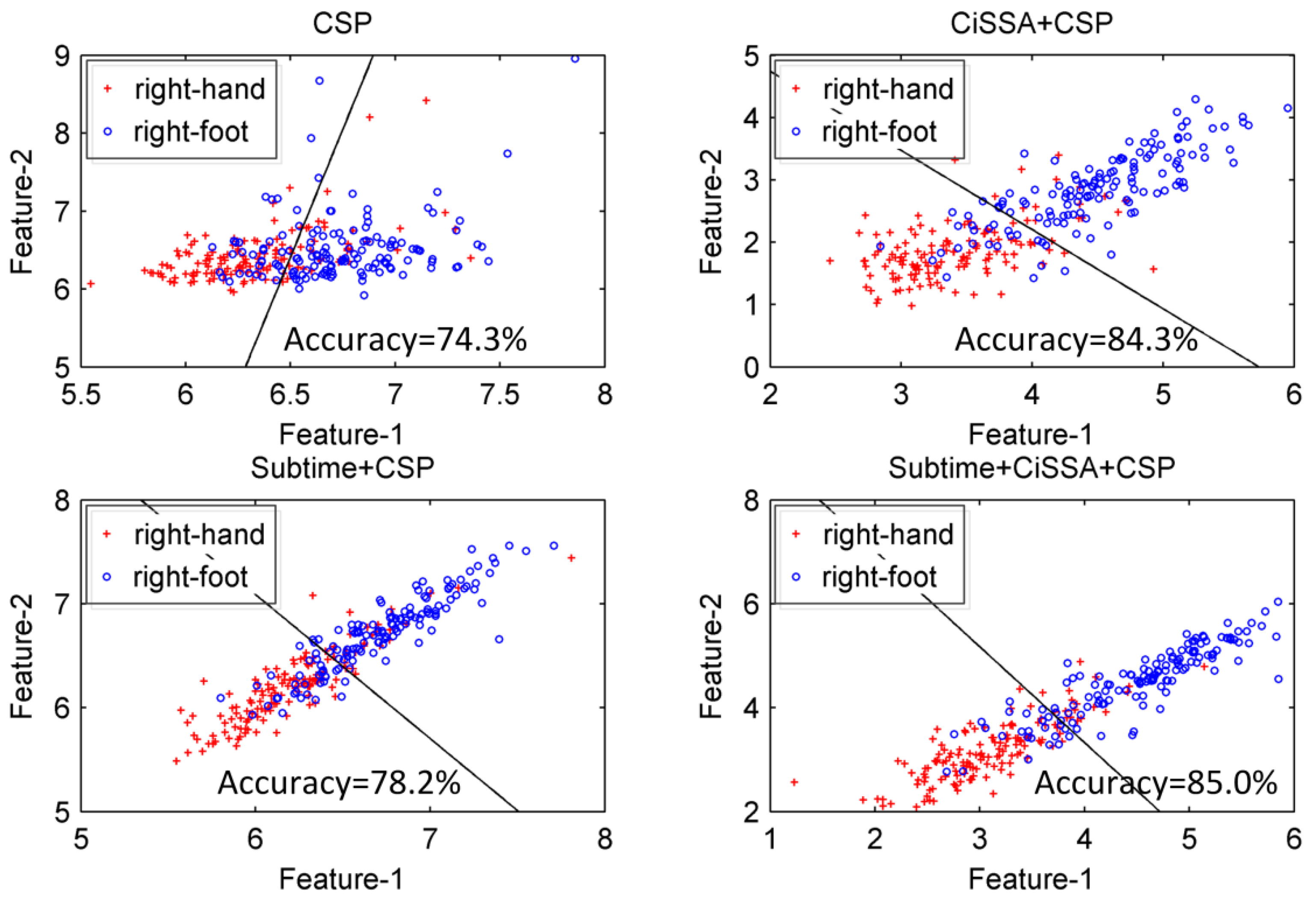


| Method | Classification Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| aa | al | av | aw | ay | Average | |
| CSP | 78.6 ± 11.4 | 96.4 ± 3.8 | 69.6 ± 10.7 | 75.0 ± 6.3 | 88.6 ± 5.0 | 81.6 ± 7.4 |
| CiSSA + CSP | 94.3 ± 5.9 | 98.2 ± 3.5 | 78.6 ± 6.5 | 98.2 ± 2.5 | 92.4 ± 4.1 | 92.3 ± 4.5 |
| Subtime + CiSSA + CSP | 98.6 ± 1.8 | 99.3 ± 1.5 | 83.2 ± 6.1 | 97.9 ± 3.0 | 95.7 ± 2.8 | 94.9 ± 3.0 |
| Subtime + CiSSA + CSP + MIBIF | 94.3 ± 6.6 | 98.2 ± 1.9 | 79.6 ± 7.4 | 98.2 ± 2.5 | 97.9 ± 3.8 | 93.6 ± 4.4 |
| Subtime + CiSSA + CSP + PCA | 98.2 ± 3.0 | 99.3 ± 1.5 | 87.5 ± 7.6 | 100 ± 0 | 97.1 ± 2.8 | 96.4 ± 3.0 |
| Method | Classification Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| aa | al | av | aw | ay | Average | |
| FIR + CSP | 85.7 ± 8.8 | 95.4 ± 3.8 | 78.6 ± 8.8 | 97.1 ± 2.3 | 93.2 ± 4.6 | 90.0 ± 5.7 |
| IIR + CSP | 87.1 ± 9.9 | 93.9 ± 4.1 | 76.8 ± 12.3 | 97.9 ± 3.0 | 91.4 ± 4.5 | 89.4 ± 6.8 |
| WDec + CSP | 93.9 ± 8.4 | 96.8 ± 3.6 | 72.6 ± 10.4 | 97.9 ± 3.8 | 90.7 ± 4.2 | 90.4 ± 6.1 |
| ICA + CSP | 81.1 ± 6.5 | 95.0 ± 5.1 | 71.1 ± 10.0 | 77.5 ± 6.1 | 94.3 ± 3.5 | 83.6 ± 6.2 |
| ICA + FIR + CSP | 90.4 ± 8.1 | 93.6 ± 2.8 | 81.1 ± 7.7 | 94.3 ± 3.8 | 95.7 ± 2.3 | 91.0 ± 4.9 |
| CiSSA + CSP | 94.3 ± 5.9 | 98.2 ± 3.5 | 78.6 ± 6.5 | 98.2 ± 2.5 | 92.4 ± 4.1 | 92.3 ± 4.5 |
| Bandwidth (Hz) | L | Classification Accuracy (%) | |||||
|---|---|---|---|---|---|---|---|
| aa | al | av | aw | ay | Average | ||
| 1 | 100 | 93.5 ± 4.1 | 98.2 ± 2.5 | 84.3 ± 7.3 | 91.0 ± 4.8 | 94.1 ± 4.7 | 92.2 ± 4.7 |
| 2 | 50 | 88.3 ± 6.6 | 97.4 ± 2.3 | 79.6 ± 6.7 | 96.4 ± 2.8 | 92.3 ± 6.3 | 90.8 ± 4.9 |
| 4 | 25 | 94.3 ± 5.9 | 98.2 ± 3.5 | 78.6 ± 6.5 | 98.2 ± 2.5 | 92.4 ± 4.1 | 92.3 ± 4.5 |
| 6 | 16 | 90.7 ± 6.1 | 97.5 ± 2.9 | 78.9 ± 11.0 | 97.1 ± 2.8 | 94.3 ± 4.8 | 91.7 ± 5.5 |
| 8 | 12 | 88.6 ± 9.3 | 98.6 ± 1.8 | 73.6 ± 9.7 | 92.9 ± 4.8 | 92.5 ± 3.9 | 89.2 ± 5.9 |
| Time-Window Length (s) | Classification Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| aa | al | av | aw | ay | Average | |
| 1 | 98.3 ± 2.4 | 100 | 79.9 ± 3.8 | 96.1 ± 1.7 | 94.3 ± 2.4 | 93.7 ± 2.1 |
| 1.5 | 96.5 ± 2.5 | 99.6 ± 1.1 | 85.3 ± 5.4 | 97.6 ± 1.1 | 94.3 ± 1.5 | 94.7 ± 2.3 |
| 2 | 98.6 ± 1.8 | 99.3 ± 1.5 | 83.2 ± 6.1 | 97.9 ± 3.0 | 95.7 ± 2.8 | 94.9 ± 3.0 |
| 2.5 | 96.8 ± 2.6 | 99.0 ± 1.1 | 82.5 ± 8.0 | 97.9 ± 3.0 | 91.1 ± 5.1 | 93.5 ± 4.0 |
| 3 | 97.1 ± 2.8 | 99.0 ± 1.5 | 81.1 ± 6.1 | 97.5 ± 3.4 | 92.9 ± 6.1 | 93.5 ± 4.0 |
| Subject | MIBIF | PCA | ||
|---|---|---|---|---|
| Accuracy (%) | Dimension (k) | Accuracy (%) | Dimension (k) | |
| aa | 98.6 ± 1.8 | 57 | 98.2 ± 2.5 | 5 |
| al | 99.6 ± 1.1 | 28 | 99.6 ± 1.1 | 11 |
| av | 85.7 ± 7.9 | 25 | 87.9 ± 6.8 | 12 |
| aw | 99.6 ± 1.1 | 10 | 100 | 9 |
| ay | 97.9 ± 3.8 | 8 | 97.5 ± 4.7 | 16 |
| Average | 96.3 ± 3.1 | 96.6 ± 3.0 | ||
| Method | Classification Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| aa | al | av | aw | ay | Average | |
| FBCSP [14] | 83.6 | 94.6 | 51.4 | 93.9 | 88.2 | 82.4 |
| CTFSP [6] | 86.1 | 98.6 | 52.1 | 96.1 | 92.1 | 85.0 |
| Fusion [18] | 80.0 | 96.8 | 70.0 | 92.5 | 91.1 | 86.1 |
| TWFBCSP-MVO [24] | 89.6 | 99.3 | 69.3 | 96.1 | 92.1 | 89.3 |
| SFBCSP [16] | 91.5 | 98.6 | 77.4 | 98.0 | 94.7 | 92.0 |
| STFSCSP [39] | 92.5 | 98.6 | 79.4 | 97.8 | 95.0 | 92.7 |
| DFBCSP [40] | 92.3 | 99.3 | 78.1 | 99.3 | 95.1 | 92.8 |
| CC-LR [37] | 100 | 94.2 | 100 | 100 | 75.3 | 93.9 |
| ISSPL [41] | 93.6 | 100 | 79.3 | 99.6 | 98.6 | 94.2 |
| Class Separability [35] | 95.6 | 99.7 | 90.5 | 98.4 | 95.7 | 96.0 |
| Our method (MIBIF) | 98.6 | 99.6 | 85.7 | 99.6 | 97.9 | 96.3 |
| Our method (PCA) | 98.2 | 99.6 | 87.9 | 100 | 97.5 | 96.6 |
| Methods | Testing Time (ms) |
|---|---|
| FBCSP | 78.8 |
| CTFSP | 143.2 |
| DFBCSP | 146.6 |
| Fusion | 23.4 |
| STFSCSP | 45.2 |
| Class Separability | 72.6 |
| Our method (MIBIF) | 156.4 |
| Our method (PCA) | 156.7 |
| Subject | Classification Accuracy (%) | ||||
|---|---|---|---|---|---|
| CSP | CiSSA + CSP | Subtime + CiSSA +CSP | Subtime + CiSSA +CSP + MIBIF | Subtime + CiSSA +CSP + PCA | |
| S1 | 70.4 ± 6.1 | 97.5 ± 2.9 | 96.4 ± 4.1 | 93.6 ± 5.0 | 95.4 ± 4.5 |
| S2 | 68.2 ± 10.6 | 87.5 ± 5.1 | 91.4 ± 3.0 | 86.1 ± 6.4 | 91.8 ± 3.8 |
| S3 | 61.8 ± 11.9 | 95.4 ± 2.4 | 95.4 ± 4.1 | 95.0 ± 4.2 | 97.9 ± 2.5 |
| S4 | 66.8 ± 9.4 | 85.7 ± 7.5 | 88.9 ± 3.9 | 88.9 ± 6.8 | 91.8 ± 5.8 |
| S5 | 76.1 ± 14.8 | 88.6 ± 6.9 | 87.1 ± 10.1 | 87.1 ± 13.7 | 90.4 ± 11.3 |
| S6 | 51.4 ± 10.3 | 80.8 ± 10.1 | 85.0 ± 9.0 | 77.1 ± 15.7 | 86.8 ± 10.7 |
| S7 | 61.1 ± 6.2 | 77.1 ± 7.6 | 86.1 ± 8.2 | 78.6 ± 6.9 | 89.6 ± 7.8 |
| S8 | 73.6 ± 6.1 | 90.0 ± 5.8 | 87.9 ± 6.1 | 92.5 ± 4.9 | 87.9 ± 7.8 |
| S9 | 77.9 ± 7.1 | 93.2 ± 4.9 | 95.0 ± 4.8 | 91.4 ± 7.4 | 96.8 ± 4.3 |
| S10 | 88.6 ± 9.0 | 92.9 ± 5.3 | 91.8 ± 5.8 | 90.7 ± 8.3 | 93.9 ± 5.8 |
| S11 | 85.0 ± 6.0 | 92.1 ± 6.7 | 90.7 ± 5.1 | 91.8 ± 5.1 | 94.3 ± 4.5 |
| S12 | 89.3 ± 7.7 | 93.6 ± 5.5 | 95.7 ± 4.4 | 90.7 ± 5.9 | 95.4 ± 4.1 |
| S13 | 77.5 ± 11.2 | 91.1 ± 6.6 | 93.6 ± 5.5 | 90.4 ± 8.6 | 95.7 ± 6.0 |
| S14 | 87.9 ± 4.8 | 90.0 ± 2.8 | 95.4 ± 3.4 | 91.8 ± 3.8 | 93.9 ± 5.1 |
| S15 | 82.9 ± 5.8 | 95.7 ± 5.3 | 93.6 ± 5.0 | 90.0 ± 5.3 | 94.6 ± 3.0 |
| S16 | 75.7 ± 9.6 | 92.9 ± 5.3 | 93.9 ± 4.1 | 92.5 ± 3.9 | 97.9 ± 3.8 |
| S17 | 73.9 ± 7.0 | 92.1 ± 5.3 | 97.1 ± 2.8 | 92.5 ± 6.6 | 97.1 ± 3.8 |
| S18 | 83.6 ± 5.4 | 85.7 ± 7.5 | 92.1 ± 6.3 | 91.1 ± 4.8 | 92.5 ± 4.3 |
| S19 | 63.6 ± 12.5 | 91.1 ± 7.4 | 93.6 ± 4.4 | 88.2 ± 9.4 | 95.7 ± 7.1 |
| S20 | 79.3 ± 4.7 | 95.4 ± 3.8 | 95.7 ± 6.0 | 95.0 ± 5.9 | 97.9 ± 3.5 |
| Average | 74.7 ± 8.3 | 90.4 ± 5.7 | 92.3 ± 5.3 | 89.8 ± 6.8 | 93.9 ± 5.5 |
| CSP | CiSSA + CSP | Subtime + CiSSA +CSP | Subtime + CiSSA +CSP + MIBIF | Subtime + CiSSA +CSP + PCA | |
|---|---|---|---|---|---|
| p-value | - | 0.0000 | 0.0018 | 0.0006 | 0.0001 |
| Subject | MIBIF | PCA | ||
|---|---|---|---|---|
| Accuracy (%) | Dimension (k) | Accuracy (%) | Dimension (k) | |
| S1 | 97.5 ± 4.5 | 39 | 98.6 ± 2.5 | 17 |
| S2 | 91.8 ± 4.5 | 15 | 93.2 ± 3.1 | 11 |
| S3 | 97.1 ± 3.7 | 32 | 98.2 ± 2.5 | 8 |
| S4 | 90.4 ± 6.3 | 17 | 93.9 ± 4.5 | 3 |
| S5 | 88.2 ± 10.5 | 55 | 91.8 ± 11.6 | 7 |
| S6 | 85.4 ± 11.1 | 69 | 90.0 ± 6.3 | 28 |
| S7 | 87.9 ± 7.9 | 28 | 90.7 ± 5.4 | 14 |
| S8 | 92.5 ± 4.9 | 9 | 92.9 ± 5.6 | 23 |
| S9 | 95.4 ± 5.1 | 67 | 98.2 ± 2.5 | 15 |
| S10 | 92.5 ± 6.2 | 11 | 95.0 ± 5.4 | 11 |
| S11 | 93.9 ± 4.5 | 5 | 94.6 ± 4.5 | 14 |
| S12 | 96.8 ± 3.6 | 47 | 96.4 ± 3.8 | 8 |
| S13 | 94.3 ± 6.3 | 17 | 95.7 ± 6.0 | 9 |
| S14 | 96.1 ± 4.9 | 63 | 95.4 ± 3.4 | 62 |
| S15 | 95.7 ± 5.5 | 30 | 96.8 ± 3.6 | 14 |
| S16 | 94.6 ± 4.2 | 45 | 97.9 ± 3.8 | 9 |
| S17 | 97.5 ± 2.4 | 60 | 97.5 ± 2.9 | 13 |
| S18 | 93.6 ± 4.1 | 24 | 93.6 ± 5.5 | 19 |
| S19 | 95.0 ± 3.5 | 23 | 95.7 ± 7.1 | 9 |
| S20 | 98.6 ± 3.0 | 36 | 98.6 ± 3.5 | 15 |
| Average | 93.7 ± 5.3 | 95.2 ± 4.7 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Pu, Z.; Li, H.; Liu, Z.; Wang, P. Learning Optimal Time-Frequency-Spatial Features by the CiSSA-CSP Method for Motor Imagery EEG Classification. Sensors 2022, 22, 8526. https://doi.org/10.3390/s22218526
Hu H, Pu Z, Li H, Liu Z, Wang P. Learning Optimal Time-Frequency-Spatial Features by the CiSSA-CSP Method for Motor Imagery EEG Classification. Sensors. 2022; 22(21):8526. https://doi.org/10.3390/s22218526
Chicago/Turabian StyleHu, Hai, Zihang Pu, Haohan Li, Zhexian Liu, and Peng Wang. 2022. "Learning Optimal Time-Frequency-Spatial Features by the CiSSA-CSP Method for Motor Imagery EEG Classification" Sensors 22, no. 21: 8526. https://doi.org/10.3390/s22218526
APA StyleHu, H., Pu, Z., Li, H., Liu, Z., & Wang, P. (2022). Learning Optimal Time-Frequency-Spatial Features by the CiSSA-CSP Method for Motor Imagery EEG Classification. Sensors, 22(21), 8526. https://doi.org/10.3390/s22218526






