An Improved Split-Ring Resonator-Based Sensor for Microfluidic Applications
Abstract
:1. Introduction
2. Working Principle and Sensor Design
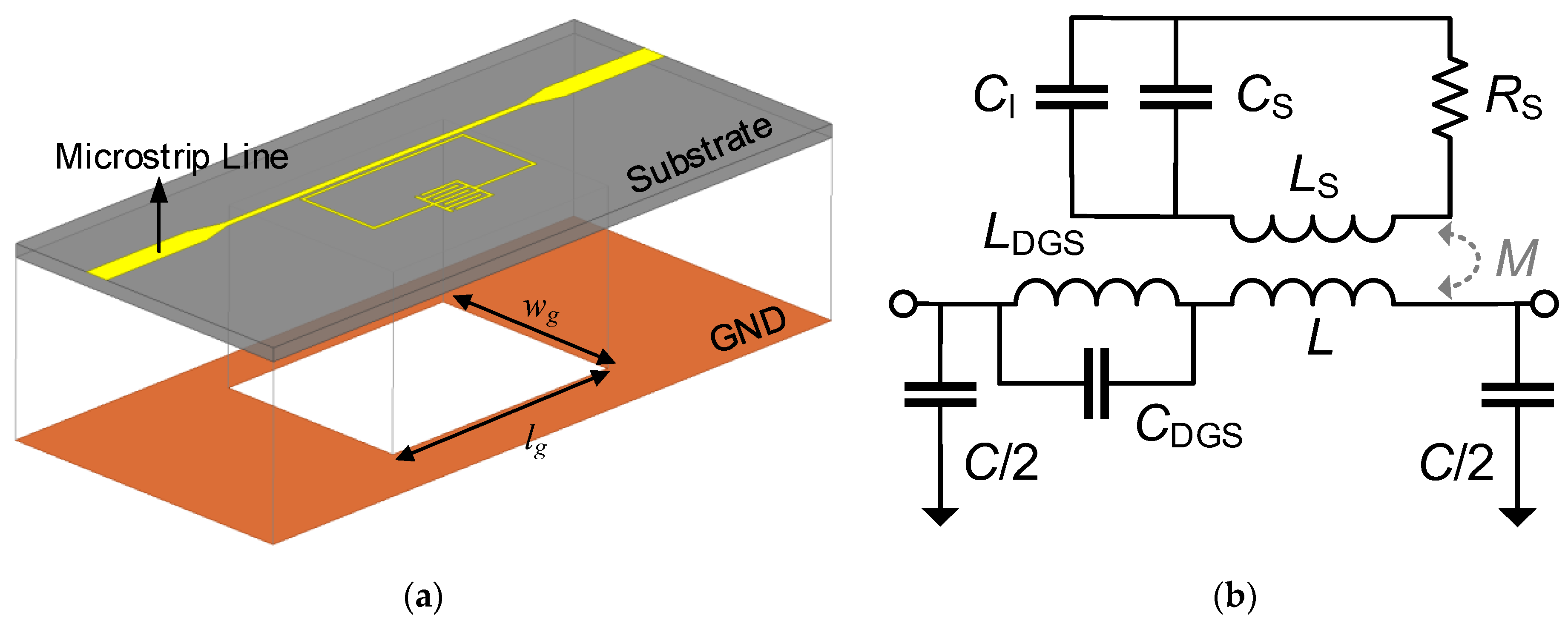
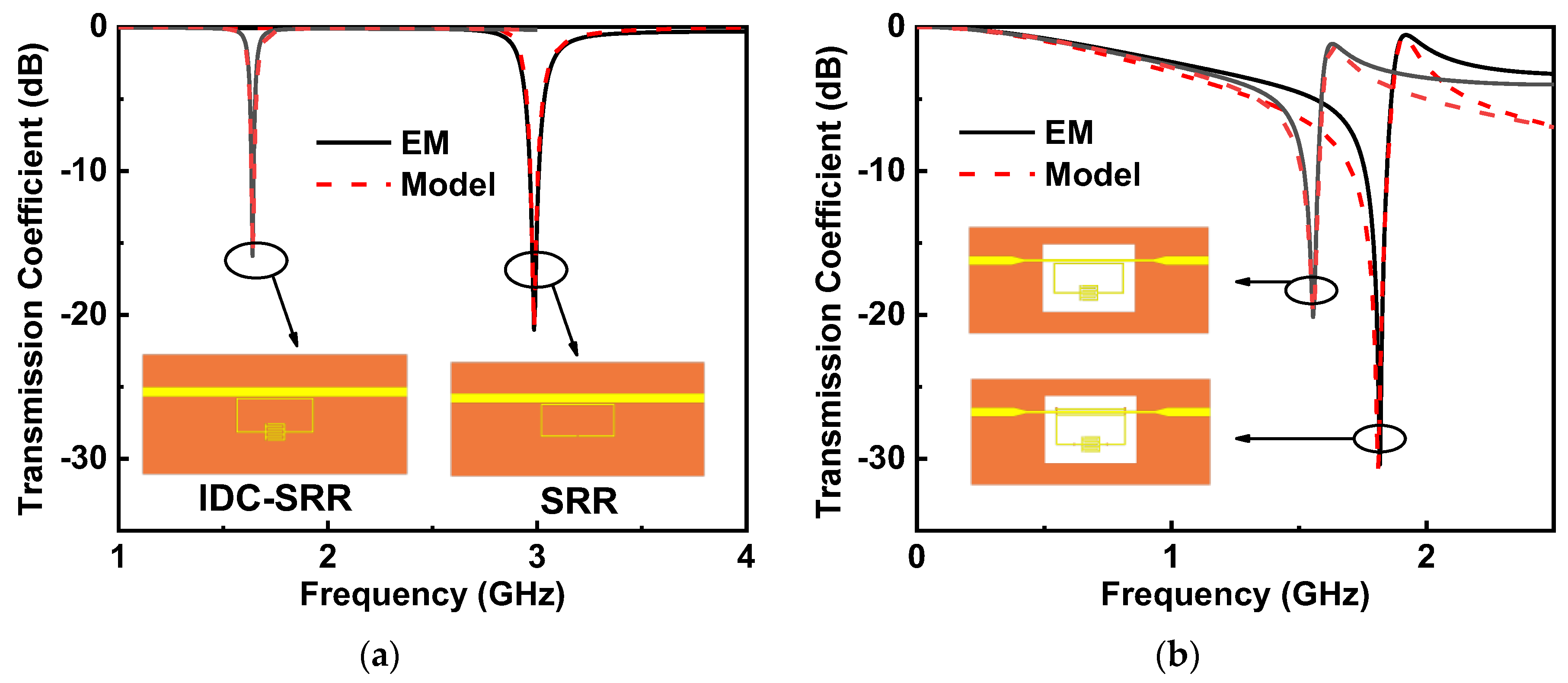
2.1. IDC-SRR-Based Sensor
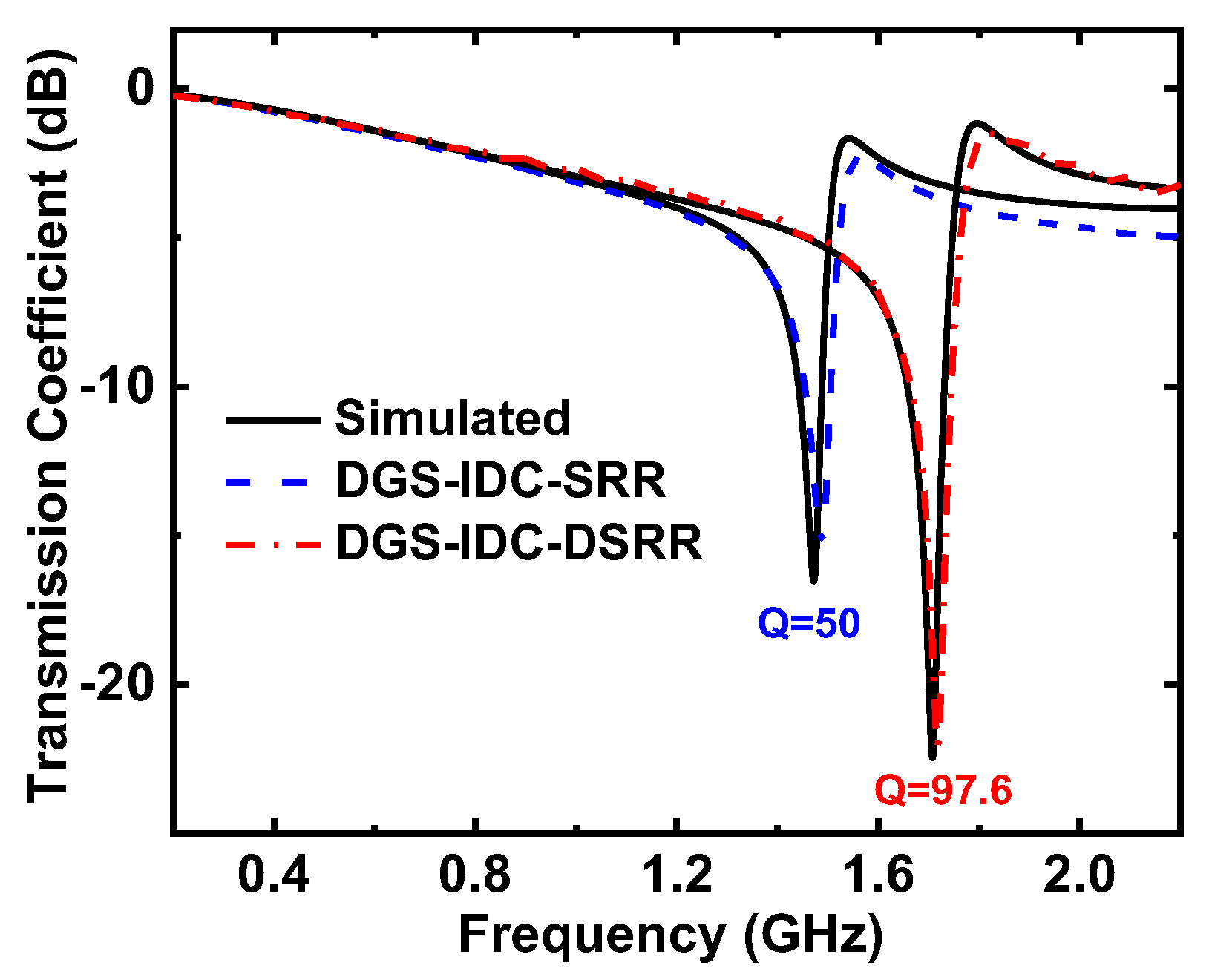
2.2. DGS-IDC-SRR-Based Sensor
2.3. DGS-IDC-DSRR-Based Sensor
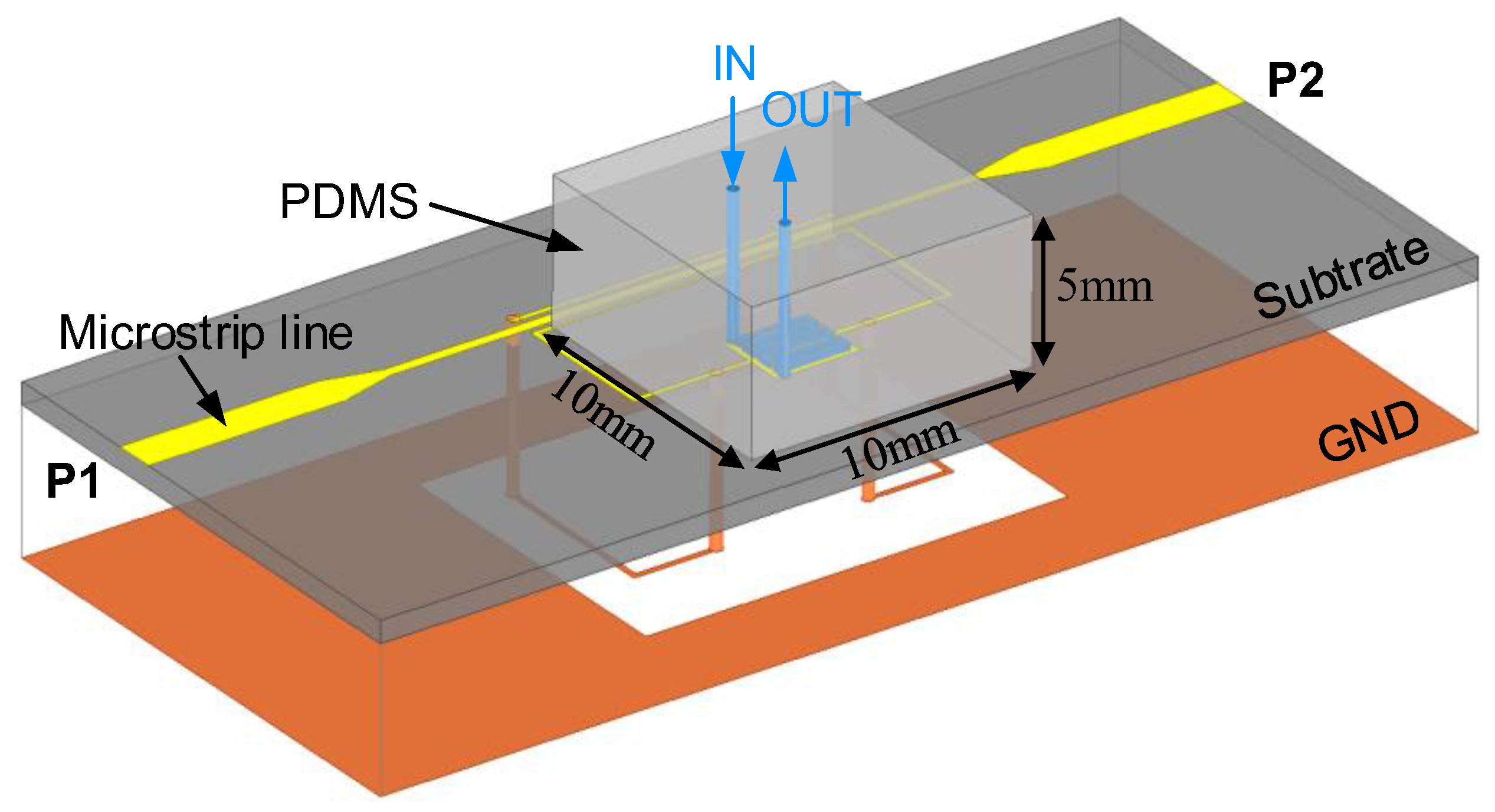
3. Experimental Validation
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Mayani, M.G.; Herraiz-Martínez, F.J.; Domingo, J.M.; Giannetti, R. Resonator-based microwave metamaterial sensors for instrumentation: Survey, classification, and performance comparison. IEEE Trans. Instrum. Meas. 2021, 70, 9503414. [Google Scholar] [CrossRef]
- Zhu, P.-W.; Wang, X.; Zhao, W.-S.; Wang, J.; Wang, D.-W.; Hou, F.; Wang, G. Design of H-shaped planar displacement microwave sensors with wide dynamic range. Sens. Actuators A Phys. 2021, 333, 113311. [Google Scholar] [CrossRef]
- Gil, M.; Vélez, P.; Aznar-Ballesta, F.; Muñoz-Enano, J.; Martín, F. Differential sensor based on electroinductive wave transmission lines for dielectric constant measurements and defect detection. IEEE Trans. Antennas Propag. 2020, 68, 1876–1886. [Google Scholar] [CrossRef]
- Adhikari, K.K.; Kim, N. Ultrahigh-Sensitivity mediator-free biosensor based on a microfabricated microwave resonator for the detection of micromolar glucose concentrations. IEEE Trans. Microw. Theory Tech. 2016, 64, 319–327. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Ultrahigh-sensitivity microwave sensor for microfluidic complex permittivity measurement. IEEE Trans. Microw. Theory Tech. 2019, 67, 4269–4277. [Google Scholar] [CrossRef]
- Wu, W.-J.; Zhao, W.-S.; Wang, D.-W.; Yuan, B.; Wang, G.-F. Ultrahigh-sensitivity microwave microfluidic sensors based on modified complementary electric-LC and split-ring resonator structures. IEEE Sens. J. 2021, 21, 18756–18763. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Fang, S. Dielectric characterization of liquid mixtures using EIT-like transmission window. IEEE Sens. J. 2021, 21, 17859–17867. [Google Scholar] [CrossRef]
- Fan, L.-C.; Zhao, W.-S.; Wang, D.-W.; Liu, Q.; Chen, S.; Wang, G. An ultrahigh sensitivity microwave sensor for microfluidic applications. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 1201–1204. [Google Scholar] [CrossRef]
- Mohammadi, S.; Adhikari, K.K.; Jain, M.C.; Zarifi, M.H. High-resolution, sensitivity-enhanced active resonator sensor using substrate-embedded channel for characterizing low-concentration liquid mixtures. IEEE Trans. Microw. Theory Tech. 2022, 70, 576–586. [Google Scholar] [CrossRef]
- Gan, H.-Y.; Zhao, W.-S.; Liu, Q.; Wang, D.-W.; Dong, L.; Wang, G.; Yin, W.-Y. Differential microwave microfluidic sensor based on microstrip complementary split-ring resonator (MCSRR) structure. IEEE Sens. J. 2020, 20, 5876–5884. [Google Scholar] [CrossRef]
- Varshney, P.K.; Kapoor, A.; Akhtar, M.J. Highly sensitive ELC resonator based differential sensor. IEEE Trans. Instrum. Meas. 2021, 70, 8004710. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Tsai, C.-H.; Wu, T.-L. A novel time domain method to extract equivalent circuit model of patterned ground structures. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 486–488. [Google Scholar] [CrossRef]
- Vélez, P.; Muñoz-Enano, J.; Ebrahimi, A.; Herrojo, C.; Paredes, F.; Scott, J.; Ghorbani, K.; Martín, F. Single-frequency amplitude-modulation sensor for dielectric characterization of solids and microfluidics. IEEE Sens. J. 2021, 21, 12189–12201. [Google Scholar] [CrossRef]
- Liu, Q.; Deng, H.; Meng, P.; Sun, H. High sensitivity sensor loaded with octagonal spiral resonators for retrieval of solid material permittivity. IEEE Sens. J. 2021, 32, 20010–20017. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Jaruwongrungsee, K.; Tuantranont, A.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sens. Actuators A Phys. 2012, 189, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-sensitivity metamaterial-inspired sensor for microfluidic dielectric characterization. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.-J.; Zhao, W.-S.; Wang, D.-W.; Yuan, B.; Wang, G. A temperature-compensated differential microstrip sensor for microfluidic applications. IEEE Sens. J. 2021, 21, 24075–24083. [Google Scholar] [CrossRef]
- Jang, C.; Park, J.-K.; Lee, H.-J.; Yun, G.-H.; Yook, J.-G. Sensitivity-enhanced fluidic glucose sensor based on a microwave resonator coupled with an interferometric system for noninvasive and continuous detection. IEEE Trans. Biomed. Circuits Syst. 2022, 15, 1017–1026. [Google Scholar] [CrossRef]
- Shaw, T.; Mitra, D. Electromagnetic metamaterial based sensor design for chemical discrimination. In Proceedings of the 2017 IEEE MTT-S International Microwave and RF Conference (IMaRC), Ahmedabad, India, 11–13 December 2017; pp. 271–274. [Google Scholar]
- Vélez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Microwave microfluidic sensor based on a microstrip splitter/combiner configuration and split ring resonators (SRRs) for dielectric characterization of liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef] [Green Version]
- Bahar, A.A.M.; Zakaria, Z.; Isa, A.A.M.; Alahnomi, R.A.; Rahman, N.A. Complex permittivity measurement based on planar microfluidic resonator sensor. In Proceedings of the 18th International Symposium Antenna Technology and Applied Electromagnetics (ANTEM), Waterloo, ON, Canada, 19–22 December 2018; pp. 1–5. [Google Scholar]
- Bao, X.; Zhang, M.; Ocket, I.; Bao, J.; Kil, D.; Liu, Z.; Puers, R.; Schreurs, D.; Nauwelaers, B. Integration of interdigitated electrodes in split-ring resonator for detecting liquid mixtures. IEEE Trans. Microw. Theory Tech. 2020, 68, 2080–2089. [Google Scholar] [CrossRef]
- Ma, J.; Tang, J.; Wang, K.; Guo, L.; Gong, Y.; Wang, S. Complex permittivity characterization of liquid samples based on a split ring resonator (SRR). Sensors 2021, 21, 3385. [Google Scholar] [CrossRef] [PubMed]
- Baena, J.D.; Bonache, J.; Martin, F.; Sillero, R.; Falcone, F.; Lopetegi, T.; Laso, M.; Garcia-Garcia, J.; Gil, I.; Portillo, M.; et al. Equivalent-circuit models for split-ring resonators and complementary split-ring resonators coupled to planar transmission lines. IEEE Trans. Microw. Theory Tech. 2005, 53, 1451–1461. [Google Scholar] [CrossRef]
- Albishi, A.M.; Alshebeili, S.A.; Ramahi, O.M. Three-dimensional split-ring resonators-based sensors for fluid detection. IEEE Sens. J. 2021, 21, 9138–9147. [Google Scholar] [CrossRef]
- Govind, G.; Akhtar, M.J. Metamaterial-Inspired microwave microfluidic sensor for glucose monitoring in aqueous solutions. IEEE Sens. J. 2019, 19, 11900–11907. [Google Scholar] [CrossRef]
- Karmakar, N.C.; Roy, S.M.; Balbin, I.; Swiegers, G.F. Quasi-Static analysis of defected ground structure. In Proceedings of the TENCON 2005-2005 IEEE Region 10 Conference, Melbourne, VIC, Australia, 21–24 November 2005; pp. 1–6. [Google Scholar]
- Bao, J.-Z.; Swicord, M.L.; Davis, C.C. Microwave dielectric characterization of binary mixtures of water, methanol, and ethanol. J. Chem. Phys. 1996, 104, 4441–4450. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly enhanced sensitivity in planar microwave sensors based on metamaterial coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef]









| Ref. | Resonant Type | S.V. (μL) | |||
|---|---|---|---|---|---|
| [8] | CSRR | 2.226 | 0.52 | 0.249 × 0.435 | 0.98 |
| [6] | CSRR | 2.45 | 1.67 | 0.536 × 0.334 | 1.444 |
| [7] | EIT-like | 0.97 | 1000 | 0.13 × 0.13 | 0.05 |
| [10] | MCSRR | 1.62 | 0.39 | 0.763 × 0.490 | 0.626 |
| [5] | Series LC | 1.91 | 0.39 | N/A | 0.635 |
| [29] | SRR | 2.5 | 5 | 1.167 × 0.375 | 0.27 |
| This work | DGS-IDC-SRR | 1.49 | 0.68 | 0.326 × 0.166 | 1.430 |
| DGS-IDC-DSRR | 1.72 | 0.68 | 0.373 × 0.173 | 1.461 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, W.; Wang, D.-W.; Wang, J.; Wang, G.; Zhao, W.-S. An Improved Split-Ring Resonator-Based Sensor for Microfluidic Applications. Sensors 2022, 22, 8534. https://doi.org/10.3390/s22218534
Ye W, Wang D-W, Wang J, Wang G, Zhao W-S. An Improved Split-Ring Resonator-Based Sensor for Microfluidic Applications. Sensors. 2022; 22(21):8534. https://doi.org/10.3390/s22218534
Chicago/Turabian StyleYe, Wei, Da-Wei Wang, Jing Wang, Gaofeng Wang, and Wen-Sheng Zhao. 2022. "An Improved Split-Ring Resonator-Based Sensor for Microfluidic Applications" Sensors 22, no. 21: 8534. https://doi.org/10.3390/s22218534
APA StyleYe, W., Wang, D.-W., Wang, J., Wang, G., & Zhao, W.-S. (2022). An Improved Split-Ring Resonator-Based Sensor for Microfluidic Applications. Sensors, 22(21), 8534. https://doi.org/10.3390/s22218534








