Flat Photonic Crystal Fiber Plasmonic Sensor for Simultaneous Measurement of Temperature and Refractive Index with High Sensitivity
Abstract
:1. Introduction
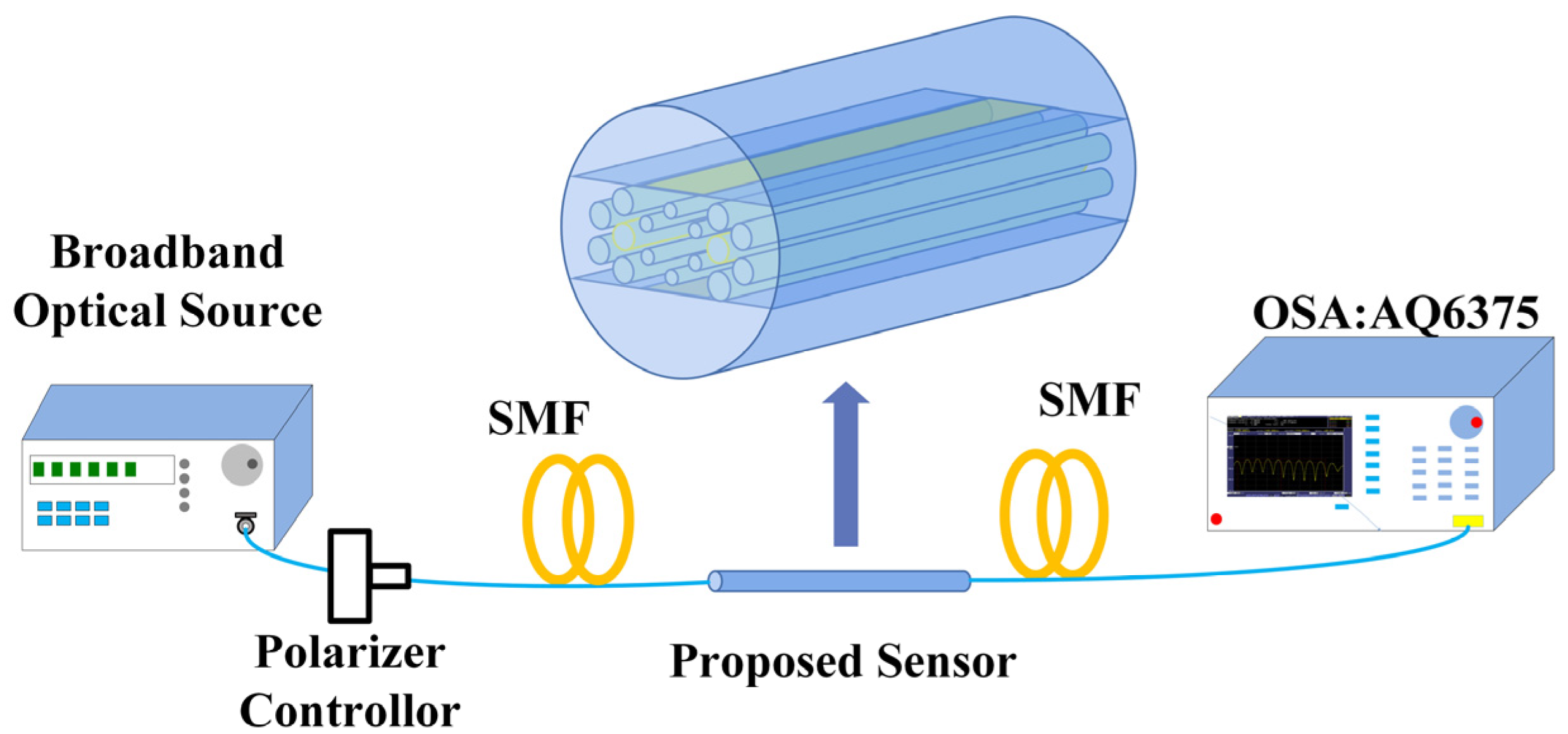
2. Theory and Model Design
3. Results and Discussion
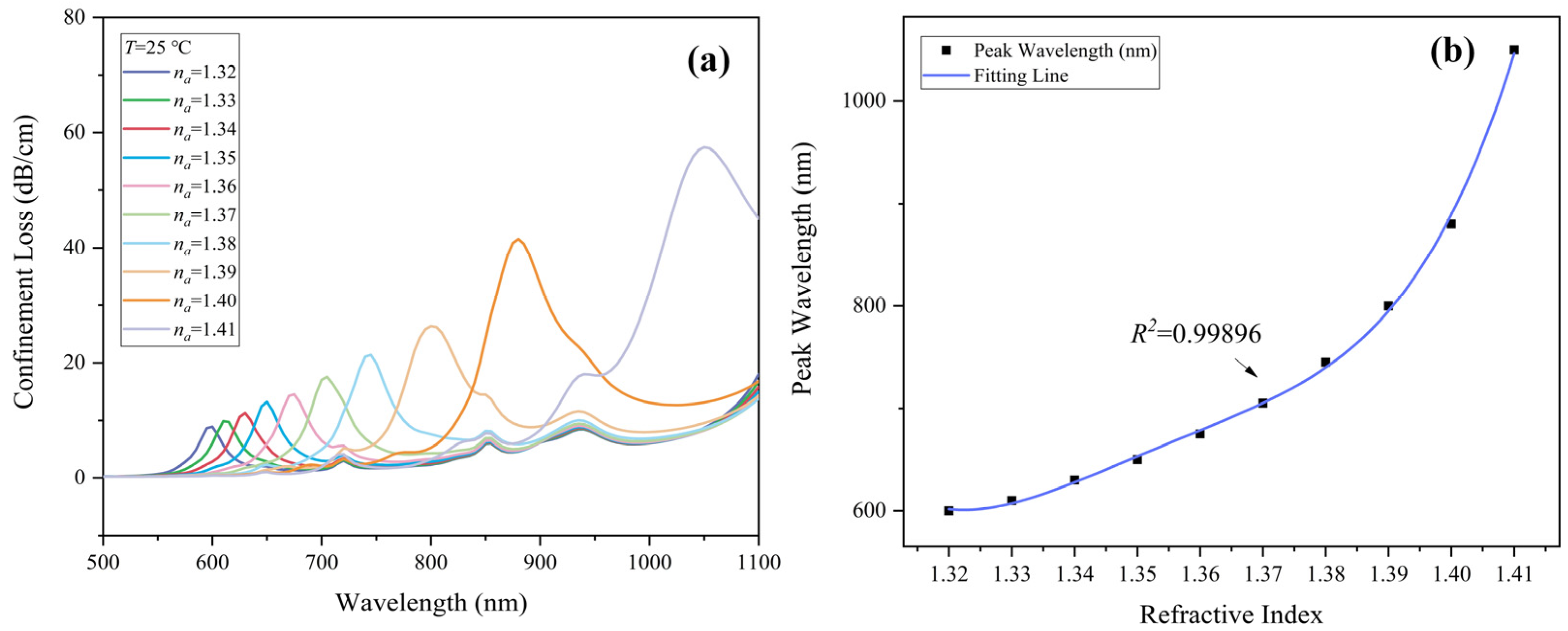
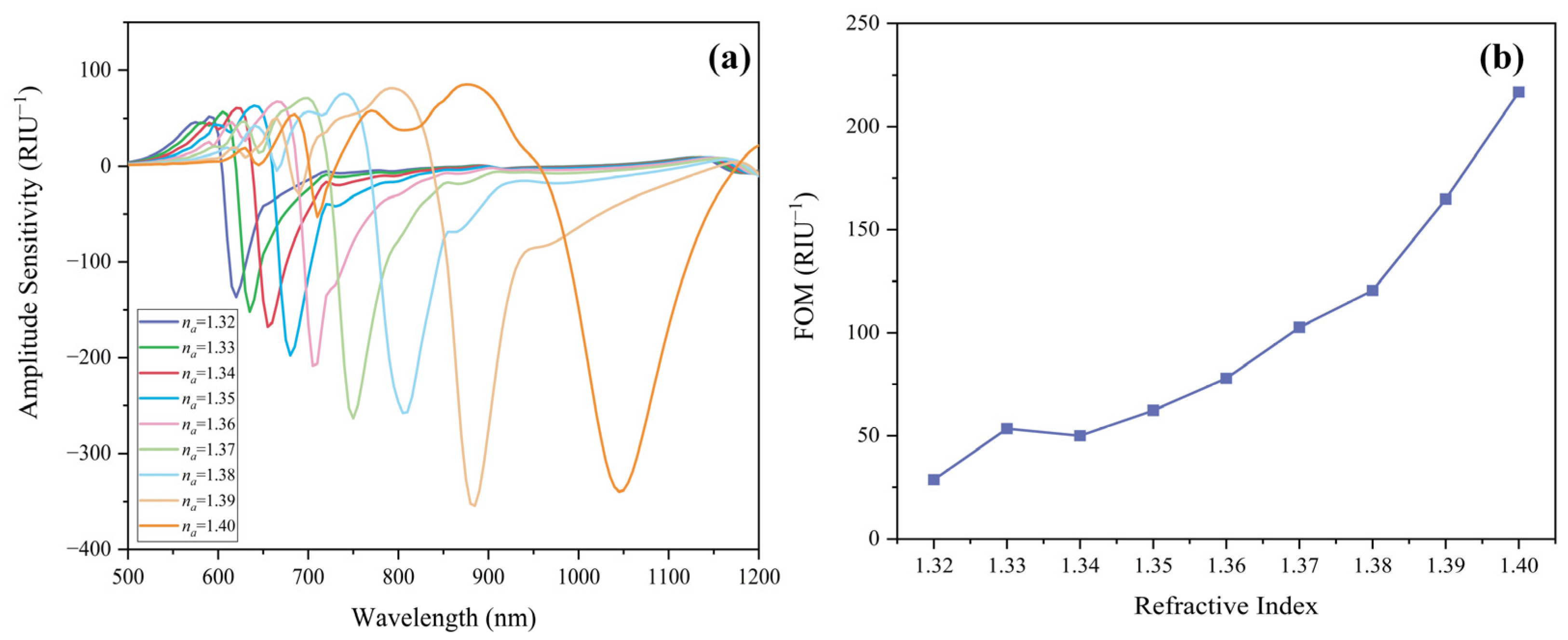
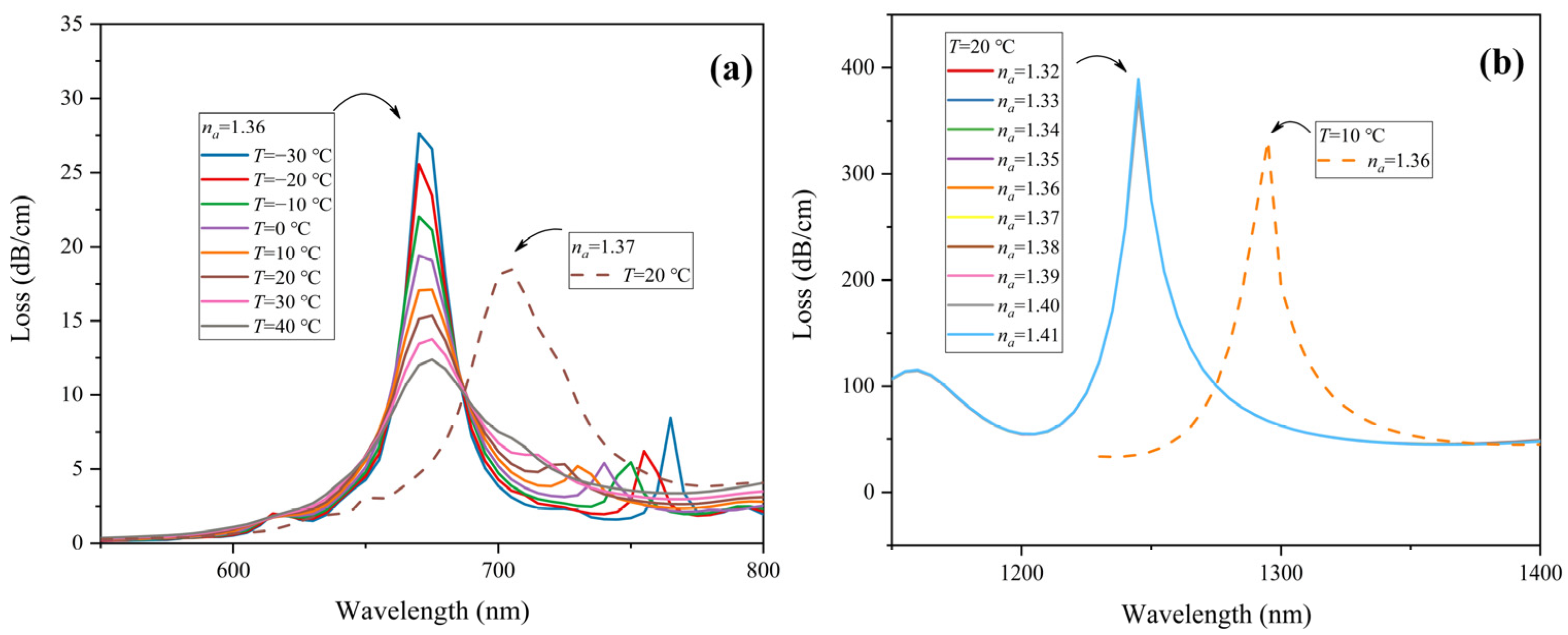
3.1. RI Sensing
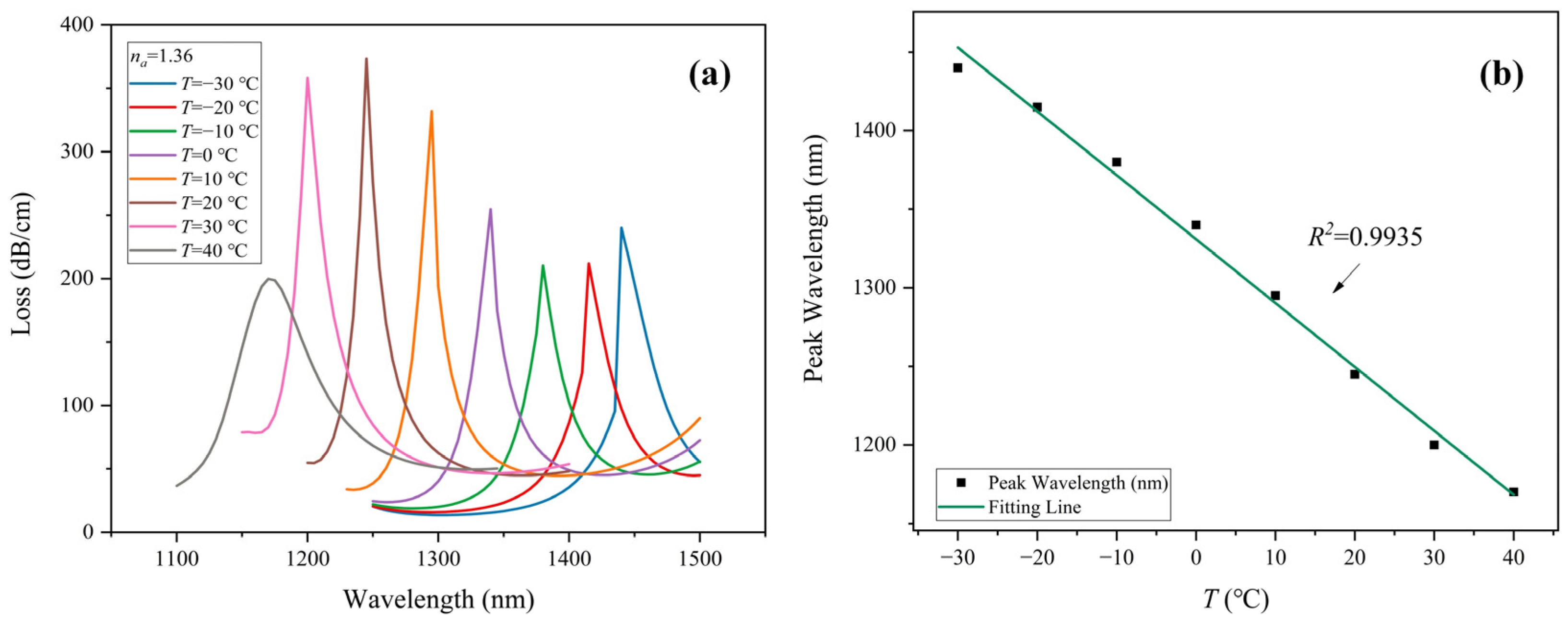
3.2. Temperature Sensing
3.3. Independence Analysis of Dual Parameter Sensing
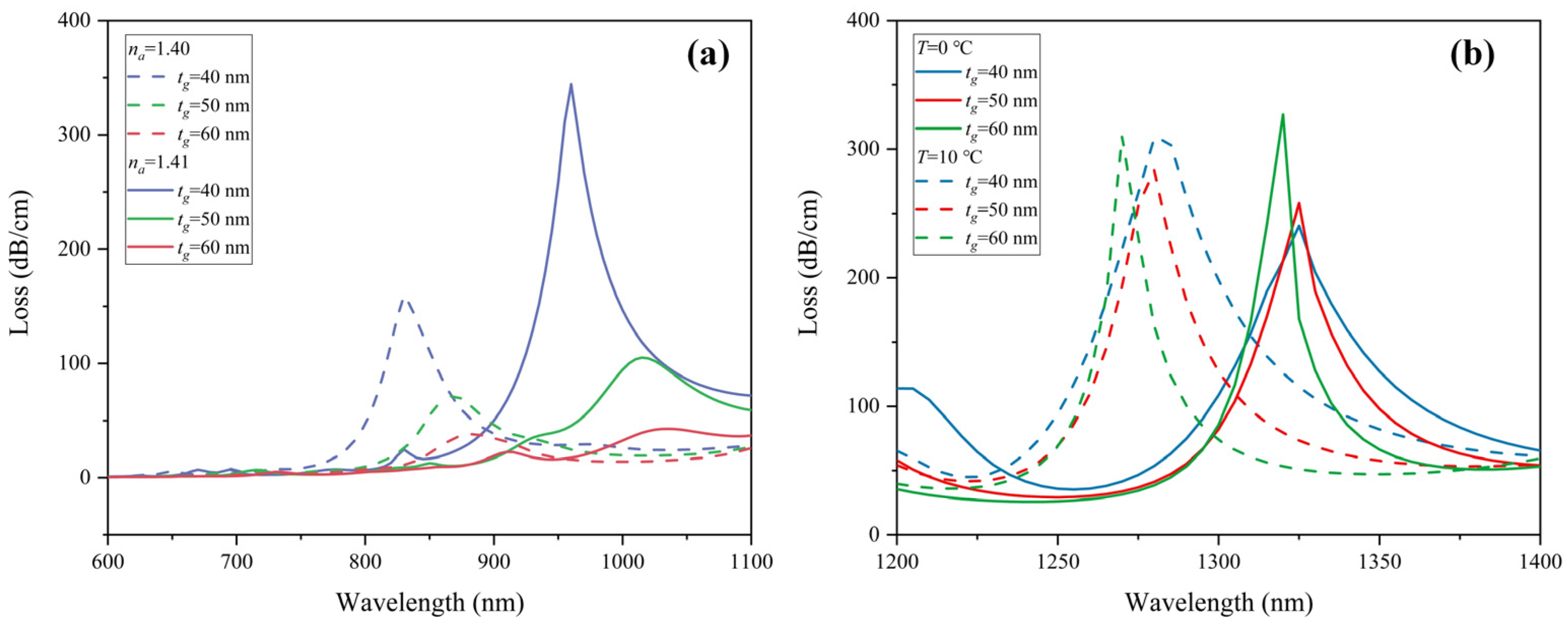
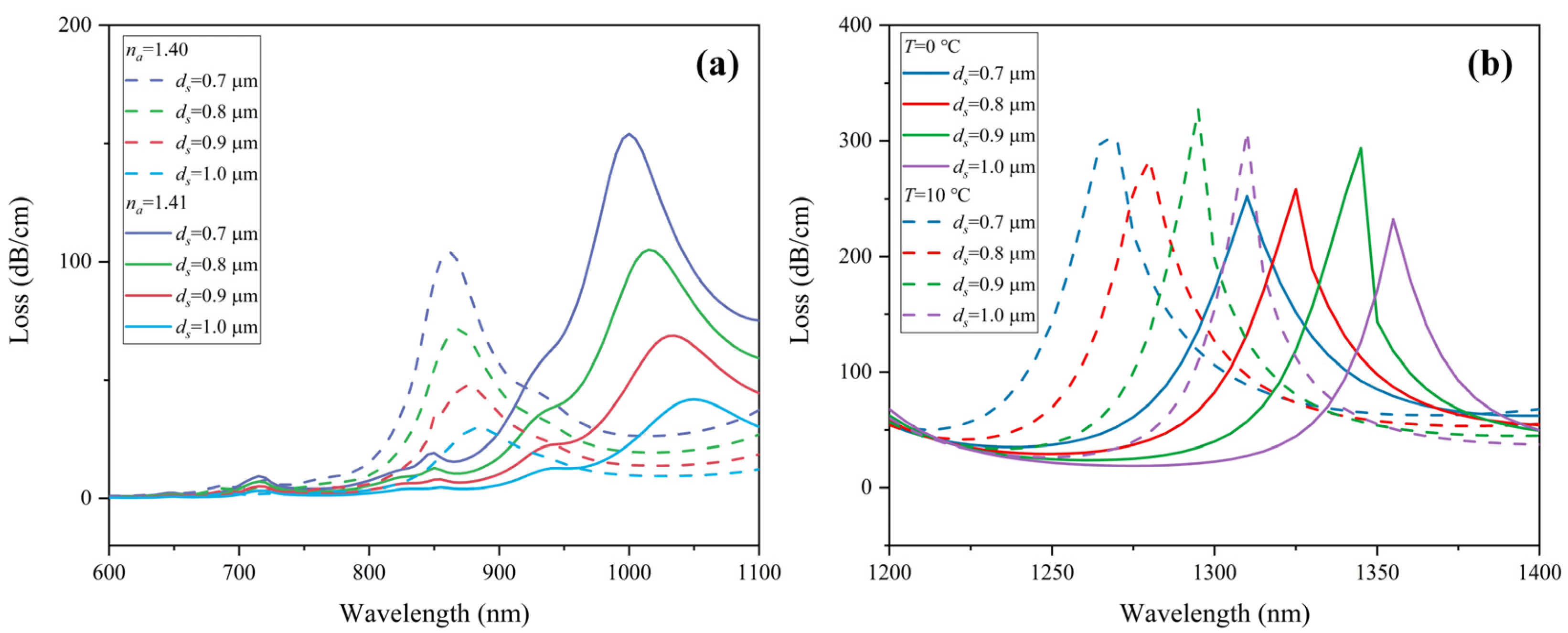
4. Structure Parameter Optimization
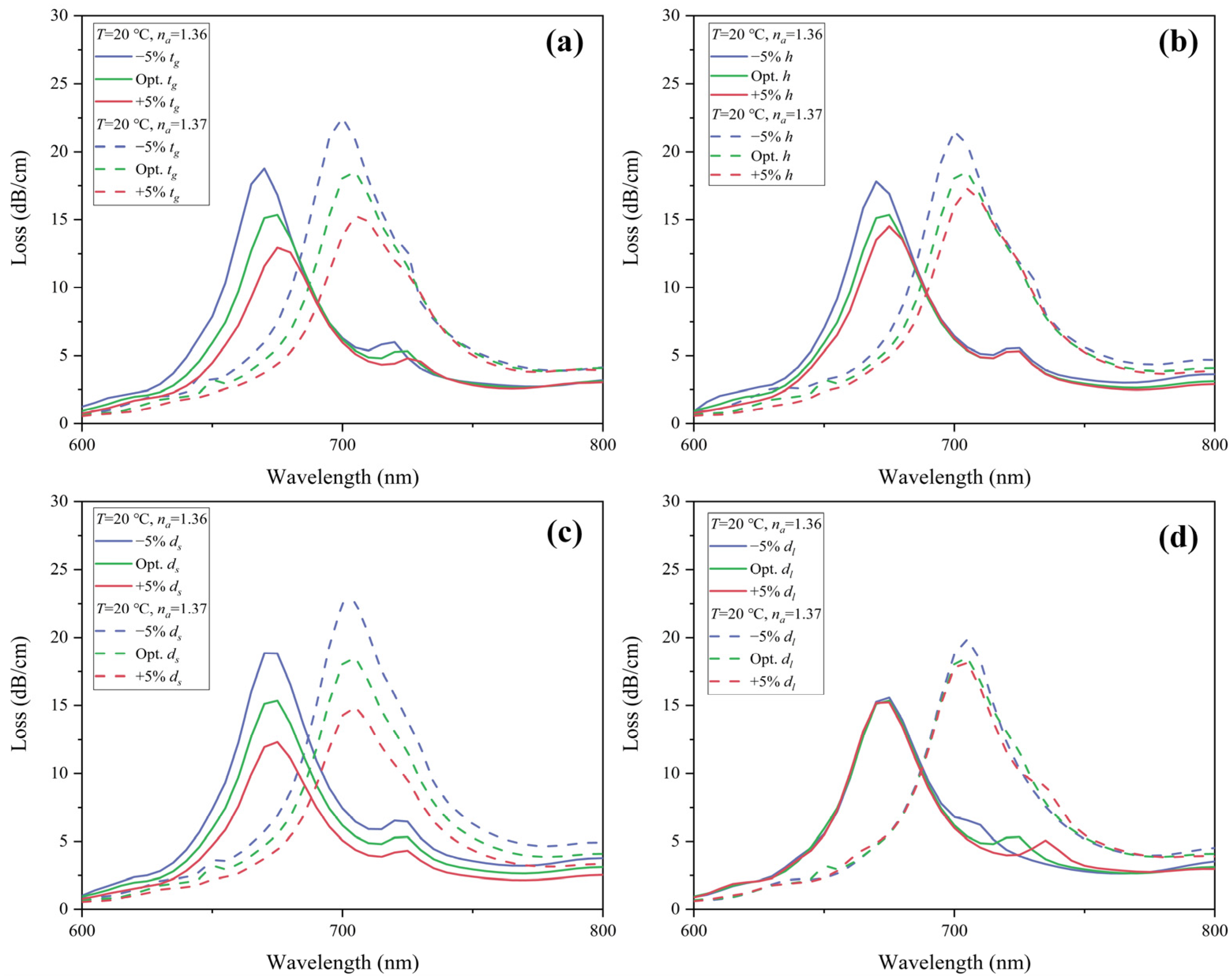
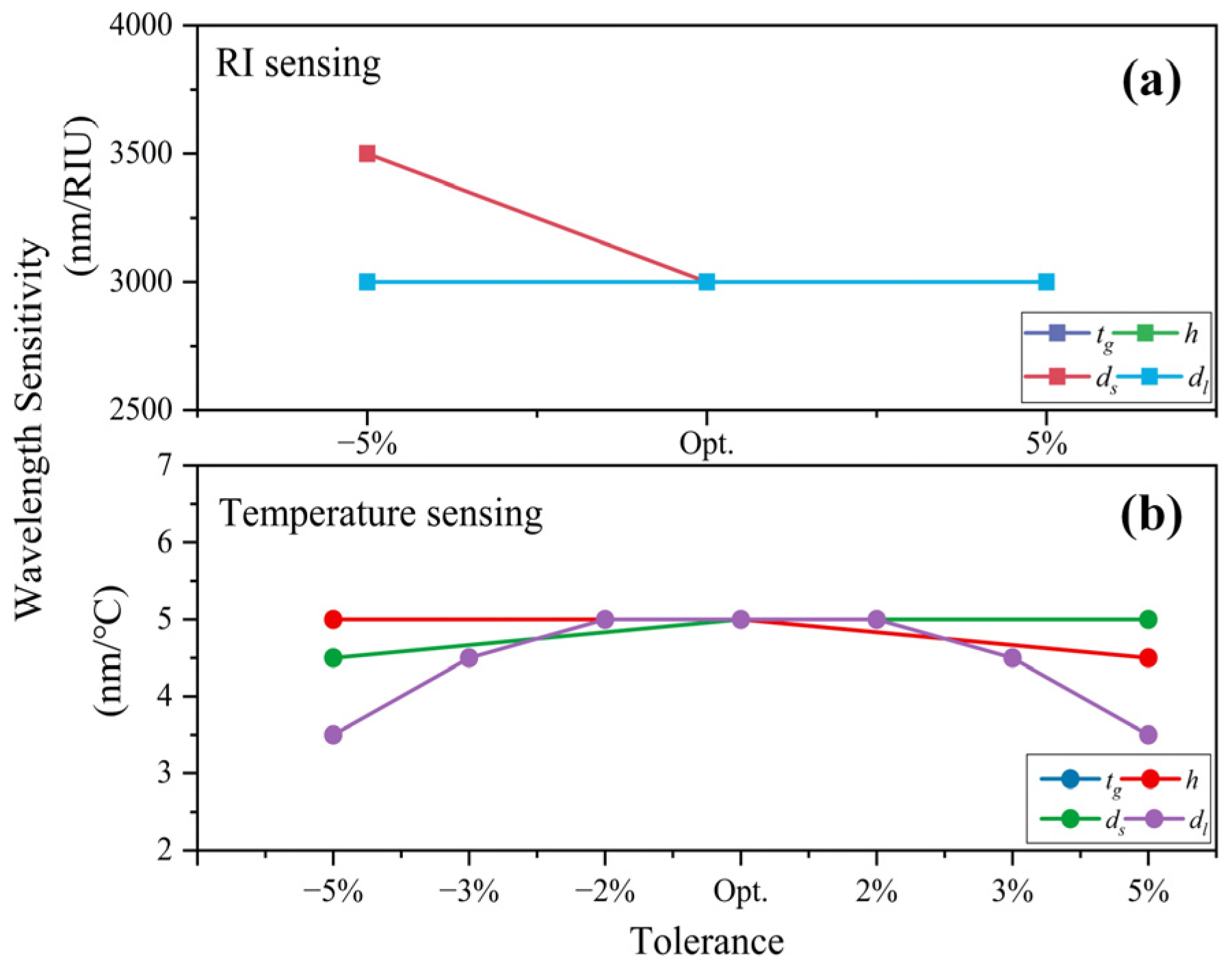
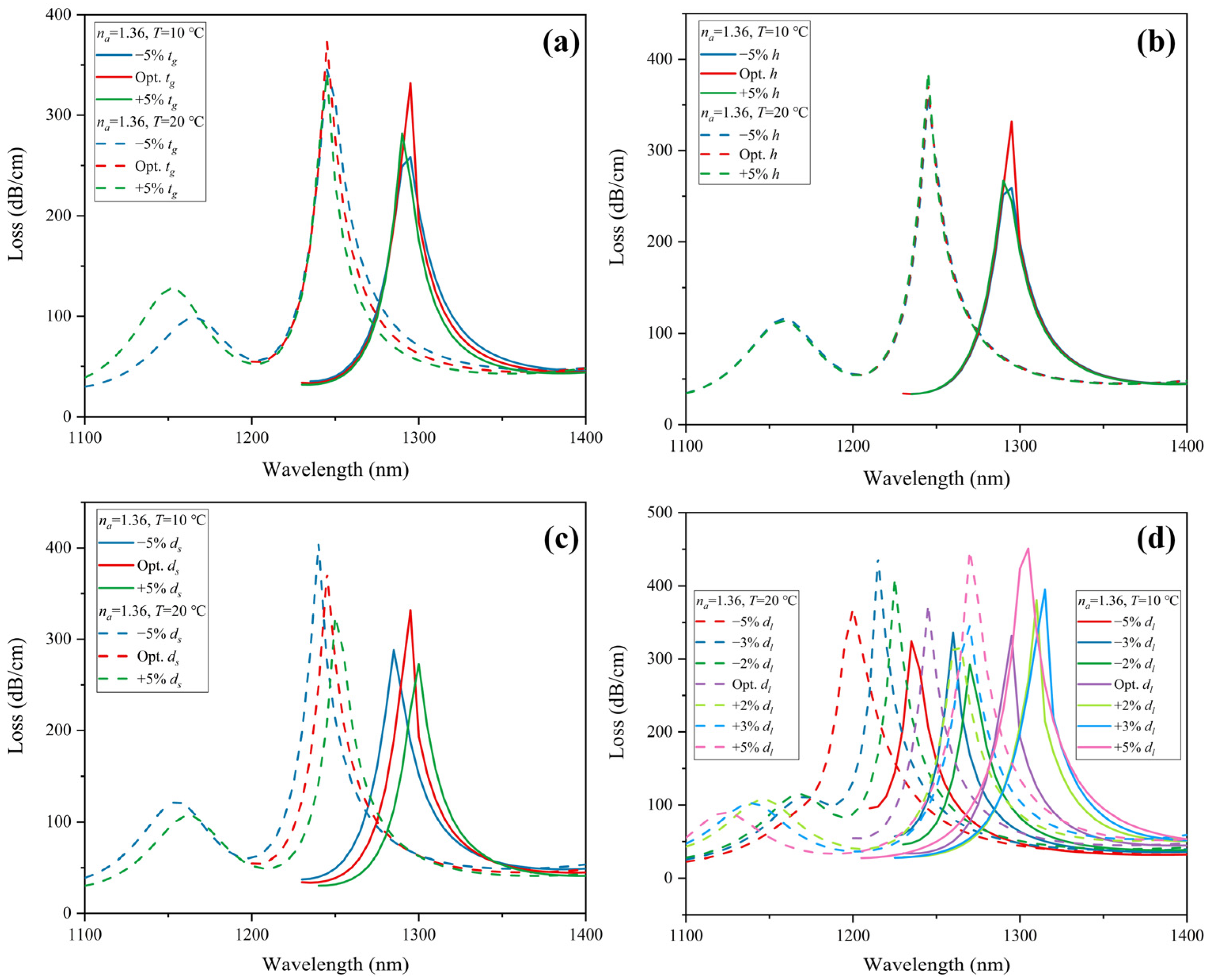
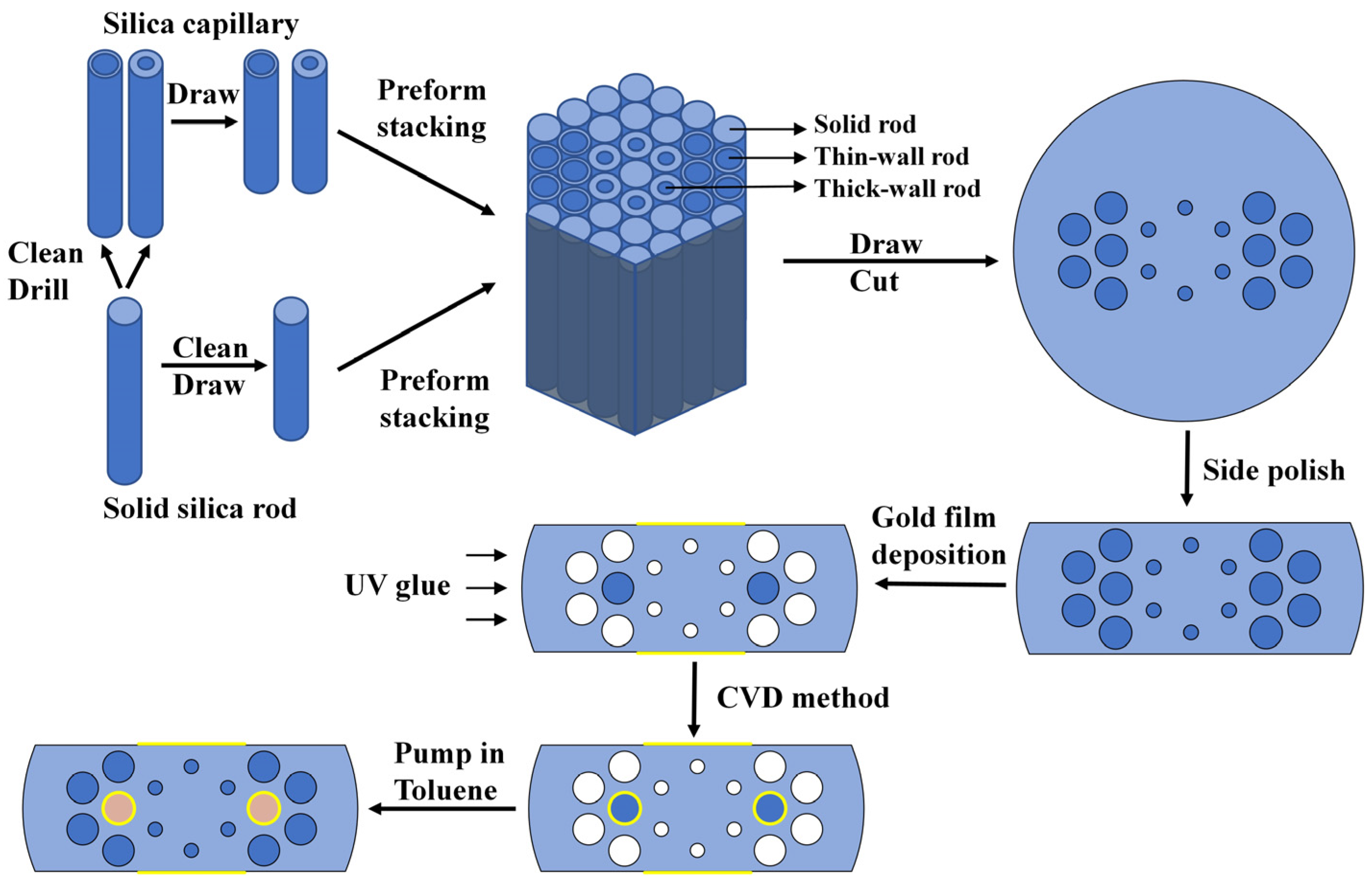
5. Fabrication Tolerance and Manufacturing Process Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Homola, J. Surface Plasmon Resonance Sensors for Detection of Chemical and Biological Species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef]
- Silva, S.; Roriz, P.; Frazão, O. Refractive Index Measurement of Liquids Based on Microstructured Optical Fibers. Photonics 2014, 1, 516–529. [Google Scholar] [CrossRef] [Green Version]
- Qin, W.; Li, S.; Yao, Y.; Xin, X.; Xue, J. Analyte-filled core self-calibration microstructured optical fiber based plasmonic sensor for detecting high refractive index aqueous analyte. Opt. Lasers Eng. 2014, 58, 1–8. [Google Scholar] [CrossRef]
- Jorge, P.A.; Silva, S.O.; Gouveia, C.; Tafulo, P.; Coelho, L.; Caldas, P.; Viegas, D.; Rego, G.; Baptista, J.M.; Santos, J.L.; et al. Fiber optic-based refractive index sensing at INESC Porto. Sensors 2012, 12, 8371–8389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, S.; Shao, Y.; Wang, Y.; Wu, T.; Zhang, L.; Huang, Y.; Zhang, F.; Liao, C.; He, J.; Wang, Y. Highly sensitive surface plasmon resonance biosensor based on a low-index polymer optical fiber. Opt. Express 2018, 26, 3988–3994. [Google Scholar] [CrossRef] [Green Version]
- Klantsataya, E.; Jia, P.; Ebendorff-Heidepriem, H.; Monro, T.M.; Francois, A. Plasmonic Fiber Optic Refractometric Sensors: From Conventional Architectures to Recent Design Trends. Sensors 2016, 17, 12. [Google Scholar] [CrossRef] [Green Version]
- Chau, Y.-F.; Liu, C.-Y.; Yeh, H.-H.; Tsai, D.P. A Comparative Study of High Birefringence and Low Confinement Loss Photonic Crystal Fiber Employing Elliptical Air Holes in Fiber Cladding with Tetragonal Lattice. Prog. Electromagn. Res. B 2010, 22, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Li, J.; Guo, Y.; Li, S.; Zhang, S.; Liu, Y.; Cheng, T. Analysis of Double Peak Detection in a D-Shaped Photonic Crystal Fiber Plasmonic Sensor. Plasmonics 2021, 16, 761–768. [Google Scholar] [CrossRef]
- Siddik, A.B.; Hossain, S.; Paul, A.K.; Rahman, M.; Mollah, A. High sensitivity property of dual-core photonic crystal fiber temperature sensor based on surface plasmon resonance. Sens. Bio-Sens. Res. 2020, 29, 100350. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Wang, M.; Liu, Y.; Fan, X.; Chen, Q.; Wu, B. Simultaneous measurement of refractive index and temperature of seawater based on surface plasmon resonance in a dual D-type photonic crystal fiber. Mater. Res. Express 2021, 8, 085201. [Google Scholar] [CrossRef]
- Zhao, Y.; Wua, Q.-L.; Zhanga, Y.-N. Theoretical analysis of high-sensitive seawater temperature and salinity measurement based on C-type micro-structured fiber. Sens. Actuators B 2018, 258, 822–828. [Google Scholar] [CrossRef]
- Chen, A.; Yu, Z.; Dai, B.; Li, Y. Highly Sensitive Detection of Refractive Index and Temperature Based on Liquid-Filled D-Shape PCF. IEEE Photonics Technol. Lett. 2021, 33, 529–532. [Google Scholar] [CrossRef]
- Li, B.; Zhang, F.; Yan, X.; Zhang, X.; Wang, F.; Li, S.; Cheng, T. Numerical Analysis of Dual-Parameter Optical Fiber Sensor With Large Measurement Range Based on Surface Plasmon Resonance. IEEE Sens. J. 2021, 21, 10719–10725. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Y.; Pan, S.; Shum, P.; Yan, M.; Leviatan, Y.; Li, C. A selectively coated photonic crystal fiber based surface plasmon resonance sensor. J. Opt. 2009, 12, 015005. [Google Scholar] [CrossRef] [Green Version]
- Vial, A.; Grimault, A.-S.; Macías, D.; Barchiesi, D.; de la Chapelle, M.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Lin, K.; Lu, Y.; Luo, Z.; Zheng, R.; Wang, P.; Ming, H. Numerical and experimental investigation of temperature effects on the surface plasmon resonance sensor. Chin. Opt. Lett. 2009, 7, 428–431. [Google Scholar]
- Lawrence, W.E. Electron-electron scattering in the low-temperature resistivity of the noble metals. Phys. Rev. B 1976, 13, 5316–5319. [Google Scholar] [CrossRef]
- Holstein, T. Optical and Infrared Volume Absorptivity of Metals. Phys. Rev. 1954, 96, 535–536. [Google Scholar] [CrossRef]
- Ozdemir, S.K.; Turhan-Sayan, G. Temperature effects on surface plasmon resonance: Design considerations for an optical temperature sensor. J. Light. Technol. 2003, 21, 805–814. [Google Scholar] [CrossRef]
- Harvey, A.H.; Gallagher, J.S.; Sengers, J.L. Revised Formulation for the Refractive Index of Water and Steam as a Function of Wavelength, Temperature and Density. J. Phys. Chem. Ref. Data 1998, 27, 761–774. [Google Scholar] [CrossRef]
- Wang, R.; Yao, J.; Miao, Y.; Lu, Y.; Xu, D.; Luan, N.; Musideke, M.; Duan, L.; Hao, C. A reflective photonic crystal fiber temperature sensor probe based on infiltration with liquid mixtures. Sensors 2013, 13, 7916–7925. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Han, H.; Lian, Y.; Luan, N.; Liu, J. Theoretical analysis of all-solid D-type photonic crystal fiber based plasmonic sensor for refractive index and temperature sensing. Opt. Fiber Technol. 2019, 50, 165–171. [Google Scholar] [CrossRef]
- Hassani, A.; Skorobogatiy, M. Design criteria for microstructured-optical-fiberbased surface-plasmon-resonance sensors. J. Opt. Soc. Am. B 2007, 24, 1423–1429. [Google Scholar] [CrossRef]
- Otupiri, R.; Akowuah, E.K.; Haxha, S. Multi-channel SPR biosensor based on PCF for multi-analyte sensing applications. Opt. Express 2015, 23, 15716–15727. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Li, S. Surface plasmon resonance sensor based on symmetrical side-polished dual-core photonic crystal fiber. Opt. Fiber Technol. 2019, 51, 96–100. [Google Scholar] [CrossRef]
- Hautakorpi, M.; Mattinen, M.; Ludvigsen, H. Surface-plasmon-resonance sensor based on three-hole microstructured optical fiber. Opt. Express 2008, 16, 8427–8432. [Google Scholar] [CrossRef]
- Gandhi, M.S.A.; Senthilnathan, K.; Babu, P.R.; Li, Q. Highly Sensitive Localized Surface Plasmon Polariton Based D-Type Twin-Hole Photonic Crystal Fiber Microbiosensor: Enhanced Scheme for SERS Reinforcement. Sensors 2020, 20, 5248. [Google Scholar] [CrossRef]
- Luan, N.; Wang, R.; Lv, W.; Lu, Y.; Yao, J. Surface plasmon resonance temperature sensor based on photonic crystal fibers randomly filled with silver nanowires. Sensors 2014, 14, 16035–16045. [Google Scholar] [CrossRef] [Green Version]
- Paul, A.K.; Hassan, M.Z.; Islam, M.R.; Zhu, J.G. Graphene/gold based photonic crystal fiber plasmonic temperature sensor for electric vehicle applications. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Qiu, S.; Yuan, J.; Zhou, X.; Qu, Y.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; Long, K.; Yu, C. Highly sensitive temperature sensing based on all-solid cladding dual-core photonic crystal fiber filled with the toluene and ethanol. Opt. Commun. 2020, 477, 126357. [Google Scholar] [CrossRef]
- Meng, F.; Wang, H.; Fang, D. Research on D-Shape Open-Loop PCF Temperature Refractive Index Sensor Based on SPR Effect. IEEE Photonics J. 2022, 14, 1–5. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, J.; Yang, H.; Liu, H.; Zeng, G.; Huang, B.; Jia, J. Double U-groove temperature and refractive index photonic crystal fiber sensor based on surface plasmon resonance. Appl. Opt. 2022, 61, 7225–7230. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhang, Y.; Li, X.; Fan, X.; Chen, Q.; Wu, B.; Chen, H. A gold film coated dual-core photonic crystal fiber for refractive index and temperature sensing with high isolation. Opt. Fiber Technol. 2022, 72, 102975. [Google Scholar] [CrossRef]
- Yu, Y.-L.; Kishikawa, H.; Liaw, S.-K.; Goto, N.; Liu, W.-F. Simultaneous measurement of temperature and refractive index based on an SPR Silicon core fiber sensor with a fused silica grating design. Opt. Quantum Electron. 2022, 54, 63. [Google Scholar] [CrossRef]
- Reeves, W.H.; Knight, J.C.; Russell, P.S.J. Demonstration of ultra-flattened dispersion in photonic crystal fibers. Opt. Express 2002, 10, 609–613. [Google Scholar] [CrossRef]
- Mahdiraji, G.A.; Chow, D.M.; Sandoghchi, S.R.; Amirkhan, F.; Dermosesian, E.; Yeo, K.S.; Kakaei, Z.; Ghomeishi, M.; Poh, S.Y.; Gang, S.Y.; et al. Challenges and Solutions in Fabrication of Silica-Based Photonic Crystal Fibers: An Experimental Study. Fiber Integr. Opt. 2014, 33, 85–104. [Google Scholar] [CrossRef]
- Li, J.; Yan, H.; Dang, H.; Meng, F. Structure design and application of hollow core microstructured optical fiber gas sensor: A review. Opt. Laser Technol. 2021, 135, 106658. [Google Scholar] [CrossRef]
- Tseng, S.-M.; Chen, C.-L. Side-polished fibers. Appl. Opt. 1992, 31, 3438–3447. [Google Scholar] [CrossRef]
- Das, S.; Guha, S.; Das, P.P.; Ghadai, R.K. Analysis of morphological, microstructural, electrochemical and nano mechanical characteristics of TiCN coatings prepared under N2 gas flow rate by chemical vapour deposition (CVD) process at higher temperature. Ceram. Int. 2020, 46, 10292–10298. [Google Scholar] [CrossRef]
- Griffiths, M.B.E.; Pallister, P.J.; Mandia, D.J.; Barry, S.T. Atomic Layer Deposition of Gold Metal. Chem. Mater. 2016, 28, 44–46. [Google Scholar] [CrossRef]
- Wijaya, E.; Lenaerts, C.; Maricot, S.; Hastanin, J.; Habraken, S.; Vilcot, J.-P.; Boukherroub, R.; Szunerits, S. Surface plasmon resonance-based biosensors: From the development of different SPR structures to novel surface functionalization strategies. Curr. Opin. Solid State Mater. Sci. 2011, 15, 208–224. [Google Scholar] [CrossRef]
- Shakya, A.K.; Singh, S. Design of novel Penta core PCF SPR RI sensor based on fusion of IMD and EMD techniques for analysis of water and transformer oil. Measurement 2022, 188, 110513. [Google Scholar] [CrossRef]




| Structure Configuration | RI Range | Temp. Range | Operating Wavelength [nm] | Wavelength Sensitivity (RI/Temp.) |
Amplitude Sensitivity (RI/Temp.)
[RIU−1/°C−1] | Wavelength Resolution (RI/Temp.) [RIU/°C] | FOM (RI) [RIU−1] |
|---|---|---|---|---|---|---|---|
| Liquid-filled D-shape PCF [12] | 1.35–1.40 | 20–60 °C | 550–850 | 3940 nm/RIU/ 1.075 nm/°C | 152.23/ 539.42 | N/A | N/A |
| No-core fiber [13] | 1.33–1.44 | 0–180 °C | 400–1200 | 12,530 nm/RIU/ −3.465 nm/°C | N/A | N/A | N/A |
| Double U-groove PCF [33] | 1.32–1.4 | −30–50 °C | 1300–2500 | 4715 nm/RIU/ 18 nm/°C | 48.44/ 1.01 × 10−1 | 2.12 × 10−5/ 5.55 × 10−3 | N/A |
| Dual-core D-shaped PCF [34] | 1.33–1.39 | −50–40 °C | 500–900 | 8100 nm/RIU/ 1.3 nm/°C | N/A | N/A | N/A |
| Grating-assisted SPR silicon core sensor [35] | 1.28–1.38 | 15–40 °C | 1800–2800 | 1949.8 nm/RIU/ 1.6 nm/°C | N/A | N/A | N/A |
| Proposed Flat PCF Plasmonic Sensor | 1.32–1.41 | −30–40 °C | 500–1500 | 17,000 nm/RIU/ −5 nm/°C | 354.39/ N/A | 5.88 × 10−6/ 0.02 | 216.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, W.; Li, C.; Wang, D.; Chen, W.; Guo, S.; Gao, S.; Zhang, C. Flat Photonic Crystal Fiber Plasmonic Sensor for Simultaneous Measurement of Temperature and Refractive Index with High Sensitivity. Sensors 2022, 22, 9028. https://doi.org/10.3390/s22239028
An W, Li C, Wang D, Chen W, Guo S, Gao S, Zhang C. Flat Photonic Crystal Fiber Plasmonic Sensor for Simultaneous Measurement of Temperature and Refractive Index with High Sensitivity. Sensors. 2022; 22(23):9028. https://doi.org/10.3390/s22239028
Chicago/Turabian StyleAn, Wei, Chao Li, Dong Wang, Wenya Chen, Shijing Guo, Song Gao, and Chunwei Zhang. 2022. "Flat Photonic Crystal Fiber Plasmonic Sensor for Simultaneous Measurement of Temperature and Refractive Index with High Sensitivity" Sensors 22, no. 23: 9028. https://doi.org/10.3390/s22239028
APA StyleAn, W., Li, C., Wang, D., Chen, W., Guo, S., Gao, S., & Zhang, C. (2022). Flat Photonic Crystal Fiber Plasmonic Sensor for Simultaneous Measurement of Temperature and Refractive Index with High Sensitivity. Sensors, 22(23), 9028. https://doi.org/10.3390/s22239028






