Proportional Fair Trajectory Design and Resource Allocation for UAV-Assisted SWIPT System
Abstract
:1. Introduction
- Considering that the improvements of the average spectral efficiency (SE), as well as user fairness are important for providing reliable quality-of-service to GNs, we formulate a problem to maximize the sum of the logarithmic average SE of the GNs while guaranteeing the average harvested energy requirement.
- To solve the formulated nonconvex problem, we convert the original problem into a tractable convex form using the quadratic transform and first-order Taylor expansion. In addition, we propose an iterative algorithm that finds the optimal trajectory and transmit power of the UAV, as well as the PS ratio of the GNs.
- Simulation results verify that the proposed scheme outperforms the state-of-the-art max–min scheme in terms of the average SE and provides a similar level of user fairness. This implies that the design of the UAV strategy in a proportional fair manner is effective in supporting fair and high data rates for GNs.
2. System Model and Problem Statement
3. Proposed Algorithm
3.1. Transmit Power Optimization
3.2. Power-Splitting Ratio Optimization
3.3. Trajectory Optimization
| Algorithm 1 Proposed algorithm. |
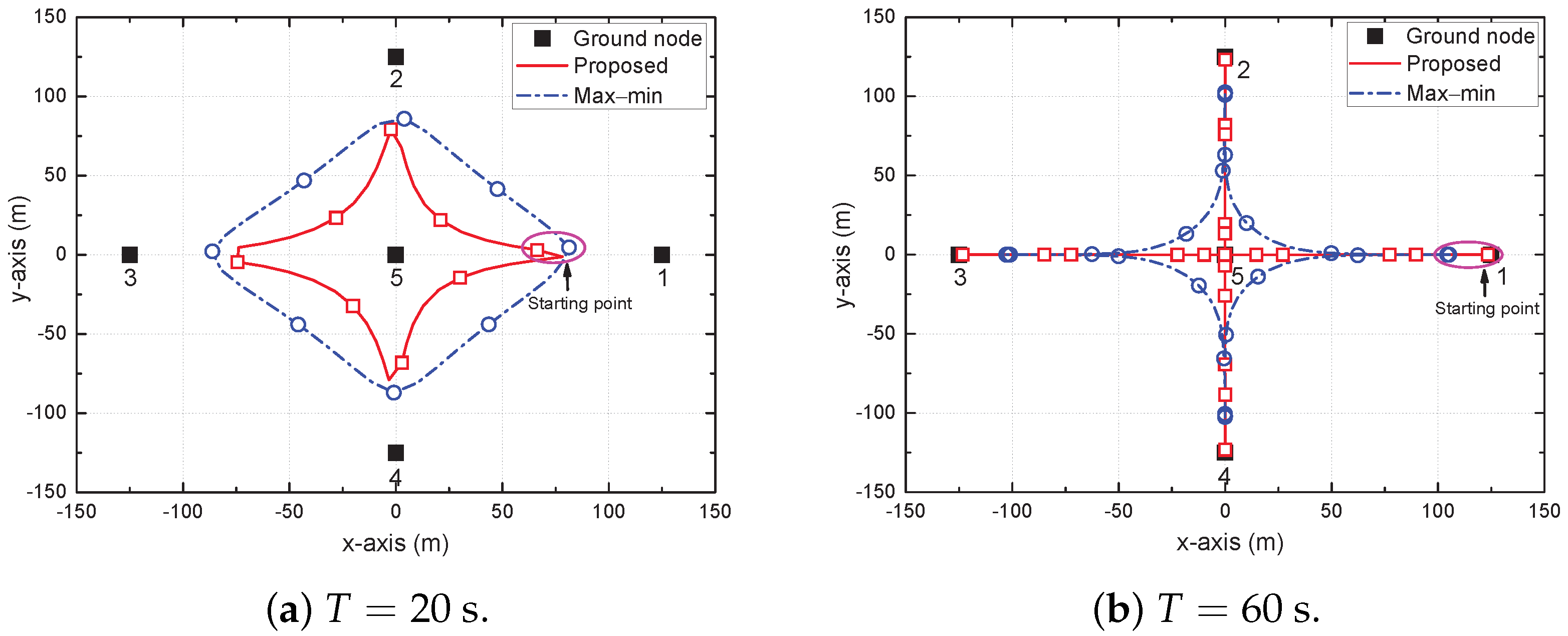
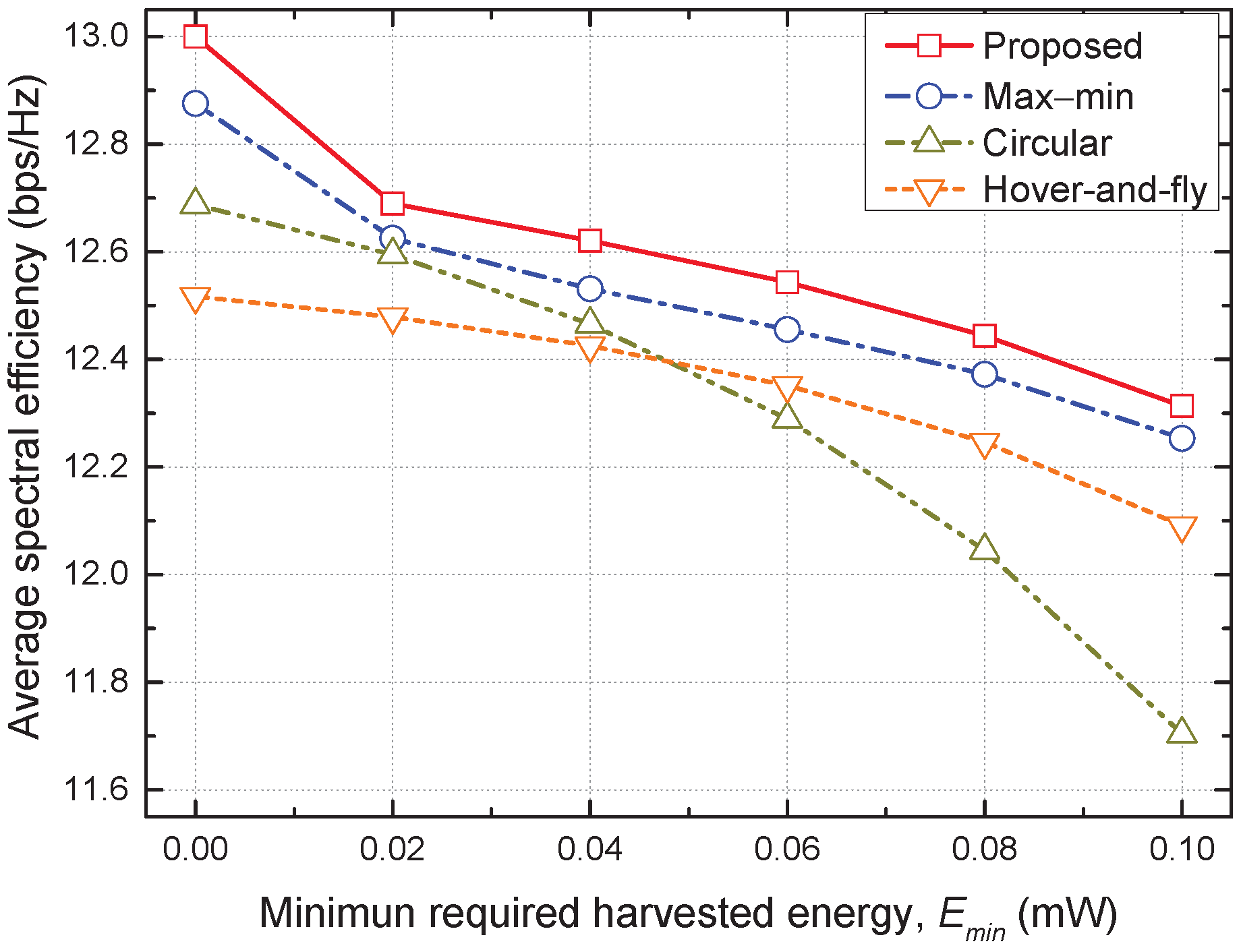
4. Simulation Results and Discussion
- Proposed scheme: The transmit power and trajectory of the UAV and the PS ratio of the GNs are determined using Algorithm 1.
- Max–min scheme: The transmit power and trajectory of the UAV and the PS ratios of the GNs are determined to maximize the minimum average achievable SE among all GNs while guaranteeing the average harvested energy requirement [14].
- Circular scheme: The UAV has a circular trajectory with a radius of area/4 centered at the geometric mean of the GNs’ coordinates. The transmit power of the UAV and the PS ratio of the GNs are determined in the same way as in the proposed scheme.
- Hover-and-fly scheme: The UAV hovers sequentially at the coordinates of the GNs and flies in a straight line from one user to the other at a constant speed. The transmit power of the UAV and the PS ratio of the GNs are determined in the same way as in the proposed scheme.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Zhan, P.; Yu, K.; Swindlehurst, A.L. Wireless relay communications with unmanned aerial vehicles: Performance and optimization. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2068–2085. [Google Scholar] [CrossRef]
- Tuna, G.; Nefzi, B.; Conte, G. Unmanned aerial vehicle-aided communications system for disaster recovery. J. Netw. Comput. Appl. 2014, 41, 27–36. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K. Uav-assisted emergency networks in disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef] [Green Version]
- Motlagh, N.H.; Taleb, T.; Arouk, O. Low-altitude unmanned aerial vehicles-based internet of things services: Comprehensive survey and future perspectives. IEEE Internet Things J. 2016, 3, 899–922. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, X.; Zhang, R. Trajectory design for completion time minimization in uav-enabled multicasting. IEEE Trans. Wirel. Commun. 2018, 17, 2233–2246. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R. Energy-efficient uav communication with trajectory optimization. IEEE Trans. Wirel. Commun. 2017, 16, 3747–3760. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Duo, B.; Wang, Z.; Lin, X.; Gao, C. Aerial cooperative jamming for cellular-enabled uav secure communication network: Joint trajectory and power control design. Sensors 2019, 19, 4440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, J.; Zeng, Y.; Zhang, R. Uav-enabled wireless power transfer: Trajectory design and energy optimization. IEEE Trans. Wirel. Commun. 2018, 17, 5092–5106. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Lee, H.; Eom, S.; Lee, I. Uav-aided wireless powered communication networks: Trajectory optimization and resource allocation for minimum throughput maximization. IEEE Access 2019, 7, 134978–134991. [Google Scholar] [CrossRef]
- Xie, L.; Xu, J.; Zhang, R. Throughput maximization for uav-enabled wireless powered communication networks. IEEE Internet Things J. 2019, 6, 1690–1703. [Google Scholar] [CrossRef] [Green Version]
- Hong, X.; Liu, P.; Zhou, F.; Guo, S.; Chu, Z. Resource allocation for secure uav-assisted swipt systems. IEEE Access 2017, 7, 10403–10421. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Wang, H.; Ding, G.; Xue, Z.; Yang, Y.; Song, F. Uav-assisted swipt in internet of things with power splitting: Trajectory design and power allocation. IEEE Access 2019, 7, 68260–68270. [Google Scholar] [CrossRef]
- Kang, J.-M.; Chun, C.-J. Joint trajectory design, tx power allocation, and rx power splitting for uav-enabled multicasting swipt systems. IEEE Syst. J. 2020, 14, 3740–3743. [Google Scholar] [CrossRef]
- Zhao, Y.; Foong, L.K. Predicting electrical power output of combined cycle power plants using a novel artificial neural network optimized by electrostatic discharge algorithm. Measurement 2022, 198, 111405. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z. Subset simulation with adaptable intermediate failure probability for robust reliability analysis: An unsupervised learning-based approach. Struct. Multidiscip. Optim. 2022, 65, 6. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Jo, O.; Cho, D.-H. Cooperative resource allocation for guaranteeing intercell fairness in femtocell networks. IEEE Commun. Lett. 2011, 15, 214–216. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. cvx: Matlab Software for Disciplined Convex Programming, Version 2.1. Available online: http://cvxr.com/cvx (accessed on 1 October 2022).
- Shen, K.; Yu, W. Fractional programming for communication systems–part i: Power control and beamforming. IEEE Trans. Signal Process. 2018, 66, 2616–2630. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.; Vandenberghe, L.; Press, C.U. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ben-Tal, A.; Nemirovskiaei, A.S. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]




| Parameter | Value |
|---|---|
| Flight period | s |
| Length of time slot | s |
| Number of GNs | |
| Flight altitude | m |
| Maximum flying speed | m/s |
| Average power budget | dBm |
| Peak power budget | |
| Minimum required harvested energy | mW |
| Energy conversion efficiency | |
| Channel power gain at 1 m | dB |
| Antenna noise power | dBm |
| Baseband noise power | dBm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, K.; Lee, K. Proportional Fair Trajectory Design and Resource Allocation for UAV-Assisted SWIPT System. Sensors 2022, 22, 9359. https://doi.org/10.3390/s22239359
Heo K, Lee K. Proportional Fair Trajectory Design and Resource Allocation for UAV-Assisted SWIPT System. Sensors. 2022; 22(23):9359. https://doi.org/10.3390/s22239359
Chicago/Turabian StyleHeo, Kanghyun, and Kisong Lee. 2022. "Proportional Fair Trajectory Design and Resource Allocation for UAV-Assisted SWIPT System" Sensors 22, no. 23: 9359. https://doi.org/10.3390/s22239359
APA StyleHeo, K., & Lee, K. (2022). Proportional Fair Trajectory Design and Resource Allocation for UAV-Assisted SWIPT System. Sensors, 22(23), 9359. https://doi.org/10.3390/s22239359






