Prediction of IGS RTS Orbit Correction Using LSTM Network at the Time of IOD Change
Abstract
:1. Introduction
2. Background and Methods
2.1. Overview of RTS Correction
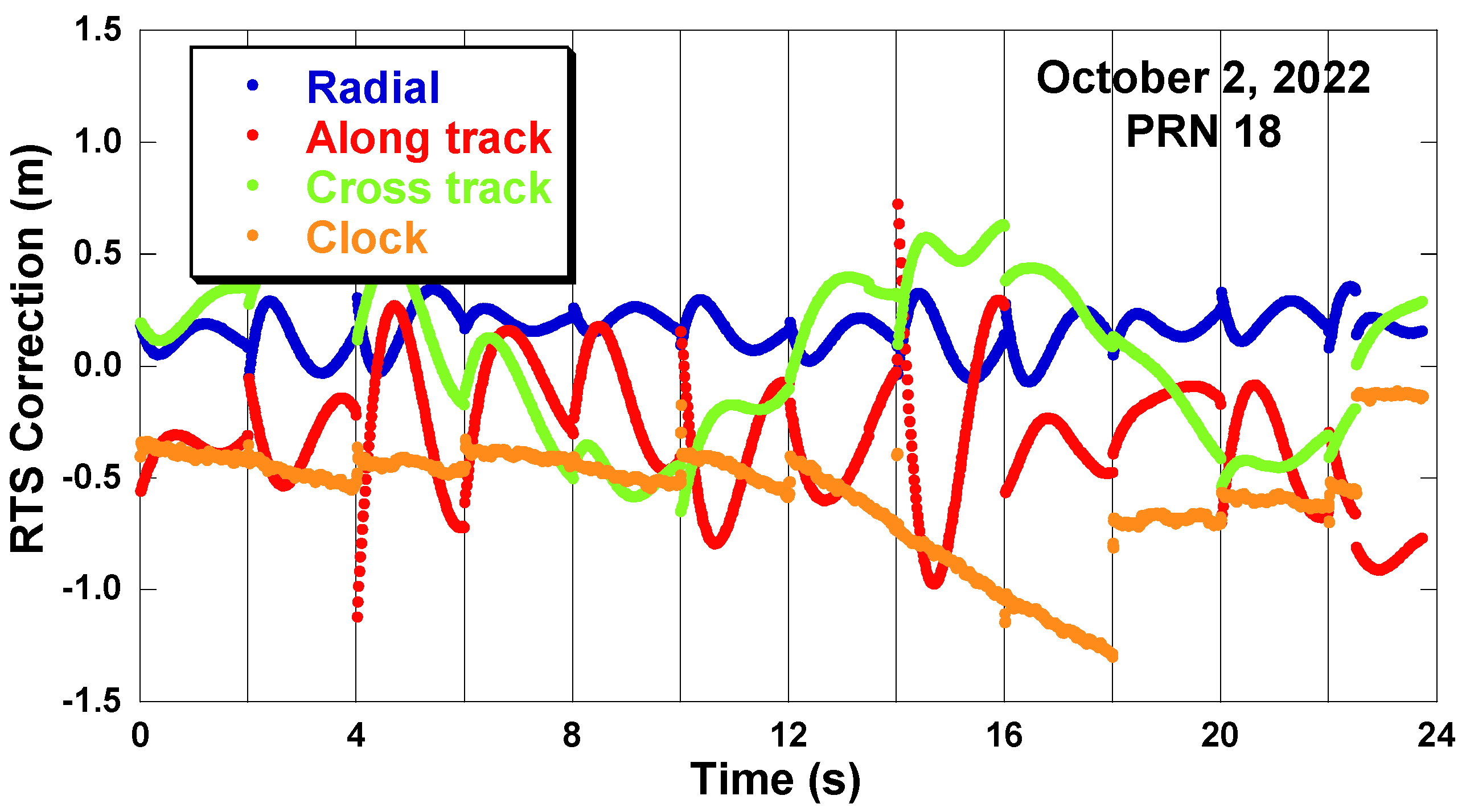
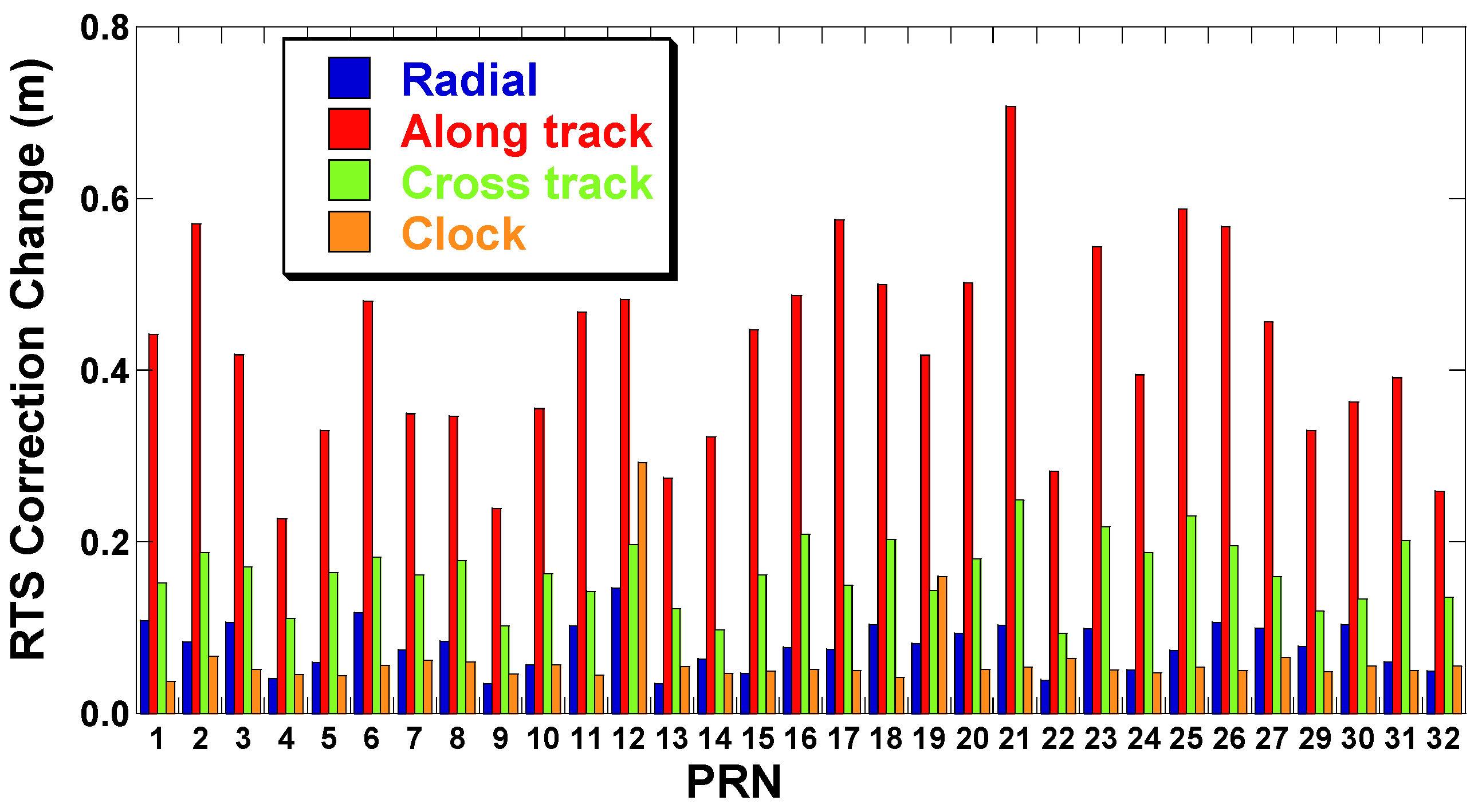
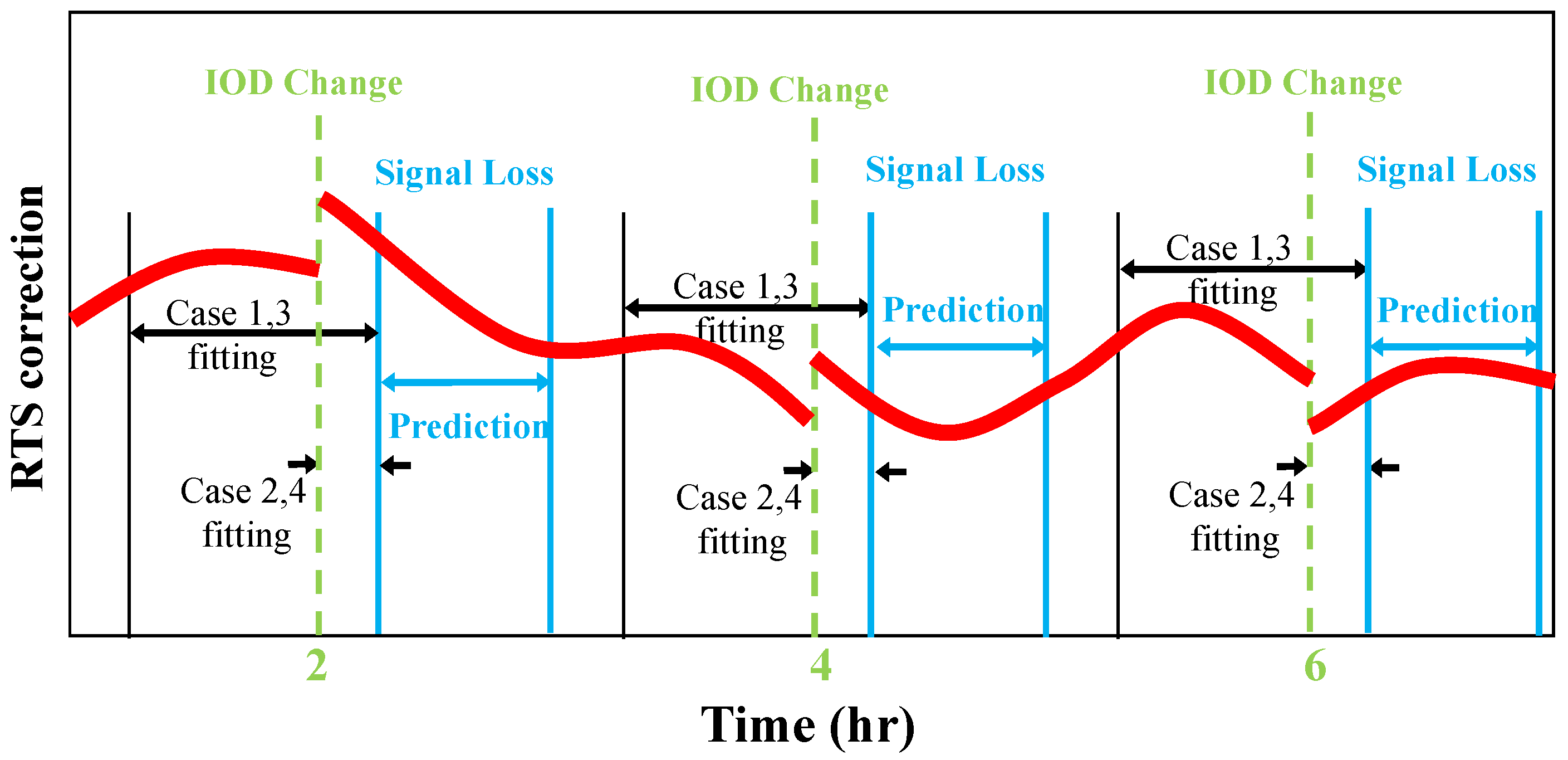
2.2. Analysis of the RTS Correction at the Time of IOD Change
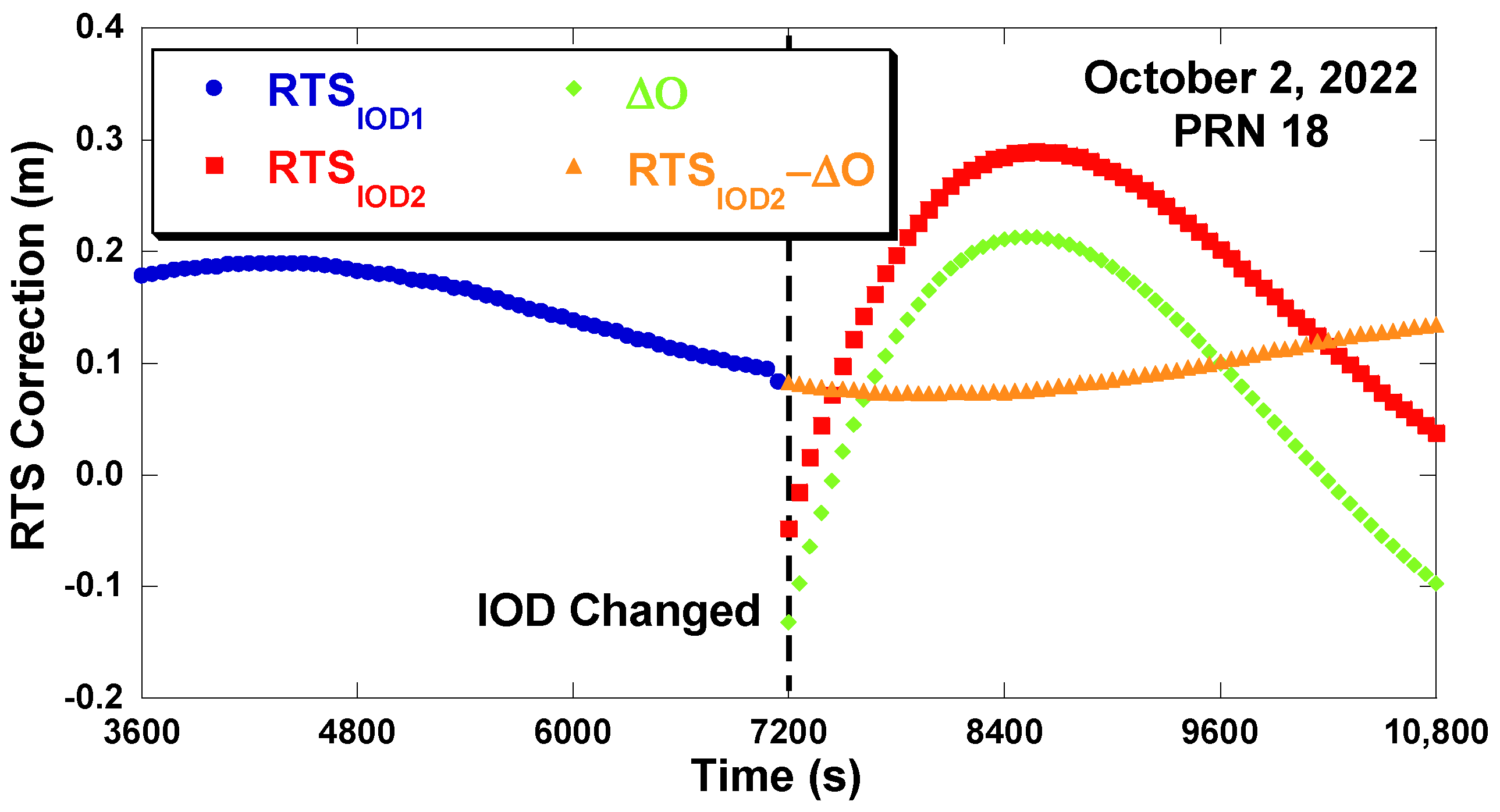
2.3. Change in RTS Correction and Navigation Message at the Time of IOD Change
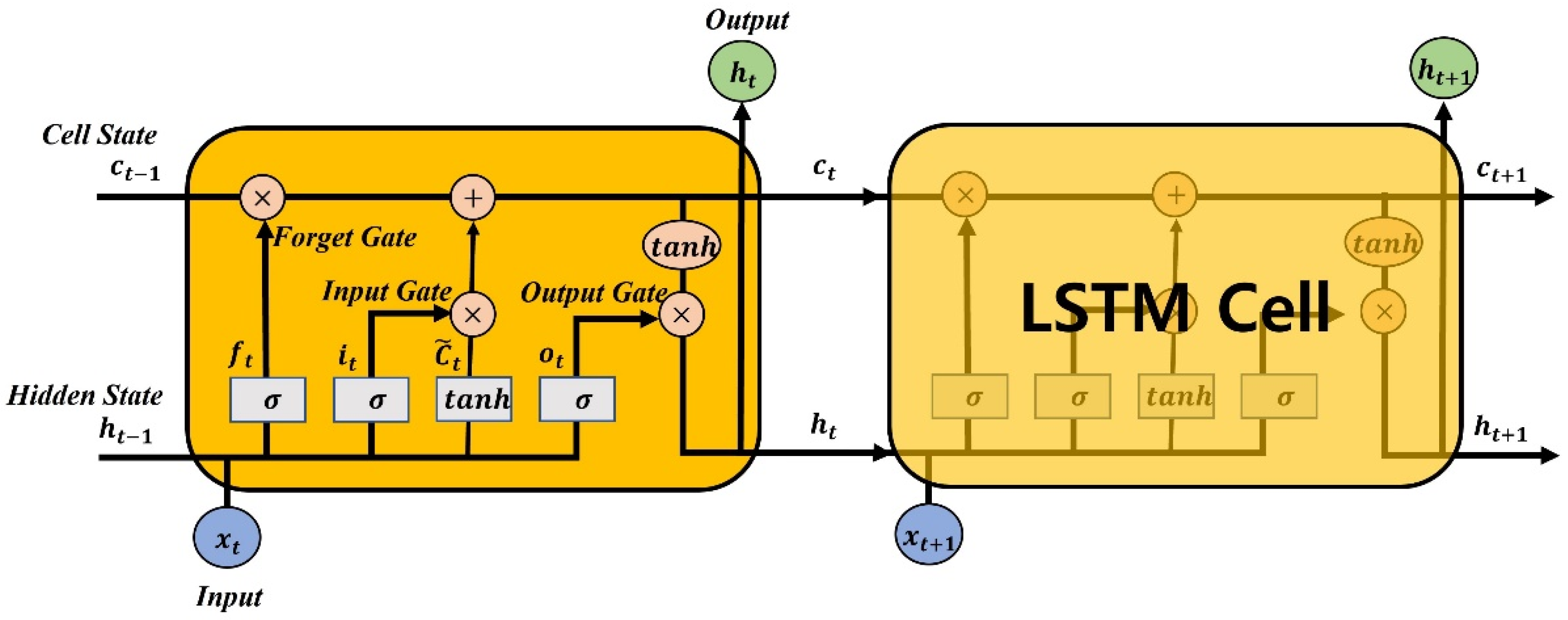
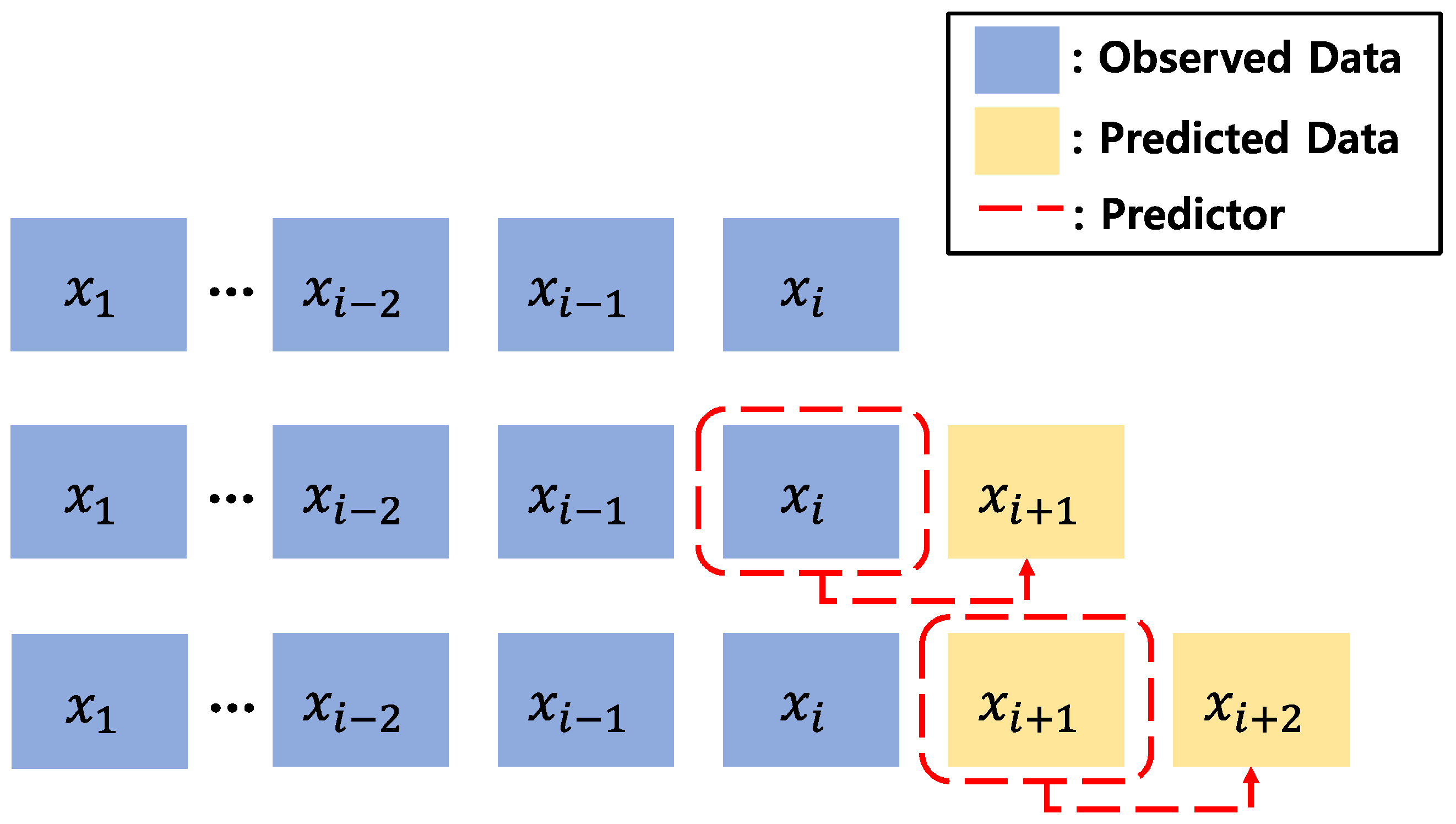
2.4. LSTM Network
3. Data Processing
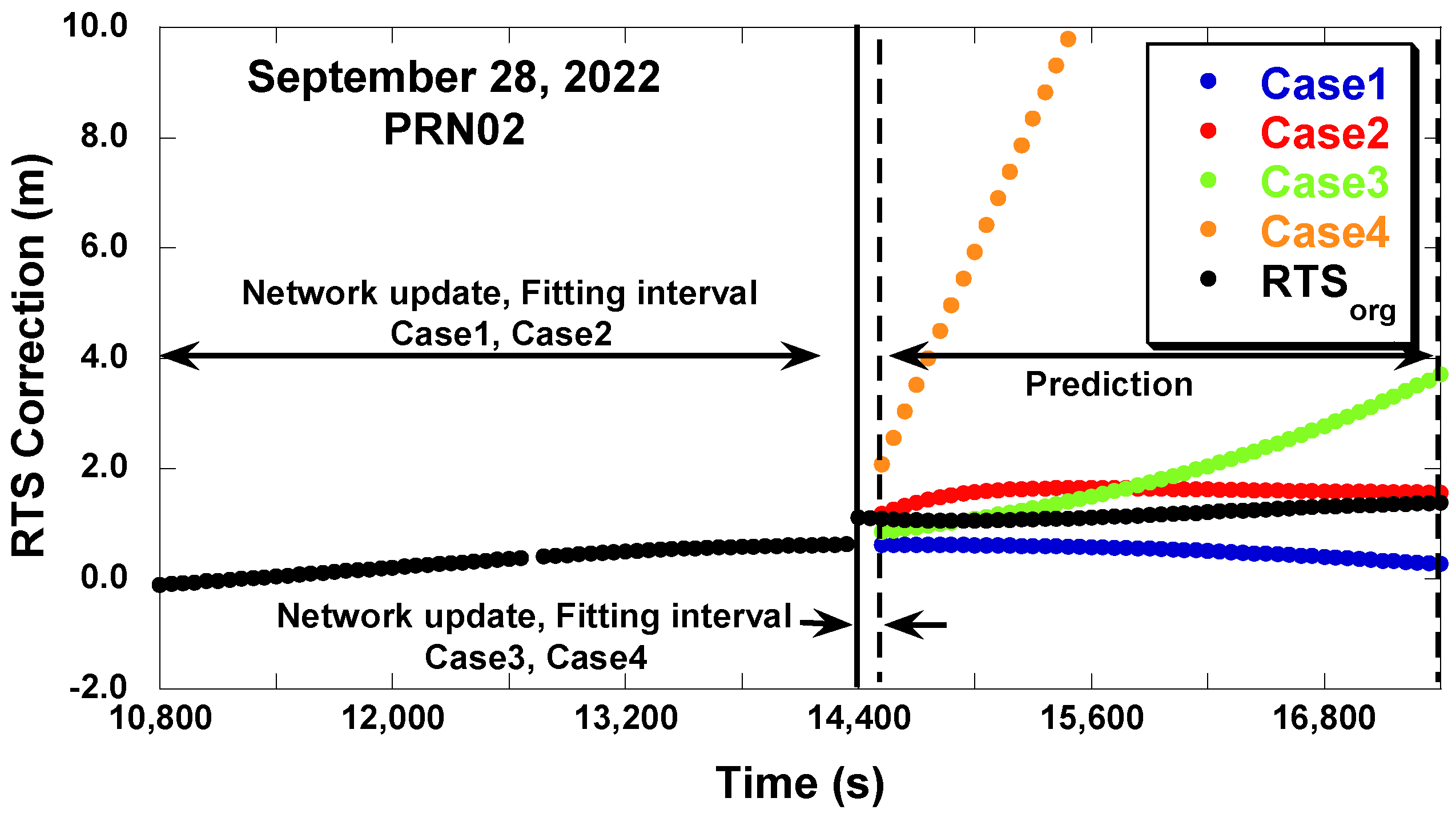
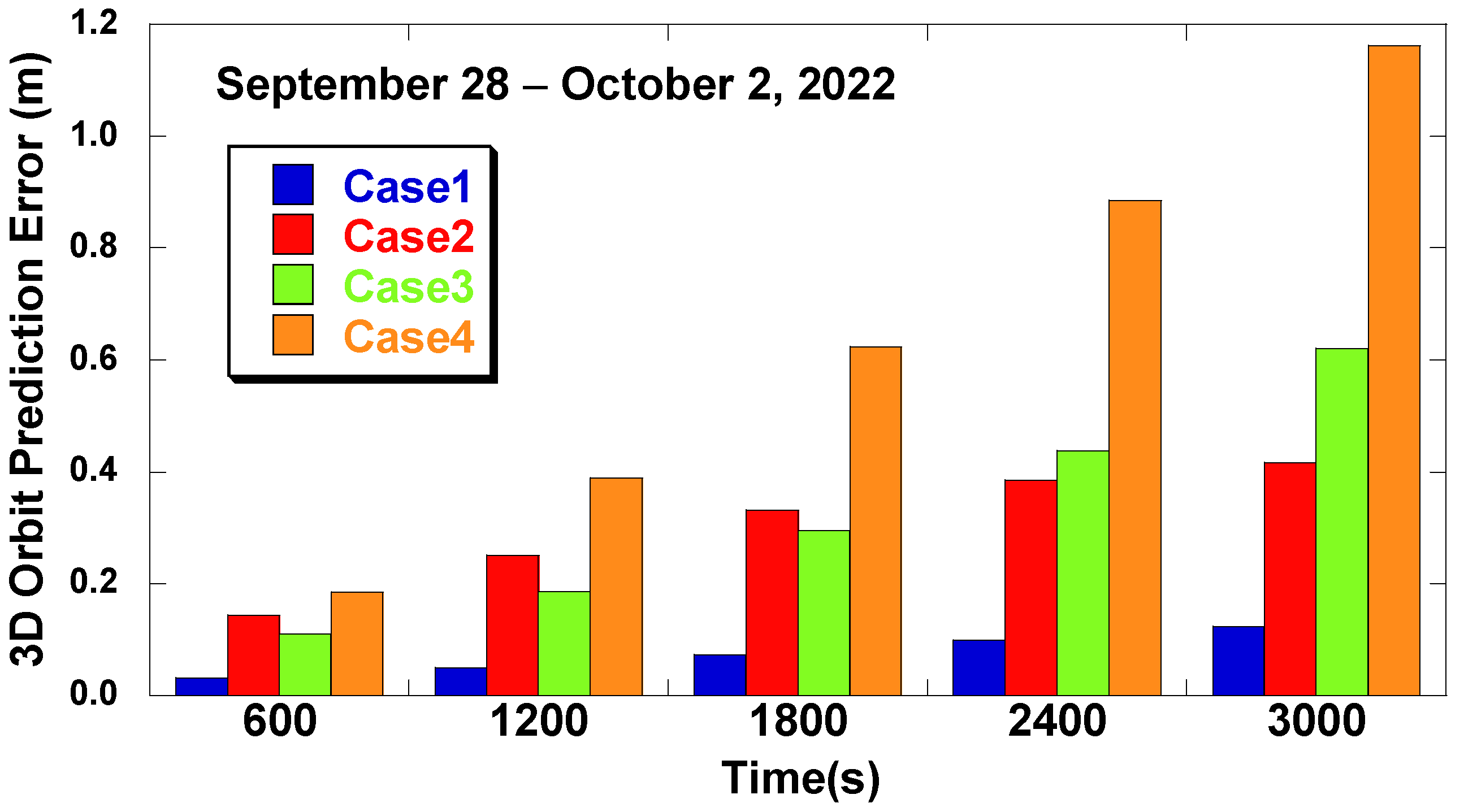
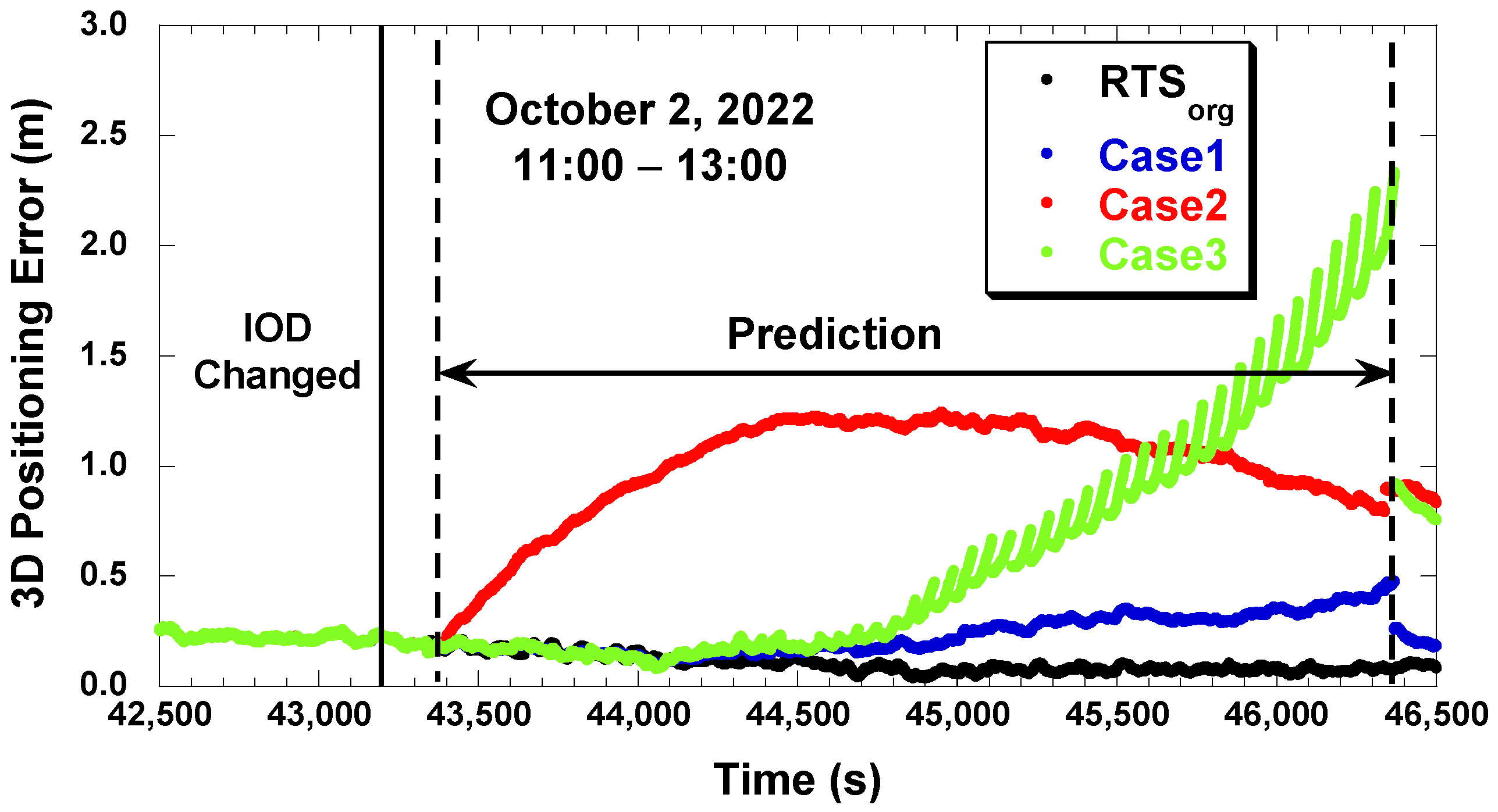
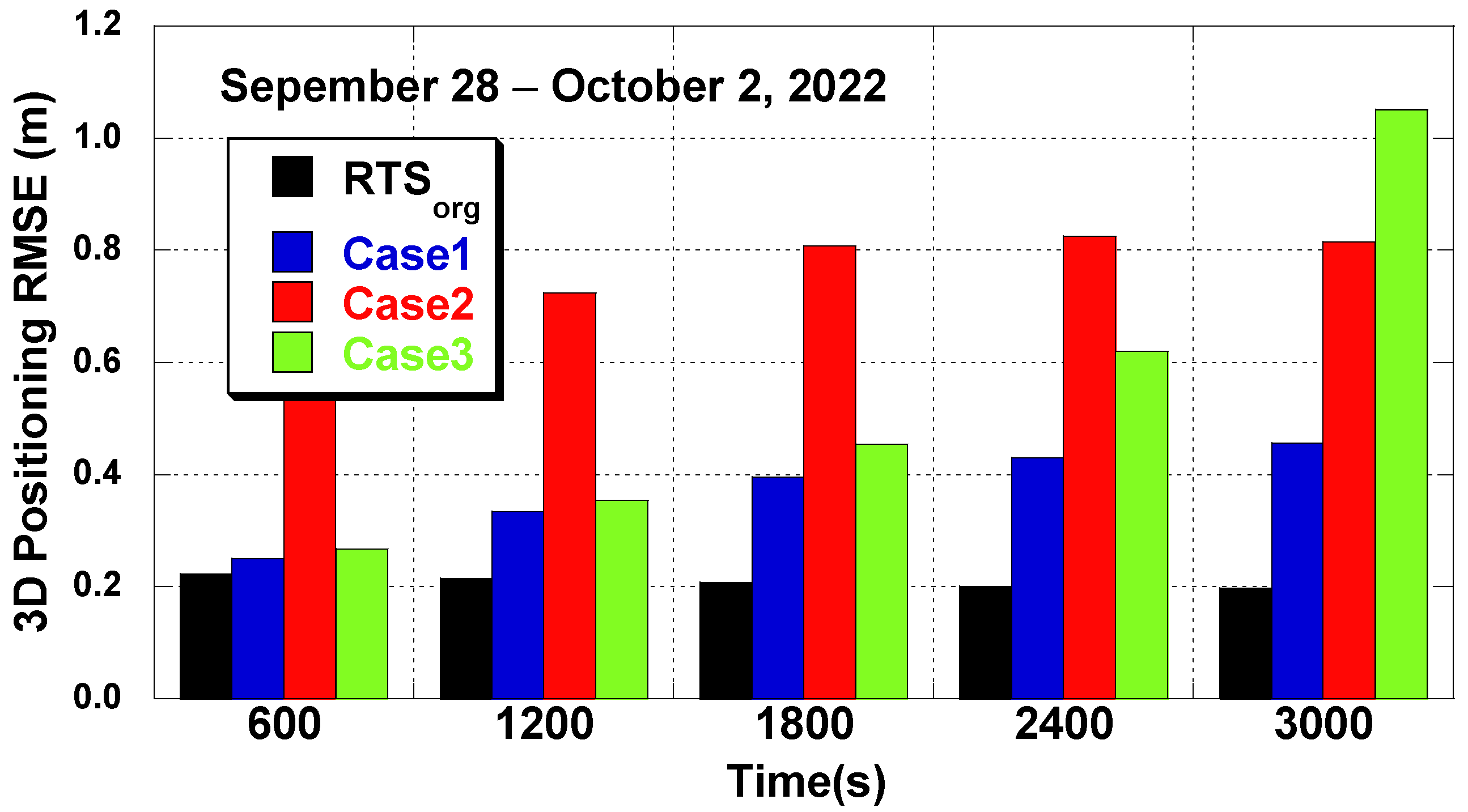
4. RTS Prediction Results
5. PPP Performance Analysis Using RTS Predictions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bhattarai, S.; Ziebart, M. A performance analysis of the IGS predictions of the GPS satellite clocks. In Proceedings of the IGS Workshop, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Ray, J.; Griffiths, J. Status of IGS ultra-rapid products for realtime applications. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 18 December 2008. [Google Scholar]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef] [Green Version]
- Nie, Z.; Gao, Y.; Wang, Z.; Ji, S.; Yang, H. An approach to GPS clock prediction for real-time PPP during outages of RTS stream. GPS Solut. 2017, 22, 14. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Deo, M.; Kubo, N. Maintaining real-time precise point positioning during outages of orbit and clock corrections. GPS Solut. 2017, 21, 937–947. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Li, J.; Zhang, S.; Pan, L.; Kuang, K. Performance assessment of uncombined precise point positioning using multi-GNSS real-time streams: Computational efficiency and RTS interruption. Adv. Space Res. 2018, 62, 3133–3147. [Google Scholar] [CrossRef]
- Lv, Y.; Dai, Z.; Zhao, Q.; Yang, S.; Zhou, J.; Liu, J. Improved Short-Term Clock Prediction Method for Real-Time Positioning. Sensors 2017, 17, 1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, M.; Kim, J. Predicting IGS RTS corrections using ARMA neural networks. Math. Probl. Eng. 2015, 2015, 851761. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Kim, J. GA-ARMA model for predicting IGS RTS corrections. Int. J. Aerosp. Eng. 2017, 2017, 6316590. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Kim, J. A short-term prediction method of the IGS RTS clock correction by using LSTM network. J. Position. Navig. Timing 2019, 8, 209–214. [Google Scholar]
- Kim, B.; Kim, M.; Kim, J.; Bu, S.; Lee, C. Real-time LSTM Prediction of RTS Correction for PPP by a Low-cost Positioning Device. J. Adv. Navig. Technol. 2022, 26, 119–124. [Google Scholar]
- Kim, M.; Kim, J.; Kim, J. Prediction of the IGS RTS Correction using Polynomial Model at IOD Changes. J. Adv. Navig. Technol. 2020, 24, 533–539. [Google Scholar]
- Weber, G.; Mervart, L.; Lukes, Z.; Rocken, C.; Dousa, J. Real-time clock and orbit corrections for improved point positioning via NTRIP. In Proceedings of the ION GNSS 2007, FortWorth, TX, USA, 25–28 September 2007; pp. 1992–1998. [Google Scholar]
- Elsobeiey, M.; Al-Harbi, S. Performance of real-time precise point positioning using IGS real-time service. GPS Solut. 2016, 20, 565–571. [Google Scholar] [CrossRef]
- International GNSS Service RTS Products. Available online: https://igs.org/rts/products/ (accessed on 13 October 2022).
- RTCM Special Committee. RTCM Standard 10403.3 Differential GNSS (Global Navigation Satellite Systems) Services-Version 3, No. 104; RTCM Special Committee: Arlington, TX, USA, 2016. [Google Scholar]
- Li, G.; Lin, Y.; Shi, F.; Liu, J.; Yang, Y.; Shi, J. Using IGS RTS Products for Real-Time Subnanosecond Level Time Transfer. In Proceedings of the 9th China Satellite Navigation Conference, Harbin, China, 23–25 May 2018. [Google Scholar]
- Kim, M.; Myung, J.; Kim, J. A performance analysis of the IGS real-time service. In Proceedings of the 2016 Korean GNSS Society Conference, Jeju, Republic of Korea, 2–4 November 2016. [Google Scholar]
- Kim, M.; Kim, J.; Kim, J. An analysis of the IGS RTS correction changes after IOD changes. In Proceedings of the Korean Navigation Institute Conference, Online, 23 October 2020. [Google Scholar]
- Kim, J. Development of Real-Time Precise Satellite Navigation Device Using RTS Correction with Bidirectional LSTM Algorithm. Master’s Dissertation, Korea Aerospace University, Goyang, Republic of Korea, February 2021. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Deep Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction. In Proceedings of the International Workshop on Urban Computing, London, UK, 19 August 2018. [Google Scholar]
- Zhang, G.; Li, X.; Wang, X.; Zhang, Z.; Hu, G.; Li, Y.; Zhang, R. Research on the Prediction Problem of Satellite Mission Schedulability Based on Bi-LSTM Model. Aerospace 2022, 9, 676. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.; Koutnik, J.; Steunebrink, B.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Hadas, T.; Kaplon, J.; Wilgan, K.; Bosy, J.; Sierny, J. Verification of real-time IGS products and their influence on Precise Point Positioning. In Proceedings of the GNSS PPP Workshop: Reaching Full Potential, Ottawa, ON, Canada, 12–14 June 2013. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- RTKLIB: An Open-Source Program Package for GNSS Positioning. Available online: https://rtklib.com/ (accessed on 13 October 2022).


| Product | Description | Ref Point | Satellite System |
|---|---|---|---|
| SSRA01IGS1 | Single-Epoch Combination | APC | GPS |
| SSRC01IGS1 | Single-Epoch Combination | CoM | GPS |
| SSRA02IGS1 | Kalman Filter Combination | APC | GPS, GLONASS, Galileo |
| SSRC02IGS1 | Kalman Filter Combination | CoM | GPS, GLONASS, Galileo |
| SSRA03IGS1 | Kalman Filter Combination | APC | GPS, GLONASS, Galileo, BeiDou |
| SSRC03IGS1 | Kalman Filter Combination | CoM | GPS, GLONASS, Galileo, BeiDou |
| Parameter | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| IOD use | Past + Recent | Recent | Past + Recent | Recent |
| Prediction Method | LSTM | LSTM | 4th Polynomial | 1st Polynomial |
| Fitting length | 3600 s | 180 s | 3600 s | 180 s |
| Case 1 | Case 2 | Case 3 | ||
|---|---|---|---|---|
| H Mean | 0.14 | 0.29 | 0.42 | 0.46 |
| V Mean | 0.10 | 0.27 | 0.51 | 0.56 |
| H STD | 0.04 | 0.12 | 0.13 | 0.33 |
| V STD | 0.06 | 0.14 | 0.21 | 0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.; Kim, J. Prediction of IGS RTS Orbit Correction Using LSTM Network at the Time of IOD Change. Sensors 2022, 22, 9421. https://doi.org/10.3390/s22239421
Kim B, Kim J. Prediction of IGS RTS Orbit Correction Using LSTM Network at the Time of IOD Change. Sensors. 2022; 22(23):9421. https://doi.org/10.3390/s22239421
Chicago/Turabian StyleKim, Beomsoo, and Jeongrae Kim. 2022. "Prediction of IGS RTS Orbit Correction Using LSTM Network at the Time of IOD Change" Sensors 22, no. 23: 9421. https://doi.org/10.3390/s22239421
APA StyleKim, B., & Kim, J. (2022). Prediction of IGS RTS Orbit Correction Using LSTM Network at the Time of IOD Change. Sensors, 22(23), 9421. https://doi.org/10.3390/s22239421






