Physical Simulation of Ultrasonic Imaging Logging Response
Abstract
1. Introduction
2. Experimental System and Methods
2.1. Experimental Equipment
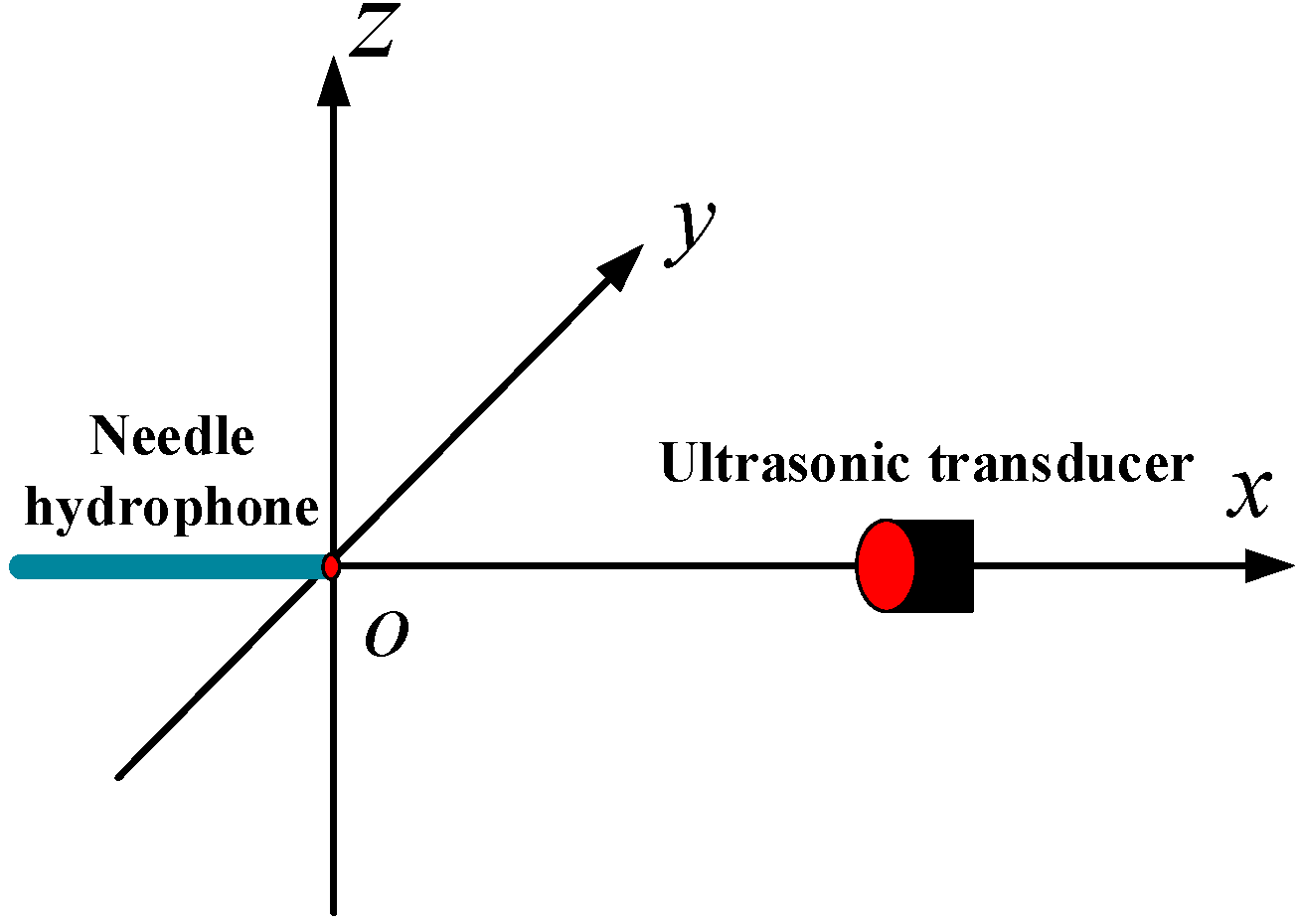
2.1.1. Experimental Measurement System
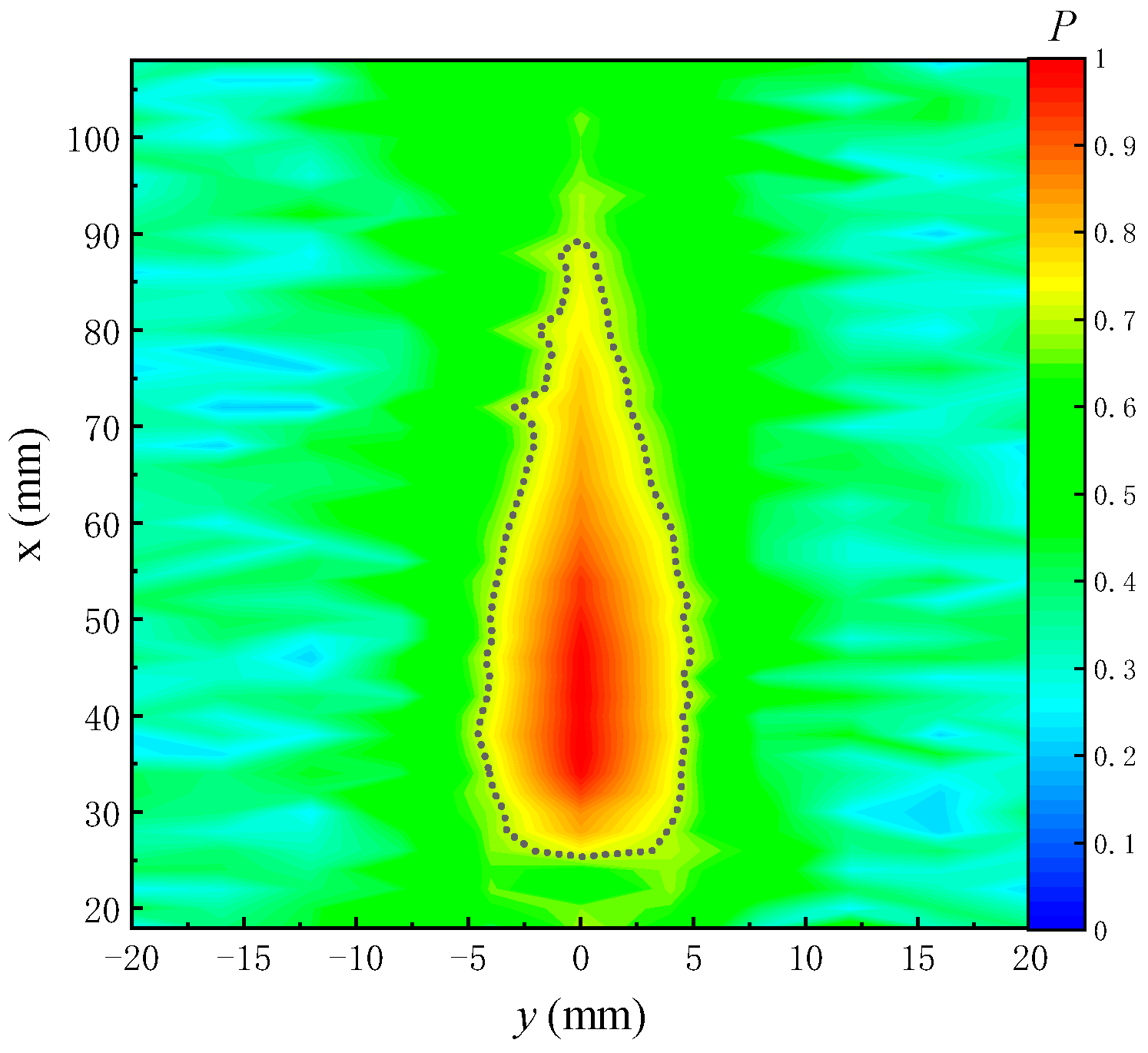
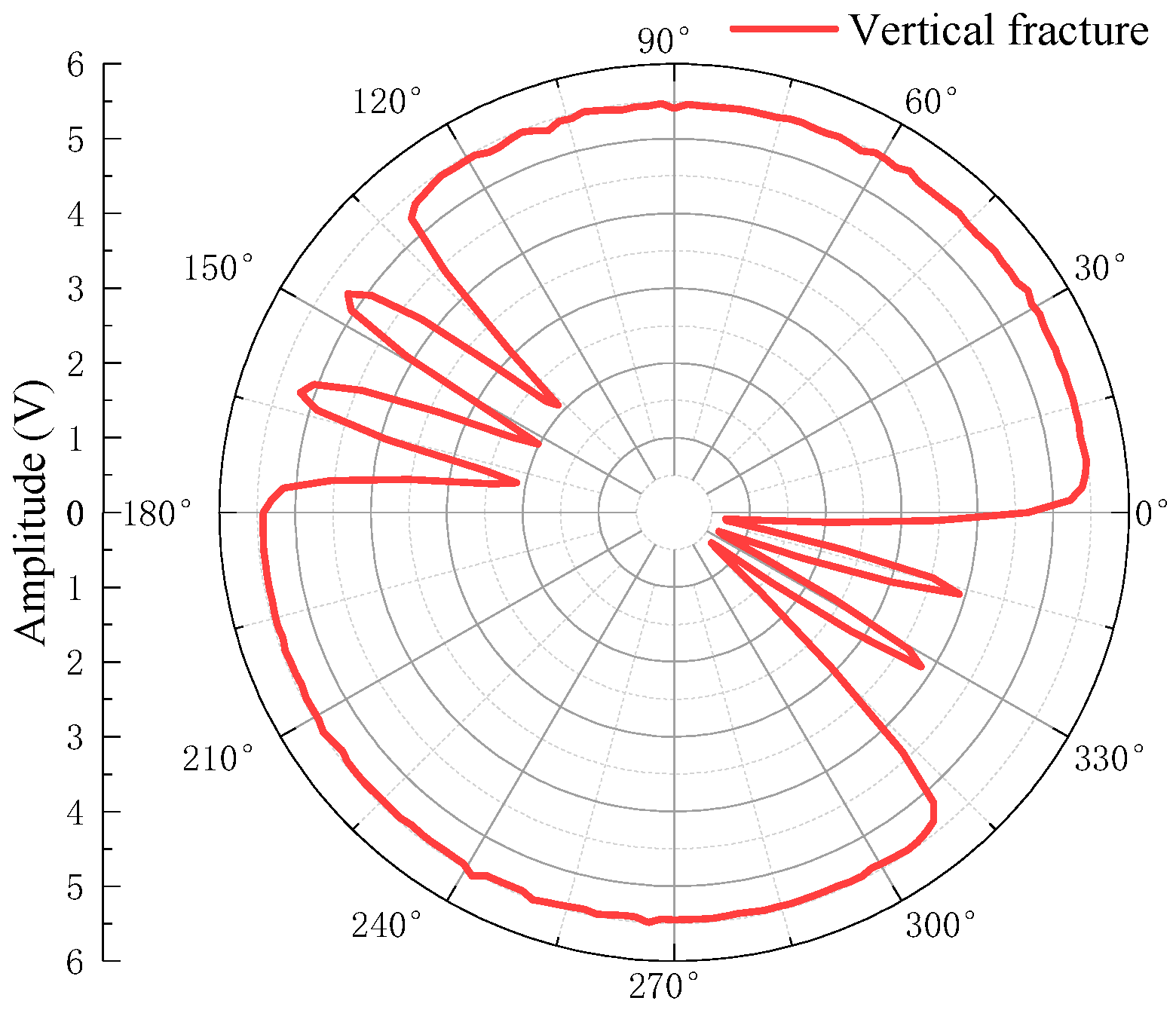
2.1.2. Ultrasonic Transducer and Its Radiated Sound Field Distribution
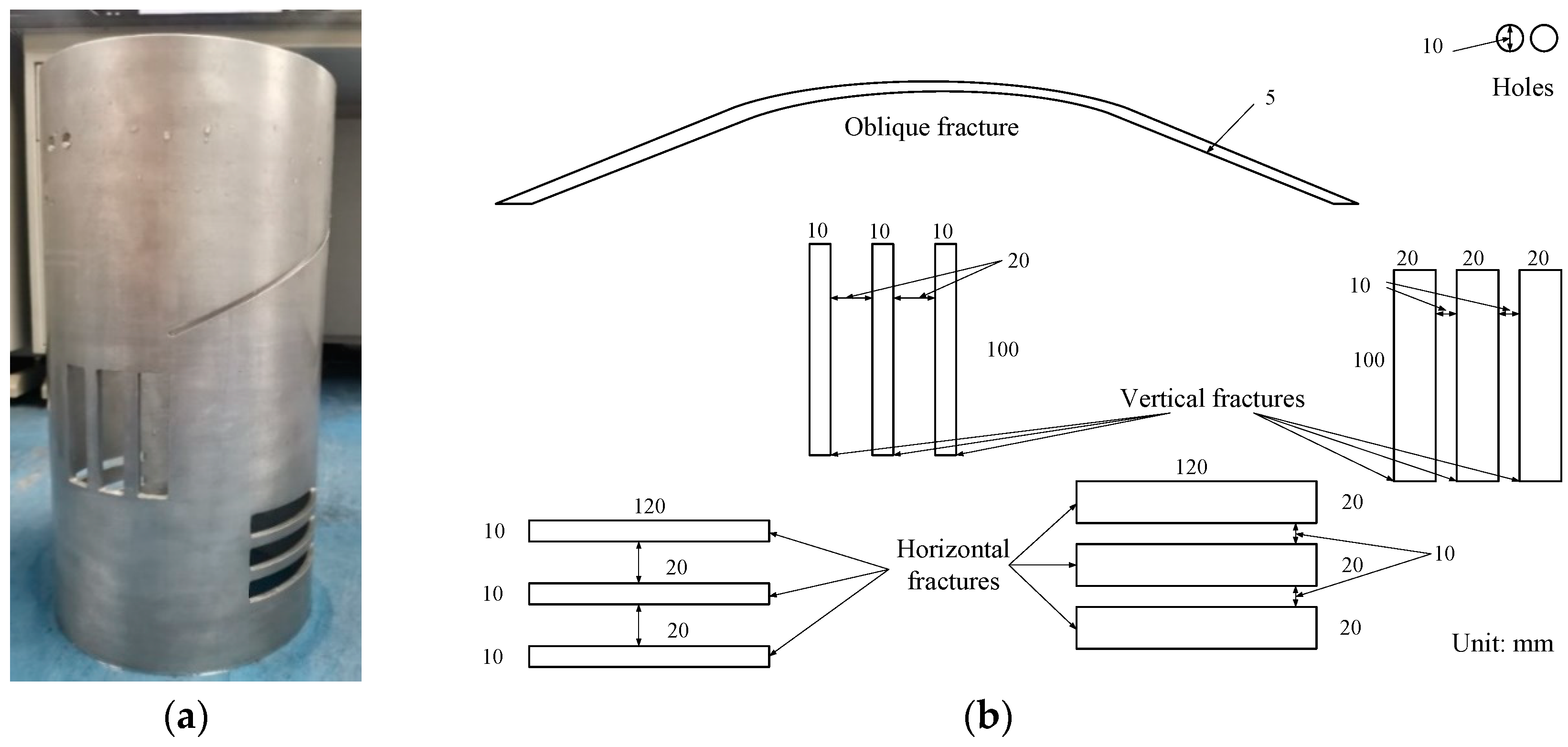
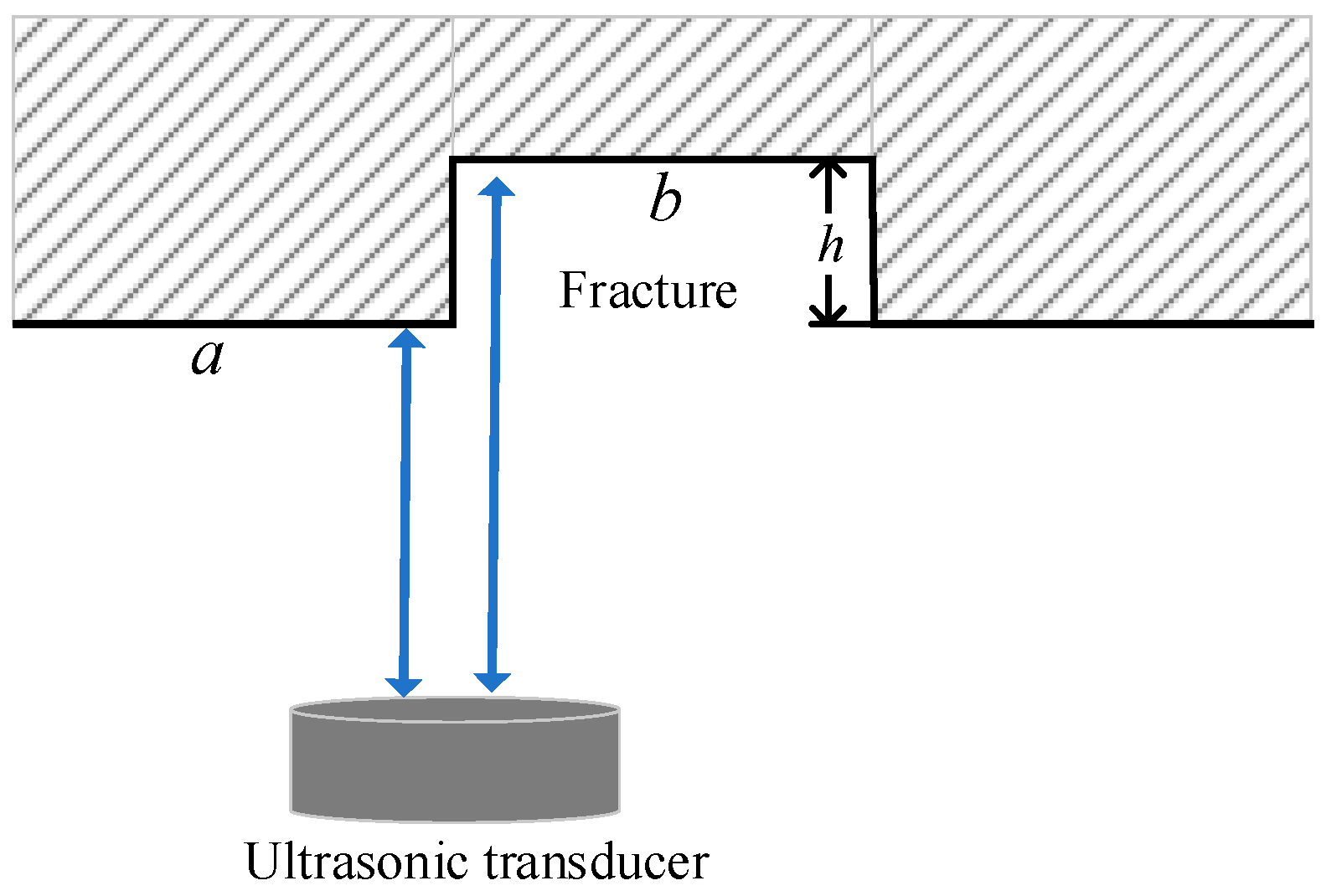
2.1.3. Experimental Measurement Samples
- (1)
- Plate reflector samples
- (2)
- Simulated borehole sample
2.2. Experimental Procedure
2.2.1. Ultrasonic Imaging of Plate Reflector Samples
2.2.2. Ultrasonic Imaging of the Simulated Borehole
3. Experimental Data Processing and Analysis
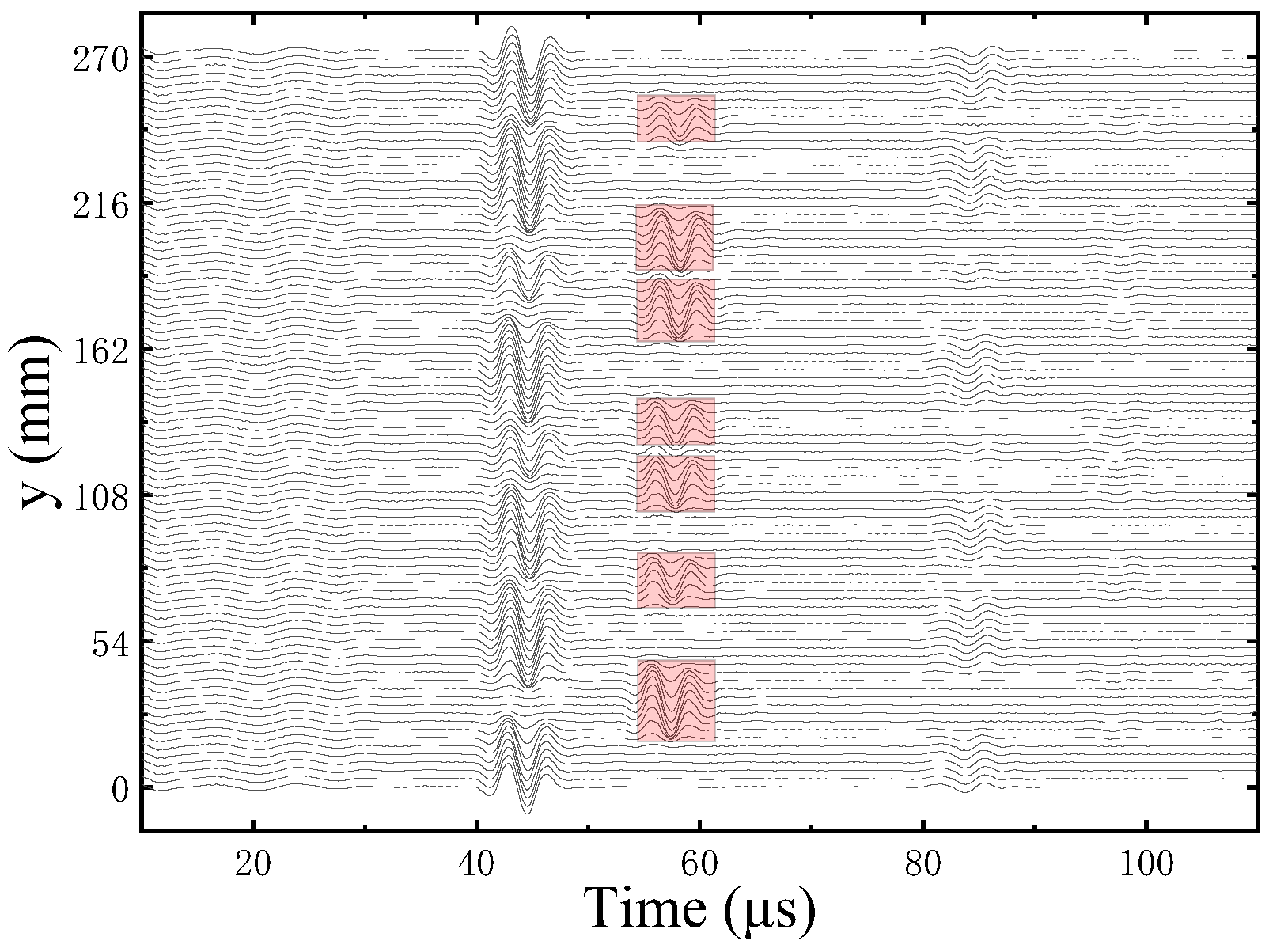
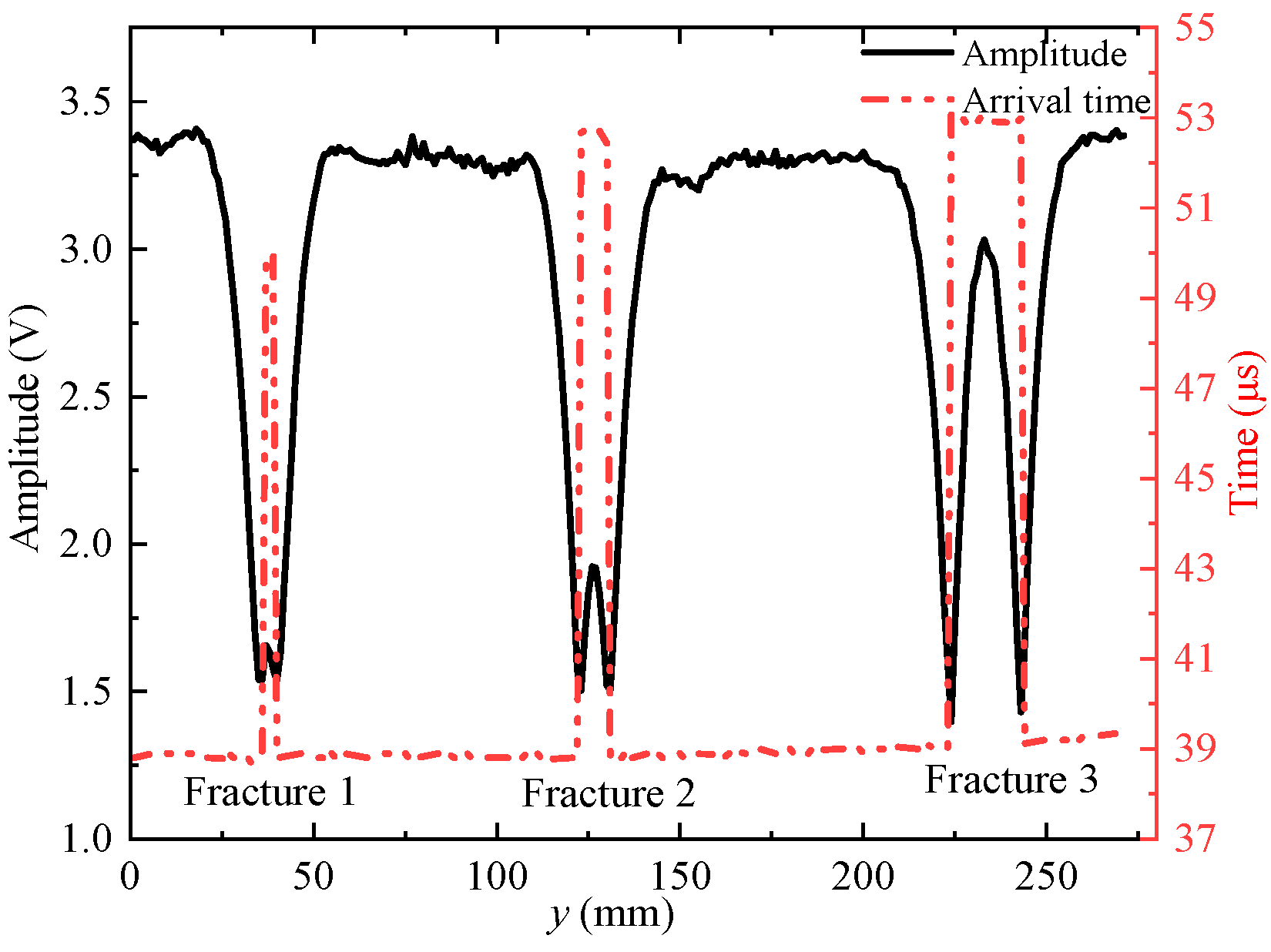
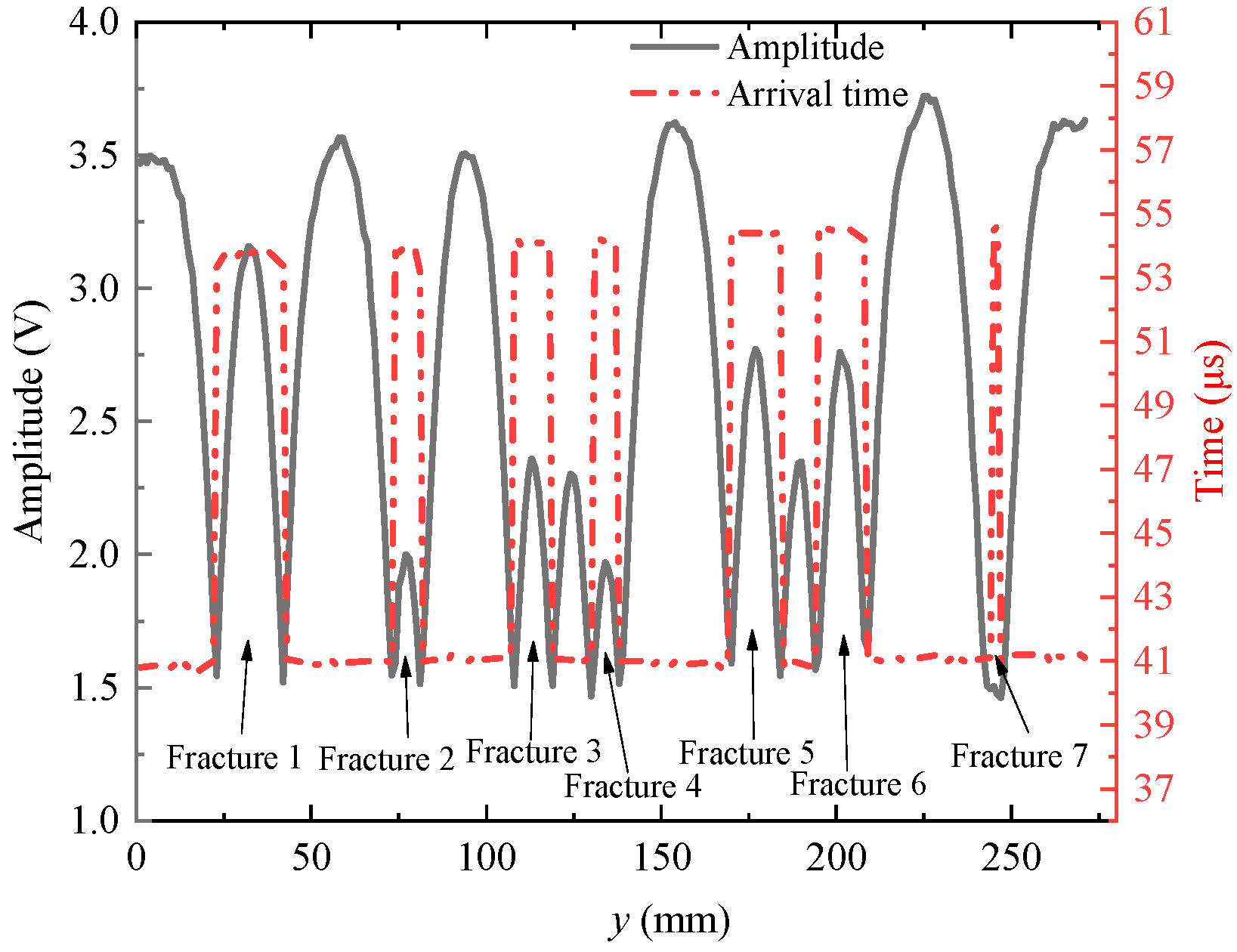
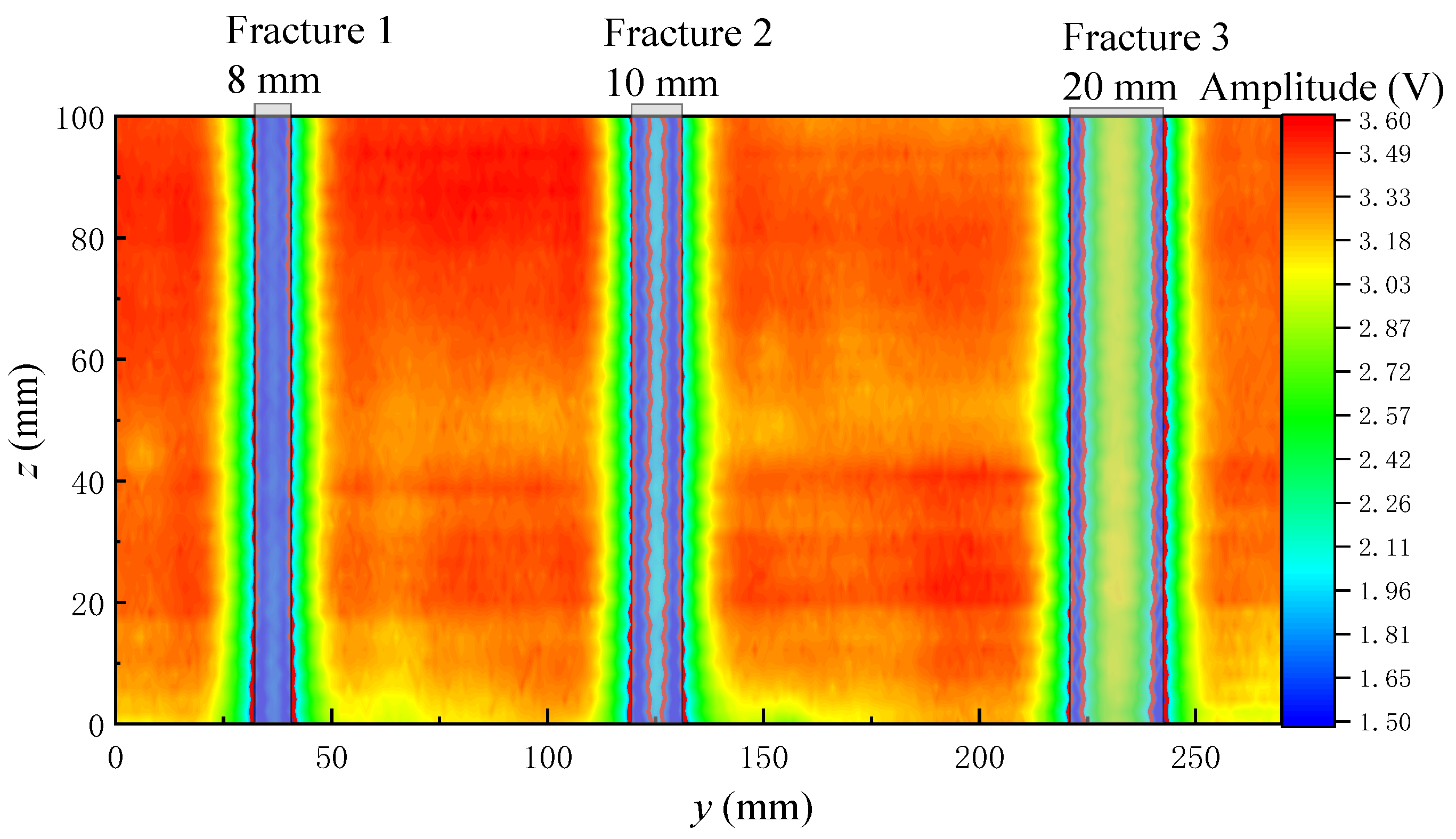
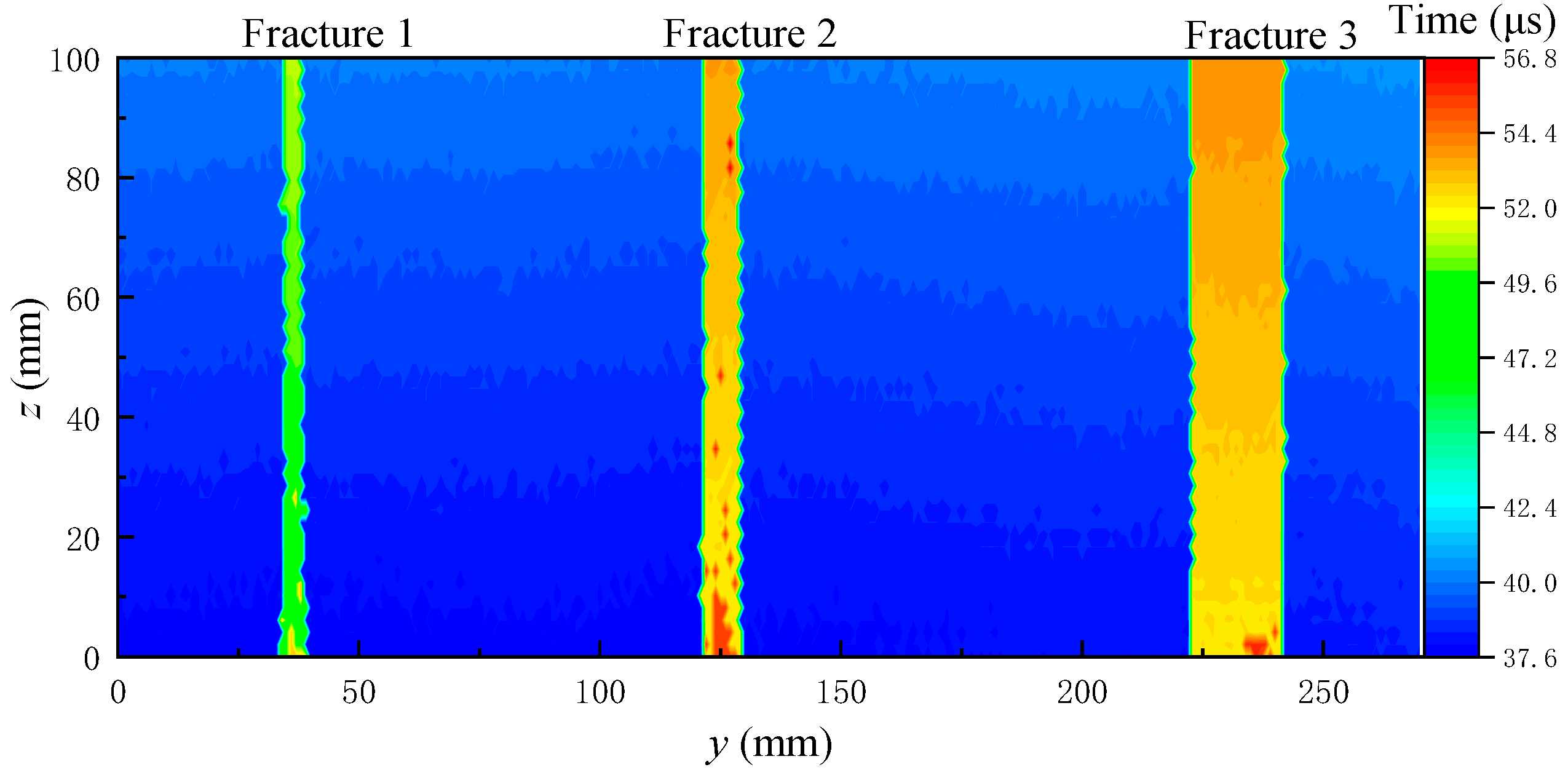
3.1. Experimental Results and Analysis of Plate Reflector Samples
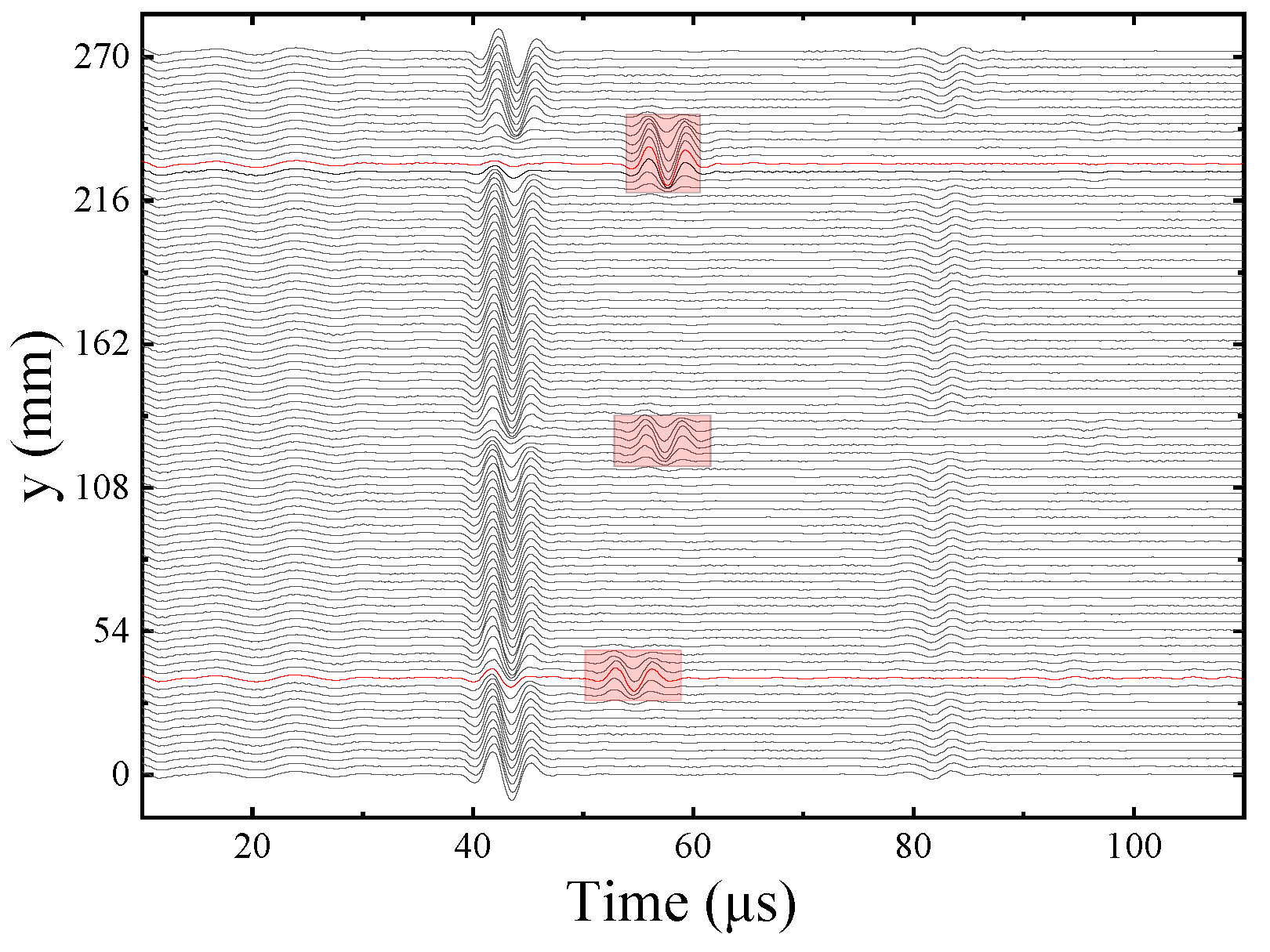
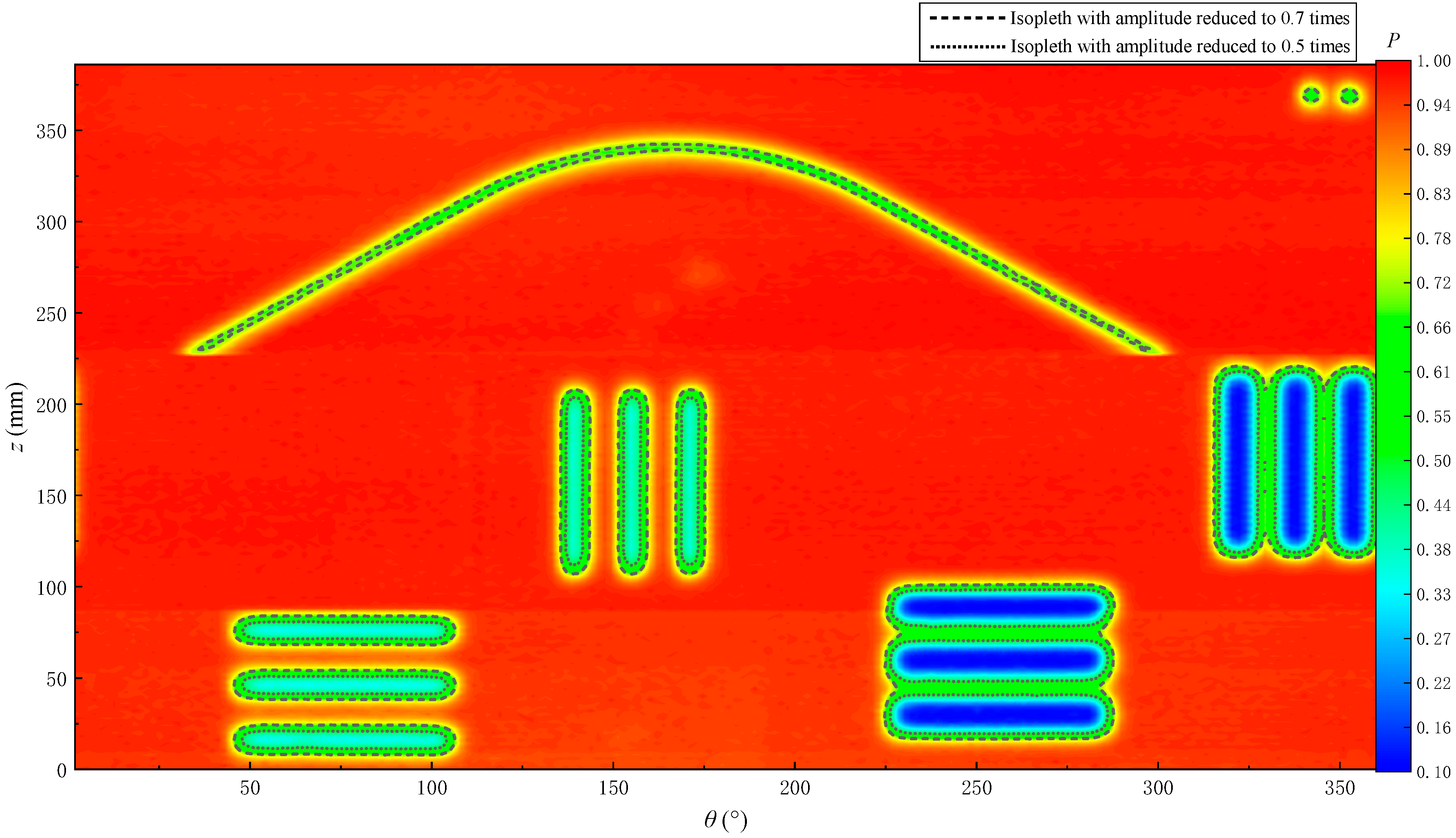
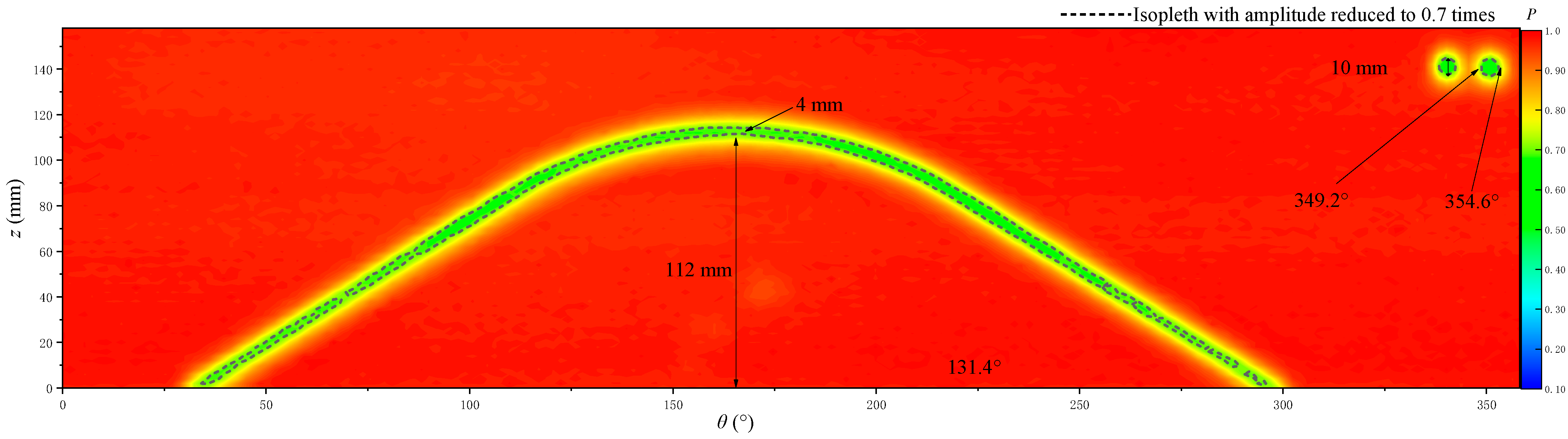
3.2. Experimental Results and Analysis of the Simulated Borehole

4. Conclusions
- (1)
- When the ultrasonic transducer is at the fracture boundary and the fracture depth is greater than a quarter of the ultrasonic signal wavelength, two wave packets will appear in the reflected echo waveform. The arrival times of two wave packets are extracted and imaged and the depth of the fracture can be determined.
- (2)
- The fracture identification accuracy of the ultrasonic imaging logging is related to the acoustic spot diameter radiated by the ultrasonic transducer on the reflecting surface. A fracture with a width equal to or greater than 8 mm of the ultrasonic transducer’s sound spot diameter and multiple fractures with a fracture spacing greater than or equal to the sound spot diameter can be effectively identified.
- (3)
- When the simulated borehole is measured, the distance between the transducer and reflective surface is small and the diameter of the acoustic spot is reduced. Fractures with a width of 5 mm can be effectively detected. Large fracture depths and great attenuation of the echo wave at the fracture are conducive to the identification of fractures.
- (4)
- The position and scale of fractures and holes can be identified by combining the echo amplitude imaging and arrival time imaging. If the fracture and hole are small, then the arrival time of the scattered wave from the edge is basically consistent with that of the reflected wave from the surface without fractures and holes. Thus, the arrival time of the echo wave alone cannot be used to identify the fracture and must be combined with the echo amplitude.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Che, X.; Zhao, T.; Qiao, W.; Lu, W.; Fan, J. Fracture identification and evaluation of multi-pole acoustic logging. Oil Gas Geol. 2020, 41, 1263–1272. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, W.; Pan, H. Principles and Applications of Acoustic Logging; Petroleum Industry Press: Beijing, China, 2009; pp. 1–20. [Google Scholar]
- Gan, Q.; Zhang, C.; Zhu, L.; Yang, S. Analysis of fracture identification effect of ultrasonic imaging logger under oil-based mud. Energy Environ. Prot. 2017, 39, 57–63. [Google Scholar] [CrossRef]
- Felice, M.; Fan, Z. Sizing of flaws using ultrasonic bulk wave testing: A review. Ultrasonics 2018, 88, 26–42. [Google Scholar] [CrossRef] [PubMed]
- Lefever, G.; Snoeck, D.; De Belie, N.; Van Vlierberghe, S.; Van Hemelrijck, D.; Aggelis, D. The contribution of elastic wave NDT to the characterization of modern cementitious media. Sensors 2020, 20, 2959. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhao, J.; Pan, Y. Surface circular-arc defects interacted by laser-generated Rayleigh wave. Ultrasonics 2020, 103, 106085. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Cho, Y.; Kim, J.; Malikov, A.; Kim, Y.; Yi, J.; Li, W. Non-destructive evaluation of coating thickness using water immersion ultrasonic testing. Coatings 2021, 11, 1421. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, C.; Qin, D.; Luo, Y.; Momayez, M. Estimating ultrasonic time-of-flight through echo signal envelope and modified Gauss Newton method. Measurement 2016, 94, 355–363. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Z.; Li, Y. Application of ultrasonic array method for the inspection of TC18 addictive manufacturing titanium alloy. Sensors 2019, 19, 4371. [Google Scholar] [CrossRef] [PubMed]
- Dhutti, A.; Tumin, S.; Balachandran, W.; Kanfoud, J.; Gan, T. Development of ultrasonic guided wave transducer for monitoring of high temperature pipelines. Sensors 2019, 19, 5443. [Google Scholar] [CrossRef] [PubMed]
- Sinclair, A.; Malkin, R. Sensors for ultrasonic nondestructive testing (NDT) in harsh environments. Sensors 2020, 20, 456. [Google Scholar] [CrossRef] [PubMed]
- Zemanek, J.; Caldwell, R.; Holcomb, S.; Holcomb, S.; Norton, L.; Straus, A. The borehole televiewer-A new logging concept for fracture location and other types of borehole inspection. J. Pet. Technol. 1969, 21, 762–774. [Google Scholar] [CrossRef]
- Liu, G. Research on High-Performance Ultrasonic Imaging Logging Instrument. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2008. [Google Scholar]
- He, Y. Research and Implementation of Echo Signal Detection Algorithm for Ultrasonic Well Logger. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2012. [Google Scholar]
- Lu, F.; Gao, H.; Li, J. High performance ultrasonic TV imaging logging instrument. Well Logging Technol. 2009, 33, 275–278. [Google Scholar] [CrossRef]
- Zhang, J. Application of ultrasonic technology in imaging logging instrument. Ship Electron. Eng. 2005, 25, 92–95. [Google Scholar]
- Blyth, M.; Sakiyama, N.; Hori, H.; Yamamoto, H.; Nakajima, H.; Din, S.; Haecker, A.; Kittridge, M. Revealing hidden information: High-resolution logging-while-drilling slowness measurements and imaging using advanced dual ultrasonic technology. Petrophysics 2021, 62, 89–108. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, C. Extraction of longitudinal and transverse wave information from acoustic full-wave column logs by long and short time window energy ratio method. J. Oil Gas (J. Jianghan Inst. Pet.) 2006, 28, 72–75. [Google Scholar]
- Wang, W.; Gao, X.; Liu, X. Comparative analysis of several first-to-automatic pickup algorithms for tunnel over detection by seismic wave method. Tunn. Constr. (Engl. Chin.) 2019, 39, 1239–1246. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, J.; Zhang, Z. A new correction method for formation dip angle in electrical imaging logs. China Offshore Oil Gas 2017, 29, 52–56. [Google Scholar] [CrossRef]









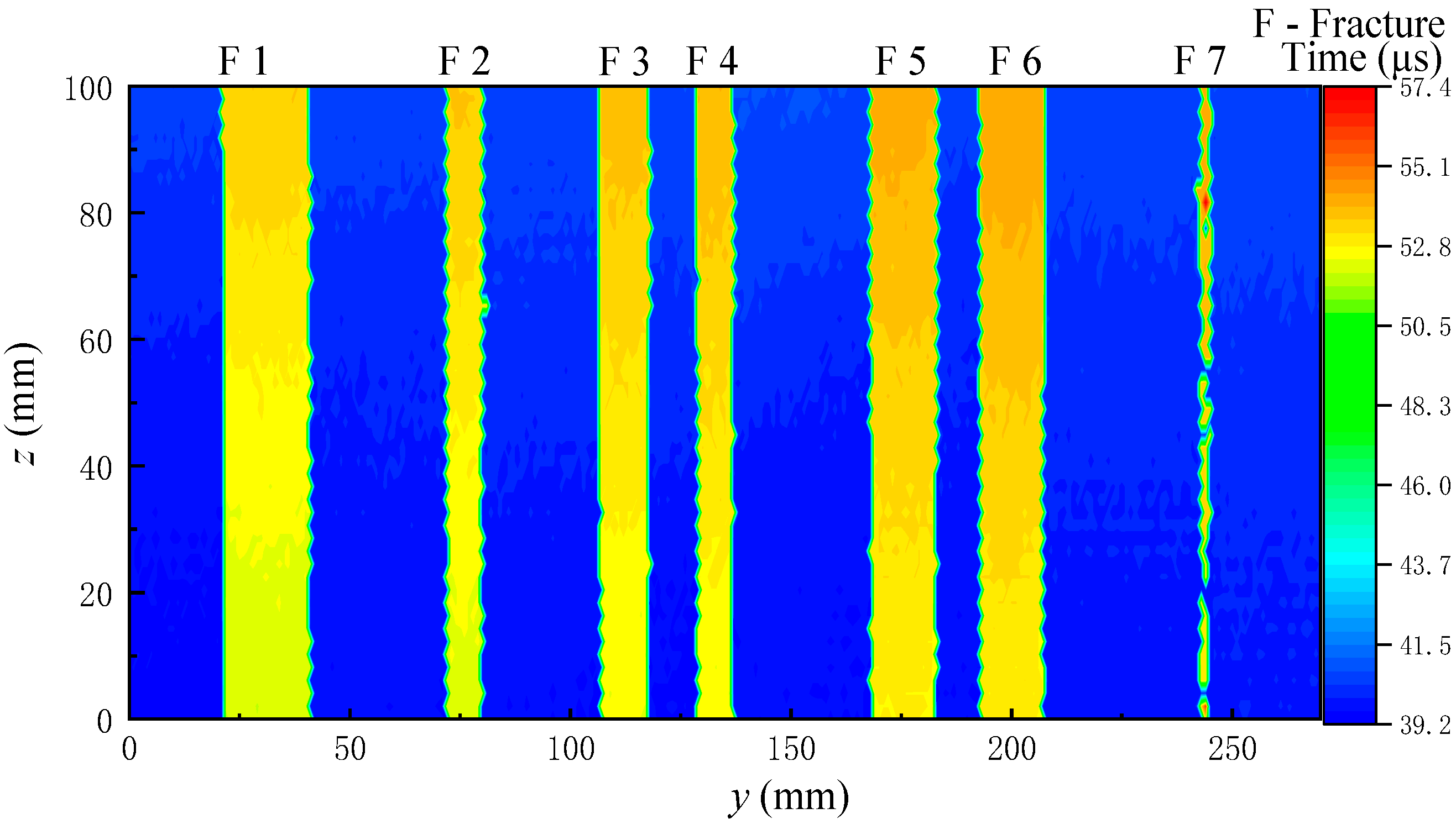



| Fracture No | Identified (mm) Width/mm | Real (mm) Width/mm | Error (mm) | Relative Error (%) | |
|---|---|---|---|---|---|
| Grooved sandstone Plate 1 | Fracture 1 | 8 | 8 | 0 | 0 |
| Fracture 2 | 10 | 10 | 0 | 0 | |
| Fracture 3 | 22 | 20 | 2 | 10 | |
| Grooved sandstone Plate 2 | Fracture 1 | 22 | 21 | 1 | 4.7 |
| Fracture 2 | 11 | 11 | 0 | 0 | |
| Fracture 3 | 14 | 13 | 1 | 7.7 | |
| Fracture 4 | 11 | 11 | 0 | 0 | |
| Fracture 5 | 17 | 16 | 1 | 6.3 | |
| Fracture 6 | 16 | 16 | 0 | 0 | |
| Fracture 7 | 8 | 9 | 1 | 11.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Han, J.; Wu, J.; Che, X.; Qiao, W.; Wang, J.; Chen, X. Physical Simulation of Ultrasonic Imaging Logging Response. Sensors 2022, 22, 9422. https://doi.org/10.3390/s22239422
Lu J, Han J, Wu J, Che X, Qiao W, Wang J, Chen X. Physical Simulation of Ultrasonic Imaging Logging Response. Sensors. 2022; 22(23):9422. https://doi.org/10.3390/s22239422
Chicago/Turabian StyleLu, Junqiang, Jiyong Han, Jinping Wu, Xiaohua Che, Wenxiao Qiao, Jiale Wang, and Xu Chen. 2022. "Physical Simulation of Ultrasonic Imaging Logging Response" Sensors 22, no. 23: 9422. https://doi.org/10.3390/s22239422
APA StyleLu, J., Han, J., Wu, J., Che, X., Qiao, W., Wang, J., & Chen, X. (2022). Physical Simulation of Ultrasonic Imaging Logging Response. Sensors, 22(23), 9422. https://doi.org/10.3390/s22239422








