Optimal Underwater Acoustic Warfare Strategy Based on a Three-Layer GA-BP Neural Network
Abstract
:1. Introduction
2. Materials and Methods
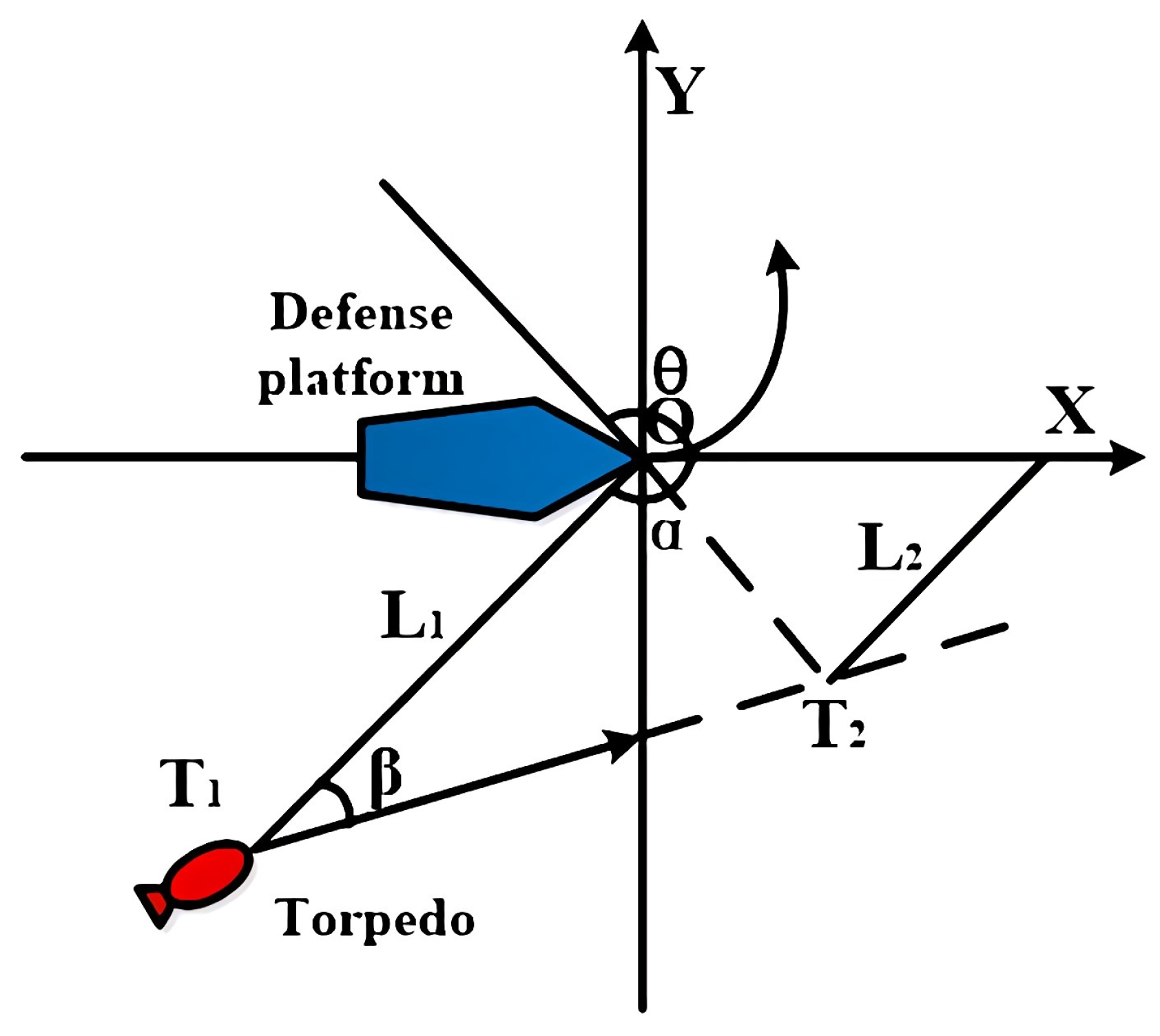
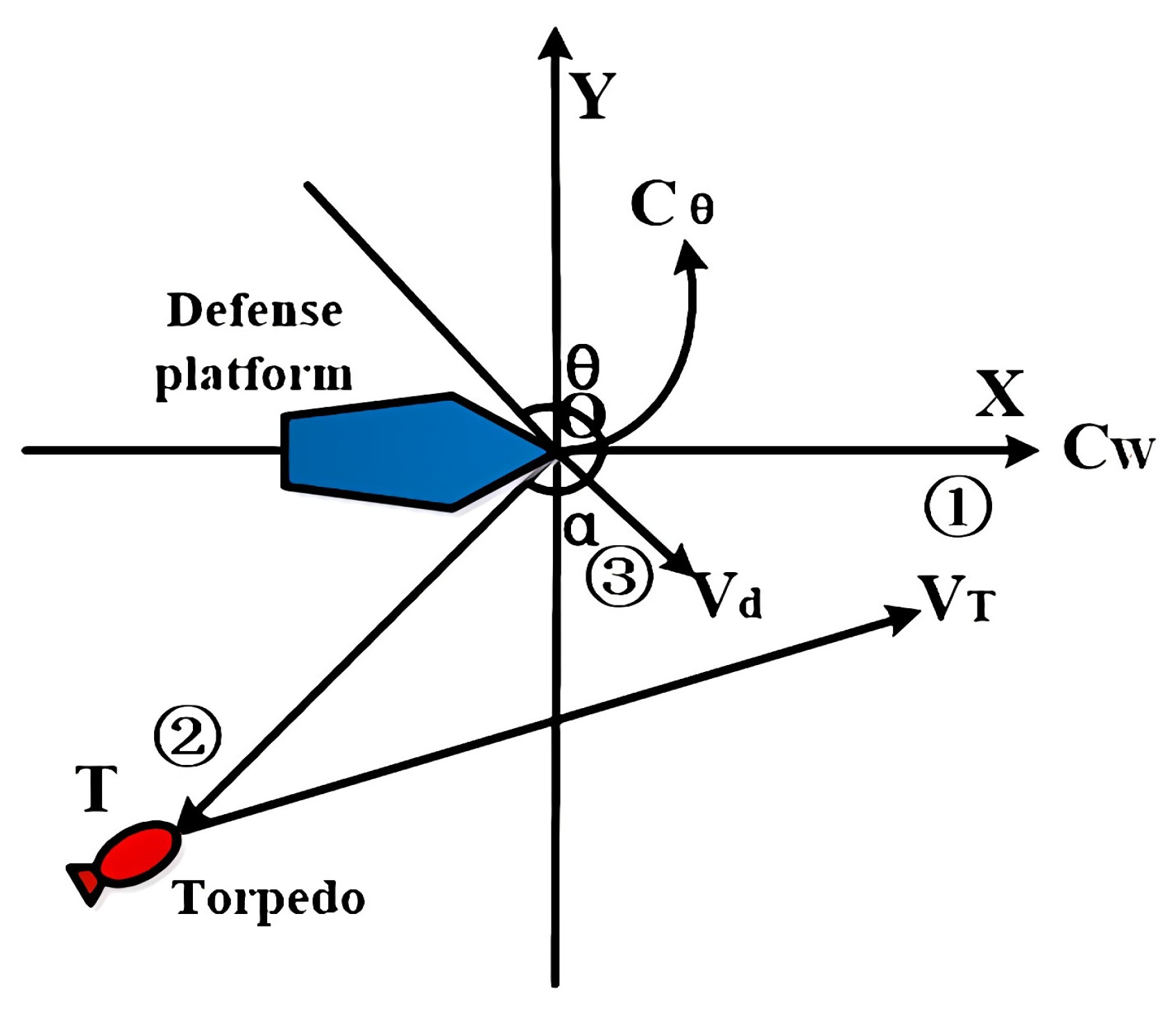
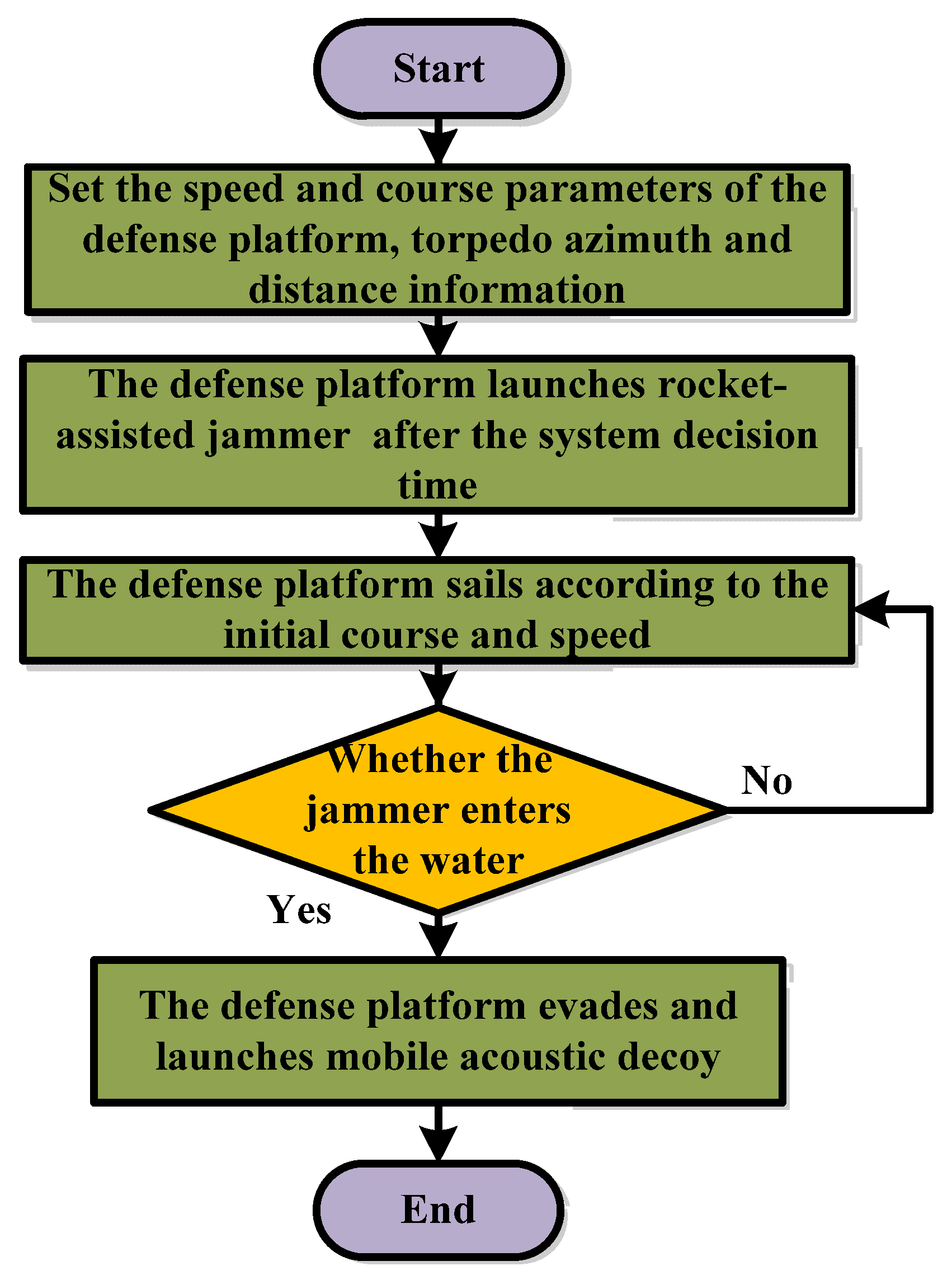
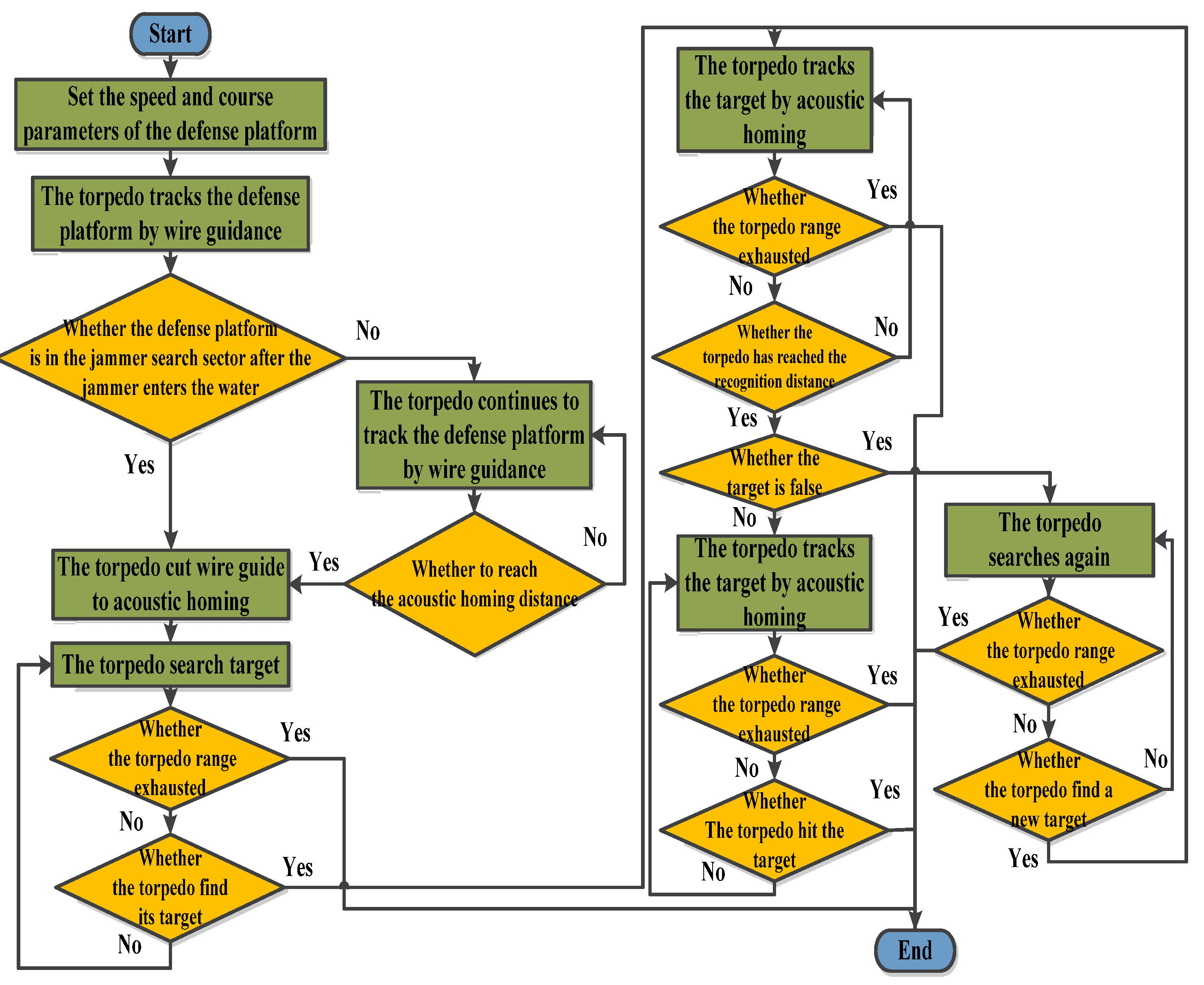
2.1. Defense Platform Maneuver Evasion Strategy
2.2. Jammer Deployment Strategy
2.3. Acoustic Decoy Deployment Strategy
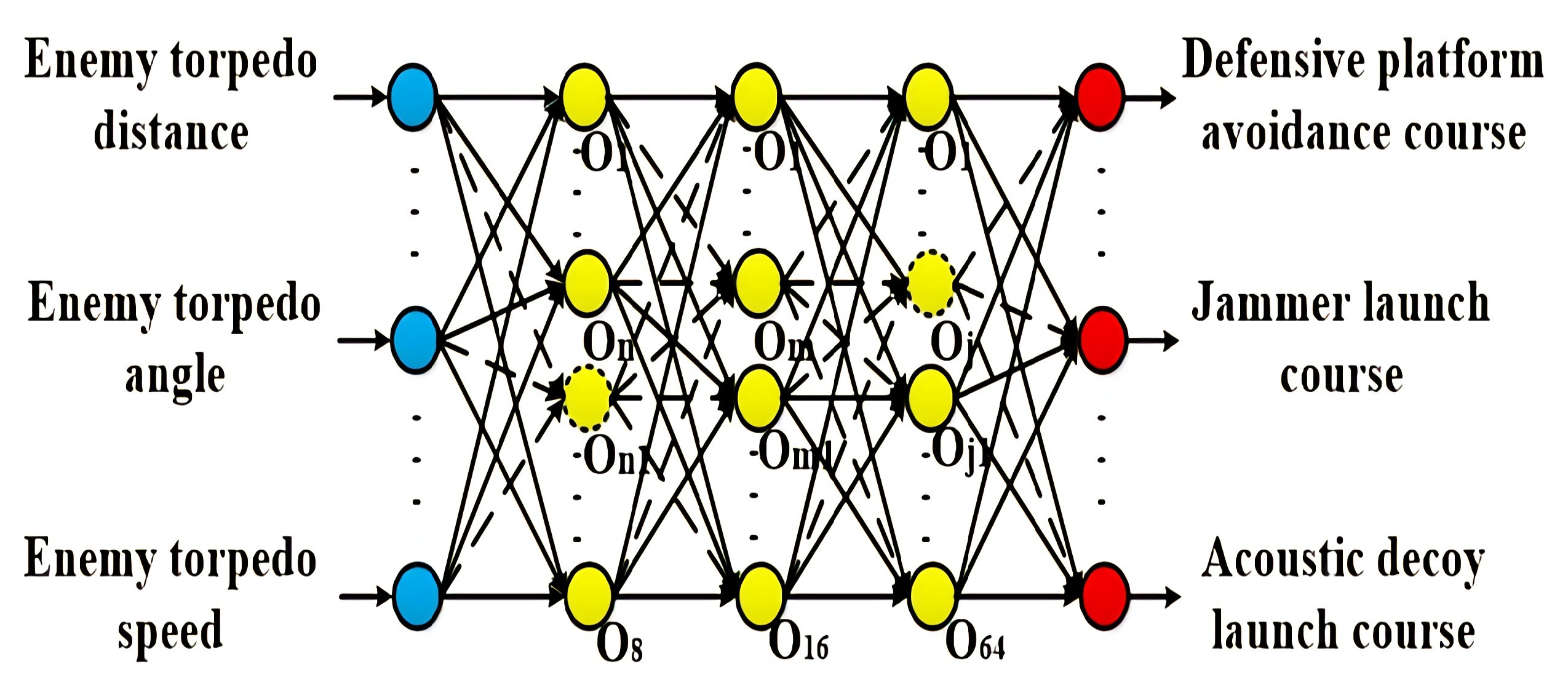
2.4. Back Propagation Neural Network Theory
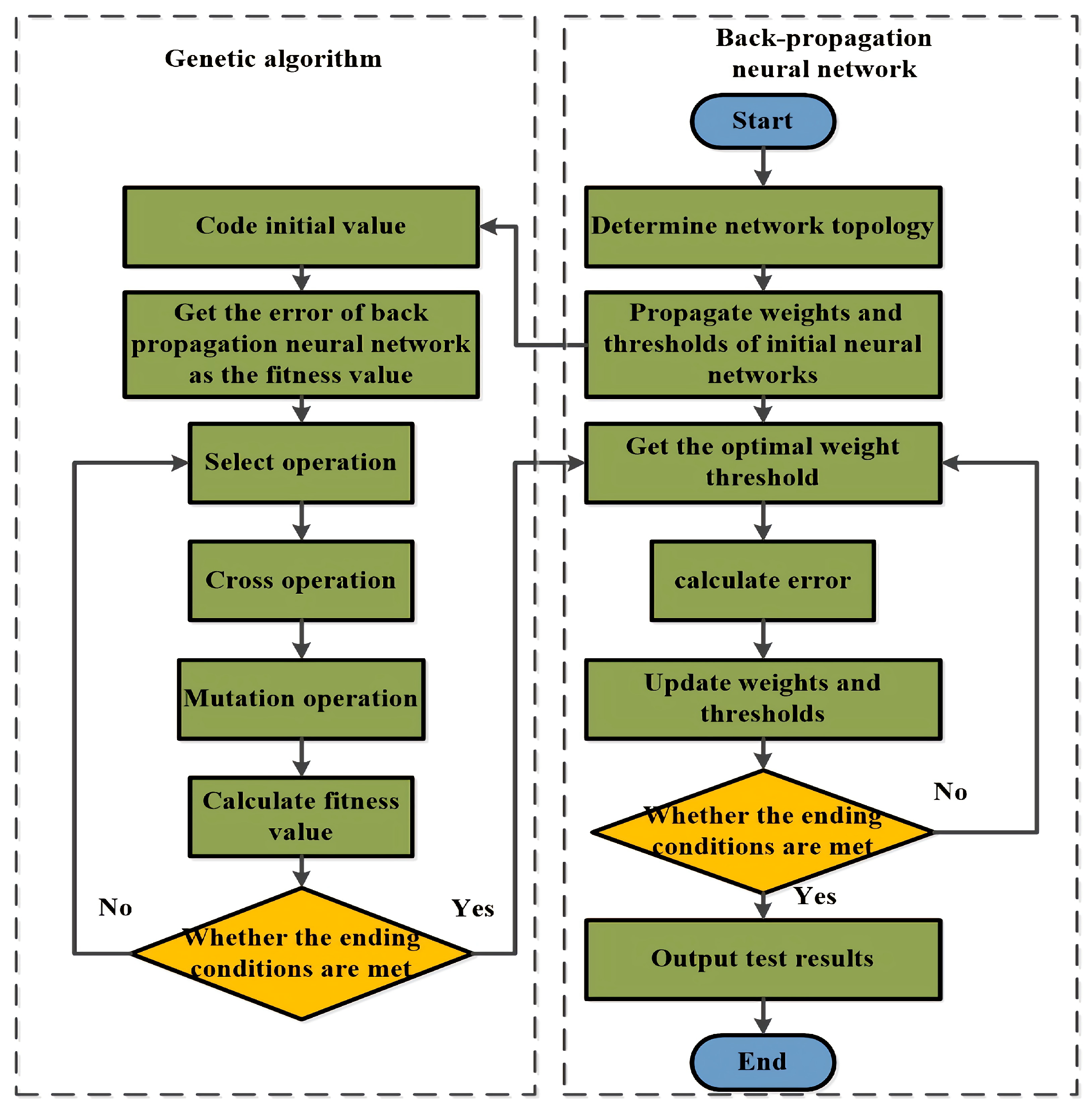
2.5. Genetic Algorithm to Optimize BP Neural Network Method
- Input normalized training data.
- Determine the BP neural network topology.
- Encode using the real number encoding method and initial each chromosome in the population, which includes the connection weights and thresholds of the BP neural network, whose chromosome length L can be derived by the following equation:Among them, l, m, and n are the nodes in the input layer, the hidden layer, and the output layer.
- Substitute the initialized network weights and thresholds into the BP neural network. We can obtain the fitness value of each chromosome by the absolute value of the difference between the predicted and the actual results.
- Genetic evolution is achieved by the roulette wheel method for selection and the real number crossover method.
- We judge whether the genetic evolution reaches the set maximum times, and if the genetic evolution reaches the maximum evolution, the GA stops running and obtains the last generation population. Otherwise, it returns to step 5.
- We decode the chromosome with the optimal fitness value from the last generation population in GA and substitute it into the BP neural network to obtain the initialized connection weights and thresholds to start the training. The BP neural network completes training when the network reaches the set accuracy or the maximum number of iterations.
- The output obtains the prediction results of the network model.
3. Results and Discussion
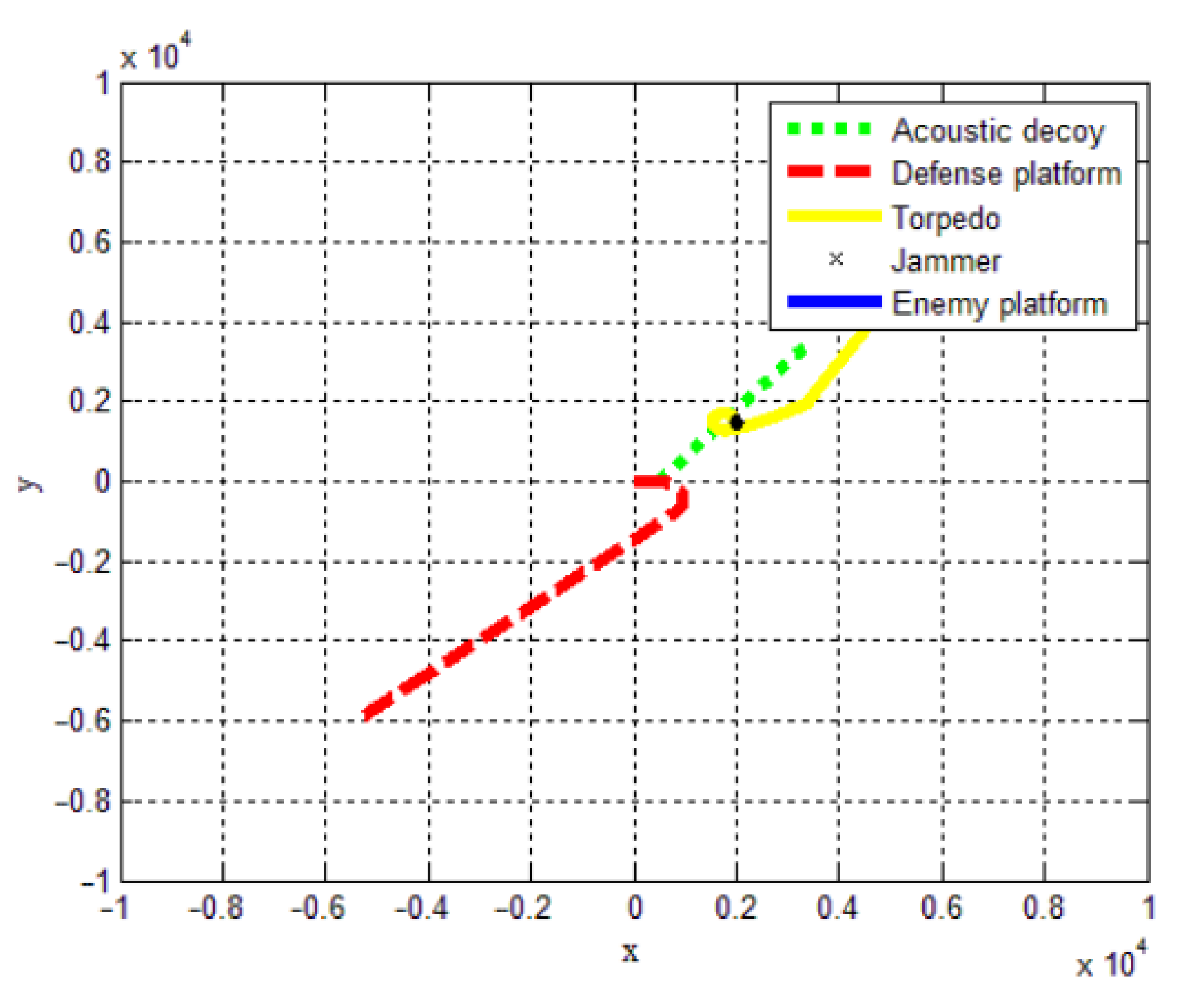
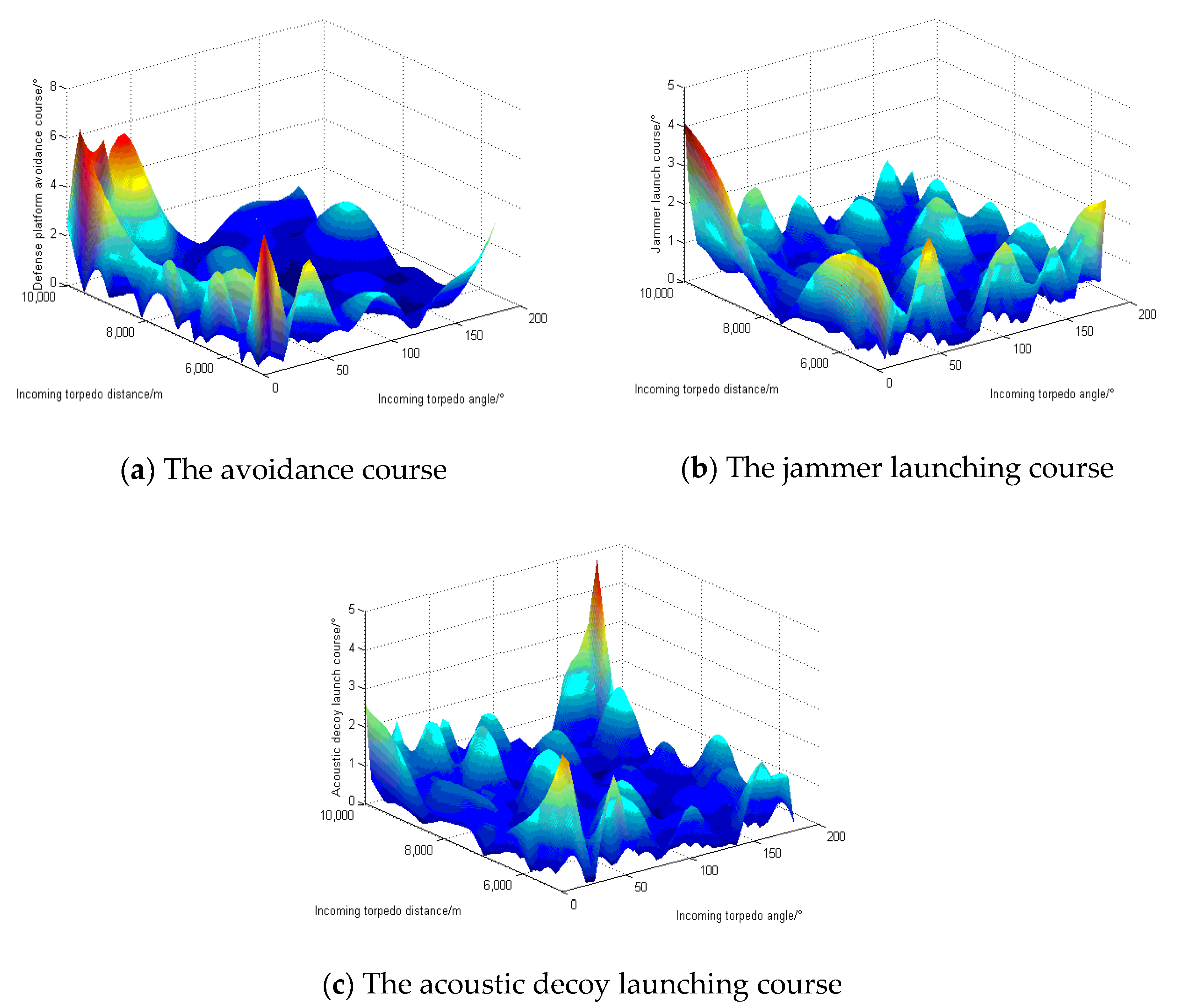
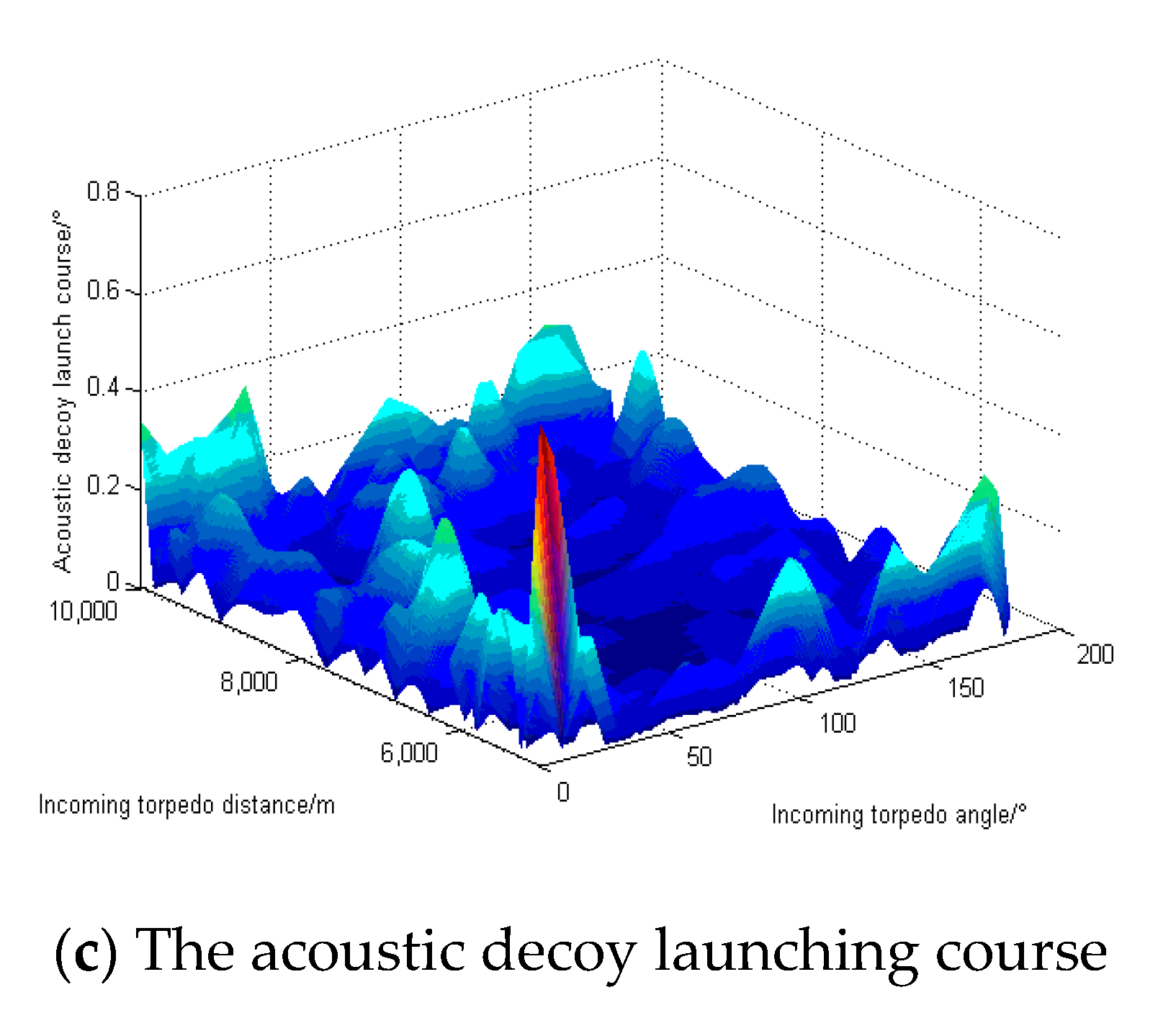
3.1. Optimal Warfare Strategy Planning for Defense Platforms under Monte-Carlo
3.2. Normalization of Values
3.3. Setting of Network Training Parameters
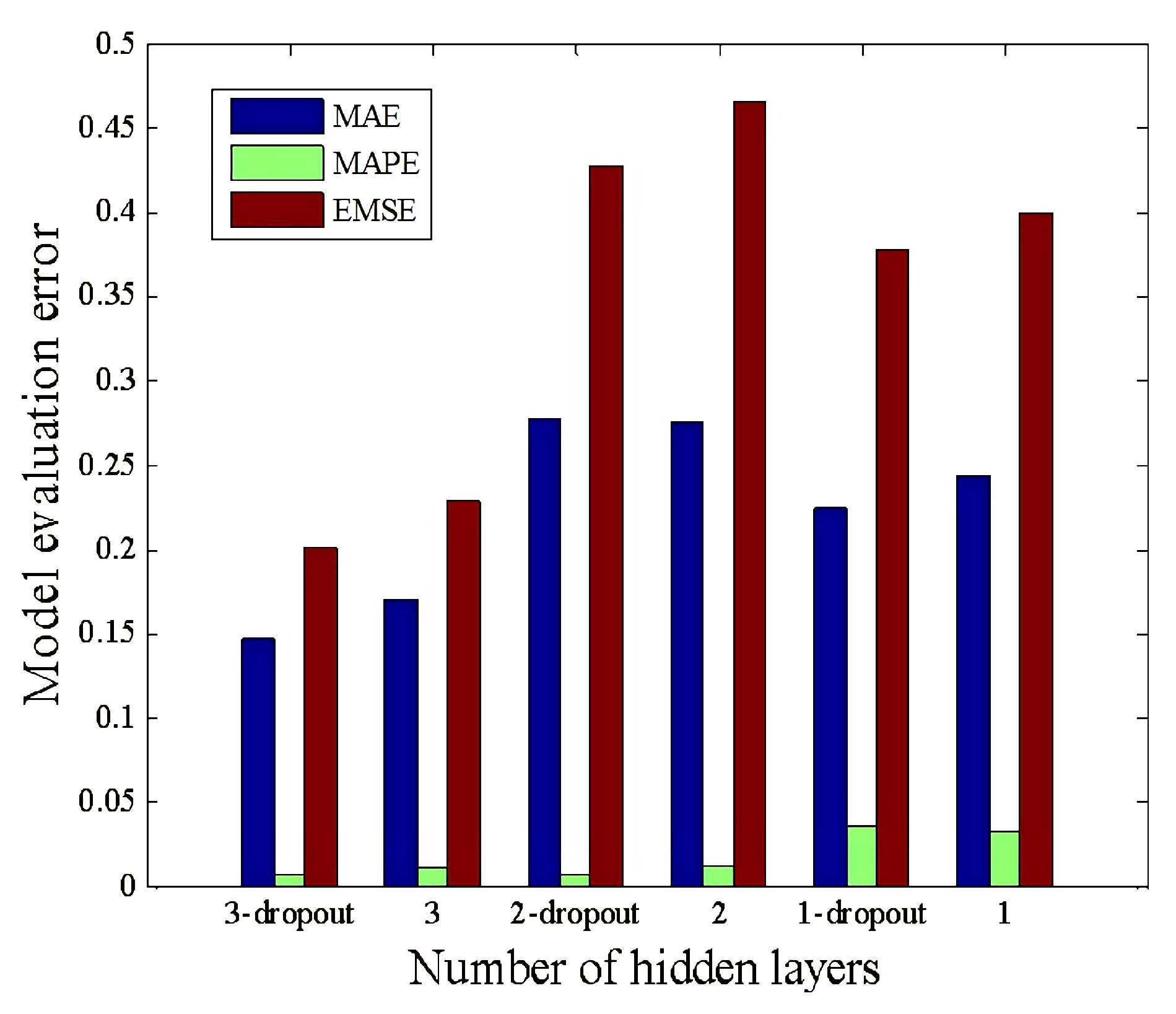
3.4. Confirmation of Optimized GA-BP Neural Network Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Lautour, N.J.; Trevorrow, M. Initial Study on Expendable Acoustic Countermeasures for Torpedo Defence; Defence Technology Agency: Auckland, New Zealand, 2012. [Google Scholar]
- Hui, L.; Wang, K.M. Torpedo performance Markov model. Expert Syst. Appl. 2015, 42, 9129–9136. [Google Scholar] [CrossRef]
- Lei, R.; Yue, J.; Wen-zhe, L. Research on Comprehensive Scheme of Shipboard Hard and Soft Torpedo Defense Weapons Against Intelligent Torpedoes. Acta Armamentarii 2015, 36, 2336. [Google Scholar] [CrossRef]
- Carreño, R.M.; Martínez, J.; Bouza, J.B. An Approach for Integrating Uncertainty When Selecting an Anti-Torpedo Decoy in Brand New Warships. Math. Comput. Appl. 2019, 24, 5. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Wang, Y.J.; Cai, L.; Wei, R. Research on the Combination of Underwater Acoustic Countermeasure Equipments against Torpedo. MATEC Web Conf. 2016, 40, 02018. [Google Scholar] [CrossRef] [Green Version]
- Zhan, K.; Yu, B.; Wang, J. Simulations of the anti-torpedo tactic of the conventional submarine using decoys and jammers. Appl. Mech. Mater. 2011, 65, 165–168. [Google Scholar] [CrossRef]
- Chen, Y.C.; Guo, Y.H. Optimal combination strategy for two swim-out acoustic decoys to countermeasure acoustic homing torpedo. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 1061–1065. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wang, L. Optimal combination strategy for underwater acoustic countermeasure at close distance. In Proceedings of the The Fourth International Workshop on Advanced Computational Intelligence, Wuhan, China, 19–21 October 2011; pp. 92–96. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, Z.; Zou, Y.; Zhao, J.; Ke, Y. A Prediction Model of Defecation Based on BP Neural Network and Bowel Sound Signal Features. Sensors 2022, 22, 7084. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, H.; Li, D.-a. Channel Prediction Based on BP Neural Network for Backscatter Communication Networks. Sensors 2020, 20, 300. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Lv, X.; Qian, L.; Liu, X. An Optimal BP Neural Network Track Prediction Method Based on a GA–ACO Hybrid Algorithm. J. Mar. Sci. Eng. 2022, 10, 1399. [Google Scholar] [CrossRef]
- Lv, D.; Liu, G.; Ou, J.; Wang, S.; Gao, M. Prediction of GPS Satellite Clock Offset Based on an Improved Particle Swarm Algorithm Optimized BP Neural Network. Remote Sens. 2022, 14, 2407. [Google Scholar] [CrossRef]
- Bharati, P.V.; Rao, S.K.; Krishna, A.R. Generation and analysis of tactics for anti-torpedo defense system. In Proceedings of the 2013 IEEE Conference on Information & Communication Technologies, Thuckalay, India, 11–12 April 2013; pp. 382–387. [Google Scholar] [CrossRef]
- Ragesh, R.; Ratnoo, A.; Ghose, D. Analysis of evader survivability enhancement by decoy deployment. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 4735–4740. [Google Scholar] [CrossRef]
- Ragesh, R.; Ratnoo, A.; Ghose, D. Evasion strategies in decoy assisted engagements. IFAC Proc. Vol. 2014, 47, 414–420. [Google Scholar] [CrossRef]
- Liang, K.-H.; Wang, K.-M. Using simulation and evolutionary algorithms to evaluate the design of mix strategies of decoy and jammers in anti-torpedo tactics. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1299–1306. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Xu, Y. Financial security evaluation of the electric power industry in China based on a back propagation neural network optimized by genetic algorithm. Energy 2016, 101, 366–379. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP neural network algorithm in typical hydrological model for flood forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z. Water quality evaluation based on BP neural network in Nierji reservoir. J. Water Resour. Res. 2017, 6, 247–253. [Google Scholar] [CrossRef]
- Xinxin, L.; Dan, Z.; Jianxi, Y.; Haonan, C.; Weicheng, Z.; Ruiqiang, Y. Water Quality Prediction and Early Warning Model of Construction Area Based on GA-BP Neural Network. J. Chongqing Jiaotong Univ. 2020, 39, 106. [Google Scholar]
- Ding, S.; Su, C.; Yu, J. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Qie, X.; Kang, C.; Zong, G.; Chen, S. Trajectory Planning and Simulation Study of Redundant Robotic Arm for Upper Limb Rehabilitation Based on Back Propagation Neural Network and Genetic Algorithm. Sensors 2022, 22, 4071. [Google Scholar] [CrossRef]
- Song, B.W.; Li, N. In Applied Research of Simulation Method in Calculate the Hit Probability of Acoustic Homing Torpedo. Adv. Mater. Res. 2011, 148–149, 353–358. [Google Scholar] [CrossRef]
- Ping, H.; Aiping, H.; Linwei, T. Deep Learning-Based Decision-Making Model for the Submarine Evade Movement. In Proceedings of the OCEANS 2021: San Diego–Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, W.; Li, X.; Zhang, L.; Li, X.; Liu, G. Situation Cognition and Decision Modeling Method for Submarine Operation Based on Discriminant Matrix. J. Syst. Simul. 2020, 32, 182. [Google Scholar]
- Wang, Z.; Wu, J.; Wang, H.; Hao, Y.; Wang, H. A Torpedo Target Recognition Method Based on the Correlation between Echo Broadening and Apparent Angle. Appl. Sci. 2022, 12, 12345. [Google Scholar] [CrossRef]
- Murugesan, M.; Sajjad, M.; Jung, D.W. Hybrid machine learning optimization approach to predict hot deformation behavior of medium carbon steel material. Metals 2019, 9, 1315. [Google Scholar] [CrossRef] [Green Version]
- Beşikçi, E.B.; Arslan, O.; Turan, O.; Ölçer, A.I. An artificial neural network based decision support system for energy efficient ship operations. Comput. Oper. Res. 2016, 66, 393–401. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Guo, W. Research on railway passenger flow prediction method based on GA improved BP neural network. J. Comput. Commun. 2019, 7, 283–292. [Google Scholar] [CrossRef]







| Sample Number | Input Samples | Output Samples |
|---|---|---|
| 1 | [X1, Y1, Z1] | B1 |
| 2 | [X2, Y2, Z2] | B2 |
| ··· | ··· | ··· |
| 37,000 | [X100, Y37, Z10] | B37,000 |
| Network/ Index | MAE | MAPE | RMSE | Survival Probability |
|---|---|---|---|---|
| Three-layer GA-BP network after optimization | 0.147 | 0.0061 | 0.2016 | 94.34% |
| Typical single-layer GA-BP network | 0.2441 | 0.0331 | 0.3995 | 88.19% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wu, J.; Wang, H.; Wang, H.; Hao, Y. Optimal Underwater Acoustic Warfare Strategy Based on a Three-Layer GA-BP Neural Network. Sensors 2022, 22, 9701. https://doi.org/10.3390/s22249701
Wang Z, Wu J, Wang H, Wang H, Hao Y. Optimal Underwater Acoustic Warfare Strategy Based on a Three-Layer GA-BP Neural Network. Sensors. 2022; 22(24):9701. https://doi.org/10.3390/s22249701
Chicago/Turabian StyleWang, Zirui, Jing Wu, Haitao Wang, Huiyuan Wang, and Yukun Hao. 2022. "Optimal Underwater Acoustic Warfare Strategy Based on a Three-Layer GA-BP Neural Network" Sensors 22, no. 24: 9701. https://doi.org/10.3390/s22249701
APA StyleWang, Z., Wu, J., Wang, H., Wang, H., & Hao, Y. (2022). Optimal Underwater Acoustic Warfare Strategy Based on a Three-Layer GA-BP Neural Network. Sensors, 22(24), 9701. https://doi.org/10.3390/s22249701






