Tracking of a Fixed-Shape Moving Object Based on the Gradient Descent Method
Abstract
:1. Introduction
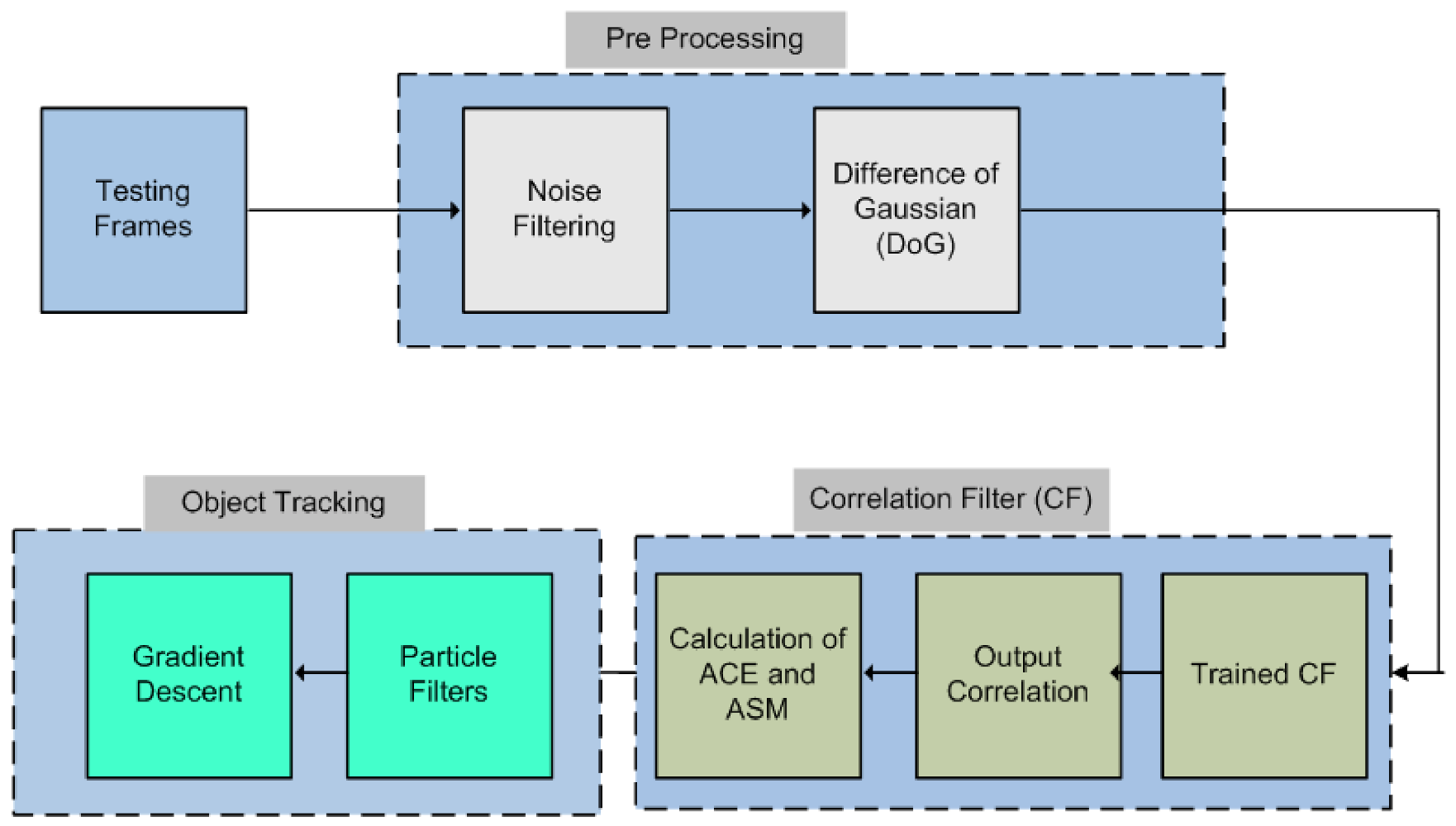
2. Proposed Methodology
2.1. Preprocessing
2.2. Object Recognition
2.3. Object Tracking
Gradient Descent-Based Particle Filtering
| Algorithm 1: Gradient Descent Algorithm |
|
3. Results and Discussion
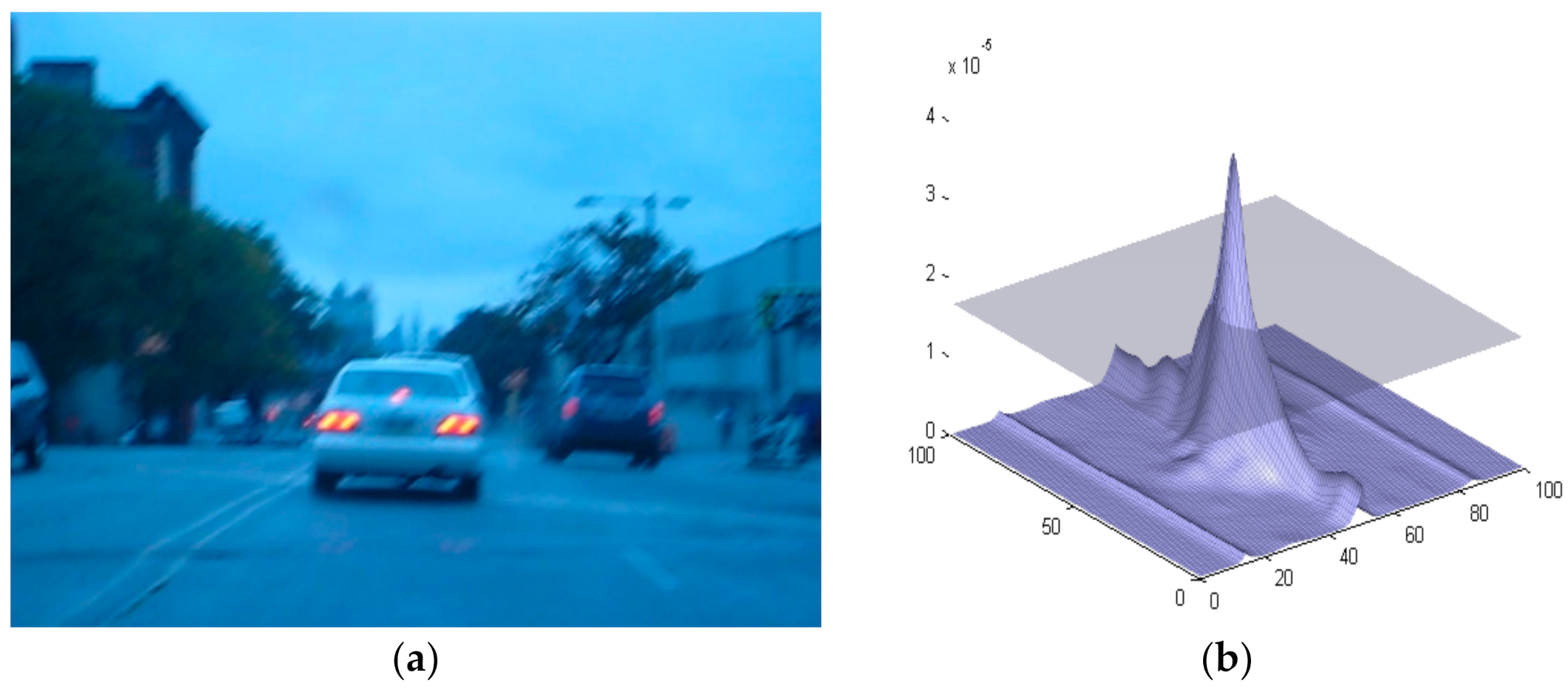
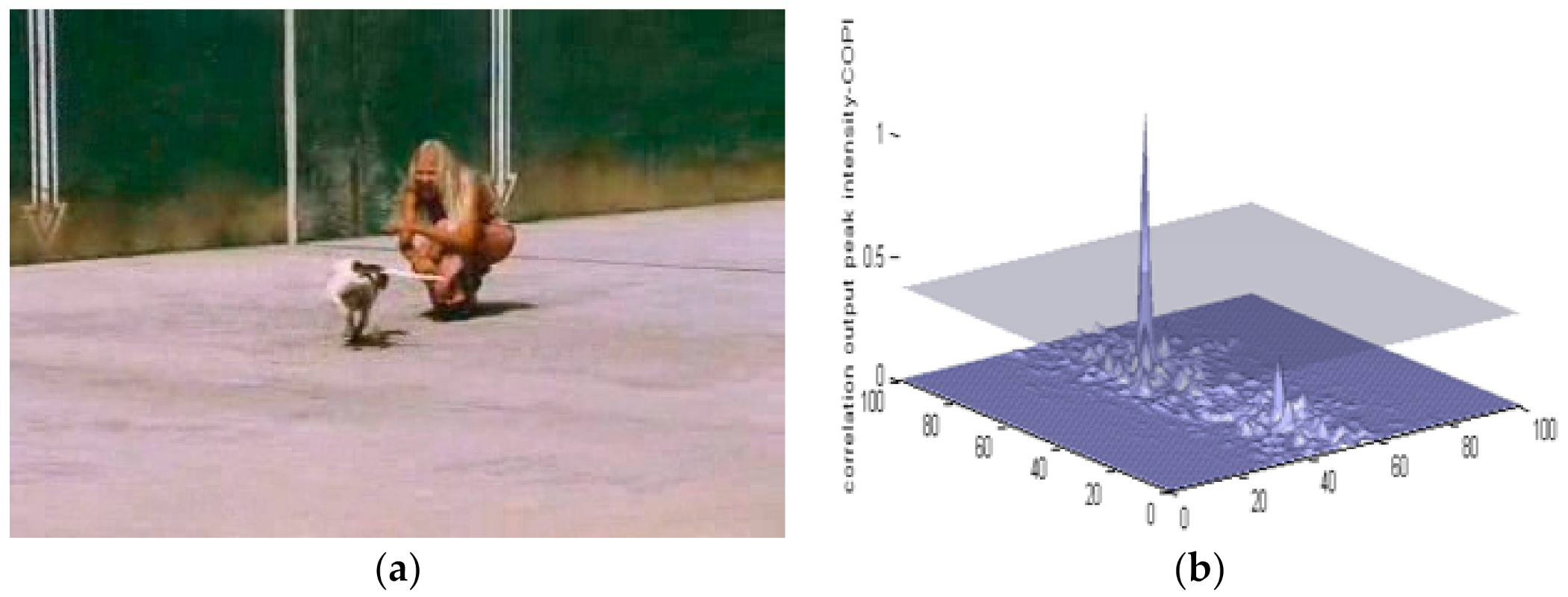
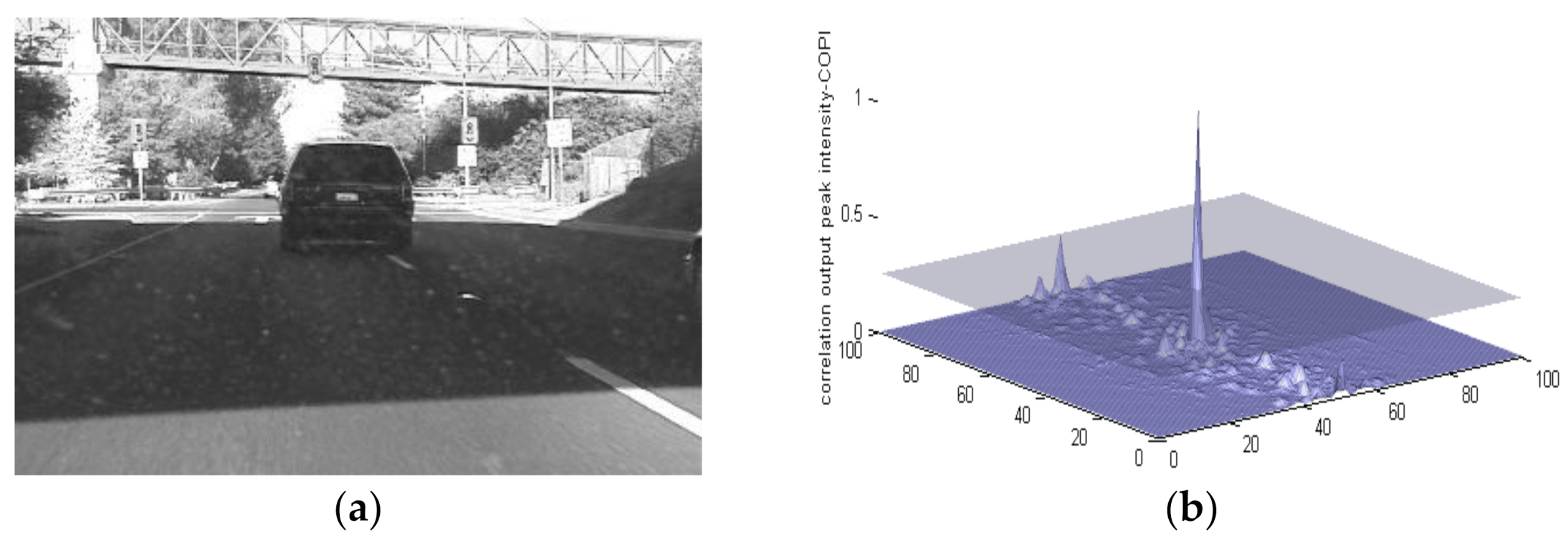
3.1. Data Sets
3.2. Discussion and Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaushal, M.; Khehra, B.S.; Sharma, A. Soft Computing based object detection and tracking approaches: State-of-the-Art survey. Appl. Soft Comput. 2018, 70, 423–464. [Google Scholar] [CrossRef]
- Bai, Z.; Li, Y.; Chen, X.; Yi, T.; Wei, W.; Wozniak, M.; Damasevicius, R. Real-Time Video Stitching for Mine Surveillance Using a Hybrid Image Registration Method. Electronics 2020, 9, 1336. [Google Scholar] [CrossRef]
- Olszewska, J.I. Active contour based optical character recognition for automated scene understanding. Neurocomputing 2015, 161, 65–71. [Google Scholar] [CrossRef]
- Mu, H.; Sun, R.; Yuan, G.; Wang, Y. Abnormal Human Behavior Detection in Videos: A Review. Inf. Technol. Control 2021, 50, 522–545. [Google Scholar] [CrossRef]
- Zhou, B.; Duan, X.; Ye, D.; Wei, W.; Woźniak, M.; Połap, D.; Damaševičius, R. Multi-Level Features Extraction for Discontinuous Target Tracking in Remote Sensing Image Monitoring. Sensors 2019, 19, 4855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolf, C.; Lombardi, E.; Mille, J.; Celiktutan, O.; Jiu, M.; Dogan, E.; Eren, G.; Baccouche, M.; Dellandréa, E.; Bichot, C.-E.; et al. Evaluation of video activity localizations integrating quality and quantity measurements. Comput. Vis. Image Underst. 2014, 127, 14–30. [Google Scholar] [CrossRef] [Green Version]
- Ge, H.; Zhu, Z.; Lou, K.; Wei, W.; Liu, R.; Damaševičius, R.; Woźniak, M. Classification of Infrared Objects in Manifold Space Using Kullback-Leibler Divergence of Gaussian Distributions of Image Points. Symmetry 2020, 12, 434. [Google Scholar] [CrossRef] [Green Version]
- Wang, X. Deep Learning in Object Recognition, Detection, and Segmentation. Found. Trends® Signal Process. 2014, 8, 217–382. [Google Scholar] [CrossRef]
- Meyer, F.; Williams, J. Scalable Detection and Tracking of Geometric Extended Objects. IEEE Trans. Signal Process. 2021, 69, 6283–6298. [Google Scholar] [CrossRef]
- Mondal, A. Occluded object tracking using object-background prototypes and particle filter. Appl. Intell. 2021, 51, 5259–5279. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Y. Moving Camera-Based Object Tracking Using Adaptive Ground Plane Estimation and Constrained Multiple Kernels. J. Adv. Transp. 2021, 2021, 8153474. [Google Scholar] [CrossRef]
- Demiroz, B.E.; Ari, I.; Eroglu, O.; Salah, A.A.; Akarun, L. Feature-based tracking on a multi-omnidirectional camera dataset. In Proceedings of the 2012 5th International Symposium on Communications, Control and Signal Processing, Rome, Italy, 2–4 May 2012. [Google Scholar]
- Masood, H.; Rehman, S.; Khan, A.; Riaz, F.; Hassan, A.; Abbas, M. Approximate Proximal Gradient-Based Correlation Filter for Target Tracking in Videos: A Unified Approach. Arab. J. Sci. Eng. 2019, 44, 9363–9380. [Google Scholar] [CrossRef]
- Wei, W.; Zhou, B.; Maskeliunas, R.; Damaševičius, R.; Połap, D.; Woźniak, M. Iterative Design and Implementation of Rapid Gradient Descent Method. In Artificial Intelligence and Soft Computing; Springer: Cham, Switzerland, 2019; pp. 530–539. [Google Scholar] [CrossRef]
- Fan, J.; Shen, X.; Wu, Y. What Are We Tracking: A Unified Approach of Tracking and Recognition. IEEE Trans. Image Process. 2012, 22, 549–560. [Google Scholar] [CrossRef]
- Xia, Y.; Qu, S.; Goudos, S.; Bai, Y.; Wan, S. Multi-object tracking by mutual supervision of CNN and particle filter. Pers. Ubiquitous Comput. 2019, 25, 979–988. [Google Scholar] [CrossRef]
- Huyan, L.; Bai, Y.; Li, Y.; Jiang, D.; Zhang, Y.; Zhou, Q.; Wei, J.; Liu, J.; Zhang, Y.; Cui, T. A Lightweight Object Detection Framework for Remote Sensing Images. Remote Sens. 2021, 13, 683. [Google Scholar] [CrossRef]
- Cui, N. Applying Gradient Descent in Convolutional Neural Networks. J. Phys. Conf. Ser. 2018, 1004, 012027. [Google Scholar] [CrossRef]
- MacLean, J.; Tsotsos, J. Fast pattern recognition using gradient-descent search in an image pyramid. In Proceedings of the 15th International Conference on Pattern Recognition (ICPR-2000), Barcelona, Spain, 3–7 September 2000. [Google Scholar] [CrossRef]
- Qiu, J.; Ma, M.; Wang, T.; Gao, H. Gradient Descent-Based Adaptive Learning Control for Autonomous Underwater Vehicles With Unknown Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5266–5273. [Google Scholar] [CrossRef]
- Iswanto, I.A.; Li, B. Visual Object Tracking Based on Mean-shift and Particle-Kalman Filter. Procedia Comput. Sci. 2017, 116, 587–595. [Google Scholar] [CrossRef]
- Ge, H.; Zhu, Z.; Lou, K. Tracking Video Target via Particle Filtering on Manifold. Inf. Technol. Control 2019, 48, 538–544. [Google Scholar] [CrossRef]
- Bhat, P.G.; Subudhi, B.N.; Veerakumar, T.; Laxmi, V.; Gaur, M.S. Multi-Feature Fusion in Particle Filter Framework for Visual Tracking. IEEE Sens. J. 2019, 20, 2405–2415. [Google Scholar] [CrossRef]
- Li, S.; Zhao, S.; Cheng, B.; Chen, J. Dynamic Particle Filter Framework for Robust Object Tracking. IEEE Trans. Circuits Syst. Video Technol. 2021. [Google Scholar] [CrossRef]
- Malviya, V.; Kala, R. Trajectory prediction and tracking using a multi-behaviour social particle filter. Appl. Intell. 2021, 1–43. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, M.; Li, J. Object tracking method based on hybrid particle filter and sparse representation. Multimed. Tools Appl. 2016, 76, 2979–2993. [Google Scholar] [CrossRef]
- Lin, S.D.; Lin, J.; Chuang, C. Particle filter with occlusion handling for visual tracking. IET Image Process. 2015, 9, 959–968. [Google Scholar] [CrossRef]
- Choe, G.; Wang, T.; Liu, F.; Choe, C.; Jong, M. An advanced association of particle filtering and kernel based object tracking. Multimed. Tools Appl. 2014, 74, 7595–7619. [Google Scholar] [CrossRef]
- Nsinga, R.; Karungaru, S.; Terada, K. A comparative study of batch ensemble for multi-object tracking approximations in embedded vision. Proc. SPIE 2021, 11794, 257–262. [Google Scholar] [CrossRef]
- Li, G.; Liang, D.; Huang, Q.; Jiang, S.; Gao, W. Object tracking using incremental 2D-LDA learning and Bayes inference. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 1568–1571. [Google Scholar] [CrossRef]
- Dhassi, Y.; Aarab, A. Visual tracking based on adaptive interacting multiple model particle filter by fusing multiples cues. Multimed. Tools Appl. 2018, 77, 26259–26292. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, Y.; Deng, N.; Yang, K. The Augmented Lagrange Multiplier for robust visual tracking with sparse representation. Optik 2015, 126, 937–941. [Google Scholar] [CrossRef]
- Kong, J.; Liu, C.; Jiang, M.; Wu, J.; Tian, S.; Lai, H. Generalized ℓP-regularized representation for visual tracking. Neurocomputing 2016, 213, 155–161. [Google Scholar] [CrossRef]
- França, G.; Robinson, D.P.; Vidal, R. Gradient flows and proximal splitting methods: A unified view on accelerated and stochastic optimization. arXiv 2019, arXiv:1908.00865. [Google Scholar] [CrossRef]
- Chen, J.-X.; Zhang, Y.-N.; Jiang, D.-M.; Li, F.; Xie, J. Multi-class Object Recognition and Segmentation Based on Multi-feature Fusion Modeling. In Proceedings of the 2015 IEEE 12th Intl Conf on Ubiquitous Intelligence and Computing and 2015 IEEE 12th Intl Conf on Autonomic and Trusted Computing and 2015 IEEE 15th Intl Conf on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom), Beijing, China, 10–14 August 2015; pp. 336–339. [Google Scholar] [CrossRef]
- Majeed, I.; Arif, O. Non-linear eigenspace visual object tracking. Eng. Appl. Artif. Intell. 2016, 55, 363–374. [Google Scholar] [CrossRef]
- Assirati, L.; da Silva, N.; Berton, L.; Lopes, A.A.; Bruno, O. Performing edge detection by Difference of Gaussians using q-Gaussian kernels. J. Phys. Conf. Ser. 2014, 490, 012020. [Google Scholar] [CrossRef] [Green Version]
- Dinc, S.; Bal, A. A Statistical Approach for Multiclass Target Detection. Procedia Comput. Sci. 2011, 6, 225–230. [Google Scholar] [CrossRef] [Green Version]
- Bone, P.; Young, R.; Chatwin, C. Position-, rotation-, scale-, and orientation-invariant multiple object recognition from cluttered scenes. Opt. Eng. 2006, 45, 077203. [Google Scholar] [CrossRef] [Green Version]
- Birch, P.; Mitra, B.; Bangalore, N.M.; Rehman, S.; Young, R.; Chatwin, C. Approximate bandpass and frequency response models of the difference of Gaussian filter. Opt. Commun. 2010, 283, 4942–4948. [Google Scholar] [CrossRef]
- Rehman, S.; Riaz, F.; Hassan, A.; Liaquat, M.; Young, R. Human detection in sensitive security areas through recognition of omega shapes using MACH filters. Proc. SPIE 2015, 9477, 947708. [Google Scholar] [CrossRef]
- Urban Lisa Dataset. Available online: http://homepages.inf.ed.ac.uk/rbf/CVonline/Imagedbase.htm (accessed on 11 October 2021).
- Visual Tracker Benchmark Dataset Webpage. Available online: http://cvlab.hanyang.ac.kr/tracker_benchmark/datasets.html (accessed on 11 October 2021).
- Zhang, L.J.; Wang, C.; Jin, X. Research and Implementation of Target Tracking Algorithm Based on Convolution Neural Network. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018. [Google Scholar] [CrossRef]
- Ming, Y.; Zhang, Y. ADT: Object Tracking Algorithm Based on Adaptive Detection. IEEE Access 2020, 8, 56666–56679. [Google Scholar] [CrossRef]
- Yang, B.; Tang, M.; Chen, S.; Wang, G.; Tan, Y.; Li, B. A vehicle tracking algorithm combining detector and tracker. EURASIP J. Image Video Process. 2020, 2020, 17. [Google Scholar] [CrossRef]
- Bumanis, N.; Vitols, G.; Arhipova, I.; Solmanis, E. Multi-object Tracking for Urban and Multilane Traffic: Building Blocks for Real-World Application. In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS), 26–28 April 2021; pp. 729–736. [Google Scholar] [CrossRef]
- Tian, X.; Li, H.; Deng, H. An improved object tracking algorithm based on adaptive weighted strategy and occlusion detection mechanism. J. Algorithms Comput. Technol. 2021, 15. [Google Scholar] [CrossRef]
- Afza, F.; Sharif, M.; Kadry, S.; Manogaran, G.; Saba, T.; Ashraf, I.; Damaševičius, R. A framework of human action recognition using length control features fusion and weighted entropy-variances based feature selection. Image Vis. Comput. 2021, 106, 104090. [Google Scholar] [CrossRef]
- Zhang, Y.-D.; Khan, S.A.; Attique, M.; Rehman, A.; Seo, S. A resource conscious human action recognition framework using 26-layered deep convolutional neural network. Multimed. Tools Appl. 2021, 80, 35827–35849. [Google Scholar]
- Nisa, M.; Shah, J.H.; Kanwal, S.; Raza, M.; Damaševičius, R.; Blažauskas, T. Hybrid malware classification method using segmentation-based fractal texture analysis and deep convolution neural network features. Appl. Sci. 2020, 10, 4966. [Google Scholar] [CrossRef]
- Nasir, I.M.; Yasmin, M.; Shah, J.H.; Gabryel, M.; Scherer, R.; Damaševičius, R. Pearson correlation-based feature selection for document classification using balanced training. Sensors 2020, 20, 6793. [Google Scholar] [CrossRef] [PubMed]
- Kadry, S.; Parwekar, P.; Damaševičius, R.; Mehmood, A.; Khan, J.A.; Naqvi, S.R. Human gait analysis for osteoarthritis prediction: A framework of deep learning and kernel extreme learning machine. Complex Intell. Syst. 2021, 11, 1–19. [Google Scholar]
- Sharif, M.I.; Alqahtani, A.; Nazir, M.; Alsubai, S.; Binbusayyis, A.; Damaševičius, R. Deep Learning and Kurtosis-Controlled, Entropy-Based Framework for Human Gait Recognition Using Video Sequences. Electronics 2022, 11, 334. [Google Scholar] [CrossRef]
- Jabeen, K.; Alhaisoni, M.; Tariq, U.; Zhang, Y.-D.; Hamza, A.; Mickus, A.; Damaševičius, R. Breast Cancer Classification from Ultrasound Images Using Probability-Based Optimal Deep Learning Feature Fusion. Sensors 2022, 22, 807. [Google Scholar] [CrossRef]
- Khan, S.; Alhaisoni, M.; Tariq, U.; Yong, H.-S.; Armghan, A.; Alenezi, F. Human Action Recognition: A Paradigm of Best Deep Learning Features Selection and Serial Based Extended Fusion. Sensors 2021, 21, 7941. [Google Scholar] [CrossRef]
- Akram, T.; Zhang, Y.-D.; Sharif, M. Attributes based skin lesion detection and recognition: A mask RCNN and transfer learning-based deep learning framework. Pattern Recognit. Lett. 2021, 143, 58–66. [Google Scholar]
- Rashid, M.; Sharif, M.; Javed, K.; Akram, T. Classification of gastrointestinal diseases of stomach from WCE using improved saliency-based method and discriminant features selection. Multimed. Tools Appl. 2019, 78, 27743–27770. [Google Scholar]
- Akram, T.; Gul, S.; Shahzad, A.; Altaf, M.; Naqvi, S.S.R.; Damaševičius, R.; Maskeliūnas, R. A novel framework for rapid diagnosis of COVID-19 on computed tomography scans. Pattern Anal. Appl. 2021, 5, 1–14. [Google Scholar]








| Comparison of Execution Time (in Seconds) of Algorithms (Min. 300 Frames) | |||||||
|---|---|---|---|---|---|---|---|
| Data Set | TTACNN | ADT | VTACDT | APGCF | AWSODM | MTUMT | Proposed Algorithm |
| Blur Car | 2.14 | 2.51 | 2.10 | 2.44 | 2.91 | 2.29 | 2.01 |
| Running Dog | 2.92 | 4.12 | 2.77 | 4.11 | 2.99 | 2.84 | 2.89 |
| Vehicle at Night | 3.04 | 3.09 | 2.91 | 3.19 | 2.71 | 2.69 | 2.72 |
| Grayscale vehicle | 2.46 | 3.01 | 2.62 | 2.90 | 2.19 | 2.90 | 2.21 |
| Singer | 2.99 | 3.71 | 2.81 | 2.81 | 2.89 | 3.11 | 2.85 |
| Average Tracking Errors (Min. 300 Frames) | |||||||
|---|---|---|---|---|---|---|---|
| Data Set | TTACNN | ADT | MTUMT | VTACDT | APGCF | AWSODM | Proposed Algorithm |
| Blur Car | 0.46 | 0.42 | 0.21 | 0.17 | 0.055 | 0.21 | 0.041 |
| Running Dog | 0.059 | 0.057 | 0.48 | 0.056 | 0.051 | 0.061 | 0.048 |
| Vehicle at Night | 0.09 | 0.088 | 0.099 | 0.094 | 0.071 | 0.041 | 0.012 |
| Grayscale vehicle | 0.10 | 0.101 | 0.118 | 0.089 | 0.09 | 0.088 | 0.079 |
| Singer | 0.14 | 0.14 | 0.211 | 0.1328 | 0.129 | 0.144 | 0.127 |
| Comparison Based on Precision (Min. 300 Frames) | |||||||
|---|---|---|---|---|---|---|---|
| Data Set | TTACNN | ADT | MTUMT | VTACDT | APGCF | AWSODM | Proposed Algorithm |
| Blur Car | 0.88 | 0.88 | 0.93 | 0.94 | 0.94 | 0.92 | 0.96 |
| Running Dog | 0.90 | 0.92 | 0.89 | 0.93 | 0.94 | 0.87 | 0.94 |
| Vehicle at Night | 0.91 | 0.95 | 0.88 | 0.92 | 0.97 | 0.86 | 0.98 |
| Gray scale vehicle | 0.96 | 0.96 | 0.91 | 0.97 | 0.99 | 0.97 | 1.00 |
| Singer | 0.94 | 0.92 | 0.95 | 0.98 | 0.97 | 0.98 | 1.00 |
| Comparison Based on MAP (Min. 300 Frames) | |||||||
|---|---|---|---|---|---|---|---|
| Data Set | TTACNN | ADT | MTUMT | VTACDT | APGCF | AWSODM | Proposed Algorithm |
| Blur Car | 69.6 | 64.8 | 69.9 | 73.9 | 70.1 | 73.8 | 74.6 |
| Running Dog | 74.0 | 66.9 | 71.0 | 73.1 | 71.9 | 71.7 | 72.9 |
| Vehicle at Night | 77.2 | 68.2 | 71.1 | 76.9 | 74.6 | 75.1 | 77.8 |
| Gray scale vehicle | 76.1 | 69.2 | 72.5 | 74.9 | 77.1 | 77.9 | 78.2 |
| Singer | 74.9 | 66.0 | 72.8 | 75.5 | 70.9 | 72,8 | 75.6 |
| Comparison Based on Recall (Min. 300 Frames) | |||||||
|---|---|---|---|---|---|---|---|
| Data Set | TTACNN | ADT | MTUMT | VTACDT | APGCF | AWSODM | Proposed Algorithm |
| Blur Car | 0.55 | 0.52 | 0.59 | 0.53 | 0.59 | 0.55 | 0.52 |
| Running Dog | 0.52 | 0.54 | 0.54 | 0.45 | 0.54 | 0.49 | 0.45 |
| Vehicle at Night | 0.46 | 0.44 | 0.39 | 0.46 | 0.49 | 0.44 | 0.41 |
| Gray scale vehicle | 0.49 | 0.46 | 0.46 | 0.42 | 0.51 | 0.44 | 0.40 |
| Singer | 0.41 | 0.38 | 0.44 | 0.44 | 0.39 | 0.39 | 0.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masood, H.; Zafar, A.; Ali, M.U.; Hussain, T.; Khan, M.A.; Tariq, U.; Damaševičius, R. Tracking of a Fixed-Shape Moving Object Based on the Gradient Descent Method. Sensors 2022, 22, 1098. https://doi.org/10.3390/s22031098
Masood H, Zafar A, Ali MU, Hussain T, Khan MA, Tariq U, Damaševičius R. Tracking of a Fixed-Shape Moving Object Based on the Gradient Descent Method. Sensors. 2022; 22(3):1098. https://doi.org/10.3390/s22031098
Chicago/Turabian StyleMasood, Haris, Amad Zafar, Muhammad Umair Ali, Tehseen Hussain, Muhammad Attique Khan, Usman Tariq, and Robertas Damaševičius. 2022. "Tracking of a Fixed-Shape Moving Object Based on the Gradient Descent Method" Sensors 22, no. 3: 1098. https://doi.org/10.3390/s22031098
APA StyleMasood, H., Zafar, A., Ali, M. U., Hussain, T., Khan, M. A., Tariq, U., & Damaševičius, R. (2022). Tracking of a Fixed-Shape Moving Object Based on the Gradient Descent Method. Sensors, 22(3), 1098. https://doi.org/10.3390/s22031098






