3D Static Point Cloud Registration by Estimating Temporal Human Pose at Multiview
Abstract
:1. Introduction
2. Multi-View Extrinsic Calibration Based on Human Pose
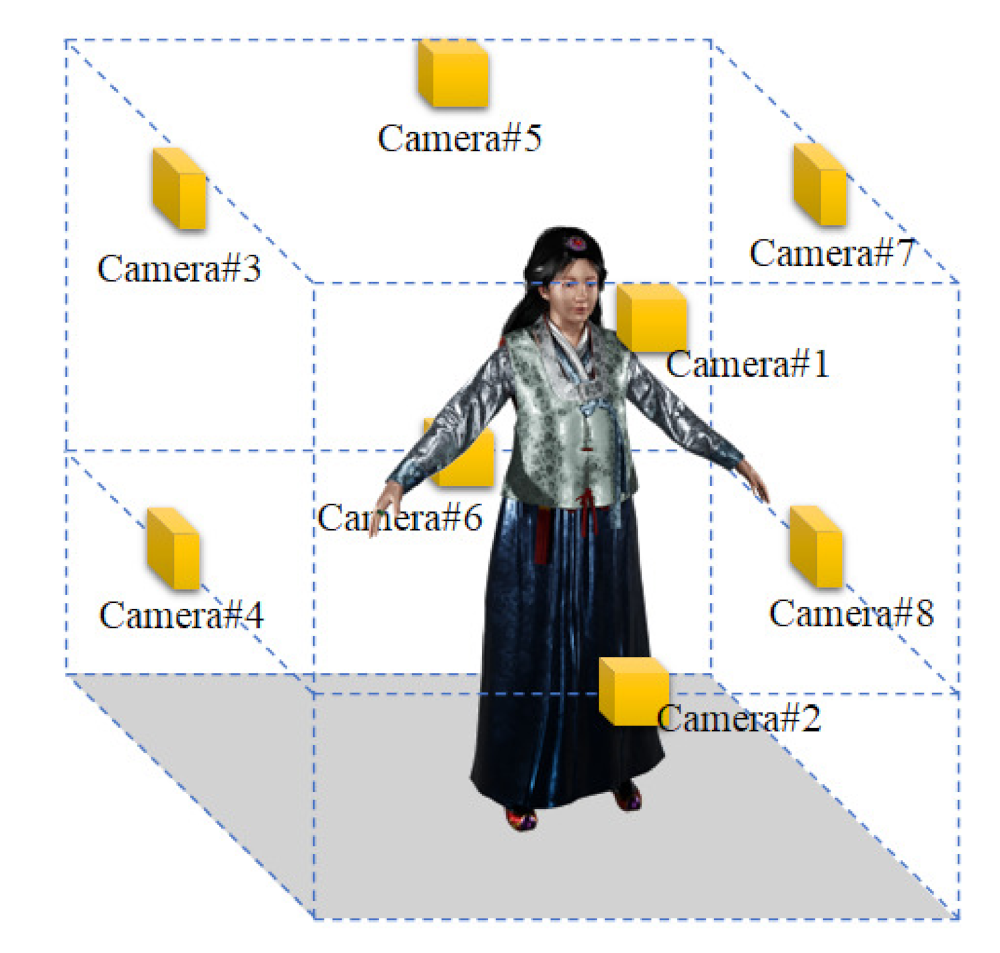
2.1. Multi-View Camera System
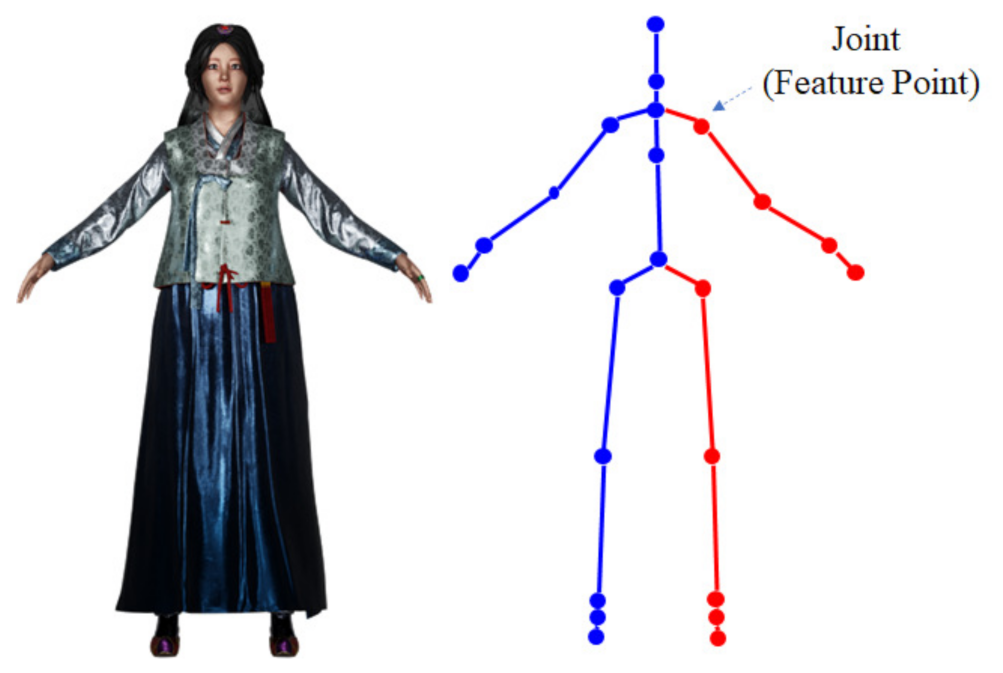
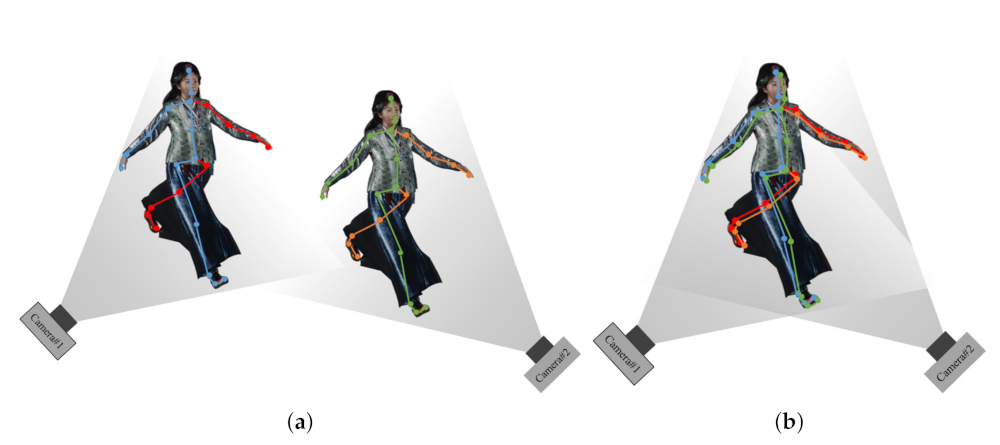
2.2. Extrinsic Calibration
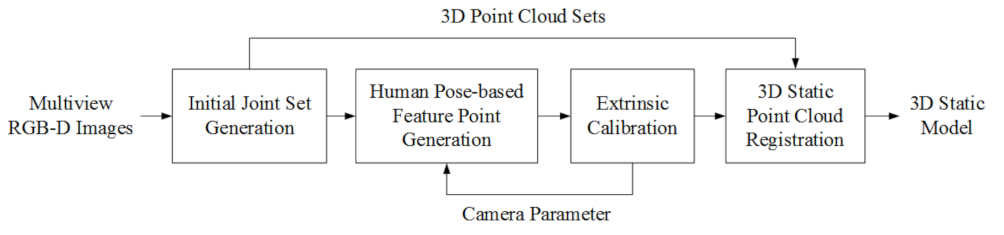
3. Proposed 3D Static Reconstruction
3.1. Extrinsic Calibration
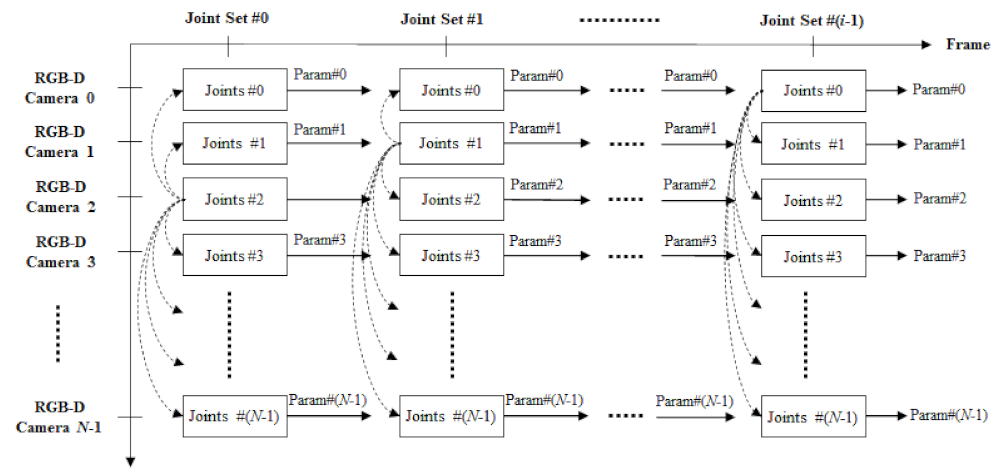
3.2. 3D Registration
4. Experimental Result
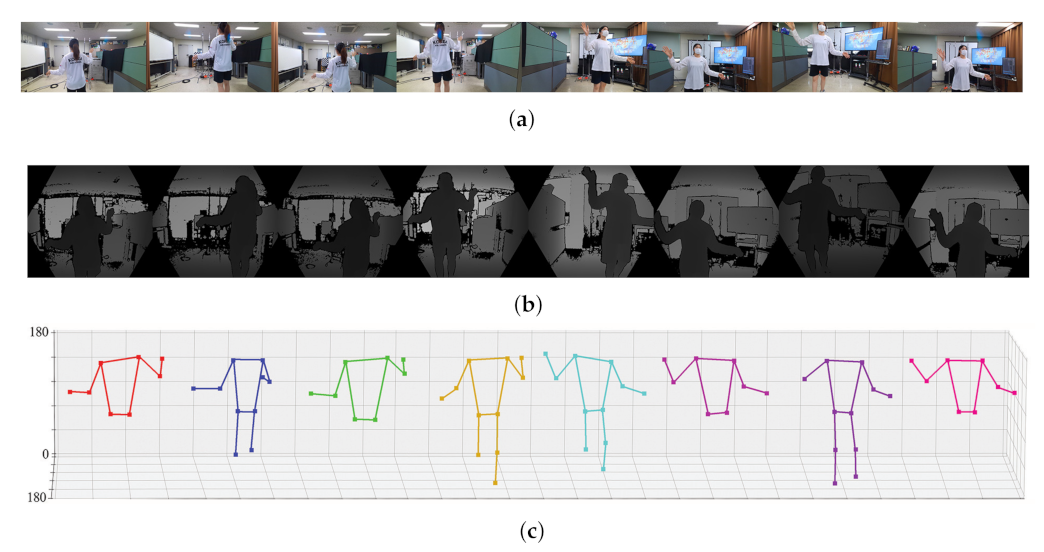
4.1. Environment
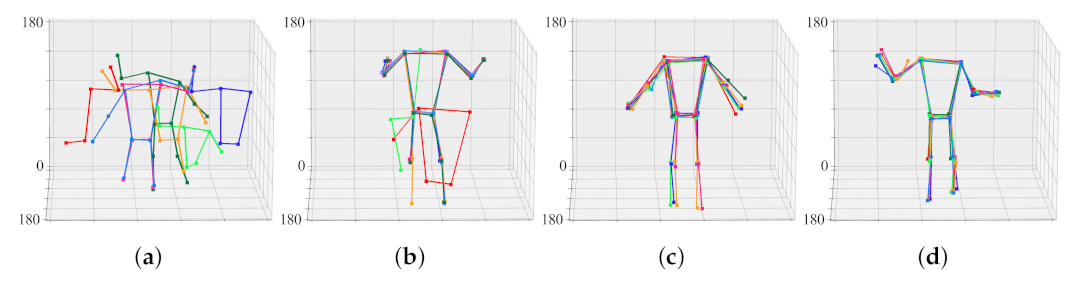
4.2. 3D Pose Estimation Result
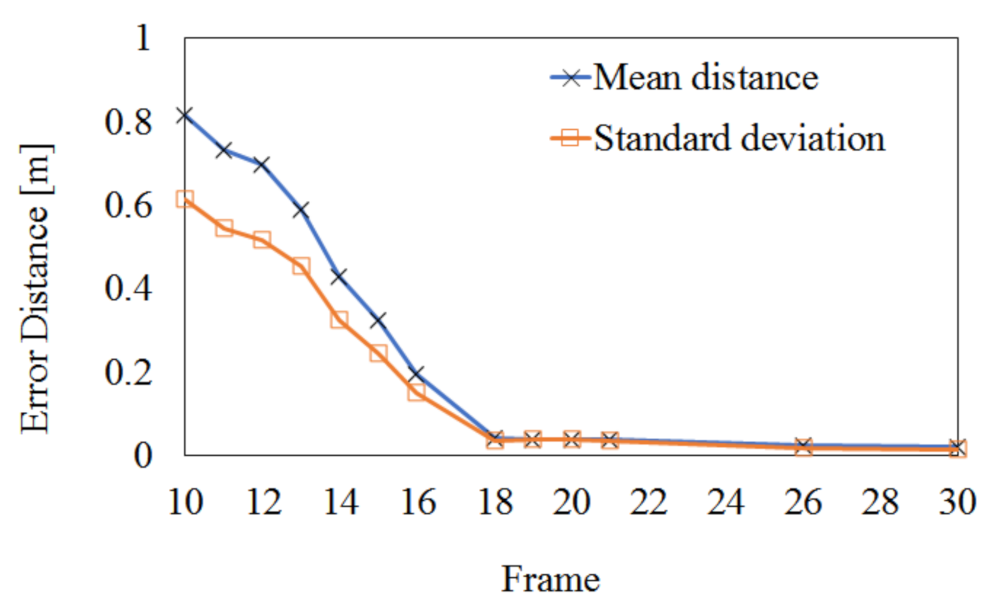
4.3. Extrinsic Calibration Result
4.4. Extrinsic Calibration Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Endres, F.; Hess, J.; Sturm, J.; Cremers, D.; Burgard, W. 3-D mapping with an RGB-D camera. IEEE Trans. Robot. 2013, 30, 177–187. [Google Scholar] [CrossRef]
- Labbe, M.; Michaud, F. Online global loop closure detection for large-scale multi-session graph-based SLAM. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2661–2666. [Google Scholar]
- Munaro, M.; Menegatti, E. Fast RGB-D people tracking for service robots. Auton. Robot. 2014, 37, 227–242. [Google Scholar] [CrossRef]
- Choi, C.; Christensen, H.I. RGB-D object tracking: A particle filter approach on GPU. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1084–1091. [Google Scholar]
- Tang, J.; Miller, S.; Singh, A.; Abbeel, P. A textured object recognition pipeline for color and depth image data. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MI, USA, 14–18 May 2012; pp. 3467–3474. [Google Scholar]
- Munea, T.L.; Jembre, Y.Z.; Weldegebriel, H.T.; Chen, L.; Huang, C.; Yang, C. The progress of human pose estimation: A survey and taxonomy of models applied in 2D human pose estimation. IEEE Access 2020, 8, 133330–133348. [Google Scholar] [CrossRef]
- Zollhöfer, M.; Stotko, P.; Görlitz, A.; Theobalt, C.; Nießner, M.; Klein, R.; Kolb, A. State of the Art on 3D Reconstruction with RGB-D Cameras. Comput. Graph. Forum. Wiley Online Libr. 2018, 37, 625–652. [Google Scholar] [CrossRef]
- Giancola, S.; Valenti, M.; Sala, R. State-of-the-art devices comparison. In A Survey on 3D Cameras: Metrological Comparison of Time-of-Flight, Structured-Light and Active Stereoscopy Technologies; Springer: Berlin/Heidelberg, Germany, 2018; pp. 29–39. [Google Scholar]
- Yun, W.J.; Kim, J. 3D Modeling and WebVR Implementation using Azure Kinect, Open3D, and Three. js. In Proceedings of the 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 21–23 October 2020; pp. 240–243. [Google Scholar]
- Photoneo. Phoxi 3D Scanner. Available online: https://www.photoneo.com/phoxi-3d-scanner/ (accessed on 8 December 2021).
- Zivid. Zivid Two. Available online: https://www.zivid.com/zivid-two (accessed on 8 December 2021).
- Lucid. Helios2, the Next Generation of Time of Flight. Available online: https://thinklucid.com/helios-time-of-flight-tof-camera/ (accessed on 8 December 2021).
- Zabatani, A.; Surazhsky, V.; Sperling, E.; Moshe, S.B.; Menashe, O.; Silver, D.H.; Karni, Z.; Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Intel® realsense™ sr300 coded light depth camera. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2333–2345. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Caire, G.; Molisch, A.F. Quality-aware streaming and scheduling for device-to-device video delivery. IEEE/ACM Trans. Netw. 2015, 24, 2319–2331. [Google Scholar] [CrossRef]
- Basso, F.; Menegatti, E.; Pretto, A. Robust intrinsic and extrinsic calibration of RGB-D cameras. IEEE Trans. Robot. 2018, 34, 1315–1332. [Google Scholar] [CrossRef] [Green Version]
- Khoshelham, K.; Elberink, S.O. Accuracy and resolution of kinect depth data for indoor mapping applications. Sensors 2012, 12, 1437–1454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mikhelson, I.V.; Lee, P.G.; Sahakian, A.V.; Wu, Y.; Katsaggelos, A.K. Automatic, fast, online calibration between depth and color cameras. J. Vis. Commun. Image Represent. 2014, 25, 218–226. [Google Scholar] [CrossRef]
- Staranowicz, A.N.; Brown, G.R.; Morbidi, F.; Mariottini, G.L. Practical and accurate calibration of RGB-D cameras using spheres. Comput. Vis. Image Underst. 2015, 137, 102–114. [Google Scholar] [CrossRef]
- Zheng, K.; Chen, Y.; Wu, F.; Chen, X. A general batch-calibration framework of service robots. In Proceedings of the International Conference on Intelligent Robotics and Applications, Wuhan, China, 15–18 August 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 275–286. [Google Scholar]
- Lindner, M.; Schiller, I.; Kolb, A.; Koch, R. Time-of-flight sensor calibration for accurate range sensing. Comput. Vis. Image Underst. 2010, 114, 1318–1328. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Rosenhahn, B. On calibration of a low-cost time-of-flight camera. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 415–427. [Google Scholar]
- Ferstl, D.; Reinbacher, C.; Riegler, G.; Rüther, M.; Bischof, H. Learning Depth Calibration of Time-of-Flight Cameras. In Proceedings of the the British Machine Vision Conference 2015, Swansea, UK, 7–10 September 2015; pp. 102–111. [Google Scholar]
- Perez-Yus, A.; Fernandez-Moral, E.; Lopez-Nicolas, G.; Guerrero, J.J.; Rives, P. Extrinsic calibration of multiple RGB-D cameras from line observations. IEEE Robot. Autom. Lett. 2017, 3, 273–280. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.h.; Yoo, J.; Park, M.; Kim, J.; Kwon, S. Robust Extrinsic Calibration of Multiple RGB-D Cameras with Body Tracking and Feature Matching. Sensors 2021, 21, 1013. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Mikami, D.; Isogawa, M.; Kimata, H. Human Pose as Calibration Pattern: 3D Human Pose Estimation with Multiple Unsynchronized and Uncalibrated Cameras. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 18566–18567. [Google Scholar] [CrossRef]
- Yoon, B.H.; Jeong, H.W.; Choi, K.S. Targetless Multiple Camera-LiDAR Extrinsic Calibration using Object Pose Estimation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 13377–13383. [Google Scholar] [CrossRef]
- Fukushima, N. Icp with depth compensation for calibration of multiple tof sensors. In Proceedings of the 2018-3DTV-Conference: The True Vision-Capture, Transmission and Display of 3D Video (3DTV-CON), Helsinki, Finland, 3–5 June 2018; pp. 1–4. [Google Scholar]
- Desai, K.; Prabhakaran, B.; Raghuraman, S. Skeleton-based continuous extrinsic calibration of multiple RGB-D kinect cameras. In Proceedings of the 9th ACM Multimedia Systems Conference, Amsterdam, The Netherlands, 12–15 June 2018; pp. 250–257. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.J.; Park, B.S.; Kim, J.K.; Kim, D.W.; Seo, Y.H. Holographic augmented reality based on three-dimensional volumetric imaging for a photorealistic scene. Opt. Express 2020, 28, 35972–35985. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.J.; Park, B.S.; Kim, D.W.; Kwon, S.C.; Seo, Y.H. Real-time 3D Volumetric Model Generation using Multiview RGB-D Camera. J. Broadcast Eng. 2020, 25, 439–448. [Google Scholar]
- Microsoft. Microsoft, Quickstart: Set Up Azure Kinect Body Tracking. Available online: https://docs.microsoft.com/en-us/azure/kinect-dk/body-sdk-setup (accessed on 26 June 2019).
- GOOGLE. MediaPipe Pose. Available online: https://google.github.io/mediapipe/solutions/pose.html (accessed on 8 December 2021).
- Kwolek, B.; Rymut, B. Reconstruction of 3D human motion in real-time using particle swarm optimization with GPU-accelerated fitness function. J. Real-Time Image Process. 2020, 17, 821–838. [Google Scholar] [CrossRef] [Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, B.-S.; Kim, W.; Kim, J.-K.; Hwang, E.S.; Kim, D.-W.; Seo, Y.-H. 3D Static Point Cloud Registration by Estimating Temporal Human Pose at Multiview. Sensors 2022, 22, 1097. https://doi.org/10.3390/s22031097
Park B-S, Kim W, Kim J-K, Hwang ES, Kim D-W, Seo Y-H. 3D Static Point Cloud Registration by Estimating Temporal Human Pose at Multiview. Sensors. 2022; 22(3):1097. https://doi.org/10.3390/s22031097
Chicago/Turabian StylePark, Byung-Seo, Woosuk Kim, Jin-Kyum Kim, Eui Seok Hwang, Dong-Wook Kim, and Young-Ho Seo. 2022. "3D Static Point Cloud Registration by Estimating Temporal Human Pose at Multiview" Sensors 22, no. 3: 1097. https://doi.org/10.3390/s22031097
APA StylePark, B.-S., Kim, W., Kim, J.-K., Hwang, E. S., Kim, D.-W., & Seo, Y.-H. (2022). 3D Static Point Cloud Registration by Estimating Temporal Human Pose at Multiview. Sensors, 22(3), 1097. https://doi.org/10.3390/s22031097






