Correlation Coefficient Based Optimal Vibration Sensor Placement and Number
Abstract
:1. Introduction
2. Theoretical Background
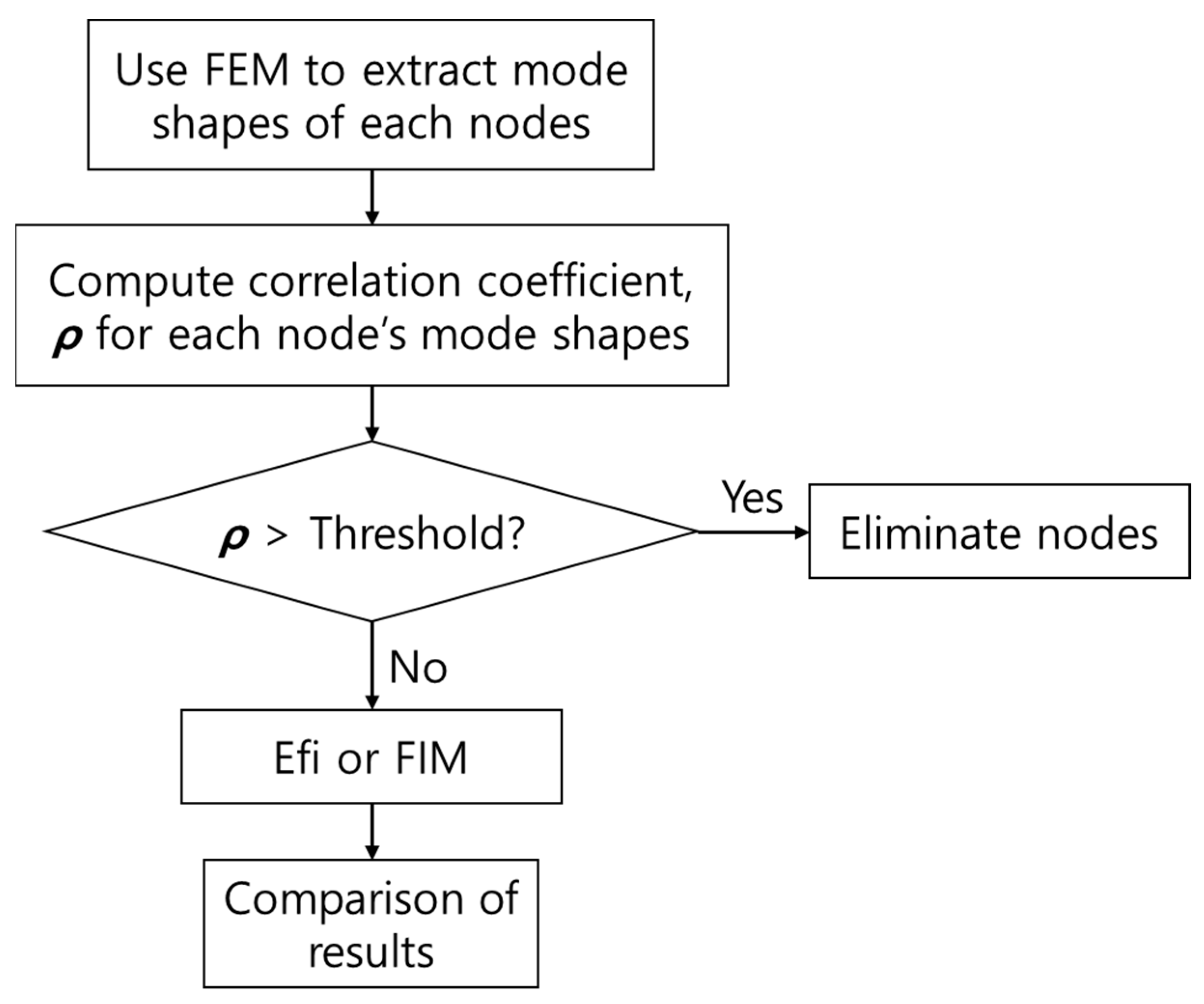
2.1. Correlation Coefficient
2.2. Fisher Information Matrix
2.3. Effective Independence
3. Numerical Example
3.1. Target Shape and Mechanical Properties
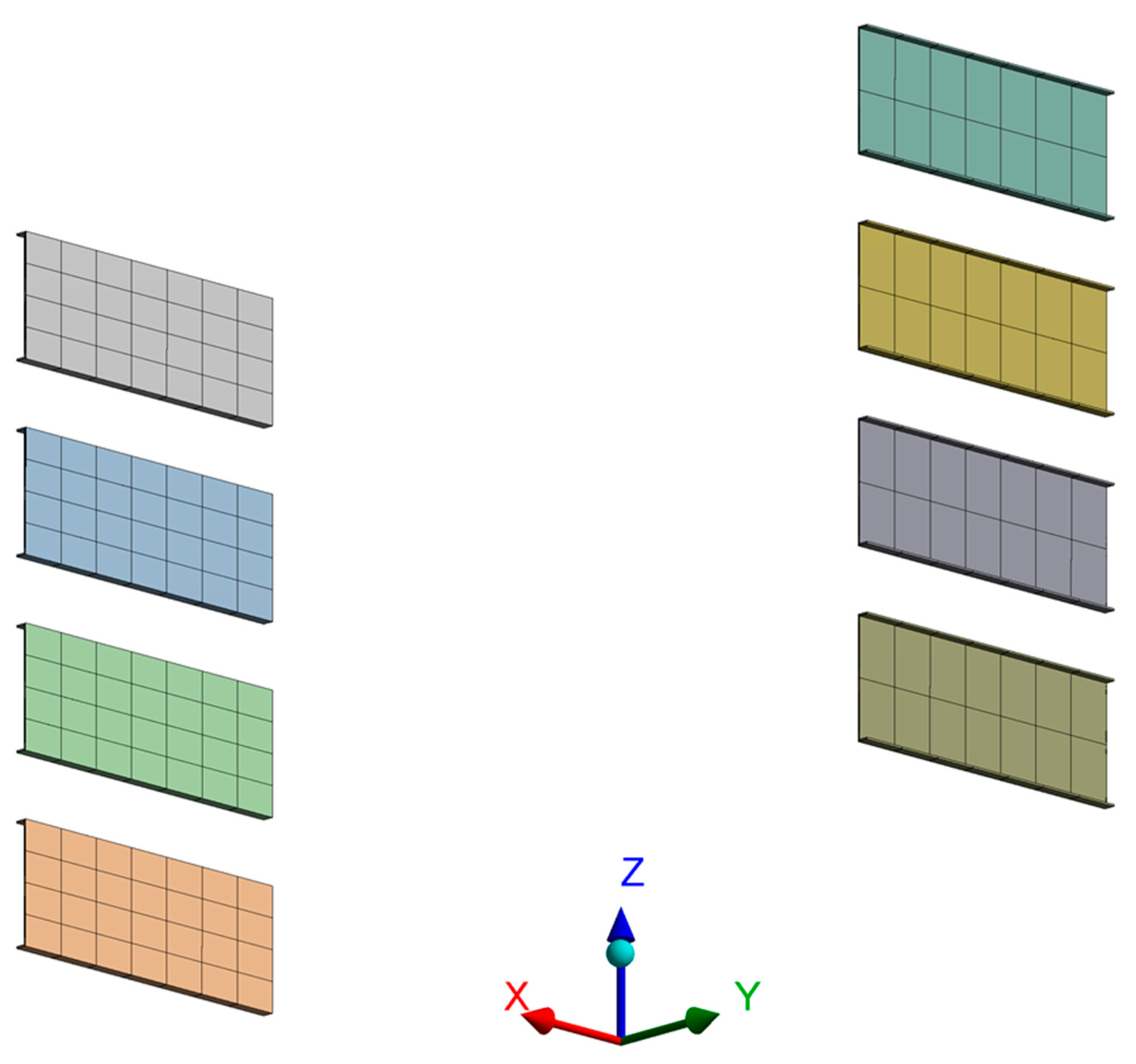
3.2. Boundary Conditions and Meshing
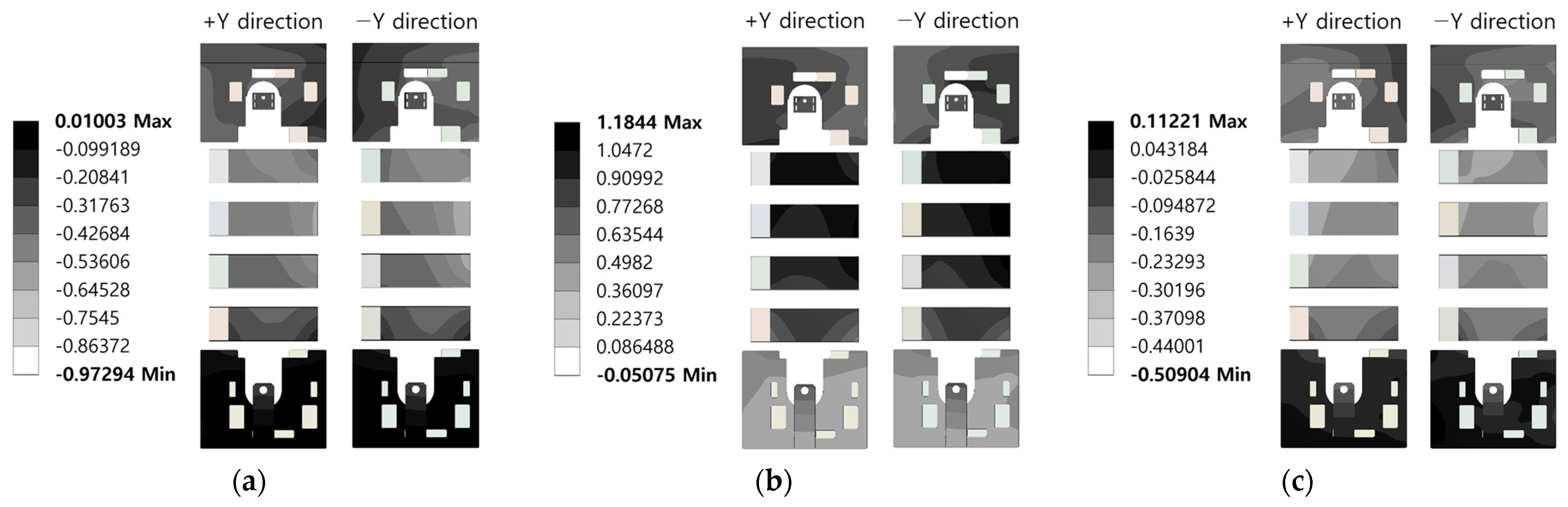
3.3. Modal Analysis Results
3.4. Optimal Sensor Placement and Number Results
3.5. Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Gao, H.; Wen, J.; Li, S.; Liu, Q. A deep learning-based recognition method for degradation monitoring of ball screw with multi-sensor data fusion. Microelectron. Reliab. 2017, 75, 215–222. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Yan, X.; Sun, Z.; Zhao, J.; Shi, Z.; Zhang, C. Fault diagnosis of rotating machinery equipped with multiple sensors using space-time fragments. J. Sound Vib. 2019, 456, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Ma, R.; Ma, R. Optimal sensor placement for modal identification in multirotary-joint solar power satellite. IEEE Sens. J. 2020, 20, 7337–7346. [Google Scholar] [CrossRef]
- Kammer, D.C.; Tinker, M.L. Optimal placement of triaxial accelerometers for modal vibration tests. Mech. Syst. Signal Processing 2004, 18, 29–41. [Google Scholar] [CrossRef]
- Yang, C. An adaptive sensor placement algorithm for structural health monitoring based on multi-objective iterative optimization using weight factor updating. Mech. Syst. Signal Processing 2021, 151, 107363. [Google Scholar] [CrossRef]
- Li, Z.N.; Tang, J.; Li, Q.S. Optimal sensor locations for structural vibration measurements. Appl. Acoust. 2004, 65, 807–818. [Google Scholar] [CrossRef]
- Martin, G.; Balmes, E.; Chancellier, T. Improved modal assurance criterion using a quantification of identification errors per mode/sensor. In Proceedings of the 2014 ISMA, Leuven, Belgium, 15 September 2014. [Google Scholar]
- Meo, M.; Zumpano, G. On the optimal sensor placement techniques for a bridge structure. Eng. Struct. 2005, 27, 1488–1497. [Google Scholar] [CrossRef]
- Suastika, I.K.; Hakim, M.L.; Nugroho, B.; Nasirudin, A.; Utama, I.K.A.P.; Monty, J.P.; Ganapathisubramani, B. Characteristics of drag due to streamwise inhomogeneous roughness. Ocean Eng. 2021, 223, 108632. [Google Scholar] [CrossRef]
- Balagangadhar, R.; Slater, J.C. On the Convergence of Nonlinear Modes of a Finite Element Model. Shock Vib. 2008, 15, 645014. [Google Scholar] [CrossRef] [Green Version]
- Sheng, S.; Zhang, L.; Gao, R.X. A systematic sensor-placement strategy for enhanced defect detection in rolling bearings. IEEE Sens. J. 2006, 6, 1346–1354. [Google Scholar] [CrossRef]
- Camelio, J.A.; Hu, S.J.; Yim, H. Sensor placement for effective diagnosis of multiple faults in fixturing of complaint parts. J. Manuf. Sci. Eng. 2005, 127, 68–74. [Google Scholar] [CrossRef]
- Kammer, D.C. Sensor Placement for On-Orbit Modal Identification and Correlation of Large Space Structures. J. Guid. Control. Dyn. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.W. A multi-domain diagnostics approach for solenoid pumps based on discriminative features. IEEE Access 2020, 8, 175020–175034. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.W. A cost-efficient MFCC-based fault detection and isolation technology for electromagnetic pumps. Electronics 2021, 10, 439. [Google Scholar] [CrossRef]
- Shifat, T.A.; Hur, J.W. ANN assisted multi sensor information fusion for BLDC motor fault diagnosis. IEEE Access 2021, 9, 9429–9441. [Google Scholar] [CrossRef]
- Chok, N.S. Pearson’s versus Spearman’s and Kendall’s Correlation Coefficients for Continuous Data. Master’s Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 26 May 2010. [Google Scholar]
- Xu, W.; Hou, Y.; Hung, Y.S.; Zou, Y. A comparative analysis of Spearman’s rho and Kendall’s tau in normal and contaminated normal models. Signal Processing 2013, 93, 261–276. [Google Scholar] [CrossRef]
- Shin, G.H.; Lee, E.Y.; Hwang, C.W.; Kuk, Y.H.; Hur, J.W. The number and location optimization of sensors for fault diagnosis of automated storage and retrieval system. In Proceedings of the PRESM 2021, Jeju, Korea, 21–23 of July 2021. [Google Scholar]
- ANSYS Inc. Contact Technology Guide; ANSYS Inc.: Canonsburg, PA, USA, 2004. [Google Scholar]
- ANSYS Inc. Theory Reference for the Mechanical APDL and Mechanical Applications; ANSYS Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Demir, M.E. Shock Analysis of an Antenna Structure Subjected to Underwater Explosions. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 8 September 2015. [Google Scholar]
- Tasdelen, E. Shock Analysis of On-board Equipment Submitted to Underwater Explosion. Master’s Thesis, University of Liege, Liege, Belgium, February 2018. [Google Scholar]
- Mo, H.; Qiu, H. Simulation and Random Vibration Test of Structural Dynamic Characteristics of Vacuum Tube. In Proceedings of the International Conference on Mechatronics, Materials, Biotechnology and Environment, Yinchuan, China, 13–14 August 2016. [Google Scholar]








| Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|
| Aluminum | 2770 | 71 | 0.33 |
| Brass | 8460 | 103 | 0.35 |
| Pre-coated steel sheet | 7800 | 204 | 0.29 |
| SS41 | 7850 | 206 | 0.29 |
| SUS304 | 8000 | 197 | 0.3 |
| Definition | Door Unit | Rotary Unit |
|---|---|---|
| Mass (kg) | 6.927 | 491.32 |
| Mass moment of inertia X (kg·m2) | 6.978 | 496.71 |
| Mass moment of inertia Y (kg·m2) | 1.341 | 356.45 |
| Mass moment of inertia Z (kg·m2) | 5.647 | 244.15 |
| Mode | Frequency (Hz) | Modal Mass (%) |
|---|---|---|
| 1 | 7.024 | 0.000 |
| 2 | 8.880 | 0.000 |
| 3 | 9.010 | 0.001 |
| ⋮ | ||
| 25 | 24.621 | 19.475 |
| 26 | 24.986 | 31.647 |
| ⋮ | ||
| 33 | 27.081 | 2.207 |
| ⋮ | ||
| 35 | 27.551 | 4.849 |
| ⋮ | ||
| 82 | 47.551 | 4.353 |
| ⋮ | ||
| 122 | 61.446 | 1.359 |
| ⋮ | ||
| 262 | 109.81 | 1.028 |
| ⋮ | ||
| 300 | 123.14 | 0.017 |
| 301 | 123.30 | 0.291 |
| 302 | 123.39 | 0.057 |
| Total | 80.051 | |
| Correlation Coefficient | Threshold | The Number of Sensors |
|---|---|---|
| Pearson | 0.7 | 10 |
| Spearman | 11 | |
| Kendall tau | 25 |
| The Number of Sensors | Node Numbers | Same Node Numbers | |
|---|---|---|---|
| Pearson-FIM | Pearson-Efi | ||
| 2 | 1,358,355, 1,406,113 | 1,351,085, 1,406,113 | 1 |
| 3 | 1,343,710, 1,358,355, 1,406,113 | 1,351,083, 1,351,085, 1,406,113 | 1 |
| 4 | 1,343,710, 1,351,085, 1,358,355, 1,406,113 | 1,343,710, 1,351,083, 1,351,085, 1,406,113 | 3 |
| 5 | 1,343,708, 1,351,083, 1,351,085, 1,358,355, 1,406,113 | 1,343,708, 1,343,710, 1,351,083, 1,351,085, 1,406,113 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, G.-H.; Hur, J.-W. Correlation Coefficient Based Optimal Vibration Sensor Placement and Number. Sensors 2022, 22, 1207. https://doi.org/10.3390/s22031207
Shin G-H, Hur J-W. Correlation Coefficient Based Optimal Vibration Sensor Placement and Number. Sensors. 2022; 22(3):1207. https://doi.org/10.3390/s22031207
Chicago/Turabian StyleShin, Geon-Ho, and Jang-Wook Hur. 2022. "Correlation Coefficient Based Optimal Vibration Sensor Placement and Number" Sensors 22, no. 3: 1207. https://doi.org/10.3390/s22031207
APA StyleShin, G.-H., & Hur, J.-W. (2022). Correlation Coefficient Based Optimal Vibration Sensor Placement and Number. Sensors, 22(3), 1207. https://doi.org/10.3390/s22031207







