Multi-Angle Optical Image Automatic Registration by Combining Point and Line Features
Abstract
:1. Introduction
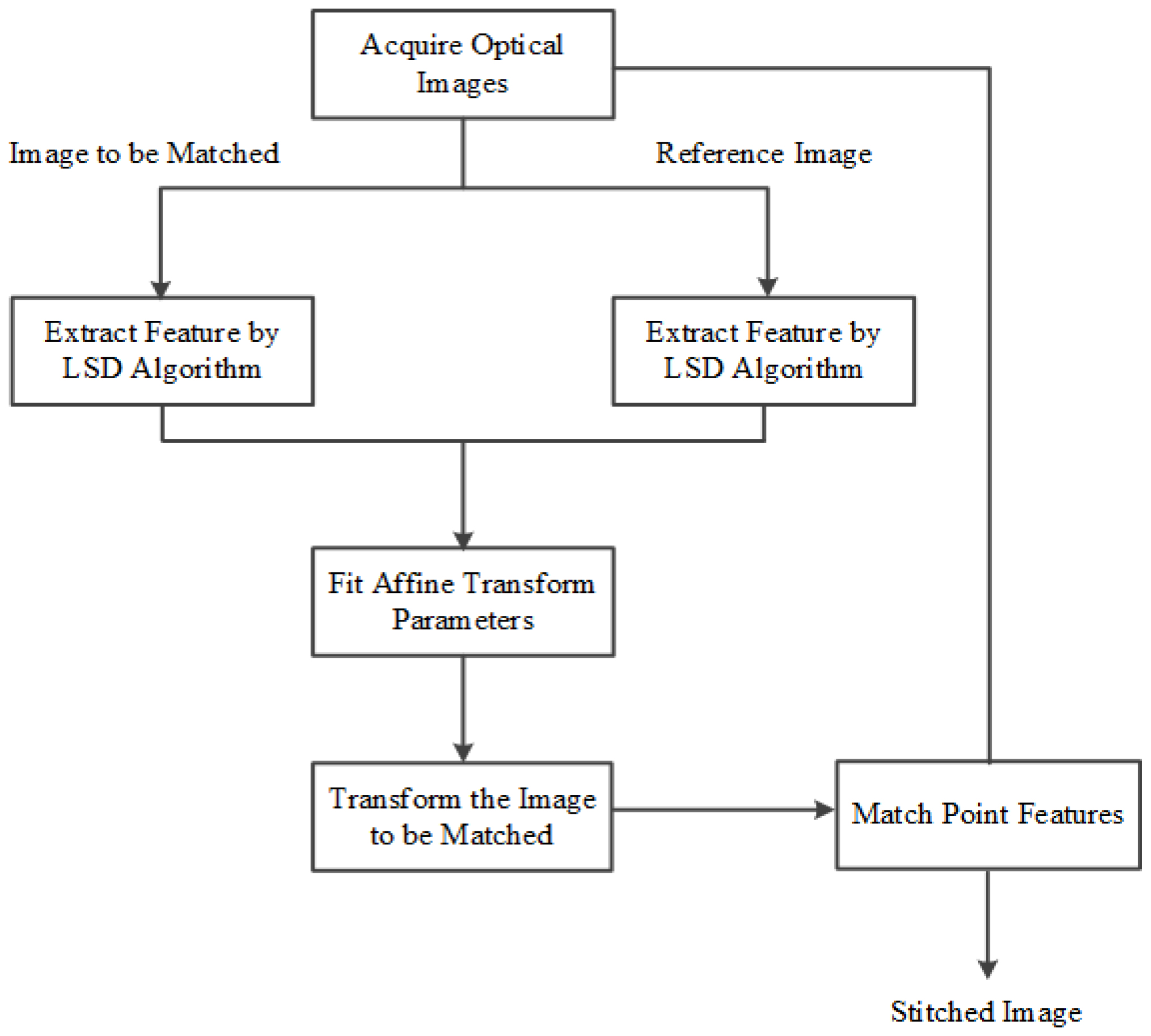
2. Methodology
2.1. Rough Matching
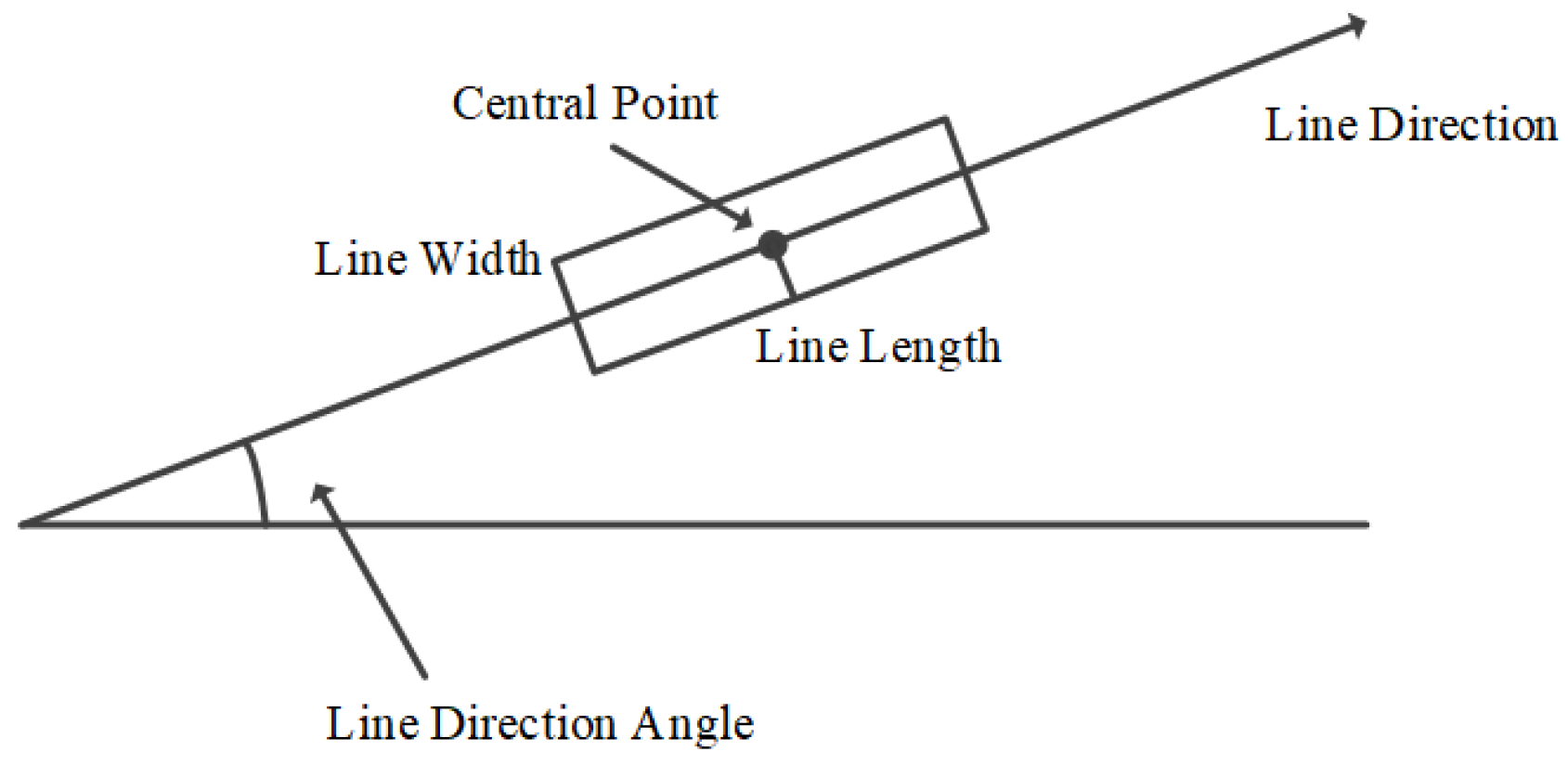
2.1.1. Line Detection by LSD
2.1.2. Matching Line Features by GMM
2.2. Fine Matching
2.2.1. Extraction and Representation of Point Features
2.2.2. Point Feature Matching
2.2.3. Elimination of Mismatches
3. Experimental Results
3.1. Rough Matching Test
3.2. Registration Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, Q.; Adu, J.; Liu, J.; Yang, J.; Xu, Y.; Gong, M. Real-time adaptive visible and infrared image registration based on morphological gradient and C_SIFT. J. Real-Time Image Process. 2020, 17, 1103–1115. [Google Scholar] [CrossRef]
- Pan, Y.; Tong, L.; Li, Y.; Xiao, F.; Wang, H. High-resolution optical and SAR image registration using local self-similar descriptor based on edge feature. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2491–2494. [Google Scholar]
- Fernández-Fabeiro, J.; Gonzalez-Escribano, A.; Llanos, D.R. Distributed programming of a hyperspectral image registration algorithm for heterogeneous GPU clusters. J. Parallel Distrib. Comput. 2021, 151, 86–93. [Google Scholar] [CrossRef]
- Hou, X.; Gao, Q.; Wang, R.; Luo, X. Satellite-borne optical remote sensing image registration based on point features. Sensors 2021, 21, 2695. [Google Scholar] [CrossRef] [PubMed]
- Hossein-Nejad, Z.; Agahi, H.; Mahmoodzadeh, A. Image matching based on the adaptive redundant keypoint elimination method in the SIFT algorithm. Pattern Anal. Appl. 2020, 24, 669–683. [Google Scholar] [CrossRef]
- Zhao, D. Rapid multimodal image registration based on the local edge histogram. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Pourfard, M.; Hosseinian, T.; Saeidi, R.; Motamedi, S.A.; Abdollahifard, M.J.; Mansoori, R.; Safabakhsh, R. KAZE-SAR: SAR image registration using KAZE detector and modified SURF descriptor for tackling speckle noise. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5207612. [Google Scholar] [CrossRef]
- Wang, X.; Duan, L.; Fan, Y.; Ning, C. A multi-sensor image matching method based on KAZE-HOG features. In Proceedings of the 2019 IEEE 4th International Conference on Image, Vision and Computing (ICIVC), Xiamen, China, 5–7 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 514–517. [Google Scholar]
- Zheng, J.; Peng, W.; Wang, Y.; Zhai, B. Accelerated RANSAC for accurate image registration in aerial video surveillance. IEEE Access 2021, 9, 36775–36790. [Google Scholar] [CrossRef]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.-M.; Randall, G. LSD: A line segment detector. Image Process. Line 2012, 2, 35–55. [Google Scholar] [CrossRef] [Green Version]
- Noorbala, L.; Niyakan, S.; Alavi, S.M.M. Development of phase congruency to estimate the direction of maximum information (tDMI) in images with straight line segments. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1413–1419. [Google Scholar]
- Yu, Q.; Ni, D.; Jiang, Y.; Yan, Y.; An, J.; Sun, T. Universal SAR and optical image registration via a novel SIFT framework based on nonlinear diffusion and a polar spatial-frequency descriptor. ISPRS J. Photogramm. Remote Sens. 2021, 171, 1–17. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Q.; Tansey, K.; Ullah, S.; Liu, F.; Zhao, H.; Yan, L. Multi-constrained optimization method of line segment extraction based on multi-scale image space. ISPRS Int. J. Geo-Inf. 2019, 8, 183. [Google Scholar] [CrossRef] [Green Version]
- Sui, Y.; Qin, Z.; Tong, X.; Li, H.; Lai, G. A cumulative projection-based automatic registration method for mobile laser scanning data. Remote Sens. Lett. 2018, 10, 86–94. [Google Scholar] [CrossRef]
- Momani, M.Q. Cross-section and GMM/SDF tests of linear factor models. Appl. Econ. Lett. 2021, 28, 590–593. [Google Scholar] [CrossRef]
- Ossimitz, C.; TaheriNejad, N. A fast line segment detector using approximate computing. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Korea, 22–28 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Liu, Y.; Xie, Z.; Liu, H. LB-LSD: A length-based line segment detector for real-time applications. Pattern Recognit. Lett. 2019, 128, 247–254. [Google Scholar] [CrossRef]
- Zhu, H.; Zou, K.; Li, Y.; Cen, M.; Mihaylova, L. Robust non-rigid feature matching for image registration using geometry preserving. Sensors 2019, 19, 2729. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Du, N.; Wang, Z.; Xiao, G. Wrapped ambiguity Gaussian mixed model with applications in sparse sampling based multiple parameter estimation. Signal Process. 2021, 179, 107825. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Shen, S.; Jiang, X. A new lateral cephalogram image stitching technique using gaussian mixture model and normalized cross-correlation. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; IEEE: Piscataway, NJ, USA, 2021; Volume 5, pp. 1574–1579. [Google Scholar]
- Wei, Z.; Jung, C.; Su, C. RegiNet: Gradient guided multispectral image registration using convolutional neural networks. Neurocomputing 2020, 415, 193–200. [Google Scholar] [CrossRef]
- Li, B.; Au, S.-K. An expectation-maximization algorithm for Bayesian operational modal analysis with multiple (possibly close) modes. Mech. Syst. Signal Process. 2019, 132, 490–511. [Google Scholar] [CrossRef]
- Hu, H.; Ao, Y.; Bai, Y.; Cheng, R.; Xu, T. An improved Harris’s Hawks optimization for SAR target recognition and stock market index prediction. IEEE Access 2020, 8, 65891–65910. [Google Scholar] [CrossRef]
- Wenying, L.; Yaobin, M.; Yi, Z. Noise detection from single image based on Harris operator. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 7293–7298. [Google Scholar]
- Etezadifar, P.; Farsi, H. A new sample consensus based on sparse coding for improved matching of SIFT features on remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5254–5263. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Liu, H. Robust optical and SAR image registration based on OS-SIFT and cascaded sample consensus. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Du, J.; Bian, F. A privacy-preserving and efficient k-nearest neighbor query and classification scheme based on k-dimensional tree for outsourced data. IEEE Access 2020, 8, 69333–69345. [Google Scholar] [CrossRef]
- Meddeber, L.; Zouagui, T.; Berrached, N. An improved registration and mosaicking method for remote sensing images under geometric and photometric constraints. In Proceedings of the 2020 1st International Conference on Communications, Control Systems and Signal Processing (CCSSP), El Oued, Algeria, 16–17 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 125–130. [Google Scholar]
- Rasmy, L.; Sebari, I.; Ettarid, M. Automatic sub-pixel co-registration of remote sensing images using phase correlation and Harris detector. Remote Sens. 2021, 13, 2314. [Google Scholar] [CrossRef]
- Rahman, M.; Li, X.; Yin, X. DL-RANSAC: An improved RANSAC with modified sampling strategy based on the likelihood. In Proceedings of the 2019 IEEE 4th International Conference on Image, Vision and Computing (ICIVC), Xiamen, China, 5–7 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 463–468. [Google Scholar]
- Yi, Z.; Wang, H.; Duan, G.; Wang, Z. An airborne LiDAR building-extraction method based on the naive Bayes–RANSAC method for proportional segmentation of quantitative features. J. Indian Soc. Remote Sens. 2021, 49, 393–404. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Van Gool, L. A comparison of affine region detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef] [Green Version]
- Ben Marzouka, W.; Solaiman, B.; Hammouda, A.; Ben Dhief, Z.; Bsaies, K. Possibilistic BRISK method for an efficient registration (PBRISK). In Proceedings of the 2020 5th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 2–5 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Ordóñez, Á.; Argüello, F.; Heras, D.B.; Demir, B. GPU-accelerated registration of hyperspectral images using KAZE features. J. Supercomput. 2020, 76, 9478–9492. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, R.; Chen, Z. Application of migration image registration algorithm based on improved SURF in remote sensing image mosaic. IEEE Access 2020, 8, 163637–163645. [Google Scholar] [CrossRef]













| Methods | The First Pair | The Second Pair | The Third Pair | |||
|---|---|---|---|---|---|---|
| NoP | Accuracy of Pairs | NoP | Correct Matching Rate | NoP | Accuracy of Pairs | |
| line matching | 152 | 92.3% | 108 | 90.2% | 50 | 84% |
| point matching | 16 | 100% | 16 | 100% | 7 | 100% |
| Images | Methods | NoP (Lines) | NoP (Points) | Correct Matching Rate | RMSE | Time (s) |
|---|---|---|---|---|---|---|
| 0° and 15° | SIFT | / | 100 | 98% | 1.1892 | 4.370 |
| BRISK | / | 58 | 100% | 1.1953 | 2.136 | |
| KAZE | / | 89 | 98% | 1.2137 | 4.678 | |
| SURF | / | 122 | 98.3% | 1.2059 | 3.733 | |
| Ours | 137 | 85 | 100% | 1.1161 | 8.527 | |
| 0° and 35° | SIFT | / | 73 | 100% | 1.1676 | 4.292 |
| BRISK | / | 52 | 99% | 1.1715 | 2.032 | |
| KAZE | / | 64 | 100% | 1.1708 | 4.489 | |
| SURF | / | 95 | 98% | 1.1803 | 3.376 | |
| Ours | 129 | 70 | 100% | 1.1389 | 8.378 |
| Methods | NoP (Lines) | NoP (Points) | Correct Matching Rate | RMSE | Time (s) |
|---|---|---|---|---|---|
| SIFT | / | 121 | 97.5% | 1.5151 | 11.934 |
| BRISK | / | 78 | 96.8% | 1.5619 | 5.466 |
| KAZE | / | 116 | 96.3% | 1.5722 | 14.659 |
| SURF | / | 134 | 97.8% | 1.5312 | 7.904 |
| Ours | 129 | 112 | 98.2% | 1.4777 | 48.315 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Meng, J.; Hou, W.; Wang, R.; Luo, X. Multi-Angle Optical Image Automatic Registration by Combining Point and Line Features. Sensors 2022, 22, 739. https://doi.org/10.3390/s22030739
Su J, Meng J, Hou W, Wang R, Luo X. Multi-Angle Optical Image Automatic Registration by Combining Point and Line Features. Sensors. 2022; 22(3):739. https://doi.org/10.3390/s22030739
Chicago/Turabian StyleSu, Jia, Juntong Meng, Weimin Hou, Rong Wang, and Xin Luo. 2022. "Multi-Angle Optical Image Automatic Registration by Combining Point and Line Features" Sensors 22, no. 3: 739. https://doi.org/10.3390/s22030739
APA StyleSu, J., Meng, J., Hou, W., Wang, R., & Luo, X. (2022). Multi-Angle Optical Image Automatic Registration by Combining Point and Line Features. Sensors, 22(3), 739. https://doi.org/10.3390/s22030739






