Laser Ablated Nanocrystalline Diamond Membrane for Infrared Applications
Abstract
:1. Introduction
2. Experimental
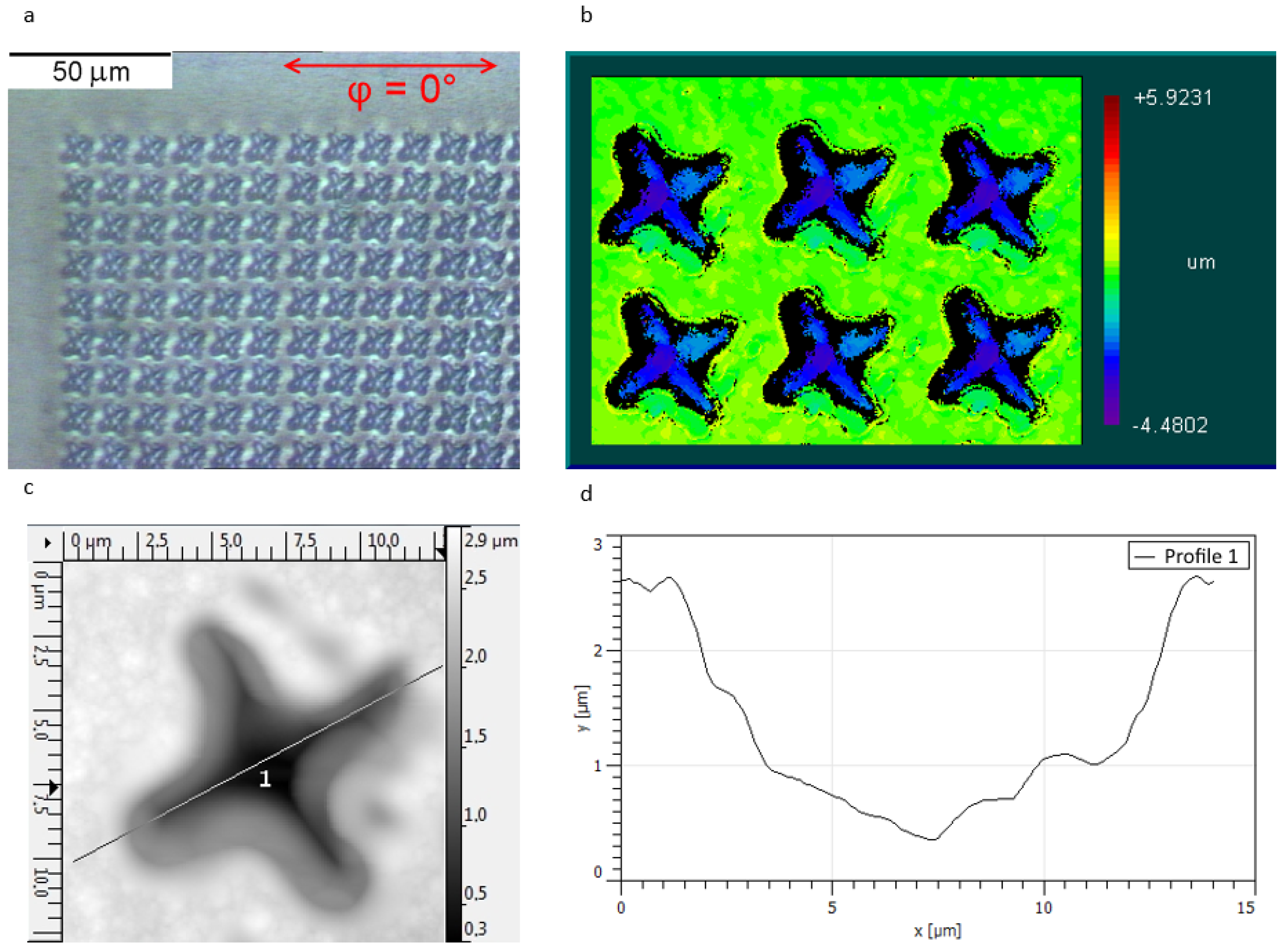
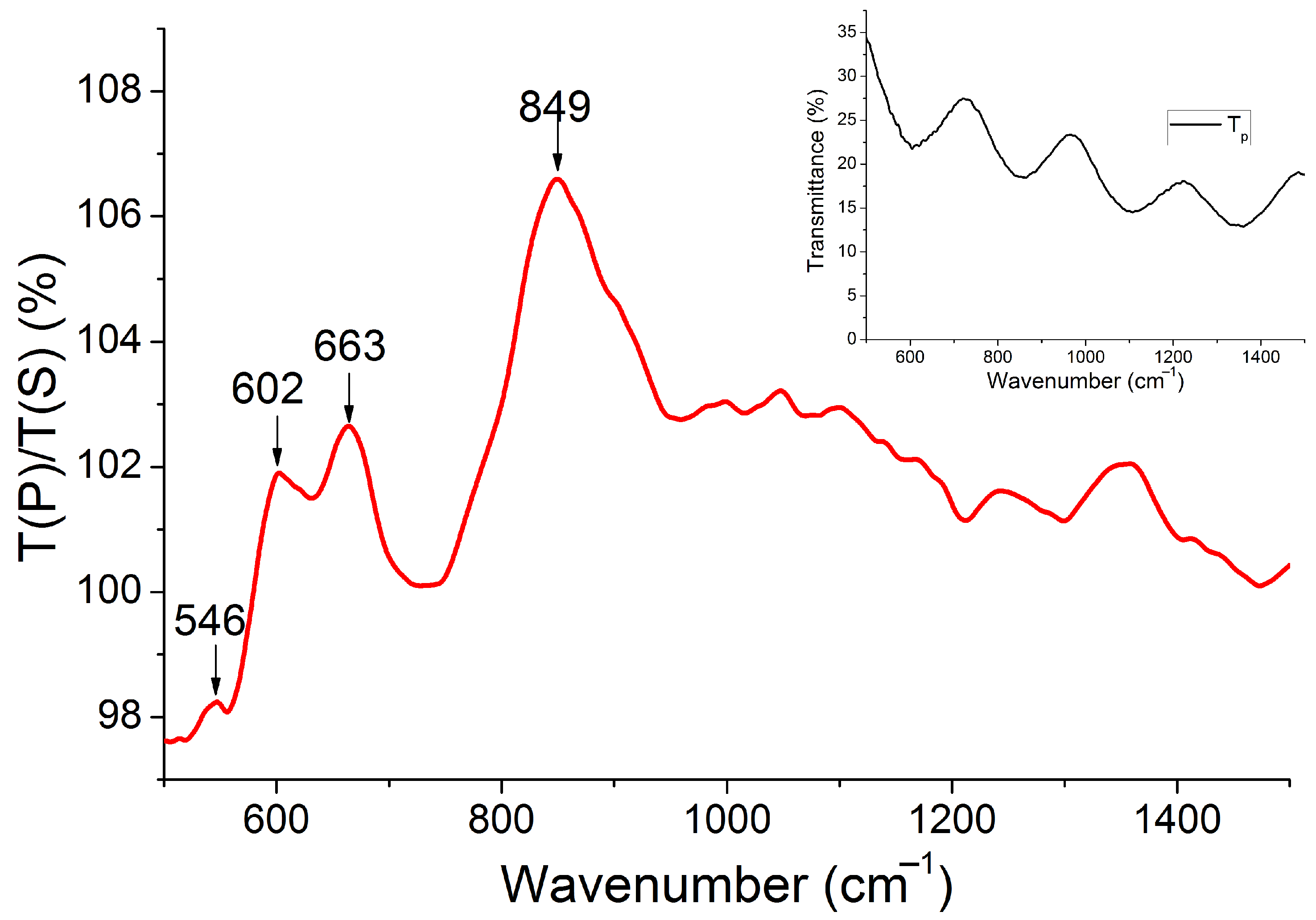
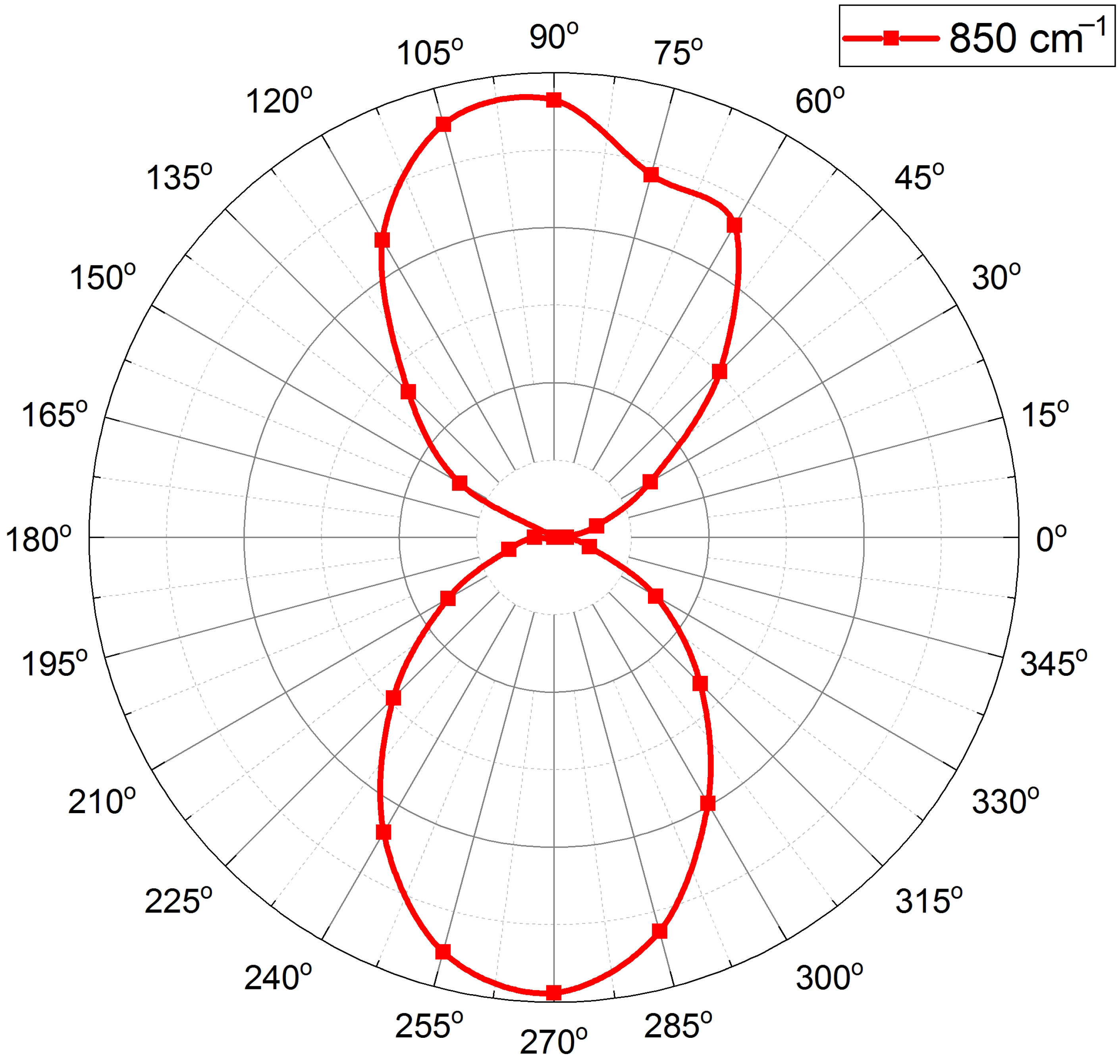
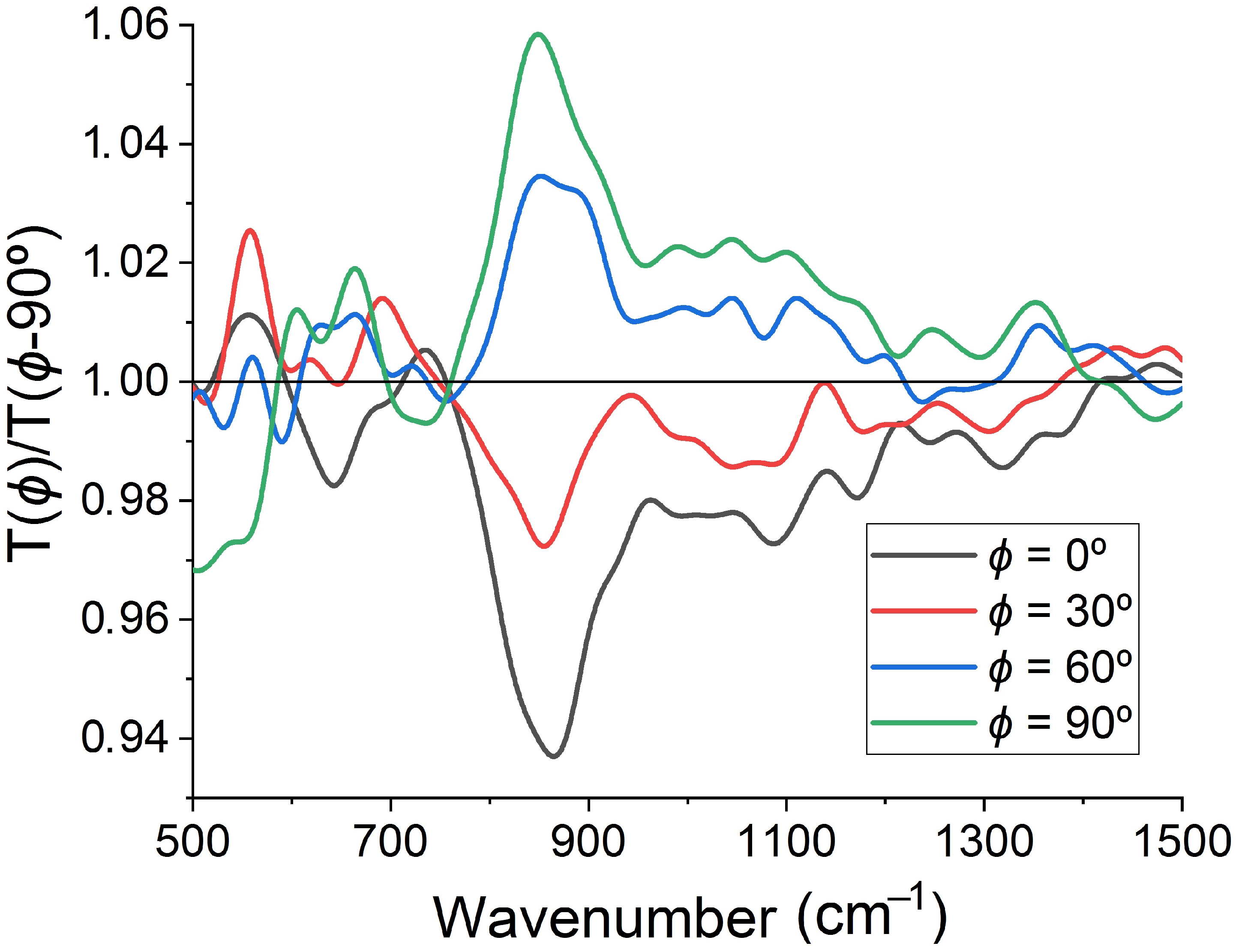
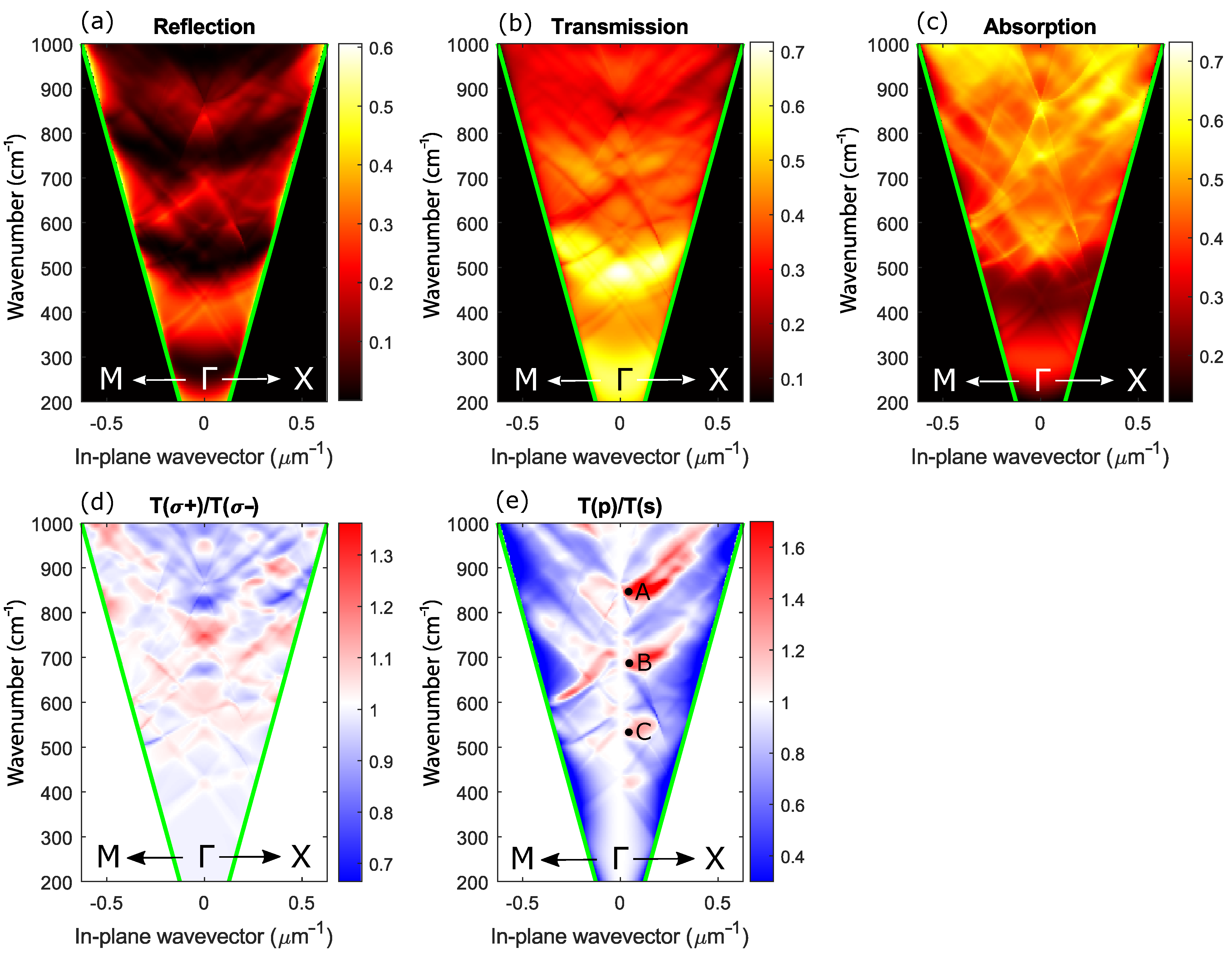
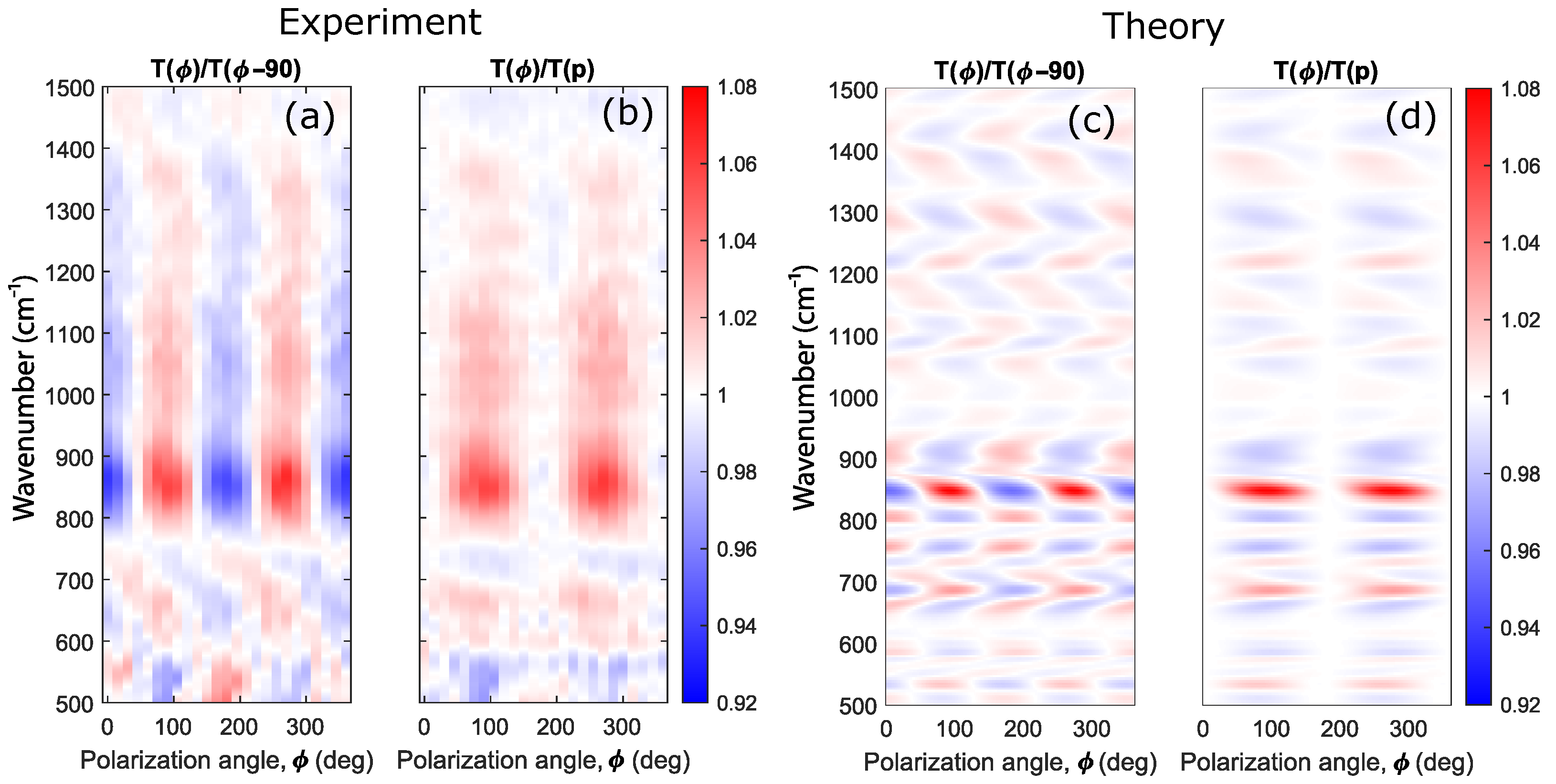
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Arju, N.; Kelp, G.; Fan, J.A.; Dominguez, J.; Gonzales, E.; Tutuc, E.; Brener, I.; Shvets, G. Spectrally selective chiral silicon metasurfaces based on infrared Fano resonances. Nat. Commun. 2014, 5, 3892. [Google Scholar] [CrossRef]
- Bossard, J.A.; Werner, D.H. Metamaterials with custom emissivity polarization in the near-infrared. Opt. Express 2013, 21, 3872–3884. [Google Scholar] [CrossRef] [PubMed]
- Wadsworth, S.L.; Clem, P.G.; Branson, E.D.; Boreman, G.D. Broadband circularly-polarized infrared emission from multilayer metamaterials. Opt. Mater. Express 2011, 1, 466–479. [Google Scholar] [CrossRef]
- Hao, F.; Sonnefraud, Y.; Dorpe, P.V.; Maier, S.A.; Halas, N.J.; Nordlander, P. Symmetry breaking in plasmonic nanocavities: Subradiant LSPR sensing and a tunable Fano resonance. Nano Lett. 2008, 8, 3983–3988. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Tang, M.L.; Hentschel, M.; Giessen, H.; Alivisatos, A.P. Nanoantenna-enhanced gas sensing in a single tailored nanofocus. Nat. Mater. 2011, 10, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Khanikaev, A.B.; Adato, R.; Arju, N.; Yanik, A.A.; Altug, H.; Shvets, G. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers. Nat. Mater. 2012, 11, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Raman, A.P.; Abou Anoma, M.; Zhu, L.; Rephaeli, E.; Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef] [PubMed]
- Hsu, P.C.; Song, A.Y.; Catrysse, P.B.; Liu, C.; Peng, Y.; Xie, J.; Fan, S.; Cui, Y. Radiative human body cooling by nanoporous polyethylene textile. Science 2016, 353, 1019–1023. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Y.; Ma, Y.; David, S.N.; Zhao, D.; Lou, R.; Tan, G.; Yang, R.; Yin, X. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling. Science 2017, 355, 1062–1066. [Google Scholar] [CrossRef] [Green Version]
- Lenert, A.; Bierman, D.M.; Nam, Y.; Chan, W.R.; Celanović, I.; Soljačić, M.; Wang, E.N. A nanophotonic solar thermophotovoltaic device. Nat. Nanotechnol. 2014, 9, 126. [Google Scholar] [CrossRef]
- Rephaeli, E.; Fan, S. Absorber and emitter for solar thermo-photovoltaic systems to achieve efficiency exceeding the Shockley-Queisser limit. Opt. Express 2009, 17, 15145–15159. [Google Scholar] [CrossRef] [PubMed]
- Dyachenko, P.N.; Molesky, S.; Petrov, A.Y.; Störmer, M.; Krekeler, T.; Lang, S.; Ritter, M.; Jacob, Z.; Eich, M. Controlling thermal emission with refractory epsilon-near-zero metamaterials via topological transitions. Nat. Commun. 2016, 7, 11089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagpal, P.; Han, S.E.; Stein, A.; Norris, D.J. Efficient low-temperature thermophotovoltaic emitters from metallic photonic crystals. Nano Lett. 2008, 8, 3238–3243. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, X.; Guo, L.J. Efficient Thermal–Light Interconversions Based on Optical Topological Transition in the Metal-Dielectric Multilayered Metamaterials. Adv. Mater. 2016, 28, 3017–3023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Bai, X.; Yang, T.; Luo, H.; Qiu, C.W. Structured thermal surface for radiative camouflage. Nat. Commun. 2018, 9, 273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, L.; Ma, H.; Liu, J.; Zhao, W.; Jia, Y.; Zhao, Q.; Liu, K.; Wu, Y.; Wei, Y.; Fan, S.; et al. Fast adaptive thermal camouflage based on flexible VO2/graphene/CNT thin films. Nano Lett. 2015, 15, 8365–8370. [Google Scholar] [CrossRef]
- Kononenko, T.; Dyachenko, P.; Konov, V. Diamond photonic crystals for the IR spectral range. Opt. Lett. 2014, 39, 6962–6965. [Google Scholar] [CrossRef]
- Deotare, P.B.; McCutcheon, M.W.; Frank, I.W.; Khan, M.; Lončar, M. High quality factor photonic crystal nanobeam cavities. Appl. Phys. Lett. 2009, 94, 121106. [Google Scholar] [CrossRef] [Green Version]
- Checoury, X.; Néel, D.; Boucaud, P.; Gesset, C.; Girard, H.; Saada, S.; Bergonzo, P. Nanocrystalline diamond photonics platform with high quality factor photonic crystal cavities. Appl. Phys. Lett. 2012, 101, 171115. [Google Scholar] [CrossRef] [Green Version]
- Ding, M.Q.; Li, L.; Feng, J. Composite diamond films for short-mm wave and THz traveling wave tube windows. Diam. Relat. Mater. 2014, 50, 129–134. [Google Scholar] [CrossRef]
- Ding, M.Q.; Li, L.; Du, Y.; Wu, X.; Cai, J.; Feng, J. Development of an extremely thin-diamond window for terahertz traveling wave tubes. Diam. Relat. Mater. 2017, 79, 173–178. [Google Scholar] [CrossRef]
- Remes, Z.; Babchenko, O.; Varga, M.; Stuchlik, J.; Jirasek, V.; Prajzler, V.; Nekvindova, P.; Kromka, A. Preparation and optical properties of nanocrystalline diamond coatings for infrared planar waveguides. Thin Solid Films 2016, 618, 130–133. [Google Scholar] [CrossRef]
- Rahmati, A.T.; Mashanovich, G.Z.; Nezhad, M.P. Suspended nanocrystalline diamond ridge waveguides designed for the mid-infrared. J. Opt. 2021, 23, 075801. [Google Scholar] [CrossRef]
- Arndt, N.; Bolwien, C.; Sulz, G.; Kühnemann, F.; Lambrecht, A. Diamond-Coated Silicon ATR Elements for Process Analytics. Sensors 2021, 21, 6442. [Google Scholar] [CrossRef] [PubMed]
- Kosowska, M.; Majchrowicz, D.; Sankaran, K.J.; Ficek, M.; Haenen, K.; Szczerska, M. Doped nanocrystalline diamond films as reflective layers for fiber-optic sensors of refractive index of liquids. Materials 2019, 12, 2124. [Google Scholar] [CrossRef] [Green Version]
- Janssens, S.D.; Vázquez-Cortés, D.; Giussani, A.; Kwiecinski, J.A.; Fried, E. Nanocrystalline diamond-glass platform for the development of three-dimensional micro-and nanodevices. Diam. Relat. Mater. 2019, 98, 107511. [Google Scholar] [CrossRef]
- Konov, V.I. Carbon photonics. Quantum Electron. 2015, 45, 1043. [Google Scholar] [CrossRef]
- Ali, B.; Litvinyuk, I.V.; Rybachuk, M. Femtosecond laser micromachining of diamond: Current research status, applications and challenges. Carbon 2021, 179, 209–226. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Bellini, M.; Corsi, C.; Gorelli, F.; Parrini, G.; Santoro, M.; Sciortino, S. Three-dimensional diamond detectors: Charge collection efficiency of graphitic electrodes. Appl. Phys. Lett. 2013, 103, 233507. [Google Scholar] [CrossRef]
- Oh, A.; Caylar, B.; Pomorski, M.; Wengler, T. A novel detector with graphitic electrodes in CVD diamond. Diam. Relat. Mater. 2013, 38, 9–13. [Google Scholar] [CrossRef]
- Salvatori, S.; Oliva, P.; Pacilli, M.; Allegrini, P.; Conte, G.; Komlenok, M.; Khomich, A.; Bolshakov, A.; Ralchenko, V.; Konov, V. Nano-carbon pixels array for ionizing particles monitoring. Diam. Relat. Mater. 2017, 73, 132–136. [Google Scholar] [CrossRef]
- Komlenok, M.; Bolshakov, A.; Ralchenko, V.; Konov, V.; Conte, G.; Girolami, M.; Oliva, P.; Salvatori, S. Diamond detectors with laser induced surface graphite electrodes. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 837, 136–142. [Google Scholar] [CrossRef]
- Komlenok, M.; Lebedev, S.; Komandin, G.; Piqué, A.; Konov, V. Fabrication and electrodynamic properties of all-carbon terahertz planar metamaterials by laser direct-write. Laser Phys. Lett. 2018, 15, 036201. [Google Scholar] [CrossRef]
- Komlenok, M.; Tikhodeev, S.; Weiss, T.; Lebedev, S.; Komandin, G.; Konov, V. All-carbon diamond/graphite metasurface: Experiment and modeling. Appl. Phys. Lett. 2018, 113, 041101. [Google Scholar] [CrossRef]
- Komlenok, M.S.; Zaniewski, A.M.; Zavedeev, E.V.; Konov, V.I.; Koeck, F.A.; Nemanich, R.J. UV laser induced changes to morphological, optical and electrical properties of conductive nanocrystalline diamond films. Diam. Relat. Mater. 2015, 58, 196–199. [Google Scholar] [CrossRef] [Green Version]
- Preclíková, J.; Kromka, A.; Rezek, B.; Malỳ, P. Laser-induced refractive index changes in nanocrystalline diamond membranes. Opt. Lett. 2010, 35, 577–579. [Google Scholar] [CrossRef]
- Komlenok, M.; Kononenko, V.; Ralchenko, V.; Pimenov, S.; Konov, V. Laser induced nanoablation of diamond materials. Phys. Procedia 2011, 12, 37–45. [Google Scholar] [CrossRef] [Green Version]
- Komlenok, M.S.; Kononenko, V.V.; Vlasov, I.I.; Ralchenko, V.G.; Arutyunyan, N.R.; Obraztsova, E.D.; Konov, V.I. “Nano” ablation of Ultrananocrystalline Diamond Films. J. Nanoelectron. Optoelectron. 2009, 4, 286–289. [Google Scholar] [CrossRef]
- Kononenko, T.V.; Pivovarov, P.A.; Khomich, A.A.; Khmelnitsky, R.A.; Plotnichenko, V.G.; Konov, V.I. Processing of polycrystalline diamond surface by IR laser pulses without interior damage. Opt. Laser Technol. 2019, 117, 87–93. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Wang, Q.; Su, H.; Fu, Y.; Xu, J. Investigation on the material removal behavior of single crystal diamond by infrared nanosecond pulsed laser ablation. Opt. Laser Technol. 2020, 126, 106086. [Google Scholar] [CrossRef]
- Konishi, K.; Nomura, M.; Kumagai, N.; Iwamoto, S.; Arakawa, Y.; Kuwata-Gonokami, M. Circularly polarized light emission from semiconductor planar chiral nanostructures. Phys. Rev. Lett. 2011, 106, 057402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lobanov, S.V.; Weiss, T.; Gippius, N.A.; Tikhodeev, S.G.; Kulakovskii, V.D.; Konishi, K.; Kuwata-Gonokami, M. Polarization control of quantum dot emission by chiral photonic crystal slabs. Opt. Lett. 2015, 40, 1528–1531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lobanov, S.; Tikhodeev, S.; Gippius, N.; Maksimov, A.; Filatov, E.; Tartakovskii, I.; Kulakovskii, V.; Weiss, T.; Schneider, C.; Geßler, J.; et al. Controlling circular polarization of light emitted by quantum dots using chiral photonic crystal slabs. Phys. Rev. B 2015, 92, 205309. [Google Scholar] [CrossRef] [Green Version]
- Demenev, A.; Kulakovskii, V.; Schneider, C.; Brodbeck, S.; Kamp, M.; Höfling, S.; Lobanov, S.; Weiss, T.; Gippius, N.; Tikhodeev, S. Circularly polarized lasing in chiral modulated semiconductor microcavity with GaAs quantum wells. Appl. Phys. Lett. 2016, 109, 171106. [Google Scholar] [CrossRef] [Green Version]
- Maksimov, A.A.; Tartakovskii, I.I.; Filatov, E.V.; Lobanov, S.V.; Gippius, N.A.; Tikhodeev, S.G.; Schneider, C.; Kamp, M.; Maier, S.; Höfling, S.; et al. Circularly polarized light emission from chiral spatially-structured planar semiconductor microcavities. Phys. Rev. B 2014, 89, 045316. [Google Scholar] [CrossRef]
- Pan, M.; Li, Q.; Hong, Y.; Cai, L.; Lu, J.; Qiu, M. Circular-polarization-sensitive absorption in refractory metamaterials composed of molybdenum zigzag arrays. Opt. Express 2018, 26, 17772–17780. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.C.W.; Chan, C. Circularly polarized thermal radiation from layer-by-layer photonic crystal structures. Appl. Phys. Lett. 2007, 90, 051912. [Google Scholar] [CrossRef]
- Thiel, M.; Von Freymann, G.; Wegener, M. Layer-by-layer three-dimensional chiral photonic crystals. Opt. Lett. 2007, 32, 2547–2549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thiel, M.; Hermatschweiler, M.; Wegener, M.; von Freymann, G. Thin-film polarizer based on a one-dimensional–three-dimensional–one-dimensional photonic crystal heterostructure. Appl. Phys. Lett. 2007, 91, 123515. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Zhao, X.; Lin, Y.; Zhu, A.; Zhu, X.; Guo, P.; Cao, B.; Wang, C. All-dielectric metasurface circular dichroism waveplate. Sci. Rep. 2017, 7, 41893. [Google Scholar] [CrossRef]
- Fedotov, V.; Mladyonov, P.; Prosvirnin, S.; Rogacheva, A.; Chen, Y.; Zheludev, N. Asymmetric propagation of electromagnetic waves through a planar chiral structure. Phys. Rev. Lett. 2006, 97, 167401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Menzel, C.; Rockstuhl, C.; Lederer, F. Advanced Jones calculus for the classification of periodic metamaterials. Phys. Rev. A 2010, 82, 053811. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Coppens, Z.J.; Besteiro, L.V.; Wang, W.; Govorov, A.O.; Valentine, J. Circularly polarized light detection with hot electrons in chiral plasmonic metamaterials. Nat. Commun. 2015, 6, 8379. [Google Scholar] [CrossRef]
- Tikhodeev, S.G.; Yablonskii, A.L.; Muljarov, E.A.; Gippius, N.A.; Ishihara, T. Quasiguided modes and optical properties of photonic crystal slabs. Phys. Rev. B 2002, 66, 045102. [Google Scholar] [CrossRef] [Green Version]
- Li, L. New formulation of the Fourier modal method for crossed surface-relief gratings. JOSA A 1997, 14, 2758–2767. [Google Scholar] [CrossRef]
- Leung, P.T.; Liu, S.Y.; Young, K. Completeness and orthogonality of quasinormal modes in leaky optical cavities. Phys. Rev. A 1994, 49, 3057–3067. [Google Scholar] [CrossRef]
- Gippius, N.A.; Tikhodeev, S.G.; Ishihara, T. Optical properties of photonic crystal slabs with an asymmetrical unit cell. Phys. Rev. B 2005, 72, 045138. [Google Scholar] [CrossRef] [Green Version]
- Gras, A.; Yan, W.; Lalanne, P. Quasinormal-mode analysis of grating spectra at fixed incidence angles. Opt. Lett. 2019, 44, 3494–3497. [Google Scholar] [CrossRef]
- Dyakov, S.A.; Stepikhova, M.V.; Bogdanov, A.A.; Novikov, A.V.; Yurasov, D.V.; Shaleev, M.V.; Krasilnik, Z.F.; Tikhodeev, S.G.; Gippius, N.A. Photonic Bound States in the Continuum in Si Structures with the Self-Assembled Ge Nanoislands. Laser Photonics Rev. 2021, 2000242. [Google Scholar] [CrossRef]
- Fano, U. The theory of anomalous Diffraction Gratings and of quasi-stationary waves on metallic surfaces (Sommerfeld’s waves). J. Opt. Soc. Am. 1941, 31, 213–222. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Dyakov, S.; Semenenko, V.; Gippius, N.; Tikhodeev, S. Magnetic field free circularly polarized thermal emission from a chiral metasurface. Phys. Rev. B 2018, 98, 235416. [Google Scholar] [CrossRef] [Green Version]
- Dyakov, S.; Gippius, N.; Fradkin, I.; Tikhodeev, S. Vertical Routing of Spinning-Dipole Radiation from a Chiral Metasurface. Phys. Rev. Appl. 2020, 14, 024090. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komlenok, M.S.; Dezhkina, M.A.; Sedov, V.S.; Klimenko, O.A.; Dyakov, S.A.; Gippius, N.A. Laser Ablated Nanocrystalline Diamond Membrane for Infrared Applications. Sensors 2022, 22, 829. https://doi.org/10.3390/s22030829
Komlenok MS, Dezhkina MA, Sedov VS, Klimenko OA, Dyakov SA, Gippius NA. Laser Ablated Nanocrystalline Diamond Membrane for Infrared Applications. Sensors. 2022; 22(3):829. https://doi.org/10.3390/s22030829
Chicago/Turabian StyleKomlenok, Maxim S., Margarita A. Dezhkina, Vadim S. Sedov, Oleg A. Klimenko, Sergey A. Dyakov, and Nikolay A. Gippius. 2022. "Laser Ablated Nanocrystalline Diamond Membrane for Infrared Applications" Sensors 22, no. 3: 829. https://doi.org/10.3390/s22030829
APA StyleKomlenok, M. S., Dezhkina, M. A., Sedov, V. S., Klimenko, O. A., Dyakov, S. A., & Gippius, N. A. (2022). Laser Ablated Nanocrystalline Diamond Membrane for Infrared Applications. Sensors, 22(3), 829. https://doi.org/10.3390/s22030829






