Abstract
The uterine electromyogram, also called electrohysterogram (EHG), is the electrical signal generated by uterine contractile activity. The EHG has been considered an expanding technique for pregnancy monitoring and preterm risk evaluation. Data were collected on the abdominal surface. It has been speculated the effect of the placenta location on the characteristics of the EHG. In this work, a preliminary exploration method is proposed using the average spectra of Alvarez waves contractions of subjects with anterior and non-anterior placental position as a basis for the triple-dispersion Cole model that provides a best fit for these two cases. This leads to the uterine impedance estimation for these two study cases. Non-linear least square fitting (NLSF) was applied for this modelling process, which produces electric circuit fractional models’ representations. A triple-dispersion Cole-impedance model was used to obtain the uterine impedance curve in a frequency band between 0.1 and 1 Hz. A proposal for the interpretation relating the model parameters and the placental influence on the myometrial contractile action is provided. This is the first report regarding in silico estimation of the uterine impedance for cases involving anterior or non-anterior placental positions.
1. Introduction
The EHG has been used as a modern tool for pregnancy monitoring and preterm risk evaluation [1,2]. It has been pointed out as having the potential to replace the tocogram in pregnancy monitoring given its superior sensitivity [3,4,5]. One of the advantages of the EHG technology is its non-invasive nature since the electrodes are in designated places in the abdominal surface. EHG electrodes capture the electric potential due to the uterine contractile activity, which is present throughout pregnancy and can be detected as early as 19 weeks of gestation [6]. Subjects with a high body mass index (BMI) reportedly may have poor tocography recordings due to the fat layer attenuation effect [7]. The EHG has been deemed to be less affected by the high BMI attenuation effect [5,8]. The question arose as to whether an anterior placenta could introduce signal EHG variations given the acquisition electrodes being in the projection line containing the involved myometrial tissue and the anterior placenta. Dermott et al. (2010) [9] reported no significant contraction differences in amplitude, frequency, and integral activity between anterior and posterior placental groups during labour. Contrarily, Kavšek el al. (1999) [10,11] observed a significant increase in the EHG contractions root mean square (RMS) value for subjects with non-anterior placenta (46.50 to 82.93 µV) and a noticeable decrease in the mean frequency (0.25 to 0.20 Hz) for the same group. The local hormonal inhibitory influence of the placenta in the surrounding uterine muscles is reported as the cause for the RMS reduction for anterior placental implantation. This research associated higher RMS results with lower mean frequency values. Basal uterine activity is, according to the work of Kavšek et al. (1999) [10], associated with increased mean frequency values, being the anterior uterine wall the main contributor for the EHG. On the other hand, Grgic et al. (2006) [12] reported no statistical significant differences between the two involved study groups for subjects in the mid- trimester of pregnancy using a bipolar EHG electrode arrangement. The used parameters were the median frequency and median amplitude of the EHG. The apparent discrepancy between these authors’ results may be related to conflicting electrical resistance calculations, namely the way the resistance is estimated, specifically if it is obtained from the real part or, otherwise, the absolute value of the impedance [13]. In an in vivo study, Gandhi et al. (2006) [14] reported an increase in the cervix electrical resistivity in pregnant women compared to non-pregnant subjects along with a trend where the resistivity increases with gestational age, suggesting that increased collagen content in the cervix weights over cervical hydration. The frequency band in this study extended from 4 kHz to 819 KHz. Roughly, given electrode areas and current path length, the electrical resistance in the second trimester was reported as being around 4 KΩ compared to 6 KΩ in the third trimester. Somewhat contradictory results were obtained in another study of Avis et al. (1996) [13], where a small sample of cervix tissue was used to evaluate the electric resistance. The results of this pilot study showed a lower R/S ratio and RC time constant for the term group compared with the preterm group. In this study, R represents the resistance of the extracellular space, S the resistance of the intracellular space, and C the capacitance of the tissue’s cells membranes for the circuit model under study.
Fractional calculus is a powerful tool for modelling phenomena in science and engineering. Although its history dates back as far as integer-order calculus, its progress over the last thirty years has been enormous and has become the object of great interest of not only of mathematicians but also other researchers in science and technology [15,16,17,18,19,20,21,22]. Fractional-order calculus has been used to generalize various types of controllers, including internal model controllers [23]. Biochemical processes modelling has been implemented using fractional calculus to facilitate the interpretation of its complex mechanisms that often are not intuitive to understand [24]. Fractional calculus can model numerous real-world phenomena better than integer-order calculus. The fractional-order models, for example, present better capabilities for electrochemical capacitors characteristics approximation than models based on the integer order [16,25,26,27,28]. Fractional-order circuit models and systems are emerging fields that have resulted of importing concepts from fractional calculus into electrical circuit theory [29]. The single-dispersion Cole-impedance model was introduced by Cole in 1942. Despite its fractional character, fractional calculus was not taken into consideration when it was proposed [30]. This model is composed of three circuit elements: a high-frequency resistor , a resistor , and a constant phase element (CPE), or fractional capacitor, with capacitance and positive real order leading to its fractional character. This model is simple and a good fit for numerous data sets collected from biological tissues and materials. By combining Cole circuit elements, the double- and triple-dispersion Cole models were created to improve fitting characteristics [28,31,32,33,34,35]. These Cole models have been applied for monitoring necrosis of human tumour xenografts during and/or after hyperthermia treatment [36]; investigating age-related changes of dentine to create non-destructive test methods [37]; assessing quality of red blood cell suspensions under storage [38]; modelling lung, beef, and veal meat impedance [39,40,41]; and numerous others [34].
On the other hand, for describing the fractional character of these fractional calculus-depending models, it is natural to consider the CPE described by the current-voltage relationship in the following differential equation:
where and are the time-dependent current and voltage, C is the capacitance, measured in Farad/, and represents the fractional derivative [42]. For describing the constant phase element in Equation (1), we use the Grünwald–Letkinov fractional derivative defined on the whole real line, which is given by [28]:
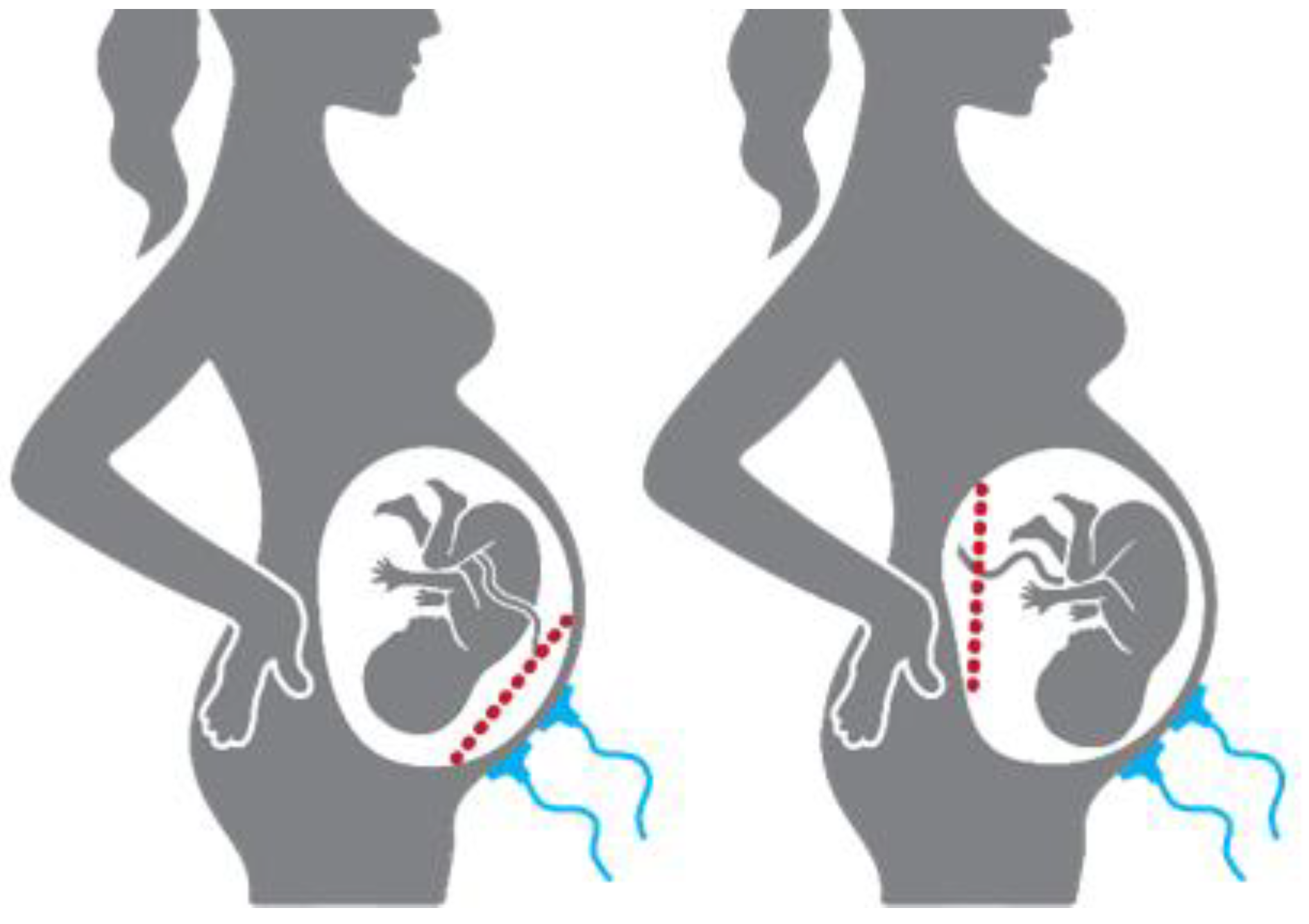
In this study, the placental position influence on the EHG spectral parameters will be investigated using a preliminary exploratory methodology. The anterior placenta is positioned at the front wall of the uterus and is therefore in the projection of the myometrium and the acquisition electrodes. This placenta position has the potential to influence the EHG characteristics. The other placenta positions, herein referred to as non-anterior, are not in the electrode’s projection. Figure 1 provides a simplified illustration regarding placental position relatively to the acquisition electrodes. Tissue impedance has been widely used as a biomarker for biological tissues, such as animal tumour growth and status evaluation, or vegetal non-destructive fruit-ripening assessment [34,36,37,43,44].
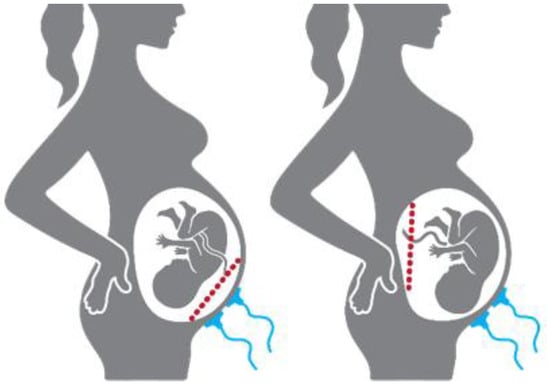
Figure 1.
Placental position relatively to the acquisition electrodes (blue): (Left) anterior placenta (red dash line); (Right) an example of non-anterior placental position (red dash line).
The main goal is to obtain the electrical impedance fractional estimation in silico model of the uterine tissue using non-invasively obtained data. Considering that anterior placenta stands in the alignment of the electrodes and the myometrium, its effect on the impedance model is concurrently studied. A tentative interpretation of the results is provided. To the best of the authors’ knowledge, this is the first study using the mentioned methodology for the uterine impedance estimation modelling.
2. Materials and Methods
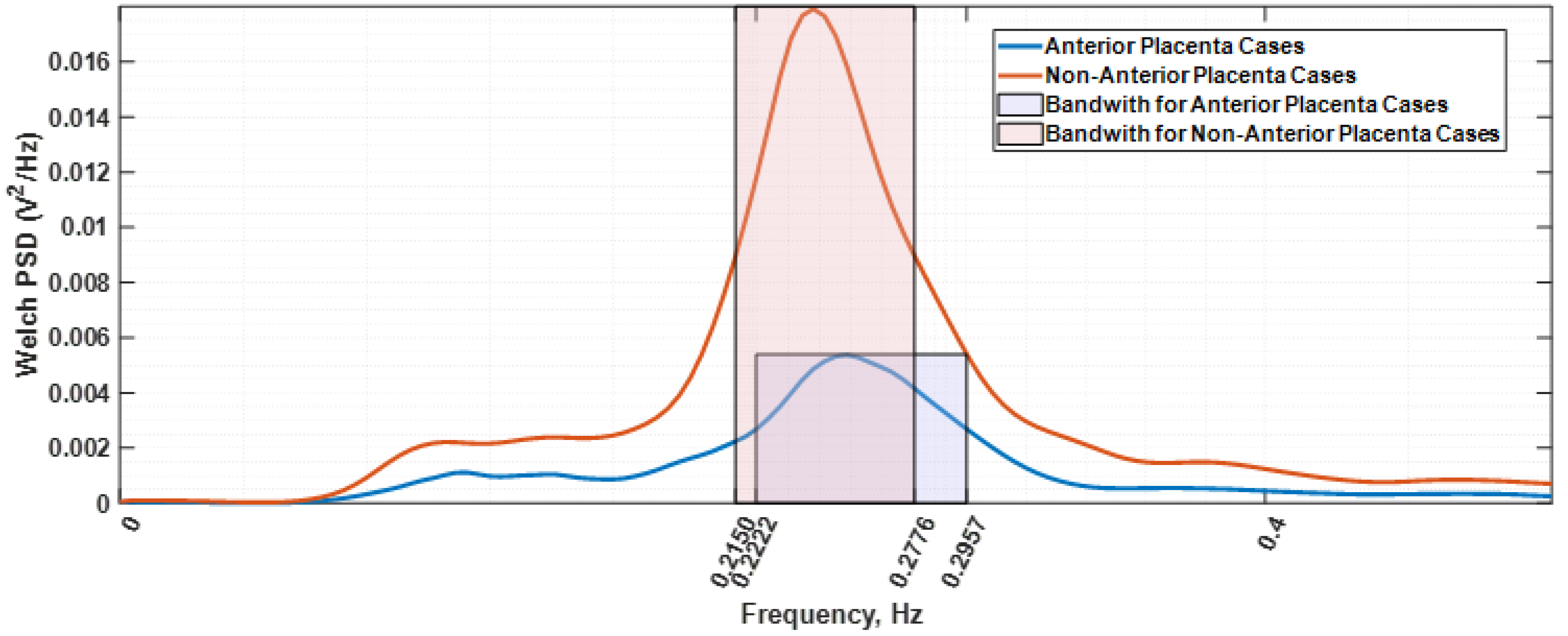
The used data were provided by the Iceland Uterine Electromyography database [45], comprising 121 EHG recordings. Each record includes about 30 min of data from a 16-channel electrode configuration, located in the abdominal surface. Database parameters are described in Table 1. To reduce maternal respiration and common mode noise interference, a bipolar arrangement between channels 4 and 10 was used. The selection criteria for this electrode arrangement can be found in Esgalhado et al. (2020) [46]. A uterine contraction detector, previously developed under the Uterine Explorer project [46,47,48,49], [50] processed the mentioned database. The obtained contraction data pool was, subsequently, the input for an unsupervised clustering classifier. The obtained clusters were identified using a retrospective correlation study involving the contraction occurrence rate and amplitude. This led to the characterization of the Alvarez and Braxton-Hicks contraction types, with the former separated into Alvarez low (AlvL) and Alvarez high (AlvH) categories [46]. For the herein presented work, both the AlvL and AlvH contraction sets could have been selected. The former was chosen. The other possible option of using the extracted Braxton-Hicks (BH) contraction dataset was rejected given that, compared with the Alvarez waves, the BH spectral estimation was found to be less smooth and would incur in higher model-fitting estimation errors and overly complexity in the obtained circuit model. The other reason for the Alvarez waves selection was that they are generated in local myometrium areas, and thus, the tissue under study is a restricted zone. Subsequently, the Alvarez dataset was divided into two categories regarding the subject placental position: anterior and non-anterior placenta. Alvarez waves have been deemed as being labour triggers, while BH components are associated with normal pregnancy progress [51,52]. Only contractions for subjects between 36 and 41 gestational weeks were selected. This exclusion criterium was established to narrow the observation interval regarding uterine maturation. Anterior placenta is in the projection of the electrodes’ location and the myometrium, and the goal here is to explore its impact on the electrical impedance of the overall tissue as far as seen by the selected electrodes. Welch power spectral density [53] of all the selected AlvL contractions were obtained and divided in two groups depending on the placenta position and subsequently averaged. Figure 2 represents the resulting spectra, a Welch periodogram estimation, where it is shown that for the non-anterior placenta case, the frequency power spectral peak (0.2124 Hz) is reduced relatively to the anterior placenta case (0.2539 Hz). The bandwidth of the anterior placental case is 0.0735 Hz, whereas for the other case, it is 0.0626 Hz. It therefore becomes clear that the anterior placenta plays a filtering role on the EHG. Additionally, it is also observed in Figure 2 an attenuation effect for the anterior placenta case that translates in an amplitude decrease in the PSD estimation for this case. This effect has also been reported elsewhere [10].

Table 1.
The Iceland Database Parameters.
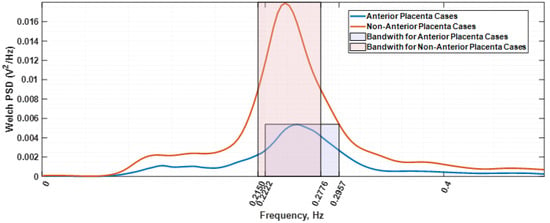
Figure 2.
Welch periodogram estimations of the average spectra for the contraction’s subjects with anterior (blue colour) and non-anterior placenta (orange colour). The respective bandwidths are shown in the shadow rectangular areas.
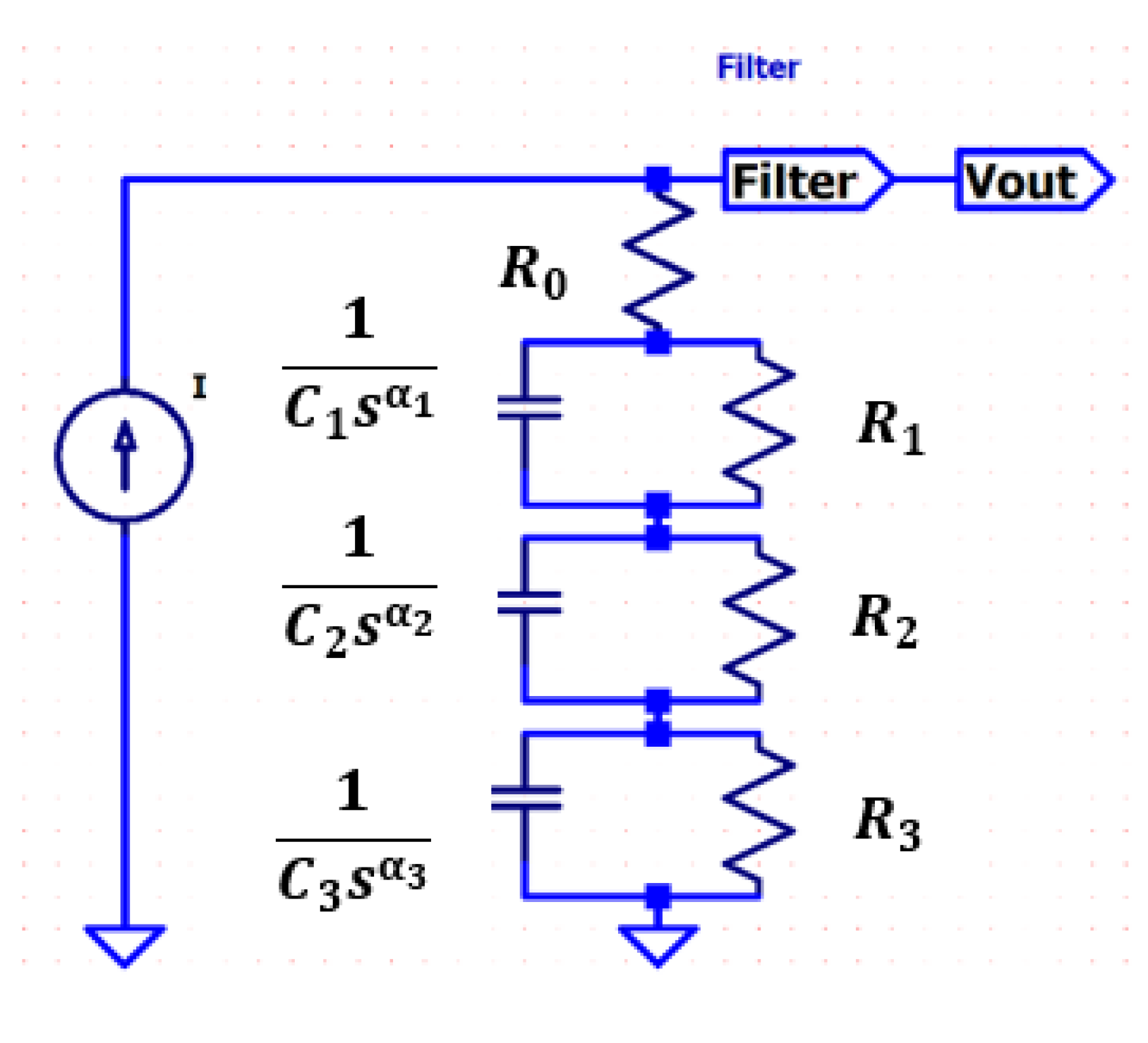
A fractional-order transfer function is obtained from Figure 3; a triple-dispersion Cole-impedance model providing a best fit to the data given by Figure 2 is to be implemented for the anterior and non-anterior placental position cases. This model produces an electric circuit representation that leads to the assessment of the placental implantation effect on the EHG. It is assumed that the current source produces a Dirac-like current waveform for which the Laplace transform has a unity value.
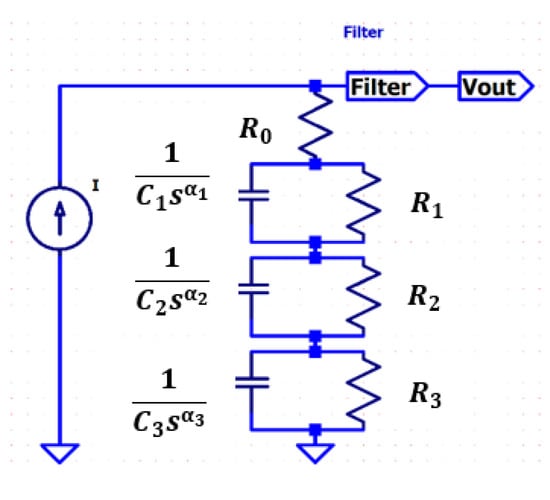
Figure 3.
Proposed triple-dispersion Cole model. The filter, F, accounts for the used filter for processing the automatically detected contractions [48].
In this work, a nonlinear least square fitting (NLSF) procedure based on the trust-region-reflective approach was performed to obtain parameters of the model in Figure 3. The Cole order model selection was performed through a trial-and-error procedure, where the criteria was to obtain the lowest model order that would fit the data within an acceptable error level. Higher model orders would result in better fitting but at a computational cost beyond a reasonable cost–benefit relation. Additionally, any possible model interpretation within the electrophysiology framework will be easier for lower model orders. The novelty of this work resides in using the spectrum of the output voltage related to the uterine contraction electromyogram for the Cole parameters estimation. The used NLSF algorithm is sensitive to the initially selected constants and lower and upper bound values for the model extracting the parameters within an acceptable estimation error. The drawback of this new approach for impedance calculation is that the obtained values should be rescaled for realistic ones. However, the impedance plot waveshape is not modified by this rescaling operation. The stability of the system of the proposed model is evaluated as well as the total error between the estimation function and the spectral function.
Fractional circuits have been used in biomedicine and biology for modelling tissue impedance [34,44,54]. Typically, the Cole-impedance model is employed, possibly in multiple dispersion modules. The triple-dispersion Cole model shown in Figure 3 consists of four resistors and three constant phase elements (CPEs) as follows:
where it is assumed that . Furthermore, it is supposed that all , , and are the unknown real nonnegative parameters since there is no physical meaning for negative valued resistors, capacitors, and Equation (4).
The parameters to be obtained in Equation (3) are real values providing best fit for anterior and non-anterior placental position cases. These parameters were extracted through an algorithm involving the MATLAB function lsqnonlin for the implementation of this NLSF process based on [55,56]. The lsqnonlin function is specified by the goal function as follows:
expressed by:
where x is the vector of parameters ( to minimize , is the spectral data, is the total number of the experimentally angular frequencies for each data point in y, and G is the estimation function:
where F is the band pass filter transfer function given by Equation (7), with coefficients and .
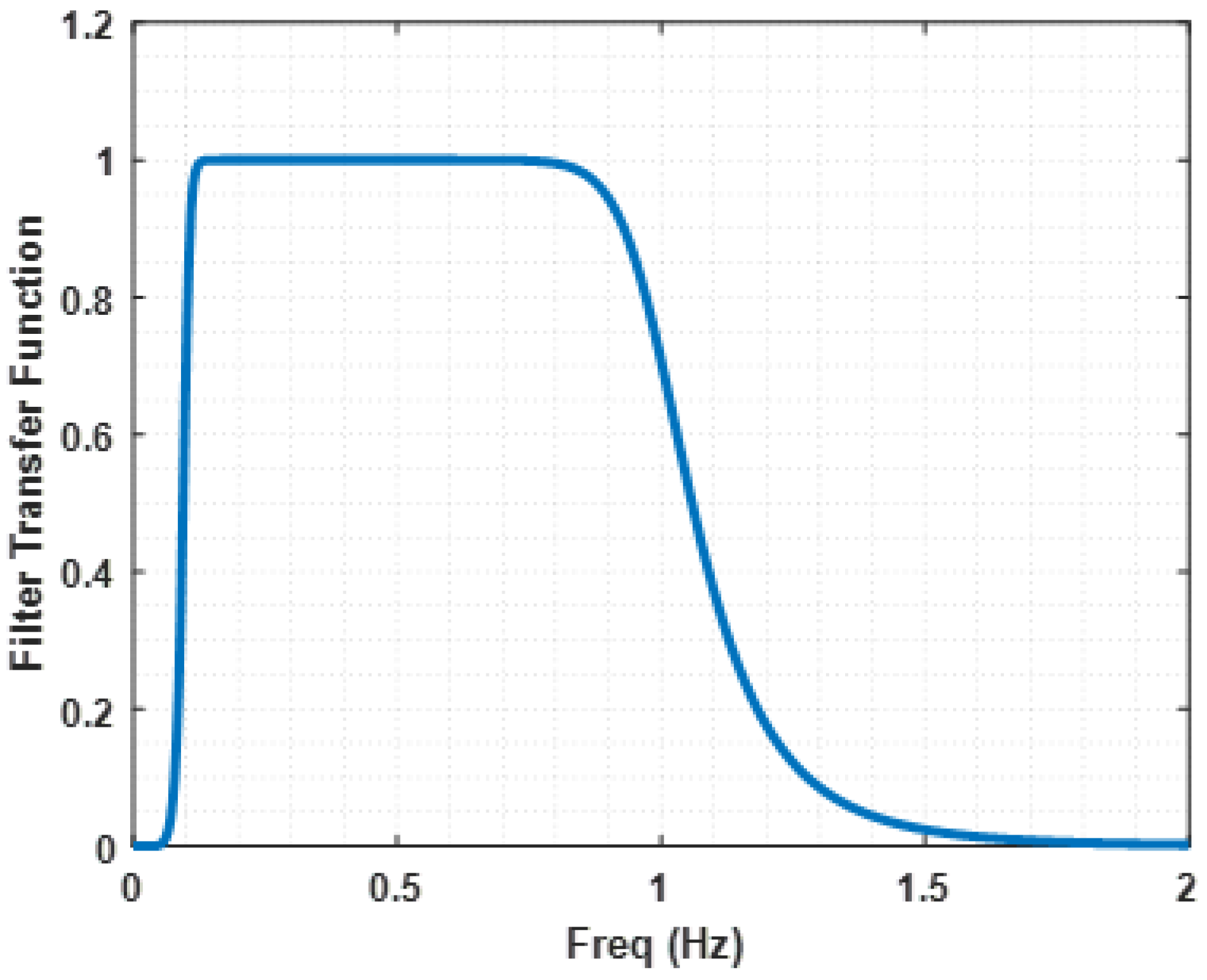
The F filter transfer function is represented in Figure 4. As mentioned in [48], this filter operates over the data to reduce interference.
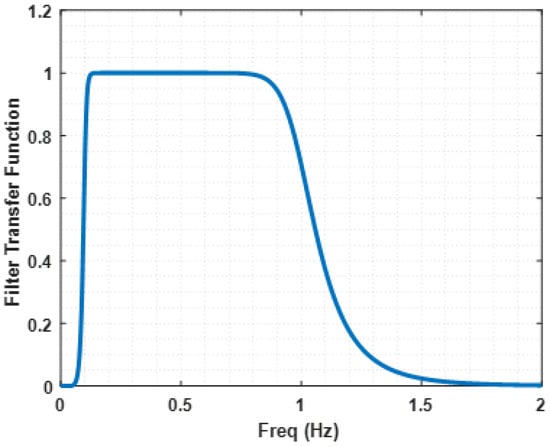
Figure 4.
Filter transfer function, F. This filter represents the one used in the automatically detected contractions processing [48].
Moreover, NLSF processing needs initial points, namely lower and upper bounds for each parameter in Equation (4). All lower bounds for are selected to be equal to 1, and all the upper bounds are restricted to be 2. The lower and the upper bound values for are specified by 0.001 and 5000 values, respectively. The lower and the upper bound values for are 0.00001 and 50, respectively. The initial point for each parameter was determined within the ranges between its lower bound and upper bound in all cases.
The optimal values of parameters of the model in Equation (3) are determined using the trust-region-reflective approach for performing the actual minimization of . In addition to this, for each case of the anterior and the non-anterior placenta positions, the algorithm shows the location of the poles of model Equation (3), which yields the stability of the system. The total error between the experimental data and the estimate function G in Equation (6) is also obtained, which determines the good quality of the approximation of the estimate function G to the spectrum.
3. Results
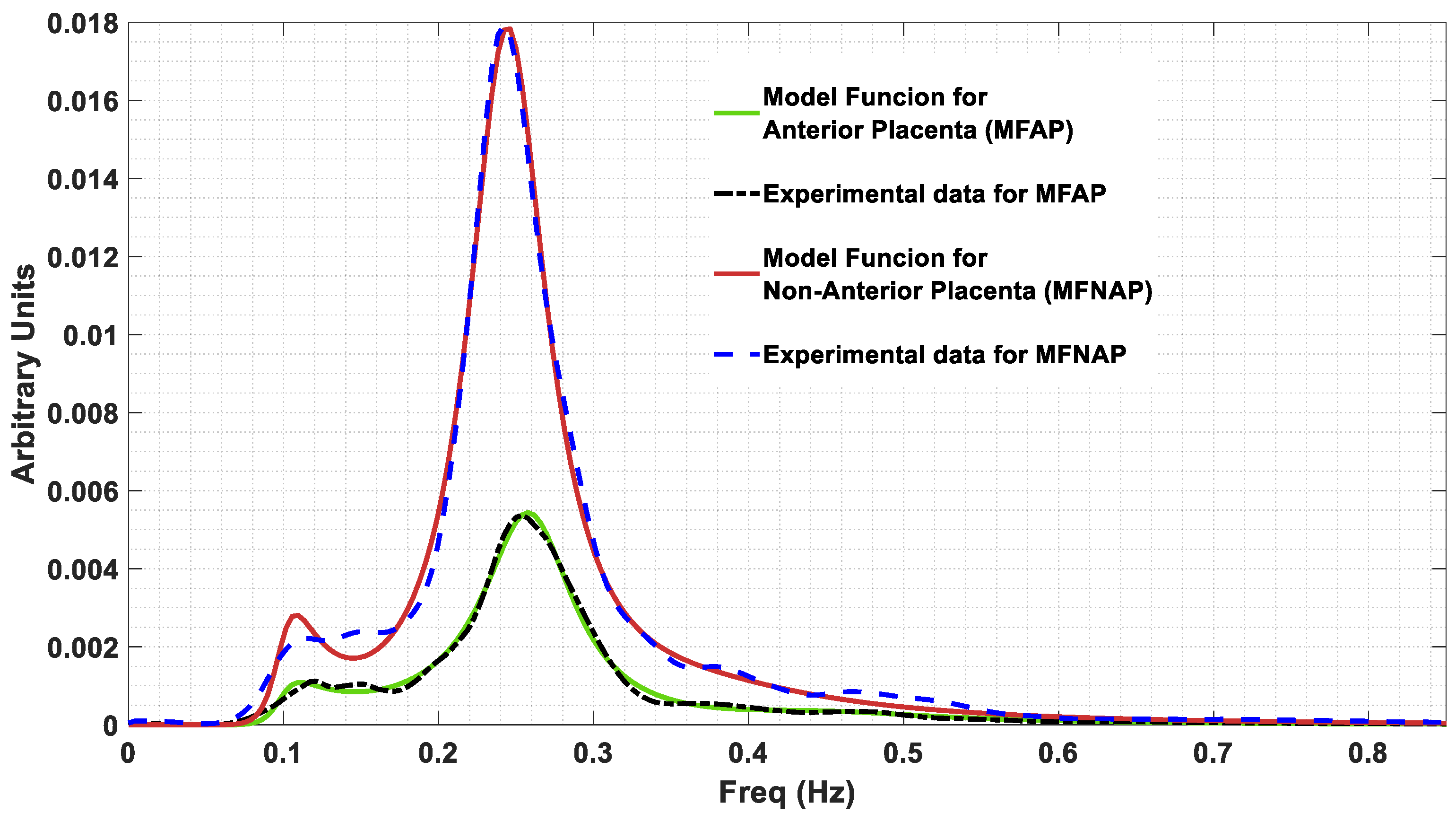
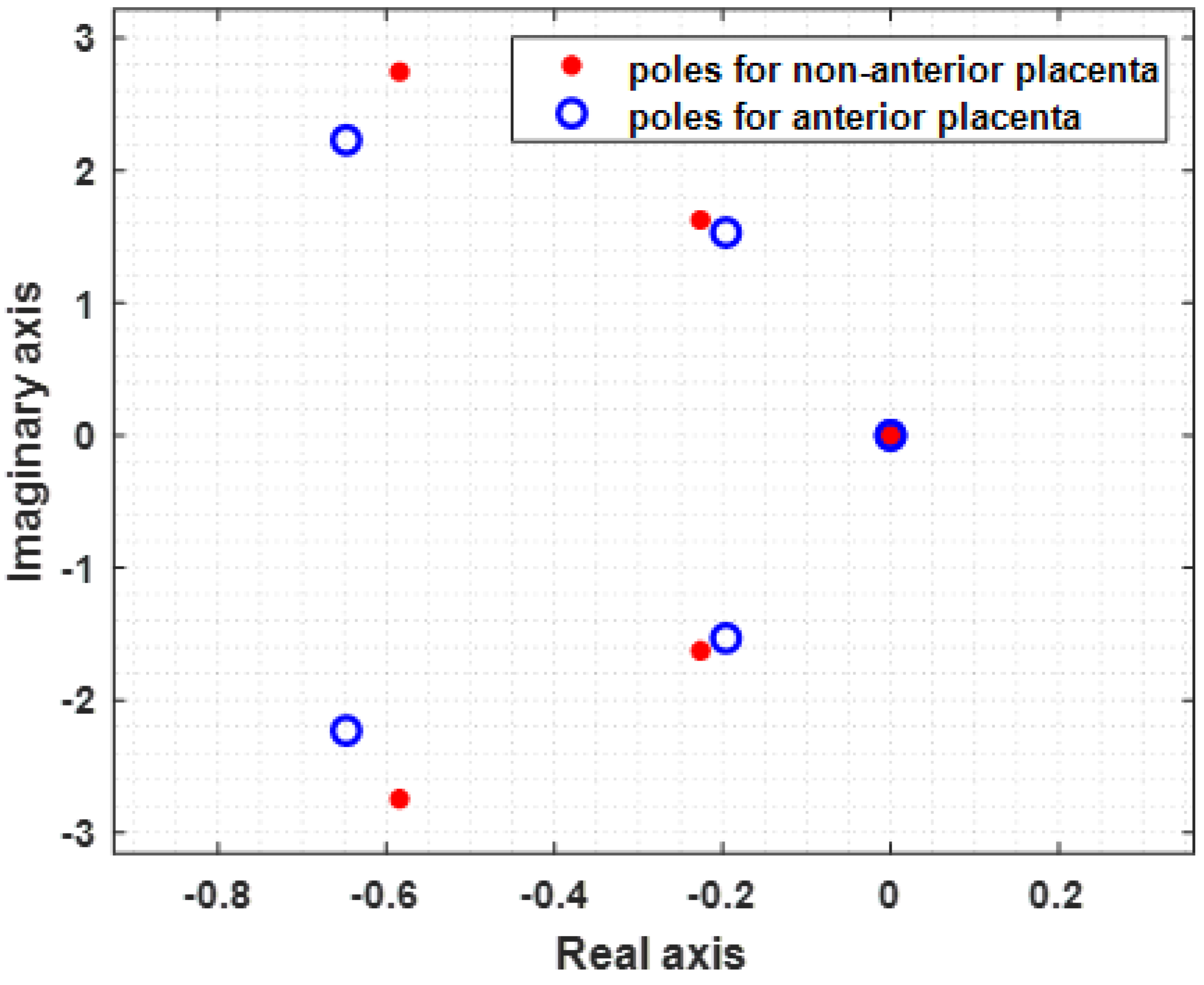
As a result of the optimization fitting procedure applied to the model given by expression (3), the values in Table 2 were extracted. The obtained α values belong to the interval 1 < α < 2. The obtained values for the resistances and the capacitances are the ones the estimator produced and do not represent the physical values, for which a rescaling would be necessary, based on some known values for these two variables. The total error between the estimate function G defined by Equation (6) and the spectrum for the anterior placental position is 1.6456 , while for the non-anterior placental position, it is 1.4436 Figure 5 shows represented the model function for anterior placenta (MFAP, green colour) and the model function for non-anterior placenta (MFNAP, red colour). Additionally, the experimental data spectra for MFAP (black colour) and the MFNAP (blue colour) are represented. A good fitting was obtained. Since all H(s) poles are located on the left-half plane, as shown in Figure 6, the system with the proposed model is stable.

Table 2.
Component estimated values for H(s).
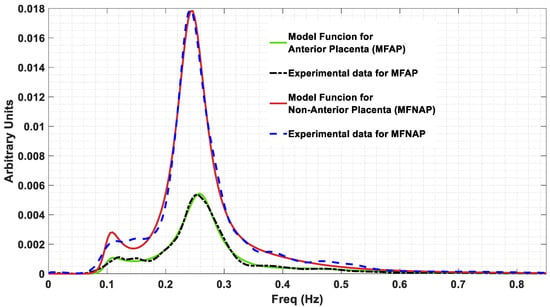
Figure 5.
Model function for anterior placenta (MFAP, green colour) and the model function for non-anterior placenta (MFNAP, red colour). The experimental data spectra for MFAP (black colour) and the MFNAP (blue colour) are represented.
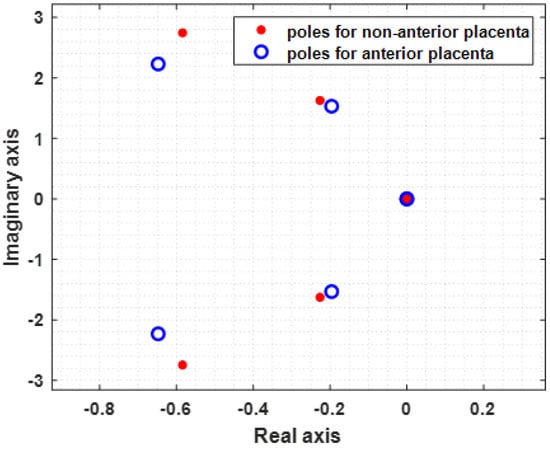
Figure 6.
Poles of H(s) for the non-anterior placenta case (blue) and anterior placenta case (red), showing system stability. All poles are in the left half Argand plane.
The time constants for the three Cole dispersion models are obtained by:
Using the classic formulation, the cut-off frequency is obtained:
Table 3 represents the time constants and cut-off frequencies for each of the single-dispersion cell in the Cole model circuit of Figure 3. To note that τ1 values in both placenta position cases represent a long-range process component of more than half an hour, corresponding to very low cut-off frequencies.

Table 3.
Time constants and cut-off frequencies for H(s).
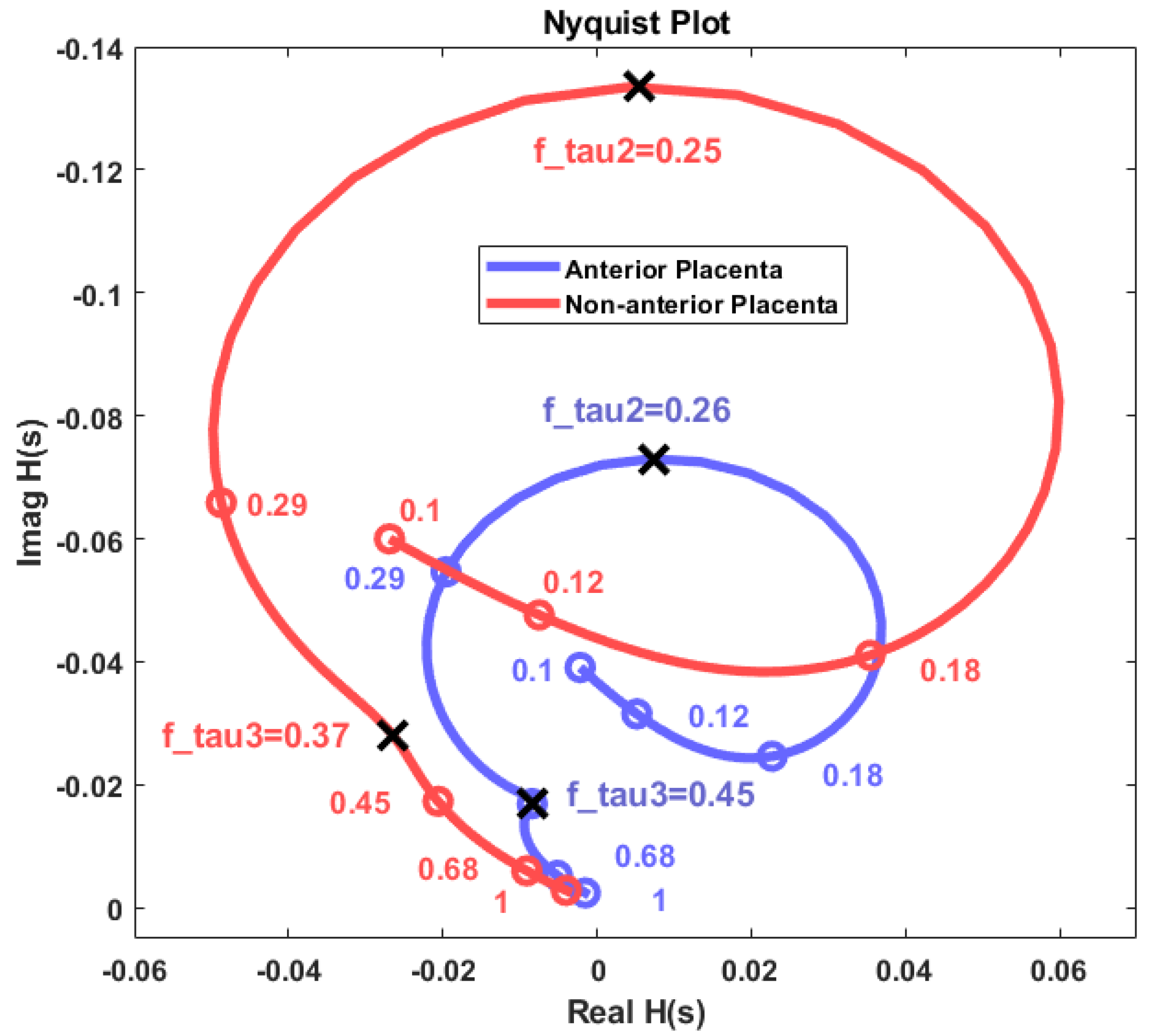
Figure 7 shows the Nyquist diagram-estimated impedance plot for the non-anterior placenta (red) and anterior placenta cases (blue). The curves represent frequency variation from 0.1 Hz to 1 Hz. The mark circles represent frequency points for the impedance estimations. Cut-off frequencies for both cases are represented and correspond to notches in the impedance curves. The long-range cut-off frequencies corresponding to τ1 have been excluded. The real and imaginary impedance axes do not represent the physical resistive or reactive components of the myometrial or myometrial plus placental tissue. The herein presented method is based on a spectral output, from which the obtained physical impedance values cannot be achieved. However, the impedance curve waveshape remains the same. Rescaling the impedance axes to physical values is possible if some physical impedance points are known. The 0.45-Hz cut-off frequency in the non-anterior placenta case is associated with a sharp impedance curve variation if compared with the corresponding 0.37-Hz cut-off frequency in the anterior placental case. This indicates that the time constant τ2 has more impact in the impedance variation for the anterior placental case.
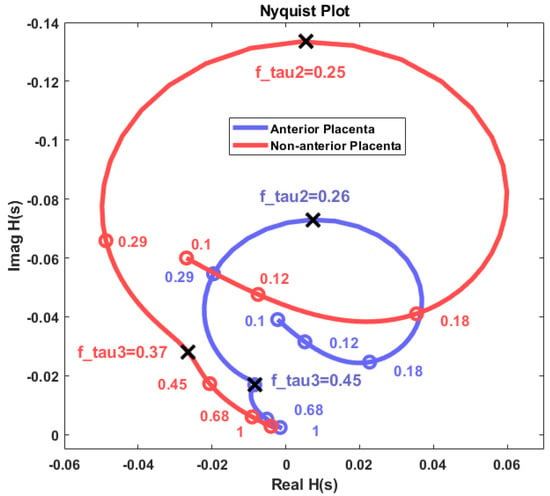
Figure 7.
Nyquist diagram for the obtained impedance estimation for the placental and non-anterior placental cases. Axes are not scaled to physical resistance (real axis) and reactance (imaginary axis) values.
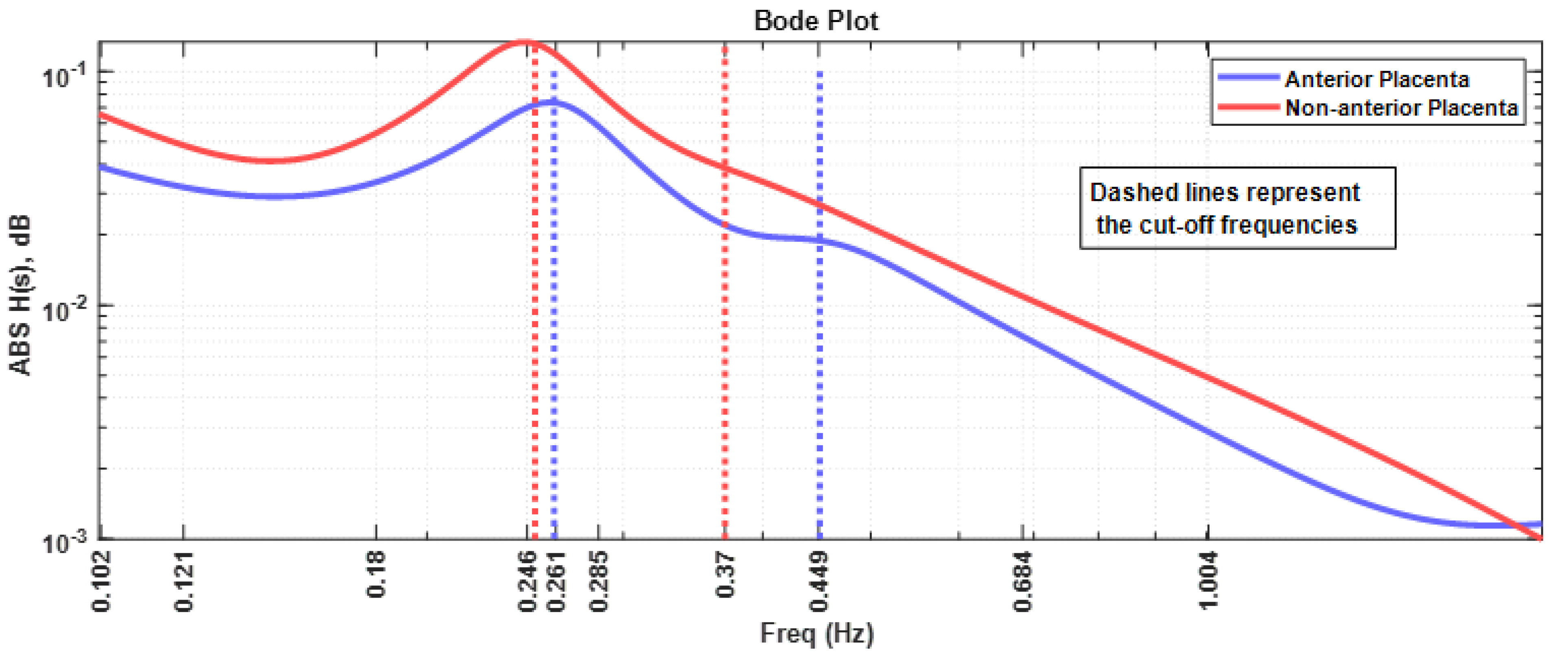
Figure 8 represents the Bode plot of the absolute value of the impedance for both placenta position cases. All the comments presented for Figure 7 apply in this case. It should be noted that the anterior placental case impedance curve is roughly 10 dB below the non-anterior placental case.
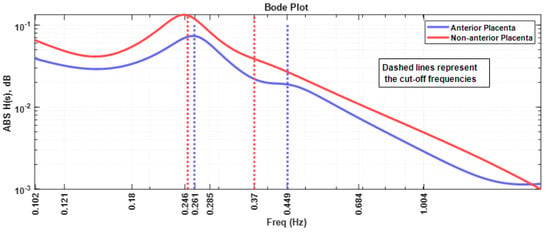
Figure 8.
Bode plot of the myometrial impedance for the anterior placental and non-anterior placental cases. The cut-off frequencies are represented by the dash lines with the same colour as the respective curves.
4. Discussion and Conclusions
The obtained fractional circuit accurately represented the original spectral estimation for the anterior and non-anterior placental cases using only a triple-dispersion Cole model. This emphasizes fractional systems as an efficient tool to model complex electrophysiological phenomena, in this case, the uterine tissue impedance. It is also indicative of the potential fractional nature of the electrical characteristics of the uterine tissue. The presented study estimated, non-invasively, uterine tissue impedance using EHG data collected in the abdominal surface and projected to the spectral domain. The elegancy of the method has, however, the drawback of not being able to estimate the physical values of the tissue impedance. What is obtained is a Nyquist plot of the uterine impedance model. Nevertheless, a scaling to realistic impedance values is possible if actual resistance and reactance value pairs are known, via, for instance, in vitro or in vivo experiments.
During early human pregnancy, the trophoblast, an embryonic structure that will originate the placenta, invades the decidualized endometrium up to the inner third of the myometrium. It migrates in a retrograde direction along the spiral arteries, transforming them into large-diameter conduit vessels of low resistance [57]. Uteroplacental vessel development has been reported to occur in two phases: the first represents the decidual segments of spiral arteries at 8 to 10 weeks of gestation, invading the border between the decidua and myometrium [58]. The second stage, at 16 to 18 weeks, involves some intramyometrial spiral arteries invasion [58]. In a healthy pregnancy, this physiological transformation or remodelling is characterized by a gradual loss of the normal musculoelastic structure of the arterial wall that converts narrow-lumen, muscular spiral arteries into dilated, low-resistance uteroplacental vessels [57,59,60,61,62].
Our results show different myometrium frequency dependent impedance curves for the anterior placenta compared to non-anterior placenta case. In view of these results, it would be possible to hypothesize that:
- The mentioned remodelling could be in favour of a decreased myometrial impedance in cases where the placenta is anterior as a result of large uteroplacental vessels implantation, allowing increased placental blood flow [63]. This is in accordance with the Nyquist plot results in Figure 7, whereas the impedance range variation for both the resistance and reactance for the anterior placental case is lower compared to the non-anterior placental case.
- Regarding the intriguing increase in the frequency for the peak impedance value (Figure 8) in the anterior placenta case (0.261 Hz), relative to the non-anterior placenta case (0.246 Hz), further studies are required in this respect. The herein presented fractional circuit model may be beneficial for the understanding of this behaviour.
- Lower energy levels for anterior placenta, as reported in Figure 2 and Figure 5, may be due to local hormonal inhibitory influence of the placenta that blocks the propagation of uterine contractile activity [10]. Kanda et al. [64] concluded that, in rats, the muscular activity in the placental region is significantly inhibited until the last stage of pregnancy.
- Low energy levels identified in our study may also be a result of blocked propagation of electrical activity from the cells of the non-placental region to the placental region [10] presumably to avoid placenta abruption.
Our results are in accordance with Kavšek et al. [10], who also verified lower RMS values for EHG contractile activity in the anterior implantation placental site. According to their study, anterior uterine wall is the main source of the EMG activity, and as a result, the contractions of the posterior uterine wall do not affect the detected signal significantly.
Contrary to the study of Kavšek et al. and the herein presented one, Dermott et al. [9] reported no significant differences in frequency or power density values between anterior and non-anterior placental cases. However, this last study was performed for women in labour, a different population from both the herein presented work and the study of Kavšek et al.: the third pregnancy trimester only, before delivery.
The field of vegetal and animal fractional tissue modelling has presented interesting outcomes. Likewise, fractional calculus has the potential to explore and model myometrium electrophysiological phenomena. This could be an important contribution in areas such as pregnancy monitoring, preterm risk evaluation, and uterine electrophysiological research.
Author Contributions
Conceptualization, M.Ş., A.B., S.R. and M.O.; funding acquisition, M.Ş., A.B., and M.O.; investigation, M.Ş., A.B., S.R., F.E., C.R.P.d.R., F.S. and M.O.; methodology, M.Ş., A.B. and M.O.; project administration, M.Ş., A.B. and M.O.; resources, M.Ş., A.B. and M.O.; software, M.Ş., A.B., F.E. and M.O., supervision, M.Ş., A.B., S.R., F.E., C.R.P.d.R., F.S. and M.O.; validation, M.Ş., A.B., S.R., F.E., C.R.P.d.R., F.S. and M.O.; visualization, M.Ş., A.B., S.R., F.E., C.R.P.d.R., F.S. and M.O.; writing—original draft, M.Ş., A.B., S.R.,C.R.P.d.R., F.S. and M.O.; writing—review and editing, M.Ş., A.B., S.R., F.E., C.R.P.d.R., F.S. and M.O. All authors have read and agreed to the published version of the manuscript.
Funding
For Arnaldo Batista and Manuel Ortigueira, this work was supported by the Portuguese National Funds through the FCT Foundation for Science and Technology within the scope of the CTS Research Unit—Center of Technology and Systems—UNINOVA, under the project UIDB/00066/2020 (FCT). For Müfit Şan, this work was supported by a research scholarship from The Scientific and Technological Research Council of Turkey (TUBITAK-BIDEB/2219-Program granted).
Data Availability Statement
The dataset used in this work is open access: https://physionet.org/content/ehgdb/1.0.0/ (Last accessed on 30 October 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marque, C.K.; Terrien, J.; Rihana, S.; Germain, G. Preterm Labour Detection by Use of a Biophysical Marker: The Uterine Electrical Activity. BMC Pregnancy Childbirth 2007, 7, S5. [Google Scholar] [CrossRef] [PubMed]
- Selvaraju, V.; Karthick, P.A.; Swaminathan, R. Analysis of Frequency Bands of Uterine Electromyography Signals for the Detection of Preterm Birth. In Public Health and Informatics: Proceedings of Medical Informatics Europe 2021; IOS Press: Athens, Greece, 2021; Volume 281, pp. 283–287. ISBN 9781643681856. [Google Scholar]
- Hadar, E.; Biron-Shental, T.; Gavish, O.; Raban, O.; Yogev, Y. A Comparison between Electrical Uterine Monitor, Tocodynamometer and Intra Uterine Pressure Catheter for Uterine Activity in Labor. J. Matern. Neonatal Med. 2015, 28, 1367–1374. [Google Scholar] [CrossRef] [PubMed]
- Euliano, T.Y.; Nguyen, M.T.; Darmanjian, S.; McGorray, S.P.; Euliano, N.; Onkala, A.; Gregg, A.R. Monitoring Uterine Activity during Labor: A Comparison of 3 Methods. Am. J. Obstet. Gynecol. 2013, 208, 66.e1–66.e6. [Google Scholar] [CrossRef] [PubMed]
- Vlemminx, M.W.C.; Thijssen, K.M.J.; Bajlekov, G.I.; Dieleman, J.P.; Der Hout-Van Der Jagt, V.; Beatrijs, M.; Oei, S.G. Could Electrohysterography Be the Solution for External Uterine Monitoring in Obese Women? J. Perinatol. 2018, 38, 580–586. [Google Scholar] [CrossRef] [PubMed]
- Duchene, J.; Devedeux, D.; Mansour, S.; Marque, C. Analyzing Uterine EMG: Tracking Instantaneous Burst Frequency. IEEE Eng. Med. Biol. Mag. 1995, 14, 125–132. [Google Scholar] [CrossRef]
- Aina-Mumuney, A.; Hwang, K.; Sunwoo, N.; Burd, I.; Blakemore, K. The Impact of Maternal Body Mass Index and Gestational Age on the Detection of Uterine Contractions by Tocodynamometry. Reprod. Sci. 2016, 23, 638–643. [Google Scholar] [CrossRef][Green Version]
- Hiersch, L.; Salzer, L.; Aviram, A.; Ben-Haroush, A.; Ashwal, E.; Yogev, Y. Factors Affecting Uterine Electrical Activity during the Active Phase of Labor prior to Rupture of Membranes. J. Matern. Neonatal Med. 2015, 28, 1633–1636. [Google Scholar] [CrossRef]
- Mc Dermott, I.; Breslin, E.; Saade, G.; Garfield, R.; Thornton, S. Comparison of Electromyographic Recordings during Labor in Women with an Anterior or Posterior Placenta. Am. J. Perinatol. 2010, 27, 325–326. [Google Scholar] [CrossRef]
- Kavšek, G.; Pajntar, M.; Leskošek, B. Electromyographic Activity of the Uterus Above the Placental Implantation Site. Gynecol. Obstet. Investig. 1999, 48, 81–84. [Google Scholar] [CrossRef]
- Fele-Žorž, G.; Kavšek, G.; Novak-Antolič, Ž.; Jager, F. A Comparison of Various Linear and Non-Linear Signal Processing Techniques to Separate Uterine EMG Records of Term and Pre-Term Delivery Groups. Med. Biol. Eng. Comput. 2008, 46, 911–922. [Google Scholar] [CrossRef]
- Grgic, O.; Matijevic, R.; Vasilj, O. Placental Site Does Not Change Background Uterine Electromyographic Activity in the Middle Trimester of Pregnancy. Eur. J. Obs. Gynecol. Reprod. Biol. 2006, 127, 209–212. [Google Scholar] [CrossRef] [PubMed]
- Avis, N.J.; Lindow, S.W.; Kleinermann, F. In Vitro Multifrequency Electrical Impedance Measurements and Modelling of the Cervix in Late Pregnancy. Physiol. Meas. 1996, 17 (Suppl. 4A), A97. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, S.V.; Walker, D.; Milnes, P.; Mukherjee, S.; Brown, B.H.; Anumba, D.O.C. Electrical Impedance Spectroscopy of the Cervix in Non-Pregnant and Pregnant Women. Eur. J. Obs. Gynecol. Reprod. Biol. 2006, 129, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier Science Inc.: New York, NY, USA, 2006; ISBN 9780444518323. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls. In Advances in Industrial Control, 1st ed.; Springer: London, UK, 2010; ISBN 978. [Google Scholar]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers. In Lecture Notes in Electrical Engineering, 1st ed.; Springer: Dordrecht, The Netherlands, 2011; ISBN 978. [Google Scholar]
- Podlubny, I. Fractional Differential Equations-An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solutions and Some of Their Applications, 1st ed.; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Herrmann, R. Fractional Calculus An Introduction for Physicists, 2nd ed.; World Scientific Publishing: Singapore, 2014; ISBN 978/981/3274/57/0. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, 1st ed.; Gordon and Breach Science Publishers: New York, NY, USA, 1993. [Google Scholar]
- Tenreiro Machado, J.A.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis, C.M.; Marcos, M.G.; Galhano, A.F. Some Applications of Fractional Calculus in Engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar] [CrossRef]
- Martynyuk, V.; Ortigueira, M.; Fedula, M.; Savenko, O. Fractional Model of the Electrochemical Capacitor Relaxation Phenomenon. Bull. Polish Acad. Sci. Tech. Sci. 2018, 66, 441–448. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.R.; Dulf, E.H. Event-Based Implementation of Fractional Order IMC Controllers for Simple FOPDT Processes. Mathematics 2020, 8, 1378. [Google Scholar] [CrossRef]
- Dulf, E.-H.; Vodnar, D.C.; Danku, A.; Muresan, C.-I.; Crisan, O. Fractional-Order Models for Biochemical Processes. Fractal Fract. 2020, 4, 12. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Measurement of Supercapacitor Fractional-Order Model Parameters From Voltage-Excited Step Response. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 367–376. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-Order Models of Supercapacitors, Batteries and Fuel Cells: A Survey. Mater. Renew. Sustain. Energy 2015, 4, 9. [Google Scholar] [CrossRef]
- Lewandowski, M.; Orzyłowski, M. Fractional-Order Models: The Case Study of the Supercapacitor Capacitance Measurement. Bull. Polish Acad. Sci. Tech. Sci. 2017, 65, 449–457. [Google Scholar] [CrossRef]
- Martynyuk, V.; Ortigueira, M. Fractional Model of an Electrochemical Capacitor. Signal Processing 2015, 107, 355–360. [Google Scholar] [CrossRef]
- Elwakil, A. Fractional-Order Circuits and Systems: An Emerging Interdisciplinary Research Area. IEEE Circuits Syst. Mag. 2010, 10, 40–50. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics II. Direct Current Characteristics. J. Chem. Phys. 1942, 10, 98–105. [Google Scholar] [CrossRef]
- Fouda, M.E.; Khorshid, A.E.; Alquaydheb, I.; Eltawil, A.; Kurdahi, F. Extracting the Cole-Cole Model Parameters of Tissue-Mimicking Materials. In Proceedings of the 2018 IEEE Biomedical Circuits and Systems Conference (BioCAS), Cleveland, OH, USA, 17–19 October 2018; pp. 1–4. [Google Scholar]
- Freeborn, T.J.; Maundy, B.; Elwakil, A. Improved Cole-Cole Parameter Extraction from Frequency Response Using Least Squares Fitting. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012; Volume 2, pp. 337–340. [Google Scholar]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Least Squares Estimation Technique of Cole-Cole Parameters from Step Response. Electron. Lett. 2012, 48, 752. [Google Scholar] [CrossRef]
- Freeborn, T.J. A Survey of Fractional-Order Circuit Models for Biology and Biomedicine. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 416–424. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Maundy, B. Extracting the Cole-Cole Impedance Model Parameters without Direct Impedance Measurement. Electron. Lett. 2010, 46, 1367. [Google Scholar] [CrossRef]
- McRae, D.A.; Esrick, M.A.; Mueller, S.C. Changes in the Noninvasive, in Vivo Electrical Impedance of Three Xenografts during the Necrotic Cell-Response Sequence. Int. J. Radiat. Oncol. 1999, 43, 849–857. [Google Scholar] [CrossRef]
- Eldarrat, A.H.; Wood, D.J.; Kale, G.M.; High, A.S. Age-Related Changes in Ac-Impedance Spectroscopy Studies of Normal Human Dentine. J. Mater. Sci. Mater. Med. 2007, 18, 1203–1210. [Google Scholar] [CrossRef]
- Sezdi, M.; Bayik, M.; Ulgen, Y. Storage Effects on the Cole-Cole Parameters of Erythrocyte Suspensions. Physiol. Meas. 2006, 27, 623–635. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Machado, J.A.T.; De Keyser, R. Modeling of the Lung Impedance Using a Fractional-Order Ladder Network With Constant Phase Elements. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 83–89. [Google Scholar] [CrossRef]
- Copot, D.; De Keyser, R.; Derom, E.; Ortigueira, M.; Ionescu, C.M. Reducing Bias in Fractional Order Impedance Estimation for Lung Function Evaluation. Biomed. Signal Process. Control 2018, 39, 74–80. [Google Scholar] [CrossRef]
- Guermazi, M.; Kanoun, O.; Derbel, N. Investigation of Long Time Beef and Veal Meat Behavior by Bioimpedance Spectroscopy for Meat Monitoring. IEEE Sens. J. 2014, 14, 3624–3630. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor Theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Lazarević, M.; Cajić, M.; Đurović, N. Biomechanical Modelling and Simulation of Soft Tissues Using Fractional Memristive Elements. In Proceedings of the Electronic 8th GRACM International Congress in Computational Mechanics, Volos, Greece, 12–15 July 2015; pp. 1–10. [Google Scholar]
- Rigaud, B.; Hamzaoui, L.; Frikha, M.R.; Chauveau, N.; Morucci, J.P. In Vitro Tissue Characterization and Modelling Using Electrical Impedance Measurements in the 100 Hz-10 MHz Frequency Range. Physiol. Meas. 1995, 16, A15–A28. [Google Scholar] [CrossRef] [PubMed]
- Alexandersson, A.; Steingrimsdottir, T.; Terrien, J.; Marque, C.; Karlsson, B. The Icelandic 16-Electrode Electrohysterogram Database. Sci. Data 2015, 2, 150017. [Google Scholar] [CrossRef] [PubMed]
- Esgalhado, F.; Batista, A.G.; Mouriño, H.; Russo, S.; Palma dos Reis, C.R.; Serrano, F.; Vassilenko, V.; Ortigueira, M. Uterine Contractions Clustering Based on Electrohysterography. Comput. Biol. Med. 2020, 123, 103897. [Google Scholar] [CrossRef]
- Batista, A.G.; Cebola, R.; Esgalhado, F.; Russo, S.; dos Reis, C.R.P.; Serrano, F.; Vassilenko, V.; Ortigueira, M. The Contractiongram: A Method for the Visualization of Uterine Contraction Evolution Using the Electrohysterogram. Biomed. Signal Process. Control 2021, 67, 102531. [Google Scholar] [CrossRef]
- Esgalhado, F.; Batista, A.G.; Mouriño, H.; Russo, S.; dos Reis, C.R.P.; Serrano, F.; Vassilenko, V.; Duarte Ortigueira, M. Automatic Contraction Detection Using Uterine Electromyography. Appl. Sci. 2020, 10, 7014. [Google Scholar] [CrossRef]
- Batista, A.G.; Najdi, S.; Godinho, D.M.; Martins, C.; Serrano, F.C.; Ortigueira, M.D.; Rato, R.T. A Multichannel Time–frequency and Multi-Wavelet Toolbox for Uterine Electromyography Processing and Visualisation. Comput. Biol. Med. 2016, 76, 178–191. [Google Scholar] [CrossRef]
- Russo, S.; Batista, A.; Esgalhado, F.; Palma dos Reis, C.R.; Serrano, F.; Vassilenko, V.; Ortigueira, M. Alvarez Waves in Pregnancy: A Comprehensive Review. Biophys. Rev. 2021, 13, 563–574. [Google Scholar] [CrossRef]
- Marquel, C.; Gondty, J.; Rossi, J.; Baaklini, N. Surveillance Des Grossesses À Risque Par Électromyographie Uterine. RBM-News 1995, 17, 25–31. [Google Scholar] [CrossRef]
- Roberts, W.F.; Perry, K.G.; Naef, R.W.; Washburne, J.F.; Morrison, J.C. The Irritable Uterus: A Risk Factor for Preterm Birth? Am. J. Obstet. Gynecol. 1995, 172, 138–142. [Google Scholar] [CrossRef]
- Welch, P. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Ulgen, Y.; Sezdi, M. Hematocrit Dependence of the Cole-Cole Parameters of Human Blood. In Proceedings of the 1998 2nd International Conference Biomedical Engineering Days, Istanbul, Turkey, 22–22 May 1998; pp. 71–74. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W.; Marquardtt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Brosens, I.; Robertson, W.B.; Dixon, H.G. The Physiological Response of the Vessels of the Placental Bed to Normal Pregnancy. J. Pathol. Bacteriol. 1967, 93, 569–579. [Google Scholar] [CrossRef]
- Medicine, S.; George, S. Uteroplacental Arterial Changes Related to Interstitial Trophoblast Migration in Early Human Pregnancy. Placenta 1983, 4, 397–413. [Google Scholar]
- Blankenship, T.N.; Enders, A.C.; King, B.F. Trophoblastic Invasion and Modification of Uterine Veins during Placental Development in Macaques. Cell Tissue Res. 1993, 274, 135–144. [Google Scholar] [CrossRef]
- Ziekenhuis, A. Trophoblastic Invasion of Human Decidua From 8 to 18 Weeks of Pregnancy. Placenta 1980, 1, 3–19. [Google Scholar]
- Sheppard, B.L.; Bonnar, J. the ultrastructure of the arterial supply of the human placenta in pregnancy complicated by fetal growth retardation. BJOG Int. J. Obstet. Gynaecol. 1976, 83, 948–959. [Google Scholar] [CrossRef]
- Khong, T.Y.; Wolf, F.; Robertson, W.B.; Brosens, I. Inadequate Maternal Vascular Response to Placentation in Pregnancies Complicated by Pre-Eclampsia and by Small-for-Gestational Age Infants. BJOG Int. J. Obstet. Gynaecol. 1986, 93, 1049–1059. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhao, S. Chapter 2: Placental Blood Circulation. In Vascular Biology of the Placenta; Morgan & Claypool Life Sciences: San Rafael, CA, USA, 2010; pp. 1–5. [Google Scholar]
- Kanda, B.Y.S.; Kuriyama, H. Specific Features of Smooth Muscle Cells Recorded from the Placental Region of the Myometrium of Pregnant Rats. J. Physiol. 1980, 50, 127–144. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).