Developmental Trends in the Application and Measurement of the Bidirectional Reflection Distribution Function
Abstract
:1. Introduction
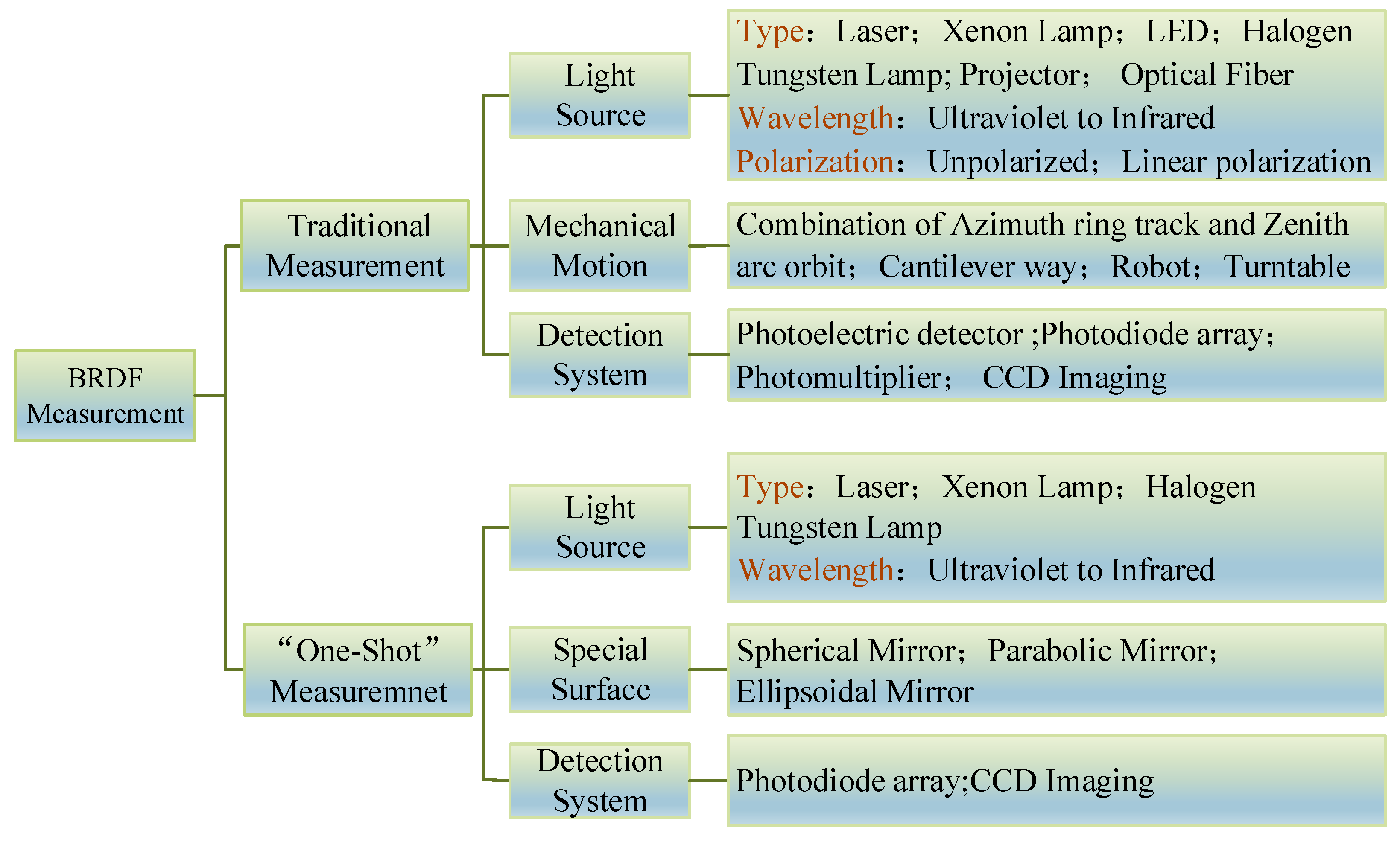
2. History of Developments in BRDF Measurements
3. Trend of Development of BRDF Measurement Devices
3.1. Summary of Development Status
3.2. Current Problems and Development Trends
- (a)
- Unachievable of time-varying BRDF detection for traditional measurement;
- (b)
- Lack of devices for fast measurement;
- (c)
- Lack of means to fuse and reconstruct BRDF data;
- (d)
- Incomplete analysis of factors affecting BRDF data.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nicodemus, F.E. Directional reflectance and emissivity of an opaque surface. Appl. Opt. 1965, 4, 767–775. [Google Scholar] [CrossRef]
- Kimes, D.S.; Sellers, P.J.; Diner, D.J. Extraction of spectral hemispherical reflectance (albedo) of surfaces from nadir and directional reflectance data. Int. J. Remote Sens. 1987, 8, 1727–1746. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Nolin, A.W. New methods to infer snow albedo from the MISR instrument with applications to the Greenland ice sheet. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1616–1625. [Google Scholar] [CrossRef]
- Pokrovsky, I.; Pokrovsky, O.; Roujean, J.L. Development of an operational procedure to estimate surface albedo from the SEVIRI/MSG observing system in using polder BRDF measurements. Remote Sens. Environ. 2003, 87, 198–214. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.M.; Wang, J.D.; Liang, S.L.; Wang, D.W.; Ma, B.; Bo, Y.C. The bidirectional reflectance signature of typical land surfaces and comparison of MISR and MODIS BRDF products. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Wu, H.; Liang, S.; Ling, T.; Tao, H. Snow BRDF characteristics from MODIS and MISR data. In Proceedings of the Geoscience & Remote Sensing Symposium IEEE, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Samain, O.; Geiger, B.; Roujean, J.L. Spectral normalization and fusion of optical sensors for the retrieval of BRDF and albedo: Application to VEGETATION, MODIS, and MERIS data sets. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3166–3179. [Google Scholar] [CrossRef]
- Comar, A.; Baret, F.; Viénot, F.; Yan, L.; De Solan, B. Wheat leaf bidirectional reflectance measurements: Description and quantification of the volume, specular and hot-spot scattering features. Remote Sens. Environ. 2012, 121, 26–35. [Google Scholar] [CrossRef]
- Comar, A.; Baret, F.; Obein, G.; Simonot, L.; Meneveaux, D.; Vienot, F.; de Solan, B. ACT: A leaf BRDF model taking into account the azimuthal anisotropy of monocotyledonous leaf surface. Remote Sens. Environ. 2014, 143, 112–121. [Google Scholar] [CrossRef]
- Roth, B.D.; Saunders, M.G.; Bachmann, C.M.; van Aardt, J.A. On leaf BRDF estimates and their fit to microfacet models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 99, 1761–1771. [Google Scholar] [CrossRef]
- Hyman, A.H.; Barnsley, M.J. On the potential for land cover mapping from multiple-view-angle (MVA) remotely sensed images. Int. J. Remote Sens. 1997, 18, 2471–2475. [Google Scholar] [CrossRef]
- Schrder, S.; Finck, A.; Katsir, D.; Duparre, A. Light scattering characterization of optical components: BRDF, BTDF, and scatter losses. In Proceedings of the Optical Design & Testing VI International Society for Optics and Photonics, Bejing, China, 5 November 2014. [Google Scholar]
- Lu, X.; Gross, H. Efficient simulation of surface scattering in symmetry-free optical systems. Opt. Express 2020, 28, 39368–39386. [Google Scholar] [CrossRef]
- Lu, C.; Li, L. Application of BRDF data in stray light analysis. In Proceedings of the Tenth International Conference On Information Optics And Photonics, CIOP100, Bejing, China, 8–11 July 2018. [Google Scholar]
- Mo, D.; Wang, Y.; Liu, D.; Chen, J.; Xu, L. Research of suppressing stray light of cold shield with different black coating. Metasurface Wave Planar Opt. 2019, 10841, 17. [Google Scholar]
- Zeidler, S.; Akutsu, T.; Torii, Y.; Aso, Y. Measuring scattering light distributions on high-absorptive surfaces for stray-light reduction in gravitational-wave detectors. Opt. Express 2019, 27, 16890. [Google Scholar] [CrossRef] [PubMed]
- Löw, J.; Kronander, J.; Ynnerman, A.; Unger, J. BRDF models for accurate and efficient rendering of glossy surfaces. Comput. Graph. 2012, 31, 1–14. [Google Scholar]
- Schwartz, C.; Sarlette, R.; Weinmann, M.; Rump, M.; Klein, R. Design and implementation of practical bidirectional texture function measurement devices focusing on the developments at the university of bonn. Sensors 2014, 14, 7753–7819. [Google Scholar] [CrossRef] [Green Version]
- Wojciech, M.; Hanspeter, P.; Matthew, B.; Leonard, M. Efficient isotropic BRDF measurement. The Eurographics Association. 2003. Available online: http://www.csbio.unc.edu/mcmillan/pubs/egsr03_matusik.pdf (accessed on 10 September 2021).
- Weyrich, T.; Matusik, W.; Pfister, H.; Bickel, B.; Donner, C.; Tu, C.; McAndless, J.; Lee, J.; Ngan, A.; Jensen, H.W.; et al. Analysis of Human Faces using a Measurement-Based Skin Reflectance Model. ACM Trans. Graph. 2006, 25, 1013–1024. Available online: https://www.merl.com/publications/docs/TR2006-071.pdf (accessed on 17 January 2022). [CrossRef]
- Hanssen, L.M.; Bintz, J.R.; Mendenhall, M.J.; Marciniak, M.A.; Bulter, S.D.; Lloyd, J.T. A novel image-based BRDF measurement system and its application to human skin. In Proceedings of the Society of Photo-optical Instrumentation Engineers, Reflection, Scattering, and Diffraction from Surfaces V, San Diego, CA, USA, 26 September 2016; Volume 996108. [Google Scholar]
- Method for Rendering Skin Material Based on BRDF and Its Apparatus. K.R. Patent KR20100062860(A), 10 June 2010. Available online: https://patentimages.storage.googleapis.com/6e/e8/ad/47b531d4ef6137/KR20100062860A.pdf (accessed on 17 January 2022).
- Hongda, T.; Zibo, Z.; Lihui, J.; Dong, S. Visibility measurement in an atmospheric environment simulation chamber. Curr. Opt. Photonics 2017, 3, 186–195. [Google Scholar]
- Park, S.; Lee, D.H.; Kim, Y.G. SI-traceable calibration of a transmissometer for meteorological optical range (MOR) observation. Hankook Kwanghak Hoeji 2015, 26, 73–82. [Google Scholar] [CrossRef] [Green Version]
- Bloemink, H.I. KNMI visibility standard for calibration of scatterometers. In Proceedings of the 4th ICEAWS International Conference on Experiences with Automatic Weather Stations, Lisboa, Portugal, 24–26 May 2006. [Google Scholar]
- Chong, W.; Bian, Z.Q.; Chu, J.H.; He, X.L.; Jiang, D.D. A method for calibrating forward scatterometers indoors. Metrologia 2020, 57, 065030. [Google Scholar]
- Bartel, F.O.; Dereniak, E.L.; Wolfe, W.L. The theory and measurement of bidirectional reflectance distribution function (brdf) and bidirectional transmittance distribution function (BTDF). Proc. SPIE-Int. Soc. Opt. Eng. 1981, 257, 154–160. [Google Scholar]
- Meister, G.; Rothkrich, A.; Hosgood, B.; Spitzer, H.; Bienlein, J. Error analysis for BRDF measurements at the European goniometric facility. Remote Sens. Rev. 2000, 19, 111–131. [Google Scholar] [CrossRef]
- Rothkirch, A.; Meister, G.; Hosgood, B.; Spitzer, H.; Bienlein, J. BRDF measurements at the EGO using a laser source: Equipment characteristics and estimation of error sources. Remote Sens. Rev. 2000, 19, 21–35. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Torrance, K.E.; Birkebak, R.C. Polarization, directional distribution, and off-specular peak phenomena in light reflected from roughened surfaces. J. Opt. Soc. America. 1966, 56, 916–924. [Google Scholar] [CrossRef] [Green Version]
- Stuhlinger, T.W.; Dereniak, E.L.; Bartell, F.O. Bidirectional reflectance distribution function of gold-plated sandpaper. Appl. Opt. 1981, 20, 2648–2655. [Google Scholar] [CrossRef] [PubMed]
- Murray-Coleman, J.F.; Smith, A.M. The automated measurement of BRDFs and their application to luminaire modeling. J. Illum. Eng. Soc. 1990, 19, 87–99. [Google Scholar] [CrossRef]
- Drolen, B.L. Bidirectional reflectance and specularity of twelve spacecraft thermal control materials. J. Thermophys. Heat Transf. 1992, 6, 672–679. [Google Scholar] [CrossRef]
- Ward, G.J. Measuring and modeling anisotropic reflection. Acm Siggraph Comput. Graph. 1992, 26, 265–272. [Google Scholar] [CrossRef]
- Marschner, S.R.; Westin, S.H.; Lafortune, E.P.F.; Torrance, K.E. Image-based bidirectional reflectance distribution function measurement. Appl. Opt. 2000, 39, 2592–2600. [Google Scholar] [CrossRef]
- Voss, K.J.; Chapin, A.; Monti, M.; Zhang, H. Instrument to measure the bidirectional reflectance distribution function of surfaces. Appl. Optics. 2000, 39, 2000. [Google Scholar] [CrossRef]
- Dana, K.J. BRDF/BTF measurement device. In Proceedings of the IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 6197–6206. [Google Scholar]
- Shen, Y.J.; Zhu, Q.Z.; Zhang, Z.M. A scatterometer for measuring the bidirectional reflectance and transmittance of semiconductor wafers with rough surfaces. Rev. Sci. Instrum. 2003, 74, 4885–4892. [Google Scholar] [CrossRef]
- Li, H.; Torrance, K.E. Validation of the Gonioreflectometer; Beijing Institute of Technology: Bejing, China, 2005. [Google Scholar]
- Li, H.; Foo, S.C.; Torrance, K.E.; Westin, S.H. Automated three-axis gonioreflectometer for computer graphics applications. Opt. Eng. 2006, 45, 043605. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Chao, Q.; Dai, J. Design of multi-spectrum BRDF measurement system. Chin. Opt. Lett. 2007, 5, 168–171. [Google Scholar]
- Liu, Y.L. Measurement Technology and Experimental System of Bidirectional Reflectance Distribution Function. Ph.D. Thesis, School of Optics an Phontonics, Bijing Institute of Technology, Bijing, China, June 2018. [Google Scholar]
- McNeil, J.R.; Wilson, S.R. Two-Dimensional Optical Scatterometer Apparatus and Process. U.S. Patent 5,241,369, 31 August 1993. [Google Scholar]
- Hatab, Z.R.; McNeil, J.R.; Naqvi, S.S.H. Sixteen-megabit dynamic random access memory trench depth characterization using two-dimensional diffraction analysis. Vac. Sci. Technol. B. 1995, 13, 174–181. [Google Scholar] [CrossRef]
- Kautz, J. Shading and shadows. Fast, arbitrary BRDF shading for low-frequency lighting using spherical harmonics. In Proceedings of the 13th Eurographics Workshop on Rendering, Pisa, Italy, 26–28 June 2002. [Google Scholar]
- Han, J.Y.; Perlin, K. Measuring bidirectional texture reflectance with a kaleidoscope. ACM Trans. Graph. 2003, 22, 741–748. [Google Scholar] [CrossRef]
- Achutha, S. BRDF Acquisition with Basis Illumination. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2006. [Google Scholar]
- Mukaigawa, Y.; Sumino, K.; Yagi, Y. High-speed measurement of BRDF using an ellipsoidal mirror and a projector. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Ben-Ezra, M.; Wang, J.; Wilburn, B.; Li, X.; Le, M. An LED-only BRDF measurement device. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Baribeau, R.; Neil, W.S. Development of a robot-based gonioreflectometer for spectral BRDF measurement. J. Mod. Opt. 2009, 56, 1497–1503. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, J.L. Measurement of surface bidirectional reflectance distribution based on optical fiber array in hemispheric space. Chin. J. Lasers 2009, 36, 3011–3014. [Google Scholar] [CrossRef]
- Ju, R.; Zhao, J. Measurement of a bidirectional reflectance distribution and system achievement based on a hemi-parabolic mirror. Opt. Lett. 2010, 35, 1458–1460. [Google Scholar] [CrossRef]
- Ju, R.; Zhao, J. Measurement of surface bidirectional reflectance distribution based on parabolic mirror. In Proceedings of the SPIE-The International Society for Optical Engineering, Shangai, China, 20 November 2009; Volume 75111H, pp. 1–8. [Google Scholar]
- Von Finck, A.; Hauptvogel, M.; Duparré, A. Instrument for close-to-process light scatter measurements of thin film coatings and substrates. Appl. Opt. 2011, 50, 321–328. [Google Scholar] [CrossRef]
- Meyen, S.; Sutter, F.; Heller, P.; Oschepkov, A. A new instrument for measuring the reflectance distribution function of solar reflector materials. Proc. Sol. Int. Conf. Energy Procedia 2014, 49, 2145–2153. [Google Scholar] [CrossRef] [Green Version]
- Obien, G.; Audenaert, J.; Ged, G.; Lelou, F. Metrological issues related to BRDF measurements around the specular direction in the particular case of glossy surfaces. In Proceedings of the Measuring, Modeling, and Reproducing Material Appearance, SPIE, San Francisco, CA, USA, 13 March 2015; p. 93980D. [Google Scholar] [CrossRef]
- Obein, G.; Ouarets, S.; Ged, G. Evaluation of the shape of the specular peak for high glossy surfaces. In Proceedings of the Measuring, Modeling, and Reproducing Material Appearance, San Francisco, CA, USA, 24 February 2014; p. 901805. [Google Scholar]
- Breton, R.L.; Ged, G.; Obein, G. Out of plane BRDF Measurement at LNE-Cnam using “ConDOR”, our primary goniospectrophotometer. In Proceedings of the 28th CIE Session-CIE 216, Manchester, UK, 27 June–4 July 2015. [Google Scholar]
- Surface Optics Coporation, “SOC-210 BDR Bidirectional Reflectometers.” SOC210-BDR Bidirectional Reflectometer. 2021. Available online: surfaceoptics.com (accessed on 9 February 2022).
- Boher, P.; Leroux, T.; Collomb-Patton, V.; Bignon, T. Fast spectral BRDF & BTDF measurements for characterization of displays and components. IEICE Trans. Electron. 2016, 99, 1255–1263. [Google Scholar] [CrossRef] [Green Version]
- Luo, D.B.; Qian, L.L.; Dong, L.W.; Shao, P.; Qin, Y. Simultaneous measurement of liquid surface tension and contact angle by light reflection. Opt. Express 2019, 27, 16703–16712. [Google Scholar] [CrossRef]
- Ohno, H. One-shot three-dimensional measurement method with color mapping of light direction. OSA Continuum. 2021, 4, 840–848. [Google Scholar] [CrossRef]
- Ohno, H.; Kamikawa, T. One-shot BRDF imaging system to obtain surface properties. Opt Rev. 2021, 28, 655–661. [Google Scholar] [CrossRef]
- Hsia, J.J.; Richmond, J.C. Bidirectional reflectometry (Part I) A high resolution laser bidirectional reflectometer with results on several optical coatings. J. Res. Natl. Inst. Stand. Technol. 1976, 80A, 189–205. [Google Scholar] [CrossRef] [PubMed]
- Mainguy, S.; Olivier, M.; Josse, M.A.; Guidon, M. Description and calibration of a fully automated infrared scatterometer. Proc Spie. 1991, 1530, 269–282. [Google Scholar] [CrossRef]
- Schiff, T.F.; Knighton, M.W.; Wilson, D.J.; Cady, F.M.; Stover, J.C.; Bulter, J.J. Design review of a high-accuracy UV to near-IR scatterometer. Opt. Scatt. Appl. Meas. Theory II. Int. Soc. Opt. Photonics 1993, 1995, 121–130. [Google Scholar]
- Castonguay, R.J.; Stover, J.C. New generation high-speed high-resolution hemispherical scatterometer. In Proceedings of the SPIE-The International Society for Optical Engineering, San Diego, CA, USA, 1 December 1993. [Google Scholar]
- Mcguckin, B.T.; Haner, D.A.; Menzies, R.T.; Esproles, C.; Brothers, A.M. Directional reflectance characterization facility and measurement methodology. Appl. Opt. 1996, 35, 4827–4834. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Bang, S.Y.; Modest, M.F.; Vladimir, S.S. Measurement of spectral, directional reflectivities of solids at high temperatures between 9 and 11 μm. Appl. Opt. 1993, 32, 3550–3558. [Google Scholar] [CrossRef]
- Barnes, P.Y.; Proctor, J.E. NIST high accuracy reference reflectometer-spectrophotometer. Natl. Inst. Stand. Technol. 1996, 101, 619–627. [Google Scholar] [CrossRef]
- Zaworski, J.R.; Welty, J.R.; Drost, M.K. Measurement and use of bi-directional reflectance. Int. J. Heat Mass Transf. 1996, 39, 1149–1156. [Google Scholar] [CrossRef]
- White, D.R.; Saunders, P.; Bonsey, S.J.; Ven, J.V.D.; Edgar, H. Reflectometer for measuring the bidirectional reflectance of rough surfaces. Appl. Opt. 1998, 37, 3450–3454. [Google Scholar] [CrossRef]
- Sandmeier, S.R. Acquisition of bidirectional reflectance factor data with field goniometers. Remote Sens. Environ. 2000, 73, 257–269. [Google Scholar] [CrossRef]
- Coburn, C.A.; Peddle, D.R. A low-cost field and laboratory goniometer system for estimating hyper spectral bidirectional reflectance. Can J Remote Sens. 2006, 32, 244–253. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Zhang, L. BRDF measuring device design and pointing accuracy analysis. Infrared Laser Eng. 2019, 48, 31–36. [Google Scholar] [CrossRef]
- Ma, W.J.H. The Measurement and modeling investigation on the spectral polarized BRDF of brass. Opt. Rev. 2020, 27, 380–390. [Google Scholar] [CrossRef]
- Feng, X.; Schott, J.R.; Gallagher, T. Comparison of methods for generation of absolute reflectance-factor values for bidirectional reflectance-distribution function studies. Appl. Opt. 1993, 32, 1234–1242. [Google Scholar] [CrossRef] [PubMed]
- Foo, S.C. A Gonioreflectometer for Measuring the Bidirectional Reflectance of Material for Use in Illumination Computation. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2001. [Google Scholar]
- Suomalainen, J.; Hakala, T.; Peltoniemi, J.; Puttonen, E. Polarized multi-angular reflectance measurements using the finish geodetic institute field goniospectro-meter. Sensors 2009, 9, 3891–3907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, G.; Ren, H.; Hu, R.; Hu, R.H.; Yan, K.; Zhang, W.M. A portable Multi-Angle Observation System. In Proceedings of the International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Bachmann, C.M.; Gray, D.; Abelev, A.; Philpot, W.; Montes, M.J.; Fusina, R.; Musser, J.; Li, R.-R.; Vermillion, M.; Smith, G.; et al. Linking goniometer measurements to hyperspectral and multisensory imagery for retrieval of beach properties and coastal characterization. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimor, MD, USA, 23–27 April 2012. [Google Scholar]
- Buchhorn, M.; Petereit, R.; Heim, B. A Manual transportable instrument platform for ground-based spectro-directional observations (ManTIS) and the resultant hyperspectral field goniometer system. Sensors 2013, 13, 16105–16128. [Google Scholar] [CrossRef]
- Li, H.; Chen, M.; Deng, C.; Liao, N.; Rao, Z. Versatile four-axis gonio-reflectometer for bidirectional reflectance distribution function measurements on anisotropic material surfaces. Opt. Eng. 2019, 58, 82–91. [Google Scholar] [CrossRef]
- Hünerhoff, D.; Grusemann, U.; Hope, A. New robot-based gonio-reflectometer for measuring spectral diffuse reflection. Metrologia 2006, 43, 11–16. [Google Scholar] [CrossRef] [Green Version]
- Yashika, A.; Swathi, R.; Roy, C.S. An optimal reflection photoplethysmographic sensor system based on skin optics. IEEE Sens. J. 2018, 18, 7233–7241. [Google Scholar] [CrossRef]
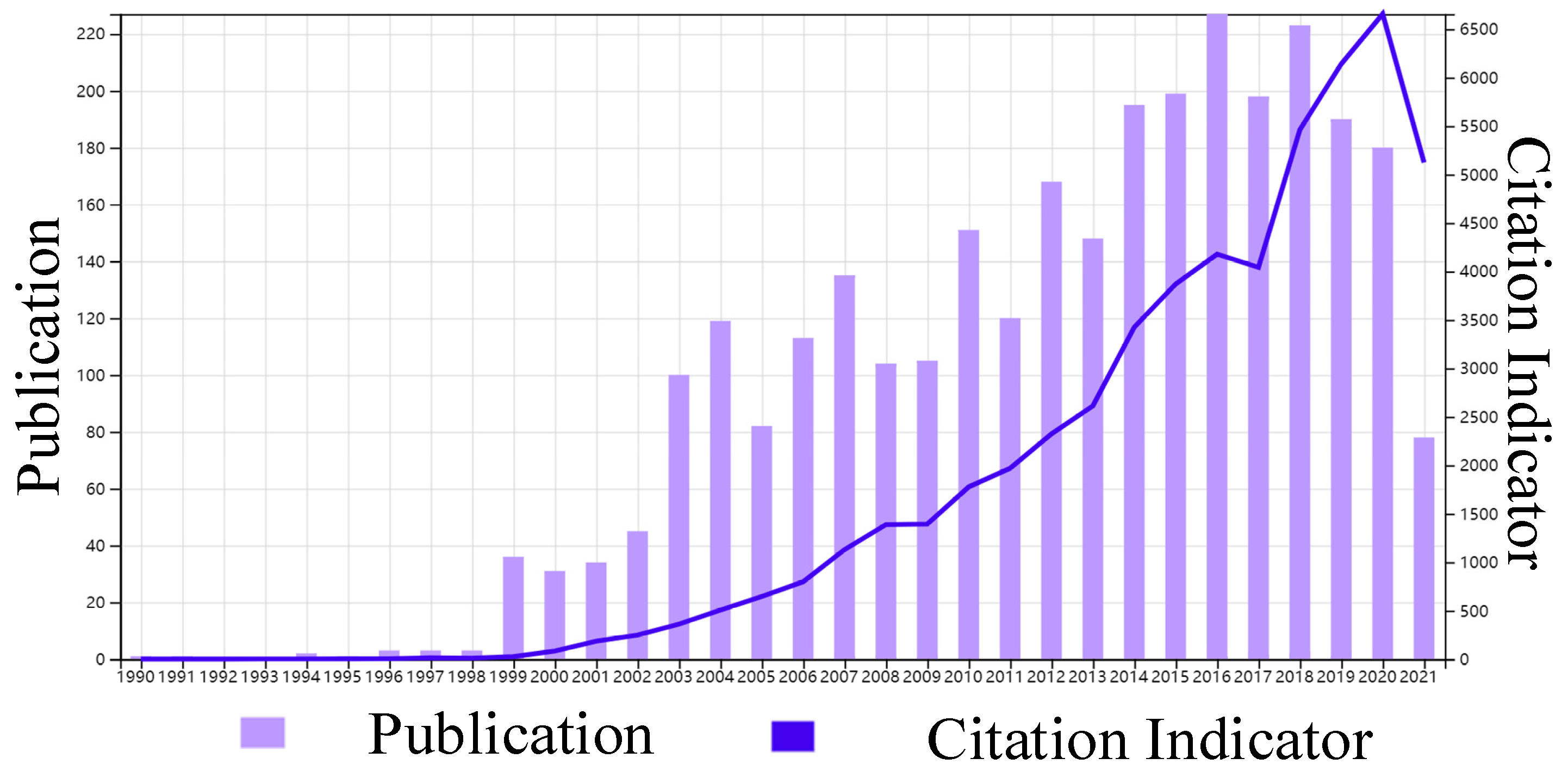

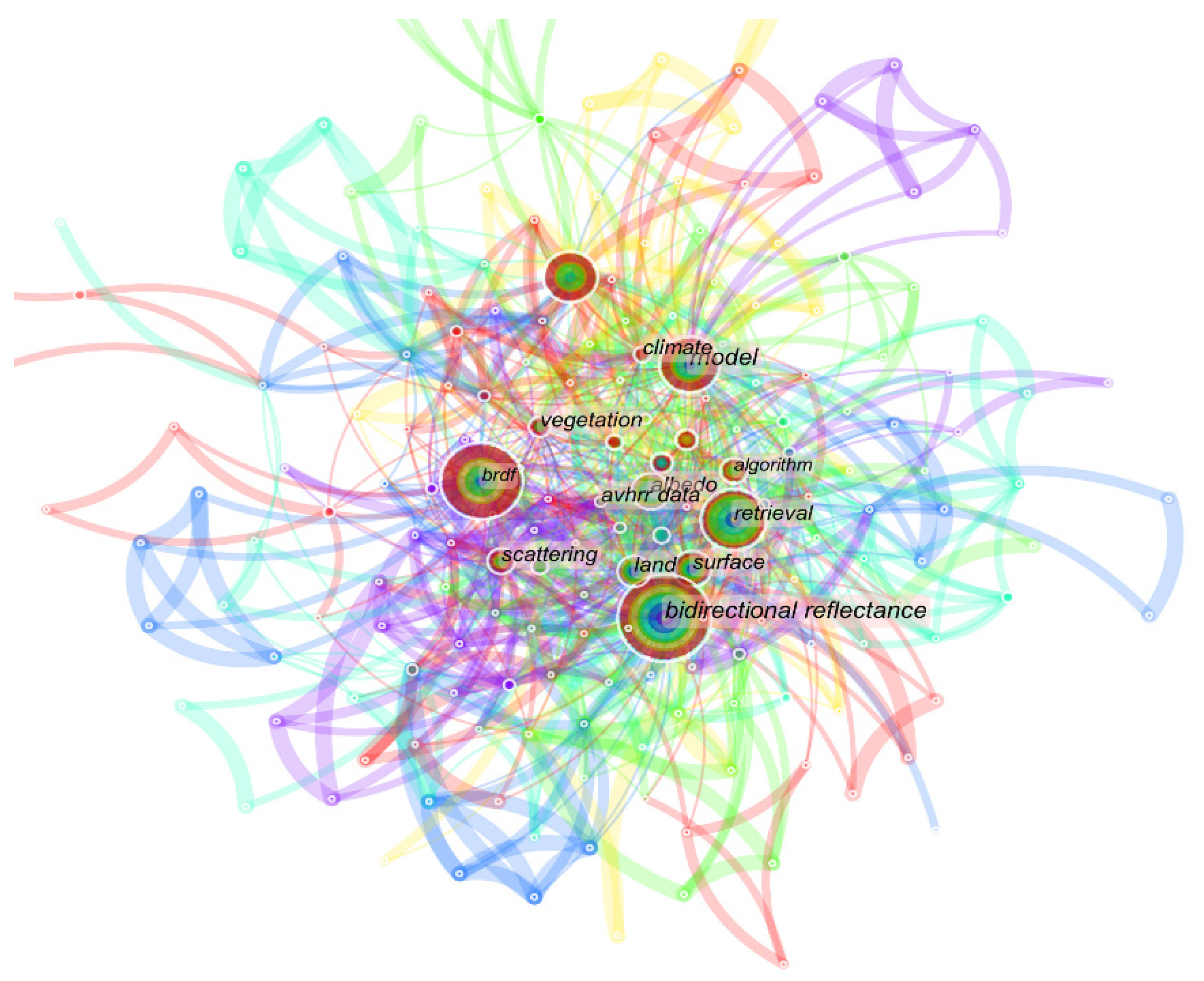
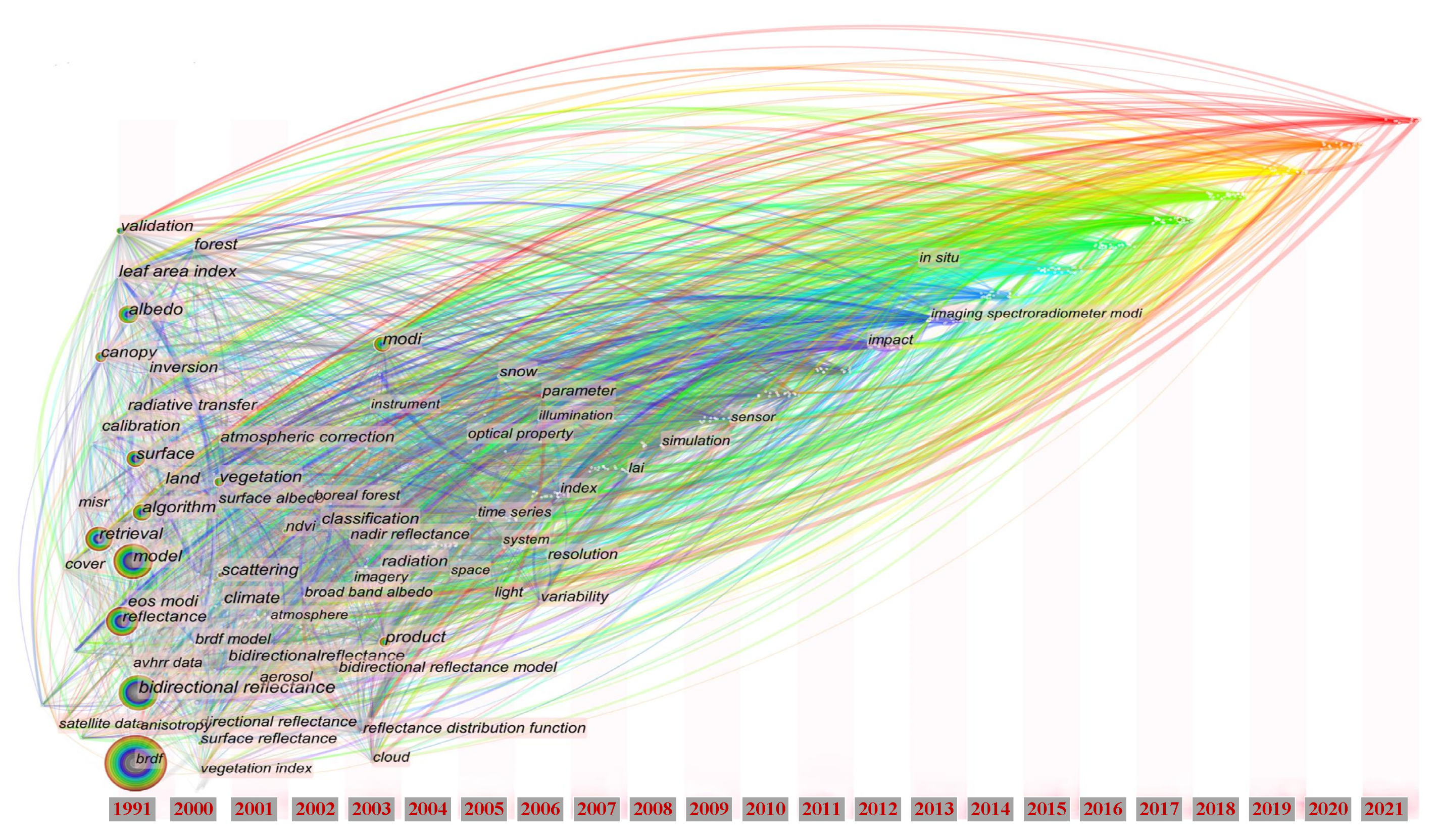
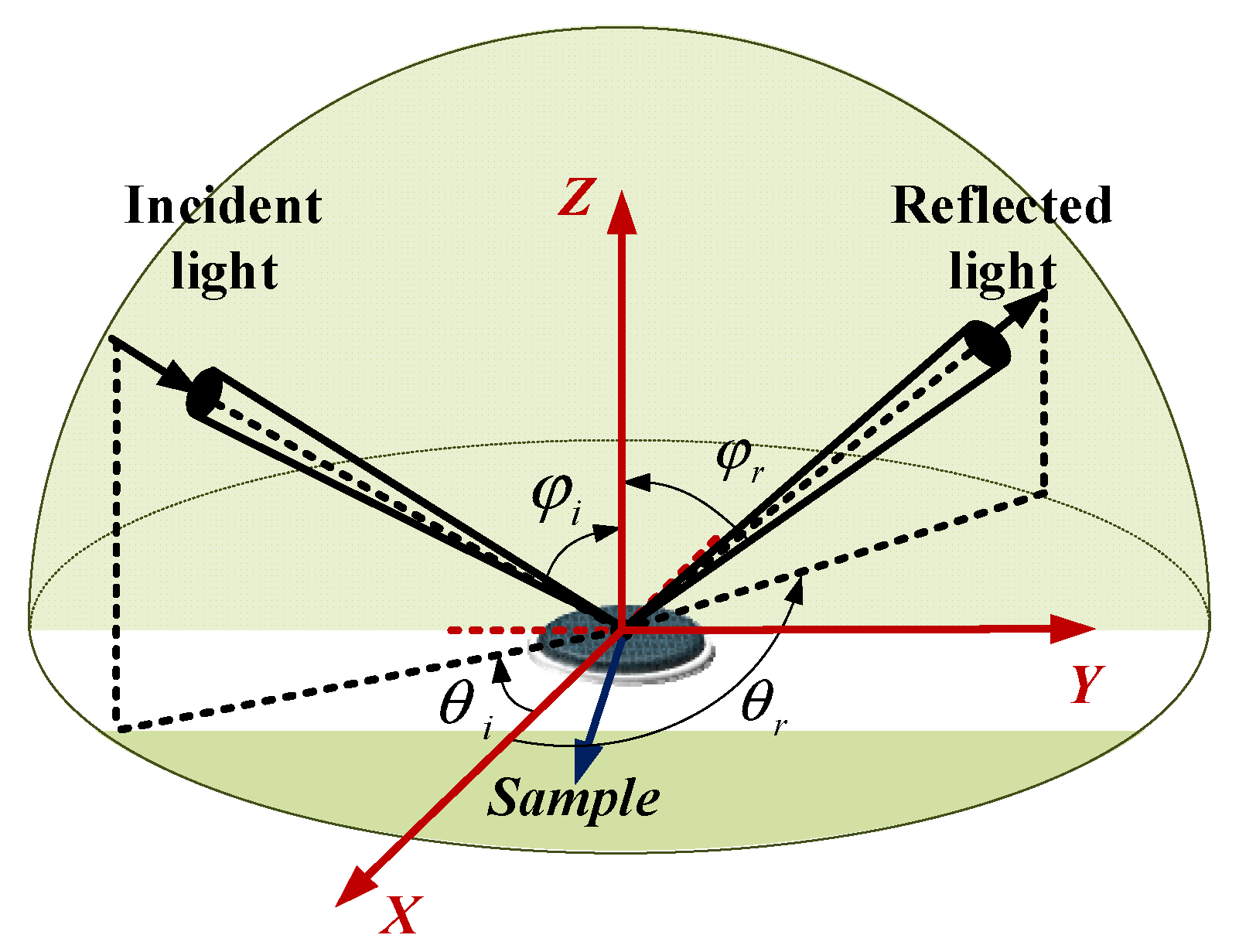
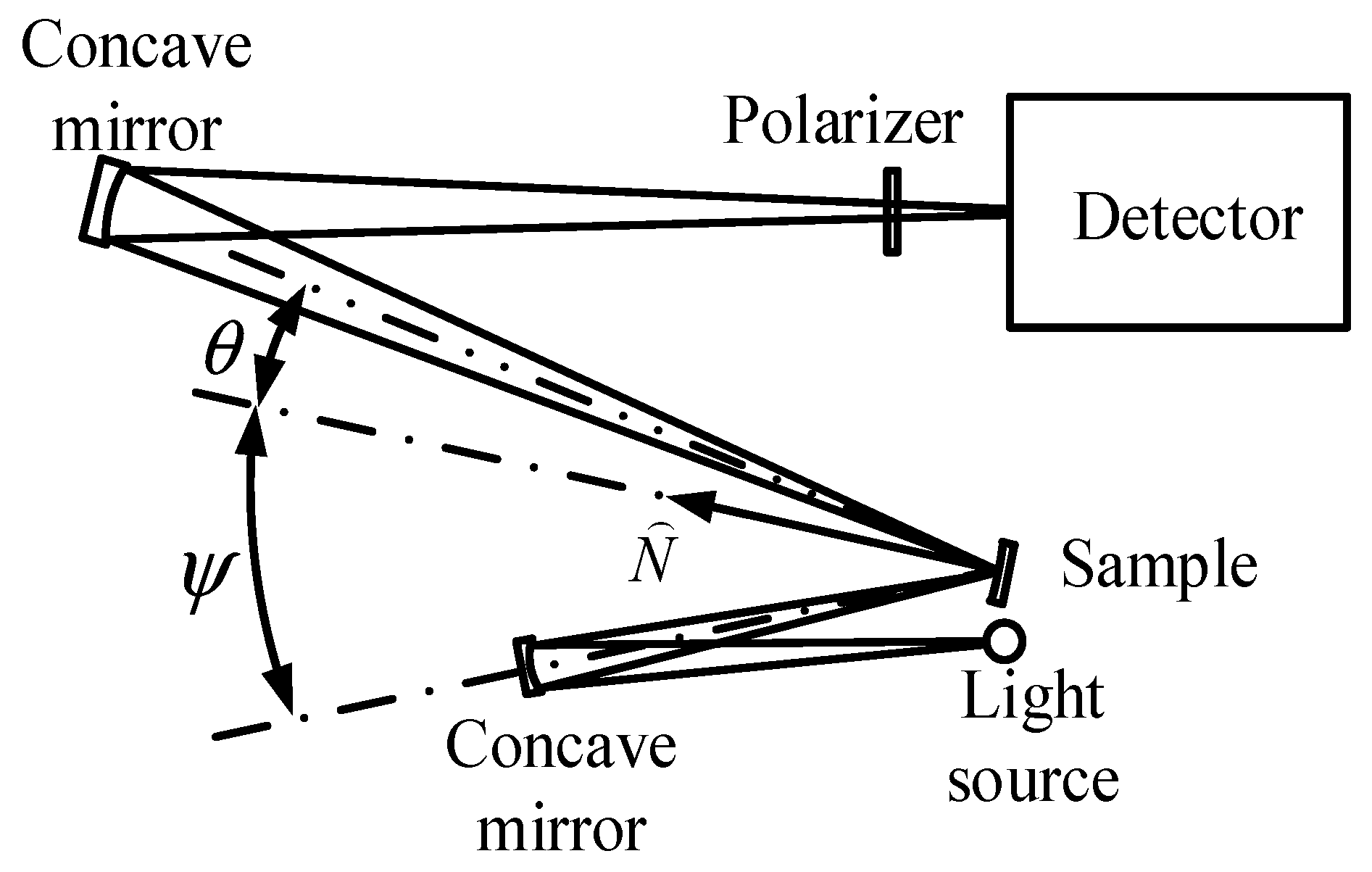

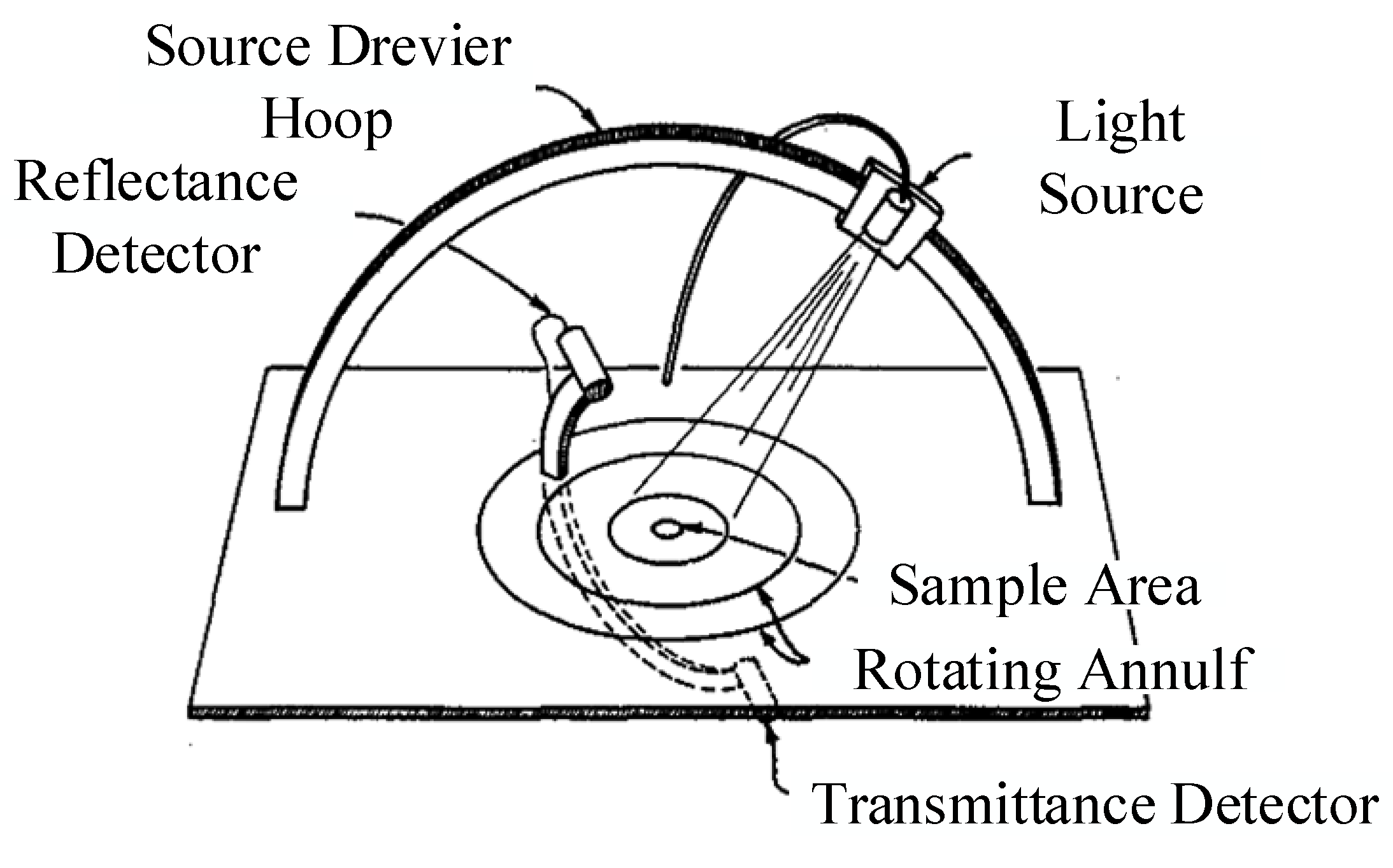
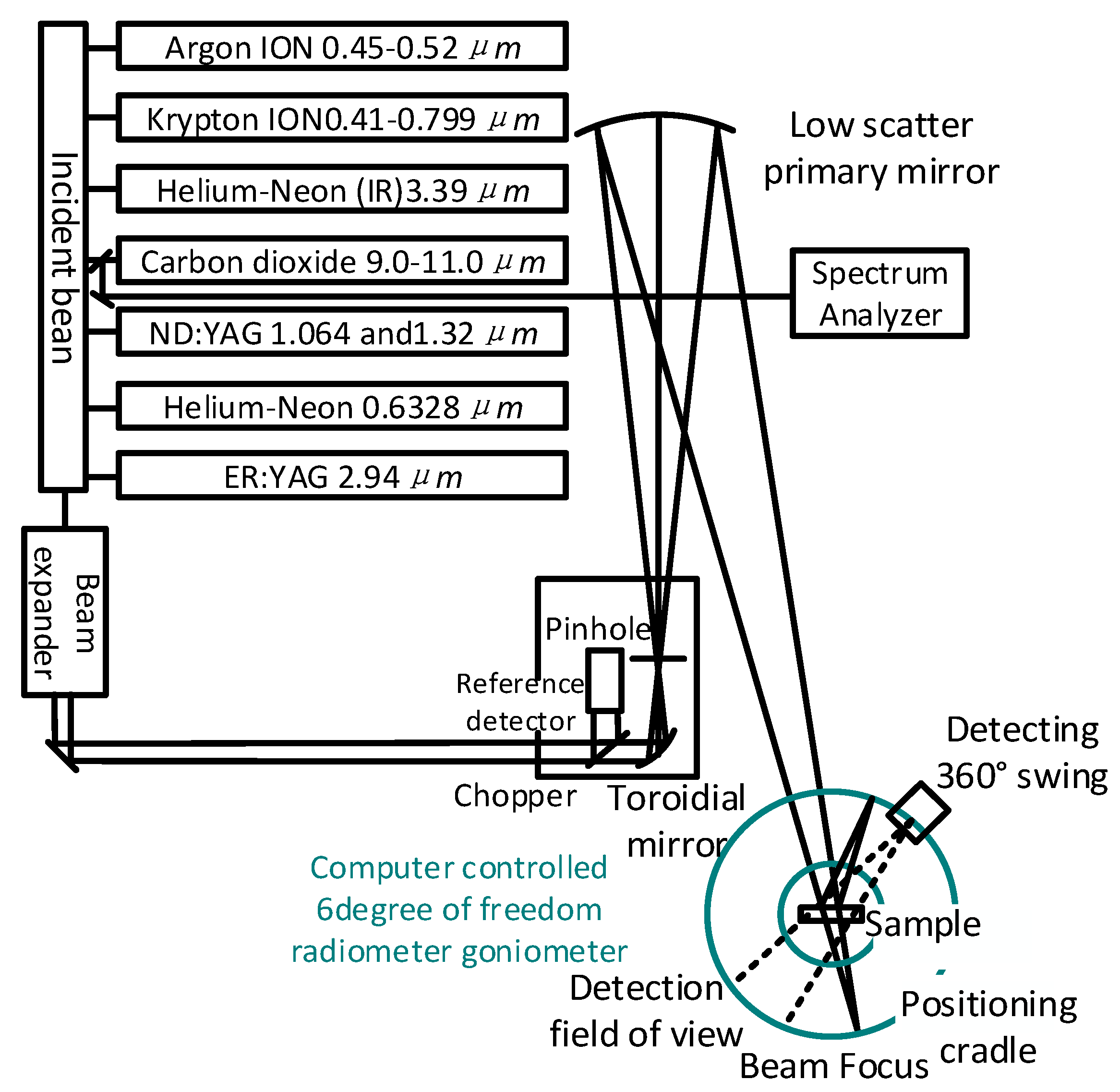
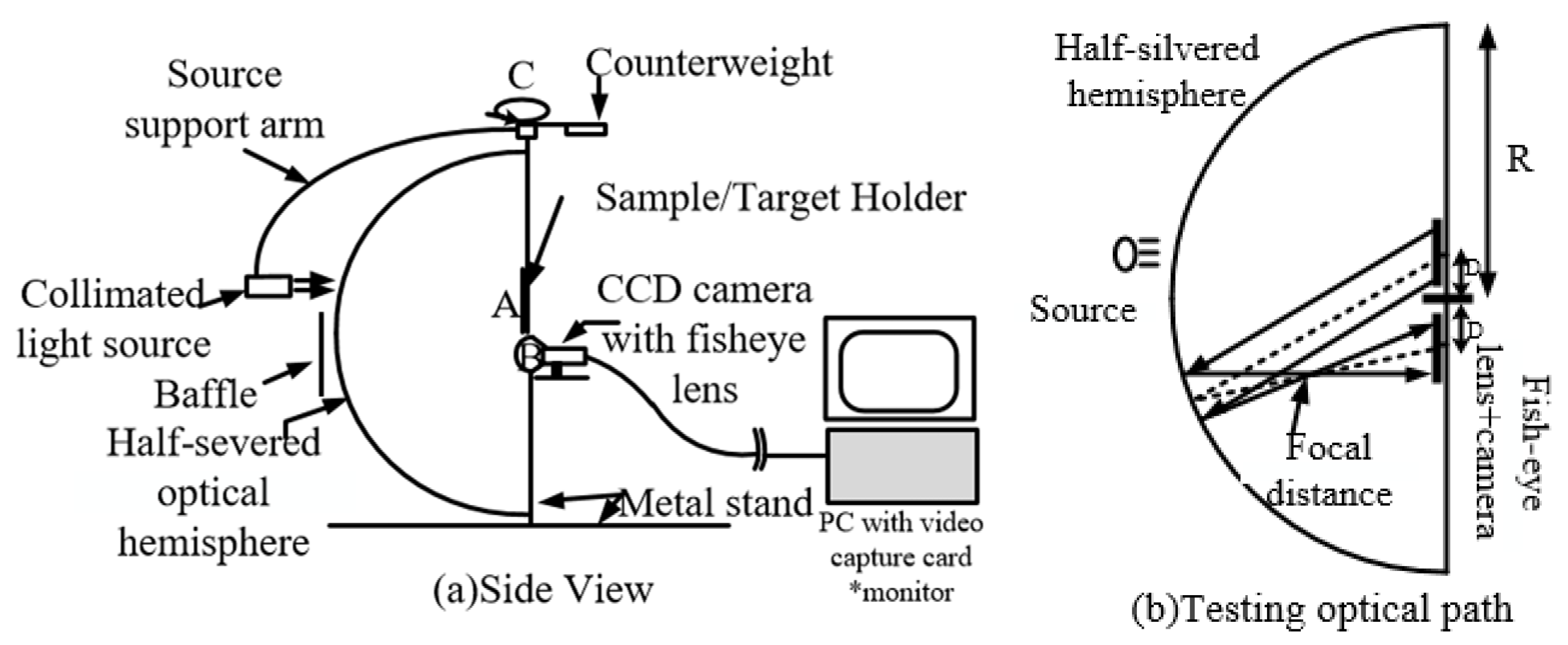

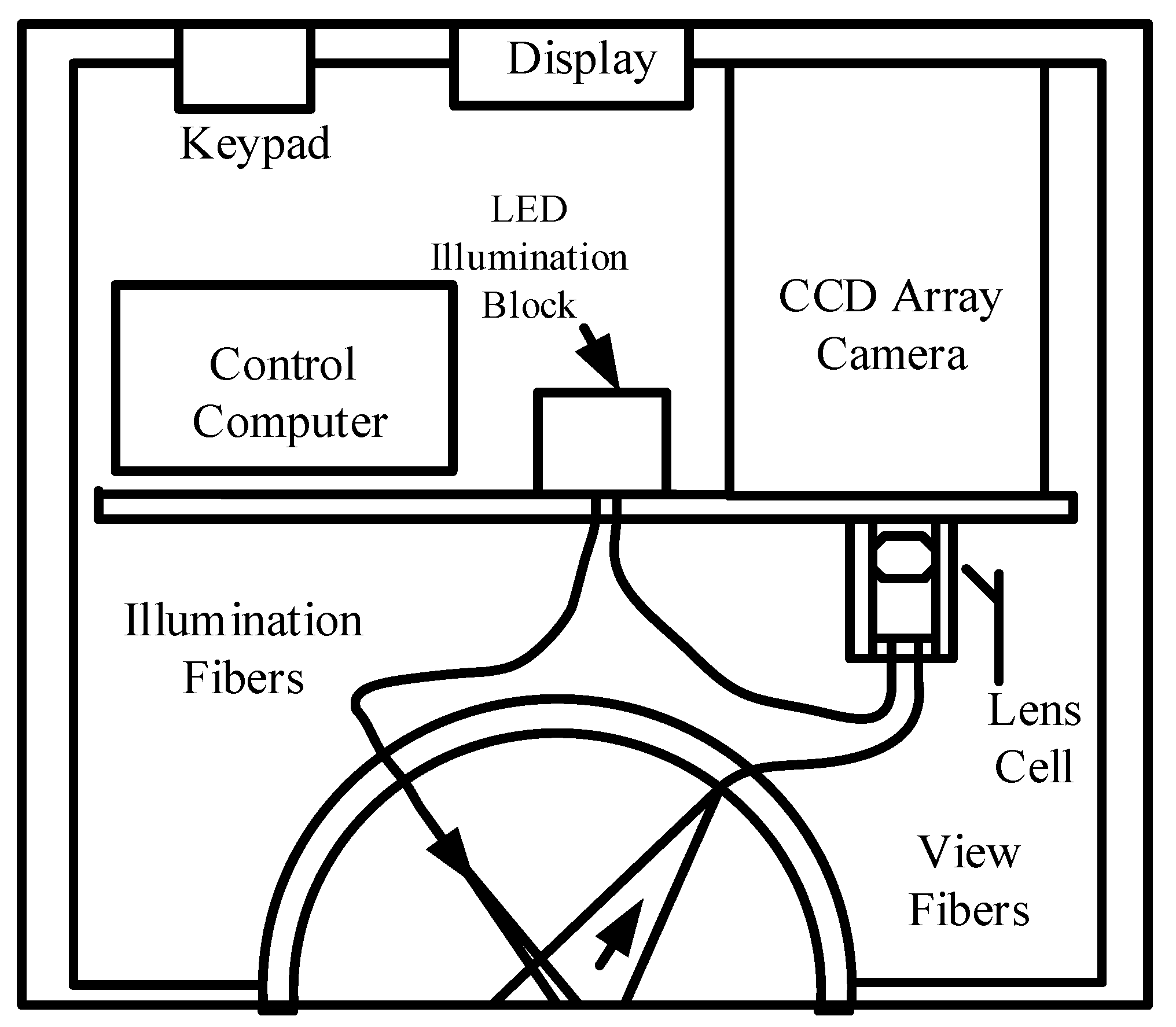


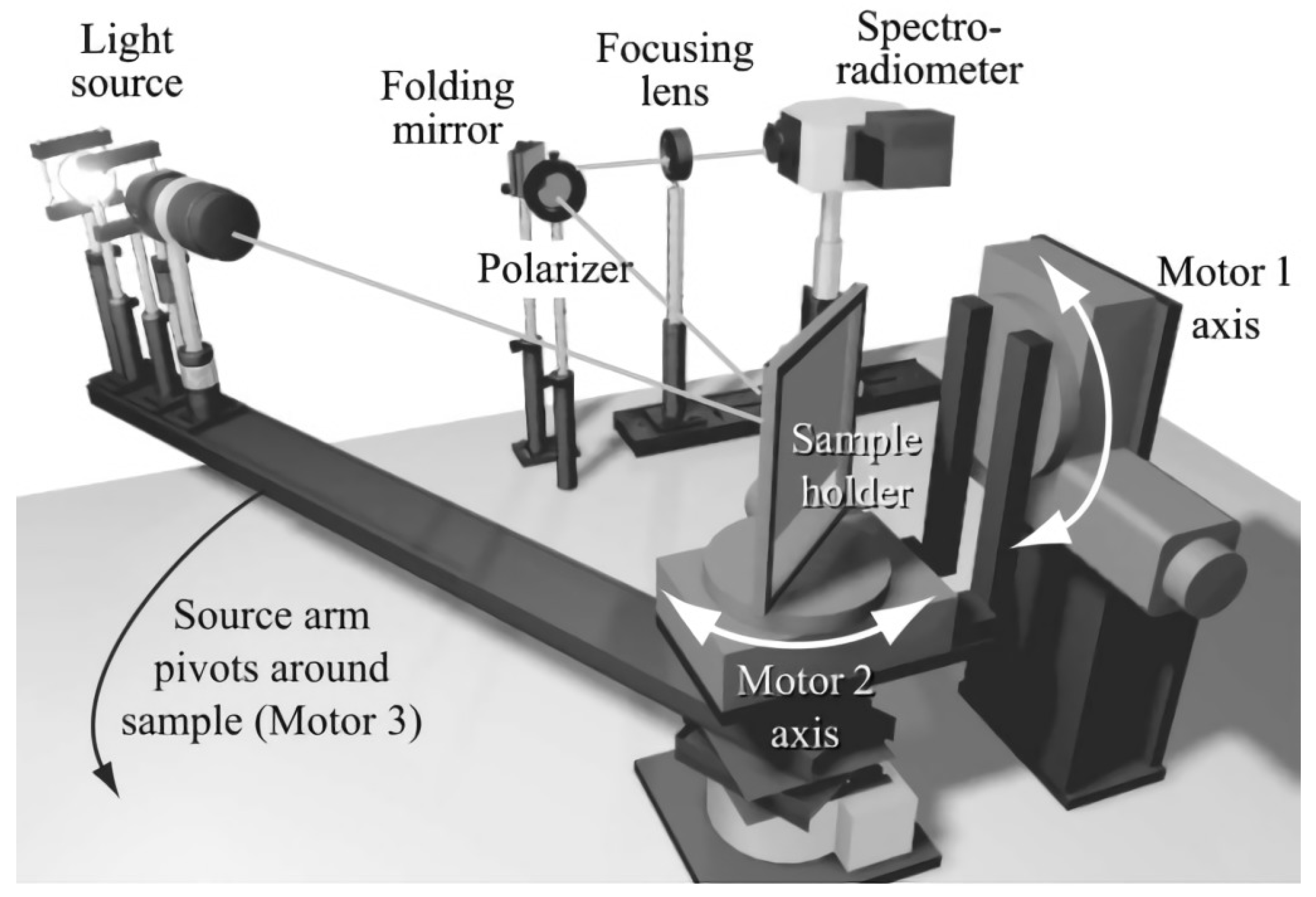
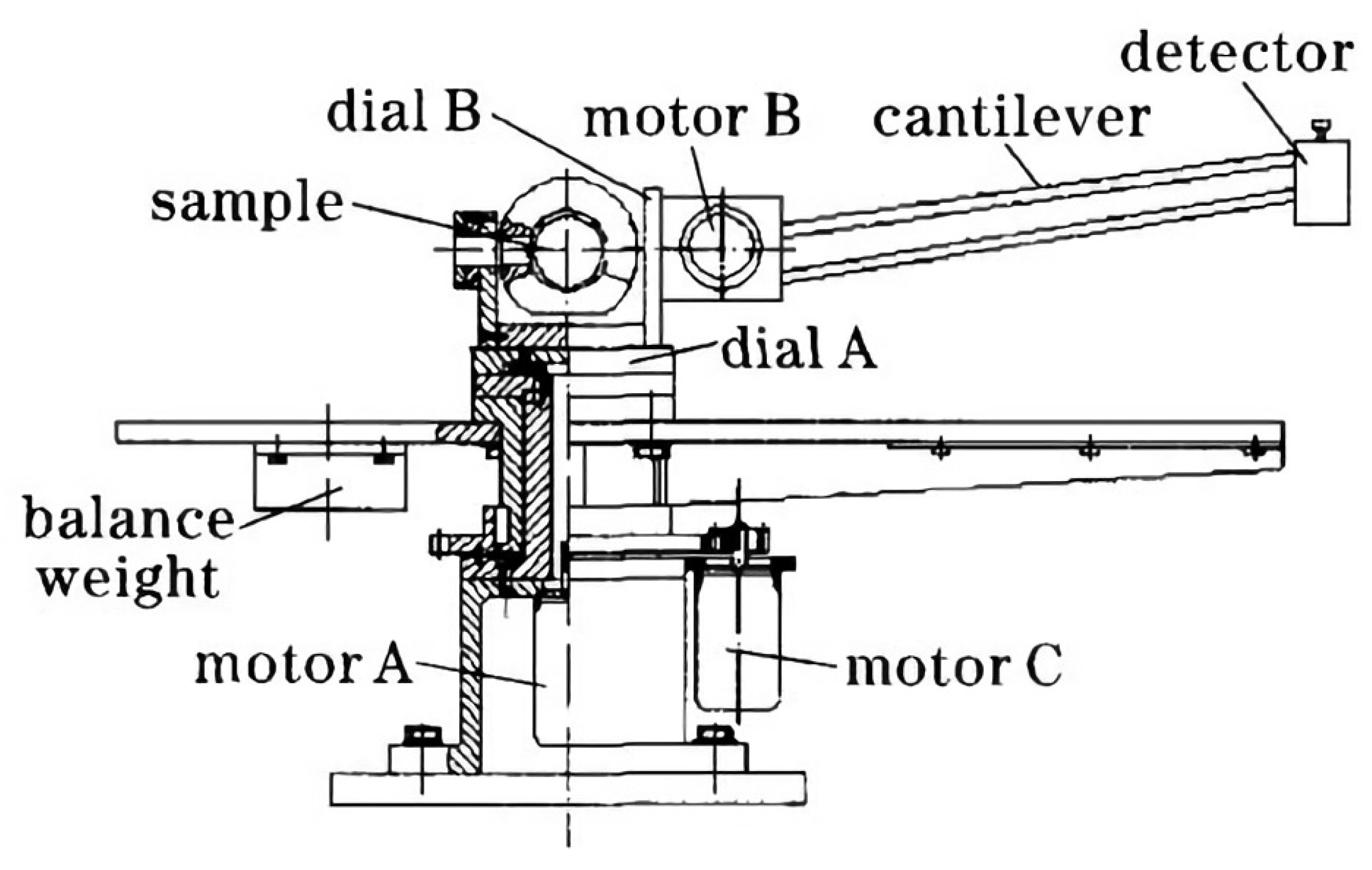
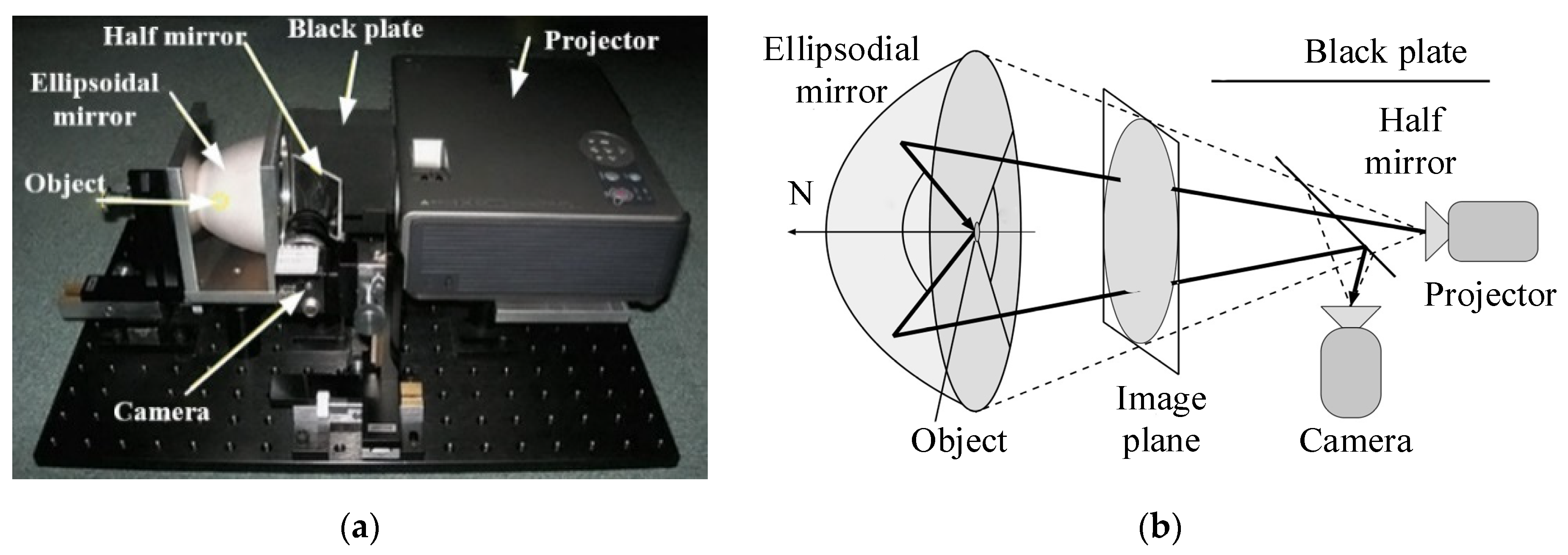

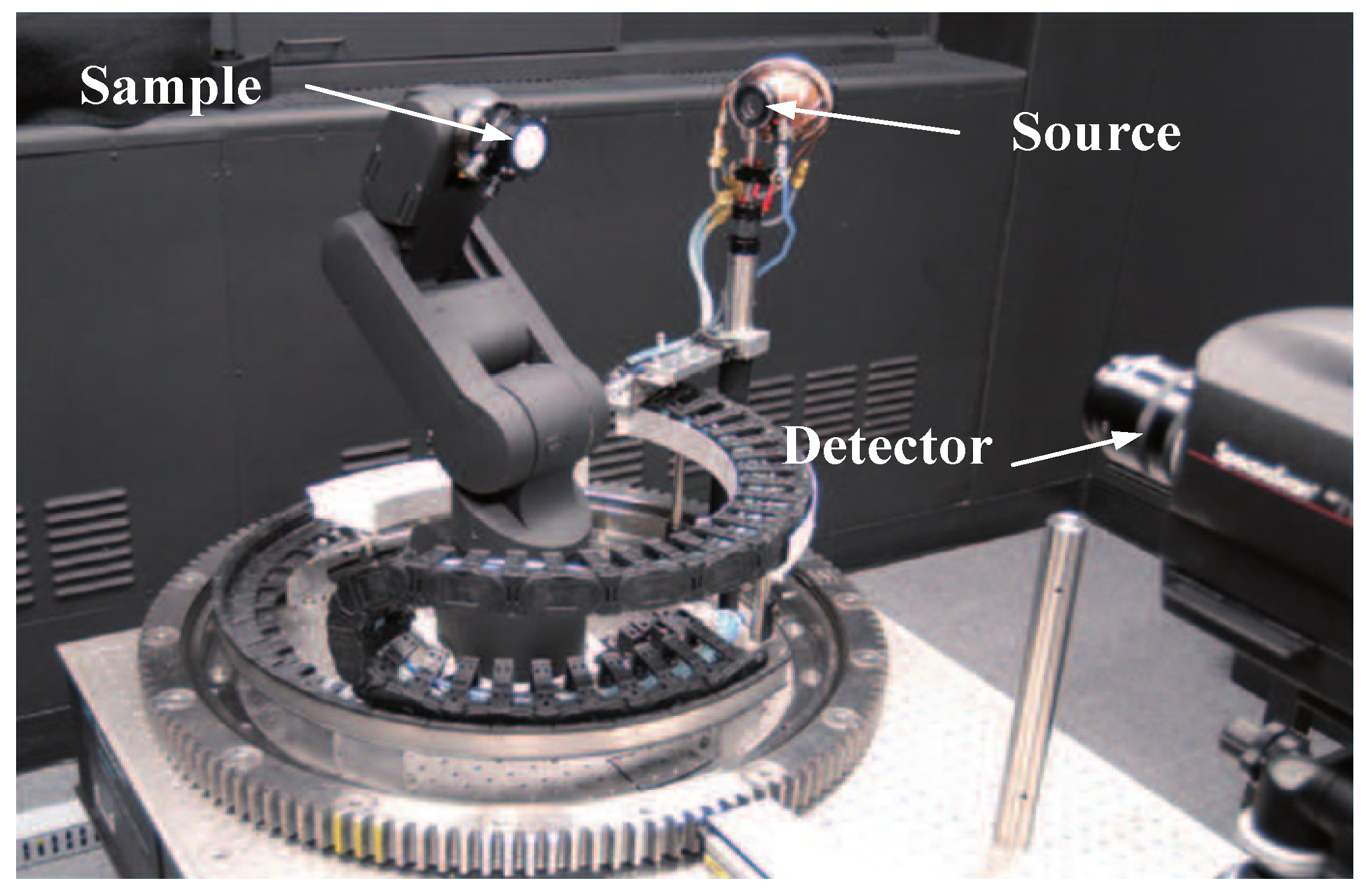

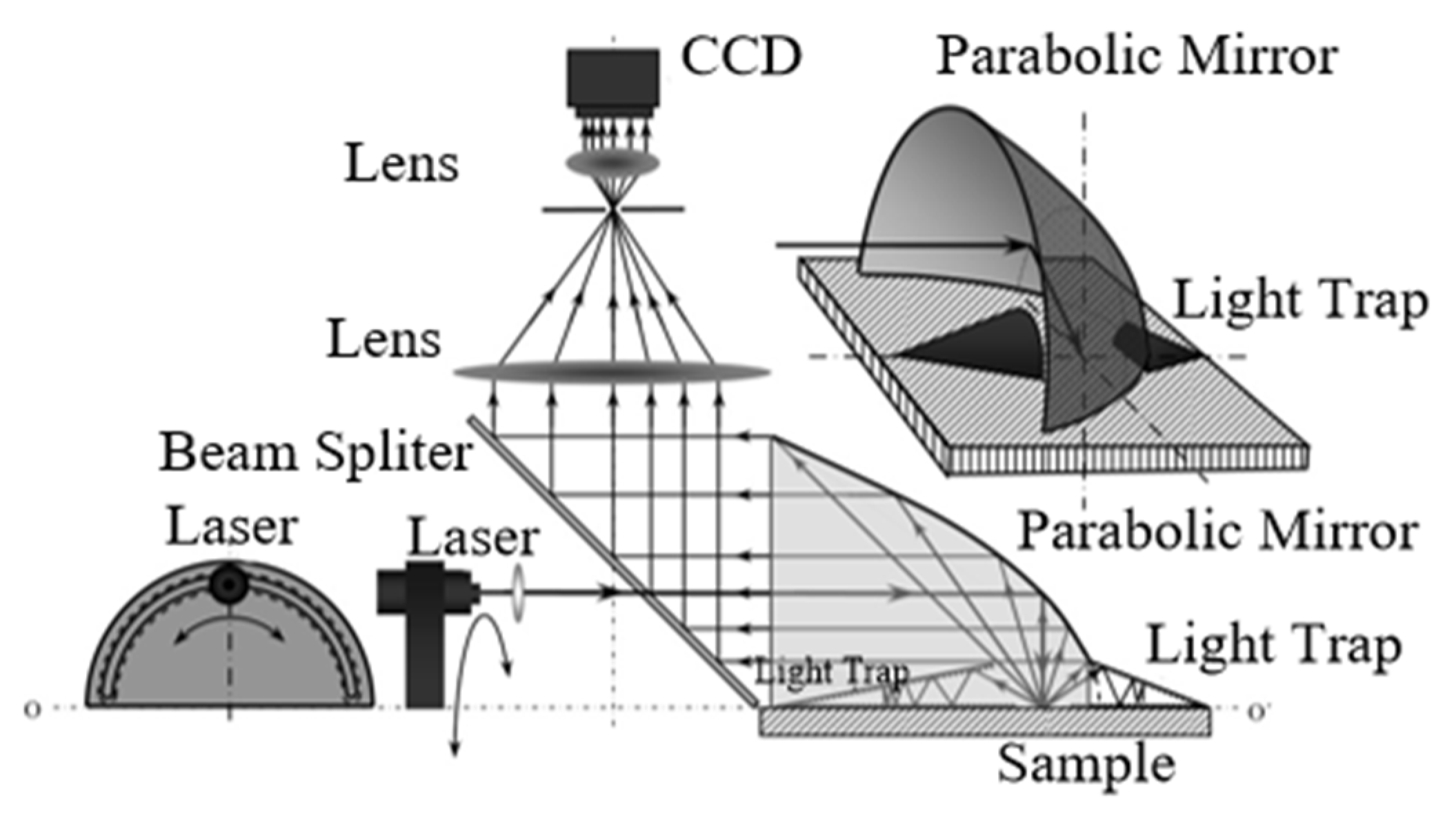

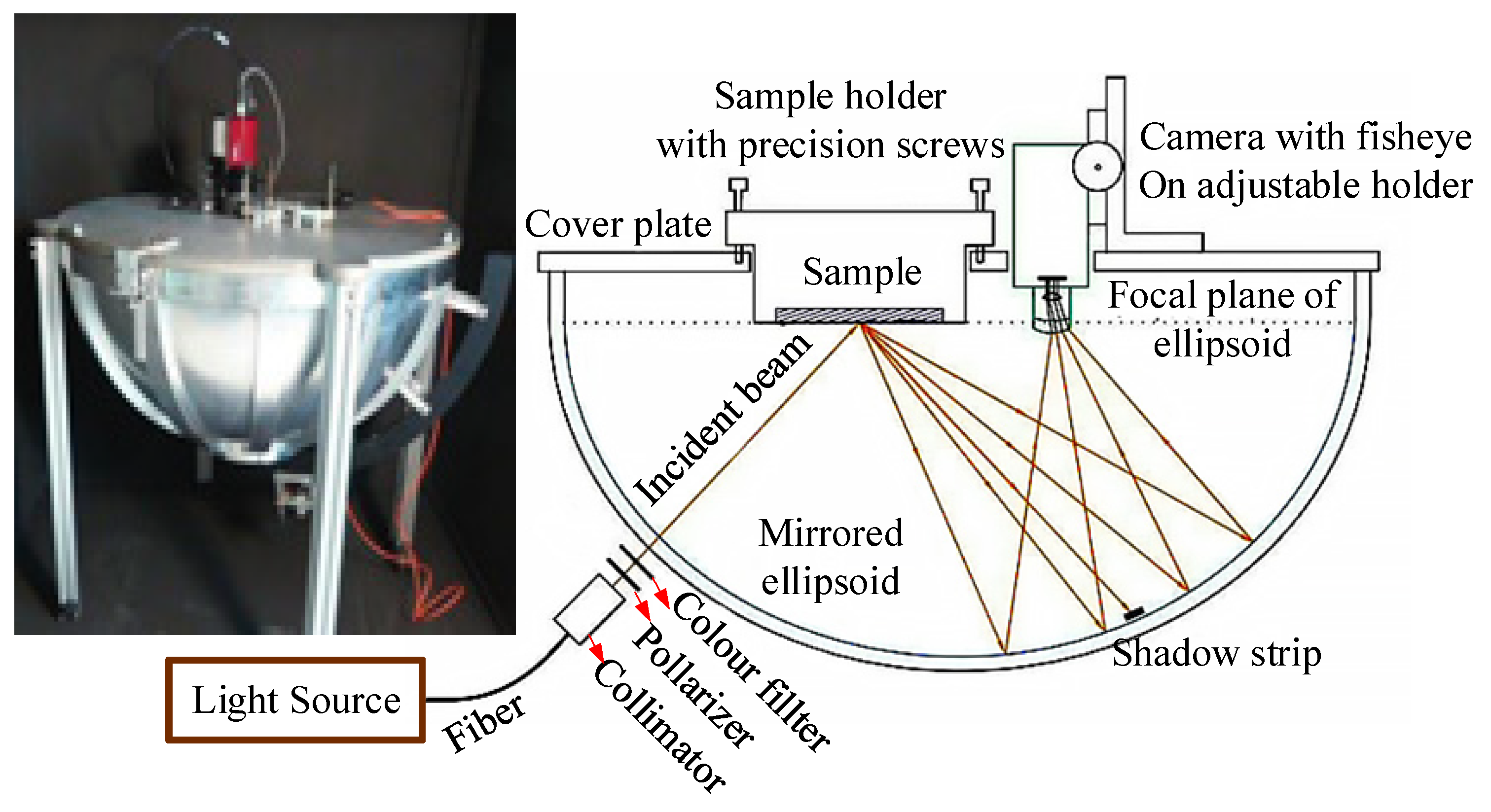

| Research Institute | Data Range | Resolution | Measurement Range | Measurement Mode |
|---|---|---|---|---|
| University of Minnesota (Figure 6) | Anisotropy and isotropy | Sampling interval: 10° | : 10–87° : 0–89° | Traditional measurement |
| Ariozona Center for Optics Sciences (Figure 7) | Anisotropy and isotropy | Sampling interval: 10° | : 0–60° : −40–80° | Traditional measurement |
| University of Colorado (Figure 8) | Anisotropy and isotropy | Minimum sampling interval: 0.5° | : ±86.5° : 0–360° : 0–78.3° : 0–360° | Traditional measurement |
| Houston Aviation (Figure 9) | Anisotropy and isotropy | Minimum sampling interval: 0.1° | : 5–78° : 0–180° : 0–180° | Traditional measurement |
| Lawrence Berkeley Laboratories (Figure 10) | Anisotropy and isotropy | Minimum sampling interval: 5° | : 0–60° : 0–90° : −90–90° | Fast measurement |
| Cornell University (Figure 11) | Isotropy | Sampling interval: 5° | : 0–85° : 0–85° | Traditional measurement |
| University of \Miami (Figure 12) | Anisotropy and isotropy | Sampling interval: 5° | : 5–65° : −180–180° : 5–65° : −180–180° | Fast measurement |
| Rutgers University (Figure 13) | Anisotropy and isotropy | -- | : −36.5–22.8° : −36.8–22.8° Reflected azimuth angle: 0–22.8° | Fast measurement |
| University of Florida (Figure 14) | Anisotropy and isotropy | Minimum sampling interval: 0.45° | : 0–88° : 0–88° : 0–180° | Traditional measurement |
| Cornell University (Figure 15) | Isotropy | Minimum sampling interval: 0.1° | : −85–85° : −85–85° : −85–85° : −85–85° | Traditional measurement |
| Harbin Institute of Technology (Figure 16) | Anisotropy and isotropy | Minimum sampling interval: 0.036° | : −90–90° : −90–90° : −55–55° : −180–180° | Traditional measurement |
| Osaka University (Figure 17) | Anisotropy and isotropy | Sampling interval: 1° | : 0.5–90°; −0.5–(−90°) : 27–180°; −27–(−180°) : 0.5–90°; −0.5–(−90°) : 27–180°; −27–(−180°) | Fast measurement |
| Microsoft Research Asia (Figure 18) | Anisotropy and isotropy | Minimum sampling interval: 30° | : −90–90° : −180–180° : −90–90° : −180–180° | Fast measurement |
| Institute for National Measurement Standards (Figure 19) | Anisotropy and isotropy | Minimum sampling interval: 0.125° | : −90–90° : −90–90° : −180–180° | Traditional measurement |
| Northwestern Polytechnical University (Figure 20) | Anisotropy and isotropy | Minimum sampling interval: 3° | : 5°, 45°, 80° : 0–85° : −180–180° | Fast measurement |
| Northwestern Polytechnical University (Figure 21) | Anisotropy and isotropy | -- | : −90–90° : −180–180° : −90–90° : −180–180° | Fast measurement |
| Fraunhofer Institute for Applied Optics and Precision Engineering (Figure 22) | Anisotropy and isotropy | Minimum sampling interval: 0.1° | : −90–90° : −90–90° : −180–180° | Traditional measurement |
| German Aerospace Design Center (Figure 23) | Anisotropy and isotropy | -- | : 6.5–45° : −90–90° : −180–180° | Fast measurement |
| Toshiba Corporation (Figure 24) | Anisotropy and isotropy | Sampling interval: 0.25° | -- | Fast measurement |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Zhang, L.; Zhang, J.; Li, B.; Lv, X. Developmental Trends in the Application and Measurement of the Bidirectional Reflection Distribution Function. Sensors 2022, 22, 1739. https://doi.org/10.3390/s22051739
Zou Y, Zhang L, Zhang J, Li B, Lv X. Developmental Trends in the Application and Measurement of the Bidirectional Reflection Distribution Function. Sensors. 2022; 22(5):1739. https://doi.org/10.3390/s22051739
Chicago/Turabian StyleZou, Yangyang, Liu Zhang, Jian Zhang, Bonan Li, and Xueying Lv. 2022. "Developmental Trends in the Application and Measurement of the Bidirectional Reflection Distribution Function" Sensors 22, no. 5: 1739. https://doi.org/10.3390/s22051739
APA StyleZou, Y., Zhang, L., Zhang, J., Li, B., & Lv, X. (2022). Developmental Trends in the Application and Measurement of the Bidirectional Reflection Distribution Function. Sensors, 22(5), 1739. https://doi.org/10.3390/s22051739






