Mid-Infrared Sensor Based on Dirac Semimetal Coupling Structure
Abstract
:1. Introduction
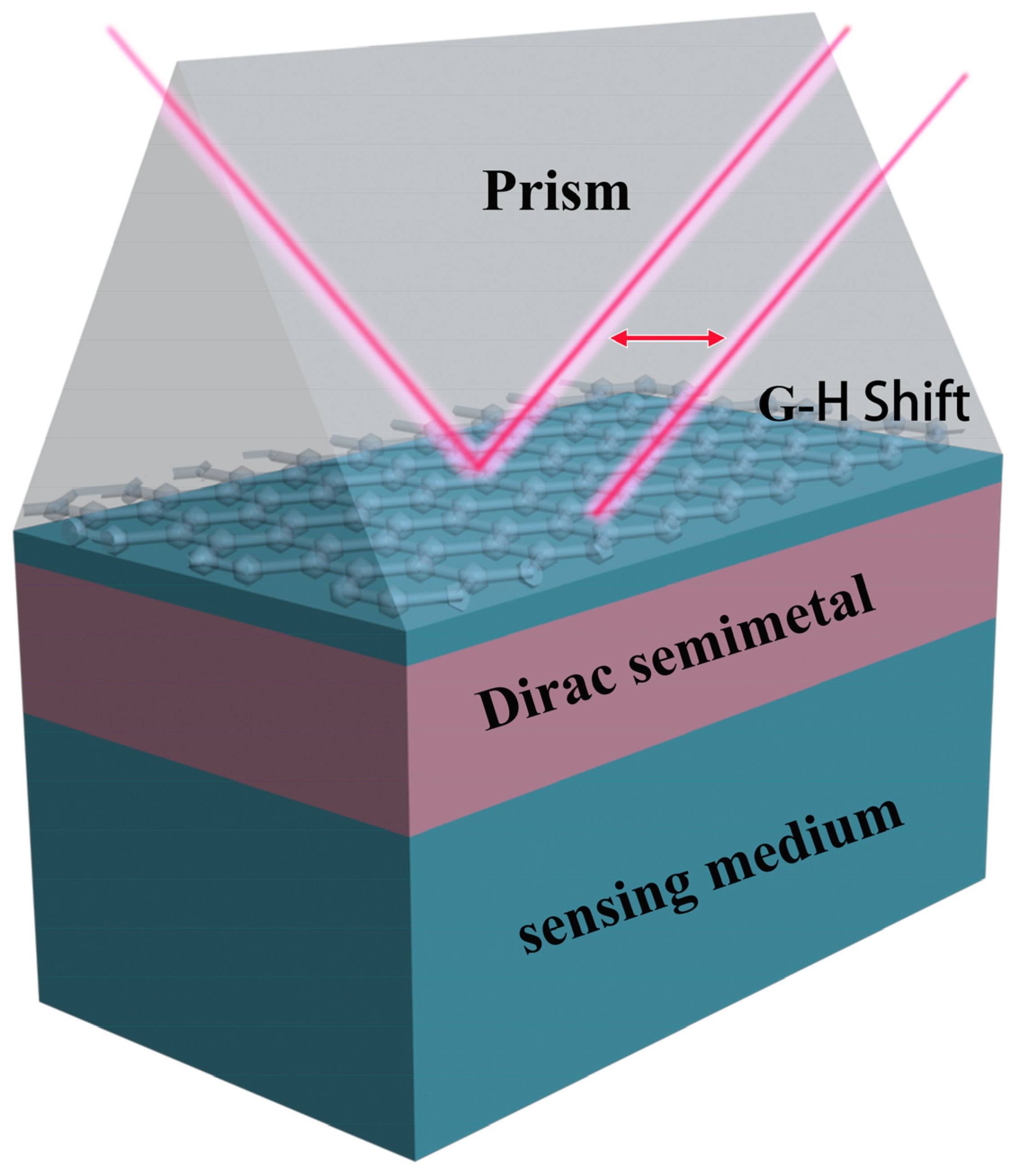
2. Theoretical Model and Method
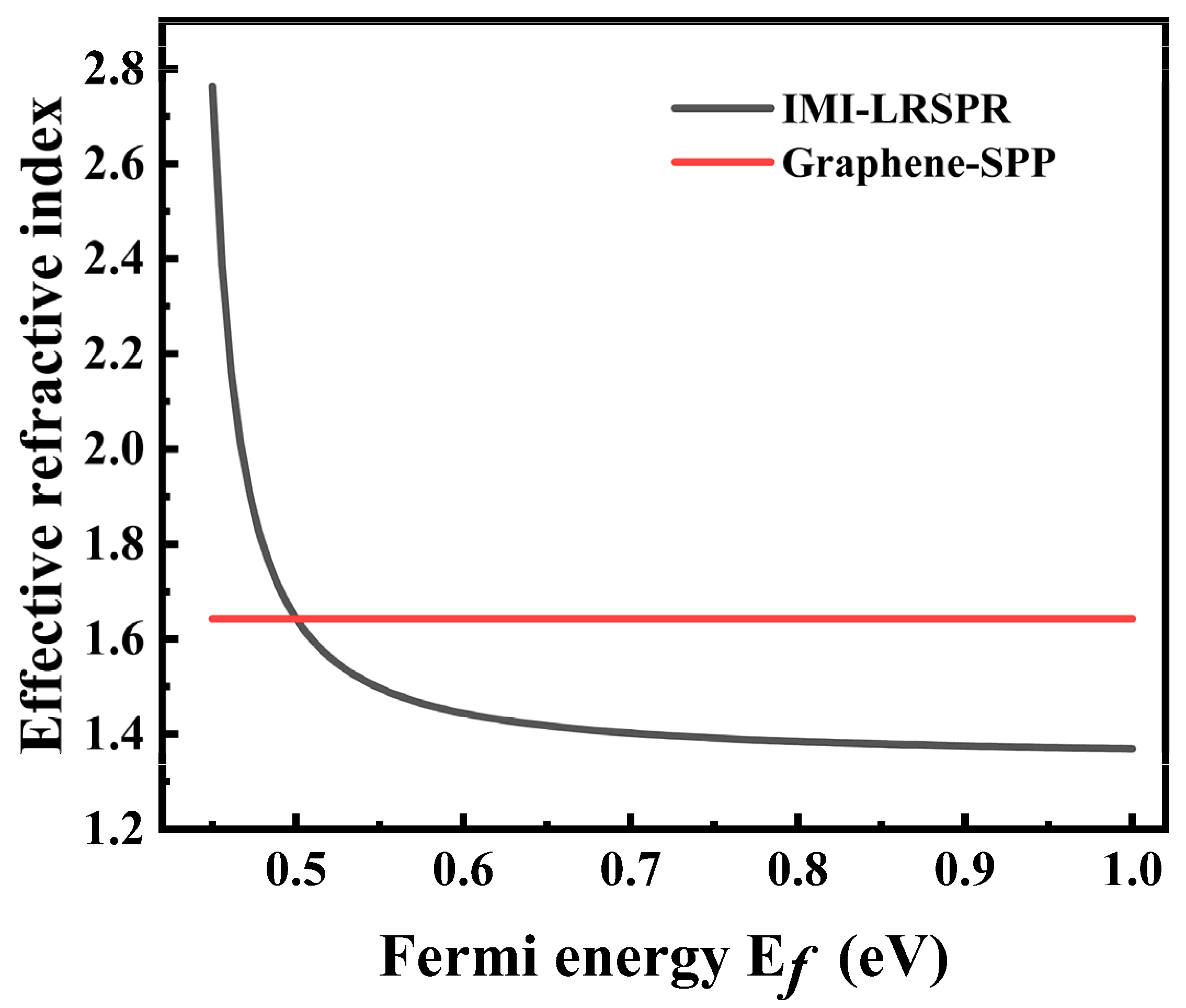
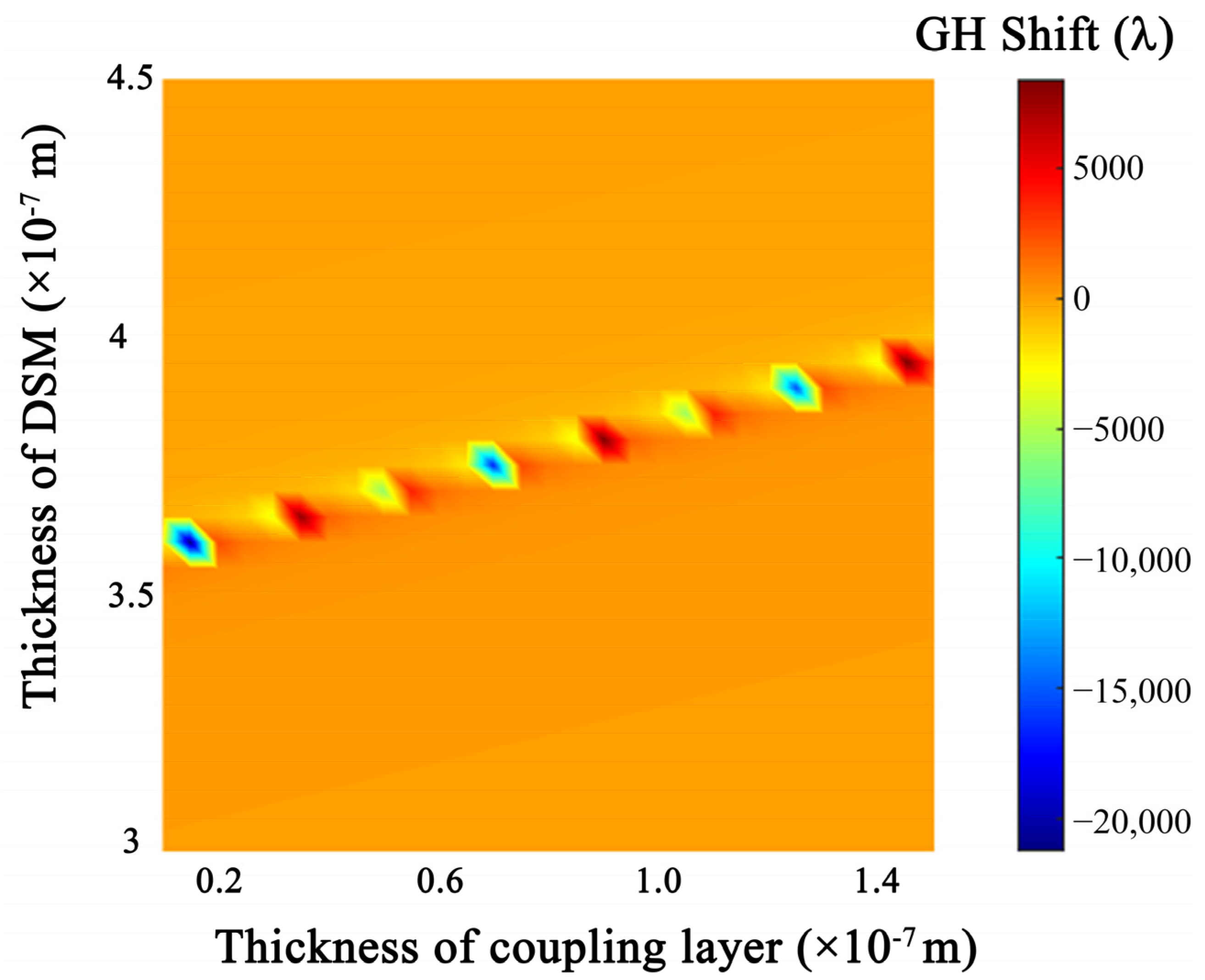
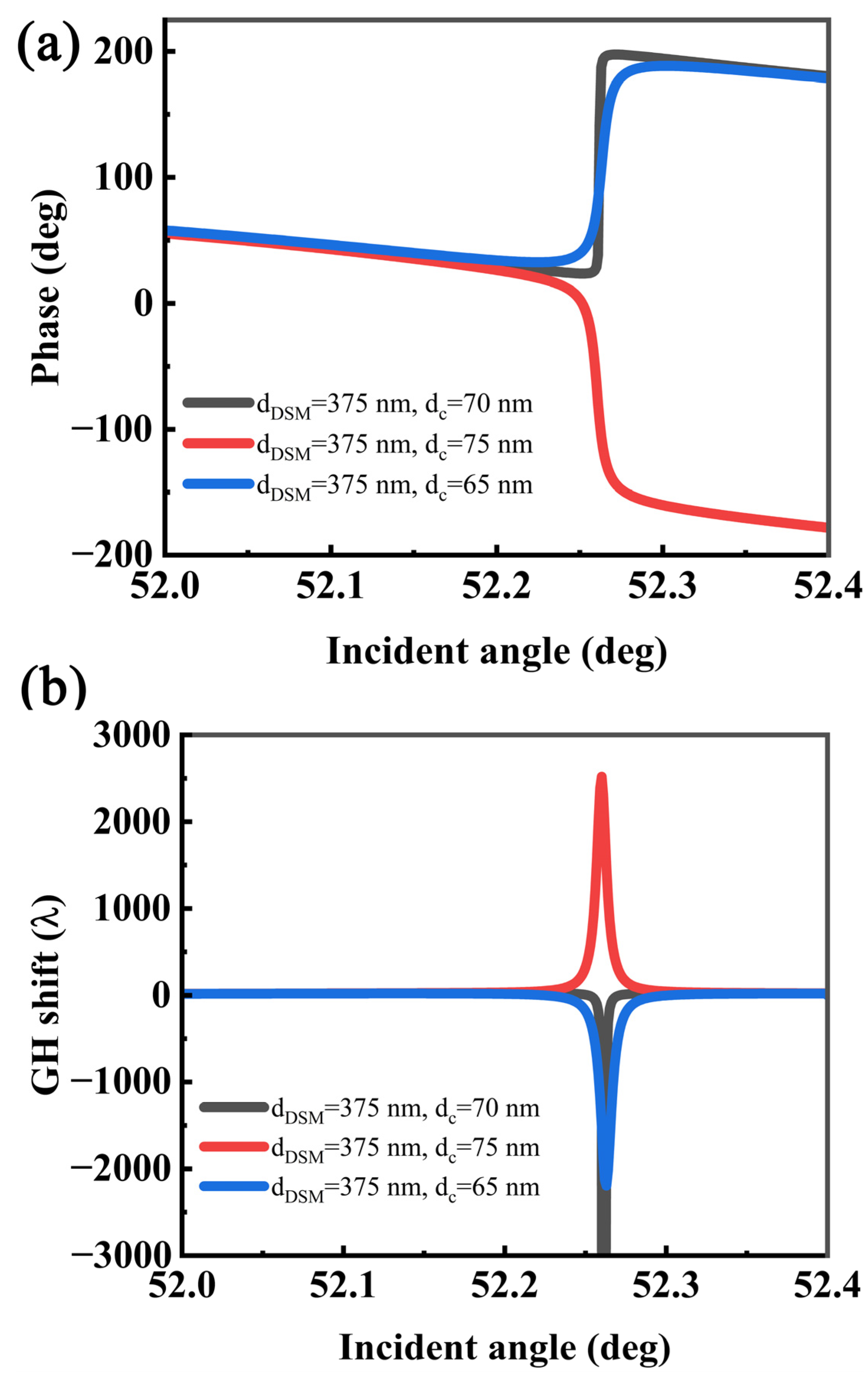
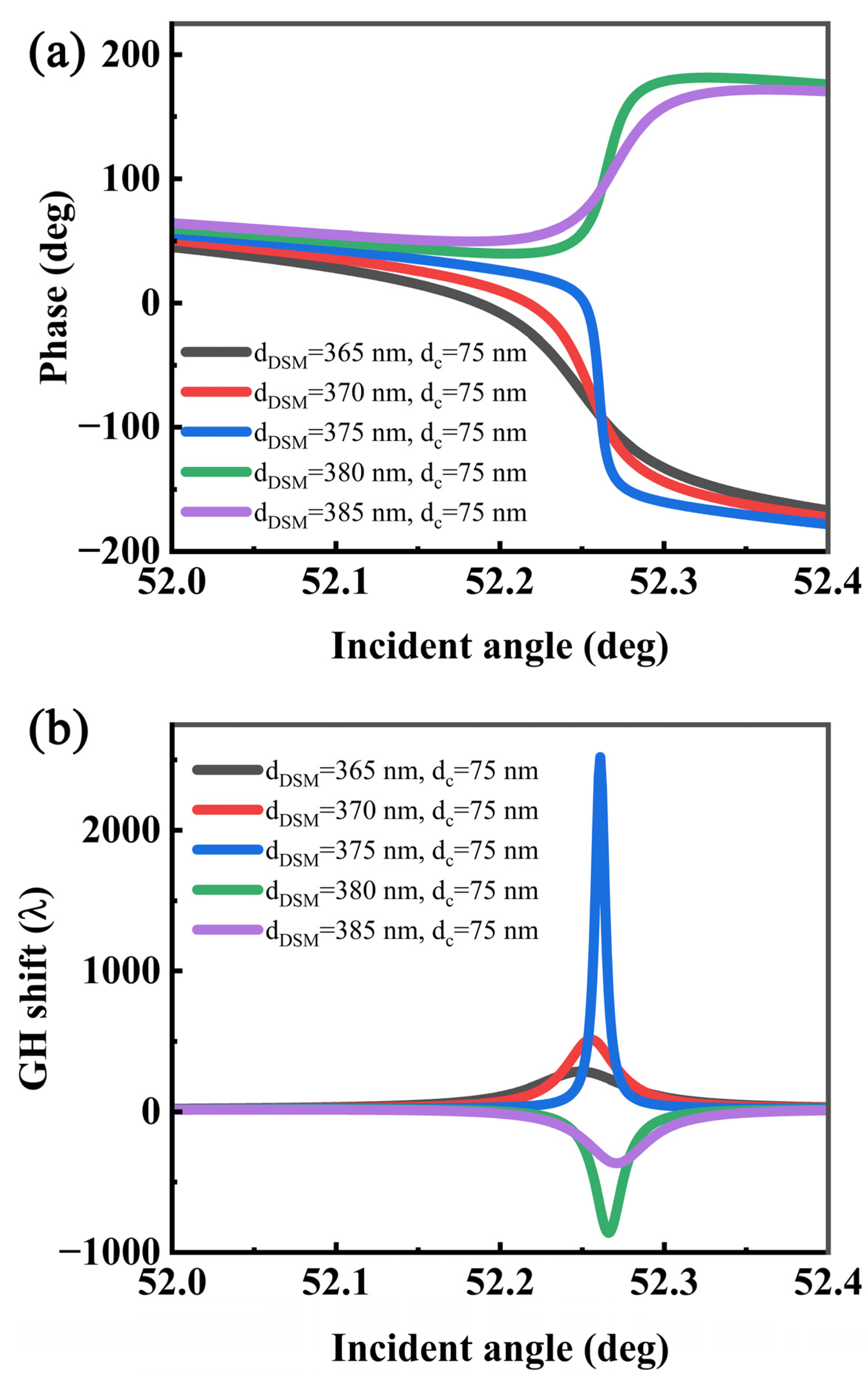
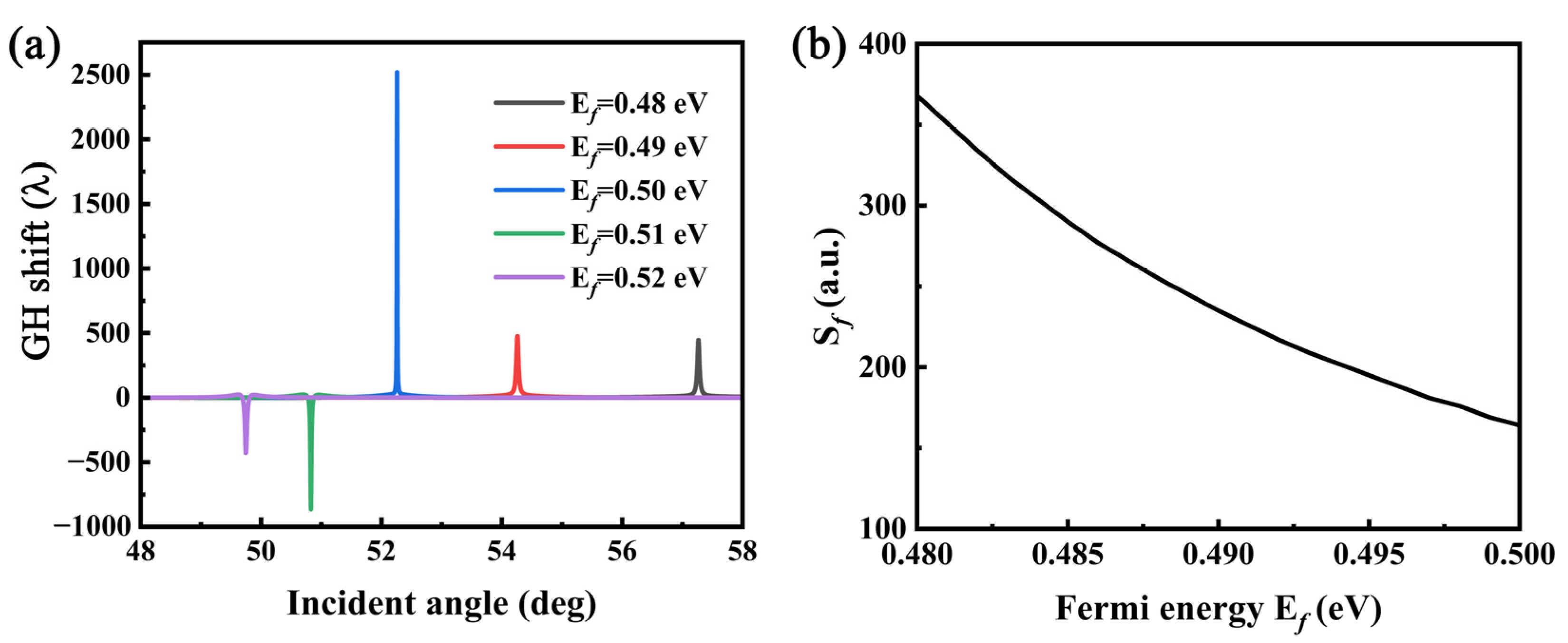
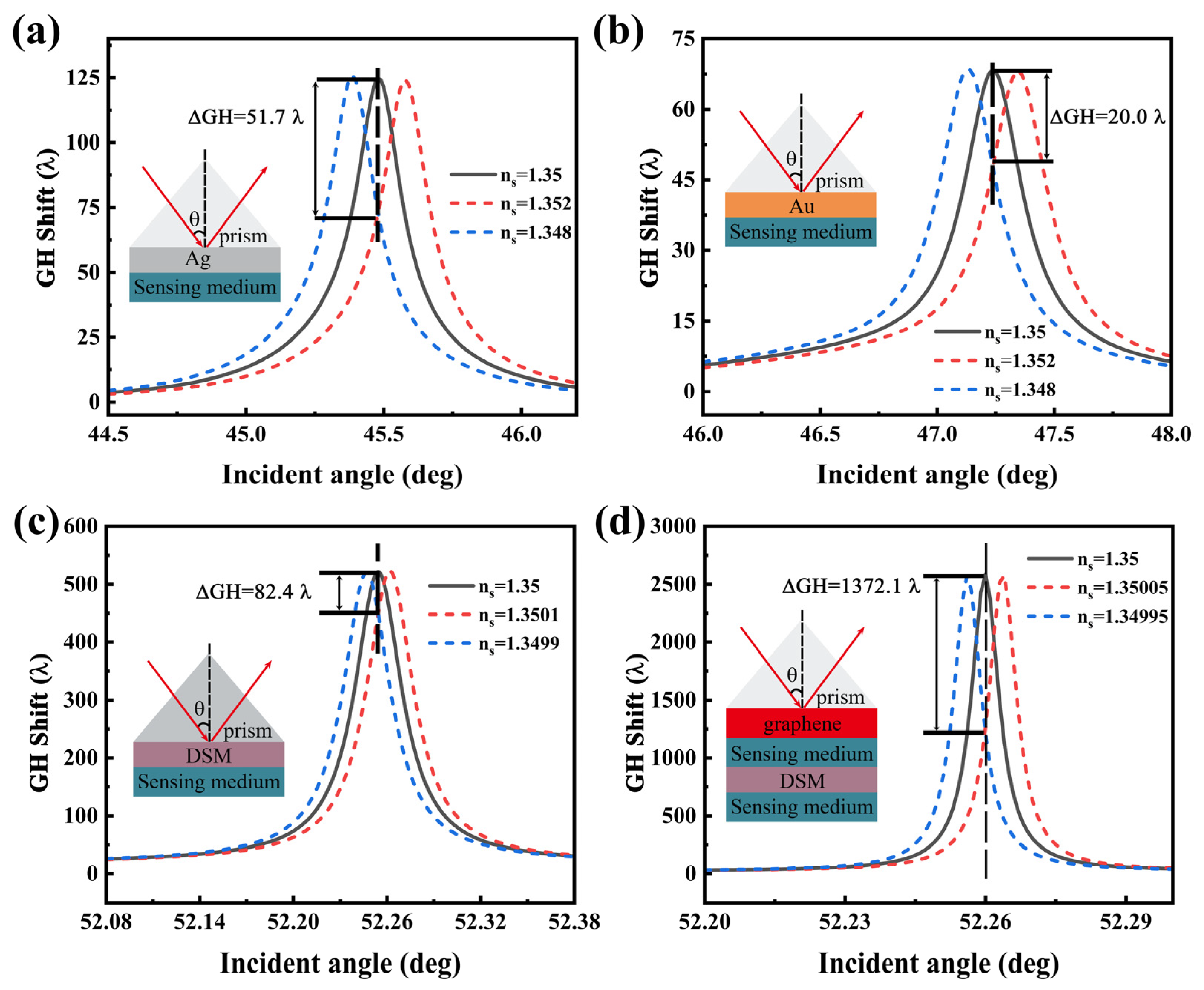
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Kane, C.L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 2008, 100, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.L.; Sankar, R.; Chang, G.Q.; Yuan, Z.J.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [Green Version]
- Lv, B.Q.; Feng, Z.L.; Xu, Q.N.; Gao, X.; Ma, J.Z.; Kong, L.Y.; Richard, P.; Huang, Y.B.; Strocov, V.N.; Fang, C.; et al. Observation of three-component fermions in the topological semimetal molybdenum phosphide. Nature 2017, 546, 627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weng, H.M.; Dai, X.; Fang, Z. Topological semimetals predicted from first-principles calculations. J. Phys.-Condes. Matter 2016, 28. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.H.; Wang, F.Q.; Meng, Y.F.; Yuan, X.; Xiu, F.X.; Luo, H.Y.; Wang, Y.Z.; Li, J.F.; Lv, X.J.; He, L.; et al. A robust and tuneable mid-infrared optical switch enabled by bulk Dirac fermions. Nat. Commun. 2017, 8, 7. [Google Scholar] [CrossRef]
- Xu, H.; Guo, C.; Zhang, J.Z.; Guo, W.L.; Hu, W.D.; Wang, L.; Chen, G.; Chen, X.S.; Lu, W. PtTe2-Based Type-II Dirac Semimetal and Its van der Waals Heterostructure for Sensitive Room Temperature Terahertz Photodetection. Small 2019, 15, 7. [Google Scholar] [CrossRef]
- Leonard, F.; Yu, W.L.; Collins, K.C.; Medlin, D.L.; Sugar, J.D.; Talin, A.A.; Pan, W. Strong Photothermoelectric Response and Contact Reactivity of the Dirac Semimetal ZrTe5. Acs Appl. Mater. Interfaces 2017, 9, 37041–37047. [Google Scholar] [CrossRef]
- Nguyen, D.A.; Park, D.Y.; Lee, J.; Duong, N.T.; Park, C.; Nguyen, D.H.; Le, T.S.; Suh, D.; Yang, H.; Jeong, M.S. Patterning of type-II Dirac semimetal PtTe2 for optimized interface of tellurene optoelectronic device. Nano Energy 2021, 86, 10. [Google Scholar] [CrossRef]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Peng, H.; Dudin, P.; et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kushwaha, S.K.; Krizan, J.W.; Feldman, B.E.; Gyenis, A.; Randeria, M.T.; Xiong, J.; Xu, S.Y.; Alidoust, N.; Belopolski, I.; Liang, T.; et al. Bulk crystal growth and electronic characterization of the 3D Dirac semimetal Na3Bi. APL Mater. 2015, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Neupane, M.; Xu, S.Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.R.; Jeng, H.T.; Lin, H.; et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 2014, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.S.; Li, C.Z.; Ge, S.F.; Li, J.G.; Lu, W.; Lai, J.W.; Liu, X.F.; Ma, J.C.; Yu, D.P.; Liao, Z.M.; et al. Ultrafast Broadband Photodetectors Based on Three-Dimensional Dirac Semimetal Cd3As2. Nano Lett. 2017, 17, 834–841. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.F.; Zhu, C.H.; Li, Y.; Yuan, X.; Xiu, F.X.; Shi, Y.; Xu, Y.B.; Wang, F.Q. Three-dimensional Dirac semimetal thin-film absorber for broadband pulse generation in the near-infrared. Opt. Lett. 2018, 43, 1503–1506. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.P.; Osgood, R.M.; Vlasov, Y.A.; Green, W.M.J. Mid-infrared optical parametric amplifier using silicon nanophotonic waveguides. Nat. Photonics 2010, 4, 557–560. [Google Scholar] [CrossRef]
- Long, M.S.; Gao, A.Y.; Wang, P.; Xia, H.; Ott, C.; Pan, C.; Fu, Y.J.; Liu, E.F.; Chen, X.S.; Lu, W.; et al. Room temperature high-detectivity mid-infrared photodetectors based on black arsenic phosphorus. Sci. Adv. 2017, 3, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dam, J.S.; Tidemand-Lichtenberg, P.; Pedersen, C. Room-temperature mid-infrared single-photon spectral imaging. Nat. Photonics 2012, 6, 788–793. [Google Scholar] [CrossRef] [Green Version]
- Chau, Y.F.C. Mid-infrared sensing properties of a plasmonic metal-insulator-metal waveguide with a single stub including defects. J. Phys. D-Appl. Phys. 2020, 53, 8. [Google Scholar] [CrossRef]
- Ye, Y.Y.; Xie, M.Z.; Ouyang, J.X.; Tang, J. Tunable mid-infrared refractive index sensor with high angular sensitivity and ultra-high figure-of-merit based on Dirac semimetal. Results Phys. 2020, 17, 6. [Google Scholar] [CrossRef]
- You, Q.; Li, Z.F.; Jiang, L.Y.; Guo, J.; Dai, X.Y.; Xiang, Y.J. Giant tunable Goos-Hanchen shifts based on surface plasmon resonance with Dirac semimetal films. J. Phys. D-Appl. Phys. 2020, 53, 7. [Google Scholar] [CrossRef]
- Kim, J.; Baik, S.S.; Ryu, S.H.; Sohn, Y.; Park, S.; Park, B.G.; Denlinger, J.; Yi, Y.; Choi, H.J.; Kim, K.S. Observation of tunable band gap and anisotropic Dirac semimetal state in black phosphorus. Science 2015, 349, 723–726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, H.; Wu, M.M.; Liu, Y.; Yang, S.A. Electric control of topological phase transitions in Dirac semimetal thin films. Sci. Rep. 2015, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.F.; Chen, P.; Li, B.; Li, J.; Ai, R.Q.; Zhang, Z.W.; Sun, G.Z.; Yao, K.K.; Lin, Z.Y.; Zhao, B.; et al. Thickness-Tunable Synthesis of Ultrathin Type-II Dirac Semimetal PtTe2 Single Crystals and Their Thickness-Dependent Electronic Properties. Nano Lett. 2018, 18, 3523–3529. [Google Scholar] [CrossRef]
- Luo, C.Y.; Guo, J.; Wang, Q.K.; Xiang, Y.J.; Wen, S.C. Electrically controlled Goos-Hanchen shift of a light beam reflected from the metal-insulator-semiconductor structure. Opt. Express 2013, 21, 10430–10439. [Google Scholar] [CrossRef]
- Cao, H.; Wiersig, J. Dielectric microcavities: Model systems for wave chaos and non-Hermitian physics. Rev. Mod. Phys. 2015, 87, 61–111. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zeng, S.W.; Crunteanu, A.; Xie, Z.M.; Humbert, G.; Ma, L.B.; Wei, Y.Y.; Brunel, A.; Bessette, B.; Orlianges, J.C.; et al. Targeted Sub-Attomole Cancer Biomarker Detection Based on Phase Singularity 2D Nanomaterial-Enhanced Plasmonic Biosensor. Nano-Micro Lett. 2021, 13, 11. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.B.; Hesselink, L. Goos-Hanchen shift surface plasmon resonance sensor. Appl. Phys. Lett. 2006, 89, 3. [Google Scholar] [CrossRef]
- Farmani, H.; Farmani, A.; Biglari, Z. A label-free graphene-based nanosensor using surface plasmon resonance for biomaterials detection. Phys. E 2020, 116, 9. [Google Scholar] [CrossRef]
- Qin, Z.R.; Yue, C.; Lang, Y.P.; Liu, Q.G. Enhancement of spin components’ shifts of reflected beam via long range surface plasmon resonance. Opt. Commun. 2018, 426, 16–22. [Google Scholar] [CrossRef]
- Wan, R.G.; Zubairy, M.S. Tunable and enhanced Goos-Hanchen shift via surface plasmon resonance assisted by a coherent medium. Opt. Express 2020, 28, 6036–6047. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.H.; Lu, F.Y.; Jiang, L.Y.; Lin, W.; Zheng, Z.W. Tunable Goos-Hanchen Shift Surface Plasmon Resonance Sensor Based on Graphene-hBN Heterostructure. Biosensors 2021, 11, 201. [Google Scholar] [CrossRef] [PubMed]
- You, Q.; Zhu, J.Q.; Guo, J.; Wu, L.M.; Dai, X.Y.; Xiang, Y.J. Giant Goos-Hanchen shifts of waveguide coupled long-range surface plasmon resonance mode. Chin. Phys. B 2018, 27, 5. [Google Scholar] [CrossRef]
- Cennamo, N.; Massarotti, D.; Conte, L.; Zeni, L. Low Cost Sensors Based on SPR in a Plastic Optical Fiber for Biosensor Implementation. Sensors 2011, 11, 11752–11760. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.J.; Li, S.G.; Wang, X.Y.; Shi, M.; Feng, X.X.; Liu, Y.D. Ultrahigh sensitivity refractive index sensor of a D-shaped PCF based on surface plasmon resonance. Appl. Opt. 2018, 57, 4002–4007. [Google Scholar] [CrossRef] [PubMed]
- Rahman-Zadeh, F.; Danaie, M.; Kaatuzian, H. Design of a highly sensitive photonic crystal refractive index sensor incorporating ring-shaped GaAs cavity. Opto-Electron. Rev. 2019, 27, 369–377. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Hameed, M.F.O.; Elkaramany, E.M.A.; Obayya, S.S.A. Highly Sensitive Terahertz Metamaterial Sensor. Ieee Sens. J. 2019, 19, 7993–7999. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Jalil, R.; Britnell, L.; Gorbachev, R.V.; Ansell, D.; Thackray, B.; Novoselov, K.S.; Geim, A.K.; Kabashin, A.V.; et al. Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection. Nat. Mater. 2013, 12, 304–309. [Google Scholar] [CrossRef]
- Hwang, E.H.; Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 2007, 75, 6. [Google Scholar] [CrossRef] [Green Version]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 8. [Google Scholar] [CrossRef] [Green Version]
- Alaee, R.; Farhat, M.; Rockstuhl, C.; Lederer, F. A perfect absorber made of a graphene micro-ribbon metamaterial. Opt. Express 2012, 20, 28017–28024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kotov, O.V.; Lozovik, Y.E. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys. Rev. B 2016, 93, 11. [Google Scholar] [CrossRef] [Green Version]
- Passler, N.C.; Paarmann, A. Generalized 4 x 4 matrix formalism for light propagation in anisotropic stratified media: Study of surface phonon polaritons in polar dielectric heterostructures. J. Opt. Soc. Am. B-Opt. Phys. 2017, 34, 2128–2139. [Google Scholar] [CrossRef] [Green Version]
- Yeh, P. Electromagnetic propagation in birefringent layered media. J. Opt. Soc. Am. 1979, 69, 742–756. [Google Scholar] [CrossRef]
- Li, C.F. Negative lateral shift of a light beam transmitted through a dielectric slab and interaction of boundary effects. Phys. Rev. Lett. 2003, 91, 4. [Google Scholar] [CrossRef]
- Chen, L.; Liu, X.B.; Cao, Z.Q.; Zhuang, S.L. Mechanism of giant Goos-Hanchen effect enhanced by long-range surface plasmon excitation. J. Opt. 2011, 13, 8. [Google Scholar] [CrossRef]
- Nishihaya, S.; Uchida, M.; Nakazawa, Y.; Kriener, M.; Kozuka, Y.; Taguchi, Y.; Kawasaki, M. Gate-tuned quantum Hall states in Dirac semimetal (Cd1-xZnx)(3)As-2. Sci. Adv. 2018, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, P.P.; Manesco, A.L.R.; Dorini, T.T.; Correa, L.E.; Weber, G.; Machado, A.J.S.; Eleno, L.T.F. Strain engineering the topological type-II Dirac semimetal NiTe2. Phys. Rev. B 2021, 103, 13. [Google Scholar] [CrossRef]
- Hellerstedt, J.; Yudhistira, I.; Edmonds, M.T.; Liu, C.; Collins, J.; Adam, S.; Fuhrer, M.S. Electrostatic modulation of the electronic properties of Dirac semimetal Na3Bi thin films. Phys. Rev. Mater. 2017, 1, 5. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.Y.; Huang, T.J.; Yin, L.Z.; Han, F.Y.; Liu, P.K. High Sensitivity Terahertz Biosensor Based on Goos-Hanchen Effect in Graphene. IEEE Photonics J. 2020, 12, 6. [Google Scholar] [CrossRef]
- Guo, X.Y.; Liu, X.H.; Zhu, W.G.; Gao, M.X.; Long, W.J.; Yu, J.H.; Zheng, H.D.; Guan, H.Y.; Luo, Y.H.; Lu, H.H.; et al. Surface plasmon resonance enhanced Goos-Hanchen and Imbert-Fedorov shifts of Laguerre-Gaussian beams. Opt. Commun. 2019, 445, 5–9. [Google Scholar] [CrossRef]
- Han, L.; Li, K.L.; Wu, C. Comparison of the Goos-Hanchen Shift Induced by Surface Plasmon Resonance in Metal-MoSe2-Graphene Structure. Plasmonics 2020, 15, 2195–2203. [Google Scholar] [CrossRef]
- Tang, T.T.; Li, J.; Luo, L.; Shen, J.; Li, C.Y.; Qin, J.; Bi, L.; Hou, J.Y. Weak measurement of magneto-optical Goos-Hanchen effect. Opt. Express 2019, 27, 17638–17647. [Google Scholar] [CrossRef] [PubMed]
- Ji, Q.Z.; Yan, B.; Han, L.; Wang, J.; Yang, M.; Wu, C. Theoretical investigation of an enhanced Goos-Hanchen shift sensor based on a BlueP/TMDC/graphene hybrid. Appl. Opt. 2020, 59, 8355–8361. [Google Scholar] [CrossRef] [PubMed]
- You, Q.; Shan, Y.X.; Gan, S.W.; Zhao, Y.T.; Dai, X.Y.; Xiang, Y.J. Giant and controllable Goos-Hanchen shifts based on surface plasmon resonance with graphene-MoS2 heterostructure. Opt. Mater. Express 2018, 8, 3036–3048. [Google Scholar] [CrossRef]
- Han, L.; Pan, J.X.; Wu, C.; Li, K.L.; Ding, H.F.; Ji, Q.Z.; Yang, M.; Wang, J.; Zhang, H.J.; Huang, T.Y. Giant Goos-Hanchen Shifts in Au-ITO-TMDCs-Graphene Heterostructure and Its Potential for High Performance Sensor. Sensors 2020, 20, 1028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, J.; Jiang, L.Y.; Dai, X.Y.; Xiang, Y.J. Tunable Fano resonances of a graphene/waveguide hybrid structure at mid-infrared wavelength. Opt. Express 2016, 24, 4740–4748. [Google Scholar] [CrossRef]
- Tang, J.; Xu, J.; Zheng, Z.W.; Dong, H.; Dong, J.; Qian, S.Y.; Guo, J.; Jiang, L.Y.; Xiang, Y.J. Graphene Tamm plasmon-induced giant Goos-Hanchen shift at terahertz frequencies. Chin. Opt. Lett. 2019, 17, 6. [Google Scholar] [CrossRef]



| Materials | Wavelength | References | ||
|---|---|---|---|---|
| Au | 632.8 nm | 12.5 | - | [54] |
| Cu-BlueP/WS2-graphene | 632.8 nm | 1004 | [55] | |
| Au-MoS2/graphene | 632.8 nm | 235.8 | [56] | |
| Au-ITO-MoS2/graphene | 632.8 nm | 801.7 | [57] | |
| Ag-Au-hBN-graphene | 632.8 nm | 182.1 | [32] | |
| DSM | 8.9 um | 361.4 | - | [21] |
| Graphene-planar waveguide | 10.6 um | less than −500 | - | [58] |
| Graphene-photonic crystals | 300 um | Less than −2000 | - | [59] |
| Graphene-medium-DSM-medium | 2.5 um | More than 2500 | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Liu, Y.; Song, G. Mid-Infrared Sensor Based on Dirac Semimetal Coupling Structure. Sensors 2022, 22, 2116. https://doi.org/10.3390/s22062116
Zou Y, Liu Y, Song G. Mid-Infrared Sensor Based on Dirac Semimetal Coupling Structure. Sensors. 2022; 22(6):2116. https://doi.org/10.3390/s22062116
Chicago/Turabian StyleZou, Yuxiao, Ying Liu, and Guofeng Song. 2022. "Mid-Infrared Sensor Based on Dirac Semimetal Coupling Structure" Sensors 22, no. 6: 2116. https://doi.org/10.3390/s22062116
APA StyleZou, Y., Liu, Y., & Song, G. (2022). Mid-Infrared Sensor Based on Dirac Semimetal Coupling Structure. Sensors, 22(6), 2116. https://doi.org/10.3390/s22062116





