Structural Damage Detection through EMI and Wave Propagation Techniques Using Embedded PZT Smart Sensing Units
Abstract
:1. Introduction
2. Mathematical Framework on EMI Technique
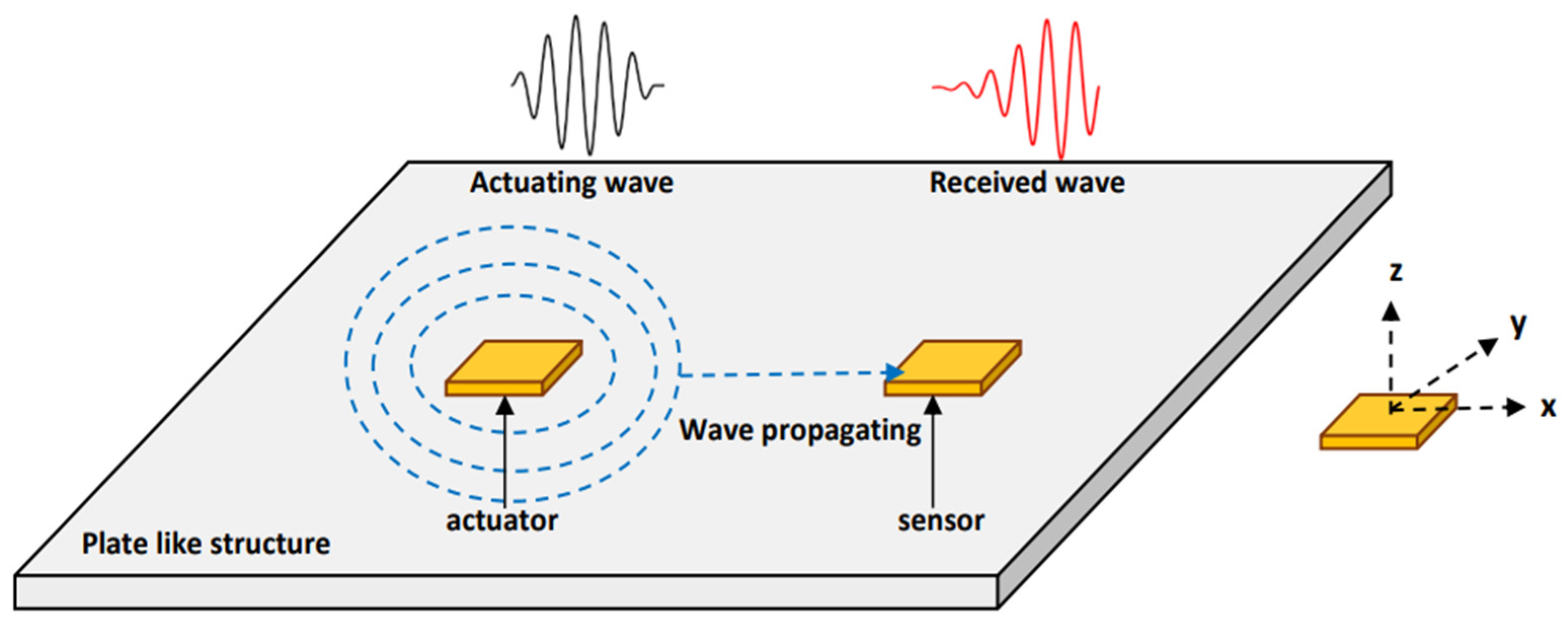
3. PZT Transducers for Understanding Wave Propagation Mechanics
4. Numerical Simulations Using the EMI Technique
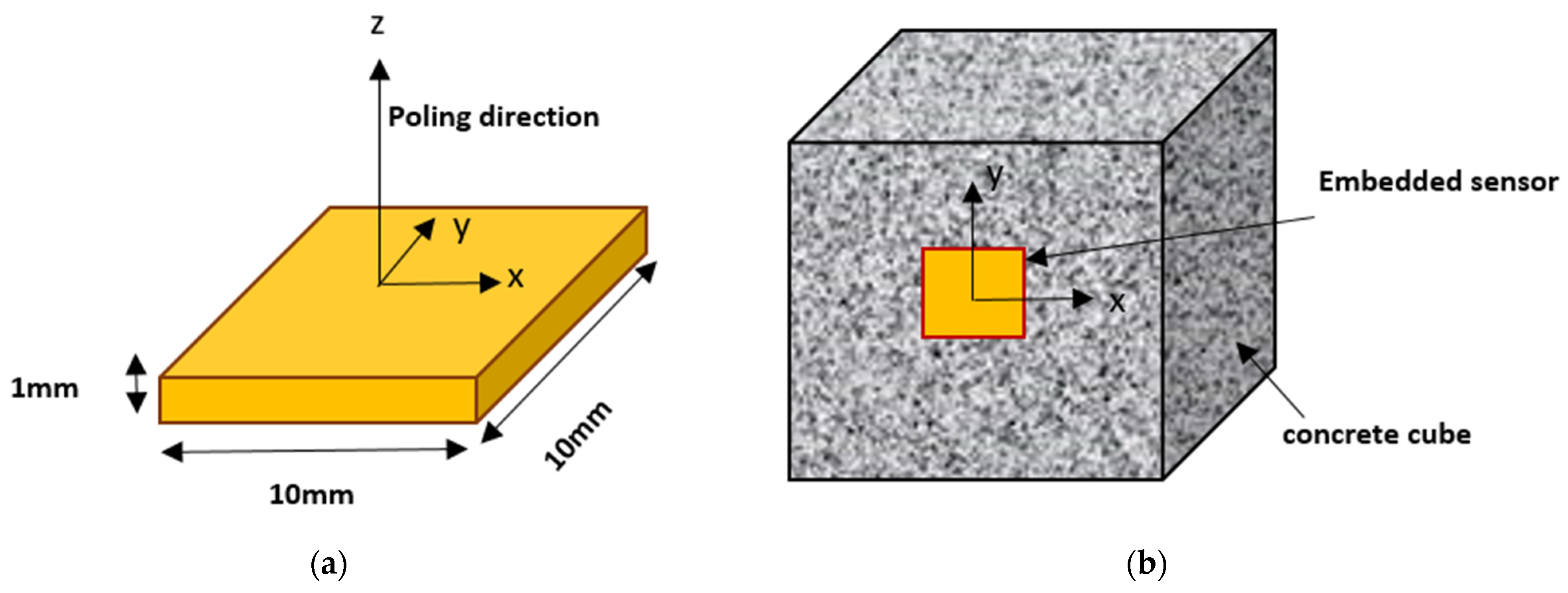
5. Modeling of Smart Sensing Units
6. Numerical Simulations Using Wave Propagation Technique
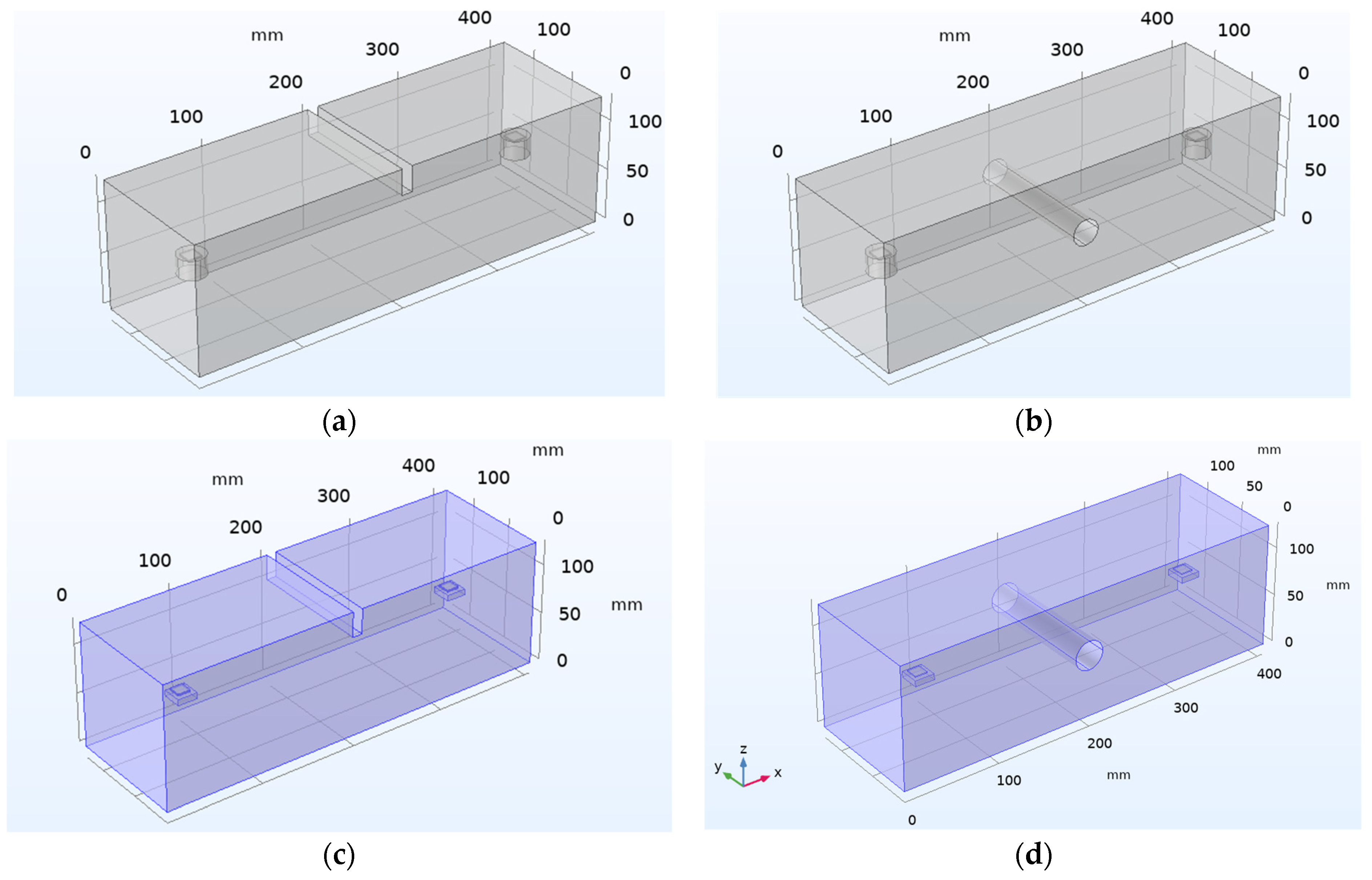
- Undamaged concrete beam with surface-mounted PZT patches;
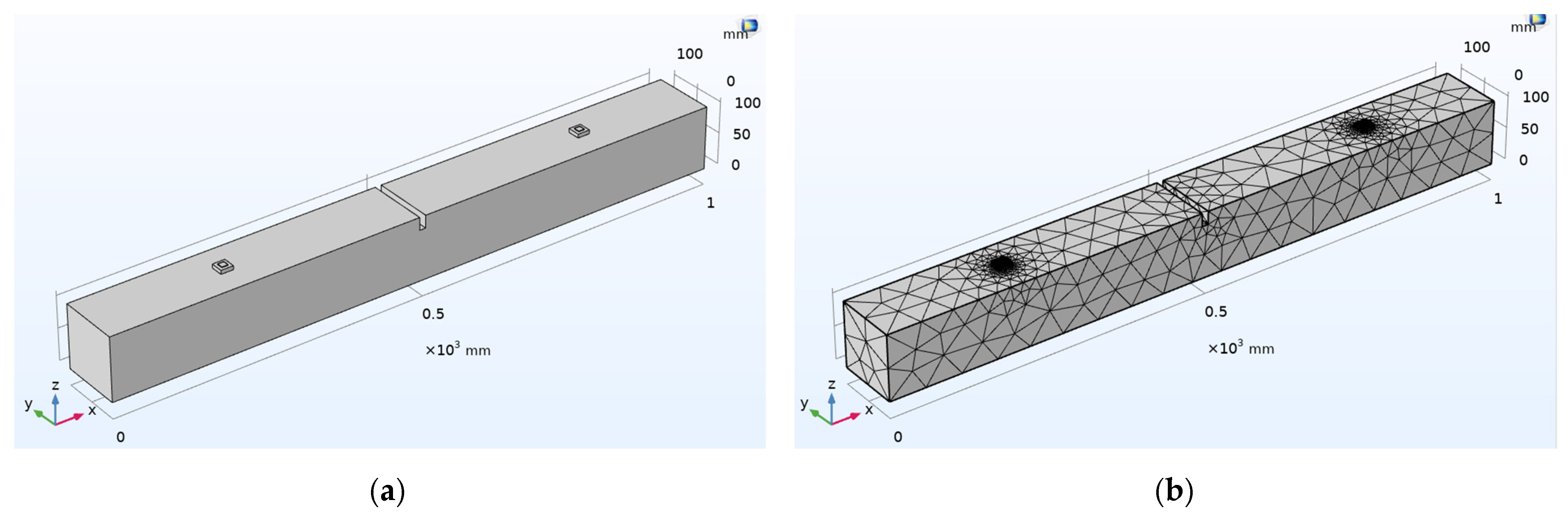
- Damaged concrete beam with surface-mounted PZT patches;
- Undamaged concrete beam with surface-mounted SSUs;
- Damaged concrete beam with surface-mounted SSUs;
- Undamaged concrete beam with embedded SSUs;
- Damaged concrete beam with embedded SSUs.
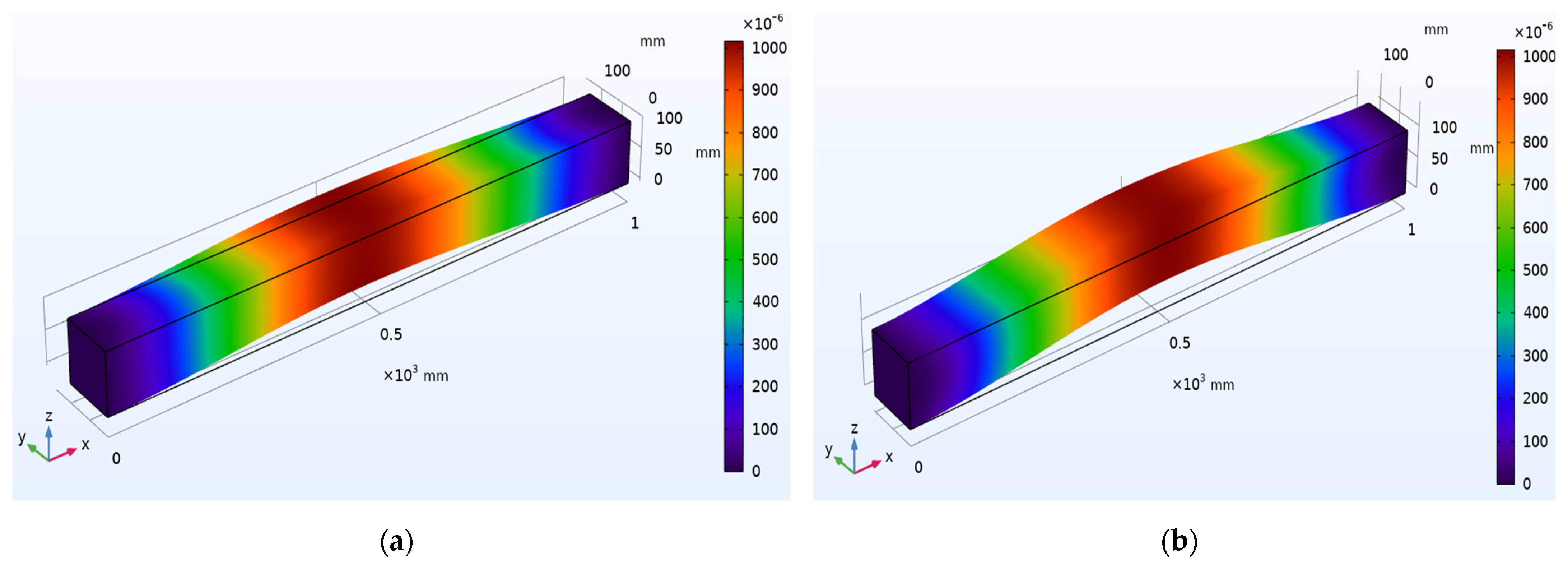
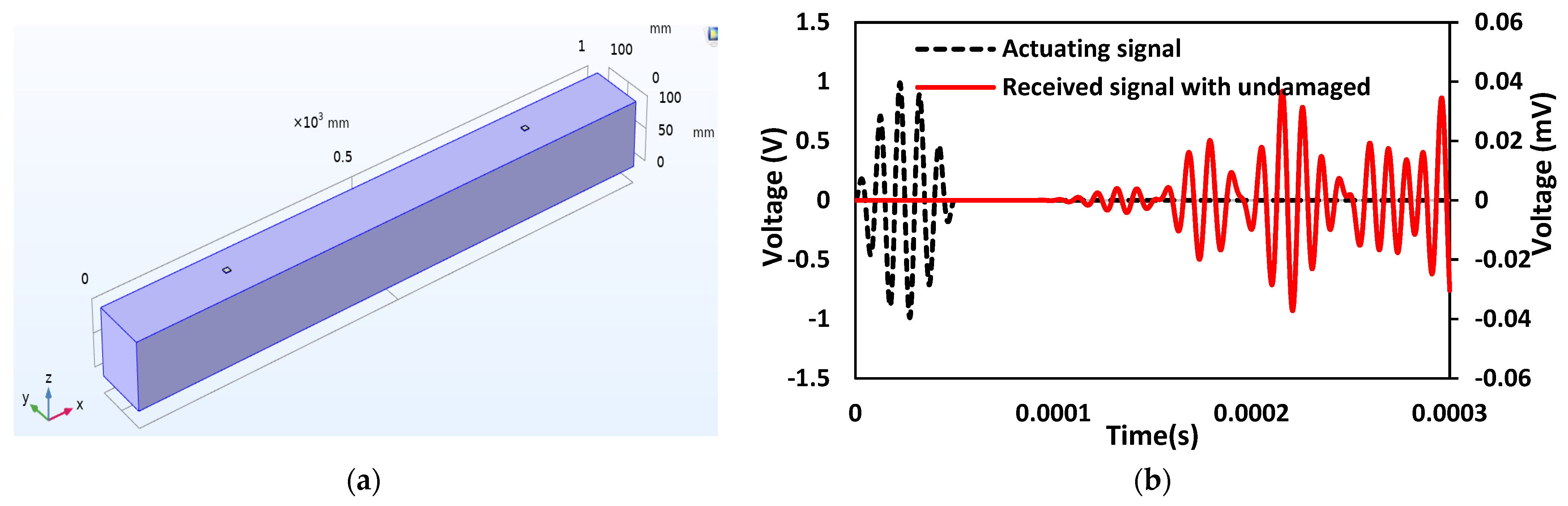
6.1. Case 1: Investigation on the Undamaged Concrete Beam with Surface-Mounted PZT Patches
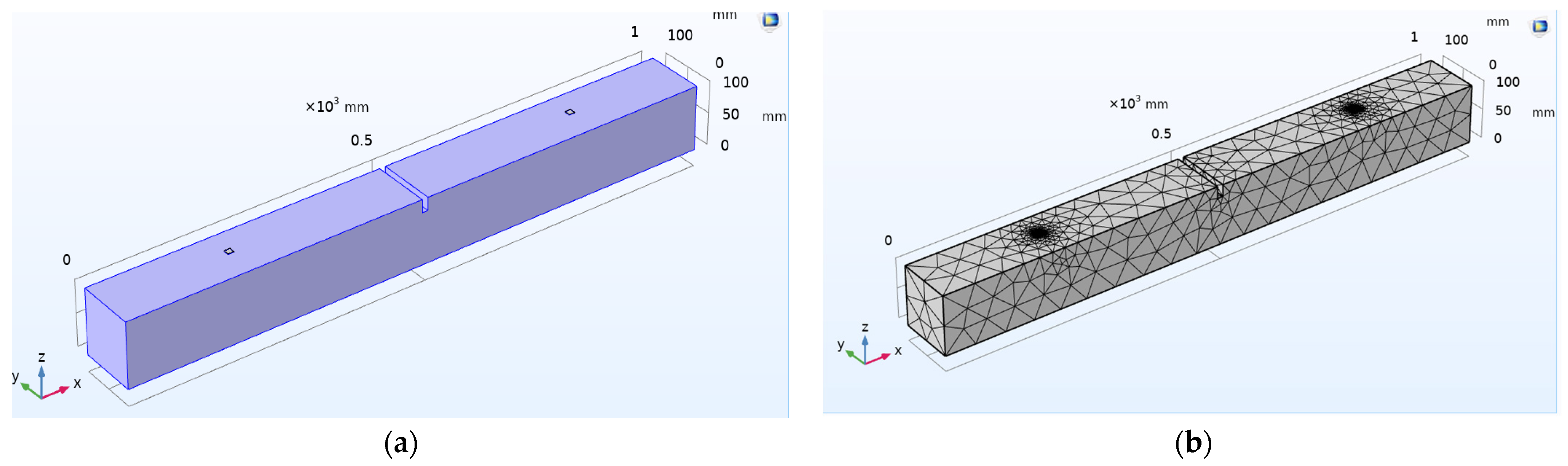
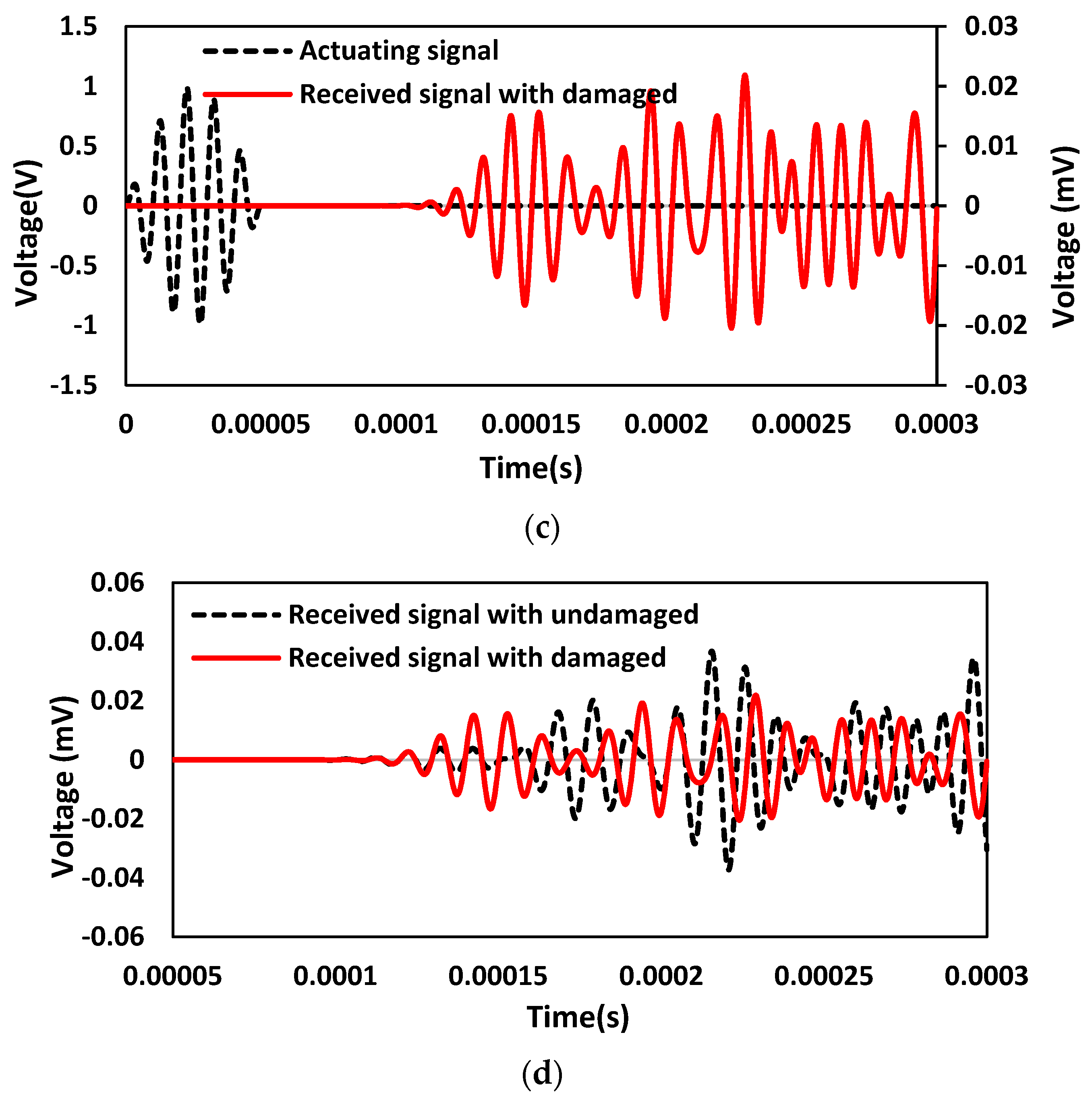
6.2. Case 2: Investigation on the Damaged Concrete Beam with Surface-Mounted PZT Patches
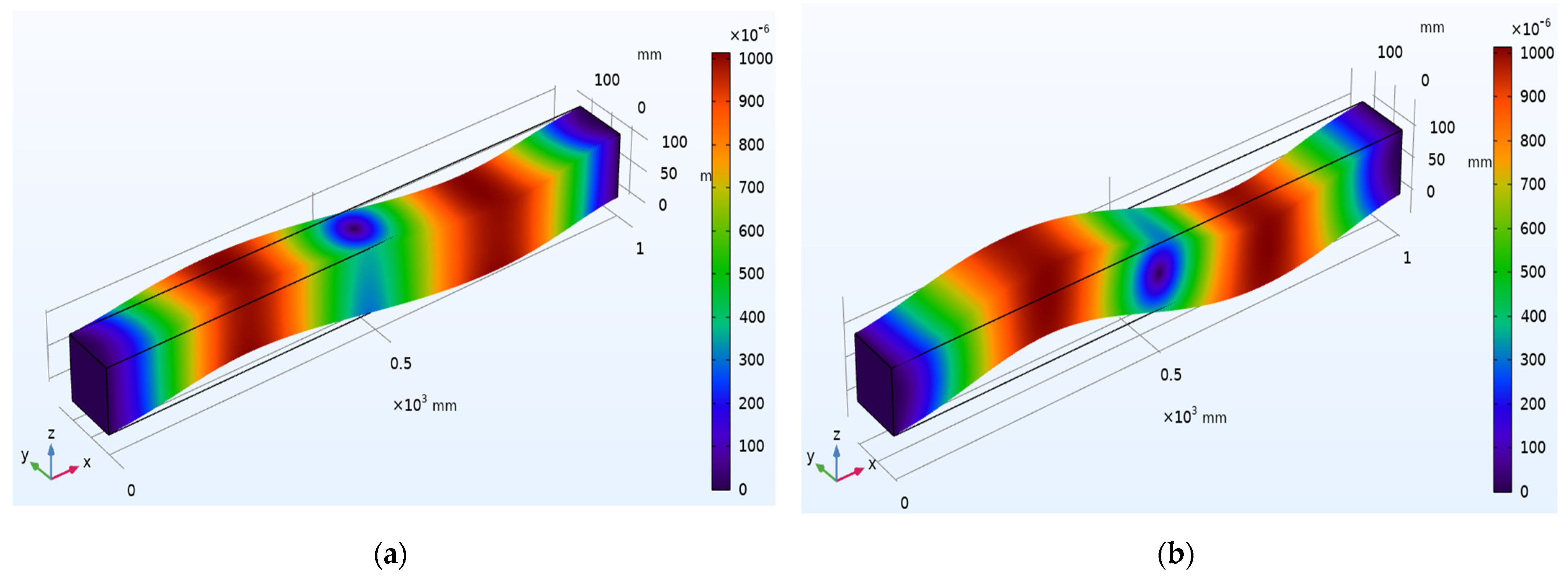
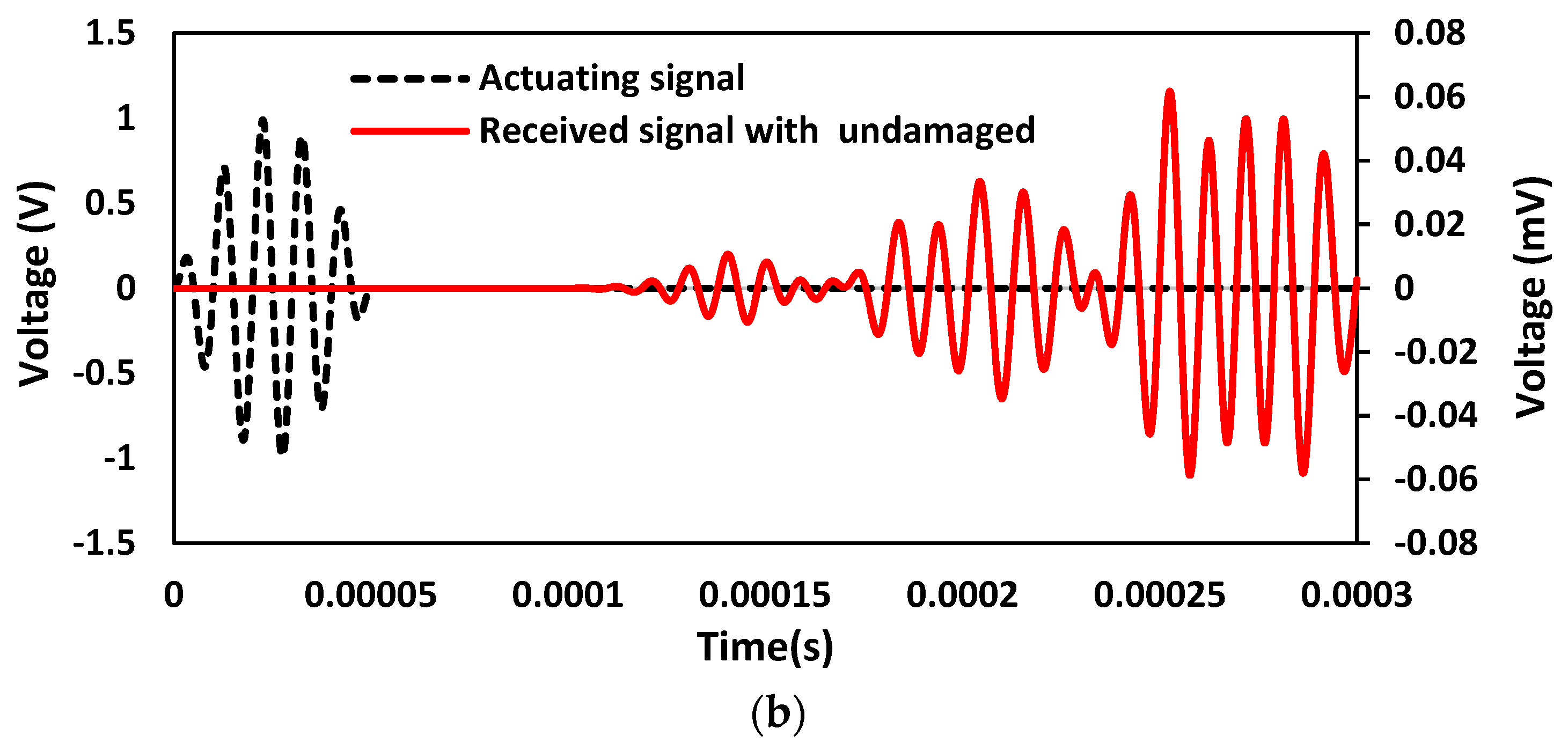
6.3. Case 3: Investigation on the Undamaged Concrete Beam with Surface-Mounted SSUs
6.4. Case 4: Investigation on the Damaged Concrete Beam with Surface-Mounted SSUs
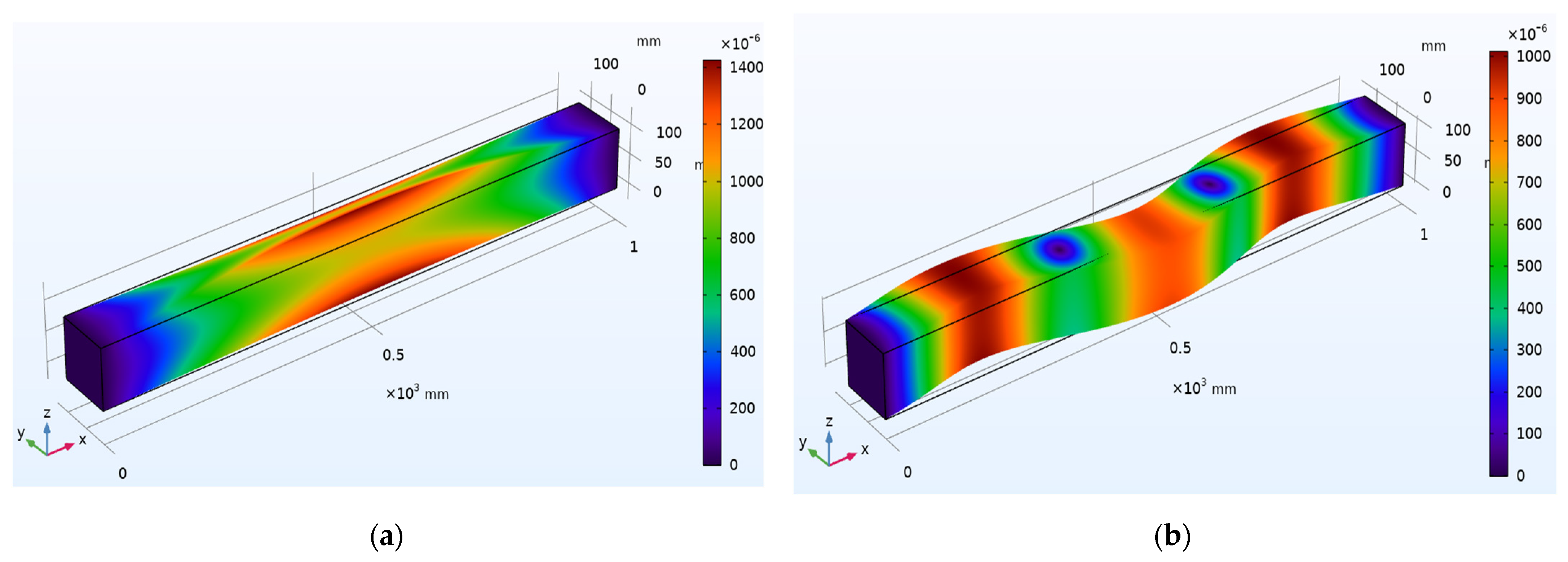
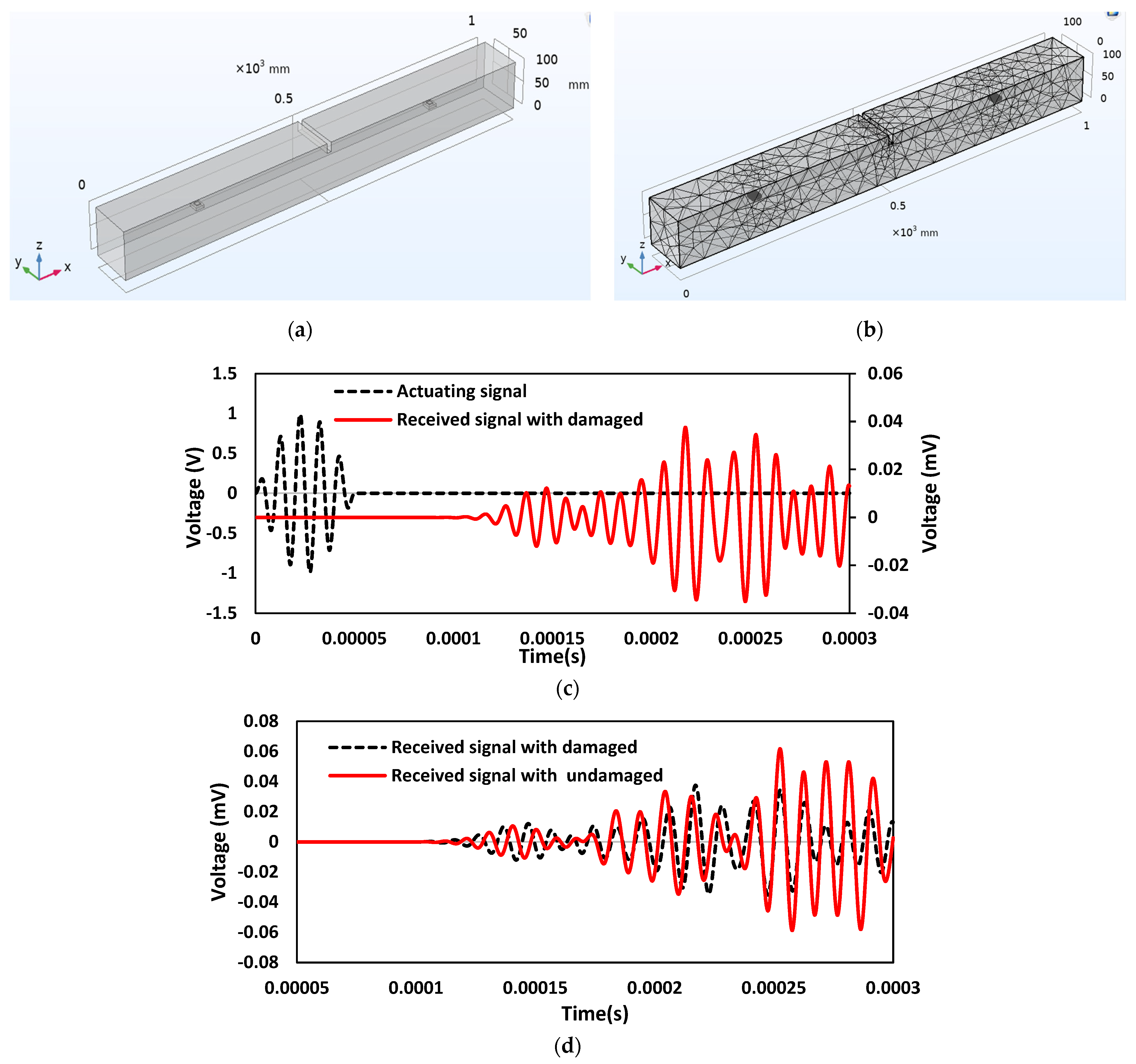
6.5. Case 5: Investigation on the Undamaged Concrete Beam with Embedded SSUs
6.6. Case 6: Investigation on the Damaged Concrete Beam with Embedded SSUs
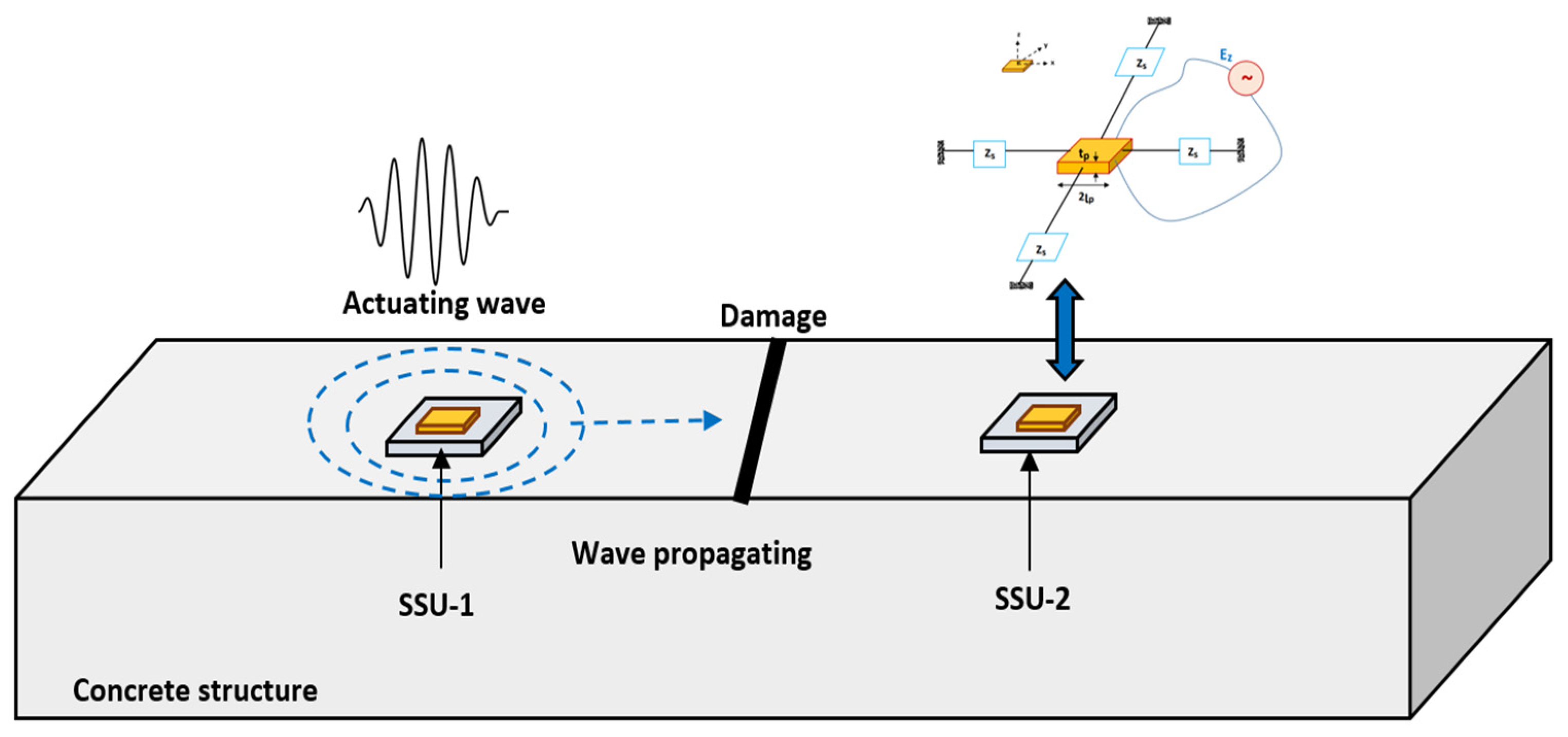
7. Combining EMI and Wave Propagation Techniques for Robust Damage Detection
- (A)
- Active wave propagation in an undamaged concrete beam;
- (B)
- Active wave propagation in damaged concrete beam;
- (C)
- EMI admittance sensor SSU-2 is activated simultaneously with a wave generator at SSU-1 in an undamaged concrete beam;
- (D)
- EMI admittance sensor SSU-2 is activated simultaneously with a wave generator at SSU-1 in a damaged concrete beam.
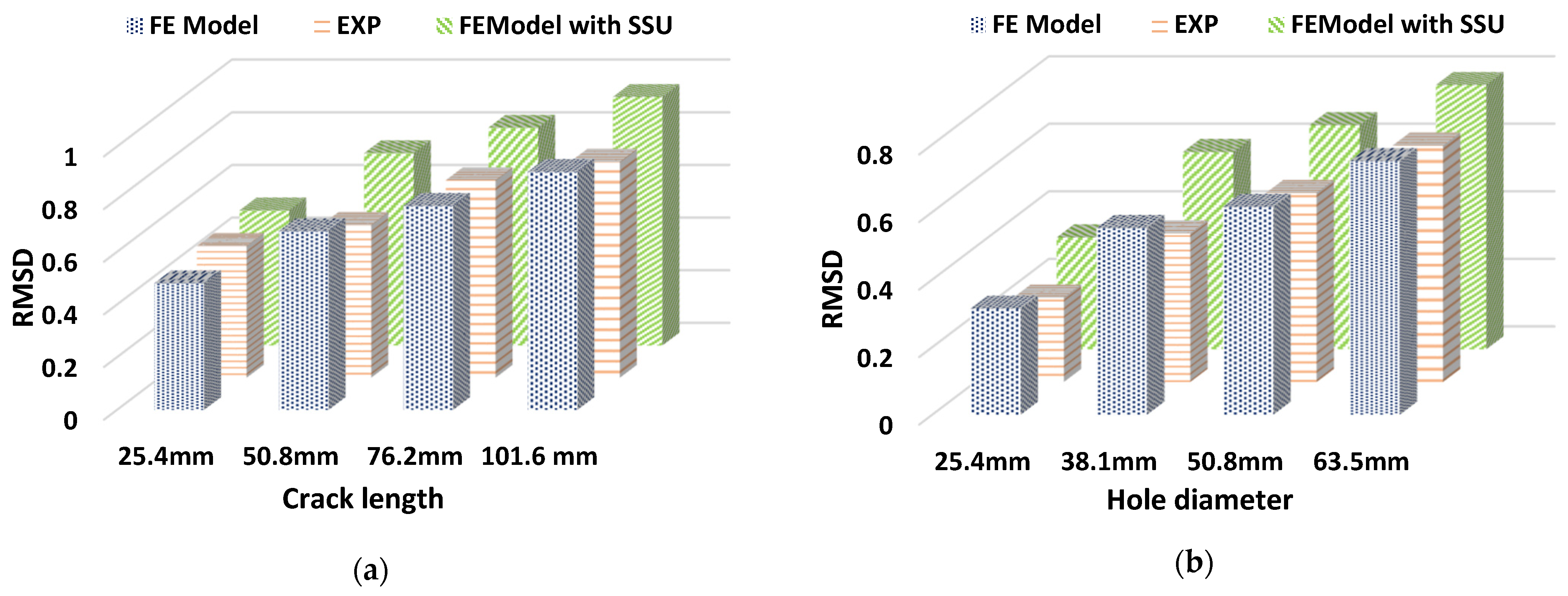
8. Experimental Validation
9. Conclusions
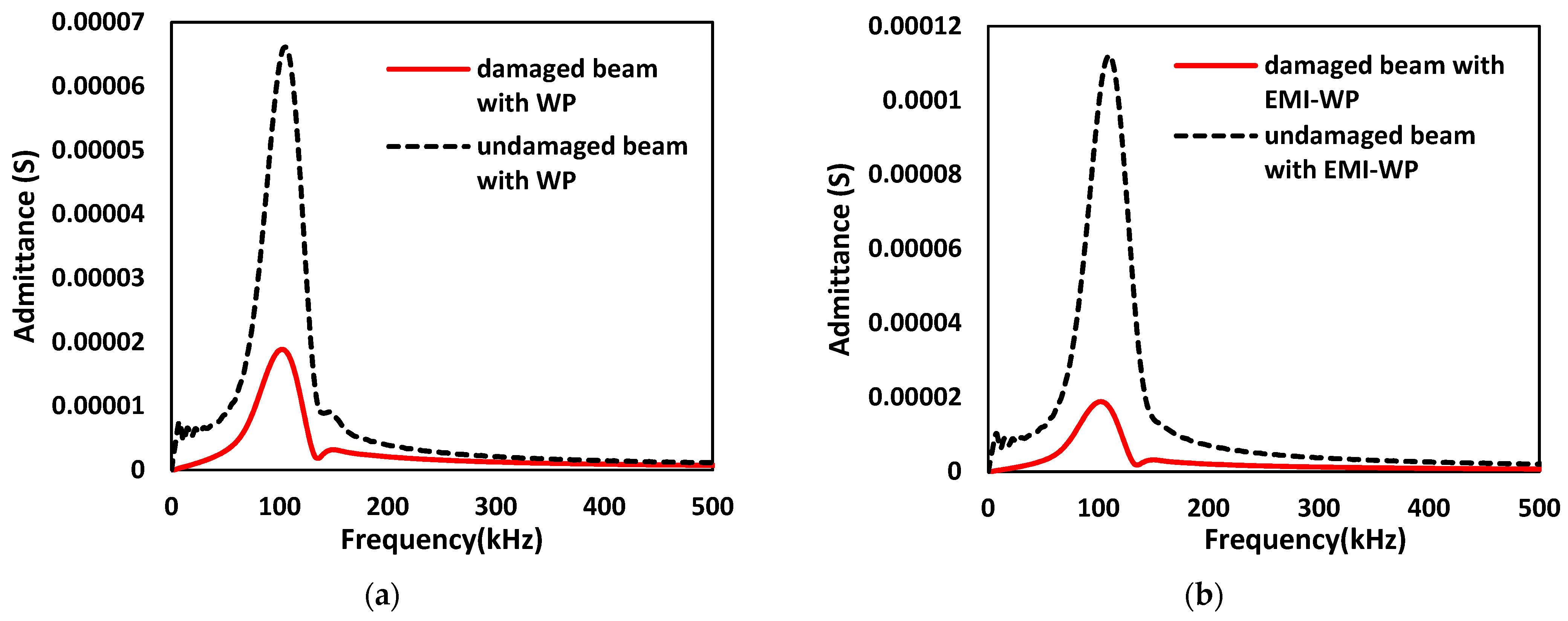
- WP-based measurement shows that damage in the structure is successfully detected utilizing the embedded SSU by observing the variation in magnitude of the received voltage signal and improved RMSD value.
- Comparing the WP response in the actuator-sensor mode of the embedded SSU, it is observed that the decrease in the magnitude of the received voltage signal is because of a crack in the transmission path, and the increase in the time of flight is due to the presence of crack along the path of the wave propagating.
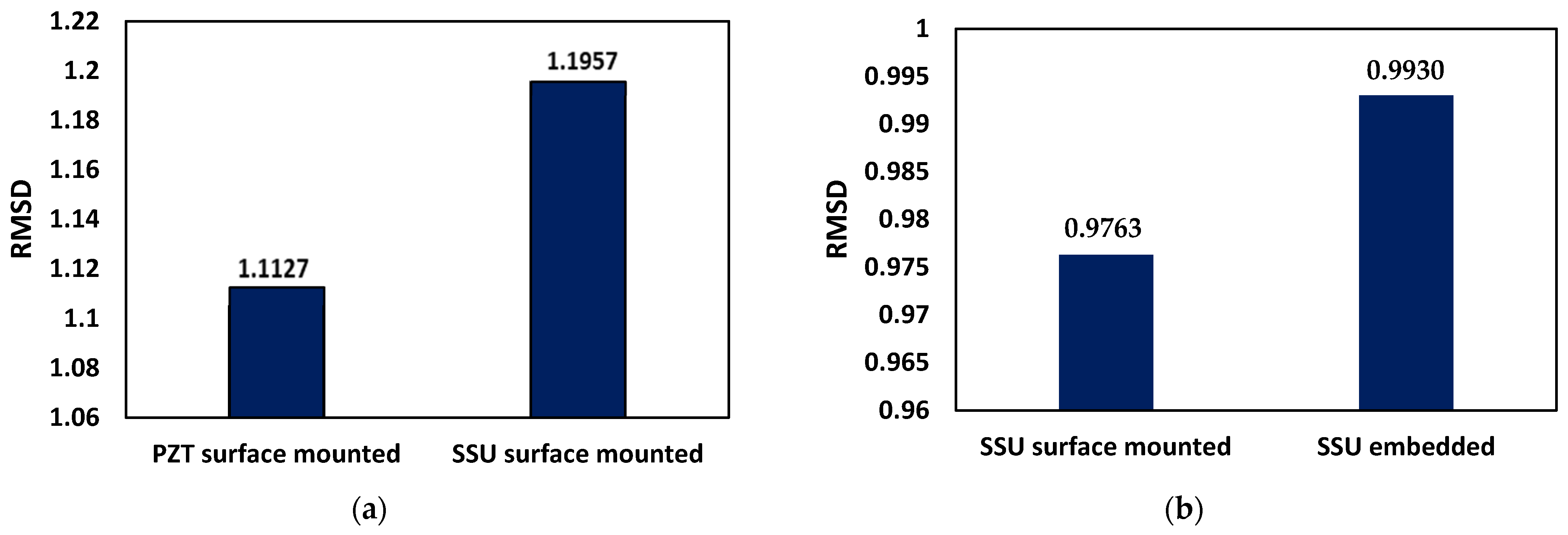
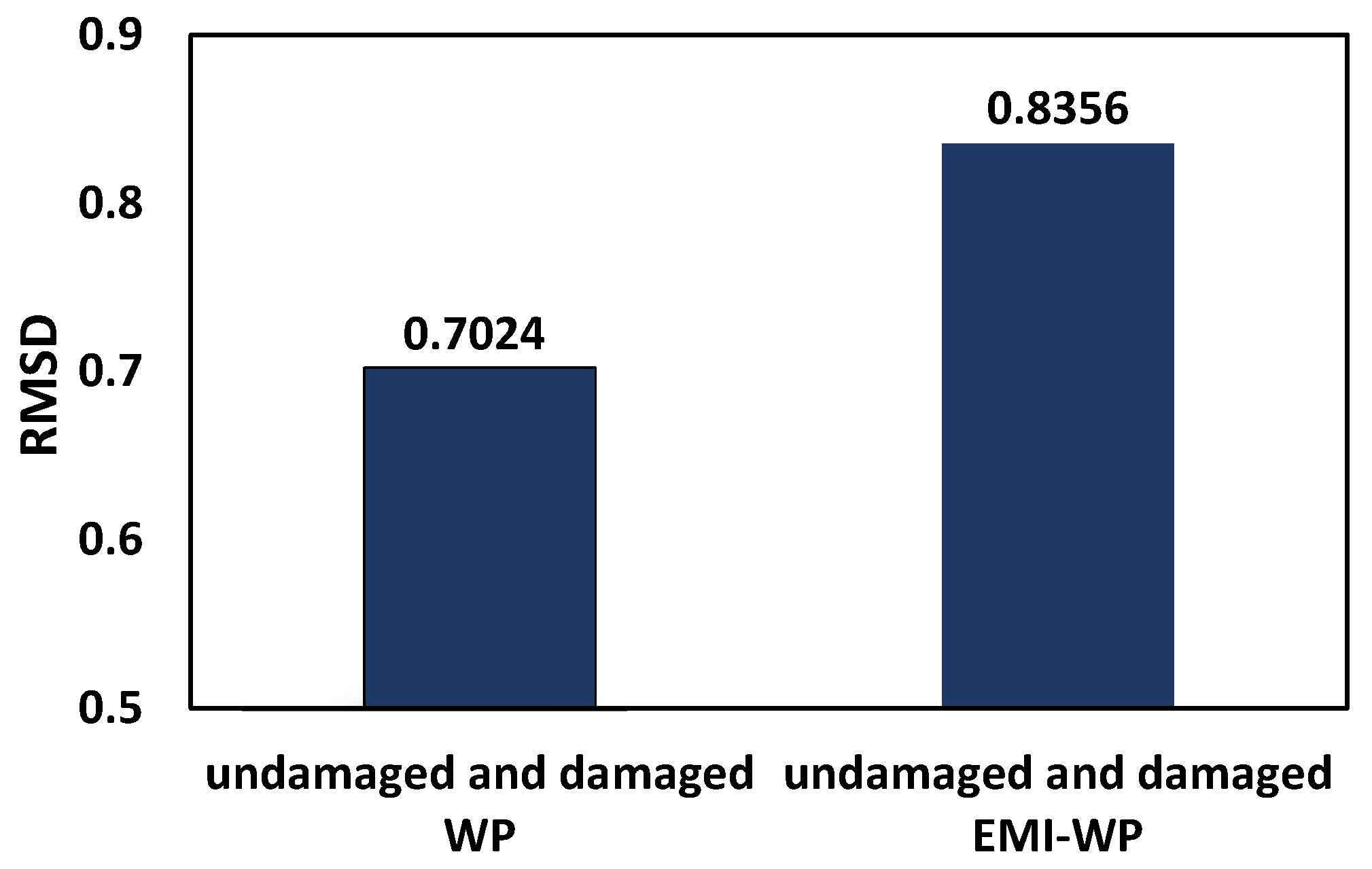
- The numerical value of the RMSD employing an SSU instead of PZT patches for damage detection exhibited by six separate cases in the wave propagation technique showed that steel–PZT models are preferable to smart material PZT-based models.
- EMI measurements are particularly important because they can detect damage to the embedded PZT patch or debond between the epoxy and concrete interface. Therefore, combining EMI and WP measurements for damage identification is useful for detecting relatively close and far damages in the structures.
- The results of the combined EMI-WP approach using four structural conditions show that the presence of damage is indicated by a change in the FFT admittance spectrum, as well as by the increment in the RMSD value from a damaged concrete beam where only wave propagation is active to EMI admittance sensor SSU-2 being activated simultaneously.
- The numerical results are compared with experimental analysis for different crack lengths and holes, which shows a good fit between the 3D FE model results and experimental results.
- The FE model results are compared with the experimentally available smart aggregate and proposed embedded SSU for damage detection, displaying enhanced damage index value. Thus, it is recommended that the embedded SSU results in a more effective modeling technique than the existing smart aggregate models for damage detection.
- The combined EMI-WP-based robust damage detection is developed by utilizing impedance and wave signals simultaneously obtained from SSUs to enhance the performance and reliability of damage diagnosis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, G.; Gu, H.; Mo, Y.-L. Smart aggregates: Multi-functional sensors for concrete structures—A tutorial and a review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Demirboga, R.; Turkmen, I.; Karakoc, M.B. Relationship between ultrasonic velocity and compressive strength for high-volume mineral-admixtured concrete. Cem. Concr. Res. 2004, 34, 2329–2336. [Google Scholar] [CrossRef]
- Brozovsky, J. High-strength concrete—NDT with rebound hammer: Influence of aggregate on test results. Nondestruct. Test. Eval. 2014, 29, 255–268. [Google Scholar] [CrossRef]
- Soh, C.K.; Tseng, K.K.; Bhalla, S.; Gupta, A.K. Performance of smart piezoceramic patches in health monitoring of a RC bridge. Smart Mater. Struct. 2000, 9, 533–542. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Radhika, M.A. Electromechanical impedance of piezoelectric transducers for monitoring metallic and non-metallic structures: A review of wired, wireless and energy-harvesting methods. J. Intell. Mater. Syst. Struct. 2013, 24, 1021–1042. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT Impedance Sensors for Damage Detection of Concrete Structures. Sensors 2008, 8, 327–346. [Google Scholar] [CrossRef] [Green Version]
- Negi, P.; Chhabra, R.; Kaur, N.; Bhalla, S. Health monitoring of reinforced concrete structures under impact using multiple piezo-based configurations. Constr. Build. Mater. 2019, 222, 371–389. [Google Scholar] [CrossRef]
- Bhalla, S.; Soh, C.K. Electromechanical Impedance Modeling for Adhesively Bonded Piezo-Transducers. J. Intell. Mater. Syst. Struct. 2004, 15, 955–972. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Soh, C.K. Fatigue life estimation of a 1D aluminum beam under model loading using the electromechanical impedance technique. Smart Mater. Struct. 2011, 20, 125001. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Gopalakrishnan, N.; Priya, C.B. Monitoring of early-age characteristics of concrete using EMI-based embedded PZT transducers on varying plate thickness. Constr. Mater. Syst. 2017, 2, 557. [Google Scholar]
- Shin, S.W.; Qureshi, A.R.; Lee, J.Y.; Yun, C.B. Piezoelectric sensor-based non-destructive active monitoring of strength gain in concrete. Smart Mater. Struct. 2008, 17, 055002. [Google Scholar] [CrossRef]
- Soh, C.K.; Bhalla, S. Calibration of piezo-impedance transducers for strength prediction and damage assessment of concrete. Smart Mater. Struct. 2005, 14, 671–684. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Balamonica, K.; Priya, C.B.; Reddy, A.L.; Gopalakrishnan, N. Comparative performance of various smart aggregates during strength gain and damage states of concrete. Smart Mater. Struct. 2015, 24, 085016. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Balamonica, K.; Priya, C.B.; Gopalakrishnan, N.; Murthy, S.G.N. Non-destructive piezo electric-based monitoring of strength gain in concrete using smart aggregate. In Proceedings of the International Symposium Non-Destructive Testing in Civil Engineering (NDT-CE), Berlin, Germany, 15–17 September 2015; pp. 15–17. [Google Scholar]
- Priya, C.B.; Saravanan, T.J.; Balamonica, K.; Gopalakrishnan, N.; Rao, A.R.M. EMI based monitoring of early-age characteristics of concrete and comparison of serial/parallel multi-sensing technique. Constr. Build. Mater. 2018, 191, 1268–1284. [Google Scholar] [CrossRef]
- Balamonica, K.; Saravanan, T.J.; Priya, C.B.; Gopalakrishnan, N. Piezoelectric sensor-based damage progression in concrete through serial/parallel multi-sensing technique. Struct. Health Monit. 2020, 19, 339–356. [Google Scholar]
- Sepehry, N.; Shamshirsaz, M.; Bastani, A. Experimental and theoretical analysis in impedance-based structural health monitoring with varying temperature. Struct. Health Monit. 2010, 10, 573–585. [Google Scholar] [CrossRef]
- Su, Y.-F.; Han, G.; Nantung, T.; Lu, N. Novel methodology on direct extraction of the strength information from cementitious materials using piezo-sensor based electromechanical impedance (EMI) method. Constr. Build. Mater. 2020, 259, 119848. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Balamonica, K.; Priya, C.B.; Gopalakrishnan, N.; Murthy, S.G.N. Piezoelectric EMI–Based Monitoring of Early Strength Gain in Concrete and Damage Detection in Structural Components. J. Infrastruct. Syst. 2017, 23, 04017029. [Google Scholar] [CrossRef]
- Tawie, R.; Lee, H.K. Characterization of cement-based materials using a reusable piezoelectric impedance-based sensor. Smart Mater. Struct. 2011, 20, 085023. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Chauhan, S.S. Study on pre-damage diagnosis and analysis of adhesively bonded smart PZT sensors using EMI technique. Measurement 2021, 188, 110411. [Google Scholar] [CrossRef]
- Parpe, A.; Saravanan, T.J. New refined analytical models for various bonding conditions of an adhesively bonded smart PZT transducer using the EMI technique. Smart Mater. Struct. 2021, 30, 125015. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Gopalakrishnan, N.; Rao, N.P. Damage detection in structural element through propagating waves using radially weighted and factored RMS. Measurement 2015, 73, 520–538. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Gopalakrishnan, N.; Hari, B.K. Damage identification in structural elements through curvature mode shapes and nonlinear energy operator. Compos. Mater. Eng. 2019, 1, 33–48. [Google Scholar]
- Thiyagarajan, J.S. Non-Destructive Testing Mechanism for Pre-Stressed Steel Wire Using Acoustic Emission Monitoring. Materials 2020, 13, 5029. [Google Scholar] [CrossRef]
- Saravanan, T.J. Elastic wave methods for non-destructive damage diagnosis in the axisymmetric viscoelastic cylindrical waveguide. Measurement 2021, 177, 109253. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Ye, L.; Wang, D. Guided waves for damage detection in rebar-reinforced concrete beams. Constr. Build. Mater. 2013, 47, 370–378. [Google Scholar] [CrossRef]
- Luo, M.; Li, W.; Hei, C.; Song, G. Concrete Infill Monitoring in Concrete-Filled FRP Tubes Using a PZT-Based Ultrasonic Time-of-Flight Method. Sensors 2006, 16, 2083. [Google Scholar] [CrossRef]
- Ihn, J.; Chang, F.K. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network: I Diagnosis. Smart Mater. Struct. 2004, 13, 609–620. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Gopalakrishnan, N.; Rao, N.P. Detection of damage through coupled axial–flexural wave interactions in a sagged rod using the spectral finite element method. J. Vib. Control 2016, 23, 3345–3364. [Google Scholar] [CrossRef]
- Saravanan, T.J.; Gopalakrishnan, N.; Rao, N.P. Experiments on coupled axial–flexural wave propagation in a sagged rod with structural discontinuity using piezoelectric transducers. J. Vib. Control 2018, 24, 2717–2731. [Google Scholar] [CrossRef]
- Krawczuk, M.; Palacz, M.; Ostachowicz, W. The dynamic analysis of a cracked Timoshenko beam by the spectral element method. J. Sound Vib. 2003, 264, 1139–1153. [Google Scholar] [CrossRef]
- Gan, C.; Wei, Y.; Yang, S. Longitudinal wave propagation in a multi-step rod with variable cross-section. J. Vib. Control 2016, 22, 837–852. [Google Scholar] [CrossRef]
- Yang, Z.-B.; Radzieński, M.; Kudela, P.; Ostachowicz, W. Two-dimensional modal curvature estimation via Fourier spectral method for damage detection. Compos. Struct. 2016, 148, 155–167. [Google Scholar] [CrossRef]
- Kumar, K.V.; Saravanan, T.J.; Sreekala, R.; Gopalakrishnan, N.; Mini, K.M. Structural damage detection through longitudinal wave propagation using spectral finite element method. Géoméch. Eng. 2017, 12, 161–183. [Google Scholar] [CrossRef]
- Song, F.; Huang, G.L.; Kim, J.H.; Haran, S. On the study of surface wave propagation in concrete structures using a piezoelectric actuator/sensor system. Smart Mater. Struct. 2008, 17, 055024. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Zagrai, A.; Bao, J. Damage identification in aging aircraft structures with piezoelectric wafer active sensors. J. Intell. Mater. Syst. Struct. 2004, 15, 673–687. [Google Scholar] [CrossRef]
- Comsol Multiphysics 5.5 Users Guide. Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 22 February 2022).
- Lim, Y.Y.; Soh, C.K. Effect of varying axial load under fixed boundary condition on admittance signatures of electromechanical impedance technique. J. Intell. Mater. Syst. Struct. 2012, 23, 815–826. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Soh, C.K. Damage detection and characterization of EMI technique under varying axial load. Smart Struct. Syst. 2013, 11, 349–364. [Google Scholar] [CrossRef]
- Saravanan, T.J. Guided ultrasonic wave-based investigation on the transient response in an axisymmetric viscoelastic cylindrical waveguide. Ultrasonics 2021, 117, 106543. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Kwong, K.Z.; Liew, W.Y.H.; Soh, C.K. Practical issues related to the application of piezoelectric based wave propagation technique in monitoring of concrete curing. Constr. Build. Mater. 2017, 152, 506–519. [Google Scholar] [CrossRef]
- Saravanan, T.J. Convergence study on ultrasonic guided wave propagation modes in an axisymmetric cylindrical waveguide. Mech. Adv. Mater. Struct. 2020, 1–18. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Kwong, K.Z.; Liew, W.Y.H.; Padilla, R.V.; Soh, C.K. Parametric study and modeling of PZT based wave propagation technique related to practical issues in monitoring of concrete curing. Constr. Build. Mater. 2018, 176, 519–530. [Google Scholar] [CrossRef]
- Saravanan, T.J. Investigation of guided wave dispersion characteristics for fundamental modes in an axisymmetric cylindrical waveguide using rooting strategy approach. Mech. Adv. Mater. Struct. 2022, 29, 495–505. [Google Scholar] [CrossRef]
- Demma, A.; Cawley, P.; Lowe, M.; Roosenbrand, A.; Pavlakovic, B. The reflection of guided waves from notches in pipes: A guide for interpreting corrosion measurements. NDT E Int. 2004, 37, 167–180. [Google Scholar] [CrossRef]
- An, Y.-K.; Sohn, H. Integrated impedance and guided wave based damage detection. Mech. Syst. Signal Process. 2012, 28, 50–62. [Google Scholar] [CrossRef]
- Hu, B.; Kundu, T.; Grill, W.; Liu, B.; Toufigh, V. Embedded piezoelectric sensors for health monitoring of concrete structures. ACI Mater. J. 2013, 110, 149. [Google Scholar]



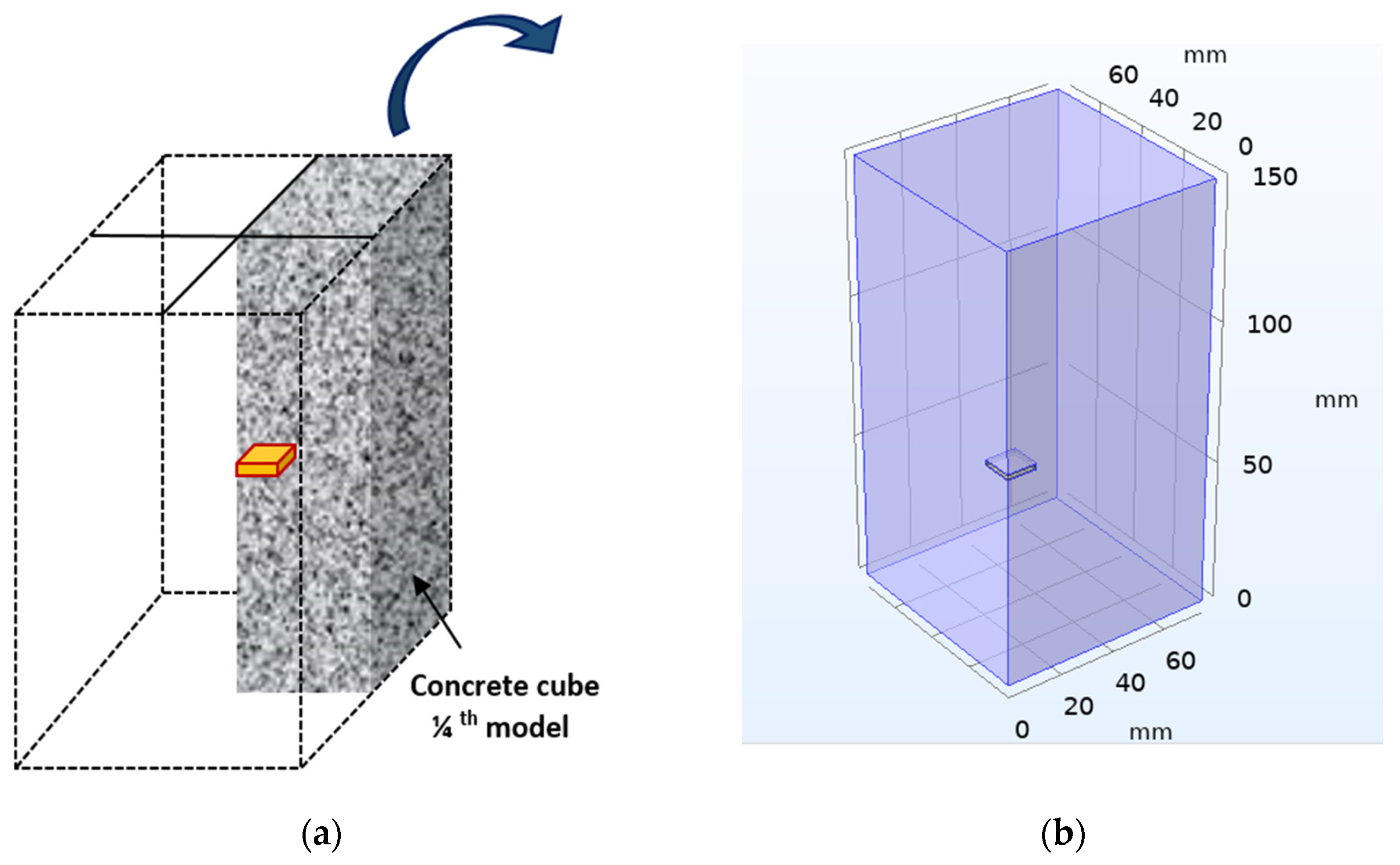
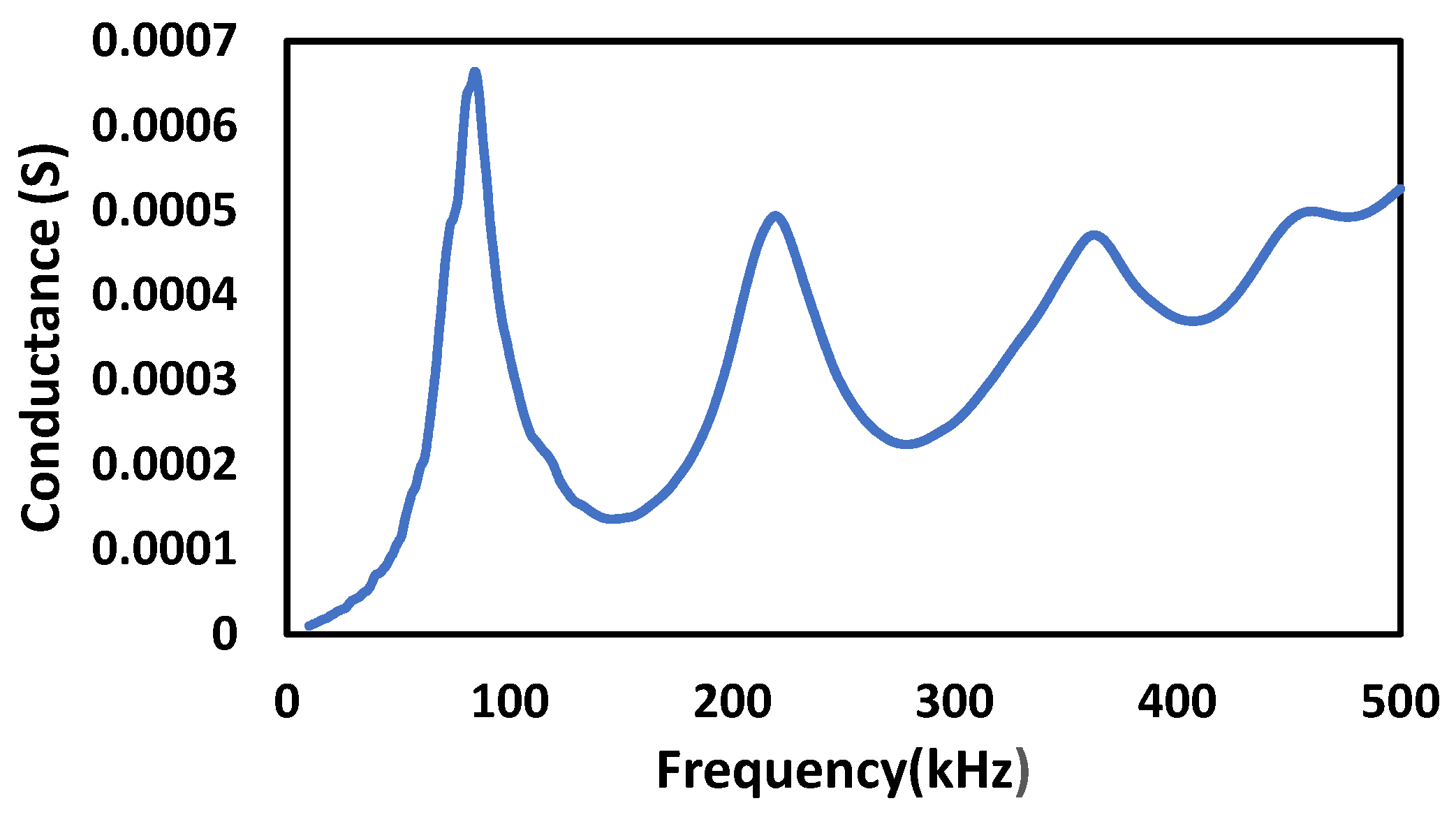

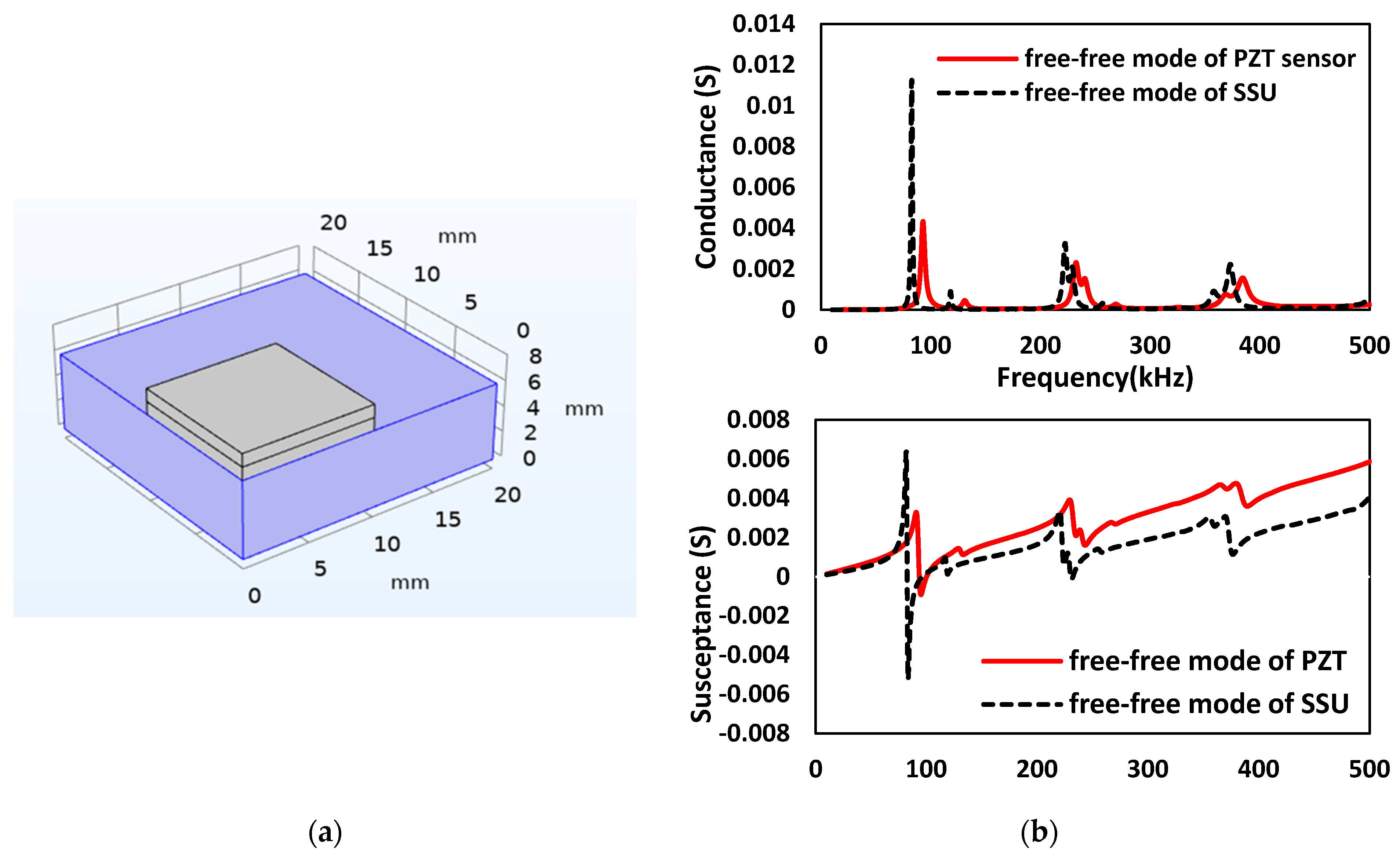
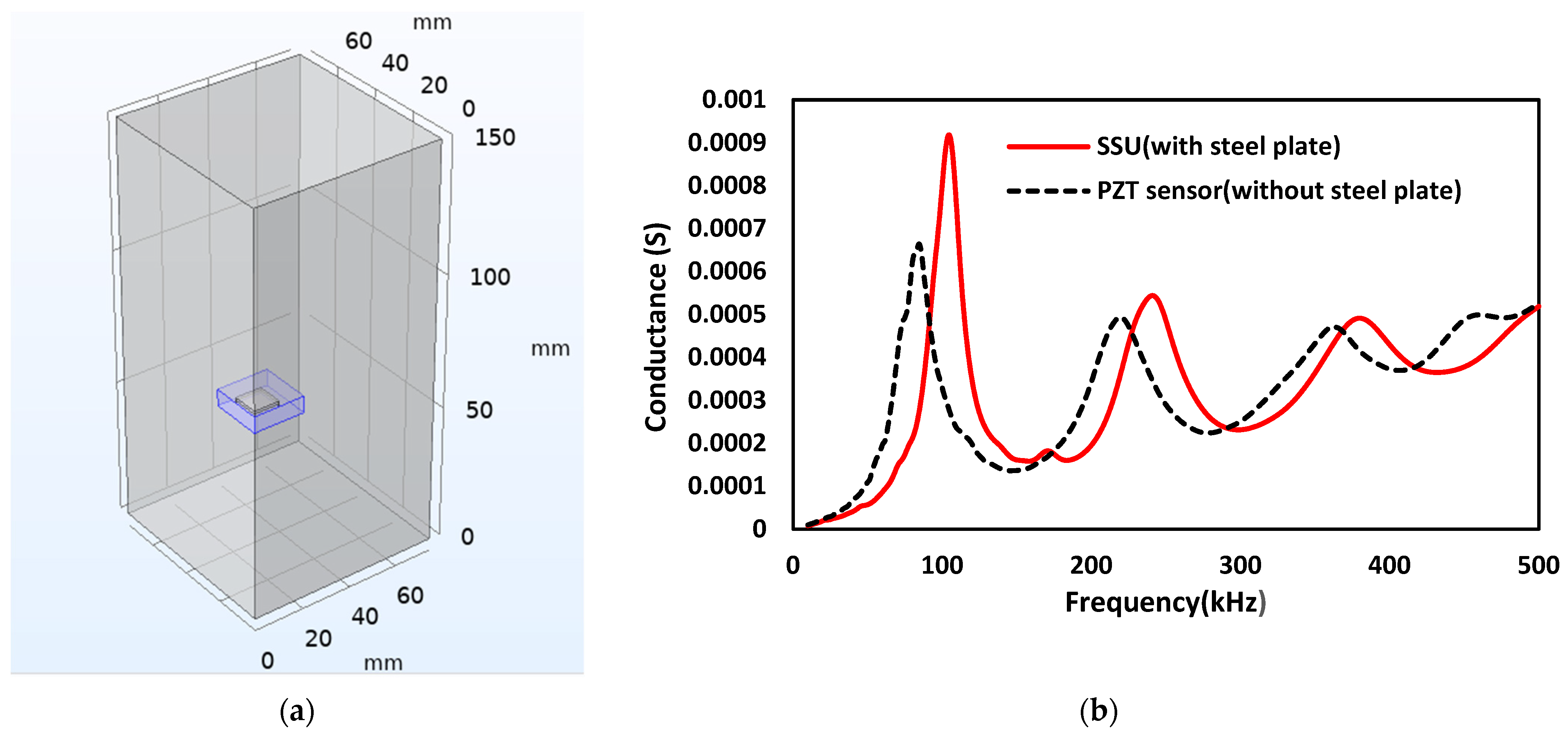








| Parameters | Value |
|---|---|
| Density, ρ [kg/m3] | 7750 |
| Poisson’s ratio, | 0.3 |
| Damping ratio, | 0.012 |
| Dielectric loss factor, | 0.0169 |
| Elasticity matrix [Pa] | |
| Piezoelectric Constants [C/N] | |
| Relative permittivity |
| Parameters | Variable | Value |
|---|---|---|
| Young’s modulus | E | 2 GPa |
| Density | 1250 kg/m3 | |
| Poisson’s ratio | 0.4 |
| Parameters | Variable | Value |
|---|---|---|
| Young’s modulus | E | 25 GPa |
| Density | 2300 kg/m3 | |
| Poisson’s ratio | 0.20 |
| Parameters | Variable | Value |
|---|---|---|
| Young’s modulus | E | 200 GPa |
| Density | 7850 kg/m3 | |
| Poisson’s ratio | 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gayakwad, H.; Thiyagarajan, J.S. Structural Damage Detection through EMI and Wave Propagation Techniques Using Embedded PZT Smart Sensing Units. Sensors 2022, 22, 2296. https://doi.org/10.3390/s22062296
Gayakwad H, Thiyagarajan JS. Structural Damage Detection through EMI and Wave Propagation Techniques Using Embedded PZT Smart Sensing Units. Sensors. 2022; 22(6):2296. https://doi.org/10.3390/s22062296
Chicago/Turabian StyleGayakwad, Himanshi, and Jothi Saravanan Thiyagarajan. 2022. "Structural Damage Detection through EMI and Wave Propagation Techniques Using Embedded PZT Smart Sensing Units" Sensors 22, no. 6: 2296. https://doi.org/10.3390/s22062296
APA StyleGayakwad, H., & Thiyagarajan, J. S. (2022). Structural Damage Detection through EMI and Wave Propagation Techniques Using Embedded PZT Smart Sensing Units. Sensors, 22(6), 2296. https://doi.org/10.3390/s22062296







