Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications
Abstract
:1. Introduction
2. Problem Definition
3. Methodology
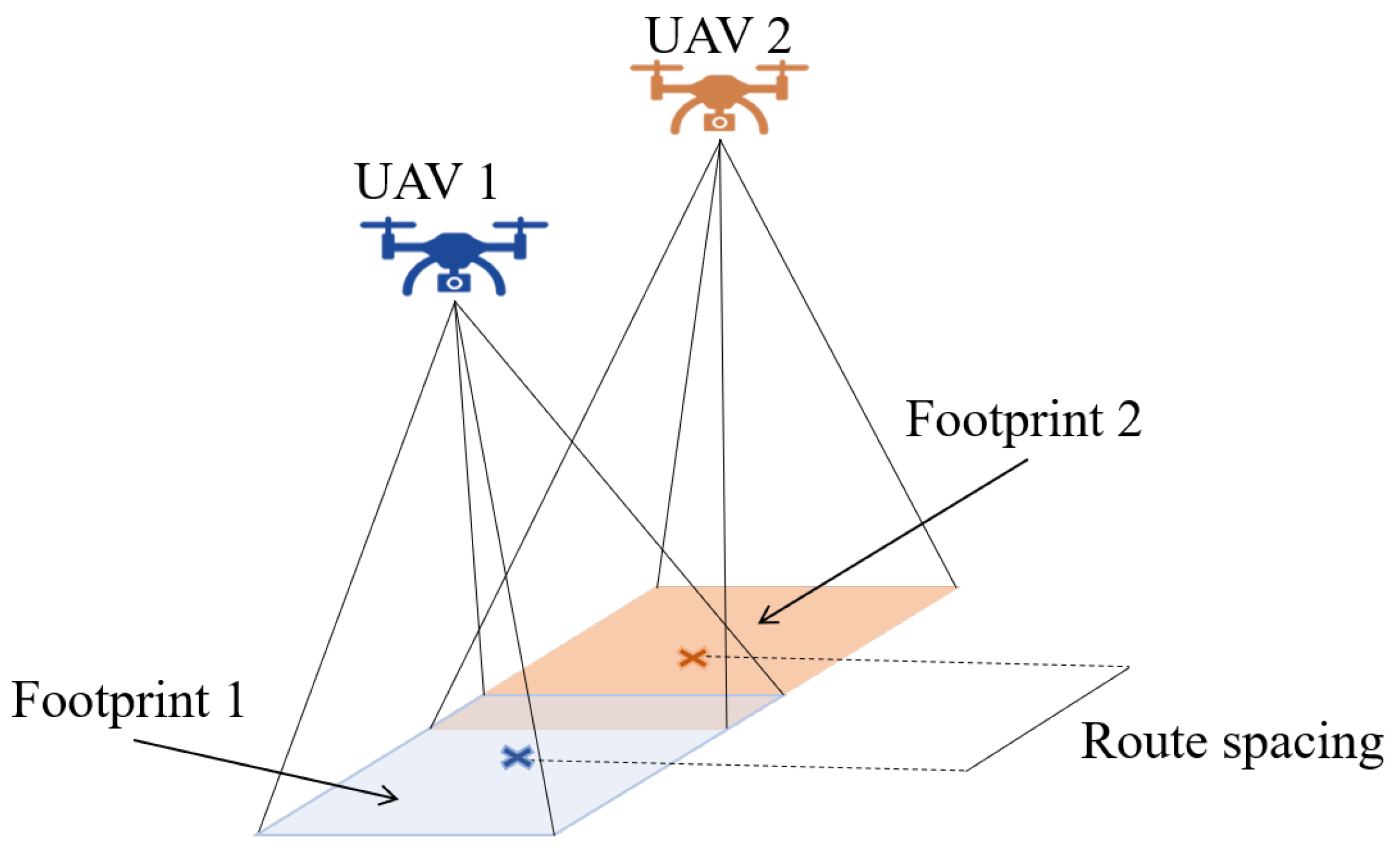
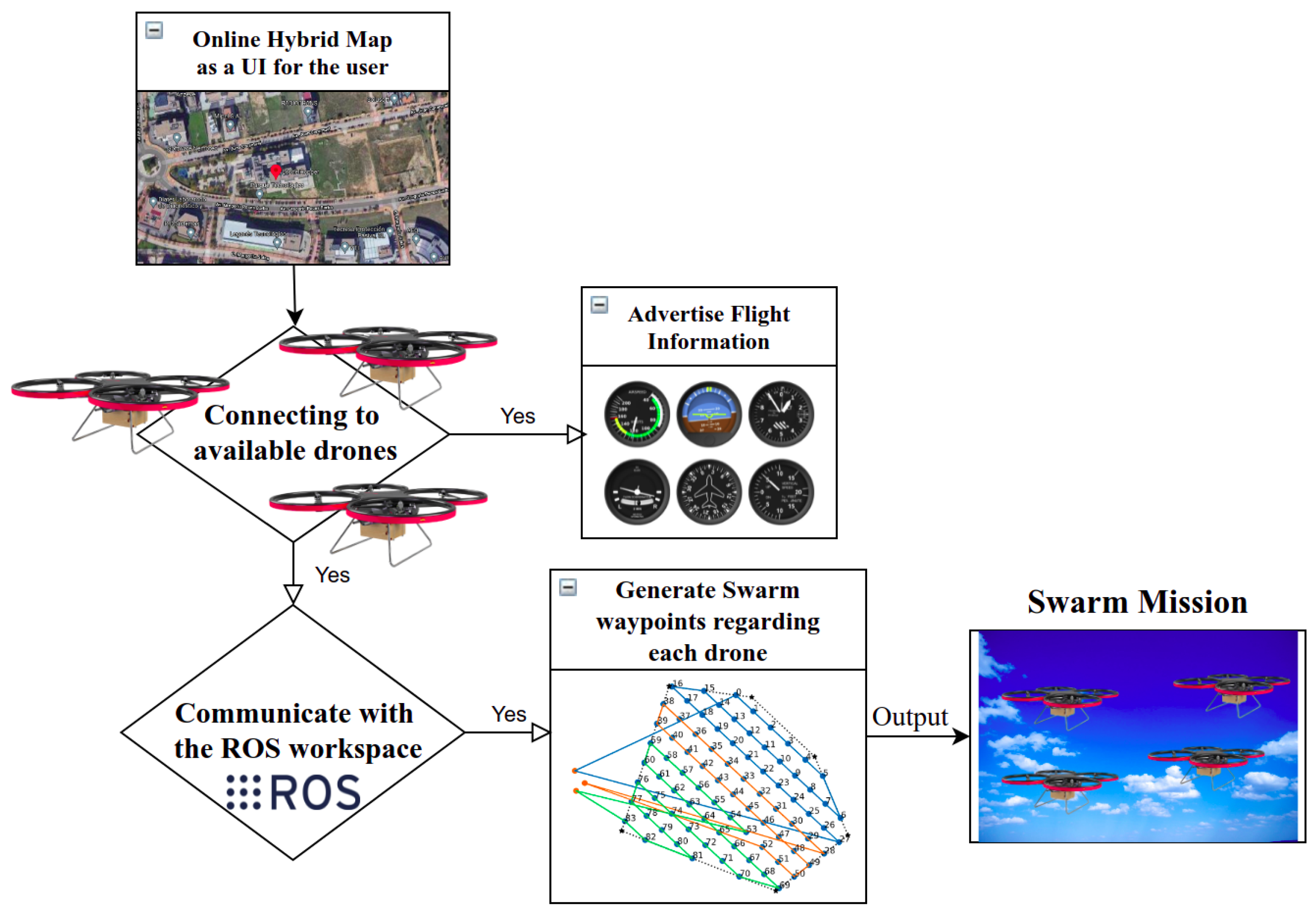
3.1. Architecture Proposal
3.2. Multi-UAV CPP Algorithm
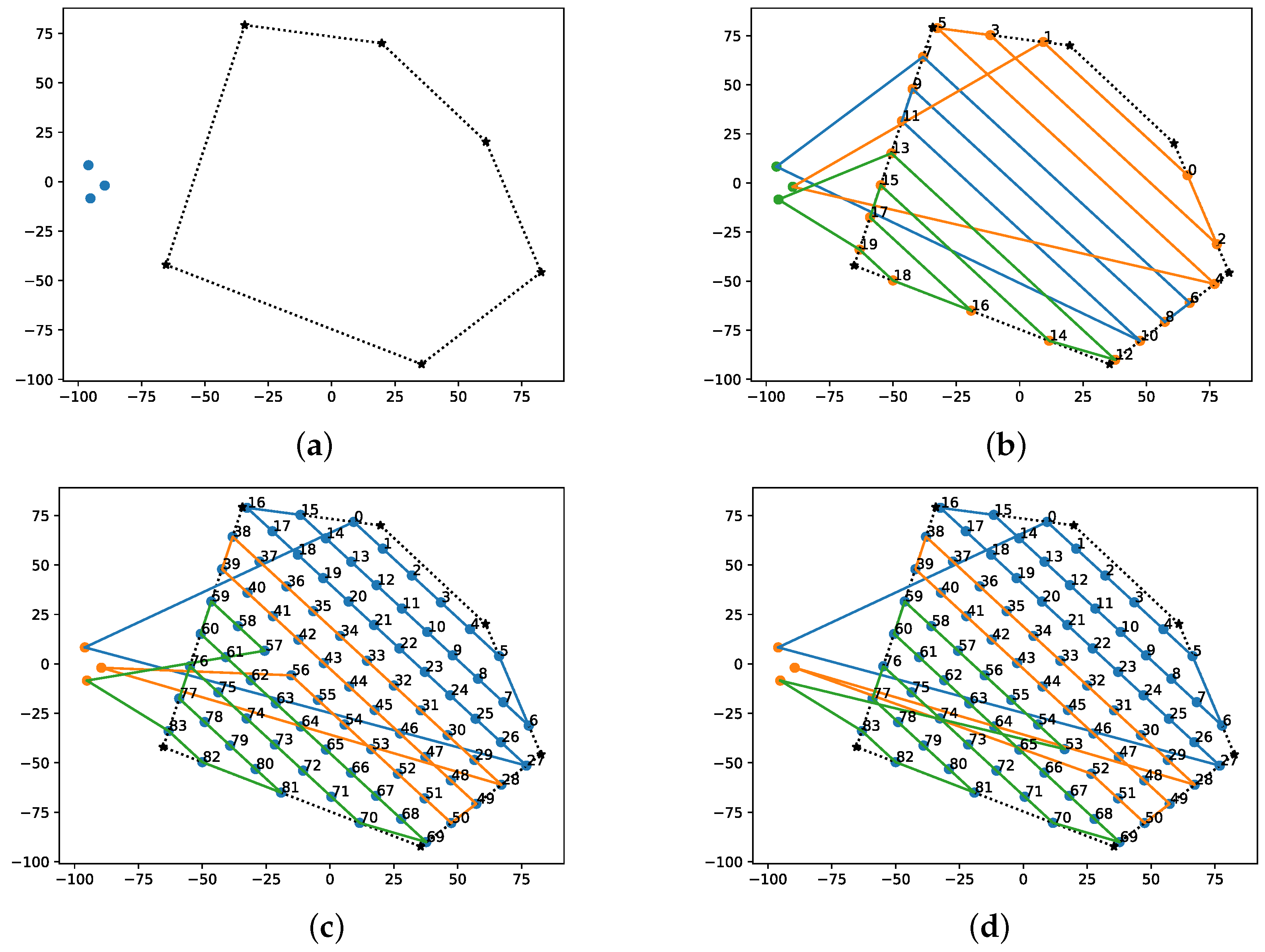
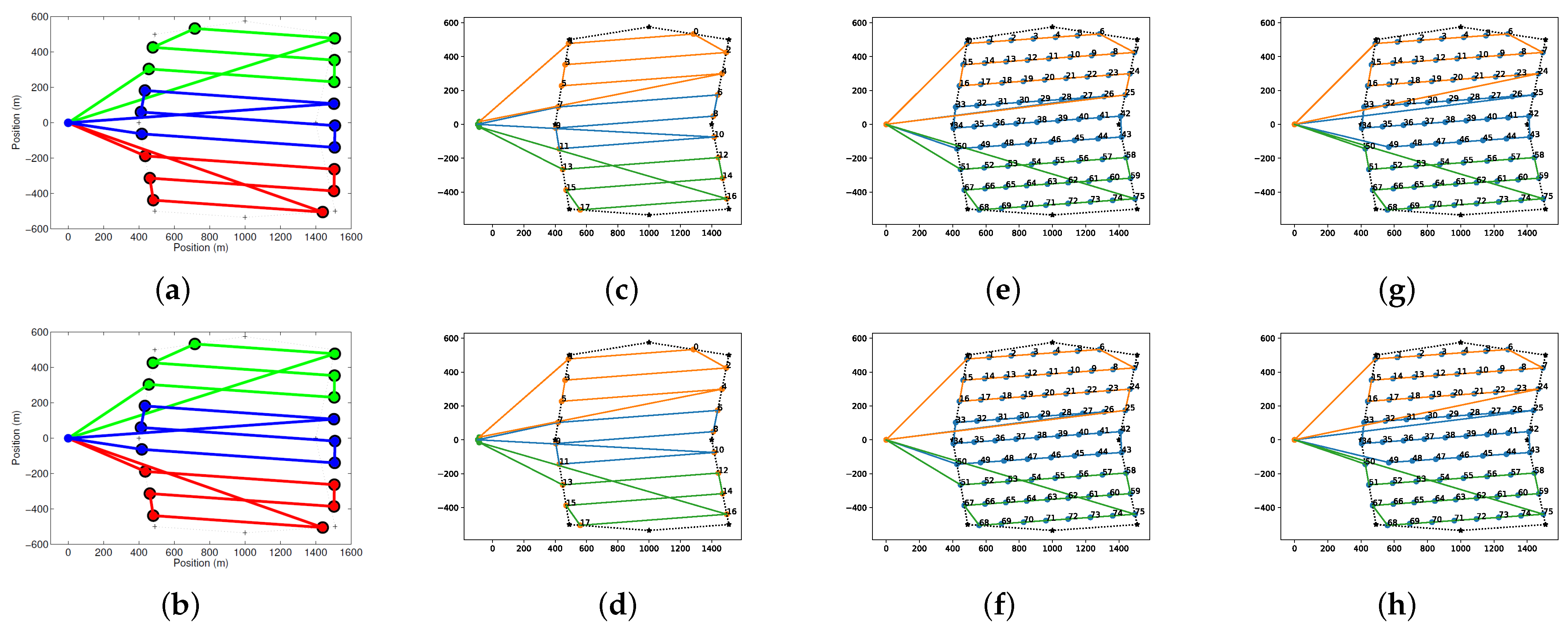
3.2.1. Area Decomposition
3.2.2. Multi-UAV Routing
| Algorithm 1: BINPAT Algorithm |
 |
| Algorithm 2: CBinPack Algorithm |
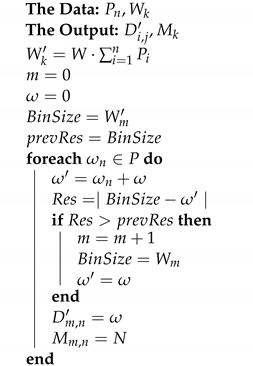 |
3.2.3. Routing Optimization
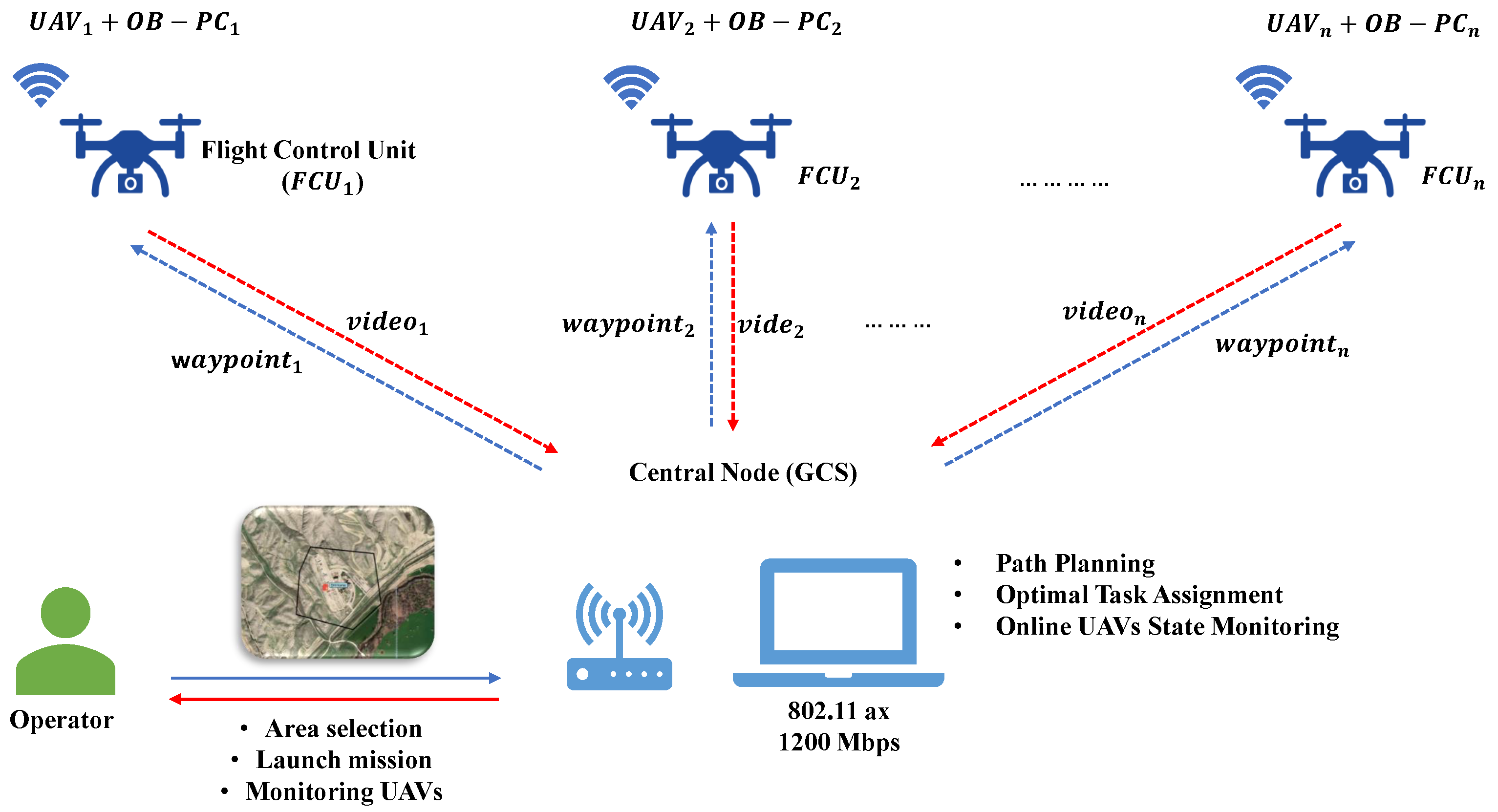
3.3. Software Implementation
3.4. Hardware Implementation
3.5. Transformation between Relative and Absolute Coordinates
4. Results and Discussion
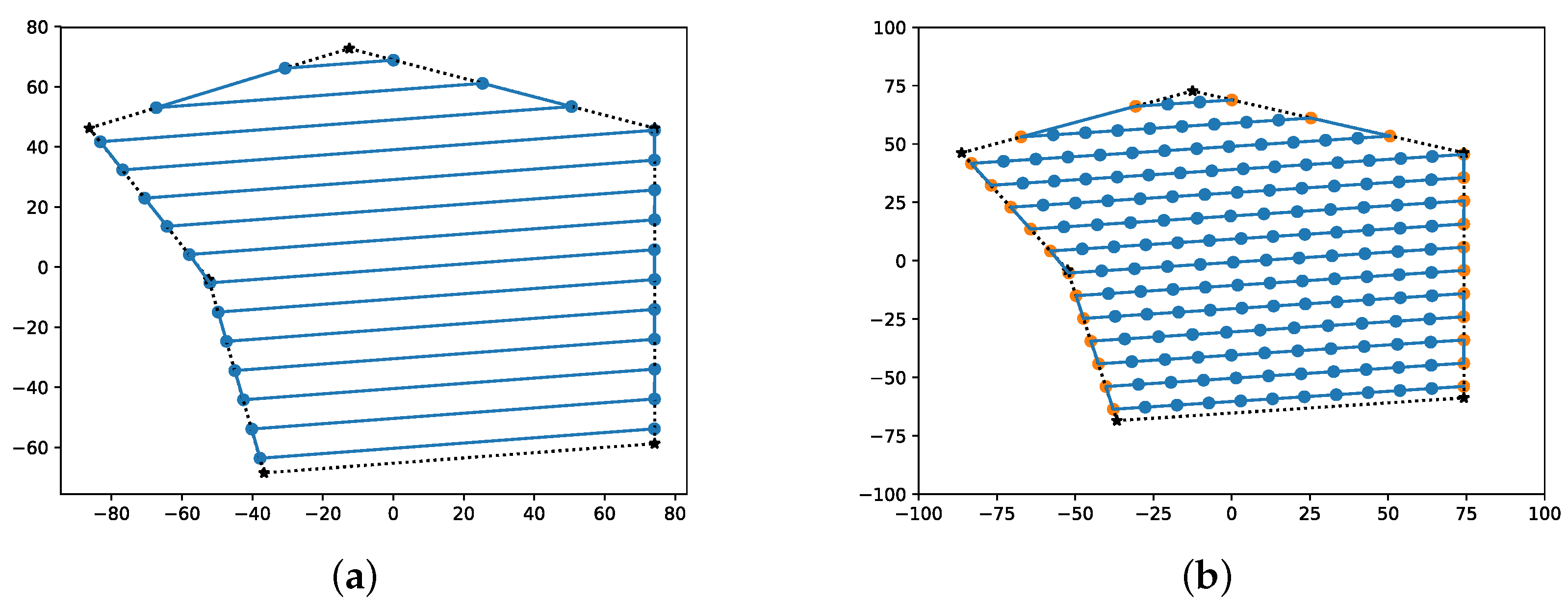
4.1. Algorithm Validation
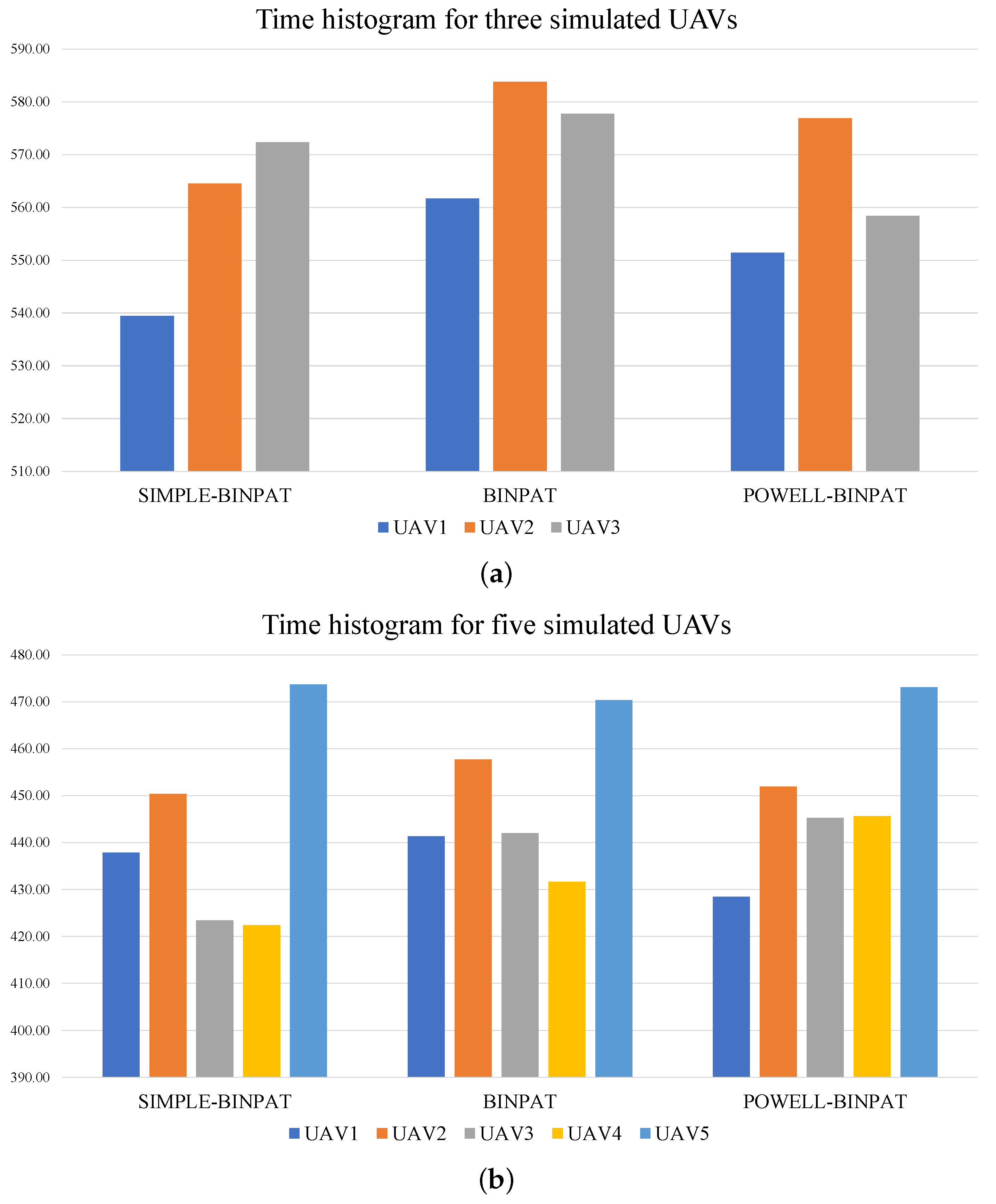
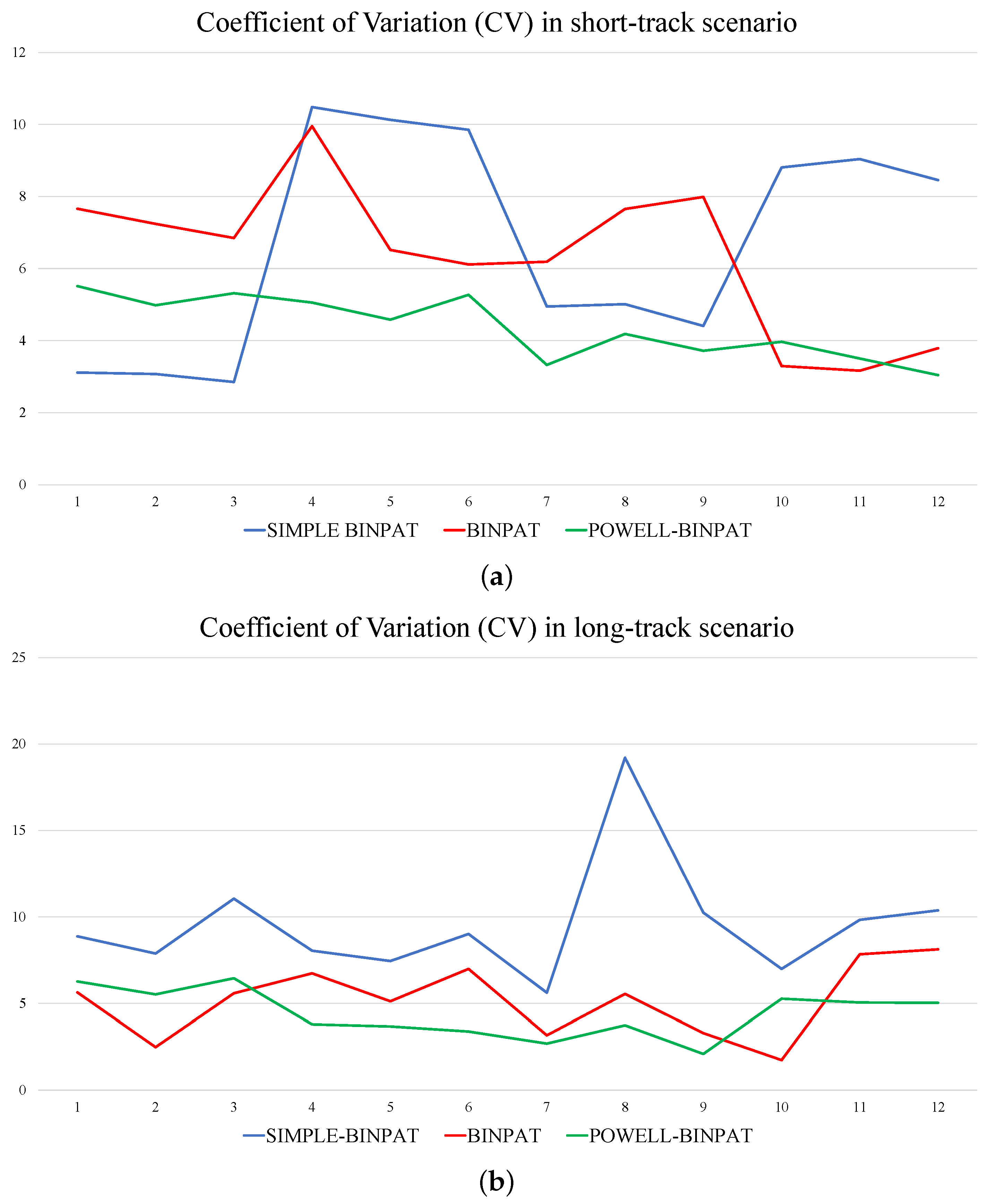
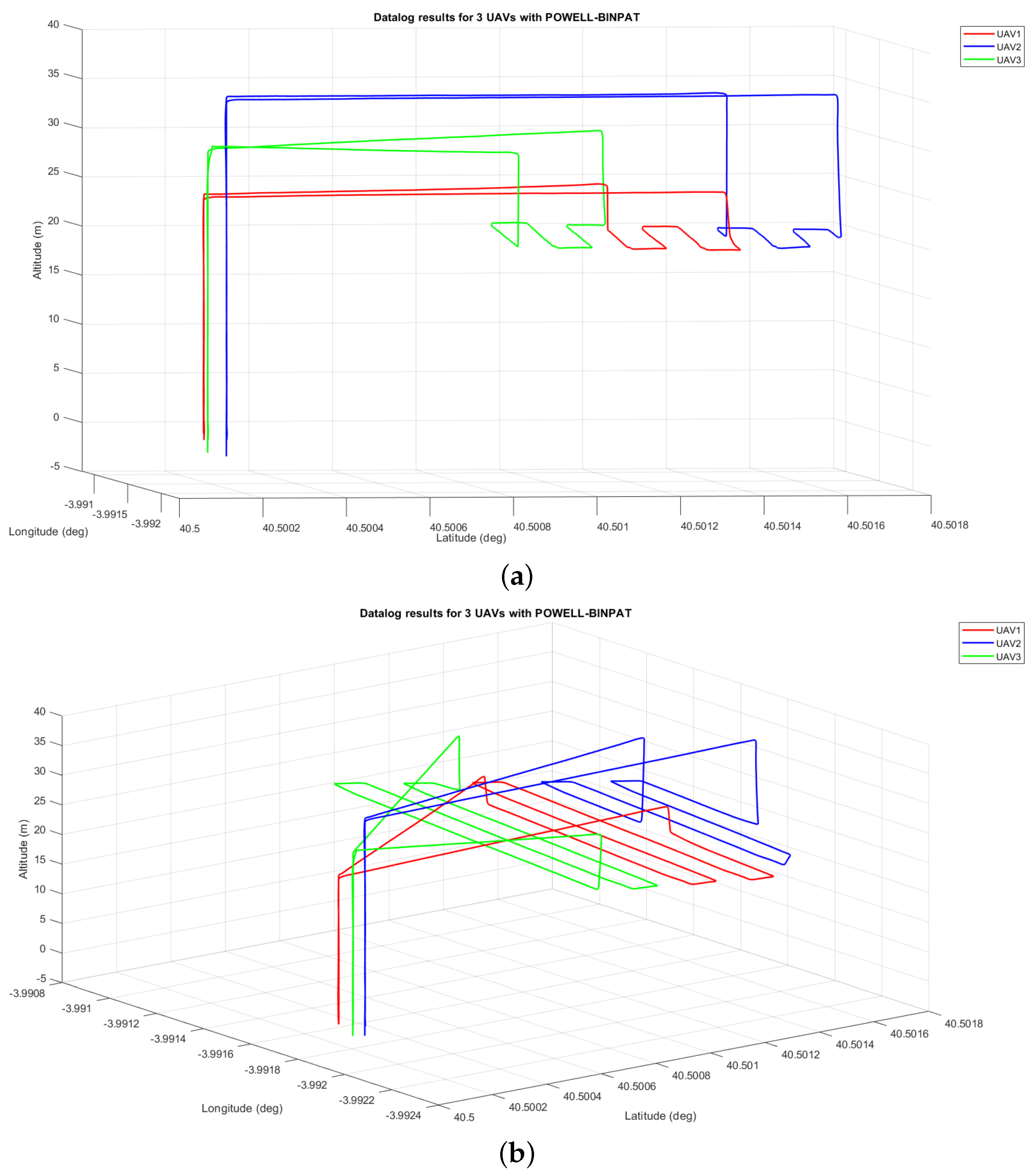
4.2. Simulation Results
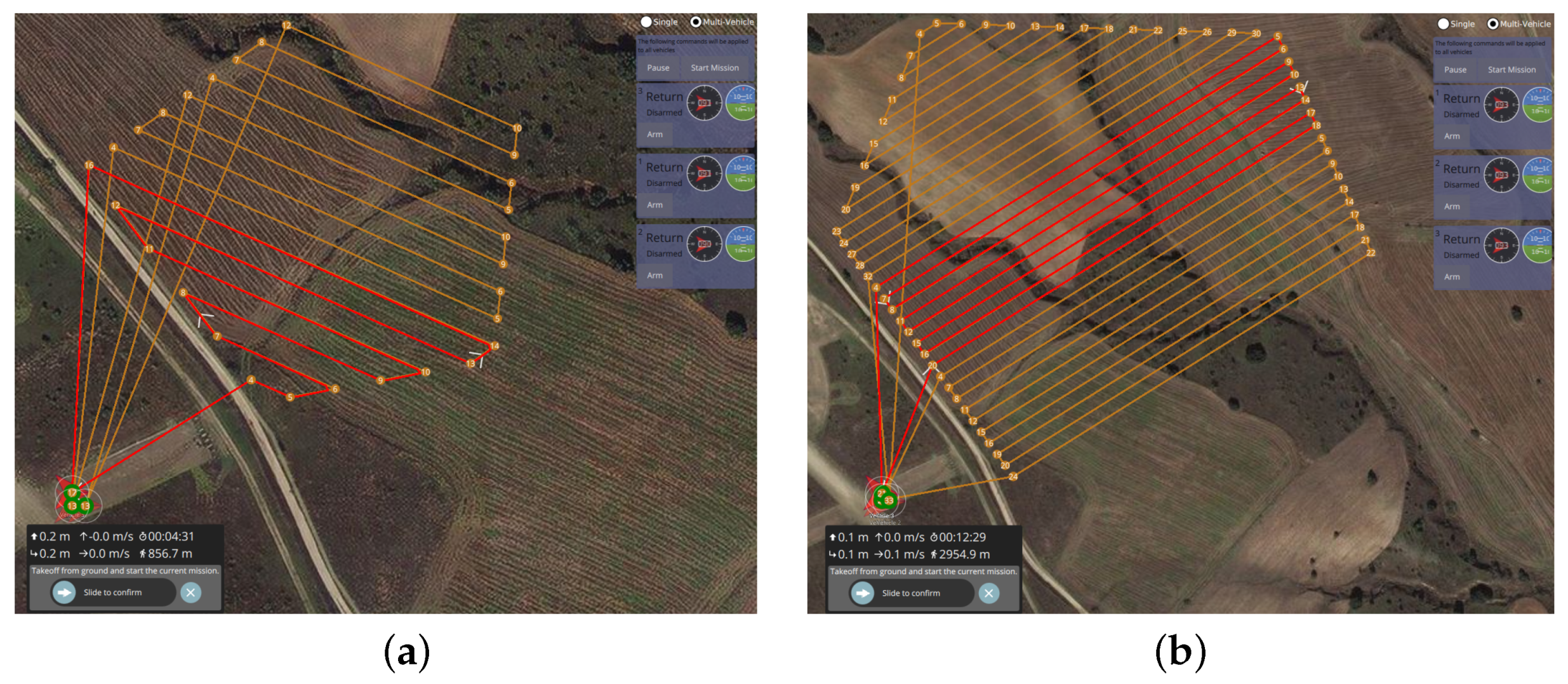
4.3. Real-Flight Test Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| UAS | Unmanned Aerial System |
| H2020 | Horizon 2020 |
| RTL | Return to Launch Point |
| GCS | Ground Control Station |
| GUI | Graphical User Interface |
| BINPAT | Bin Packing Trajectory Planner |
| CBinPack | Custom Bin Packing Algorithm |
| POWELL-BINPAT | Powell Optimized Bin Packing Trajectory Planner |
| FCU | Flight Control Unit |
| FR | First Responder |
| FASTER | First Responder Advanced Technologies for Safe and Efficient Emergency Response |
| PBD | Power Distribution Board |
| ESC | Electronic Speed Controllers |
| CPP | Coverage Path Planning |
| GNSS | Global Navigation Satellite System |
| IP | Internet Protocol |
Appendix A. Simulation Results
Appendix A.1. Time Results for Short-Track Scenario
| SIMPLE-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 318.00 | 330.00 | 344.00 | 266.00 | 277.00 | 287.00 |
| UAV2 | 331.00 | 345.00 | 356.00 | 268.00 | 280.00 | 293.00 |
| UAV3 | 312.00 | 326.00 | 337.00 | 226.00 | 237.00 | 248.00 |
| Max | 331.00 | 345.00 | 356.00 | 268.00 | 280.00 | 293.00 |
| Av | 320.33 | 333.67 | 345.67 | 253.33 | 264.67 | 276.00 |
| SD | 9.71 | 10.02 | 9.61 | 23.69 | 24.01 | 24.43 |
| CV | 3.11 | 3.07 | 2.85 | 10.48 | 10.13 | 9.85 |
| Distance | 10.00 | 10.00 | 10.00 | 5.00 | 5.00 | 5.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 214.00 | 258.00 | 280.00 | 383.00 | 385.00 | 426.00 |
| UAV2 | 232.00 | 294.00 | 313.00 | 396.00 | 399.00 | 412.00 |
| UAV3 | 244.00 | 261.00 | 272.00 | 410.00 | 411.00 | 396.00 |
| Max | 244.00 | 294.00 | 313.00 | 410.00 | 411.00 | 426.00 |
| Av | 230.00 | 271.00 | 288.33 | 396.33 | 398.33 | 411.33 |
| SD | 15.10 | 19.97 | 21.73 | 13.50 | 13.01 | 15.01 |
| CV | 6.19 | 7.65 | 7.99 | 3.29 | 3.17 | 3.79 |
| Distance | 10.00 | 10.00 | 10.00 | 5.00 | 5.00 | 5.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| POWELL-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 243.00 | 262.00 | 266.00 | 397.00 | 385.00 | 401.00 |
| UAV2 | 258.00 | 284.00 | 286.00 | 400.00 | 413.00 | 426.00 |
| UAV3 | 245.00 | 280.00 | 273.00 | 373.00 | 401.00 | 412.00 |
| Max | 258.00 | 284.00 | 286.00 | 400.00 | 413.00 | 426.00 |
| Av | 248.67 | 275.33 | 275.00 | 390.00 | 399.67 | 413.00 |
| SD | 8.14 | 11.72 | 10.15 | 14.80 | 14.05 | 12.53 |
| CV | 3.32 | 4.19 | 3.72 | 3.97 | 3.50 | 3.04 |
| Distance | 10.00 | 10.00 | 10.00 | 5.00 | 5.00 | 5.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| SIMPLE-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 225.00 | 236.00 | 249.00 | 287.00 | 302.00 | 314.00 |
| UAV2 | 232.00 | 247.00 | 259.00 | 283.00 | 302.00 | 308.00 |
| UAV3 | 249.00 | 260.00 | 271.00 | 234.00 | 246.00 | 358.00 |
| UAV4 | 222.00 | 233.00 | 245.00 | 259.00 | 271.00 | 284.00 |
| UAV5 | 222.00 | 231.00 | 245.00 | 290.00 | 304.00 | 316.00 |
| Max | 249.00 | 260.00 | 271.00 | 290.00 | 304.00 | 358.00 |
| Av | 230.00 | 241.40 | 253.80 | 270.60 | 285.00 | 316.00 |
| SD | 11.38 | 12.10 | 11.19 | 23.84 | 25.77 | 26.72 |
| CV | 4.95 | 5.01 | 4.41 | 8.81 | 9.04 | 8.46 |
| Distance | 10.00 | 10.00 | 10.00 | 5.00 | 5.00 | 5.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 237.00 | 260.00 | 258.00 | 322.00 | 335.00 | 318.00 |
| UAV2 | 204.00 | 231.00 | 231.00 | 319.00 | 332.00 | 350.00 |
| UAV3 | 210.00 | 262.00 | 260.00 | 388.00 | 298.00 | 352.00 |
| UAV4 | 229.00 | 233.00 | 233.00 | 380.00 | 295.00 | 312.00 |
| UAV5 | 244.00 | 271.00 | 269.00 | 323.00 | 336.00 | 355.00 |
| Max | 244.00 | 271.00 | 269.00 | 388.00 | 336.00 | 355.00 |
| Av | 224.80 | 251.40 | 250.20 | 346.40 | 319.20 | 337.40 |
| SD | 17.22 | 18.20 | 17.14 | 34.47 | 20.80 | 20.63 |
| CV | 7.66 | 7.24 | 6.85 | 9.95 | 6.52 | 6.12 |
| Distance | 10.00 | 10.00 | 10.00 | 5.00 | 5.00 | 5.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| POWELL-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 228.00 | 254.00 | 251.00 | 289.00 | 303.00 | 311.00 |
| UAV2 | 213.00 | 226.00 | 239.00 | 315.00 | 324.00 | 355.00 |
| UAV3 | 237.00 | 242.00 | 266.00 | 304.00 | 319.00 | 329.00 |
| UAV4 | 240.00 | 245.00 | 266.00 | 325.00 | 338.00 | 338.00 |
| UAV5 | 246.00 | 257.00 | 273.00 | 327.00 | 339.00 | 351.00 |
| Max | 246.00 | 257.00 | 273.00 | 327.00 | 339.00 | 355.00 |
| Av | 232.80 | 244.80 | 259.00 | 312.00 | 324.60 | 336.80 |
| SD | 12.83 | 12.19 | 13.77 | 15.78 | 14.88 | 17.75 |
| CV | 5.51 | 4.98 | 5.32 | 5.06 | 4.58 | 5.27 |
| Distance | 10.00 | 10.00 | 10.00 | 5.00 | 5.00 | 5.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
Appendix A.2. Time Results for Long-Track Scenario
| SIMPLE-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 817.00 | 870.00 | 985.00 | 606.00 | 693.00 | 680.00 |
| UAV2 | 834.00 | 917.00 | 856.00 | 652.00 | 843.00 | 799.00 |
| UAV3 | 749.00 | 1225.00 | 1050.00 | 567.00 | 759.00 | 832.00 |
| Max | 834.00 | 1225.00 | 1050.00 | 652.00 | 843.00 | 832.00 |
| Av | 800.00 | 1004.00 | 963.67 | 608.33 | 765.00 | 770.33 |
| SD | 44.98 | 192.83 | 98.74 | 42.55 | 75.18 | 79.95 |
| CV | 5.62 | 19.21 | 10.25 | 6.99 | 9.83 | 10.38 |
| Distance | 10.00 | 10.00 | 10.00 | 15.00 | 15.00 | 15.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 859.00 | 889.00 | 973.00 | 676.00 | 652.00 | 745.00 |
| UAV2 | 891.00 | 973.00 | 1010.00 | 675.00 | 714.00 | 697.00 |
| UAV3 | 915.00 | 986.00 | 946.00 | 696.00 | 763.00 | 633.00 |
| Max | 915.00 | 986.00 | 1010.00 | 696.00 | 763.00 | 745.00 |
| Av | 888.33 | 949.33 | 976.33 | 682.33 | 709.67 | 691.67 |
| SD | 28.10 | 52.65 | 32.13 | 11.85 | 55.63 | 56.19 |
| CV | 3.16 | 5.55 | 3.29 | 1.74 | 7.84 | 8.12 |
| Distance | 10.00 | 10.00 | 10.00 | 15.00 | 15.00 | 15.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 855.00 | 970.00 | 967.00 | 606.00 | 629.00 | 636.00 |
| UAV2 | 894.00 | 938.00 | 961.00 | 671.00 | 692.00 | 700.00 |
| UAV3 | 898.00 | 900.00 | 999.00 | 625.00 | 643.00 | 652.00 |
| Max | 898.00 | 970.00 | 999.00 | 671.00 | 692.00 | 700.00 |
| Av | 882.33 | 936.00 | 975.67 | 634.00 | 654.67 | 662.67 |
| SD | 23.76 | 35.04 | 20.43 | 33.42 | 33.08 | 33.31 |
| CV | 2.69 | 3.74 | 2.09 | 5.27 | 5.05 | 5.03 |
| Distance | 10.00 | 10.00 | 10.00 | 15.00 | 15.00 | 15.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| SIMPLE-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 579.00 | 637.00 | 682.00 | 494.00 | 653.00 | 596.00 |
| UAV2 | 619.00 | 678.00 | 752.00 | 510.00 | 596.00 | 618.00 |
| UAV3 | 583.00 | 644.00 | 686.00 | 461.00 | 542.00 | 547.00 |
| UAV4 | 544.00 | 588.00 | 596.00 | 562.00 | 581.00 | 683.00 |
| UAV5 | 685.00 | 727.00 | 801.00 | 551.00 | 639.00 | 673.00 |
| Max | 685.00 | 727.00 | 801.00 | 562.00 | 653.00 | 683.00 |
| Av | 602.00 | 654.80 | 703.40 | 515.60 | 602.20 | 623.40 |
| SD | 53.46 | 51.59 | 77.75 | 41.49 | 44.85 | 56.19 |
| CV | 8.88 | 7.88 | 11.05 | 8.05 | 7.45 | 9.01 |
| Distance | 10.00 | 10.00 | 10.00 | 15.00 | 15.00 | 15.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 614.00 | 675.00 | 737.00 | 460.00 | 525.00 | 555.00 |
| UAV2 | 633.00 | 698.00 | 756.00 | 514.00 | 595.00 | 629.00 |
| UAV3 | 577.00 | 690.00 | 698.00 | 462.00 | 549.00 | 558.00 |
| UAV4 | 608.00 | 683.00 | 717.00 | 430.00 | 538.00 | 522.00 |
| UAV5 | 672.00 | 720.00 | 806.00 | 488.00 | 576.00 | 584.00 |
| Max | 672.00 | 720.00 | 806.00 | 514.00 | 595.00 | 629.00 |
| Av | 620.80 | 693.20 | 742.80 | 470.80 | 556.60 | 569.60 |
| SD | 35.00 | 17.22 | 41.46 | 31.70 | 28.52 | 39.84 |
| CV | 5.64 | 2.48 | 5.58 | 6.73 | 5.12 | 6.99 |
| Distance | 10.00 | 10.00 | 10.00 | 15.00 | 15.00 | 15.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
| POWELL-BINPAT | ||||||
|---|---|---|---|---|---|---|
| UAV1 | 560.00 | 634.00 | 675.00 | 489.00 | 556.00 | 591.00 |
| UAV2 | 602.00 | 654.00 | 774.00 | 531.00 | 571.00 | 619.00 |
| UAV3 | 614.00 | 720.00 | 704.00 | 501.00 | 528.00 | 579.00 |
| UAV4 | 557.00 | 659.00 | 733.00 | 502.00 | 552.00 | 592.00 |
| UAV5 | 645.00 | 709.00 | 789.00 | 532.00 | 582.00 | 627.00 |
| Max | 645.00 | 720.00 | 789.00 | 532.00 | 582.00 | 627.00 |
| Av | 595.60 | 675.20 | 735.00 | 511.00 | 557.80 | 601.60 |
| SD | 37.34 | 37.28 | 47.44 | 19.40 | 20.52 | 20.39 |
| CV | 6.27 | 5.52 | 6.45 | 3.80 | 3.68 | 3.39 |
| Distance | 10.00 | 10.00 | 10.00 | 15.00 | 15.00 | 15.00 |
| Altitude | 35.00 | 45.00 | 55.00 | 35.00 | 45.00 | 55.00 |
References
- Ragab, A.R.; Isaac, M.S.A.; Luna, M.A.; Flores Peña, P. WILD HOPPER Prototype for Forest Firefighting. Int. J. Online Biomed. Eng. 2021, 17, 148–168. [Google Scholar] [CrossRef]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Rao, B.; Wang, W. UAV Swarm Intelligence: Recent Advances and Future Trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV Systems: A Survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
- Hedrick, G.; Ohi, N.; Gu, Y. Terrain-aware path planning and map update for mars sample return mission. IEEE Robot. Autom. Lett. 2020, 5, 5181–5188. [Google Scholar] [CrossRef]
- Madridano, A.; Al-Kaff, A.; Martín, D. Trajectory planning for multi-robot systems: Methods and applications. Expert Syst. Appl. 2021, 173, 114660. [Google Scholar] [CrossRef]
- Wu, H.; Li, H.; Xiao, R.; Liu, J. Modeling and simulation of dynamic ant colony’s labor division for task allocation of UAV swarm. Phys. Stat. Mech. Its Appl. 2018, 491, 127–141. [Google Scholar] [CrossRef]
- Luna, M.A.; Ragab, A.R.; Ale Isaac, M.S.; Flores Pena, P.; Campoy Cervera, P. A New Algorithm Using Hybrid UAV Swarm Control System for Firefighting Dynamical Task Allocation. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 655–660. [Google Scholar]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Jing, W.; Deng, D.; Wu, Y.; Shimada, K. Multi-UAV Coverage Path Planning for the Inspection of Large and Complex Structures. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; pp. 1480–1486. [Google Scholar]
- Barrientos, A.; Colorado, J.; Cerro, J.D.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area coverage and path planning for fleets of mini aerial robots. J. Field Robot. 2011, 28, 667–689. [Google Scholar] [CrossRef] [Green Version]
- Lottes, P.; Khanna, R.; Pfeifer, J.; Siegwart, R.; Stachniss, C. UAV-based crop and weed classification for smart farming. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3024–3031. [Google Scholar]
- Nattero, C.; Recchiuto, C.T.; Sgorbissa, A.; Wanderlingh, F. Coverage algorithms for search and rescue with uav drones. In Proceedings of the Workshop of the XIII AI*IA Symposium on Artificial Intelligence, Pisa, Italy, 10–12 December 2014; Volume 12. [Google Scholar]
- Balampanis, F.; Maza, I.; Ollero, A. Coastal areas division and coverage with multiple UAVs for remote sensing. Sensors 2017, 17, 808. [Google Scholar] [CrossRef] [Green Version]
- Cabreira, T.M.; Brisolara, L.B.; Ferreira, P.R., Jr. Survey on coverage path planning with unmanned aerial vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Valente, J.; Sanz, D.; Del Cerro, J.; Barrientos, A.; de Frutos, M.A. Near-optimal coverage trajectories for image mosaicing using a mini quad-rotor over irregular-shaped fields. Prec. Agric. 2013, 14, 115–132. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Er, M.J.; Wang, X. Coverage path planning for UAVs based on enhanced exact cellular decomposition method. Mechatronics 2011, 21, 876–885. [Google Scholar] [CrossRef]
- Coombes, M.; Chen, W.H.; Liu, C. Boustrophedon coverage path planning for UAV aerial surveys in wind. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1563–1571. [Google Scholar]
- Cabreira, T.M.; Di Franco, C.; Ferreira, P.R.; Buttazzo, G.C. Energy-aware spiral coverage path planning for uav photogrammetric applications. IEEE Robot. Autom. Lett. 2018, 3, 3662–3668. [Google Scholar] [CrossRef]
- Di Franco, C.; Buttazzo, G. Coverage path planning for UAVs photogrammetry with energy and resolution constraints. J. Intell. Robot. Syst. 2016, 83, 445–462. [Google Scholar] [CrossRef]
- Muñoz, J.; López, B.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Multi UAV Coverage Path Planning in Urban Environments. Sensors 2021, 21, 7365. [Google Scholar] [CrossRef] [PubMed]
- Nedjati, A.; Izbirak, G.; Vizvari, B.; Arkat, J. Complete coverage path planning for a multi-UAV response system in post-earthquake assessment. Robotics 2016, 5, 26. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.W.; Park, H.J.; Lee, H.; Shim, D.H.; Kim, S.Y. Coverage path planning for multiple unmanned aerial vehicles in maritime search and rescue operations. Comput. Ind. Eng. 2021, 161, 107612. [Google Scholar] [CrossRef]
- Choi, Y.; Choi, Y.; Briceno, S.; Mavris, D.N. Energy-constrained multi-UAV coverage path planning for an aerial imagery mission using column generation. J. Intell. Robot. Syst. 2020, 97, 125–139. [Google Scholar] [CrossRef]
- Maza, I.; Ollero, A. Multiple UAV cooperative searching operation using polygon area decomposition and efficient coverage algorithms. In Distributed Autonomous Robotic Systems; Springer: Tokyo, Japan, 2007; Volume 6, pp. 221–230. [Google Scholar]
- Avellar, G.S.; Pereira, G.A.; Pimenta, L.C.; Iscold, P. Multi-UAV routing for area coverage and remote sensing with minimum time. Sensors 2015, 15, 27783–27803. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y.; Jung, S.; Kim, S.; Cha, J. Autonomous Mission of Multi-UAV for Optimal Area Coverage. Sensors 2021, 21, 2482. [Google Scholar] [CrossRef] [PubMed]
- Dimou, A.; Kogias, D.G.; Trakadas, P.; Perossini, F.; Weller, M.; Balet, O.; Patriakakis, C.Z.; Zahariadis, T.; Daras, P. FASTER: First Responder Advanced Technologies for Safe and Efficient Emergency Response. Technol. Dev. Secur. Pract. 2021, 1, 447–460. [Google Scholar]
- Stanford Artificial Intelligence Laboratory. Robotic Operating System. 2018. Available online: https://www.ros.org (accessed on 12 January 2022).
- Ermakov, V. MAVROS. Available online: http://wiki.ros.org/mavros (accessed on 12 January 2022).
- Huang, W.H. Optimal line-sweep-based decompositions for coverage algorithms. In Proceedings of the 2001 ICRA, IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Korea, 21–26 May 2001; Volume 1, pp. 27–32. [Google Scholar]
- Barna, R.; Solymosi, K.; Stettner, E. Mathematical analysis of drone flight path. J. Agric. Inform. 2019, 10, 15–27. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. IEEE Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- QGroundControl. Available online: http://qgroundcontrol.com/ (accessed on 12 January 2022).
- Jonker, R.; Volgenant, A. A shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing 1987, 38, 325–340. [Google Scholar] [CrossRef]
- Crouse, D.F. On implementing 2D rectangular assignment algorithms. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1679–1696. [Google Scholar] [CrossRef]
- Powell, M.J. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E. SciPy 1.0 Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cel, M.; Dave, C. QFlightInstruments. Available online: http://marekcel.pl/?lang=en&page=qfi (accessed on 22 January 2022).
- Dauni, P.; Firdaus, M.D.; Asfariani, R.; Saputra, M.I.N.; Hidayat, A.A.; Zulfikar, W.B. Implementation of Haversine formula for school location tracking. J. Phys. Conf. Ser. 2019, 1402, 077028. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]





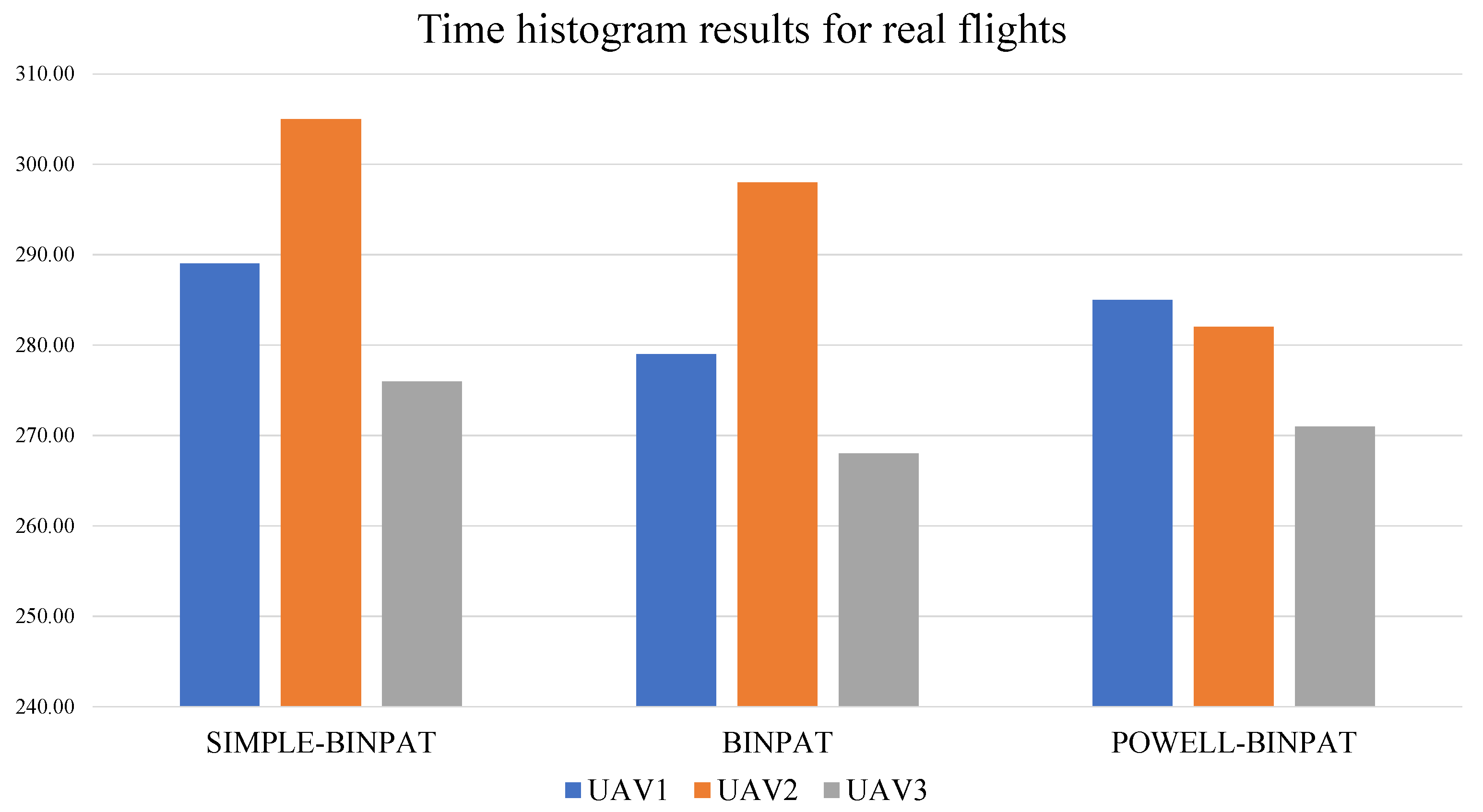
| Based Language | Role | Configuration |
|---|---|---|
| Qt C++ |
| C++ 11 Compiler qmake 3.0 |
| Qt Meta Language (qml) |
| Qt Quick JavaScript |
| Hyper Test Markup Language |
| HTML |
| Brian Fox Unix Shell (Bash) |
|
| Distance-Based Cost | |||
|---|---|---|---|
| UAV | Simple Back-and-Forth | Sampled Back-and-Forth | |
| SIMPLE-BINPAT | BINPAT | POWELL-BINPAT | |
| UAV 1 | 963.81 | 928.75 | 908.75 |
| UAV 2 | 944.65 | 900.34 | 911.77 |
| UAV 3 | 644.58 | 789.27 | 904.72 |
| SD | 179.03 | 73.7 | 3.53 |
| UAVs | SIMPLE-BINPAT | BINPAT | POWELL-BINPAT |
|---|---|---|---|
| 2 | 0.000748 | 0.0021 | 0.296894 |
| 3 | 0.001474 | 0.002244 | 0.301134 |
| 4 | 0.001522 | 0.002756 | 0.512768 |
| 5 | 0.001961 | 0.003125 | 1.419654 |
| 6 | 0.003479 | 0.003365 | 1.853162 |
| 7 | 0.004275 | 0.003924 | 1.96757 |
| Distance-Based Cost Results | ||
|---|---|---|
| UAV Number | BINPAT | POWELL-BINPAT |
| UAV1 | 390.72 | 0 |
| UAV2 | 401.93 | 370.73 |
| UAV3 | 394.62 | 383.99 |
| SIMULATION SCENARIO | ||
|---|---|---|
| Short Track | Long Track | |
| SIMPLE-BINPAT | 300.42 | 795.58 |
| BINPAT | 330.08 | 754.25 |
| POWEL-BINPAT | 322.00 | 735.42 |
| UAV | METHOD | ||
|---|---|---|---|
| SIMPLE-BINPAT | BINPAT | POWELL-BINPAT | |
| UAV1 | 289.00 | 279.00 | 285.00 |
| UAV2 | 305.00 | 298.00 | 282.00 |
| UAV3 | 276.00 | 268.00 | 271.00 |
| Max | 305.00 | 298.00 | 285.00 |
| Av | 290.00 | 281.67 | 279.33 |
| SD | 14.53 | 15.18 | 7.37 |
| CV | 5.01 | 5.39 | 2.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luna, M.A.; Ale Isaac, M.S.; Ragab, A.R.; Campoy, P.; Flores Peña, P.; Molina, M. Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications. Sensors 2022, 22, 2297. https://doi.org/10.3390/s22062297
Luna MA, Ale Isaac MS, Ragab AR, Campoy P, Flores Peña P, Molina M. Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications. Sensors. 2022; 22(6):2297. https://doi.org/10.3390/s22062297
Chicago/Turabian StyleLuna, Marco Andrés, Mohammad Sadeq Ale Isaac, Ahmed Refaat Ragab, Pascual Campoy, Pablo Flores Peña, and Martin Molina. 2022. "Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications" Sensors 22, no. 6: 2297. https://doi.org/10.3390/s22062297
APA StyleLuna, M. A., Ale Isaac, M. S., Ragab, A. R., Campoy, P., Flores Peña, P., & Molina, M. (2022). Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications. Sensors, 22(6), 2297. https://doi.org/10.3390/s22062297








