A Photolysis-Assist Molecular Communication for Tumor Biosensing
Abstract
:1. Introduction
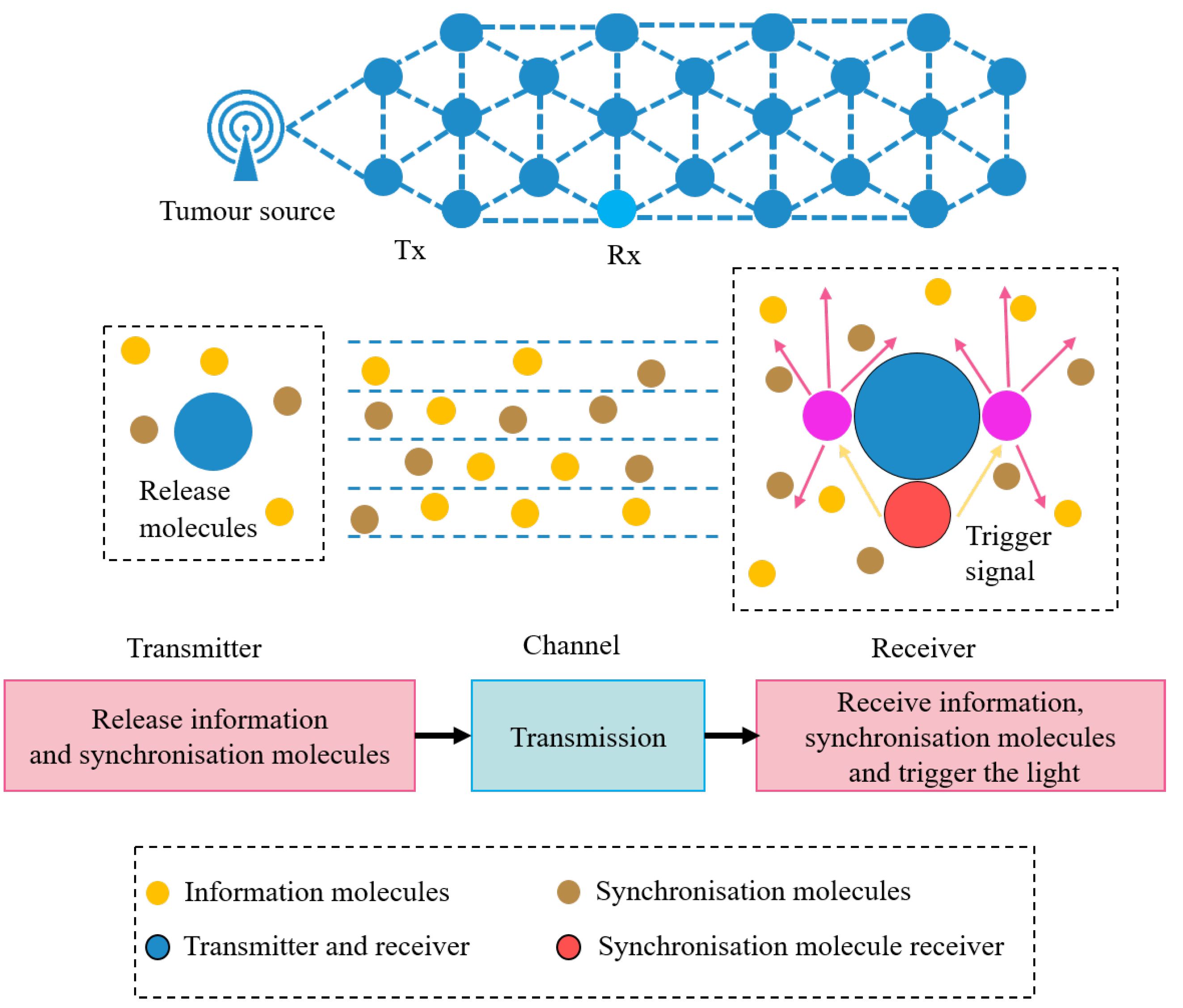
2. System Model
2.1. Biosensing for Tumor
2.2. Provitamin D3 Molecules Propagation Process
- (i)
- the propagation is unbounded,
- (ii)
- the information transmitted is modulated by concentration and UV light,
- (iii)
- the molecule reaching the receiver is considered to be fully absorbed and cannot be recycled.
2.3. Photolysis Reaction
2.4. Diffusion with Photolysis
3. Receiver Model
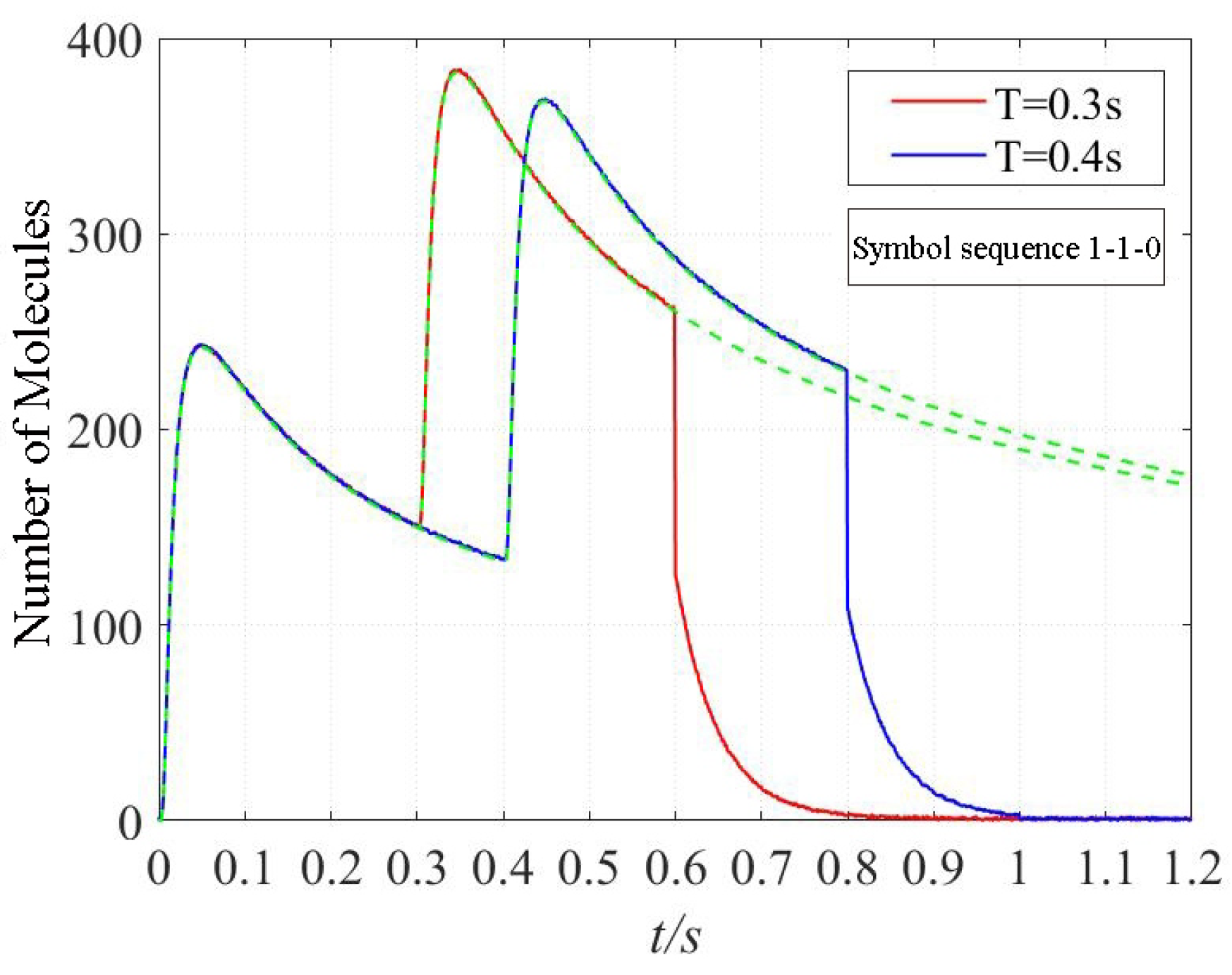
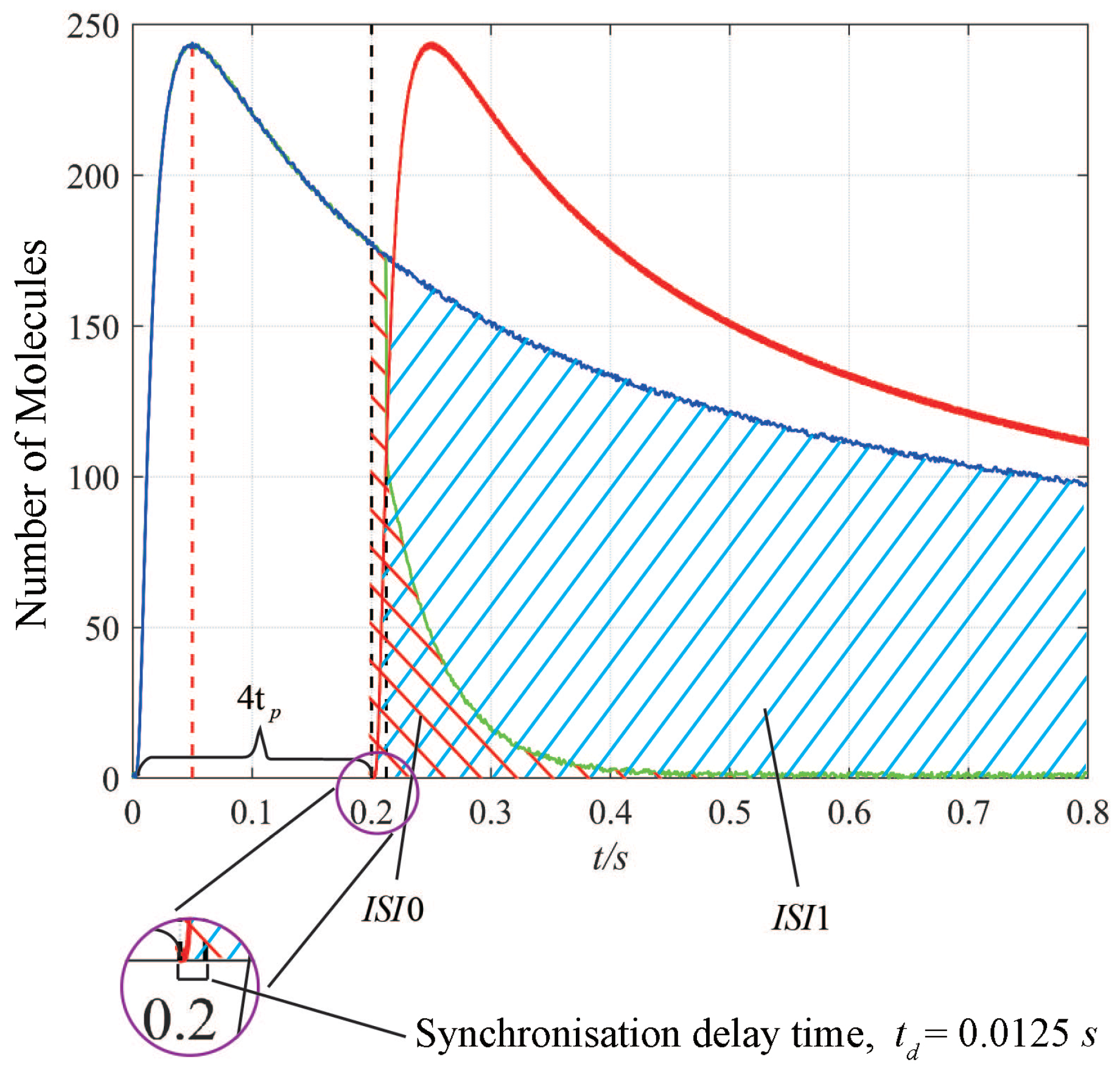
4. Numerical and Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akyildiz, I.F.; Pierobon, M.; Balasubramaniam, S. Moving Forward with Molecular Communication: From Theory to Human Health Applications. Proc. IEEE 2019, 107, 858–865. [Google Scholar]
- Dinc, E.; Akan, O.B. Theoretical Limits on Multiuser Molecular Communication in Internet of Nano-Bio Things. IEEE Trans. Nanobiosci. 2017, 16, 266–270. [Google Scholar]
- Zhao, Q.; Li, M.; Lin, L. Release Rate Optimization in Molecular Communication for Local Nanomachine-Based Targeted Drug Delivery. IEEE Trans. Nanobiosci. 2021, 20, 396–405. [Google Scholar]
- Wang, J.; Peng, M.; Liu, Y.; Liu, X.; Daneshmand, M. Performance Analysis of Signal Detection for Amplify-and-Forward Relay in Diffusion-Based Molecular Communication Systems. IEEE Internet Things J. 2020, 7, 1401–1412. [Google Scholar] [CrossRef]
- Ali, M.; Chen, Y.; Cree, M.J. Autonomous In vivo Computation in Internet-of-Nano-Bio-Things. IEEE Internet Things J. 2020. [Google Scholar] [CrossRef]
- Kuran, M.S.; Yilmaz, H.B.; Demirkol, I.; Farsad, N.; Goldsmith, A. A Survey on Modulation Techniques in Molecular Communication via Diffusion. IEEE Commun. Surv. Tutor. 2021, 23, 7–28. [Google Scholar]
- Dambri, O.A.; Cherkaoui, S. Performance Enhancement of Diffusion-Based Molecular Communication. IEEE Trans. Nanobiosci. 2020, 19, 48–58. [Google Scholar]
- Kuran, M.S.; Yilmaz, H.B.; Tugcu, T.; Akyildiz, I.F. Modulation techniques for communication via diffusion in nanonetworks. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar]
- Thakur, M.S.; Sharma, S.; Bhatia, V. Molecular Signal Detection Using Nonlinear Mapping. IEEE Wirel. Commun. Lett. 2021, 10, 547–551. [Google Scholar]
- Noel, A.; Cheung, K.C.; Schober, R. Improving receiver performance of diffusive molecular communication with Enzymes. IEEE Trans. Nanobiosci. 2014, 13, 31–43. [Google Scholar]
- Yan, H.; Chang, G.; Ma, Z.; Lin, L. Derivative-Based Signal Detection for High Data Rate Molecular Communication System. IEEE Commun. Lett. 2018, 22, 1782–1785. [Google Scholar]
- Tung, T.Y.; Mitra, U. Synchronization Error Robust Transceivers for Molecular Communication. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2019, 5, 207–221. [Google Scholar] [CrossRef]
- Jamali, V.; Ahmadzadeh, A.; Schober, R. Symbol synchronisation for Diffusion-Based Molecular Communications. IEEE Trans. Nanobiosci. 2017, 16, 873–887. [Google Scholar]
- Mukherjee, M.; Yilmaz, H.B.; Bhowmik, B.B.; Lv, Y. Block synchronisation for Diffusion-based Molecular Communication Systems. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018; pp. 1–6. [Google Scholar]
- Noel, A.; Eckford, A.W. Asynchronous peak detection for demodu- lation in molecular communication. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Baish, J.W.; Gazit, Y.; Berk, D.A.; Nozue, M.; Baxter, L.T.; Jain, R.K. Role of tumor vascular architecture in nutrient and drug delivery: An invasion percolation-based network model. Microvasc. Res. 1996, 51, 327–346. [Google Scholar] [PubMed]
- Komar, G.; Kauhanen, S.; Liukko, K.; Seppanen, M.; Kajander, S.; Ovaska, J.; Nuutila, P.; Minn, H. Decreased blood flow with increased metabolic activity: A novel sign of pancreatic tumor aggressiveness. Clin. Cancer Res. 2009, 15, 5511–5517. [Google Scholar] [PubMed] [Green Version]
- Gazit, Y.; Berk, D.A.; Leunig, M.; Baxter, L.T.; Jain, R.K. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys. Rev. Lett. 1995, 75, 2428. [Google Scholar]
- Jelski, W.; Mroczko, B. Molecular and circulating biomarkers of brain tumors. Int. J. Mol. Sci. 2021, 22, 7039. [Google Scholar] [CrossRef]
- Haidar, M.; Metheni, M.; Batteux, F.; Langsley, G. TGF-β2, catalase activity, H2O2 output and metastatic potential of diverse types of tumour. Free Radic. Biol. Med. 2019, 134, 282–287. [Google Scholar] [CrossRef]
- Langen, K.J.; Galldiks, N. Update on amino acid pet of brain tumours. Curr. Opin. Neurol. 2018, 31, 354–361. [Google Scholar] [CrossRef]
- Harney, A.S.; Arwert, E.N.; Entenberg, D.; Wang, Y.; Guo, P.; Qian, B.Z.; Oktay, M.H.; Pollard, J.W.; Jones, J.G.; Condeelis, J.S. Real-time imaging reveals local, transient vascular permeability, and tumor cell intravasation stimulated by TIE2hi macrophage–derived VEGFA. Cancer Discov. 2015, 5, 932–943. [Google Scholar]
- Liu, T.W.; Gammon, S.T.; Fuentes, D.; Piwnica-Worms, D. Multi-modal multi-spectral intravital macroscopic imaging of signaling dynamics in real time during tumor—Immune interactions. Cells 2021, 10, 489. [Google Scholar] [CrossRef]
- Deirram, N.; Zhang, C.; Kermaniyan, S.S.; Johnston, A.P.R.; Such, G.K. pH-Responsive Polymer Nanoparticles for Drug Delivery. Macromol. Rapid Commun. 2019, 40, 1–23. [Google Scholar]
- Song, S.; Chen, F.; Qi, H.; Li, F.; Xin, T.; Xu, J.; Ye, T.; Sheng, N.; Yang, X.; Pan, W. Multifunctional tumor-targeting nanocarriers based on hyaluronic acid-mediated and ph-sensitive properties for efficient delivery of docetaxel. Pharm. Res. 2014, 31, 1032–1045. [Google Scholar] [PubMed]
- Li, D.; Ding, J.; Zhuang, X.; Chen, L.; Chen, X. Drug binding rate regulates the properties of polysaccharide prodrugs. J. Mater. Chem. B 2016, 4, 5167–5177. [Google Scholar]
- Azali, N.S.; Kamarudin, N.H.N.; Jaafar, J.A.; Timmiati, S.N.; Sajab, M.S. Modification of mesoporous silica nanoparticles with pH responsive polymer poly (2-vinylpyrrolidone) for the release of 5-Florouracil. Mater. Today Proc. 2020, 31, A12–A17. [Google Scholar] [CrossRef]
- Barnoy, E.A.; Motiei, M.; Tzror, C.; Rahimipour, S.; Popovtzer, R.; Fixler, D. Biological Logic Gate Using Gold Nanoparticles and Fluorescence Lifetime Imaging Microscopy. ACS Appl. Nano Mater. 2019, 2, 6527–6536. [Google Scholar] [CrossRef]
- Li, J.; Xiang, Y.; Zhang, L.; Huang, L.; Teng, J.; Ding, S.; Cheng, W. Dynamic DNA self-assembly activated hemin-mimetic enzyme system for versatile fl uorescent biosensing. Sens. Actuators B. Chem. 2019, 288, 757–762. [Google Scholar]
- Mohammadian, H.S.; Messier, G.G.; Magierowski, S. Optimum receiver for molecule shift keying modulation in diffusion-based molecular communication channels. Nano Commun. Netw. 2012, 3, 183–195. [Google Scholar]
- Crawford, J.; Davis, D.; Chen, G.; Shetter, R.; Müller, M.; Barrick, J.; Olson, J. An assessment of cloud effects on photolysis rate coefficients: Comparison of experimental and theoretical values. J. Geophys. Res. Atmos. 1999, 104, 5725–5734. [Google Scholar]
- Osmancevic, A.; Sandström, K.; Gillstedt, M.; Landin-Wilhelmsen, K.; Larkö, O.; Larkö, A.M.; Holick, M.F.; Krogstad, A.L. Vitamin D production after UVB exposure—A comparison of exposed skin regions q. J. Photochem. Photobiol. B Biol. 2015, 143, 38–43. [Google Scholar]
- Handy, B.E.; Maciejewski, M.; Baiker, A. Vanadia, vanadia-titania, and vanadia-titania-silica gels: Structural genesis and catalytic behavior in the reduction of nitric oxide with ammonia. J. Catal. 1992, 134, 75–86. [Google Scholar]
- American National Standard Institute. American National Standard for Safe Use of Lasers (ANSI Z136.1-2014). 2014. Available online: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1852037 (accessed on 30 January 2022).
- McKenzie, A.L. Physics of thermal processes in laser-tissue interaction. Phys. Med. Biol. 1990, 35, 1175–1209. [Google Scholar] [PubMed]
- Sliney, D.H.; Trokel, S.L. Medical Lasers and Their Safe Use; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar]
- Gottfried, N.; Kaiser, W.; Braun, M.; Fuss, W.; Kompa, K.L. Ultrafast electrocyclic ring opening in previtamin D photochemistry. Chem. Phys. Lett. 1984, 110, 335–339. [Google Scholar]
- Alberts, B.; Bray, D.; Hopkin, K.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Essential Cell Biology, 3rd ed.; Garland Science: New York, NY, USA, 2010. [Google Scholar]
- Nelson, P. Biological Physics: Energy, Information, Life, 1st ed.; Freeman: San Francisco, CA, USA, 2008. [Google Scholar]
- Atakan, B.; Akan, O.B. Deterministic capacity of information flow in molecular nanonetworks. Nano Commun. Netw. 2010, 1, 31–42. [Google Scholar]
- Redner, S. A Guide to First-Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Nakano, T.; Okaie, Y.; Liu, J. Channel model and capacity analysis of molecular communication with Brownian motion. IEEE Commun. Lett. 2012, 16, 797–800. [Google Scholar]
- Mu, X.; Yan, H.; Li, B.; Liu, M.; Zheng, R.; Li, Y.; Lin, L. Low-Complexity Adaptive Signal Detection for Mobile Molecular Communication. IEEE Trans. Nanobiosci. 2020, 19, 237–248. [Google Scholar]





| Parameters | Symbol | Value |
|---|---|---|
| Released molecules | Q | 10,000 |
| Information molecules diffusion coefficient (m/s) | D | |
| Synchronization molecules diffusion coefficient (m/s) | D | |
| Distance (m) | d | 10 |
| Degradation rate (s) | J | 20 |
| Symbol interval (s) | Tb | 0.2 |
| Signal-to-noise ratio(dB) | SNR | 2–18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Bian, H.; Chen, Y. A Photolysis-Assist Molecular Communication for Tumor Biosensing. Sensors 2022, 22, 2495. https://doi.org/10.3390/s22072495
Sun Y, Bian H, Chen Y. A Photolysis-Assist Molecular Communication for Tumor Biosensing. Sensors. 2022; 22(7):2495. https://doi.org/10.3390/s22072495
Chicago/Turabian StyleSun, Yue, Huafeng Bian, and Yifan Chen. 2022. "A Photolysis-Assist Molecular Communication for Tumor Biosensing" Sensors 22, no. 7: 2495. https://doi.org/10.3390/s22072495
APA StyleSun, Y., Bian, H., & Chen, Y. (2022). A Photolysis-Assist Molecular Communication for Tumor Biosensing. Sensors, 22(7), 2495. https://doi.org/10.3390/s22072495







