Experimental Research on Vibration-Damping Effect of Combined Shear Hinge Prefabricated Steel Spring Floating Slab Track
Abstract
:1. Introduction
2. Model Building and Test Plan
2.1. Full-Scale Model of SSFST
2.2. Drop Hammer Impact Test Instrument
2.3. Fatigue Load Test System
2.4. Introduction to the Test Plan
2.4.1. Test Point Layout
2.4.2. Test Sampling Parameters and Data Processing Principles
3. Time Domain and Frequency Domain Analysis
3.1. Time Domain Analysis
- (1)
- Intercept the original signal for 0.4 s, use wavelet soft threshold denoising decomposition to denoise, and use the default threshold for the threshold. A three-level wavelet decomposition is performed on the basic vibration signal, and an approximation signal is obtained.
- (2)
- Reconstruct the decomposed signal to obtain the noise-reduced basic vibration signal for subsequent frequency domain and vibration level analysis.
- (1)
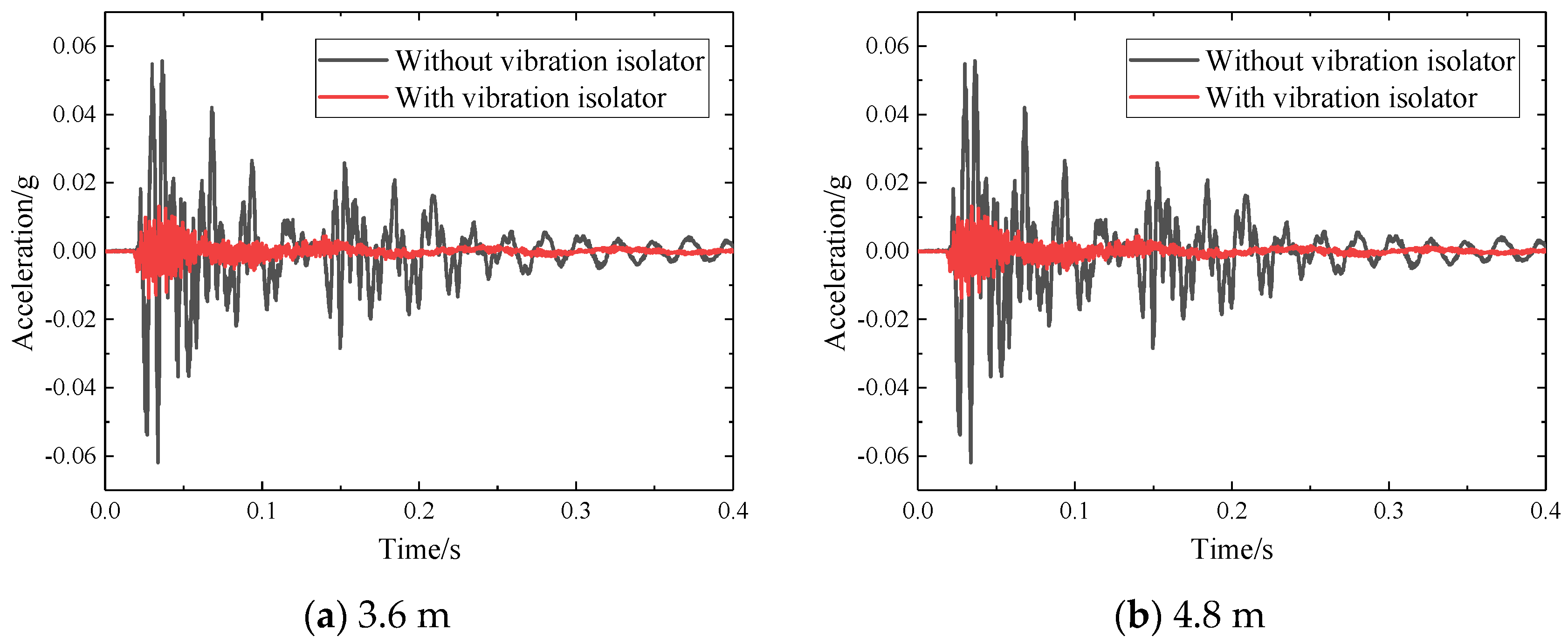
- During the SSFST drop hammer impact test, it can be seen that the positive value of acceleration at the foundation is slightly larger than its negative value. After the vibration isolator is installed, its peak acceleration is greatly reduced, and its drop is about 80%, which shows that the vibration isolator has a key effect on reducing the dynamic response of the SSFST system to the foundation.
- (2)
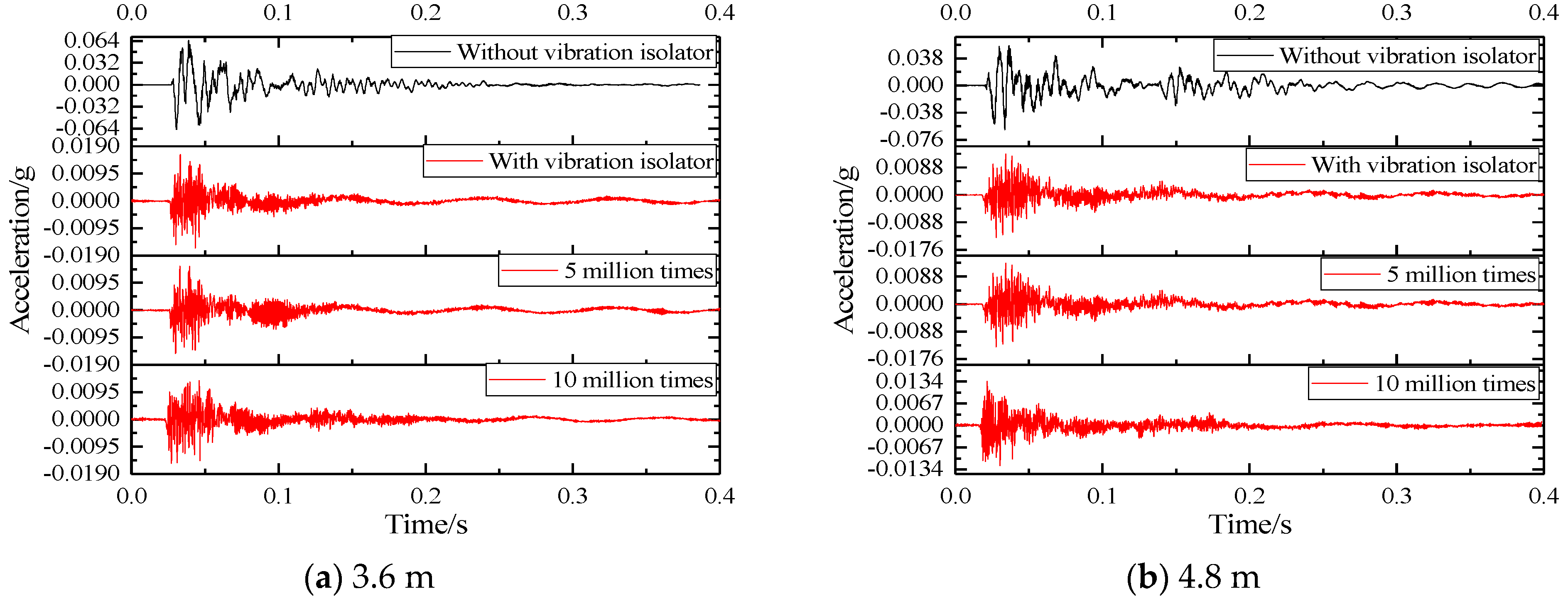
- After the prefabricated SSFST is installed with the vibration isolator, the period of shock and vibration level is continuously shortened. After the installation of the vibration isolator, the total vibration duration of the SSFST is less than the prefabricated SSFST without the vibration isolator. It can be seen that the SSFST with the vibration isolator can achieve excellent vibration energy absorption.
- (3)
- SSFST of two lengths has similar basic vibration laws, and both acceleration amplitude and attenuation waveform are similar. Among them, the acceleration of 4.8 m SSFST is slightly smaller than 3.6 m SSFST, which indicates that the length of the track slab has a small effect on the attenuation of the foundation vibration.
- (4)
- With the application of fatigue load, the waveform of the acceleration waveform at the foundation has slight changes, but the overall change is small.
- (1)
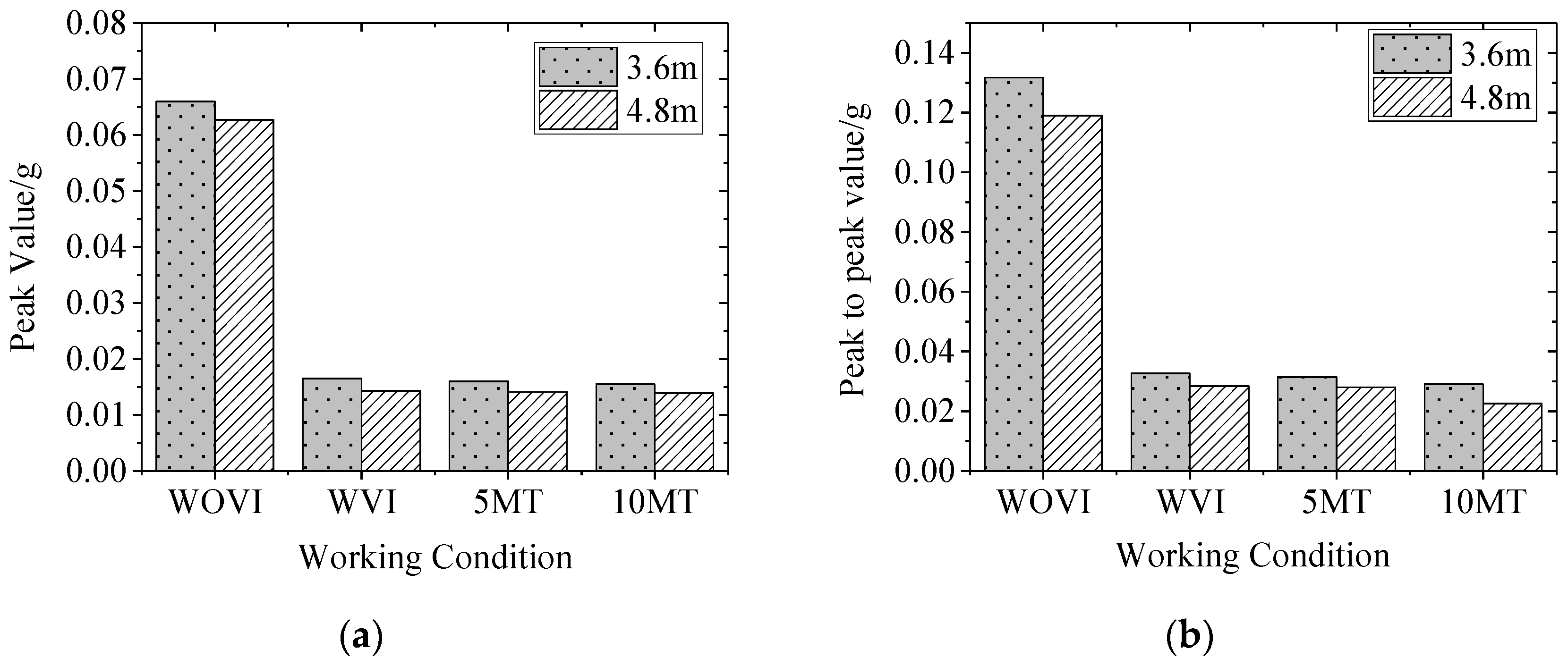
- The peak value mainly represents the maximum value of the acceleration at the foundation when the SSFST is subjected to an impact, which can directly reflect the acceleration of the foundation when the impact is received.
- (2)
- The peak-to-peak value is the difference between the maximum value and the minimum value of the acceleration at the foundation, and its magnitude has a greater correlation with the shock received at the foundation, so it can be used as an important indicator for evaluating the shock response received at the foundation.
- (3)
- The effective value is also called root-mean-square value, which can represent the vibration energy generated when the foundation is impacted.
- (1)
- After the installation of the vibration isolator, the foundation acceleration peak, peak-to-peak value, and effective value are significantly reduced, and the drop rate is about 80%. Therefore, SSFST is beneficial to reduce the vibration response level of the track structure.
- (2)
- When the number of fatigue loads increases, the maximum, minimum, peak, and effective values of the two SSFST foundations have little change, and the overall decrease slightly. It can be seen that the vibration effect of this type of SSFST is less affected by the fatigue load.
- (3)
- Comparing the peak and effective value of vibration acceleration at the foundation under different assembly conditions of vibration isolators and the number of fatigue loads, it can be seen that the vibration response amplitude of 3.6 m SSFST is slightly larger than 4.8 m SSFST, and the acceleration level of both at the foundation is generally low.
- (4)
- When laying SSFST tracks in subway tunnels, when wheel-rail impact occurs, it is beneficial to reduce the vibration response of the tunnel base and lining structure and reduce the possibility of damage to the track and tunnel structure.
3.2. Frequency Domain Analysis
4. Hilbert–Huang Transform Analysis
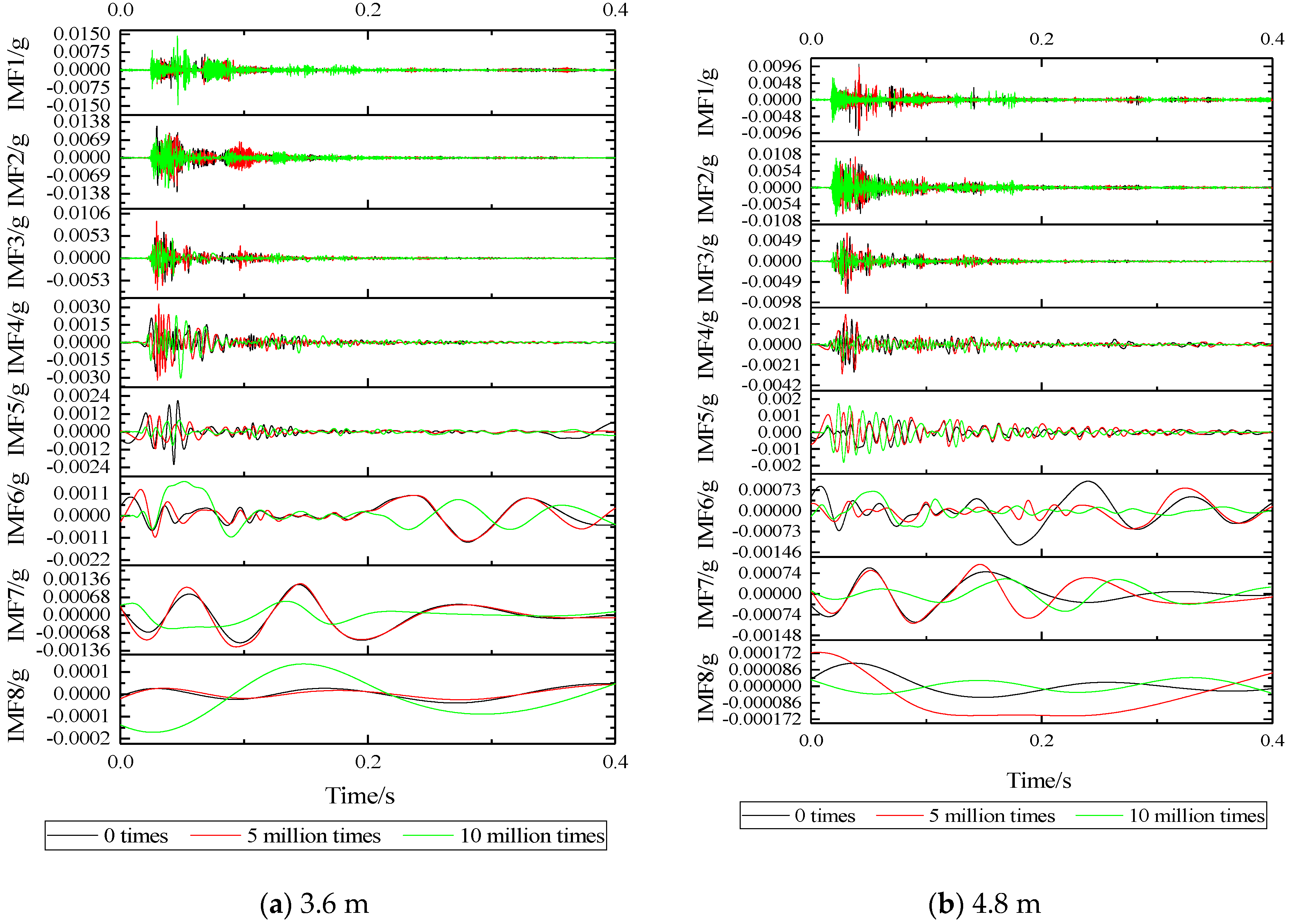
4.1. EMD Analysis
4.2. Kurtosis Analysis
- (1)
- When there is no vibration isolator, the IMF1 kurtosis value of the vibration signal at the foundation is larger, and the kurtosis value decreases sharply at IMF2 and is smaller than the working condition of the vibration isolator. After IMF3, the kurtosis value changes steadily, gradually decreases, and gradually becomes negative kurtosis at IMF7~IMF8;
- (2)
- After installing the vibration isolator, the IMF kurtosis values of each order are reduced, the IMF2~IMF4 is higher than without vibration isolators, and the peak signal density of the IMF3 frequency band is the highest. As the number of fatigue increases, the kurtosis value of this frequency range first increases and then decreases, indicating that the fatigue load will affect the distribution of the vibration acceleration IMF peak point at the foundation.
4.3. Hilbert Envelope Spectrum Analysis
5. Vibration Level Analysis
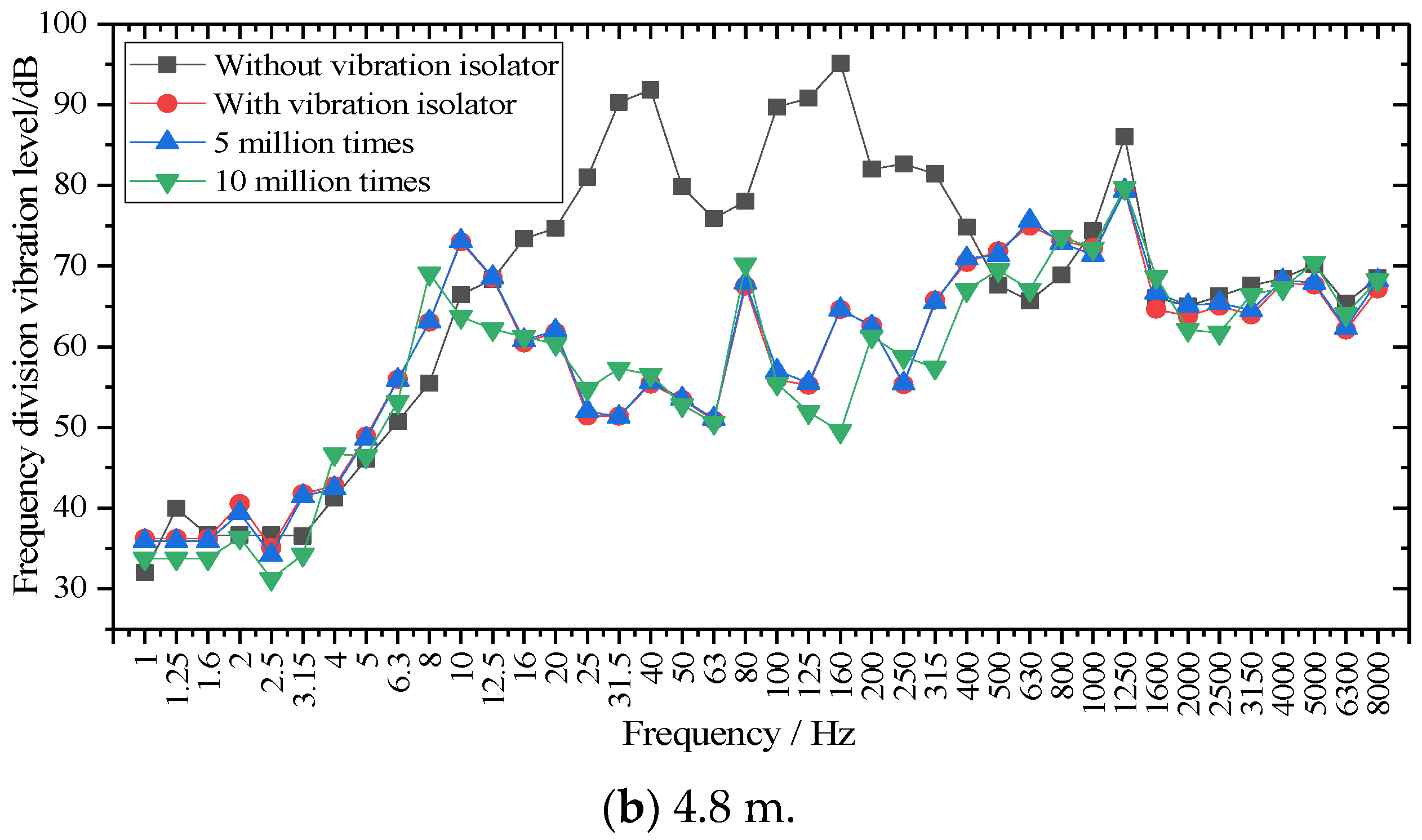
5.1. Frequency Division Vibration Level Analysis
5.2. Z Vibration Level Analysis
5.3. Comparison with Cast-in-Place SSFST Railway Field Test
- v0—the reference speed of the source intensity, in km/h;
- v—the speed of the train, in km/h.
6. Conclusions
- (1)
- Through amplitude (RMS) analysis, EMD analysis, kurtosis value analysis, Hilbert envelope spectrum analysis, and vibration level analysis, it can be seen that this novel type of combined shear hinge SSFST can have excellent isolation effect on vibration and can still maintain good vibration damping ability within 10 million fatigue loads (about 5 years).
- (2)
- By comparing the magnitude (RMS) spectrum, the IMF waveform of the EMD method, the frequency division vibration level curve and the insertion loss curve, it can be seen that the frequency of the peak point of the frequency division vibration level curve corresponds to the peak point frequency of the amplitude (RMS) spectrum. The vibration damping results of each frequency band reflected by the insertion loss curve are consistent with the IMF display results after EMD transformation, that is, the vibration-damping effect of the steel spring vibration isolator mainly acts on the middle and low-frequency bands of 16–400 Hz.
- (3)
- According to the amplitude (RMS) spectrum, frequency division vibration level curve, and insertion loss curve, it can be seen that the vibration near 10 Hz will be intensified after the vibration isolator is installed, while the human body is more sensitive to the vibration response in the frequency range of 0~80 Hz. Therefore, this problem should be improved in the subsequent SSFST design to weaken the vibration response of the floating slab to the foundation in this frequency band.
- (4)
- The vibration indicators and variation laws of the two sizes of SSFST are similar, and the acceleration amplitude and attenuation laws are consistent. The vibration response of 4.8 m SSFST is slightly smaller than that of 3.6 m SSFST. Since 3.6 m SSFST is easier to lay a smooth line, in practical applications, 3.6 m SSFST should be arranged in the curved section, and 4.8 m SSFST should be arranged in the straight-line section with higher train speed.
- (5)
- Compared with the field experiment method, the drop-weight method can also systematically study the vibration characteristics of this novel combined shear hinge SSFST before laying, and the displayed SSFST vibration damping characteristics are consistent with the field test and can conduct a comprehensive evaluation of the vibration-damping effect of SSFST at a lower cost.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grootenhuis, P. Floating track slab isolation for railways. J. Sound Vib. 1977, 51, 443–448. [Google Scholar] [CrossRef]
- Ding, D.; Liu, W.; Li, K.; Sun, X.; Liu, W. Low frequency vibration tests on a floating slab track in an underground laboratory. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2011, 12, 345–359. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, X.; Wang, W.; Zhu, Z.; Wu, Z. Comparative Research on the Vibration Transmission Law of Different Subway Track Types. J. Railw. Eng. Soc. 2021, 38, 74–79. (In Chinese) [Google Scholar]
- Ji, T.; Qiu, L.; Zhou, B. Theoretical analysis of long floating slab track(part I)—Dispersion graph and critical velocity. Chin. J. Comput. Mech. 2009, 26, 919–923. [Google Scholar]
- Cui, F.; Chew, C. The effectiveness of floating slab track system—Part I. Receptance methods. Appl. Acoust. 2000, 61, 441–453. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, X.; Wang, J.; Liu, F.; Wang, W.; Shuaibu, A. Wheel–rail stochastic dynamics and rail wear analysis of small radius waveformd sections of a tram line based on generalized probability density evolution. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 543–588. [Google Scholar] [CrossRef]
- Dere, Y. Effectiveness of the floating slab track system constructed at Konya Light Rail. Measurement 2016, 89, 48–54. [Google Scholar] [CrossRef]
- Geng, C.; Tian, M. Vibration Frequency Analysis of Floating Slab Track System. Urban Mass Transit 2007, 53, 155–164. [Google Scholar]
- Wang, L.; Xuan, Y.; Wan, J.; Jiang, J. Simulation research on the vibration insulation performance of the floating slab track structure. China Railw. Sci. 2005, 26, 48–52. [Google Scholar]
- Zhou, B.; Xie, X.; Yang, Y. Simulation of wave propagation of floating slab track-tunnel-soil system by 2d theoretical model. Int. J. Struct. Stab. Dyn. 2013, 14, 1350051. [Google Scholar] [CrossRef]
- Sun, C.; Gao, L.; Ma, J. Environmental vibration isolation tests and analysis on steel spring floating slab track used in subway. Int. Symp. Environ. Vib. 2011, 1, 840–842. [Google Scholar]
- Ding, D.; Liu, W.; Zhang, B.; Sun, X. Modal Analysis on the Floating Slab Track. J. China Railw. Soc. 2008, 30, 61–64. (In Chinese) [Google Scholar]
- Liu, W.; Ding, D.; Li, K.; Zhang, H. Experimental study of the low-frequency vibration characteristics of steel spring floating slab track. China Civ. Eng. J. 2011, 44, 118–125. (In Chinese) [Google Scholar]
- Wei, K.; Dou, Y.; Yang, Q. Random vibration analysis and parameter optimization of steel-spring floating-slab track. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 45, 115–119. [Google Scholar]
- Kang, L.; Lei, Z. Shield Tunnel Structure Modal Analysis with Floating Slab Track on Elastic Foundation. Adv. Mater. Res. 2013, 838–841, 1393–1398. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, C. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads. Int. J. Non-Linear Mech. 2014, 58, 222–232. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, J.; Wang, M.; Cai, C. Mechanical characteristic variation of ballastless track in high-speed railway: Effect of train–track interaction and environment loads. Railw. Eng. Sci. 2020, 28, 94–109. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, X.; Ye, M.; Zhu, Z.; Xiao, Y.; Peng, G.; Hu, G.; Hu, J.; Xu, R. Combined shear hinge device of floating slab track. Chin. Invent. Pat. 2021, 1–8. (In Chinese) [Google Scholar]
- Luo, J.; Zhu, S.; Zhai, W. An advanced train-slab track spatially coupled dynamics model: Theoretical methodologies and numerical applications. J. Sound Vib. 2021, 501, 116059. [Google Scholar] [CrossRef]
- Zeng, Z.; Huang, X.; Yan, B.; Wang, W.; Shuaibu, A.; He, X. Research on the fatigue performance of self-compacting concrete structure in CRTSIII slab ballastless track under the action of heavy haul train. Constr. Build. Mater. 2021, 303, 124465. [Google Scholar] [CrossRef]
- GB 10071-88; Urban Area Environmental Vibration Measurement Method. National Environmental Protection Agency: Beijing, China, 1989.
- Huang, N.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Gu, J.; Peng, Y.; Lu, H.; Cao, B.; Chen, G. Compound fault diagnosis and identification of hoist spindle device based on hilbert huang and energy entropy. J. Mech. Sci. Technol. 2021, 35, 4281–4290. [Google Scholar] [CrossRef]
- Gao, C.; Zhou, S. Wavelet transform threshold noise reduction methods in the oil pipeline leakage monitoring and positioning system. J. Elec. 2010, 27, 405–411. [Google Scholar] [CrossRef]
- Li, Y.; Lin, J.; Niu, G.; Wu, M.; Wei, X. A Hilbert–Huang Transform-Based Adaptive Fault Detection and Classification Method for Microgrids. Energies 2021, 14, 5040. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Liu, S.; Li, Z. AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform. J. Cent. South Univ. 2021, 28, 1843–1856. [Google Scholar] [CrossRef]
- Diao, Y.; Jia, D.; Liu, G.; Sun, Z.; Xu, J. Structural damage identification using modified Hilbert–Huang transform and support vector machine. J. Civ. Struct. Health Monit. 2021, 11, 1155–1174. [Google Scholar] [CrossRef]
- Murzagulov, D.; Zamyatin, A.; Romanovich, O. Approach to the Detection of Anomalies in Process Signals by Using the Hilbert–Huang Transform. Optoelectron. Instrum. Data Process. 2021, 57, 27–36. [Google Scholar] [CrossRef]
- Neukirch, M.; García-Jerez, A.; Villaseñor, A.; Luzón, F.; Ruiz, M.; Molina, L. Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform. Sensors 2021, 21, 3292. [Google Scholar] [CrossRef] [PubMed]
- Alberti, T.; Milillo, A.; Laurenza, M.; Massetti, S.; Ivanovski, S.; Ippolito, A.; Plainaki, C.; De Angelis, E.; Mangano, V.; Mura, A.; et al. Multiscale Features of the Near-Hermean Environment as Derived Through the Hilbert-Huang Transform. Front. Phys. 2021, 9, 668098. [Google Scholar] [CrossRef]
- Das, I.; Arif, M.; Oo, A.; Subhani, M. An Improved Hilbert–Huang Transform for Vibration-Based Damage Detection of Utility Timber Poles. Appl. Sci. 2021, 11, 2974. [Google Scholar] [CrossRef]
- Zhao, Y.; Shan, R.; Wang, H. Research on vibration effect of tunnel blasting based on an improved Hilbert–Huang transform. Environ. Earth Sci. 2021, 80, 206. [Google Scholar] [CrossRef]
- Ezzeiri, S.; Hamdi, E. Ultrasonic rock microcracking characterization and classification using Hilbert–Huang transform. Innov. Infrastruct. Solut. 2020, 5, 100. [Google Scholar] [CrossRef]
- AlSaleh, R.; Ni, Y. Condition assessment of a supertall structure by an improved Hilbert-Huang transform and empirical mode decomposition method. Int. J. Sustain. Mater. Struct. Syst. 2020, 4, 244–267. [Google Scholar]
- Harsuko, M.; Zulfakriza, Z.; Nugraha, A.; Sarjan, A.; Widiyantoro, S.; Rosalia, S.; Puspito, N.; Sahara, D. Investigation of Hilbert–Huang Transform and Fourier Transform for Horizontal-to-Vertical Spectral Ratio Analysis: Understanding the Shallow Structure in Mataram City, Lombok, Indonesia. Front. Earth Sci. 2020, 8, 334. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, M. Analysis of rolling bearing fault diagnosis based on EMD and kurtosis Hilbert envelope demodulation. J. Mech. Electr. Eng. 2014, 31, 1136–1167. (In Chinese) [Google Scholar]
- CJJ/T 191-2012; Technical Code for Floating Slab Track. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012. (In Chinese)
- ISO 2631/1-1985; Evaluation of Human Exposure to Whole-Body Vibration. The International Organization for Standardization: Delft, The Netherlands, 1985.
- Lian, S.; Yin, X. Theoretical Research and Practice of Floating Slab Track; China Railway Press: Beijing, China, 2021. (In Chinese) [Google Scholar]
- HJ453-2018; Technical Guidelines for Environmental Impact Assessment Urban Rail Transit. Ministry of Ecology and Environment: Beijing, China, 2018. (In Chinese)
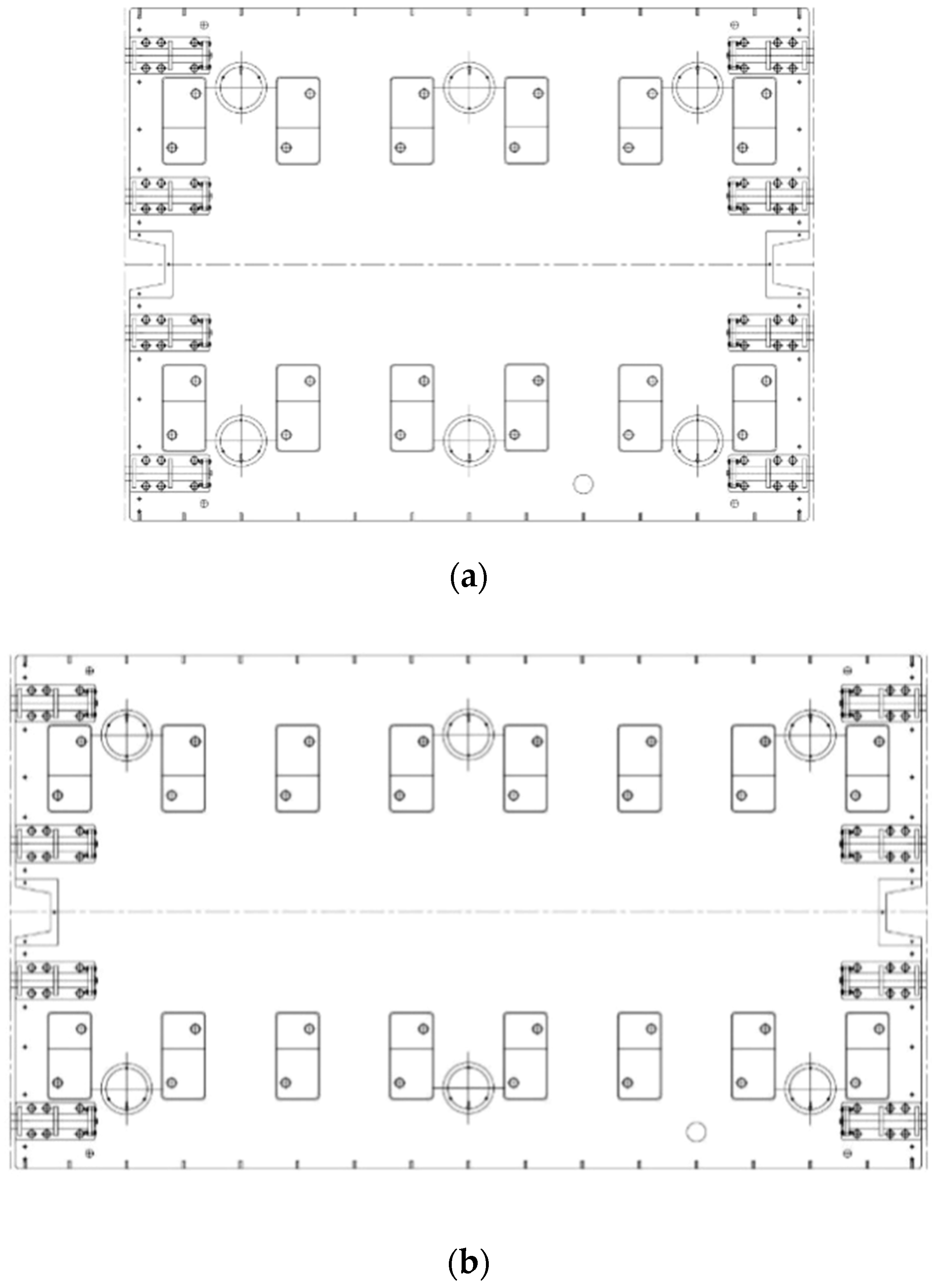
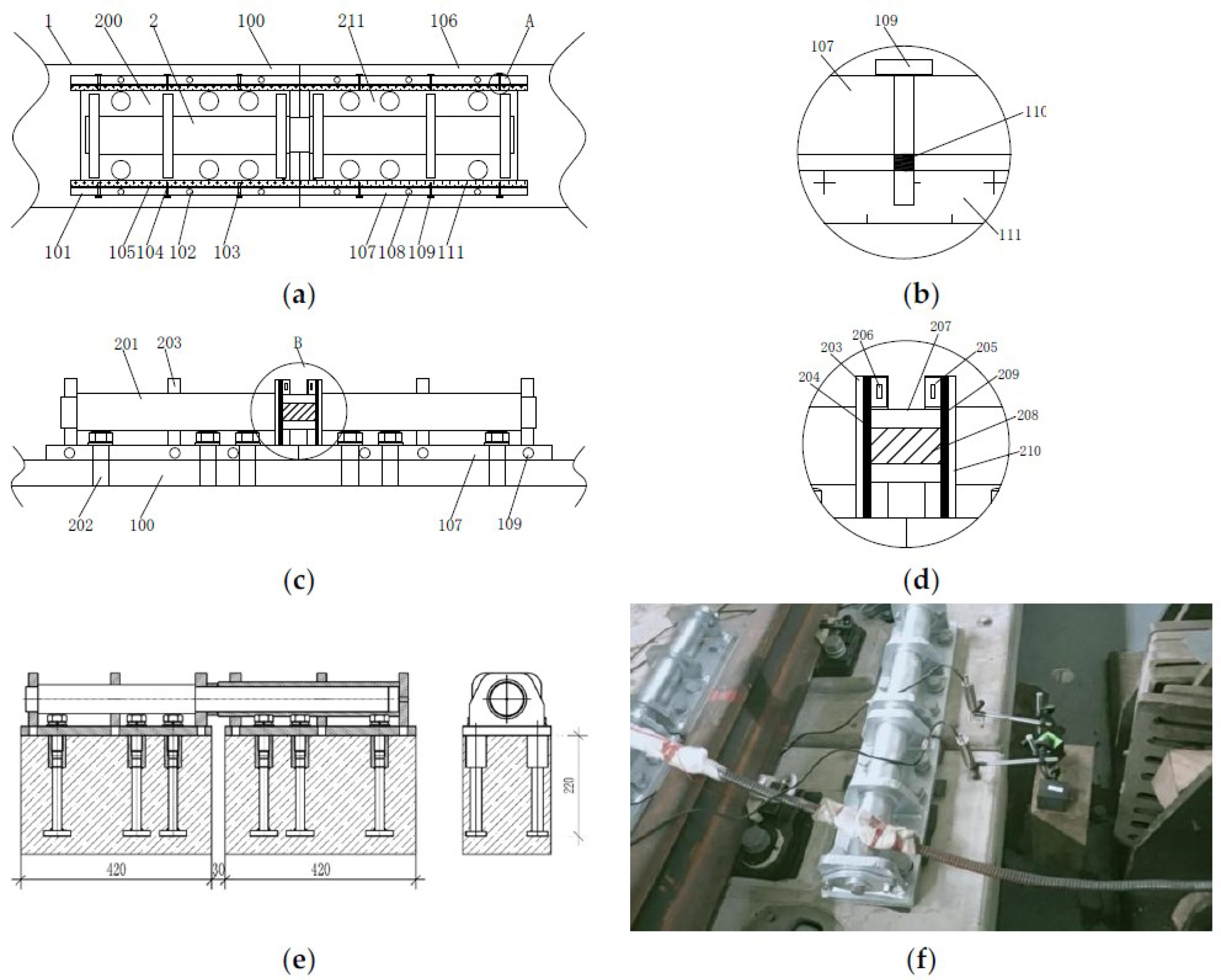
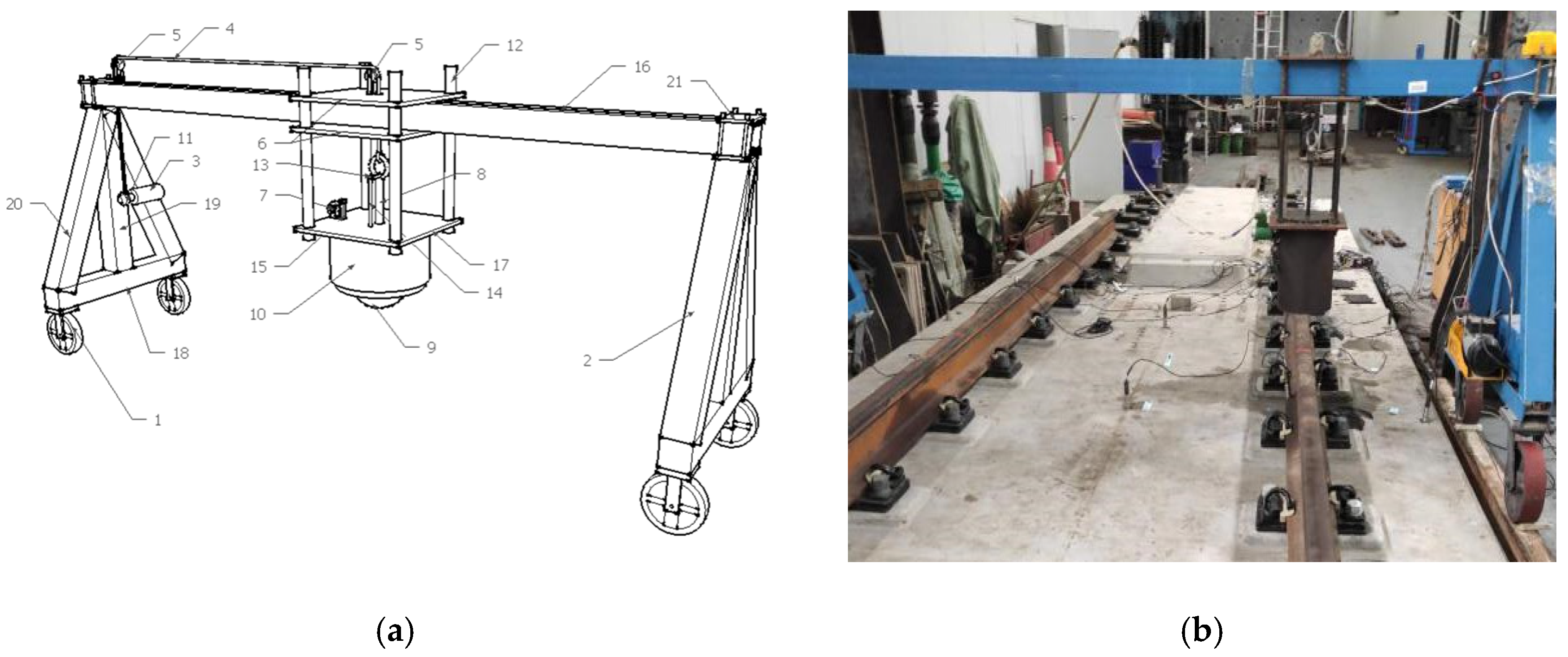




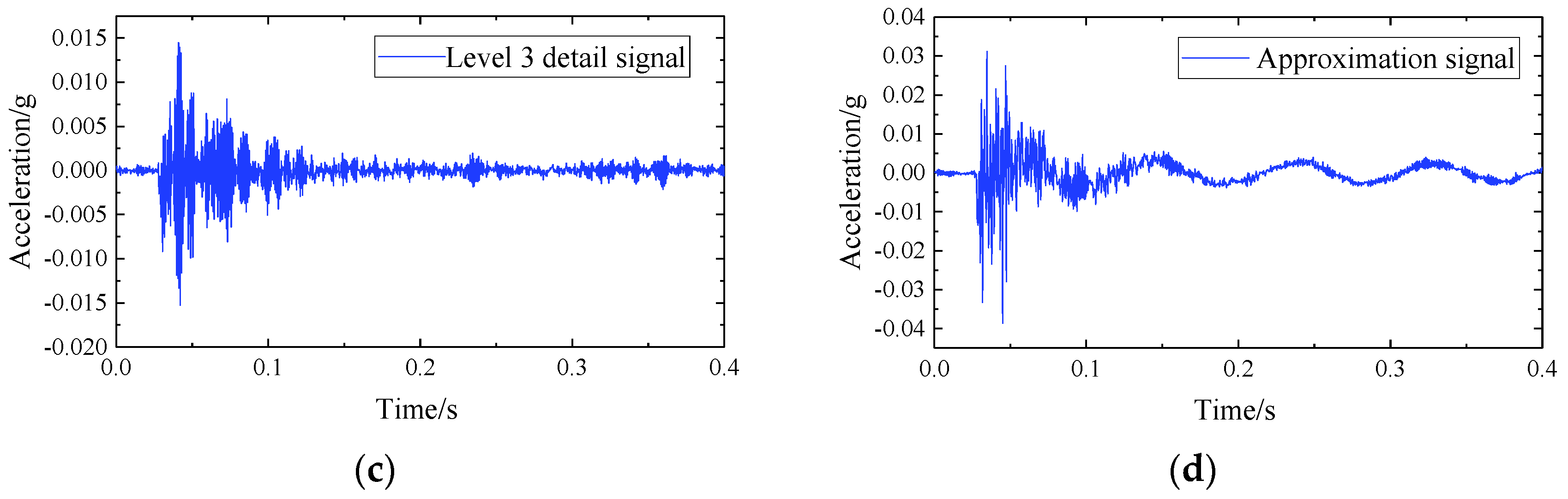













| Length | Component | Amount | Parameter |
|---|---|---|---|
| 3.6 m | Prefabricated slab | 1 | 3600 mm(length) × 2700 mm(width) × 340 mm(thickness), C50 |
| Vibration isolator | 6 | 6.66 kN/mm | |
| Shear hinge | 2 | SDT-55 × 870 | |
| 4.8 m | Prefabricated slab | 1 | 4800 mm(length) × 2700 mm(width) × 340 mm(thickness), C50 |
| Vibration isolator | 6 | 7.50 kN/mm | |
| Shear hinge | 2 | SDT-55 × 870 |
| Fatigue Load | Without Vibration Isolator (WOVI) | With Vibration Isolator (WVI) | 5 Million Times (5 MT) | 10 Million Times (10 MT) | ||||
|---|---|---|---|---|---|---|---|---|
| Type | 3.6 m | 4.8 m | 3.6 m | 4.8 m | 3.6 m | 4.8 m | 3.6 m | 4.8 m |
| Max | 0.0657 | 0.0563 | 0.0162 | 0.0143 | 0.0154 | 0.0141 | 0.0138 | 0.0127 |
| Minimum | −0.0660 | −0.0627 | −0.0165 | −0.0145 | −0.0160 | −0.0143 | −0.0153 | −0.0139 |
| Peak | −0.0660 | −0.0627 | −0.0165 | −0.0145 | −0.0160 | −0.0143 | −0.0155 | −0.0139 |
| Peak-to-peak | 0.1317 | 0.1190 | 0.0327 | 0.0284 | 0.0314 | 0.0280 | 0.0291 | 0.0226 |
| Effective value | 0.0105 | 0.0099 | 0.0021 | 0.0018 | 0.0020 | 0.0017 | 0.0018 | 0.0016 |
| Size | Working Condition | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 |
|---|---|---|---|---|---|---|---|---|---|
| 3.6 m | Without vibration isolator | −0.0112 | −0.0128 | −0.0370 | −0.0271 | −0.0248 | −0.0041 | −0.0031 | −0.0016 |
| With vibration isolator | −0.0077 | −0.0131 | −0.0062 | −0.0025 | −0.0022 | −0.0013 | −0.0011 | 0.0000 | |
| 5 million times | −0.0061 | −0.0108 | −0.0076 | −0.0032 | −0.0012 | −0.0013 | −0.0012 | 0.0000 | |
| 10 million times | −0.0145 | −0.0116 | −0.0044 | −0.0030 | −0.0009 | −0.0011 | −0.0005 | −0.0002 | |
| 4.8 m | Without vibration isolator | −0.0149 | −0.0132 | −0.0385 | −0.0314 | −0.0159 | −0.0065 | −0.0011 | −0.0004 |
| With vibration isolator | −0.0103 | −0.0084 | −0.0076 | −0.0028 | −0.0009 | −0.0012 | −0.0010 | −0.0001 | |
| 5 million times | −0.0089 | −0.0086 | −0.0077 | −0.0030 | −0.0012 | −0.0006 | −0.0010 | −0.0002 | |
| 10 million times | −0.0066 | −0.0093 | −0.0055 | −0.0017 | −0.0018 | −0.0006 | −0.0006 | 0.0000 |
| Size | Working Condition | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 |
|---|---|---|---|---|---|---|---|---|---|
| 3.6 m | Without vibration isolator | 0.0127 | 0.0122 | 0.0398 | 0.0297 | 0.0270 | 0.0048 | 0.0023 | 0.0015 |
| With vibration isolator | 0.0066 | 0.0121 | 0.0061 | 0.0021 | 0.0021 | 0.0010 | 0.0012 | 0.0000 | |
| 5 million times | 0.0051 | 0.0096 | 0.0088 | 0.0033 | 0.0011 | 0.0013 | 0.0012 | 0.0000 | |
| 10 million times | 0.0142 | 0.0089 | 0.0047 | 0.0023 | 0.0008 | 0.0017 | 0.0005 | 0.0001 | |
| 4.8 m | Without vibration isolator | 0.0169 | 0.0180 | 0.0507 | 0.0366 | 0.0155 | 0.0060 | 0.0011 | 0.0005 |
| With vibration isolator | 0.0103 | 0.0094 | 0.0058 | 0.0026 | 0.0008 | 0.0010 | 0.0009 | 0.0001 | |
| 5 million times | 0.0093 | 0.0100 | 0.0068 | 0.0031 | 0.0012 | 0.0008 | 0.0011 | 0.0002 | |
| 10 million times | 0.0064 | 0.0096 | 0.0049 | 0.0013 | 0.0017 | 0.0007 | 0.0005 | 0.0000 |
| Size | Working Condition | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 |
|---|---|---|---|---|---|---|---|---|---|
| 3.6 m | Without vibration isolator | 55.651 | 15.281 | 17.178 | 10.485 | 12.149 | 7.734 | 4.863 | 2.739 |
| With vibration isolator | 33.294 | 33.107 | 40.849 | 18.419 | 10.579 | 2.906 | 2.704 | 2.116 | |
| 5 million times | 26.238 | 30.885 | 29.416 | 18.065 | 10.149 | 2.851 | 2.531 | 2.063 | |
| 10 million times | 23.472 | 22.742 | 25.266 | 14.071 | 8.862 | 3.725 | 2.484 | 1.967 | |
| 4.8 m | Without vibration isolator | 48.728 | 16.509 | 15.663 | 15.672 | 5.911 | 7.301 | 2.058 | 1.633 |
| With vibration isolator | 28.936 | 25.593 | 40.848 | 23.911 | 7.629 | 5.288 | 3.099 | 3.227 | |
| 5 million times | 26.062 | 24.315 | 31.146 | 15.54 | 5.404 | 3.571 | 2.549 | 2.13 | |
| 10 million times | 24.424 | 20.564 | 28.221 | 9.048 | 4.728 | 2.949 | 2.288 | 1.677 |
| Size | Working Condition | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 |
|---|---|---|---|---|---|---|---|---|---|
| 3.6 m | With vibration isolator | 0.598 | 2.167 | 2.378 | 1.757 | 0.871 | 0.376 | 0.556 | 0.773 |
| 5 million times | 0.788 | 0.933 | 0.720 | 0.981 | 0.959 | 0.981 | 0.936 | 0.975 | |
| 10 million times | 0.705 | 0.687 | 0.619 | 0.764 | 0.838 | 1.282 | 0.919 | 0.930 | |
| 4.8 m | With vibration isolator | 0.594 | 1.550 | 2.608 | 1.526 | 1.291 | 0.724 | 1.506 | 1.976 |
| 5 million times | 0.901 | 0.950 | 0.762 | 0.650 | 0.708 | 0.675 | 0.823 | 0.660 | |
| 10 million times | 0.844 | 0.804 | 0.691 | 0.378 | 0.620 | 0.558 | 0.738 | 0.520 |
| Track Size | Data | Track Structure Components | |||
|---|---|---|---|---|---|
| Without Vibration Isolator | With Vibration Isolator | After 5 Million Fatigue | After 10 Million Fatigue | ||
| 3.6 m | Z vibration level | 96.0 | 73.9 | 72.8 | 72.2 |
| Insertion loss | 22.1 | 23.2 | 23.8 | ||
| 4.8 m | Z vibration level | 94.0 | 73.7 | 72.9 | 72.4 |
| Insertion loss | 20.3 | 21.1 | 21.6 | ||
| Track Bed Form | OMT | SSFST |
|---|---|---|
| VLZ (dB) | 70.83 | 46.61 |
| Speed (km/h) | 71.36 | 73.00 |
| Corrected value after the speed is unified (dB) | 0.00 | −0.20 |
| VLZ after speed correction (dB) | 70.83 | 46.41 |
| Insertion loss ΔVLZ (dB) | 24.42 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Huang, X.; Li, Z.; Wang, W.; Shi, Z.; Yuan, Y.; Shuaibu, A.A. Experimental Research on Vibration-Damping Effect of Combined Shear Hinge Prefabricated Steel Spring Floating Slab Track. Sensors 2022, 22, 2567. https://doi.org/10.3390/s22072567
Zeng Z, Huang X, Li Z, Wang W, Shi Z, Yuan Y, Shuaibu AA. Experimental Research on Vibration-Damping Effect of Combined Shear Hinge Prefabricated Steel Spring Floating Slab Track. Sensors. 2022; 22(7):2567. https://doi.org/10.3390/s22072567
Chicago/Turabian StyleZeng, Zhiping, Xudong Huang, Zhuang Li, Weidong Wang, Zixiao Shi, Yu Yuan, and Abdulmumin Ahmed Shuaibu. 2022. "Experimental Research on Vibration-Damping Effect of Combined Shear Hinge Prefabricated Steel Spring Floating Slab Track" Sensors 22, no. 7: 2567. https://doi.org/10.3390/s22072567
APA StyleZeng, Z., Huang, X., Li, Z., Wang, W., Shi, Z., Yuan, Y., & Shuaibu, A. A. (2022). Experimental Research on Vibration-Damping Effect of Combined Shear Hinge Prefabricated Steel Spring Floating Slab Track. Sensors, 22(7), 2567. https://doi.org/10.3390/s22072567






