Singular Spectrum Analysis for Modal Estimation from Stationary Response Only
Abstract
:1. Introduction
2. Research Methods
2.1. State Space Equation
2.2. Singular Spectrum Analysis
- Embedding
- Singular Value Decomposition
- Grouping
- Averaging
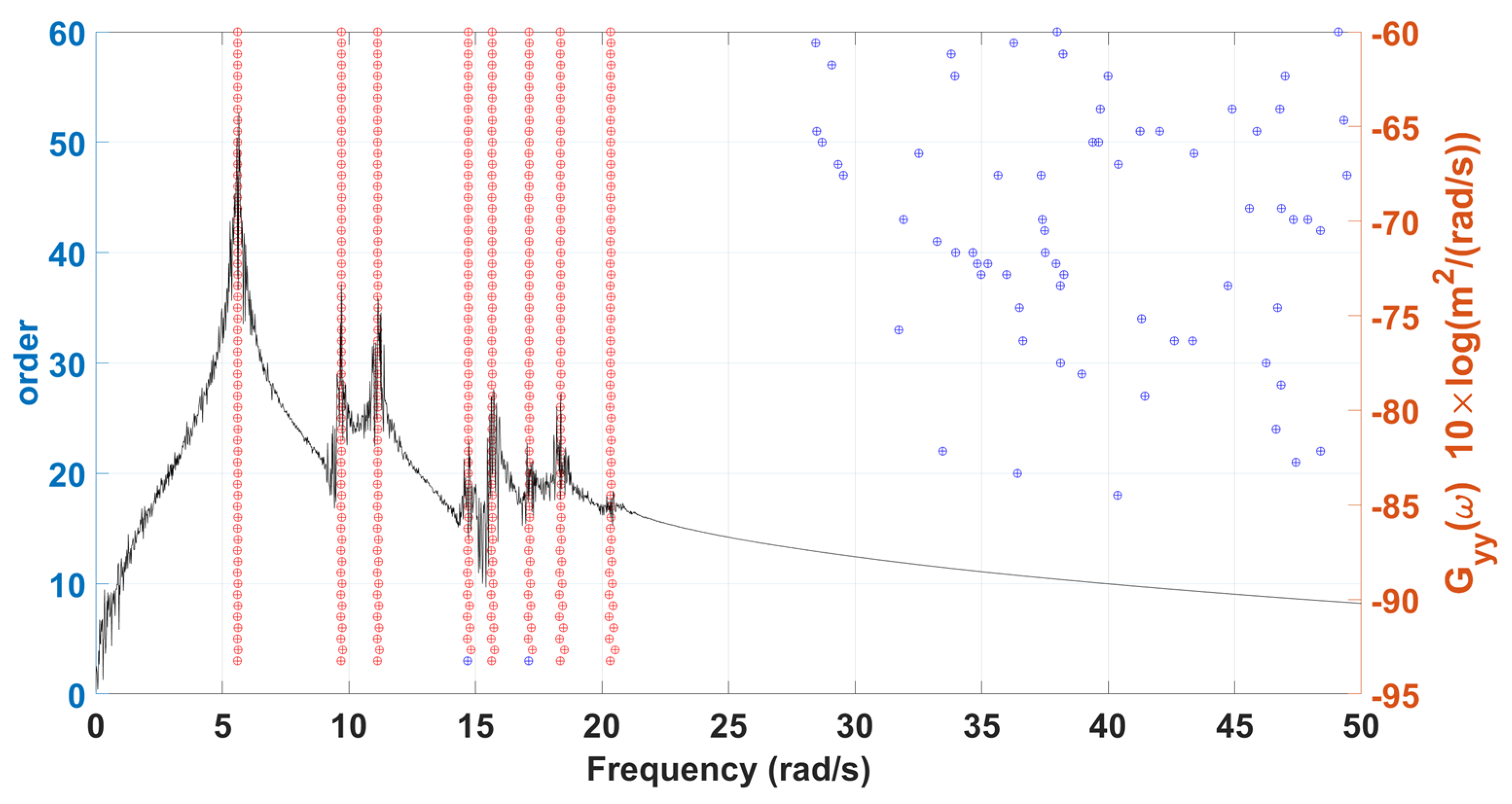
2.3. Stabilization Diagram
3. Numerical Simulations and Verifications
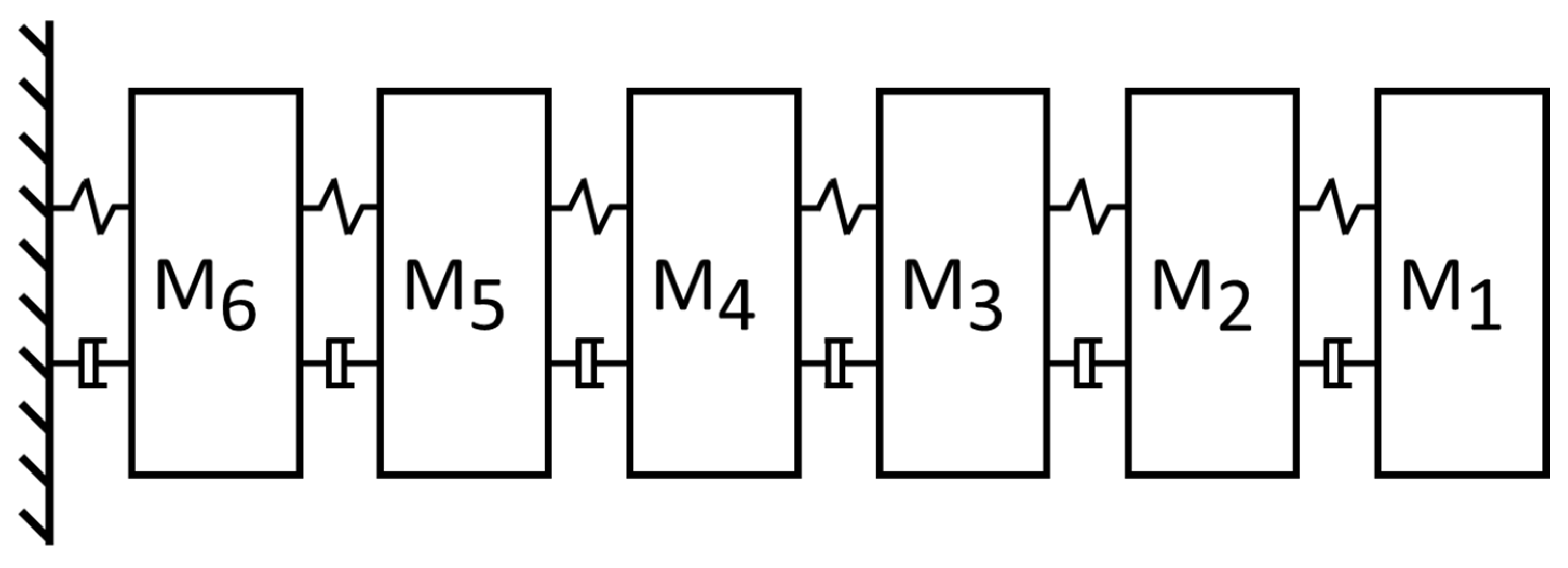
3.1. 6-DOF Chain Model
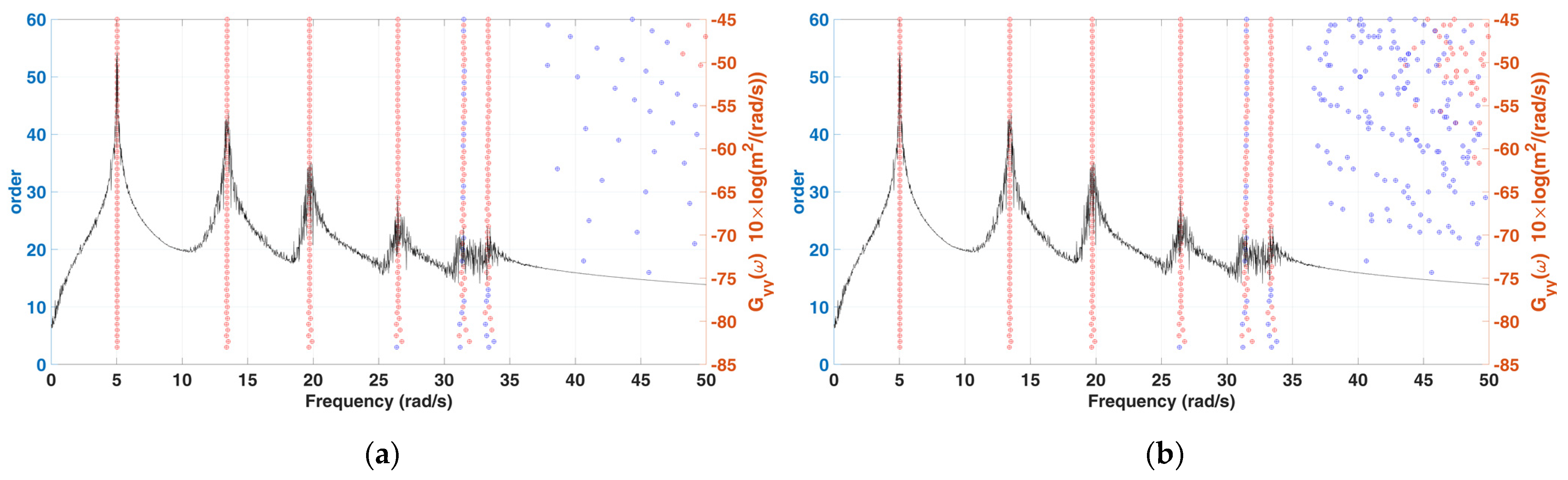
- Comparison of computation efficiency of singular spectrum analysis
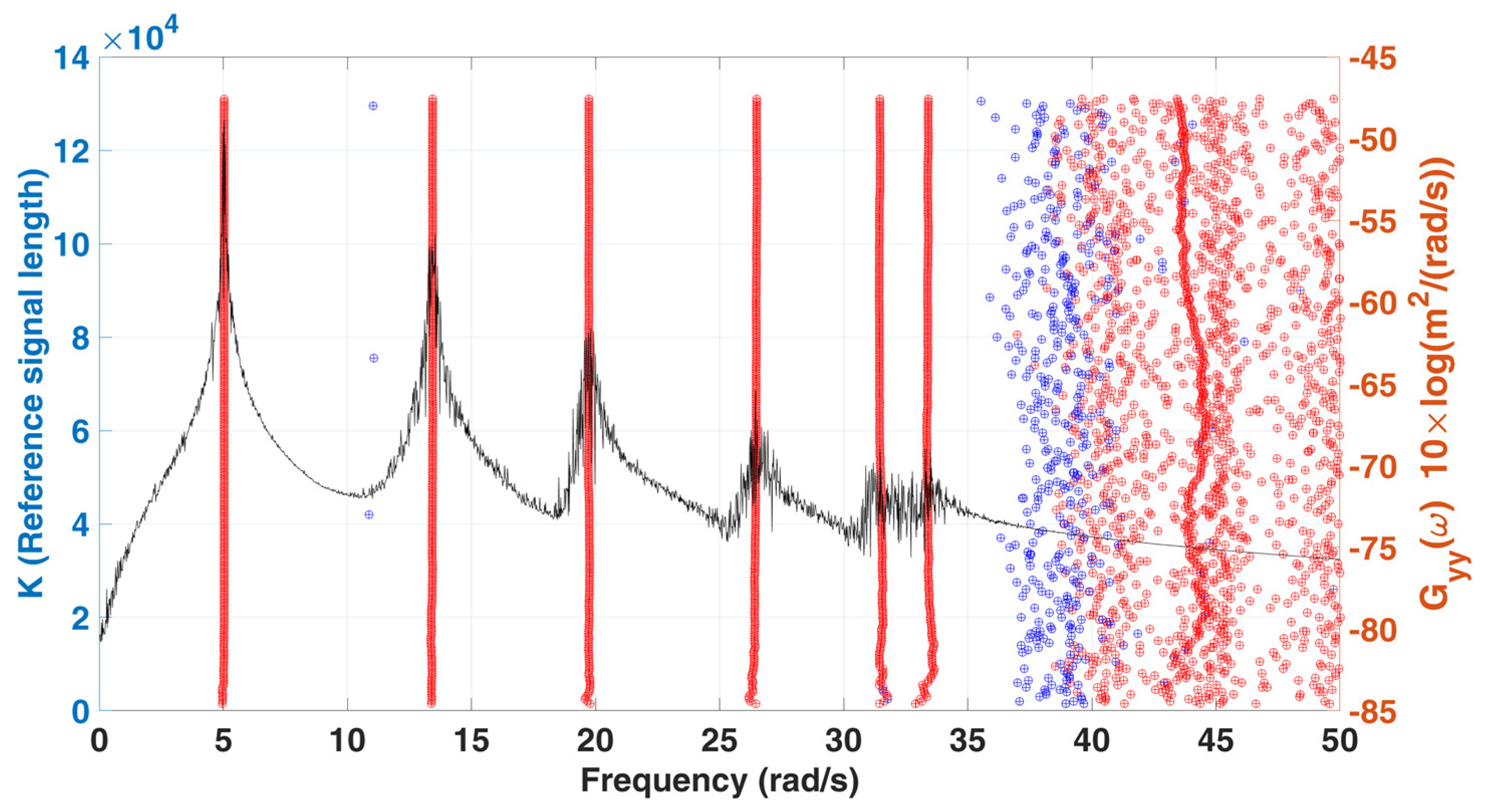
- Convergence analysis with various K (reference signal length)
- Convergence analysis with various L
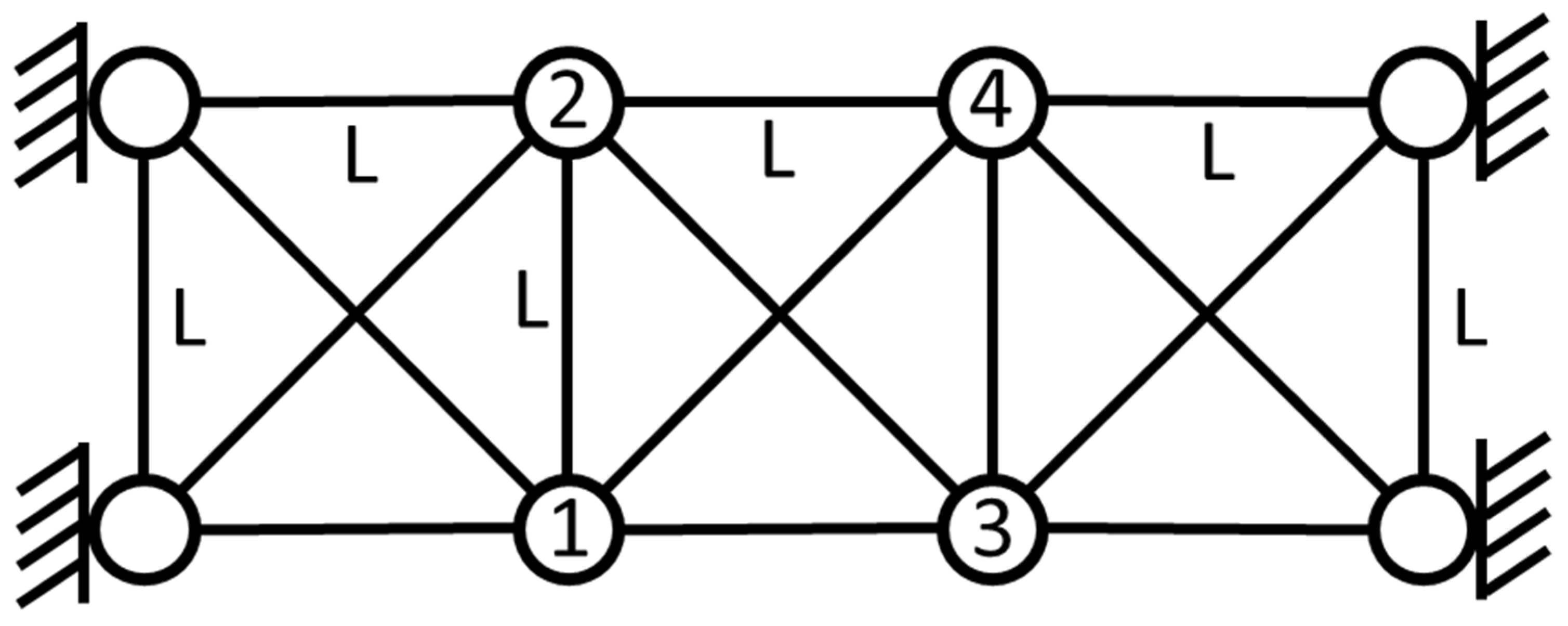
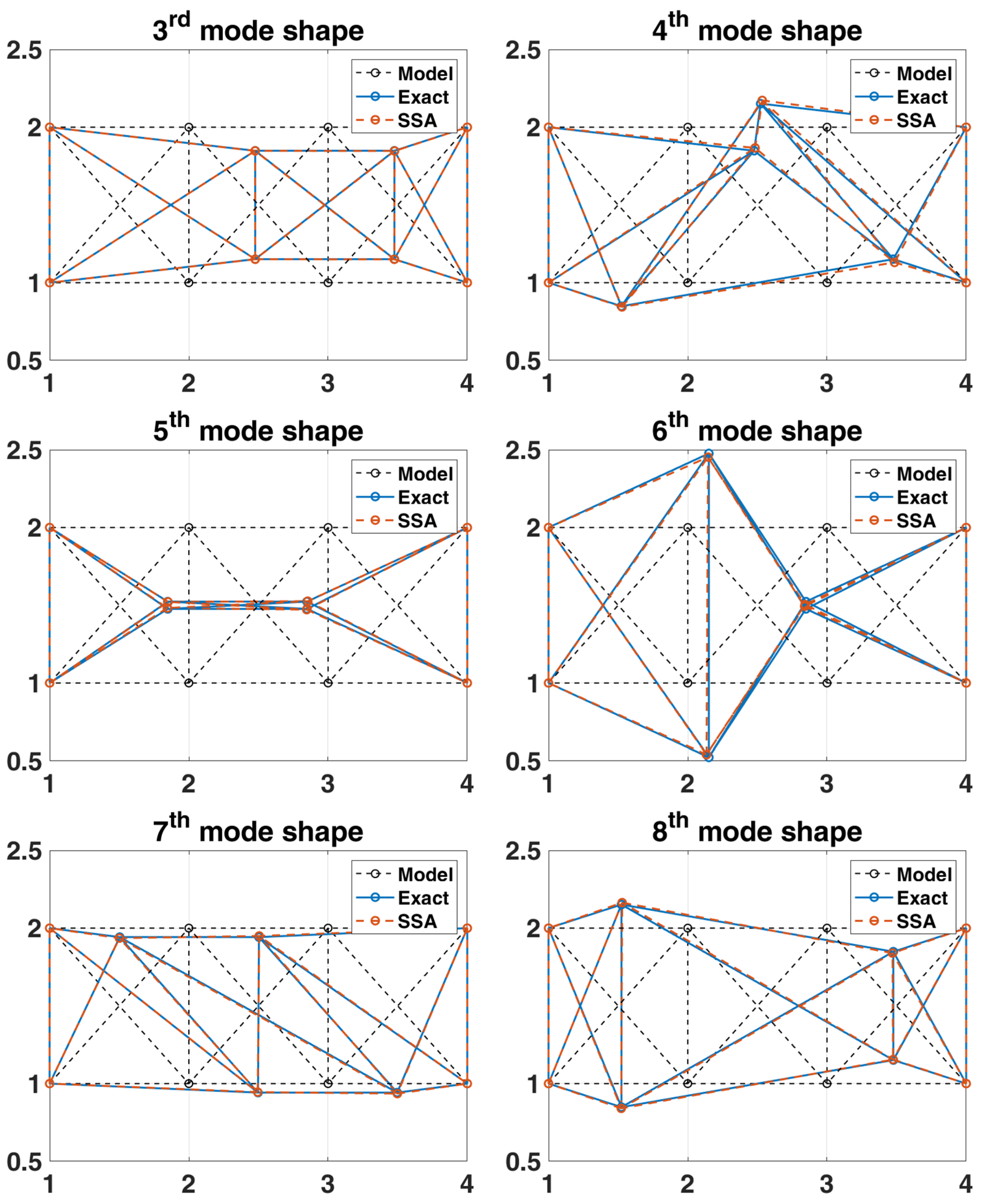
3.2. 2-D Truss Structure
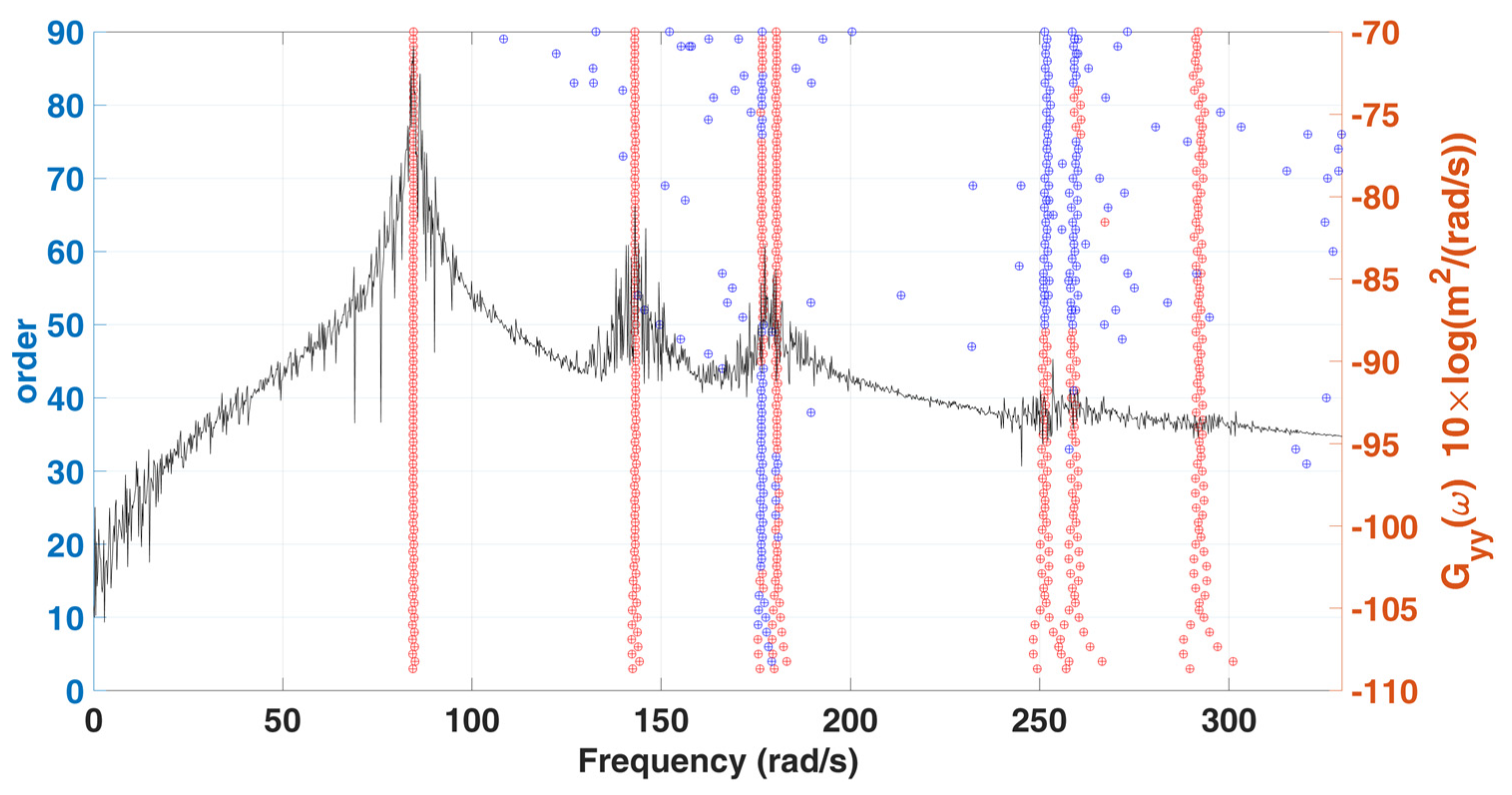
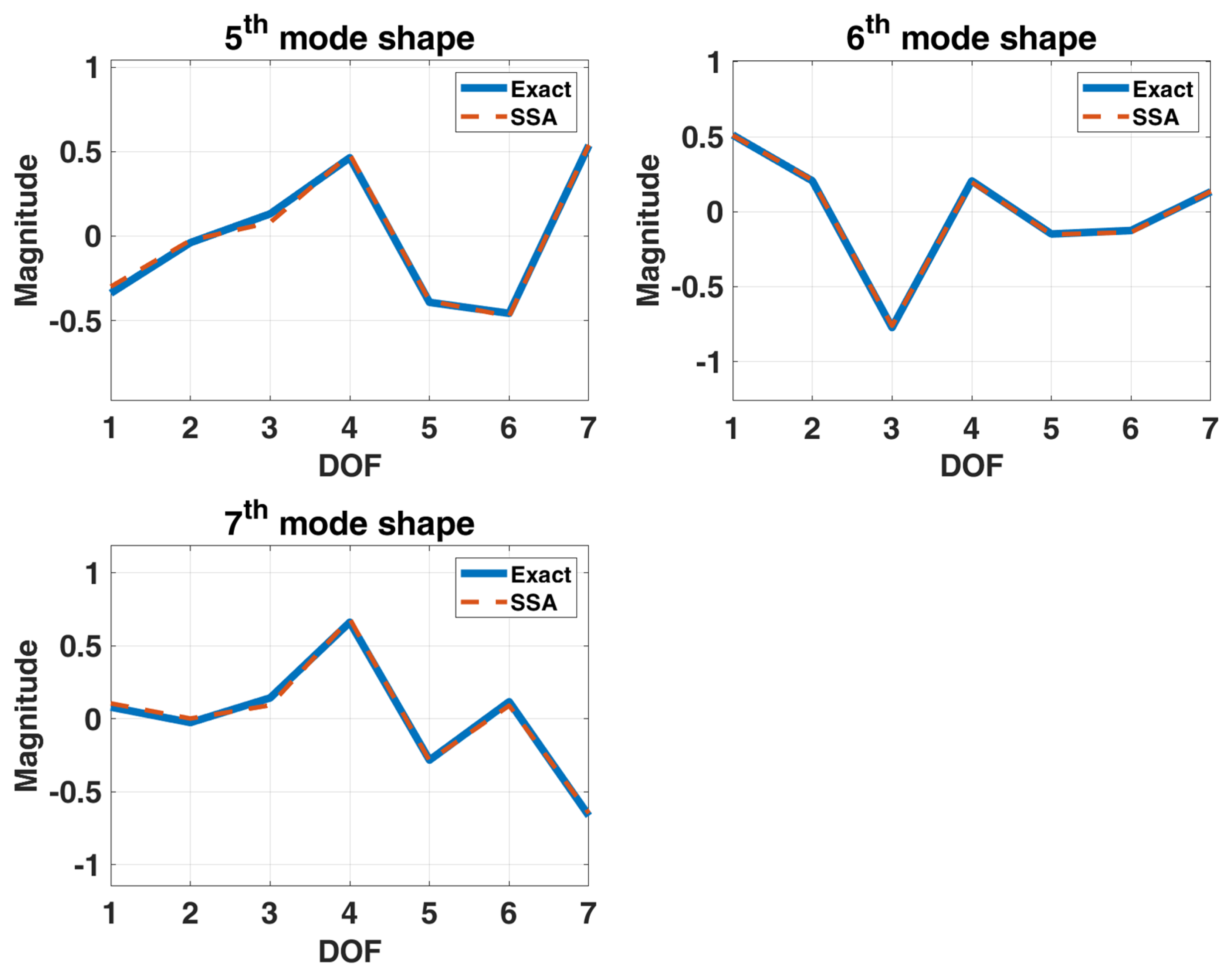
3.3. 7-DOF Model of a Sedan
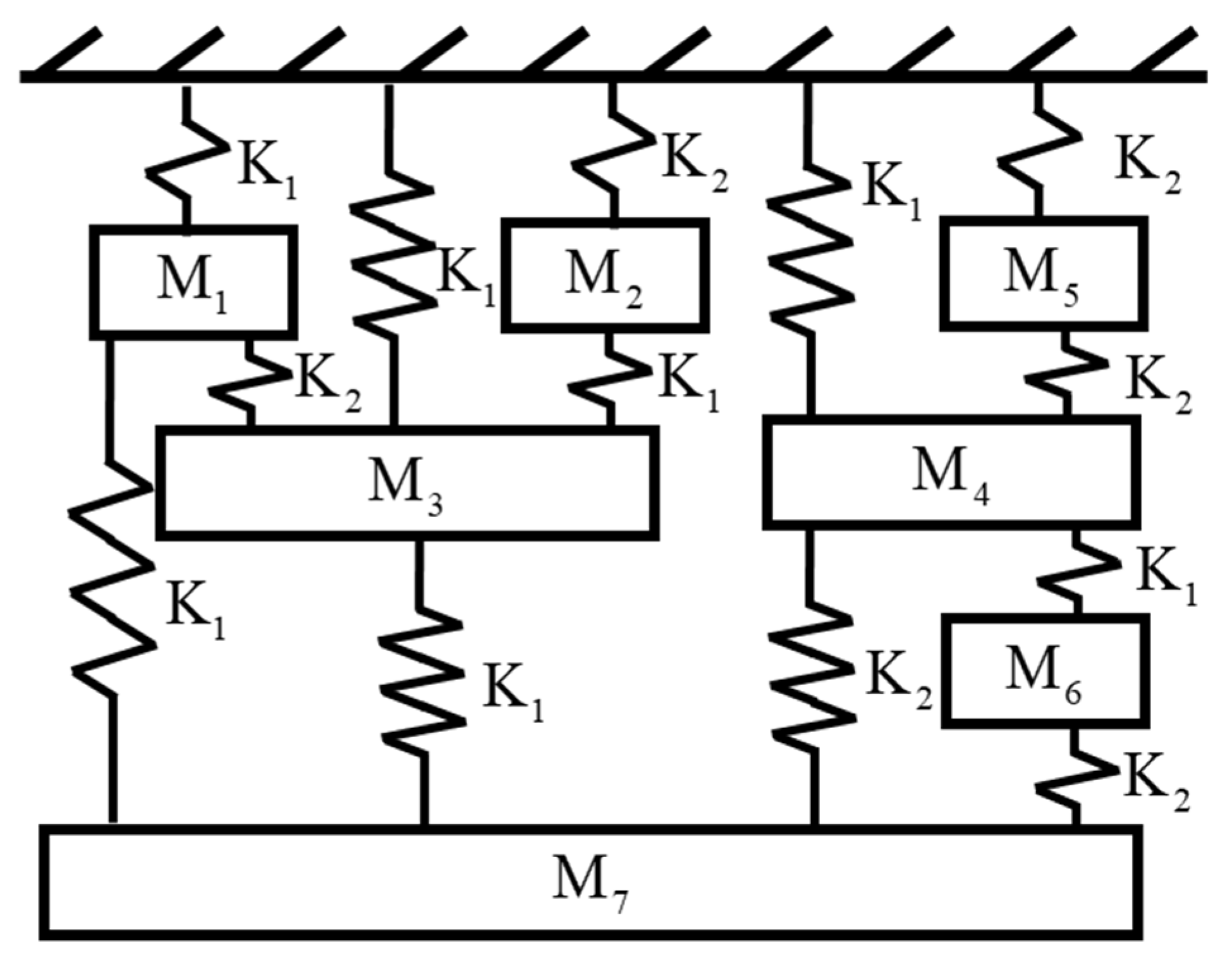
3.4. 7-DOF Highly Coupled System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ho, B.; Kalman, R. Effective construction of linear state-variable models from input/output data. In Proceedings of the 3rd Annual Allerton Conference on Circuit and System Theory, Monticello, IL, USA, 20–22 October 1965; pp. 449–459. [Google Scholar]
- Zeiger, H.; McEwen, A. Approximate linear realizations of given dimension via Ho’s algorithm. IEEE Trans. Autom. Control 1974, 19, 153. [Google Scholar] [CrossRef]
- Juang, J.-N.; Pappa, R. Effects of noise on modal parameters identified by the Eigensystem Realization Algorithm. J. Guid. Control Dyn. 1986, 9, 294–303. [Google Scholar] [CrossRef] [Green Version]
- Juang, J.-N.; Cooper, J.E.; Wright, J. An Eigensystem Realization Algorithm Using Data Correlations (ERA/DC) for Modal Parameter Identification. J. Control Theory Adv. Technol. 1988, 4, 5–14. [Google Scholar]
- Leuridan, J.; Brown, D.; Allemang, R. Time domain parameter identification methods for linear modal analysis: A unifying approach. J. Vib. Acoust. Stress Reliab. 1986, 108, 1–8. [Google Scholar] [CrossRef]
- Guan, W.; Dong, L.L.; Zhou, J.M.; Han, Y.; Zhou, J. Data-driven methods for operational modal parameters identification: A comparison and application. Measurement 2019, 132, 238–251. [Google Scholar] [CrossRef]
- Zhang, G.W.; Tang, B.P.; Chen, Z. Operational modal parameter identification based on PCA-CWT. Measurement 2019, 139, 334–345. [Google Scholar] [CrossRef]
- Yang, Y.C.; Nagarajaiah, S. Output-only modal identification with limited sensors using sparse component analysis. J. Sound Vib. 2013, 332, 4741–4765. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W.; Hester, D. Enhanced sparse component analysis for operational modal identification of real-life bridge structures. Mech. Syst. Signal Processing 2019, 116, 585–605. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Saniie, J. Singular spectrum analysis for trend extraction in ultrasonic backscattered echoes. In Proceedings of the 2015 IEEE International Ultrasonics Symposium (IUS), Taipei, Taiwan, 21–24 October 2015; pp. 1–4. [Google Scholar]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Ghil, M.; Allen, M.; Dettinger, M.; Ide, K.; Kondrashov, D.; Mann, M.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Law, S.-S.; Xia, Y.; Zhu, X. Singular spectrum analysis for enhancing the sensitivity in structural damage detection. J. Sound Vib. 2014, 333, 392–417. [Google Scholar] [CrossRef]
- Luo, S.; Cheng, J.; Zeng, M.; Yang, Y. An intelligent fault diagnosis model for rotating machinery based on multi-scale higher order singular spectrum analysis and GA-VPMCD. Measurement 2016, 87, 38–50. [Google Scholar] [CrossRef]
- Lakshmi, K.; Rao, A.R.M.; Gopalakrishnan, N. Singular spectrum analysis combined with ARMAX model for structural damage detection. Struct. Control Health Monit. 2017, 24, e1960. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Law, S.-S.; Samali, B. Drive-by blind modal identification with singular spectrum analysis. J. Aerosp. Eng. 2019, 32, 04019050. [Google Scholar] [CrossRef]
- Al-Bugharbee, H.; Trendafilova, I. A fault diagnosis methodology for rolling element bearings based on advanced signal pretreatment and autoregressive modelling. J. Sound Vib. 2016, 369, 246–265. [Google Scholar] [CrossRef] [Green Version]
- Prawin, J.; Lakshmi, K.; Rao, A.R.M. A novel singular spectrum analysis–based baseline-free approach for fatigue-breathing crack identification. J. Intell. Mater. Syst. Struct. 2018, 29, 2249–2266. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Zhang, Q.; Yang, S. An EEMD-based denoising method for seismic signal of high arch dam combining wavelet with singular spectrum analysis. Shock Vib. 2019, 2019, 4937595. [Google Scholar] [CrossRef]
- Fitzgerald, P.C.; Malekjafarian, A.; Bhowmik, B.; Prendergast, L.J.; Cahill, P.; Kim, C.-W.; Hazra, B.; Pakrashi, V.; OBrien, E.J. Scour damage detection and structural health monitoring of a laboratory-scaled bridge using a vibration energy harvesting device. Sensors 2019, 19, 2572. [Google Scholar] [CrossRef] [Green Version]
- Trendafilova, I. Singular spectrum analysis for the investigation of structural vibrations. Eng. Struct. 2021, 242, 112531. [Google Scholar] [CrossRef]
- Pappa, R.S.; Elliott, K.B.; Schenk, A. Consistent-mode indicator for the eigensystem realization algorithm. J. Guid. Control Dyn. 1993, 16, 852–858. [Google Scholar] [CrossRef]
- Bakir, P.G. Automation of the stabilization diagrams for subspace based system identification. Expert Syst. Appl. 2011, 38, 14390–14397. [Google Scholar] [CrossRef]
- Lin, C.-S.; Lin, M.-H. Output-Only Modal Estimation Using Eigensystem Realization Algorithm with Nonstationary Data Correlation. Appl. Sci. 2021, 11, 3088. [Google Scholar] [CrossRef]
- De Angelis, M.; Lus, H.; Betti, R.; Longman, R.W. Extracting physical parameters of mechanical models from identified state-space representations. J. Appl. Mech. 2002, 69, 617–625. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Tang, B.; Tang, G. An improved stochastic subspace identification for operational modal analysis. Measurement 2012, 45, 1246–1256. [Google Scholar] [CrossRef]

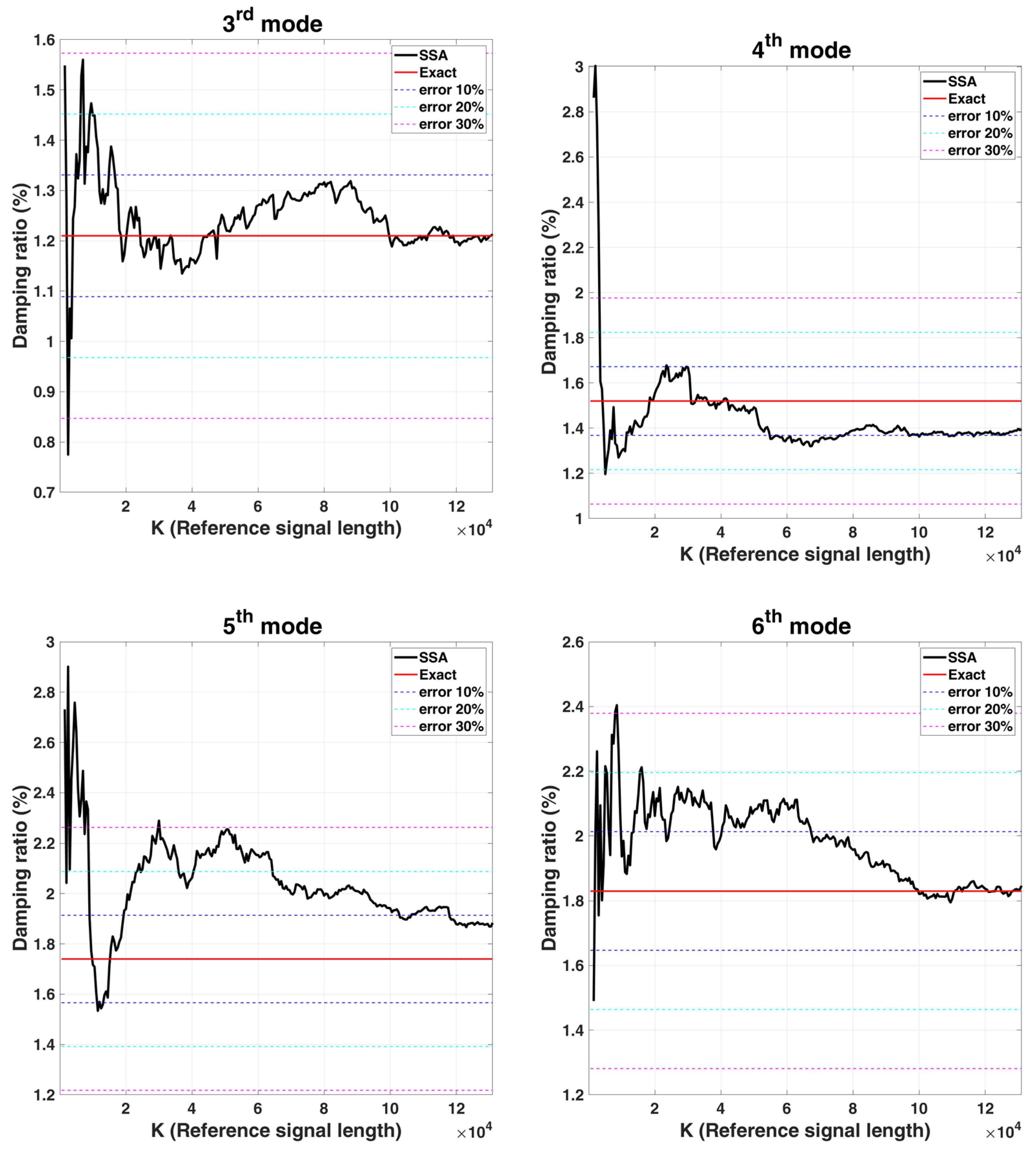
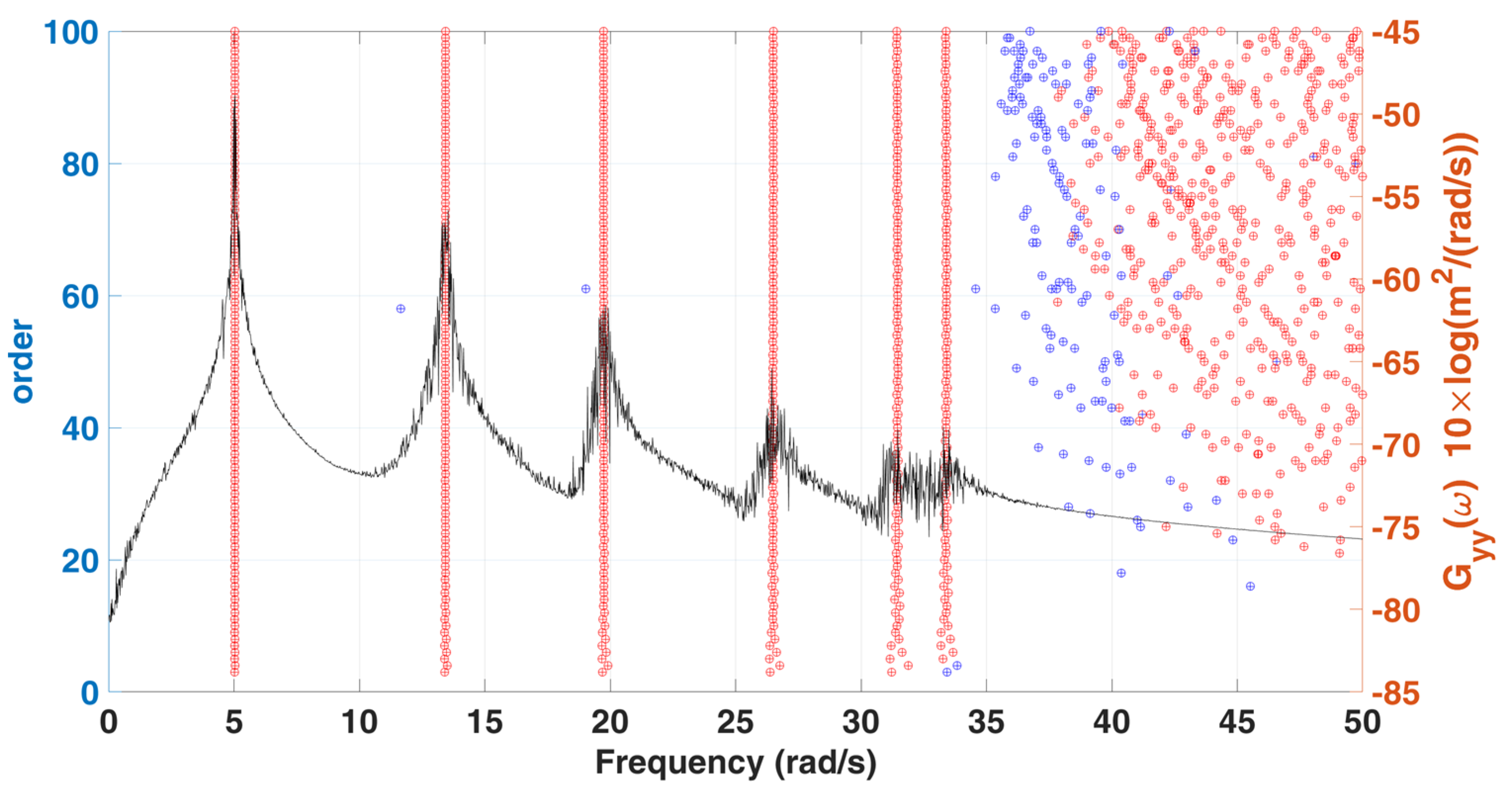
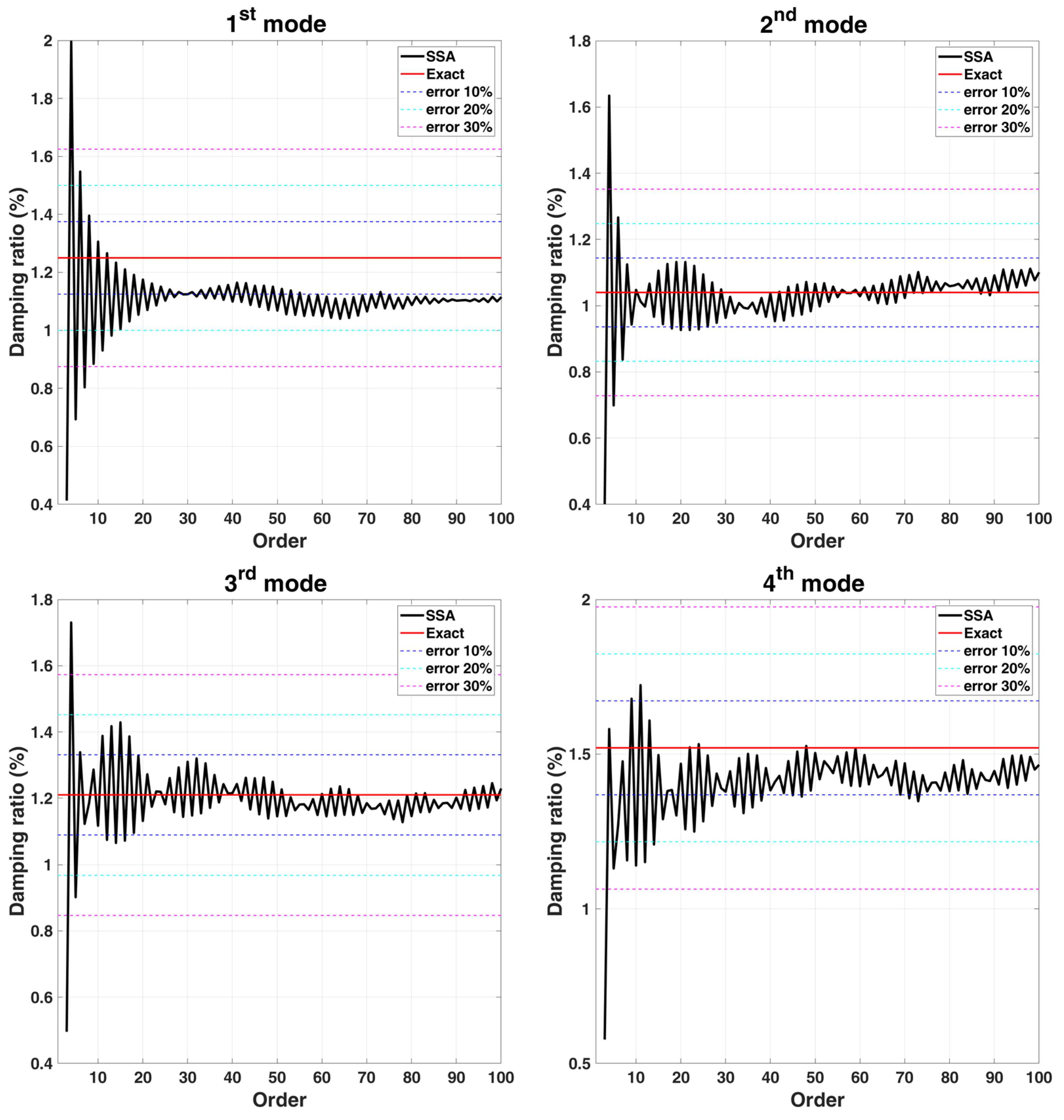

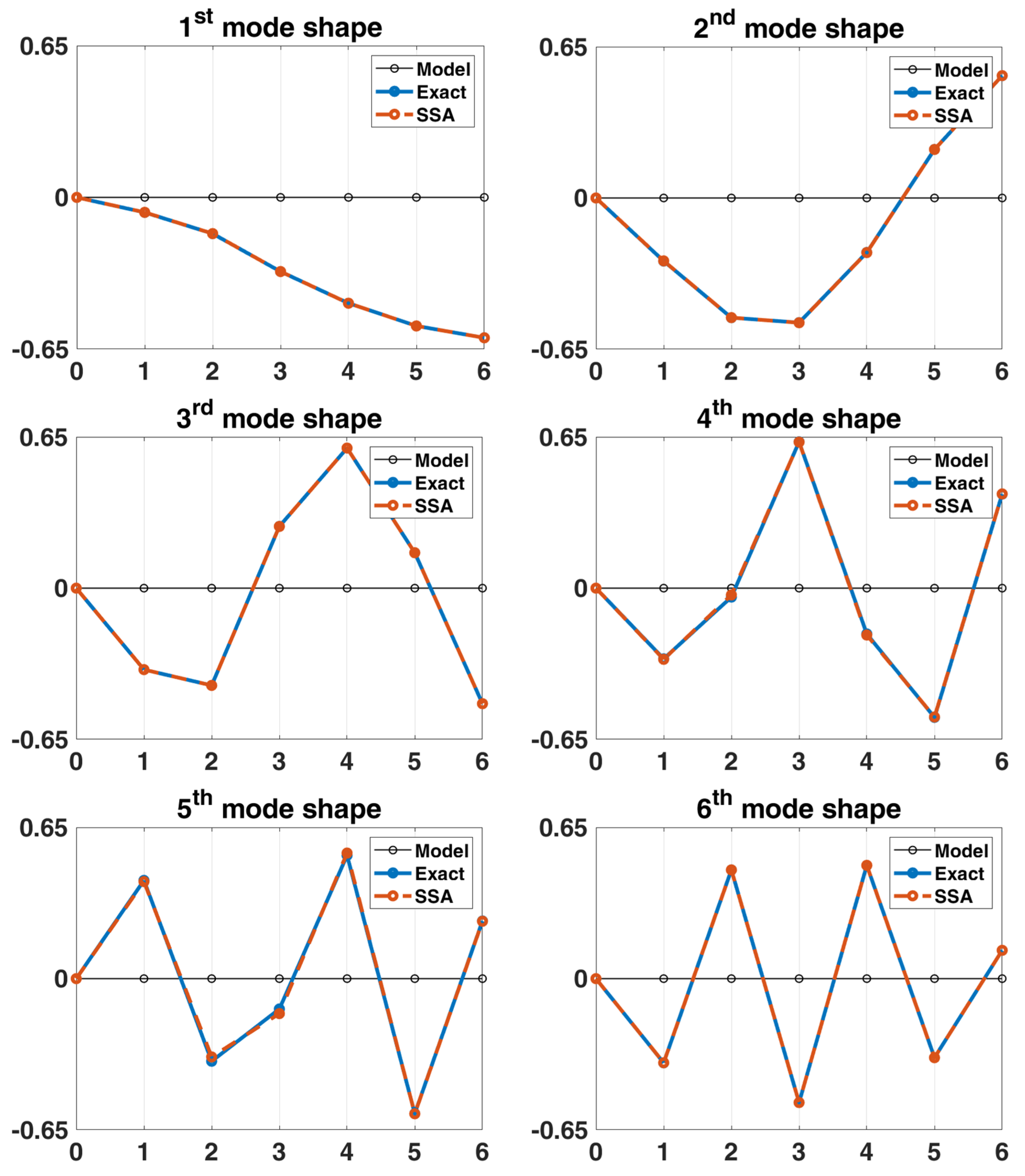






| Natural Frequency (rad/s) | ||||||
|---|---|---|---|---|---|---|
| Mode | Exact | SSA | Error (%) | MSSA | Error (%) | SSA vs MSSA Diff. (%) |
| 1 | 5.03 | 5.04 | 0.20 | 5.04 | 0.20 | |
| 2 | 13.45 | 13.43 | −0.15 | 13.43 | −0.15 | |
| 3 | 19.8 | 19.71 | −0.45 | 19.71 | −0.45 | |
| 4 | 26.69 | 26.46 | −0.86 | 26.46 | −0.86 | |
| 5 | 31.66 | 31.49 | −0.54 | 31.49 | −0.54 | |
| 6 | 33.73 | 33.36 | −1.10 | 33.36 | −1.10 | |
| Damping ratio (%) | ||||||
| Mode | Exact | SSA | Error (%) | MSSA | Error (%) | SSA vs MSSA Diff. (%) |
| 1 | 1.25 | 0.91 | −27.20 | 0.91 | −27.20 | |
| 2 | 1.04 | 1.18 | 13.46 | 1.18 | 13.46 | |
| 3 | 1.24 | 1.23 | −0.81 | 1.23 | −0.81 | |
| 4 | 1.52 | 1.49 | −1.97 | 1.49 | −1.97 | |
| 5 | 1.74 | 2.24 | 28.74 | 2.24 | 28.74 | |
| 6 | 1.83 | 2.08 | 13.66 | 2.08 | 13.66 | |
| Natural Frequency (rad/s) | Damping Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|
| Mode | Exact | SSA | Error (%) | Exact | SSA | Error (%) | MAC |
| 1 | 5.03 | 5.03 | −0.02 | 1.25 | 1.11 | −10.45 | 1.00 |
| 2 | 13.45 | 13.44 | −0.10 | 1.04 | 1.10 | 5.43 | 1.00 |
| 3 | 19.80 | 19.74 | −0.31 | 1.24 | 1.23 | −1.07 | 1.00 |
| 4 | 26.69 | 26.51 | −0.66 | 1.52 | 1.47 | −3.72 | 1.00 |
| 5 | 31.66 | 31.43 | −0.73 | 1.74 | 1.89 | 8.50 | 1.00 |
| 6 | 33.73 | 33.39 | −0.98 | 1.83 | 1.89 | 3.08 | 1.00 |
| Natural Frequency (rad/s) | Damping Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|
| Mode | Exact | SSA | Error (%) | Exact | SSA | Error (%) | MAC |
| 1 | 5.59 | 5.60 | 0.26 | 1.80 | 1.59 | −11.94 | 1.00 |
| 2 | 9.74 | 9.71 | −0.33 | 1.36 | 1.33 | −2.42 | 1.00 |
| 3 | 11.14 | 11.14 | −0.03 | 1.32 | 1.48 | 12.10 | 1.00 |
| 4 | 14.74 | 14.72 | −0.11 | 1.31 | 1.10 | −16.20 | 1.00 |
| 5 | 15.70 | 15.66 | −0.24 | 1.33 | 1.19 | −10.62 | 1.00 |
| 6 | 17.17 | 17.12 | −0.29 | 1.35 | 1.19 | −12.19 | 1.00 |
| 7 | 18.42 | 18.35 | −0.37 | 1.38 | 1.33 | −3.94 | 1.00 |
| 8 | 20.43 | 20.34 | −0.43 | 1.44 | 1.42 | −1.51 | 1.00 |
| Natural Frequency (rad/s) | Damping Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|
| Mode | Exact | SSA | Error (%) | Exact | SSA | Error (%) | MAC |
| 1 | 5.03 | 5.05 | 0.45 | 1.25 | 0.92 | −26.35 | 1.00 |
| 2 | 7.82 | 7.81 | −0.08 | 1.03 | 1.03 | −0.33 | 1.00 |
| 3 | 18.47 | 18.40 | −0.36 | 1.19 | 1.24 | 4.41 | 1.00 |
| 4 | 73.79 | 70.25 | −4.79 | 3.76 | 2.77 | −26.38 | 0.91 |
| 5 | 73.87 | 71.02 | −3.86 | 3.76 | 3.42 | −9.05 | 0.93 |
| 6 | 87.83 | 81.79 | −6.87 | 4.45 | 3.82 | −14.15 | 0.66 |
| 7 | 88.07 | 82.00 | −6.89 | 4.46 | 3.94 | −11.59 | 0.75 |
| Natural Frequency (rad/s) | Damping Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|
| Mode | Exact | SSA | Error (%) | Exact | SSA | Error (%) | MAC |
| 1 | 84.11 | 84.55 | 0.53 | 1.38 | 1.78 | 28.90 | 1.00 |
| 2 | 143.56 | 143.05 | −0.36 | 2.22 | 2.40 | 7.99 | 1.00 |
| 3 | 177.02 | 176.66 | −0.20 | 2.71 | 2.38 | −12.06 | 0.99 |
| 4 | 181.38 | 180.39 | −0.55 | 2.78 | 2.52 | −9.50 | 0.98 |
| 5 | 252.24 | 251.34 | −0.36 | 3.82 | 3.68 | −3.57 | 0.99 |
| 6 | 260.03 | 258.59 | −0.55 | 3.94 | 4.35 | 10.35 | 0.98 |
| 7 | 294.68 | 291.79 | −0.98 | 4.45 | 3.99 | −10.36 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-S.; Wu, Y.-X. Singular Spectrum Analysis for Modal Estimation from Stationary Response Only. Sensors 2022, 22, 2585. https://doi.org/10.3390/s22072585
Lin C-S, Wu Y-X. Singular Spectrum Analysis for Modal Estimation from Stationary Response Only. Sensors. 2022; 22(7):2585. https://doi.org/10.3390/s22072585
Chicago/Turabian StyleLin, Chang-Sheng, and Yi-Xiu Wu. 2022. "Singular Spectrum Analysis for Modal Estimation from Stationary Response Only" Sensors 22, no. 7: 2585. https://doi.org/10.3390/s22072585







