1. Introduction
The recent advances in information and communication technology (ICT) have promoted the evolution of the conventional computer-aided industry into the smart industry [
1]. In the transformation, the Internet of Things (IoT) has an essential role in linking the physical industrial space and cyberspace. However, the current IoT is not well-suited to the needs of the industry in terms of privacy and security. Thanks to the continuous progress of blockchain technology, the combination of IoT and blockchain is becoming more and more popular among security personnel. For example, the study [
2] provides a worthwhile research solution for data privacy transfers in the security domain. Yet blockchain still is experiencing security issues of its own while solving IoT privacy and security problems. Currently, the security of smart contracts has become one of the key blockchain security issues.
Smart contracts in blockchain are automated, programable, verifiable, and open and transparent. Using these features of smart contracts transforms them into programed, executable, and verifiable ways for decentralized execution, thereby significantly reducing the underhanded operations and unfair practices that exist in decentralized systems. More and more individual developers or industry practitioners can develop Decentralized Applications (DApps) [
3], such as Decentralized Finance (DeFi), etc. In the metaverse, users can also co-edit the world, realize the value exchange through smart contracts, and guarantee the transparent enforcement of system rules. However, previous research has shown that many real-world smart contracts deployed on blockchains have serious vulnerabilities [
3], for example, the DAO attack [
4] and the Parity attack [
5]. The DAO attack exploits a recursive call vulnerability to transfer one third of the DAO funds to a malicious account (worth about USD 50 million). The Parity attack exploits a vulnerability in the library contract to steal over 150,000 ETH to a malicious account (worth about USD 30 million).
Recent studies have reported many methods for smart contract vulnerability prediction. In general, these methods can be classified into two categories: (1) expert rule-based approach, considering static symbolic analysis [
6,
7], dynamic symbolic execution [
8], combined dynamic and static methods [
9], and XPath [
10]; and (2) data-driven approach, i.e., using NN approach [
11,
12,
13,
14,
15,
16,
17].
In symbolic-execution-based approaches, symbolic execution models are often used together with experimental data to accomplish the task of contract vulnerability prediction. In the last few years, many successes have been achieved using symbol-execution-based methods. However, constructing an accurate symbolic execution model is not an easy task, as it often requires extensive knowledge of Solidity programing (Solidity is used as an example in this paper) or experimental data obtained under well-designed and controlled conditions, which are often untimely or too time-consuming.
As an alternative to expert rule-based methods, data-driven methods for smart contract vulnerability prediction have gained popularity in recent years. The data-driven approach relies entirely on the data themself and usually does not require much knowledge of how the data work exactly. In the data-driven approach to contract vulnerability prediction, contract vulnerability prediction can be performed by learning complex features extracted from the operational sequence dependencies of a contract, and this dependency can be learned with various ML methods. The focus of the work in this paper is to apply different NNs to contractual vulnerability prediction. NN is a structure consisting of multiple layers of interconnected “neurons” that map input features to outputs (such as the vulnerability labels in this paper) [
12,
13,
14,
15,
16]. NN-based deep learning methods have recently attracted the attention of researchers working in cybersecurity because of their ability to automatically extract features and their good generalization performance. Huang et al. [
11] designed a multi-task NN model based on an attention mechanism. The model uses a shared embedding layer with the sequence of operations of a smart contract as its input, and each subtask uses the shared embedding features. The effectiveness of the proposed NN approach in vulnerability prediction is also verified on three vulnerabilities. Recently, Hongjun Wu et al. [
17] proposed a model using key data flow graphs and pretraining techniques for smart contract vulnerability prediction based on code graphs. The method converts the smart contract source code into an abstract syntax tree (AST), finds the locations and relationships of variables in the contract, and constructs a code graph for verifying the model performance by using the variables associated with vulnerabilities as nodes.
Although these data-driven methods can provide satisfactory accuracy in vulnerability prediction, they focus on improving the underlying model or single accuracy and need to be backed by a large-scale training dataset. At the same time, the time and human costs of collecting data are rarely mentioned in the studies of these methods. In many real-world scenarios, collecting contract vulnerability data is an expensive and time-consuming process. To alleviate this problem, this paper proposes an EL-based vulnerability prediction approach, called SCVDIE-ENSEMBLE, which is based on seven different neural networks using contract vulnerability data for contract-level vulnerability detection. The accuracy and robustness of the proposed method can be improved by using EL, where the final decision is reached by weighting the individual predictions (i.e., the vulnerability prediction labels of a single NN model).
The proposed SCVDIE-ENSEMBLE approach consists of four main steps, which are outlined below.
First,
-fold cross-validation (CV) is performed using the source dataset, including the original contract data collected from DEDAUB [
18], to obtain
pretraining results, which will help create more diverse NN models and their parameters. The diversity of these independent models comes from the different training subsets used for pretraining, where each independent NN model focuses on fitting a different sub-sample of the source dataset.
Second, a multi-layer perceptron is used to combine the vulnerability prediction results of individual NN models. This approach causes the good predictions to be amplified and the bad predictions to be attenuated.
The experimental results show that the proposed SCVDIE-ENSEMBLE method can provide more accurate and robust vulnerability prediction. Compared to some other ML methods including each NN model, the proposed SCVDIE-ENSEMBLE method can provide more accurate vulnerability predictions using a relatively small training dataset. To the best of our knowledge, this is the first attempt to use EL methods on smart contract vulnerabilities to improve the performance of deep learning in predicting contract vulnerabilities from operational sequence data.
In this study, several contributions were made, as detailed below.
First, this paper proposes the SCVDIE-ENSEMBLE model for predicting the possibility that smart contracts contain vulnerabilities, and their source code is public [
19]. The experimental results in this paper show that: (1) SCVDIE-ENSEMBLE outperforms other ML methods; and (2) EL can improve the robustness of SCVDIE-ENSEMBLE models.
Second, the effectiveness of the proposed SCVDIE-ENSEMBLE model in making accurate vulnerability predictions is based on more than 21,667 smart contracts manually collected and tagged from DEDAUB, of which 11,756 are vulnerable smart contracts and 9911 are nonvulnerable smart contracts; this process took more than 2 weeks.
Third, in this paper, the performance of eight deep learning models is experimentally demonstrated by using different size datasets for training. The conclusions show that integrating EL can not only reduce the size of the training dataset with the same error of the model, but also effectively improve the accuracy and robustness of vulnerability prediction.
The remainder of this paper is structured as follows:
Section 2 reviews the existing studies, including conventional methods, general ML methods, and software bug analysis research applying EL. In
Section 4, the research design of the experiments in this paper is described. The way of building the dataset is also introduced. In
Section 5, the experiments and results of SCVDIE are presented, and the conclusions of the analysis. In
Section 6, SCVDIE’s characteristics and limitations are analyzed. In
Section 7, the conclusion of this paper and future work is discussed.
3. Methodology
In this subsection, the design and implementation of SCVDIE are presented, as well as a novel dataset constructed that can be used to build an integrated system for smart contract vulnerability detection by using the NN model. SCVDIE analyzes COS (i.e., critical opcodes sequences directly related to the vulnerability) from the source code and tries to extract vulnerable opcode fragments. Then, vulnerability identification is designed as a classification task, where each sequence is assigned a vulnerability probability. Sequences with higher probability will be considered fragile. With enough training, SCVDIE can learn the possible patterns of vulnerabilities, as reflected by the different parameters of the model, i.e., the diversity of parameters. These different parameters are applied to samples with similar characteristics not seen in the model, and predictions are made accordingly.
3.1. Overall Architecture
Identifying smart contract vulnerabilities can be seen as classifying the corresponding opcodes into vulnerable/invulnerable sequences. Therefore, the problem of identifying vulnerable smart contracts is defined as identifying vulnerable operations.
Figure 1 illustrates the overall design of the proposed SCVDIE in this paper. Both the training and testing phases consist of three main steps: constructing
from co-occurrence frequencies, embedding
into the matrix space, training or predicting them, and aggregating the results of different NN models to output a final decision. Before starting to present the specific structure of SCVDIE, it is very critical to provide a global description of the notation used in this paper to enhance its readability, as shown in
Table 1.
3.2. Building Vectorized IGs
3.2.1. Determine the Same (Co-) Present Relationship
The frequency of co-occurrences was calculated from the opcodes of all contract samples in this paper, where the opcodes of individual smart contracts can be counted from the Solidity compiler.
Figure 2 shows the co-occurrence frequency matrix of the 20 operands with the highest co-occurrence frequency.
Taking MSTORE in the first row as an example, it can be seen that the vertical co-ordinate with the highest frequency corresponds to ISZERO, and the lowest frequency corresponds to EQ. In building , the ISZERO node is the closest to MSTORE, and EQ and MSTORE have the farthest distance from each other. The operands that belong to the same horizontal or vertical co-ordinate are ordered according to the order of their appearance in the contract.
3.2.2. Building Graph
The purpose of this work is to evaluate the vulnerability of smart contracts. SCVDIE is pretrained in a supervised learning environment, the tags of smart contracts are initially labeled by static recognition tools, potential COS are identified by predefined rules, and, finally, COS is used as input data to construct an infographic
based on co-occurrence relations to represent the vulnerability pattern information of the program (the infographic part in
Figure 1). The nodes of
are composed of opcodes, and all nodes are connected according to the position–frequency relationship, and opcodes belonging to the same class are connected in the order of their occurrence so that all edges and nodes form a unilateral connected digraph (UCD). This paper considers that
consists of a set of nodes and undirected edges, denoted
, where
denotes the set of nodes of
and
represents the set of edges connecting these nodes. Given an infographic
, one goal of the vulnerability identification task is to uncover hidden vulnerability features by identifying the connection patterns between nodes. Therefore, this paper constructed the samples in the dataset as
, where
,
denote the label of the
th sample,
denotes the number of nodes of
, and
is the original number of samples in the experimental dataset.
3.2.3. Graph Vectorization
When plotting these embedding matrices in a vector space, the original input code sequence is transformed into a meaningful matrix where nodes with similar relationships are located very closely together, which allows the neural network to learn from rich relationships. To vectorize the node content into a matrix, this paper first constructed the of all sample contracts, and then extracted all paths of each . Based on these paths, a set containing many operation sequences was built, and, finally, embedding models such as Word2vec were trained with the set. For each path, this paper concatenated the token embeddings corresponding to the path nodes as the initial representation of the path. Just like human language, the same word has different meanings in different contexts. A smart contract contains multiple functions, and the same operation may have different results in different functions, so this paper designed a novel node embedding method to vectorize the node into , where is the embedding dimension. The contains all the embedded nodes of the graph and is defined as . Given a sample , then input the vectorized graph into a neural network model to learn node information representation . A good model can fully embed the semantic information of nodes and their contexts, so this paper input the semantic embedding corresponding to each node into the classifier, and then calculated the vulnerability probability of each node. More precisely, the learned were fed into a linear layer with trainable weights and biases to obtain a score for each node, where is the hidden dimension of the model, followed by a layer with probability . Considering the vulnerability probability of each node, this paper took the most likely edge and the index of the corresponding node as the predicted value and calculated the cross-entropy loss compared with the true value.
To facilitate the model to quickly switch between different embedding methods to adapt to different embedding tasks, in addition to Word2vec, this method also encapsulates two other mainstream embedding methods, namely: GloVe [
45] and FastText [
46]. Bert [
47] is also a common embedding method at present. It was proposed by Google in 2018. When using the Bert model for embedding, the token position needs to be considered. The current maximum length of position embedding is 512. However, the operation code of each smart contract is a very long sequence, the length of the operation sequence of some smart contracts can even exceed 3000. If Bert is used for code embedding, a large part of the operation sequence will be discarded and a lot of feature information may be lost.
3.3. Identifying Vulnerable Paths with a Single Model
Given an , this method uses the following three main steps to predict its vulnerabilities:
- (1)
Extract all paths and nodes.
- (2)
Embed all paths and nodes to obtain the embedding matrix.
- (3)
Use the embedded matrix as input data to make predictions.
To give the label of the contract corresponding to
conveniently, this method considers adding an artificial node that does not contain any semantic information at the position where the index of
is 0. This artificial node serves as a classification for the entire graph, indicating whether the graph contains vulnerabilities. If a sample has no loopholes, this method uses index 0 as the ground truth label of the contract. If there are loopholes, the number composed of the sequence number corresponding to the path is used as its label. For example, in the red route in the testing phase in
Figure 1, the contract token will be recorded as 1246, and the probability that this route has a real vulnerability is preserved. Note that this is just one path for the example; in practice, most contracts have multiple red paths.
To identify vulnerabilities accurately, each single NN model should understand opcode sequences through multiple views. Learning such global and local combinations is necessary for every single NN model to successfully identify fragile contracts. Convolutional and recurrent neural networks can process sequential data efficiently. However, the ability to learn global dependencies is limited by the length of the corresponding path. Due to the computational cost, the acceptable path length is limited, so the independent path is usually processed. Such processing creates additional limitations for them. In contrast, Transformer allows learning latent patterns from a holistic perspective. Six models, such as CNN and RNN, pass information to edges with different weights and pass the initial vectorized node representation and edge list of each independent path to models such as CNN. It should be noted that, unlike the GNN, this paper uses the UCD, so two paths are considered; one is the sub-path in each graph and the second is the overall path of the UCD. For each sub-path, the output of models such as CNN and RNN will be the converted path vulnerability probability representation, denoted as , where represents the number of sub-paths corresponding to each sample .
To learn the implicit dependencies of the sequence, this method takes all the nodes in the overall path of the sample as a sequence and passes it to the transformer to learn the vectorized representation of the overall path. Removing connecting edges forces the model to learn long-distance dependencies more efficiently since it no longer depends on the effects of node calls that are far apart. In this paper, all nodes are sorted by distance and frequency relationship, for example, the three opcodes MSSTORE, CALLVALUE, and JUMPI. If MSSTORE and CALLVALUE are placed before JUMPI in the source program, then, when building the input sequence, MSSTORE will be placed before all nodes belonging to JUMPI; CALLVALUE is also based on the same rules. With the help of the multi-head self-attention mechanism, the final node converted by the model represents the global vulnerability probability of the contract, denoted as .
Then, the result vector representation from each model is fed into a multilayer perceptron, and this layer is used to assign weights to the models. For models such as CNN and RNN, the comprehensive score of each sub-path is calculated by Equation (1),
, and, for Transformer, the score of the overall path is calculated by Equation (2),
. During the training process, all vulnerability scores are passed into the
layer to obtain the vulnerability probability of all paths and calculate the cross-entropy loss. This paper noted that each model is trained independently, backpropagating and updating the weights without crossover.
3.4. Integrating Results
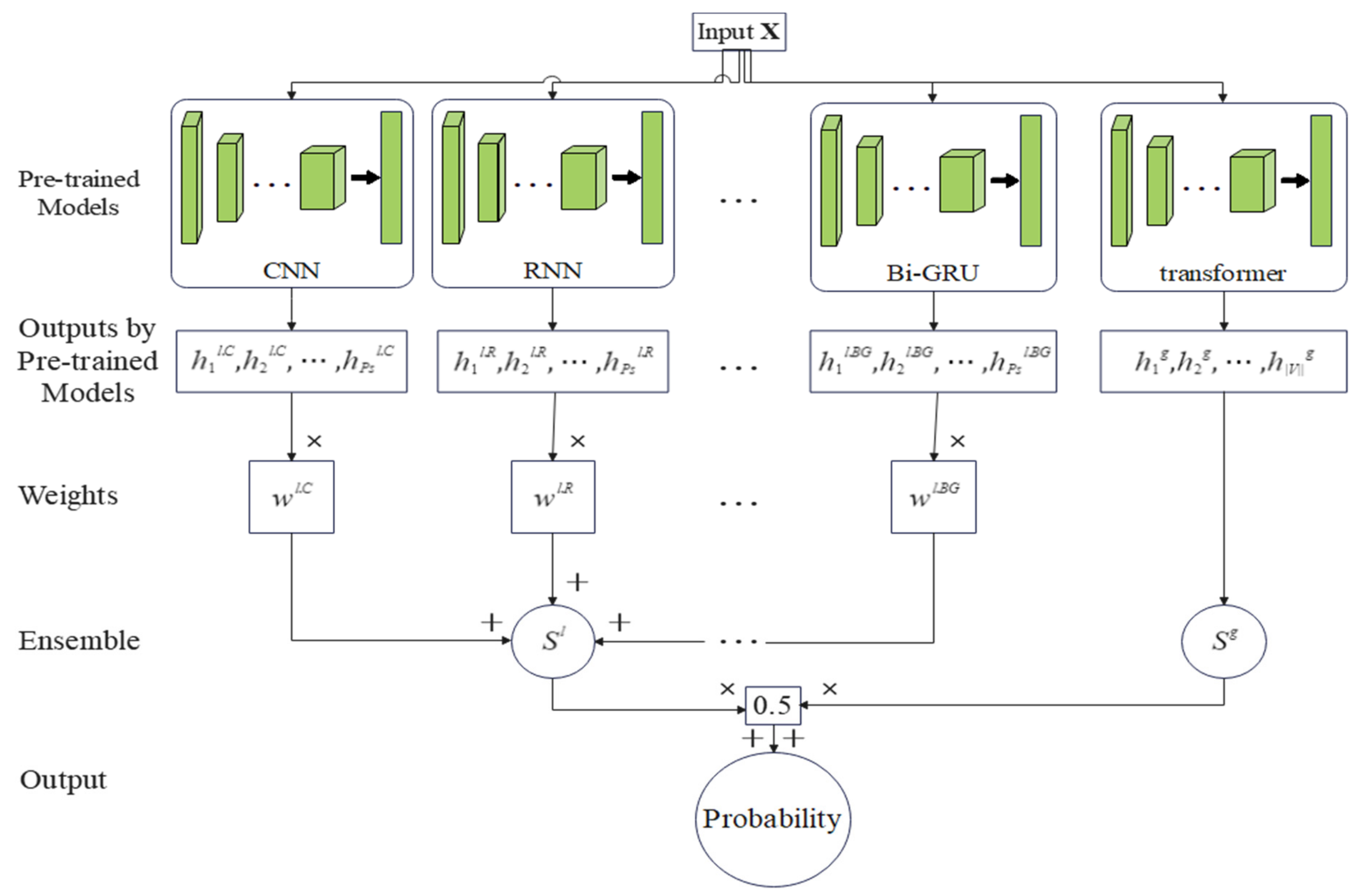
One of the goals of this paper is to combine the learning knowledge of multiple models, improve the accuracy and robustness of a single model, and reduce the probability of selecting a single model with poor performance. Therefore, this paper proposes an ensemble method to aggregate the prediction results of multiple models. The structure of the implemented SCVDIE-Ensemble in this study is shown in
Figure 3. SCVDIE-Ensemble integrates seven mainstream classification models: CNN, RNN, RCNN, DNN, GRU, Bi-GRU, and Transformer. Using different sub-classifiers, vulnerability patterns can be learned from different aspects. In the inference phase, the user can input the vectorized data into the pretrained model to obtain the recognition result. Specifically, this paper inputs the vectorized code graphs into these seven trained models, and then they output the transformed path representations
and
, then calculate the vulnerability scores
and
, where
is calculated by Equation (3).
Finally, this paper summarized the prediction results through the weighted average method and calculates the sample contract vulnerability score . If it exceeds the threshold (0.5), the contract corresponding to the graph will be considered vulnerable.
Integrating multiple methods is technically straightforward, but it is not equivalent to simple addition, which works quite well in practice [
48]. In
Section 5, this paper demonstrates the effectiveness of SCVDIE in reducing the size of training data and empirically demonstrates that different models can indeed learn different aspects of fragile patterns, as intuitively expected.
5. Results and Discussion
This paper evaluated SCVDIE through the following research questions:
RQ1: Vulnerability assessment and classification. Can SCVDIE detect static scan tool tags without vulnerabilities? How big is the gap with unsupervised learning without static tool labels?
RQ2: Ensemble strategy evaluation. Is the integrated model an effective method for combining global and local environments compared to existing methods? Does the dynamic change of the prediction result weights have any effect on the global result?
5.1. RQ1: Vulnerability Assessment and Classification
First, this paper tests the ability of SCVDIE-Ensemble to identify vulnerable contracts in a realistic environment. In a real-world environment, there is no way to know in advance if a contract is vulnerable. This simulates a typical static analysis environment in which the static analyzer aims to find as many contractual vulnerabilities as possible. The experiments in this paper can be considered as vulnerability assessment and classification, where SCVDIE classifies a smart contract as vulnerable/invulnerable, and then gives a determination result by combining different patterns learned from multiple models. In RQ1, this paper focuses on the comparison between SCVDIE-Ensemble and rule-based static analysis tools. This discussion is given priority in this paper because one of the goals of this paper is to improve the overall performance of static analysis tools using a data-driven approach to further ease the debugging efforts of developers. To comprehensively evaluate the effectiveness of the method in this paper, SCVDIE is compared with a static analyzer and a variant of SCVDIE. They are SCVDIE-Ensemble, SCVDIE-CNN, SCVDIE-RNN, SCVDIE-RCNN, SCVDIE-DNN, SCVDIE-GRU, SCVDIE-Bi-GRU, and SCVDIE-Transformer. As mentioned in
Section 3.1, to incorporate nonvulnerable contracts into SCVDIE, this paper adds an artificial node to each virtual node with index 0 without any syntactic and semantic information. If the sample is vulnerability-free, then
will be marked as 0, which is the index of the artificial node; otherwise,
will be a value consisting of the indexes of the nodes contained in the vulnerability path.
Table 5 and
Table 6 show the comparative results of RMSE, accuracy, precision, recall, F1, and prediction accuracy of different models on the combination of fragile and nonfragile contracts, respectively. In view of these results, three significant observations can be made and are listed as follows.
First, based on these results, the performance of the SCVDIE-ENSEMBLE was better than that of the SCVDIE-CNN, SCVDIE-RNN, SCVDIE-RCNN, SCVDIE-DNN, SCVDIE-GRU, SCVDIE-Bi-GRU, and SCVDIE-Transformer methods, as shown in
Figure 9. Combining the RMSEs and fuzzy matrix results, SCVDIE-Ensemble is also able to make more accurate vulnerability predictions in a single CV. Although the RMSEs of SCVDIE-Ensemble do not remain the lowest in every CV, the combined RMSE of SCVDIE-ENSEMBLE outperforms other methods, which means that SCVDIE-ENSEMBLE can still maintain a low error in obtaining high accuracy prediction results.
Second, the combined RMSE of SCVDIE-ENSEMBLE is 1.419%, which indicates that the proposed method can provide more accurate vulnerability information, even if the training set is relatively small. When compared with other variants of SCVDIE, for example, SCVDIE-Transformer (3.395%) and SCVDIE-CNN (5.039%), it can be concluded that combining different knowledge learned by different neural networks helps to improve the vulnerability prediction generalization of any single model.
Third, SCVDIE significantly outperformed static analysis tools, reducing the false-positive and false-negative rates dramatically. The best performing SCVDIE-ENSEMBLE achieved 97.57% of the evaluated F1 scores, while the rule-based static analysis tool could only achieve 46.1% accuracy at most. In the contract-level vulnerability detection setup, the SCVDIE variant has significantly higher precision, recall, and F1 than all baseline static analysis tools. These results objectively validate the fact that SCVDIE helps to alleviate developers’ concerns about the FP/FN problem of rule-based static analyzers.
Overall, these results show the effectiveness of the integrated approach when combined with the seven-class model. However, this paper also observed that the single Transformer model is more accurate than the integrated model in terms of classification accuracy, although this value is within 1%. This is because the global nature of the Transformer model allows it to perform better on more general vulnerability detection tasks, but this advantage is slightly diminished when combined with models such as CNN.
5.2. RQ2: Aggregate Strategy Evaluation
This paper had demonstrated the effectiveness of the integrated model in global and local vulnerability assessment. The model is more effective globally compared to a single model in terms of a comprehensive understanding of global and local factors.
The integration strategy of SCVDIE outperforms existing models that aggregate global and local contexts. As shown in
Table 7, the integrated approach shows a more powerful learning capability compared to existing models. Compared with the existing models studied in this paper, its learning capability is more powerful. SCVDIE-ENSEMBLE outperforms other single policies in both the vulnerability-only and mixed settings. Specifically, in the real world, SCVDIE-ENSEMBLE illustrates the versatility of the integration approach to understand complex real-world vulnerability patterns. This result empirically suggests that integrating models is a more direct and effective way to combine global and local knowledge than stacking different models, since stacked models still share learned knowledge during training, which may prevent them from learning a more diverse set of vulnerability patterns.
5.3. Effect of the Training Dataset Size
The number of smart contracts used in this paper is only the tip of the iceberg of many contracts, and the relative reliability of the experimental results cannot be guaranteed without more datasets. To thoroughly investigate the impact of using a relatively small dataset on the performance of the proposed SCVDIE-ENSEMBLE model, we dynamically change the number of samples in the original training dataset and construct 10 sub-training datasets of different sizes. The maximum number of samples in each training dataset is called
, and the range of values is
to
,
. When
, there is no need to make any adjustments to the original dataset used. To validate the generalization of the model, each of these 10 training sets used the same test dataset during the testing phase. Moreover, the SCVDIE-ENSEMBLE model was compared with variants of SCVDIE trained with datasets of different sizes. As is known, NNs trained from the small-scale training set may suffer from overfitting problems. Especially when the number of samples in the training set does not exceed
, i.e.,
, this phenomenon is easier to detect.
Figure 10 shows the performance changes of different models with the size of the training set, from which the following conclusions can be drawn.
First, when comparing different independent models and ensemble models, it can be found that the performance of the ensemble model is greatly improved compared to that of the independent model because different deep neural networks can recognize different patterns of features. The performance improvement of SCVDIE-ENSEMBLE becomes obvious as the training data set decreases, which indicates that EL is a powerful tool to improve vulnerability prediction precision, which further supports the inference made earlier in this paper. The SCVDIE-ENSEMBLE converged near ; the number is more than five times that required for a standalone NN to achieve a satisfactory horizon of performance. For example, the overall average RMSE of SCVDIE-DNN = 6.854% at . With the number of training samples increasing, the performance boost from SCVDIE-ENSEMBLE diminishes gradually. This is because, when there are enough training data samples, a single model can also grasp a relatively more comprehensive feature pattern. In other words, each independent model can achieve similar performance at the expense of a larger training dataset. In the case of , the RMSE metric of SCVDIE-ENSEMBLE is 2.456%, while each independent model requires a training dataset 5 to 10 times larger than SCVDIE-ENSEMBLE to reduce the error to this level. However, this requires a greater investment of labor and time costs to obtain larger datasets. Thereby, in the case of limited time and samples, using EL instead of training individual NNs is a better method to improve the accuracy of smart contract vulnerability prediction.
Second, SCVDIE-ENSEMBLE has a shorter error range compared to the standalone NN model. This suggests that more confident vulnerability prediction can be obtained by the combination of NN and EL than by not using EL. The SCVDIE-ENSEMBLE model consists of seven different NN models, each of which can be responsible for a different focus, and more patterns can be learned under the same conditions, which is also consistent with the first conclusion.
Finally, as mentioned at the beginning of this subsection, training a complex deep learning model with a small amount of data can lead to overfitting. Although the proposed SCVDIE-ENSEMBLE model has a complex structure consisting of seven individual NN models and the training dataset used in this study is relatively small (i.e., ), the model is not expected to be overfitted in this paper. The SCVDIE-ENSEMBLE was tested by comparing the overall test RMSE achieved when trained on a progressively larger dataset (i.e., ) with the RMSE achieved when trained using the original dataset (i.e., ). The overall RMSEs converge almost to a horizontal asymptote when the size of the training dataset increases, which suggests that the overall test RMSEs do not decrease significantly if more training samples are provided. Therefore, the proposed SCVDIE-ENSEMBLE model does not appear to be overfitted.
The above conclusions are a preliminary analysis of the experimental results, mainly for the comparison of SCVDIE-ENSEMBLE with other models, but still lacking in the analysis of other single models. We will discuss the results more fully and in greater depth below. The first to say is that the CNN and RNN models, which are closer to the performance of the integrated model, are more similar. In
Figure 10, it can be seen that, when the dataset is small, the loss value of CNN is greater than RNN, but, when the sample of the dataset increases, the advantage of RNN disappears and, instead, CNN achieves good results. This indicates that the CNN requires a higher amount of data than the RNN in this task. In addition, both CNNs showed better recognition results when the number of data samples increased rapidly, which can be interpreted as a higher performance of CNNs than RNNs in this task when there are enough samples. Secondly, this paper also identifies an interesting phenomenon. In NLP, Transformer has achieved significant performance gains over other models, yet its performance in this task is mediocre. This paper argues that this may be because, although the Transformer can handle longer sequences of operations and retain more information than other single models, and this paper also preprocesses the sequences to reduce their length, there are still a small number of contract sequences that are too long, and these overly long sequences lead to a lot of data noise that affects the Transformer’s performance. In contrast, the rest of the single model deals with data that are a sequence corresponding to each sub-path, which is relatively much smaller in length and more conducive to adequate feature extraction. Another object that deserves to be discussed is the GRU model, due to its relatively worst performance. GRU and Bi-GRU as optimization models for RNNs can solve the RNN gradient vanishing problem, but they also bring another potential problem: a large number of parameters, where GRU has three times more parameters than Navie RNN, which seriously increases the model spatial complexity. Therefore, this explains the superiority of the RNN model when dealing with relatively short sequences of sub-path operations.
6. Further Discussions
The specialty of this paper’s approach in dealing with smart contracts. The opcode of a smart contract is a sequence of specific characters, containing many nonlinear call relations, similar to the assembly language of a traditional program. In contrast to existing methods of extracting contract sequences using source code, this paper combines both the sequence features of individual contracts and the overall features. This has the obvious advantage of not only extracting features from a single linear sequence of operands, but also of segmenting them to find potential features in multiple dimensions, which greatly reduces the length of a single input sequence and effectively reduces the dimensionality of the data embedding. To this end, we have also built a unique opcode-based IG structure diagram for the first time, which better represents the relationship between the local and the whole. Ultimately, the superior performance of the proposed method in this paper was demonstrated in a quantitative manner using extensive experiments. Both the mean F1 score and the mean prediction accuracy achieved optimal values of 97.57% and 97.42%, respectively, and achieved lower relative RMSEs on different size datasets.
Findings. EL has been successful in a variety of areas, yet little has been reported on blockchain and IoT security. To this end, this paper designs a novel EL model and conducts multiple sets of comparative experiments using real-world smart contracts. The results confirm that EL can produce better results with fewer data to train. This performance improvement over popular methods, such as symbol-based execution, is easy to explain. This is because methods based on symbolic execution face significant challenges, such as path explosion, which limits the performance of these popular methods. This performance improvement over a single-model-based approach can be attributed to the fact that different classification models can specialize in different parts of the dataset. In other words, different models focus on different vulnerability features, which improves the performance of SCVDIE while paving the way for less dependence on the dataset for SCVDIE. This is because every single NN focuses on a different vulnerability feature that the integrated model can be used to learn more features when the dataset is limited, thus increasing the utilization of the dataset.
Limitations. Despite these new findings, the following limitations of this work remain. For example, while SCVDIE can reduce the amount of data required by the model, and thus reduce the human and time costs required to collect the data, this implementation is indirect and does not directly address the resources spent on collecting a certain amount of vulnerability data. In addition, this paper uses binary numbers to indicate whether a contract contains vulnerabilities and, in the future, will explore how to make the classification results more intelligent. For example, exploring how to output separate results for different vulnerabilities.
7. Conclusions and Future Work
In this study, we proposed innovatively an EL-based approach called Ensemble Learning Based Smart Contract Vulnerability Prediction (SCVDIE-ENSEMBLE) to predict vulnerabilities in Ethereum smart contracts. The proposed SCVDIE-ENSEMBLE method incorporated multiple NNs, which are CNN, RNN, RCNN, DNN, GRU, Bi-GRU, and Transformer. Each NN has its unique role to play, which allows SCVDIE-ENSEMBLE to increase the efficiency of data utilization while having a more accurate and robust performance on unseen data. We have also investigated a novel approach to data classification that underpins a wide range of experiments.
We have proven the performance of SCVDIE-ENSEMBLE with numerous experiments. First, a fivefold CV experiment was conducted on the benchmark dataset for the seven single models and the overall model integrated by SCVDIE-ENSEMBLE. Quantitative experimental results demonstrate that SCVDIE-ENSEMBLE has a smaller error in classification results. Next, the performance of these eight models and three popular methods are compared. The average prediction accuracy of SCVDIE-ENSEMBLE was experimentally demonstrated to be better than other methods. The performance of the SCVDIE-ENSEMBLE integration strategy is then further demonstrated by comparison with the general approach. Finally, the contribution of SCVDIE-ENSEMBLE to reducing the model’s reliance on large datasets, and hence the cost of data collection, is demonstrated in multiple dimensions by varying the size of the dataset.
We believe this work is an important step toward alleviating the challenges of data collection and IoT security. For future work, since the SCVDIE-ENSEMBLE model relies on existing learnable features, as with other NNs, we will focus on breaking this limitation by combining the underlying NN model with other deep learning methods, such as transfer learning that can be extended to similar domains.