Comparison of Different Linewidth Measuring Methods for Narrow Linewidth Laser
Abstract
:1. Introduction
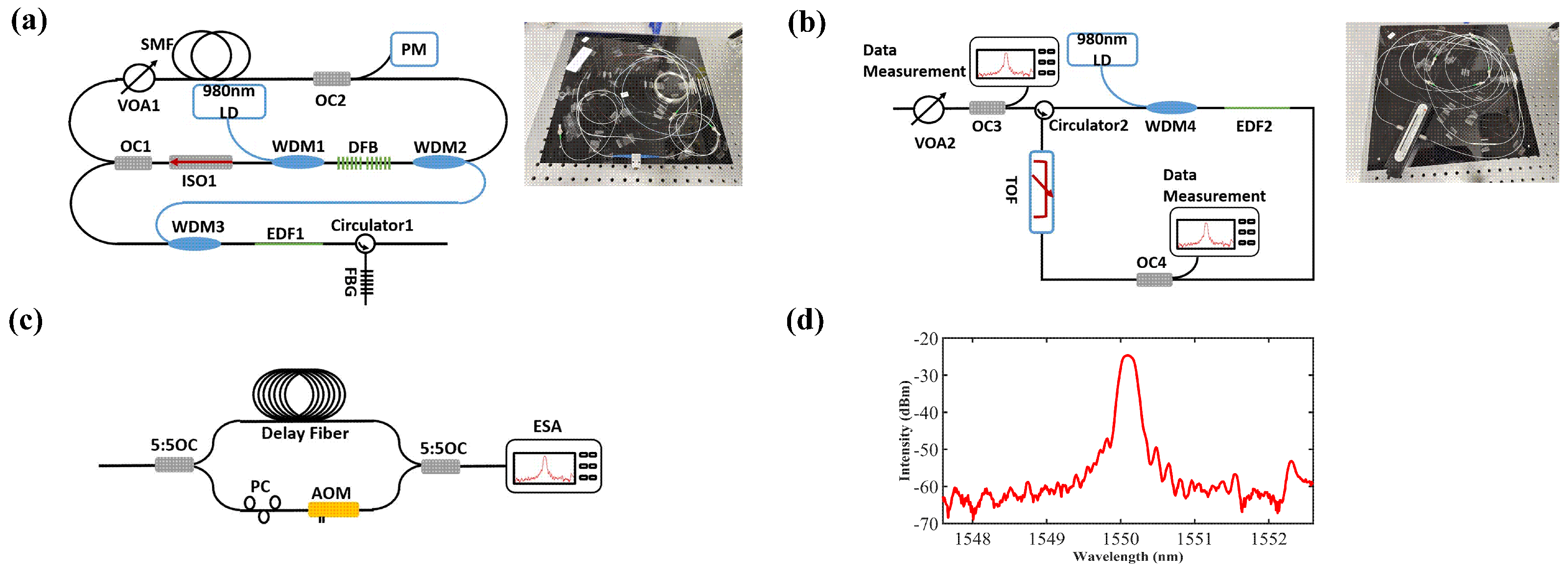
2. Experimental Setup
3. Results
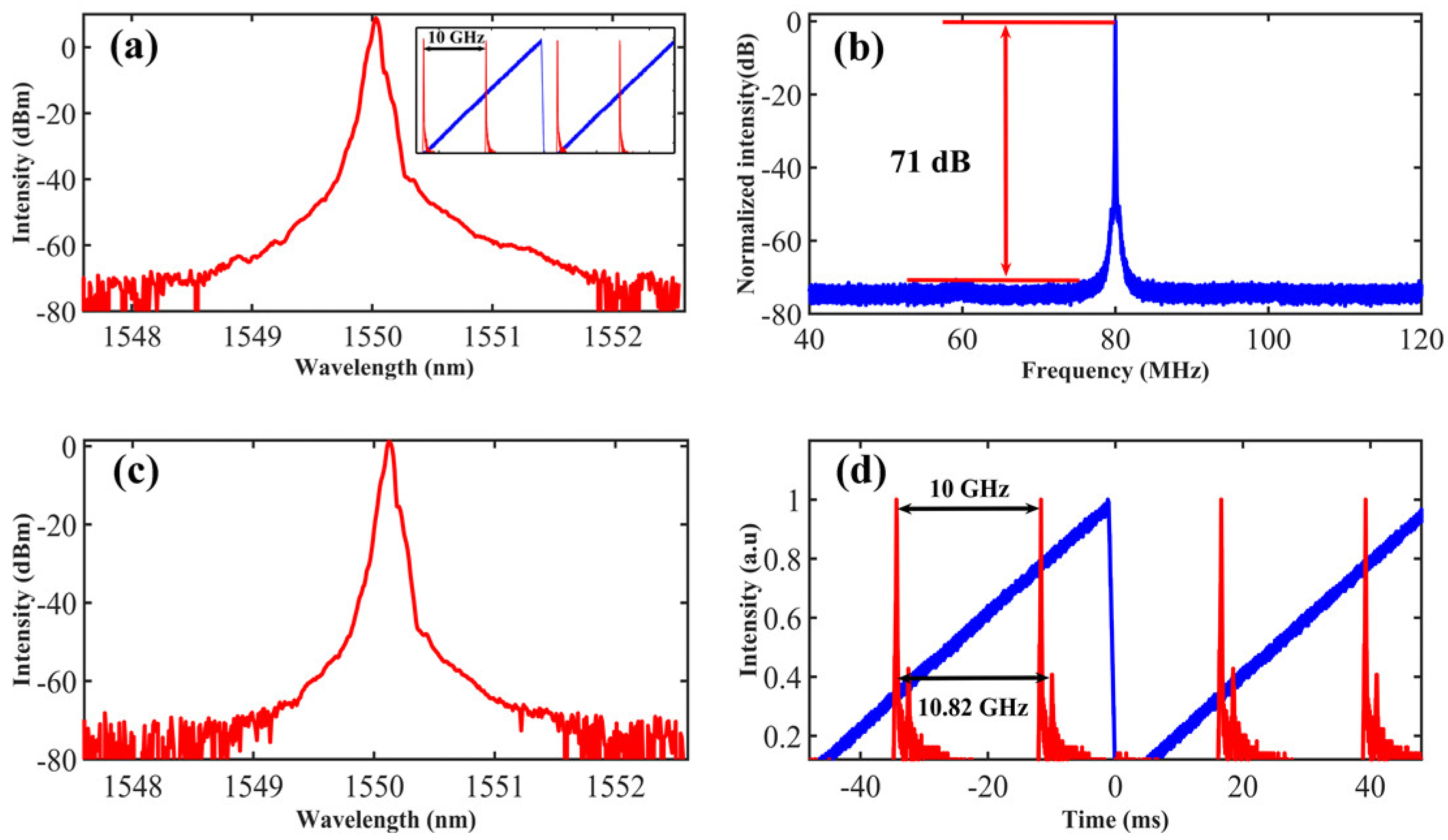
3.1. Spectral Properties
3.2. Linewidth Measurement with DSHI
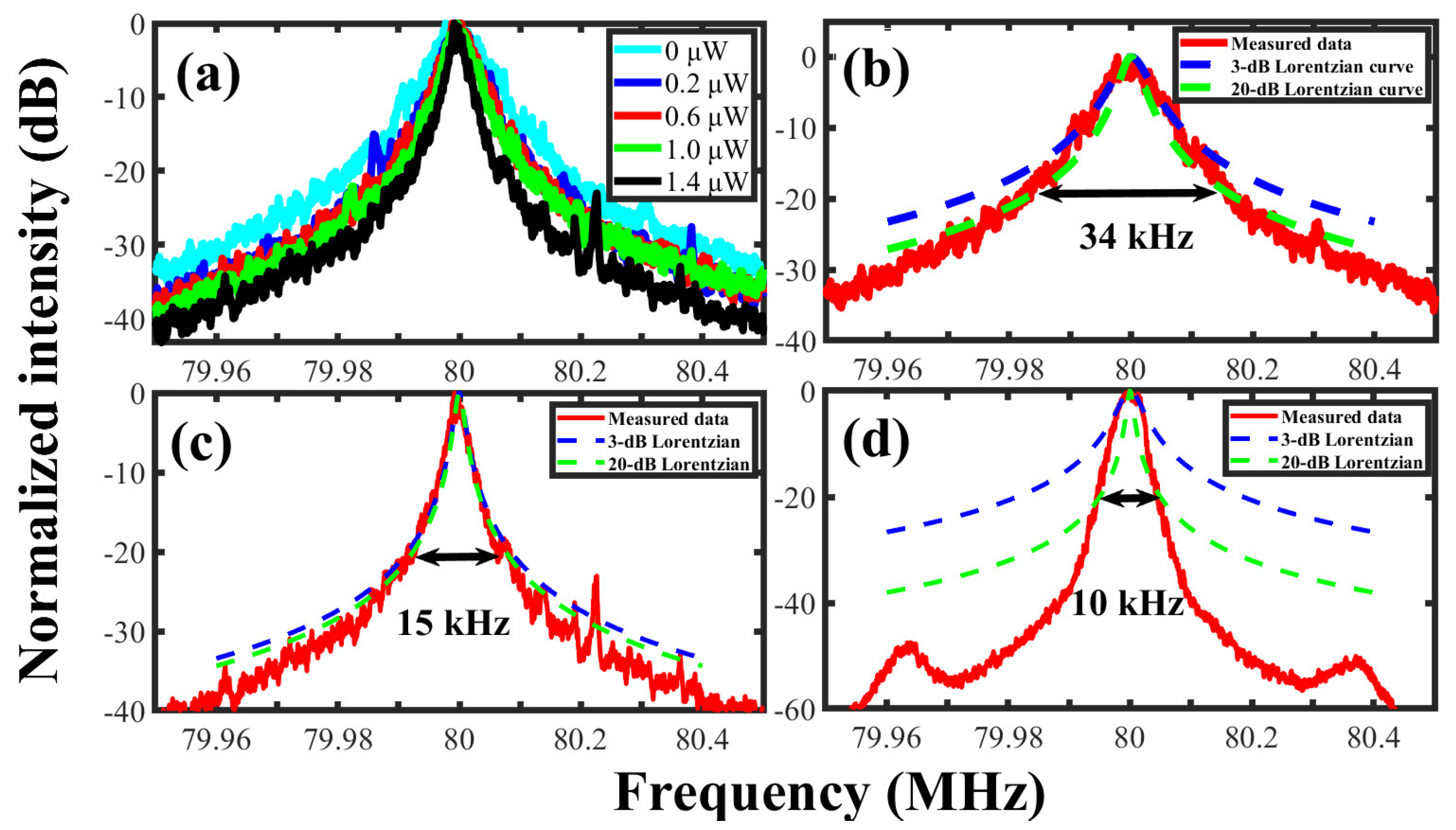
3.3. Linewidth Measurement with SCELD
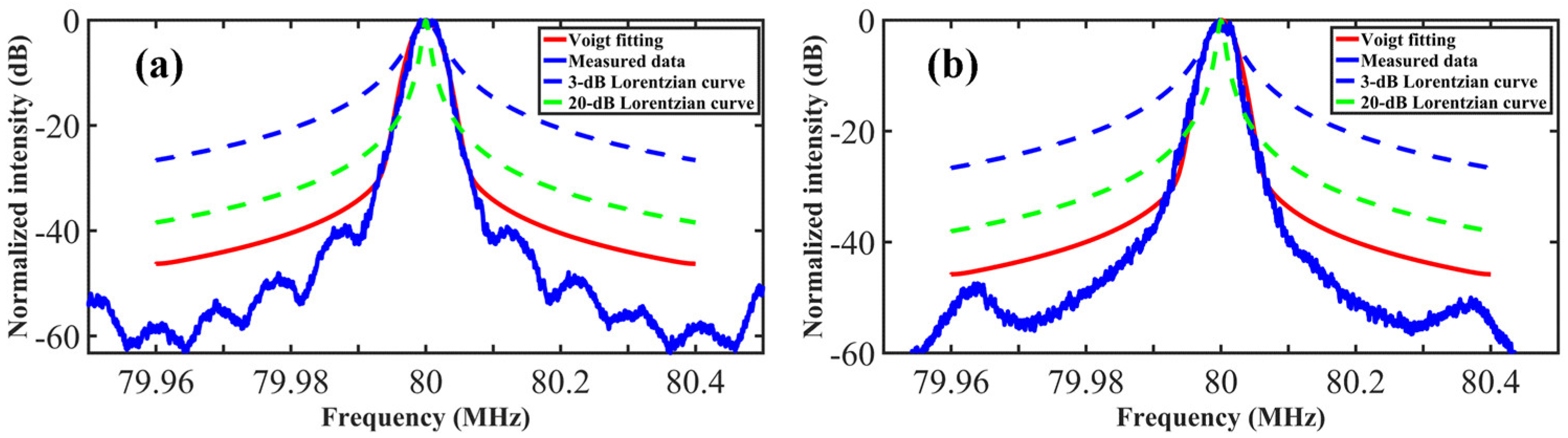
3.4. Linewidth Measurement with Voigt Fitting
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, P.; Ma, Y.; Wang, X.; Ma, H.; Xu, X.; Liu, Z. Coherent beam combination of three two-tone fiber amplifiers using stochastic parallel gradient descent algorithm. Opt. Lett. 2009, 34, 2939–2941. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Lorini, L.; Swann, W.C.; Bergquist, J.C.; Coq, Y.L.; Oates, C.W.; Quraishi, Q.; Stalnaker, J.; Diddams, S.A.; Newbury, N.R. Multi-Octave Optical Coherence Spanning Hundreds of Meters. In Proceedings of the 2007 Conference on Lasers and Electro-Optics (CLEO), Baltimore, MD, USA, 6–11 May 2007; pp. 1–2. [Google Scholar]
- Feng, Z.Y.; Cheng, Y.; Chen, M.; Yuan, L.B.; Hong, D.; Li, L.T. Temperature-Compensated Multi-Point Strain Sensing Based on Cascaded FBG and Optical FMCW Interferometry. Sensors 2022, 22, 3970. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.; Pustovoit, V. Small-Sized Interferometer with Fabry-Perot Resonators for Gravitational Wave Detection. Sensors 2021, 21, 1877. [Google Scholar] [CrossRef]
- Shi, L.; Tao, Z.; Qian, H.; Huang, S. Effect of Laser Linewidth on Phase-OTDR Based Distributed Vibration Sensing Regime. In Proceedings of the International Conference on Optical Fibre Sensors, Santander, Spain, 2 June 2014; p. 91576H-91576H-91574. [Google Scholar]
- Geng, J.H.; Spiegelberg, C.; Jiang, S.B. Narrow linewidth fiber laser for 100-km optical frequency domain reflectometry. IEEE Photonics Technol. Lett. 2005, 17, 1827–1829. [Google Scholar] [CrossRef]
- Mo, S.P.; Huang, X.; Xu, S.H.; Feng, Z.M.; Li, C.; Yang, C.S.; Yang, Z.M. Compact slow-light single-frequency fiber laser at 1550 nm. Appl. Phys. Express 2015, 8, 082703. [Google Scholar] [CrossRef]
- Black, E.D. An introduction to Pound-Drever-Hall laser frequency stabilization. Am. J. Phys. 2001, 69, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Martin, M.J.; Benko, C.; Hall, J.L.; Ye, J.; Hagemann, C.; Legero, T.; Sterr, U.; Riehle, F.; Cole, G.D.; et al. Reduction of residual amplitude modulation to 1 × 10−6 for frequency modulation and laser stabilization. Opt. Lett. 2014, 39, 1980–1983. [Google Scholar] [CrossRef]
- Yang, R.T.; Lv, H.S.; Luo, J.; Hu, P.C.; Yang, H.X.; Fu, H.J.; Tan, J.B. Ultrastable Offset-Locking Continuous Wave Laser to a Frequency Comb with a Compound Control Method for Precision Interferometry. Sensors 2020, 20, 1248. [Google Scholar] [CrossRef] [Green Version]
- Hao, L.Y.; Wang, X.H.; Guo, D.J.; Jia, K.P.; Fan, P.F.; Guo, J.; Ni, X.; Zhao, G.; Xie, Z.D.; Zhu, S.N. Narrow-linewidth self-injection locked diode laser with a high-Q fiber Fabry-Perot resonator. Opt. Lett. 2021, 46, 1397–1400. [Google Scholar] [CrossRef]
- Huang, S.H.; Zhu, T.; Yin, G.L.; Lan, T.Y.; Li, F.H.; Huang, L.G.; Liu, M. Dual-cavity feedback assisted DFB narrow linewidth laser. Sci. Rep. 2017, 7, 1185. [Google Scholar] [CrossRef]
- Tkach, R.; Chraplyvy, A. Regimes of feedback effects in 1.5-µm distributed feedback lasers. J. Light. Technol. 1986, 4, 1655–1661. [Google Scholar] [CrossRef]
- Huang, S.H.; Zhu, T.; Yin, G.L.; Lan, T.Y.; Huang, L.G.; Li, F.H.; Bai, Y.Z.; Qu, D.R.; Huang, X.B.; Qiu, F. Tens of hertz narrow-linewidth laser based on stimulated Brillouin and Rayleigh scattering. Opt. Lett. 2017, 42, 5286–5289. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Meng, Z.; Zhou, H.J. Low-Threshold, Single-Mode, Compact Brillouin/Erbium Fiber Ring Laser. J. Light. Technol. 2013, 31, 1980–1986. [Google Scholar] [CrossRef]
- Hambali, N.; Mahdi, M.A.; Al-Mansoori, M.H.; Saripan, M.I.; Abas, A.F. Optimization of output coupling ratio on the performance of a ring-cavity Brillouin-erbium fiber laser. Appl. Opt. 2009, 48, 5055–5060. [Google Scholar] [CrossRef]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef]
- Xu, D.; Yang, F.; Chen, D.J.; Wei, F.; Cai, H.W.; Fang, Z.J.; Qu, R.H. Laser phase and frequency noise measurement by Michelson interferometer composed of a 3 × 3 optical fiber coupler. Opt. Express 2015, 23, 22386–22393. [Google Scholar] [CrossRef]
- Okoshi, T.; Kikuchi, K.; Nakayama, A. Novel method for high resolution measurement of laser output spectrum. Electron. Lett. 1980, 16, 630–631. [Google Scholar] [CrossRef]
- Huang, S.H.; Zhu, T.; Liu, M.; Huang, W. Precise measurement of ultra-narrow laser linewidths using the strong coherent envelope. Sci. Rep. 2017, 7, 41988. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Meng, Z.; Wang, J.F.; Chen, W. Ultra-narrow linewidth measurement based on Voigt profile fitting. Opt. Express 2015, 23, 6803–6808. [Google Scholar] [CrossRef]
- Mercer, L.B. 1/f frequency noise effects on self-heterodyne linewidth measurements. J. Light. Technol. 1991, 9, 485–493. [Google Scholar] [CrossRef]
- Richter, L.E.; Mandelberg, H.I.; Kruger, M.S.; McGrath, P.A. Linewidth determination from self-heterodyne measurements with subcoherence delay times. IEEE J. Quantum Electron. 1986, 22, 2070–2074. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Luo, Q.; Wang, X.; Ma, X.; Zhang, W.; Fang, W.; Chen, X.; Huang, S.; Zhou, Y.; Gao, W. Comparison of Different Linewidth Measuring Methods for Narrow Linewidth Laser. Sensors 2023, 23, 122. https://doi.org/10.3390/s23010122
Zheng Z, Luo Q, Wang X, Ma X, Zhang W, Fang W, Chen X, Huang S, Zhou Y, Gao W. Comparison of Different Linewidth Measuring Methods for Narrow Linewidth Laser. Sensors. 2023; 23(1):122. https://doi.org/10.3390/s23010122
Chicago/Turabian StyleZheng, Ziqi, Qiaoxia Luo, Xian Wang, Xiaohui Ma, Wei Zhang, Wentan Fang, Xiaolin Chen, Song Huang, Yong Zhou, and Weiqing Gao. 2023. "Comparison of Different Linewidth Measuring Methods for Narrow Linewidth Laser" Sensors 23, no. 1: 122. https://doi.org/10.3390/s23010122
APA StyleZheng, Z., Luo, Q., Wang, X., Ma, X., Zhang, W., Fang, W., Chen, X., Huang, S., Zhou, Y., & Gao, W. (2023). Comparison of Different Linewidth Measuring Methods for Narrow Linewidth Laser. Sensors, 23(1), 122. https://doi.org/10.3390/s23010122





