Efficient Polar Coded Selective Decode-and-Forward with Cooperative Decision Threshold in Cooperative Multi-Relay Transmissions
Abstract
:1. Introduction
- Polar codes with specific rates are designed for fading channels. A new construction approach is proposed using polar codes in fading channels. The information bit and frozen indices are reselected based on the channel states. In addition, an optimally designed SNR is used in code design with fixed data rate. Thus, coding gain is obtained and the complexity is reduced by using the improved polar codes.
- Optimal selection is obtained for multi-relay cooperation. The scheme provides a candidate relay set to choose the optimally selected relays and sets a cooperative threshold at the destination to decide whether the relay takes part in cooperative communications. Several relays with good channel gain ratios are chosen and combined in order to exceed the decision threshold for joint cooperative reception. In addition, the OP for different numbers of relays are analyzed theoretically using the proposed PCSDF scheme for more accurate analytical expression.
- The influence of distance between the source and the optimal relay is numerically analyzed for better performance. The distance between the source and the optimal relay is a crucial factor in determining overall performance. Through numerical analyses, the relationship of the distance between the source and optimal relay is obtained. The link status associated with the proposed relay position obviously affects the cooperative schemes, which can be adopted in practice.
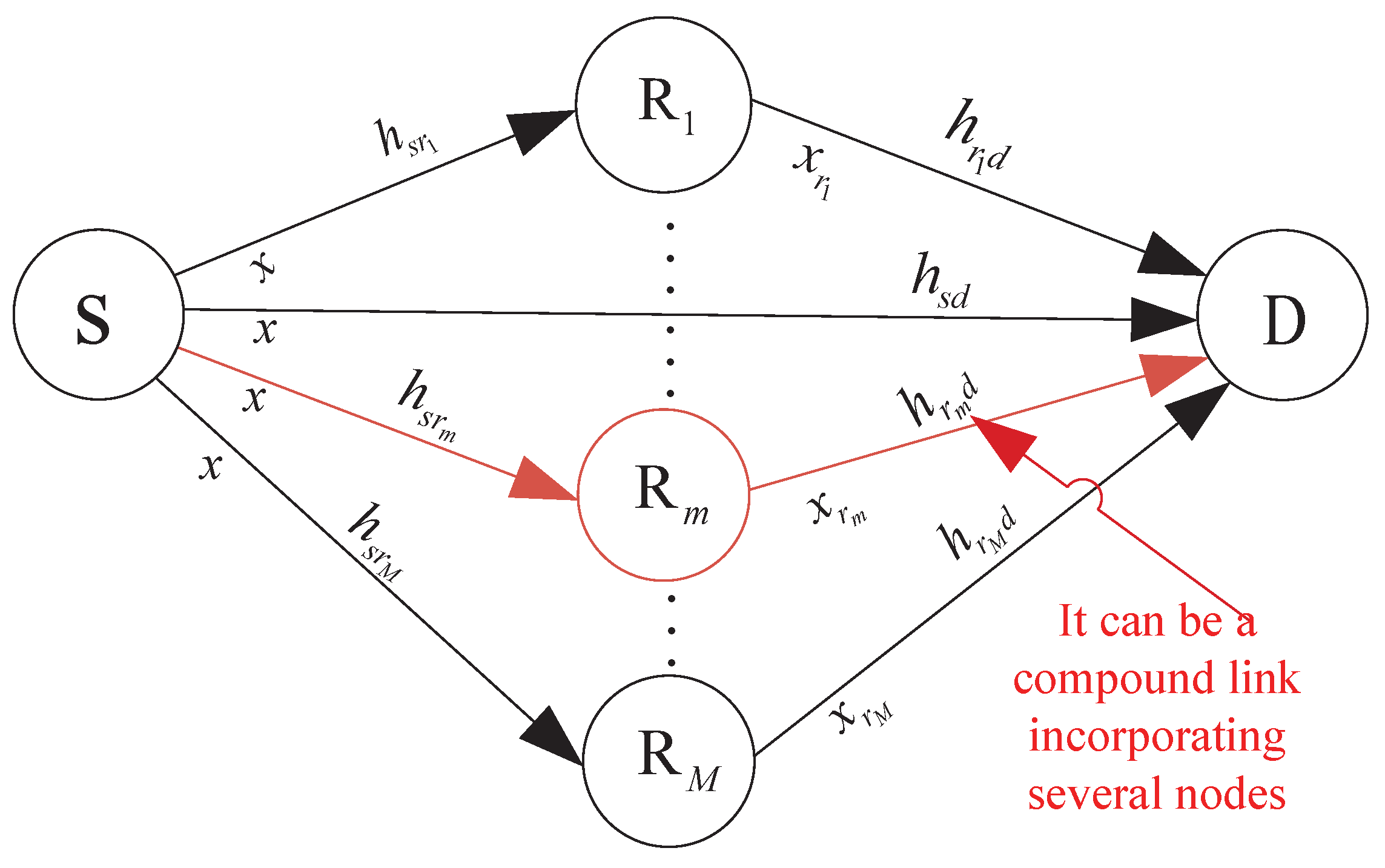
2. System Model of the SDF Cooperation
3. Polar Coded SDF Cooperation
3.1. Polar Encoding and Decoding
- Channel polarization
- Polar encoding
- Polar successive cancellation (SC) decoding
- Construction of polar codes in fading channels
- (i)
- Input a channel fading vector , the limit of the channel value , data rate R, code length N, M and , where is selected as a tradeoff between BER performance and decreased code rate. Here, is a channel index matrix chosen according to the quality of the bit channels and M.
- (ii)
- Count the number of bit channels where is less than , denoted as . If is larger than M, the actual number of unreliable channel is represented as . Otherwise, .
- (iii)
- The number of new frozen bits is expressed as , where c is the calculated channel capacity according to the operation SNR = and the capacity in (13).
- (iv)
- The indices of information bits are and those of frozen bits are . Both of them are ranked in the natural sequence.
3.2. Proposed PCSDF Cooperation
4. Theoretical Analysis of the Proposed PCSDF Cooperation Scheme
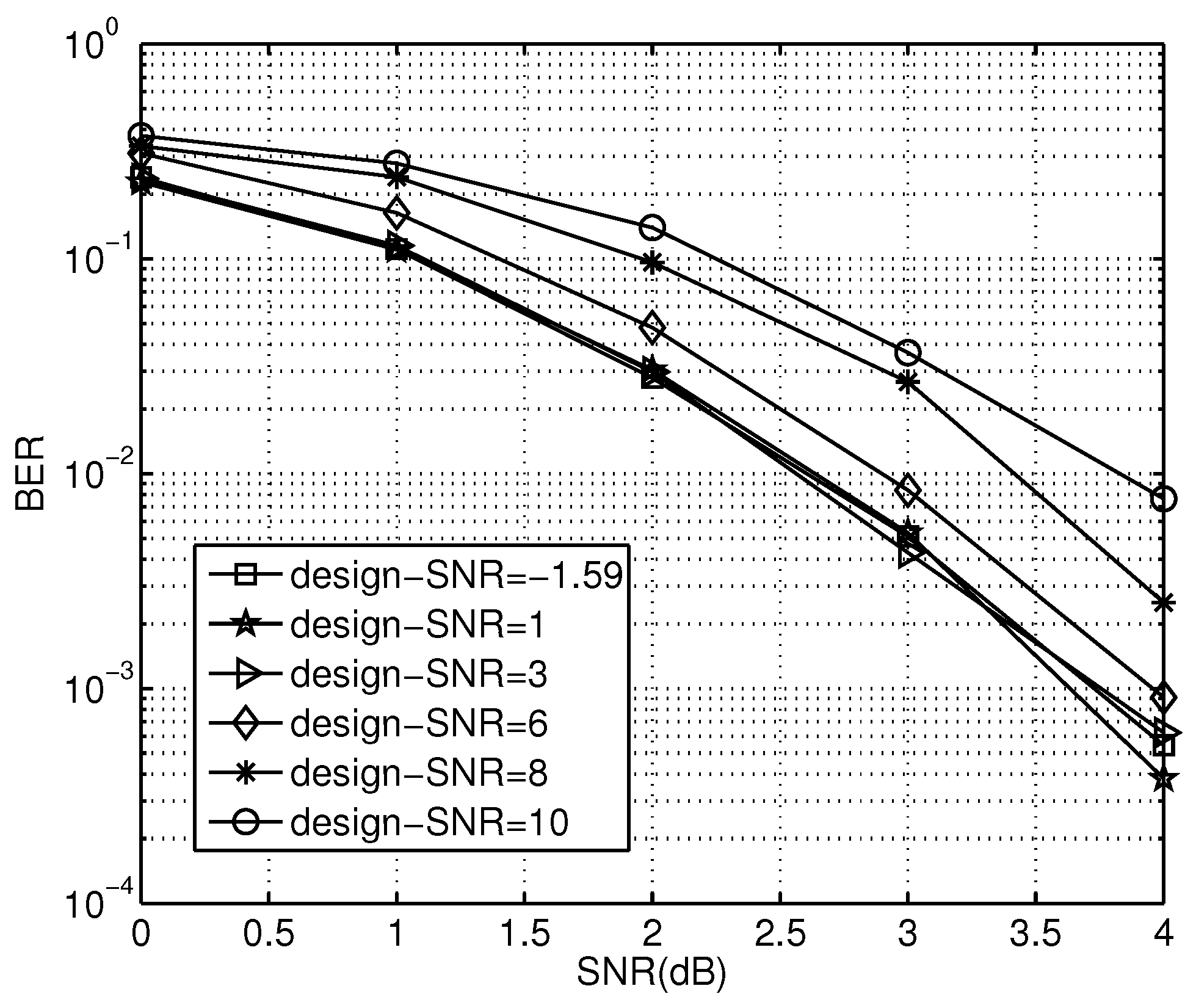
4.1. Analysis of Optimal Design-SNR in Proposed Scheme
4.2. Analyses of Outage Probability in Proposed Scheme
- (i)
- The outage probability that refers to that the source S re-transmits messages to the destination D when .
- (ii)
- The outage probability relates to the failure of the optimal relay when and .
- (iii)
- The outage probability of the optimal relay is used to forward messages when and .
5. Numerical Simulations and Analysis of Results
5.1. BER Performance of Polar-Coded Cooperation Transmission over Fading Channels
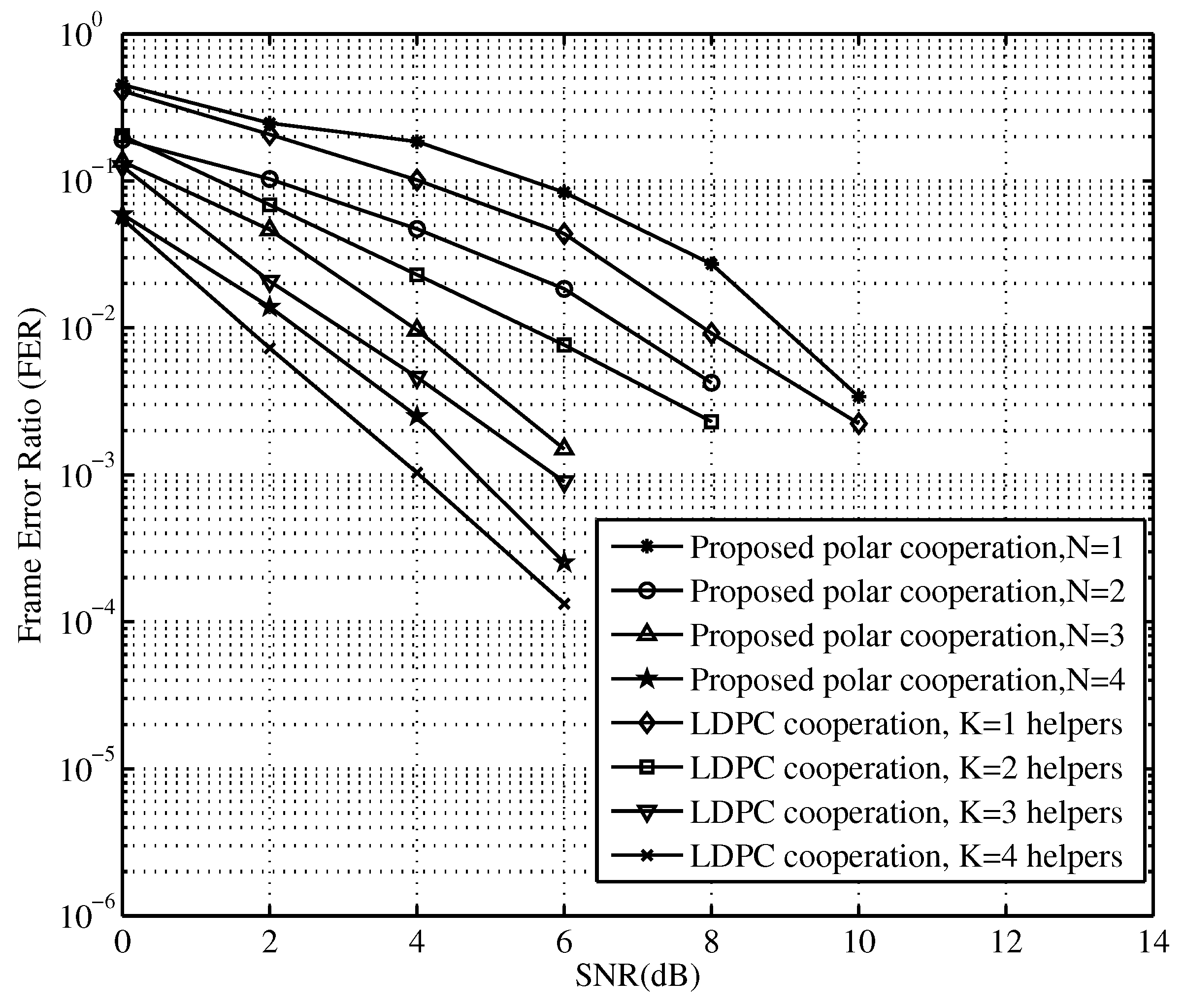
5.2. Simulations and Analyses of the Proposed PCSDF Cooperation
5.3. Computational Complexity Analysis of the Proposed PCSDF Cooperation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, J.-S.; Baek, J.-S.; Jeon, S.; Seo, J.-S. Cooperative networks with amplify-and-forward multiple-full-duplex relays. IEEE Trans. Wirel. Commun. 2014, 13, 2134–2149. [Google Scholar] [CrossRef]
- Sharma, P.K.; Garg, P. Performance analysis of full duplex decode-and-forward cooperration relaying over Nakagami-mfading channels. Trans. Emerg. Telecommun. Technol. 2014, 25, 905–913. [Google Scholar] [CrossRef]
- Vu, T.X.; Duhamel, P.; Renzo, M.D. Performance analysis of network coded cooperation with channel coding and adaptive DF-based relaying in Rayleigh fading channels. IEEE Signal Process. Lett. 2015, 22, 1354–1358. [Google Scholar] [CrossRef] [Green Version]
- Sendonaris, A.; Erkip, E.; Aazhang, B. User cooperation diversity. Part I. System description. IEEE Trans. Commun. 2003, 51, 1927–1938. [Google Scholar] [CrossRef] [Green Version]
- Sendonaris, A.; Erkip, E.; Aazhang, B. User cooperation diversity-Part II: Implementation aspects and performance analysis. IEEE Trans. Commun. 2003, 51, 1939–1948. [Google Scholar] [CrossRef] [Green Version]
- Li, Y. Distributed coding for cooperative wireless networks: An overview and recent advances. IEEE Commun. Mag. 2009, 47, 71–77. [Google Scholar]
- Valenti, M.; Zhao, B. Distributed turbo codes: Towards the capacity of the relay channel. In Proceedings of the 2003 IEEE Vehicular Technology Conference (VTC’2003), Orlando, FL, USA, 6–9 October 2003; Volume 1, pp. 322–326. [Google Scholar]
- Souryal, M.; Vojcic, B. Performance of amplify-and-forward and decode-and-forward relaying in Rayleigh fading with turbo codes. In Proceedings of the 2006 IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP’2006), Toulouse, France, 14–19 May 2006; Volume 1, pp. 1–5. [Google Scholar]
- Razaghi, P.; Yu, W. Bilayer low-density parity-check codes for decode-and-forward in relay channels. IEEE Trans. Inf. Theory 2007, 53, 3723–3739. [Google Scholar] [CrossRef] [Green Version]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Vangala, H.; Viterbo, E.; Hong, Y. A Comparative Study of Polar Code Constructions for AWGN Channel. 2015; Volume 1, pp. 1–9. Available online: https://arxiv.org/abs/1501.02473v1 (accessed on 10 December 2022).
- Zheng, M.; Tao, M.; Chen, W.; Ling, C. Secure polar coding for the two-way wiretap channel. IEEE Access 2018, 6, 21731–21744. [Google Scholar] [CrossRef]
- Balogun, P.R.; Marsland, I.D.; Gohary, R.H.; Yanikomeroglu, H. Polar code design for irregular multidimensional constellations. IEEE Access 2017, 5, 21941–21953. [Google Scholar] [CrossRef]
- Karzand, M. Polar codes for degraded relay channels. In Proceedings of the 2012 International Zurich Seminar on Communications (IZS’2012), Zurich, Switzerland, 29 February–2 March 2012; Volume 1, pp. 59–62. [Google Scholar]
- Ejaz, S.; Yang, F.; Soliman, T.H.M. Network polar coded cooperation with joint SC decoding. Electron. Lett. 2015, 51, 695–697. [Google Scholar] [CrossRef]
- Tannious, R.; Nosratinia, A. Spectrally-efficient relay selection with limited feedback. IEEE J. Sel. Areas Commun. 2015, 26, 1419–1428. [Google Scholar] [CrossRef]
- Michalopoulos, D.S.; Karagiannidis, G.K. Performance analysis of single relay selection in rayleigh fading. IEEE Trans. Wirel. Commun. 2008, 7, 3718–3724. [Google Scholar] [CrossRef]
- Yi, Z.; Kim, I.-M. Diversity order analysis of the decode-and-forward cooperative networks with relay selection. IEEE Trans. Wirel. Commun. 2008, 7, 1354–1358. [Google Scholar]
- Eghbali, H.; Muhaidat, S.; Hejazi, S.A.; Ding, Y. Relay selection strategies for single-carrier frequency-domain equalization multi-relay cooperative networks. IEEE Trans. Wirel. Commun. 2013, 12, 2034–2045. [Google Scholar] [CrossRef]
- Wang, X.; Sun, Y.; Yu, H.; Feng, T.; Tang, W.; Zhang, Y. Outage performance analysis of amplify-and-forward cognitive relay networks with partial relay selection. In Proceedings of the 2015 Int’l Conference on Wireless Communications & Signal Processing (WCSP’2015), Nanjing, China, 15–17 October 2015; Volume 22, pp. 1354–1358. [Google Scholar]
- Mohamad, A.; Visozj, R.; Berthet, A.O. Dynamic selective decode and forward in wireless relay networks. In Proceedings of the 2015 7th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT’2015), Brno, Czech Republic, 6–8 October 2015; Volume 1, pp. 189–195. [Google Scholar]
- Al-Mistarihi, M.F.; Sharaqa, A.; Mohaisen, R.; Abu-Alnadi, O.; Abu-Seba, H. Performance analysis of multi-user diversity in multi-user two-hop amplify and forward cooperative multi-relay wireless networks. In Proceedings of the 2012 35th International Convention MIPRO, Opatija, Croatia, 21–25 May 2012; Volume 1, pp. 647–651. [Google Scholar]
- Wang, H.; Yang, S.; Lin, J.; Zhong, Y. Single relay selection with feedback and power allocation in multi-source multi-destination cooperative networks. IEEE Signal Process. Lett. 2010, 17, 997–1000. [Google Scholar] [CrossRef]
- Bletsas, A.; Shin, H.; Win, M.Z. Cooperative communications with outage-optimal opportunistic relaying. IEEE Trans. Wirel. Commun. 2007, 6, 3450–3460. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Lee, J.H. Outage probability of decode-and-forward opportunistic relaying in a multi-cell environment. IEEE Trans. Veh. Technol. 2011, 60, 1925–1930. [Google Scholar] [CrossRef]
- Miao, Q.; Bai, B.; Chen, W. Adaptive AF/DF selection with FD/HD switching in two-way relay networks. IEEE Access 2017, 5, 11594–11605. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, C.; Thompson, J.; Poor, H.V. Recovering multiplexing loss through successive relaying using repetition coding. IEEE Trans. Wirel. Commun. 2007, 6, 4484–4493. [Google Scholar] [CrossRef] [Green Version]
- Alves, H.; Souza, R.D. Selective decode-and-forward using fixed relays and packet accumulation. IEEE Signal Process. Lett. 2011, 15, 707–709. [Google Scholar] [CrossRef]
- Liu, K.J.R.; Sadek, A.; Su, W.; Kwasinski, A. Cooperative Communications and Networking; Cambridge University Press: Cambridge, UK, 2009; Volume 25, pp. 241–244. [Google Scholar]
- Sun, Q.; Bao, J.; Liu, C.; Jiang, B.; Zhu, F.; He, J. Improved polar selective decoding and forwarding cooperation. Telecommun. Sci. 2020, 36, 77–87. [Google Scholar]
- Sasoglu, E.; Telatar, E.; Arikan, E. Polarization for arbitrary discrete memoryless channels. In Proceedings of the 2009 IEEE Information Theory Workshop, Sicily, Italy, 11–16 October 2009; pp. 144–148. [Google Scholar]
- Tal, I.; Vardy, A. How to construct polar codes. IEEE Trans. Inf. Theory 2013, 59, 6562–6582. [Google Scholar] [CrossRef]
- Zribi, A.; Song, S.; Matsumoto, T. LDPC-based multi-relay lossy forwarding for correlated source transmission over orthogonal Rayleigh fading channels. In Proceedings of the 2021 IEEE Conference on Antenna Measurements & Applications (CAMA’2021), Antibes Juan-les-Pins, France, 15–17 November 2021; pp. 579–5823. [Google Scholar]


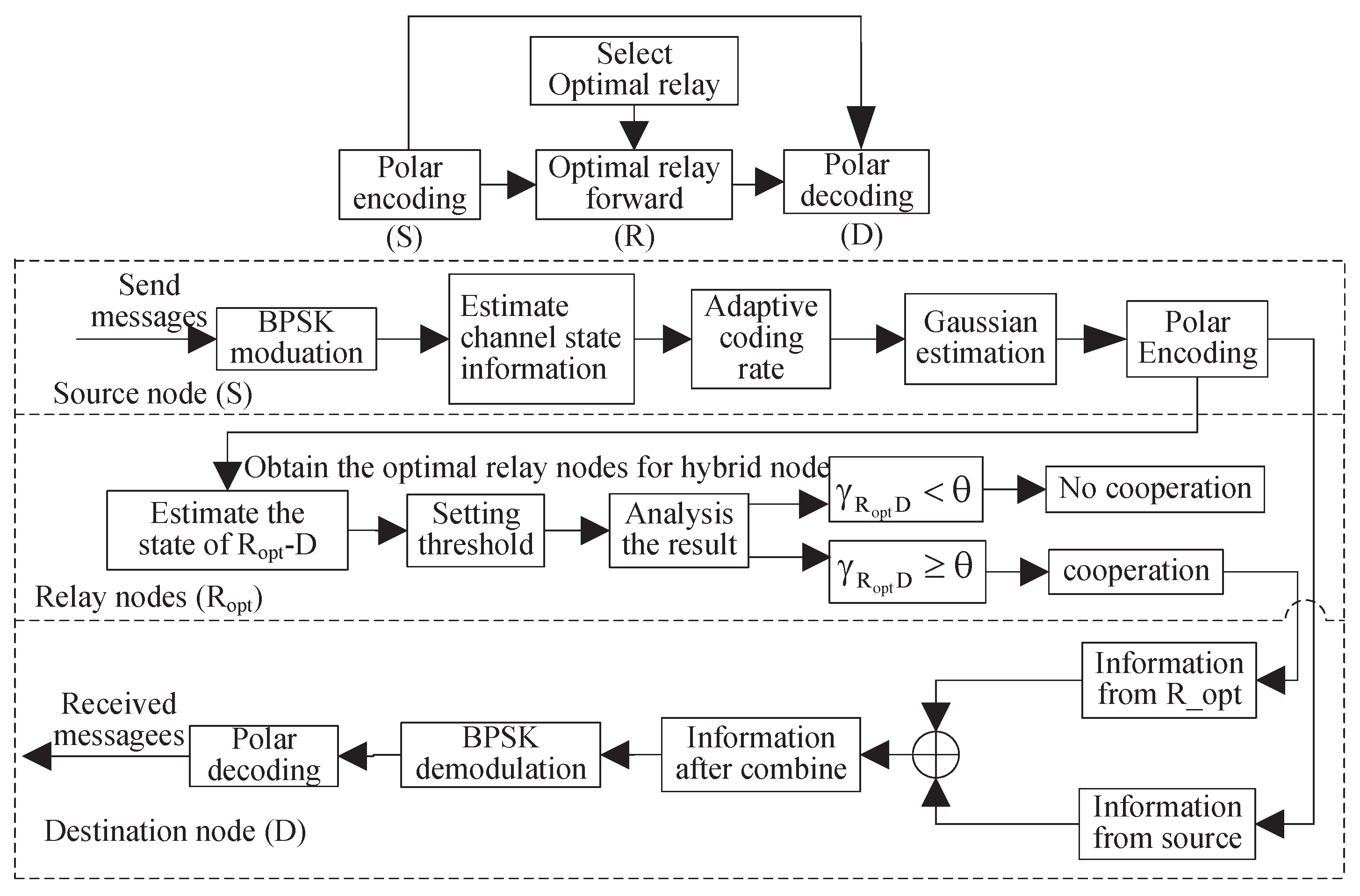





| Procedures of the improved PCSDF cooperation scheme. |
| Step (1). First, The source node broadcasts messages to the destination and all relays. Then they estimate and , respectively, to obtain the gain of link S-D and the capacity of the relay channel . |
| Step (2). Compare the capacity of the relay channel with the information transmit rate V. if , the relay is selected into the candidate relay set . Then, goto step (3). |
| Step (3). If is empty, the source transmits messages to the destination. Otherwise, the optimally selected relay are chosen from the candidate relay set . Here, can be a simple relay or a compound one composed of several relays. And the latter is jointly combined by several relays for the same channel coefficient with the maximum ratio combination (MRC) criterion. Subsequently, the cooperative capacity of the optimal relay is obtained. Then, goto step (4). |
| Step (4). Compare the relationship between and . If , the optimal relay forwards source messages. Otherwise, the optimal relay keeps silent in the whole process. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Tang, Y.; Bao, J.; Liu, C.; Shang, Y. Efficient Polar Coded Selective Decode-and-Forward with Cooperative Decision Threshold in Cooperative Multi-Relay Transmissions. Sensors 2023, 23, 165. https://doi.org/10.3390/s23010165
Jiang B, Tang Y, Bao J, Liu C, Shang Y. Efficient Polar Coded Selective Decode-and-Forward with Cooperative Decision Threshold in Cooperative Multi-Relay Transmissions. Sensors. 2023; 23(1):165. https://doi.org/10.3390/s23010165
Chicago/Turabian StyleJiang, Bin, Yue Tang, Jianrong Bao, Chao Liu, and Yanhai Shang. 2023. "Efficient Polar Coded Selective Decode-and-Forward with Cooperative Decision Threshold in Cooperative Multi-Relay Transmissions" Sensors 23, no. 1: 165. https://doi.org/10.3390/s23010165
APA StyleJiang, B., Tang, Y., Bao, J., Liu, C., & Shang, Y. (2023). Efficient Polar Coded Selective Decode-and-Forward with Cooperative Decision Threshold in Cooperative Multi-Relay Transmissions. Sensors, 23(1), 165. https://doi.org/10.3390/s23010165







