Low-Altitude Windshear Estimation Method Based on Four-Dimensional Frequency Domain Compensation for Fuselage Frustum Conformal Array
Abstract
:1. Introduction
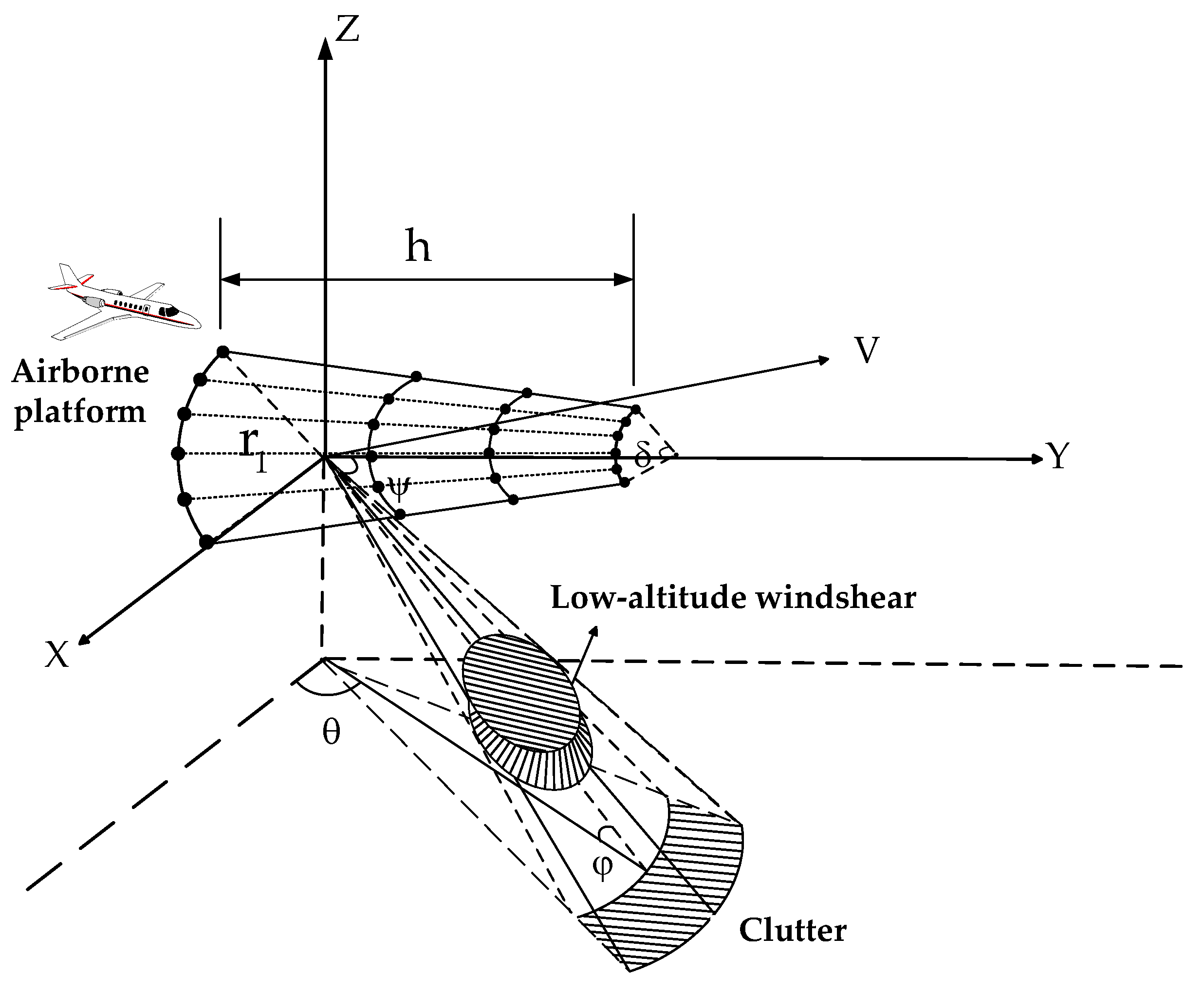
2. Fuselage Frustum Conformal Array Signal Model
2.1. The Echo Signal Model
2.2. Ground Clutter Signal
2.3. Low-Altitude Windshear Signal
3. Low-Altitude Windshear Speed Estimation Method Based on Four-Dimensional Frequency Domain Compensation Method
3.1. Covariance Matrix Estimation Based on Four-Dimensional Frequency Domain Compensation Method
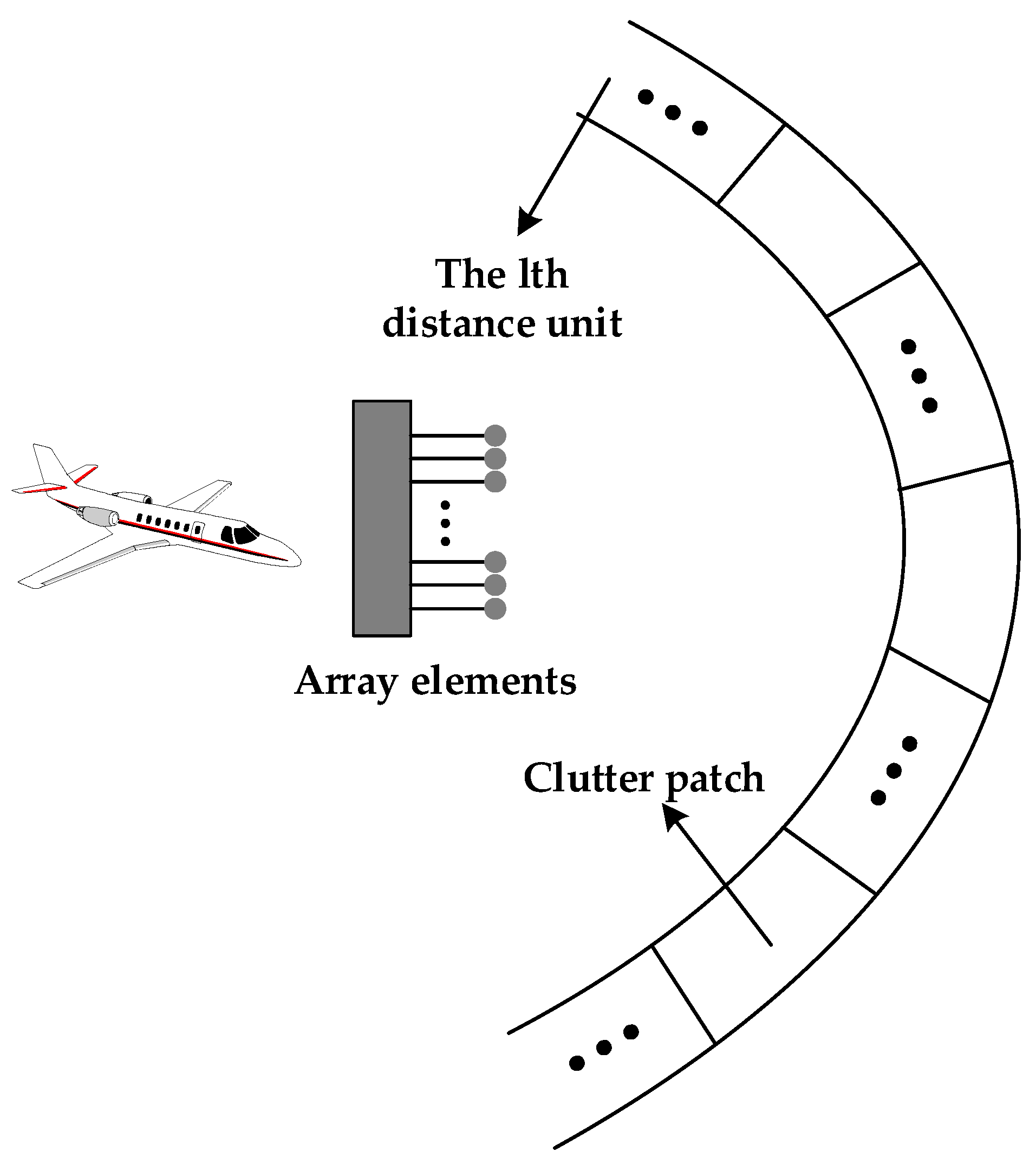
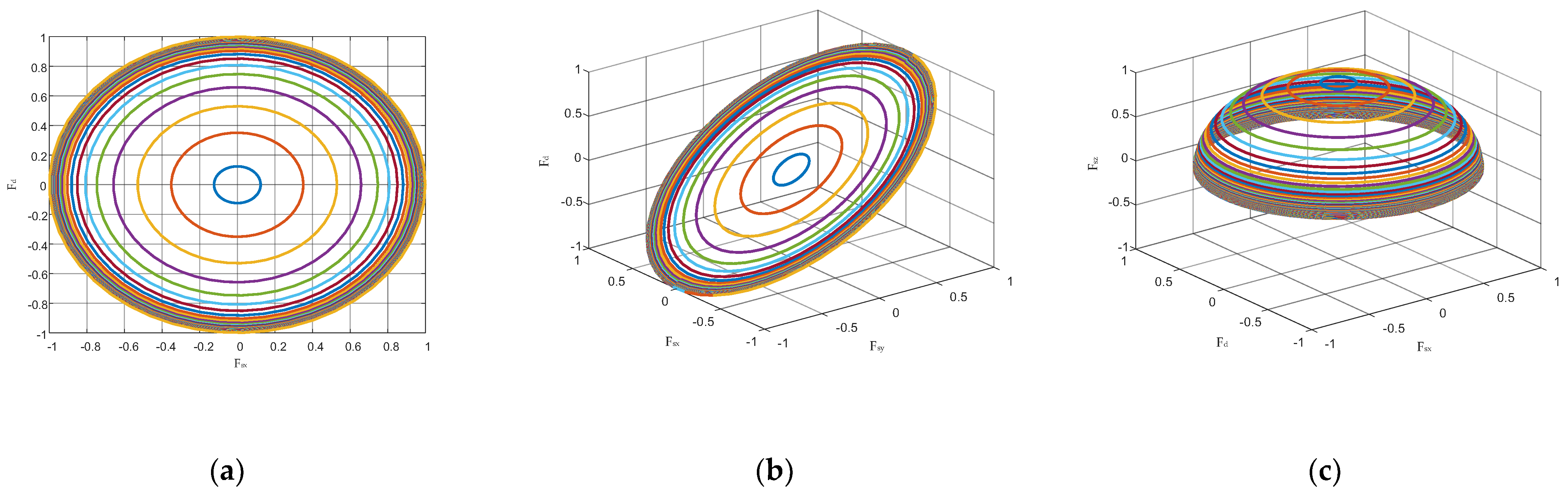
3.1.1. Analysis of the Clutter Characteristics of the Fuselage Frustum Conformal Array
3.1.2. Covariance Matrix Estimation Based on Four-Dimensional Frequency Domain Compensation Method
3.2. STAP-Based Wind Speed Estimation Method
3.3. Method Flow
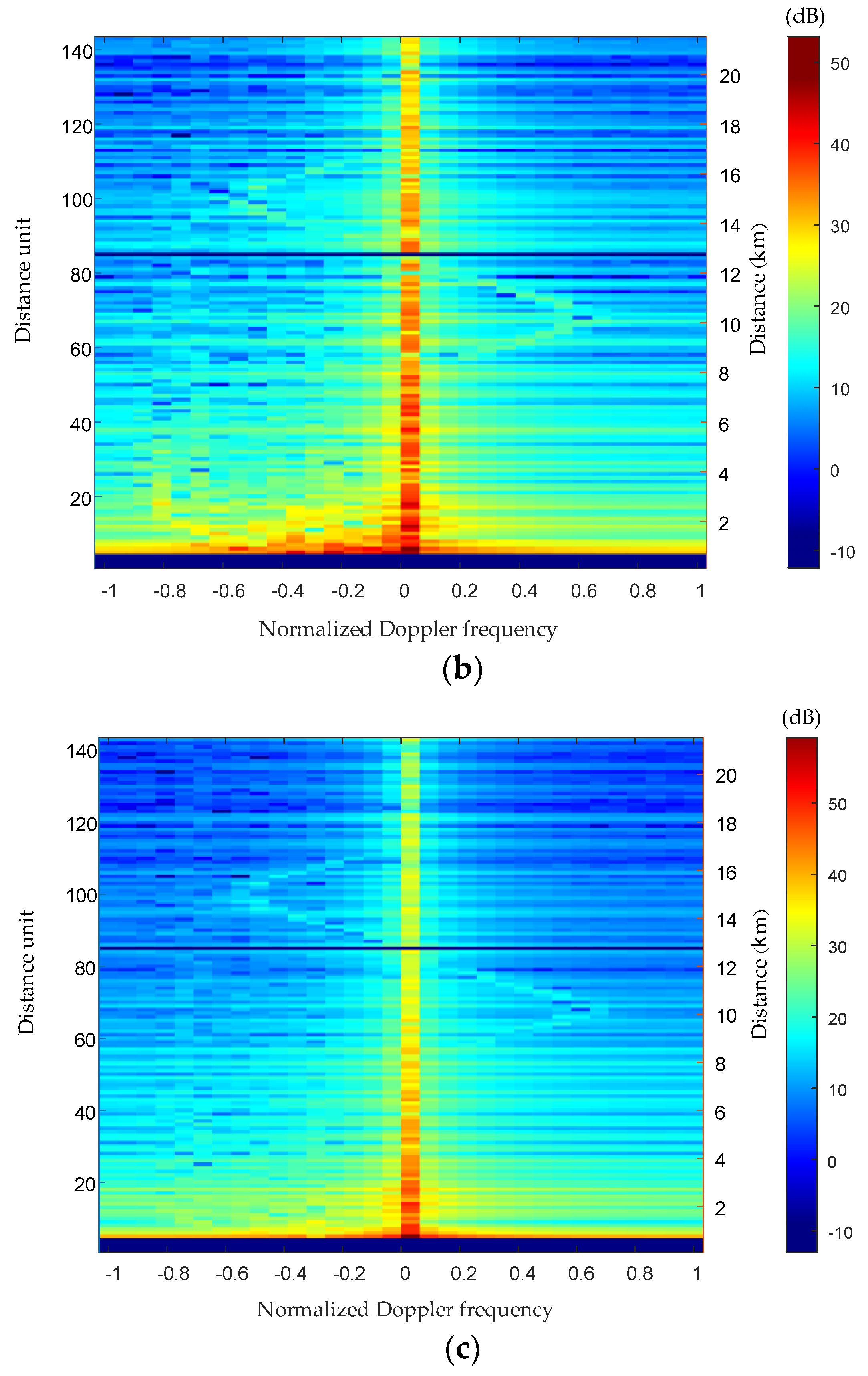
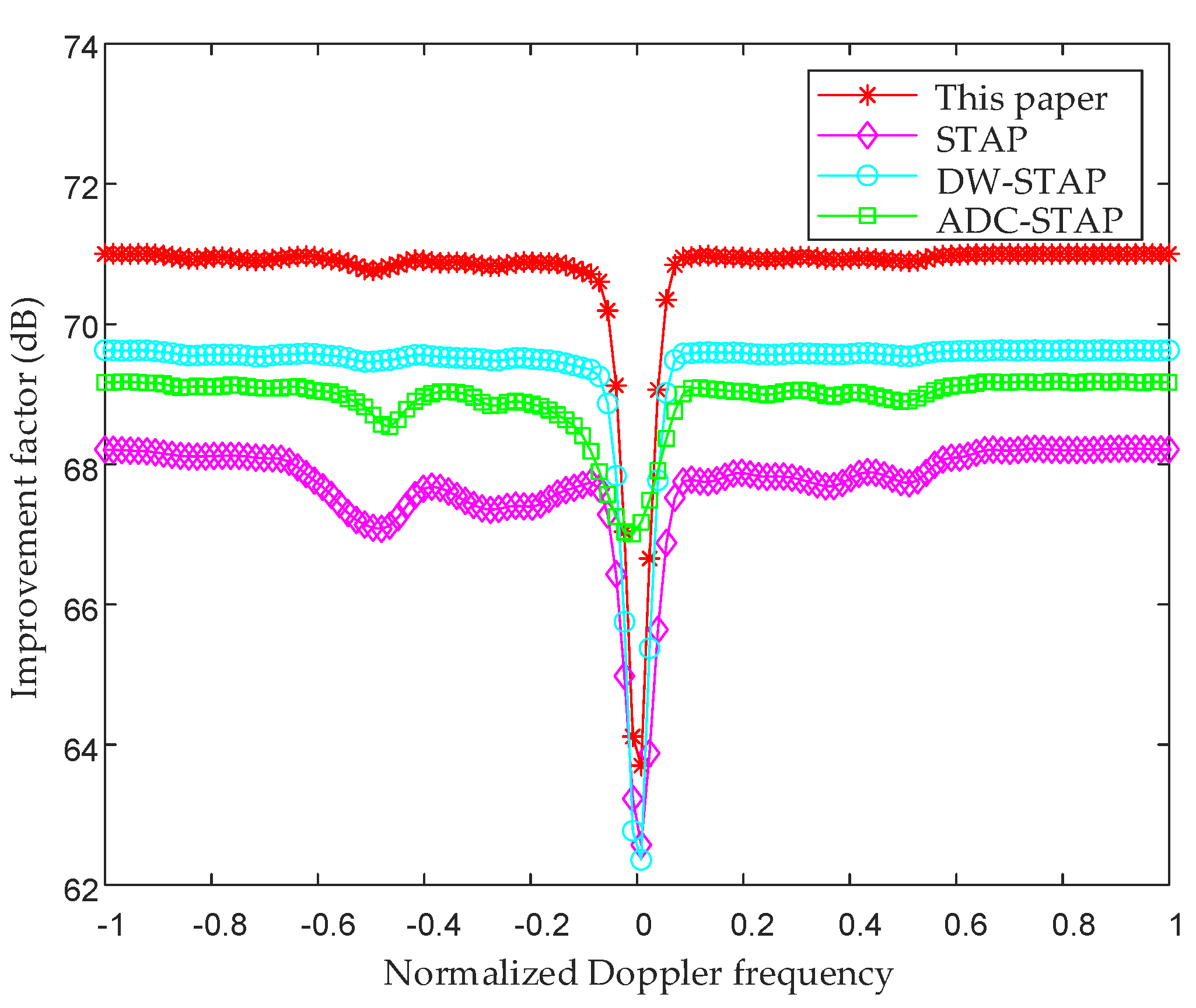
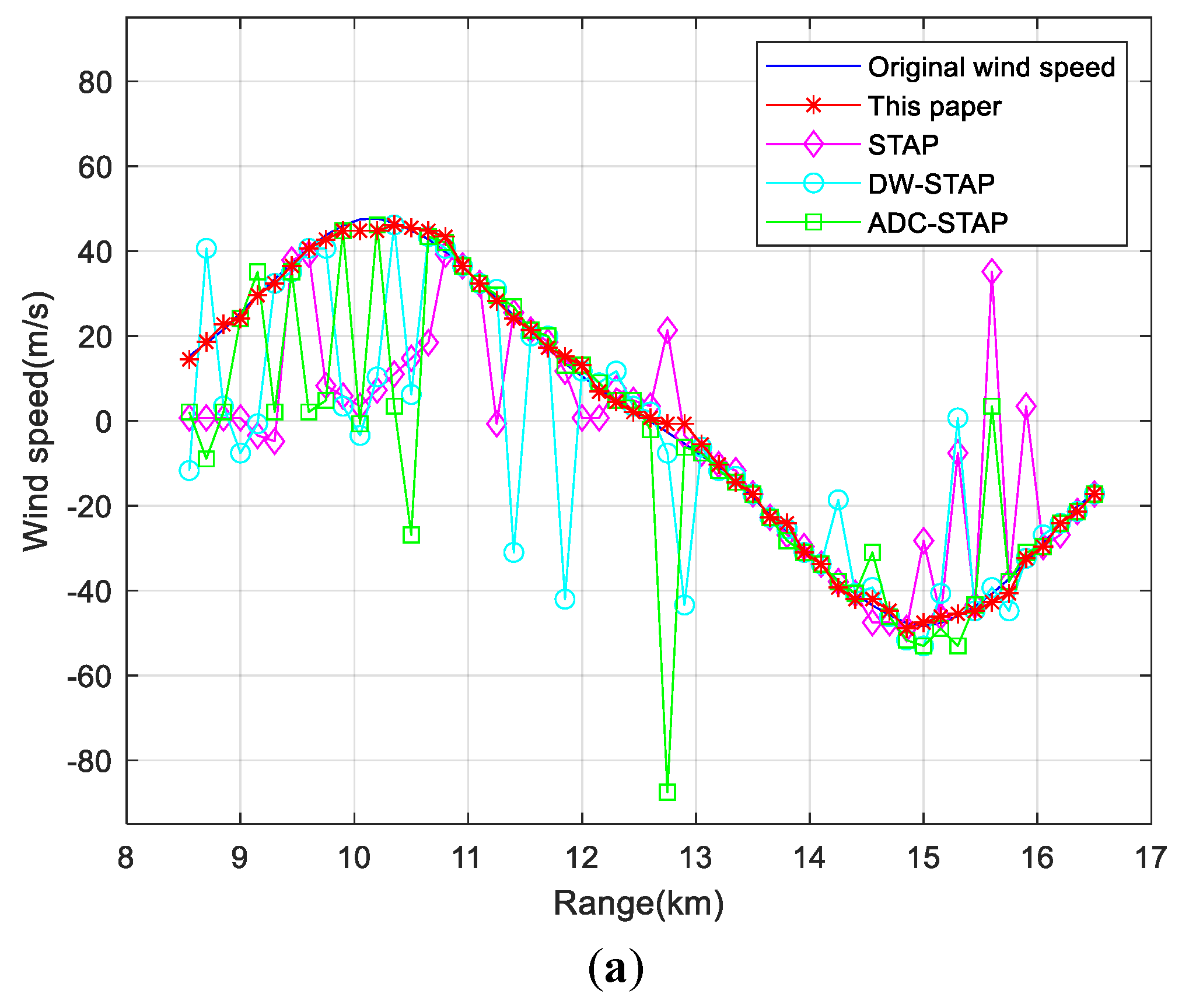
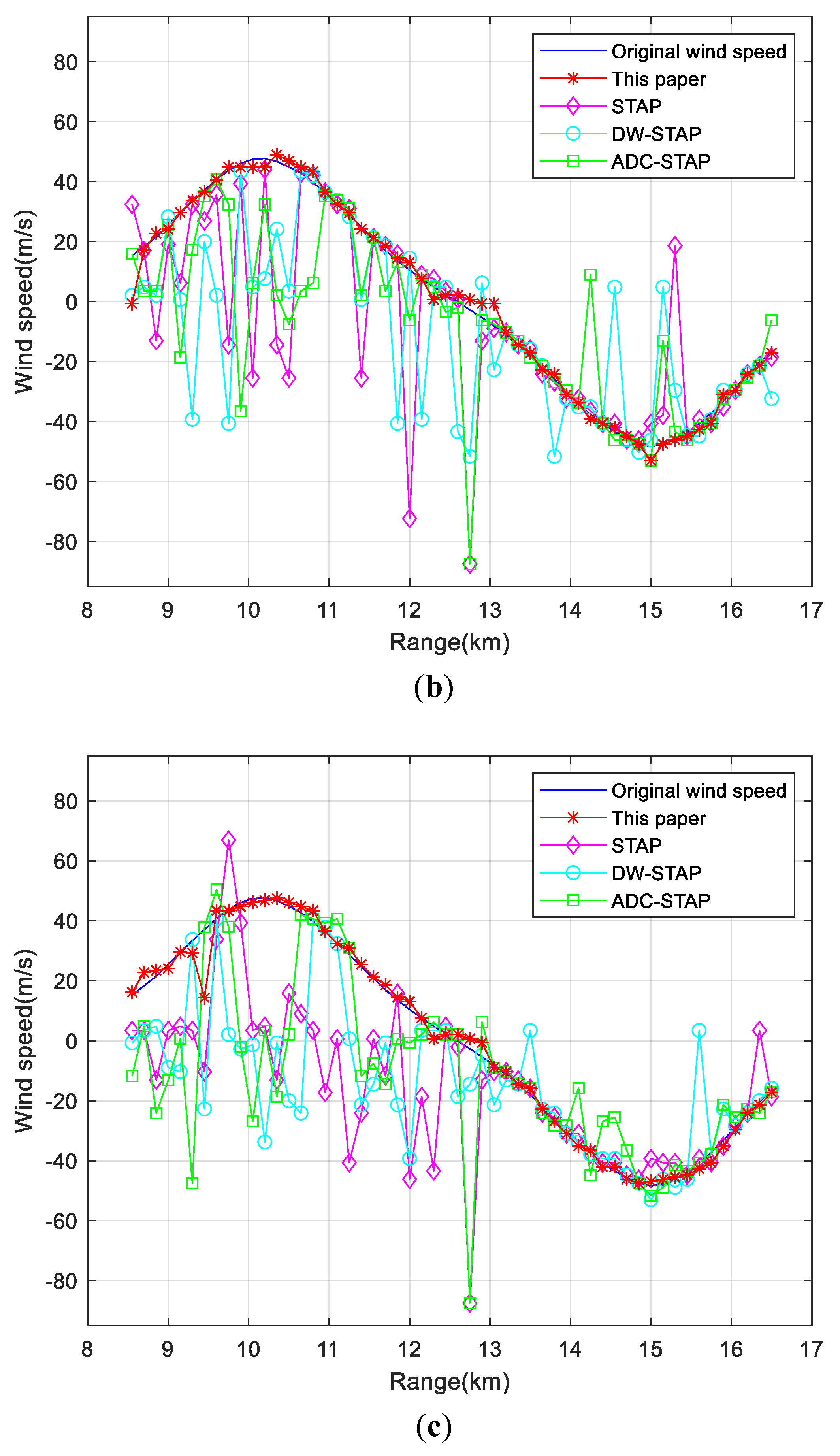
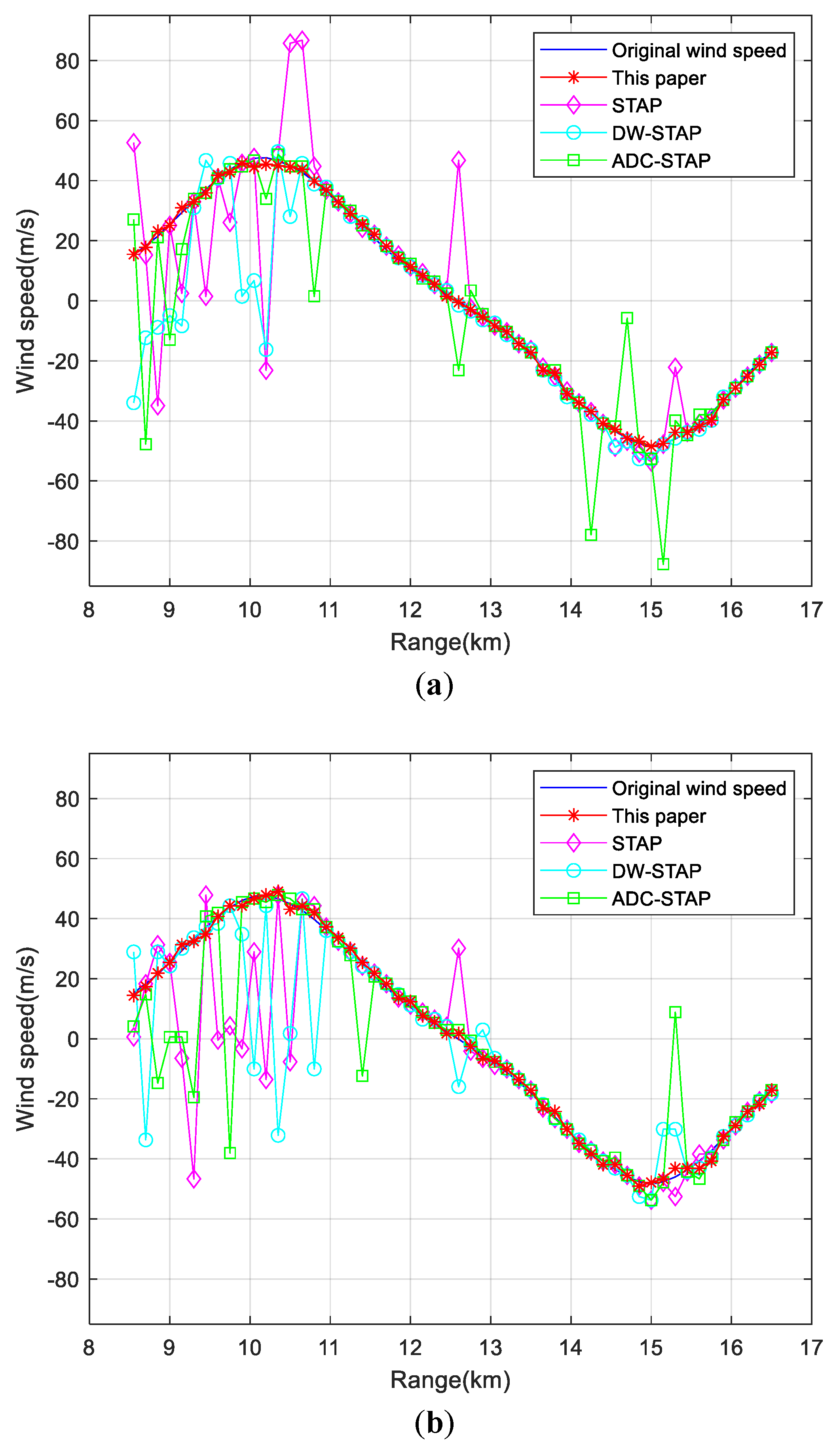
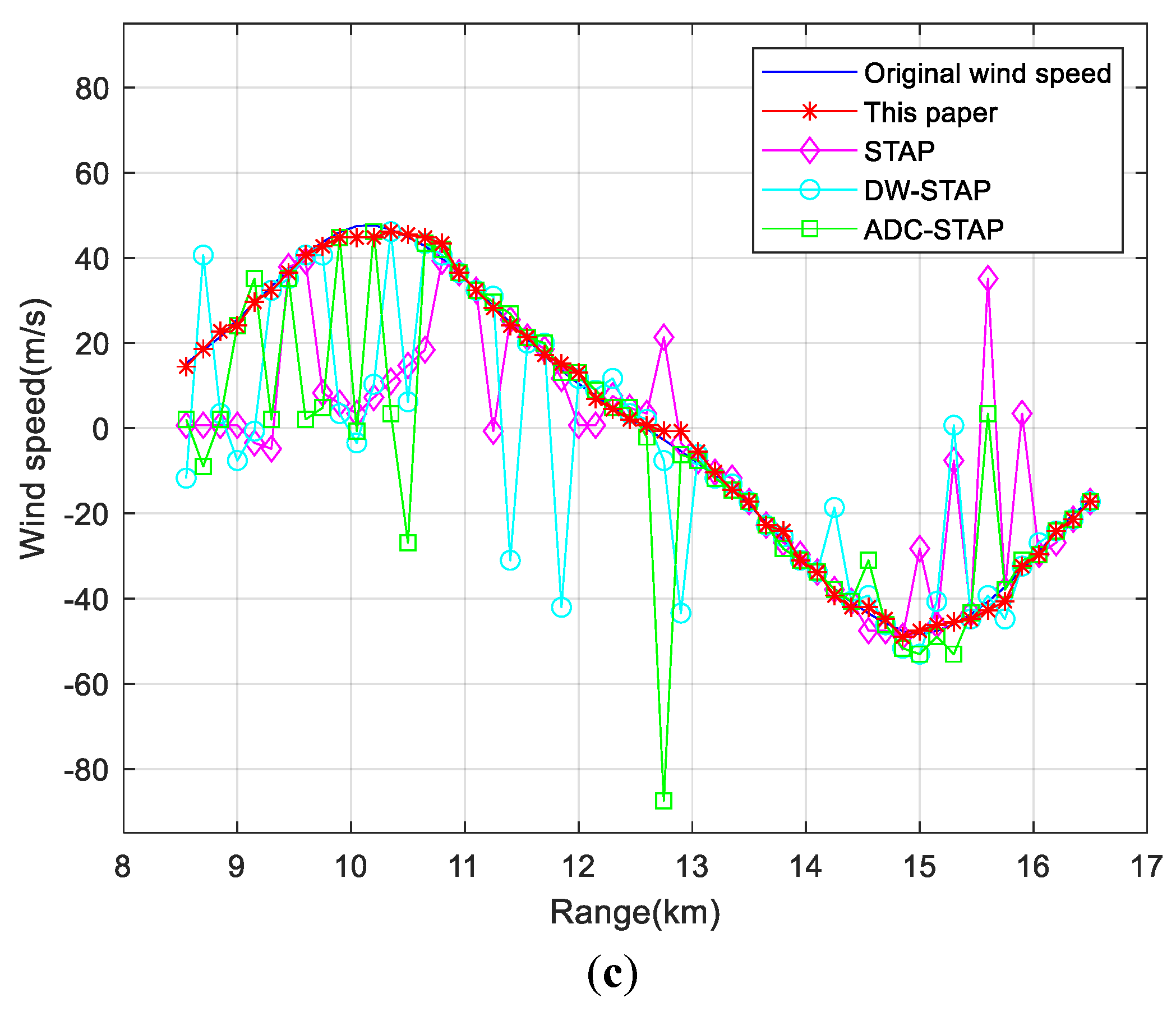
4. Simulation Results and Analysis
4.1. Simulation Condition Settings
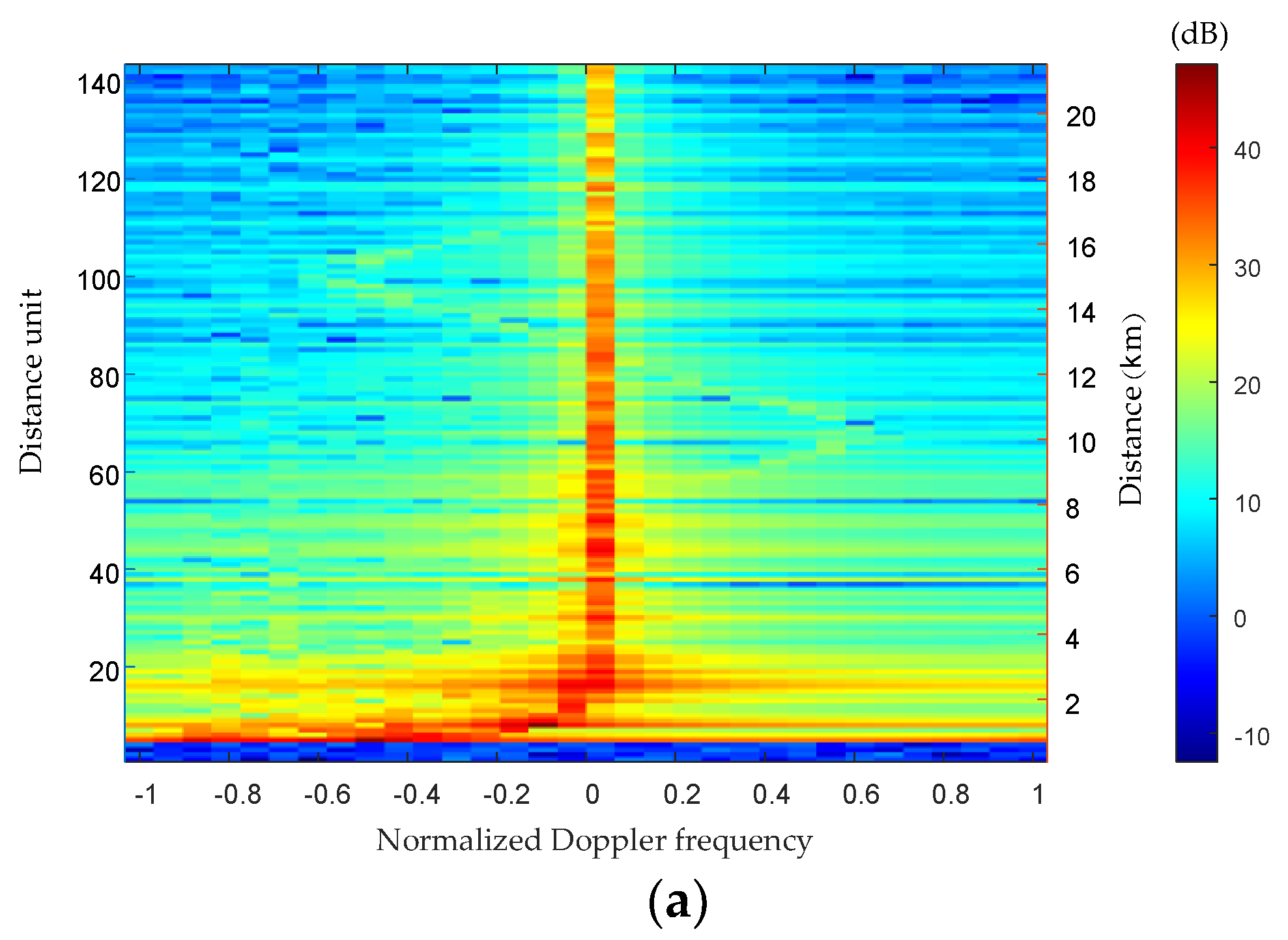
4.2. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, L. Study on the Formation Mechanism of Aviation Calamity and the Early Warning System. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2004. [Google Scholar] [CrossRef]
- Biao, Z. Detection of Low-altitude Windshear with Airborne Weather Radar Based on STAP. Ph.D. Thesis, Civil Aviation University of China, Tianjin, China, 2015. [Google Scholar]
- Zhenxing, G. Research on Real-Time Flight Simulation of Large Aircraft in Complex Atmospheric Disturbances. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2009. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Li, Y.; Cheng, Y.F. Application of Bimodal Spectrum Model in Detection of Wind-shear. Comput. Meas. Control. 2011, 19, 1636–1638. [Google Scholar] [CrossRef]
- Wu, R.B.; Lu, X.G.; Li, H.; Han, Y.F. Overview on Airborne Forward-Looking Weather Radar with Windshear Detection Capability. J. Data Acquis. Process. 2014, 29, 496–507. [Google Scholar] [CrossRef]
- Wu, R.B.; Zhang, B.; Li, H.; Lu, X.G.; Han, Y.F. Wind Speed Estimation for Low-attitude Windshear Based on Space-time Adaptive Processing. J. Electron. Inf. Technol. 2015, 37, 631–636. [Google Scholar] [CrossRef]
- Qingquan, J. Review of civil airborne weather radar development. J. China Acad. Electron. Inf. Technol. 2004, 39–46. [Google Scholar] [CrossRef]
- Li, B.; Gu, Q.T.; Li, R.Y.; Cao, J.W.; Wang, X. Analyses on disastrous weather monitoring capability of CINRAD and future development. Meteorol. Mon. 2013, 39, 265–280. [Google Scholar] [CrossRef]
- Ping, W.C. Space-Time Two-Dimensional Signal Processing Method for Airborne Conformal Array. Ph.D. Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2018. [Google Scholar]
- Wang, G.; Zhang, B.Q.; Zhang, M.H.; Sang, W.M.; Yuan, C.S.; Li, D. Research progress and prospect for conceptual and aerodynamic technology of blended-wing-body civil aircraft. Acta Aeronaut. Astronaut. Sin. 2019, 40, 7–35. [Google Scholar] [CrossRef]
- Liao, H.J.; Zhang, S.G. Design of cabin layout for blended wing body passenger transports. J. Beijing Univ. Aeronaut. Astronaut. 2009, 35, 986–989. [Google Scholar] [CrossRef]
- Jiang, J.; Zhong, B.W.; Fu, S. Influence of overall configuration parameters on aerodynamic characteristics of a blended-wing-body civil aircraft. Acta Aeronaut. Astronaut. Sin. 2016, 37, 278–289. [Google Scholar] [CrossRef]
- Tong, W. Study of Simplified STAP and Its Application to Airborne Radar. Ph.D. Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2001. [Google Scholar] [CrossRef]
- Pearson, F.; Borsari, G. Simulation and Analysis of Adaptive Interference Suppression for Bistatic Surveillance Radars. 2001, pp. 1–22. Available online: https://apps.dtic.mil/sti/pdfs/ADA422434.pdf (accessed on 7 November 2022).
- Borsari, G.K. Mitugating effects on STAP processing caused by an inclined array. In Proceedings of the IEEE National Radar Conference, Dallas, TX, USA, 14 May 1998; pp. 135–140. [Google Scholar]
- Himed, B.; Zhang, Y.H.; Hajjari, A. STAP with angle-Doppler compensation for bistatic airborne radars. In Proceedings of the IEEE Radar Conference, Long Beach, CA, USA, 25 April 2002. [Google Scholar] [CrossRef]
- Ying, L.Y. Research on Signal Processing Technology of Airborne Conformal Array Antenna. Ph.D. Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2019. [Google Scholar] [CrossRef]
- Li, H.; Zhou, M.; Wu, R.; Han, Y. Wind Speed Estimation of Low-Altitude Windshear Based on Multi-channel LFMCW Radar. J. Signal Process. 2019, 35, 1800–1809. [Google Scholar] [CrossRef]
- Yijing, L. Detection of Low-altitude windshear with Airborne Weather Radar under Complex Trajectories. Ph.D. Thesis, Civil Aviation University of China, Tianjin, China, 2019. [Google Scholar] [CrossRef]
- Zhiqiang, Z. Detection of Low-altitude windshear Based on Rank-Reduced STAP. Ph.D. Thesis, Civil Aviation University of China, Tianjin, China, 2017. [Google Scholar]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar Data Systems; Lincoln Laboratory of MIT: Lexington, MA, USA, 1994; pp. 25–45. [Google Scholar] [CrossRef]
- Zhihui, X. Multi-Channel Sea Clutter Modeling and Obtaining of Maritime Target Information. Ph.D. Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2017. [Google Scholar]
- Yanfei, H. Detection of Low-Altitude Windshear in Strong Clutter. Ph.D. Thesis, Civil Aviation University of China, Tianjin, China, 2013. [Google Scholar]
- Jiao, C.S.; Shen, C.L.; Zhang, Y. Principles of Meteorological Radar; Meteorological Press: Beijing, China, 2005; pp. 302–329. [Google Scholar]
- Cheong, B.L.; Palmer, R.D.; Xue, M. A Time Series Weather Radar Simulator Based on High-Resolution Atmospheric Models. J. Atmos. Ocean. Technol. 2008, 25, 230–243. [Google Scholar] [CrossRef] [Green Version]
- Duan, K.Q.; Xie, W.C.; Wang, Y.L. Nonstationary clutter suppression for airborne conformal array radar. Sci. Sin. 2011, 41, 1507–1516. [Google Scholar] [CrossRef]
- Hersey, R.K.; Melvin, W.L.; Mcclellan, J.H.; Culpepper, E. Adaptive ground clutter suppression for conformal array radar systems. IET Radar Sonar Navig. 2009, 3, 357–372. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, Y.H.; Liao, G.S.; Wang, Y.L.; Wu, R.B. Space-Time Signal Processing for Airborne Radars. Mod. Radar 1994, 16, 38–48. [Google Scholar] [CrossRef]

| Parameters | Parameter Value | Parameters | Parameter Value |
|---|---|---|---|
| Height of aircraft (m) | 600 | Number of rows | 4 |
| Speed of aircraft (m/s) | 87.5 | Number of columns | 12 |
| Radius of the bottom surface of the frustum (m) | 0.6 | Sampling pulse number | 32 |
| Height of Frustum (m) | 0.3 | Pulse repetition frequency (Hz) | 7000 |
| Inclination of frustum (°) | 45 | Signal to Noise Ratio (dB) | 5 |
| Center of circle angle (°) | 22.5 | Clutter to Noise Ratio (dB) | 40 |
| CNR | Wind Speed Estimation Method | RMS Error (m/s) |
|---|---|---|
| 40 dB | STAP | 21.0683 |
| DW-STAP | 19.8742 | |
| ADC-STAP | 21.1224 | |
| This paper | 1.5196 | |
| 50 dB | STAP | 27.4548 |
| DW-STAP | 26.5530 | |
| ADC-STAP | 24.0274 | |
| This paper | 2.9997 | |
| 60 dB | STAP | 28.4267 |
| DW-STAP | 28.0813 | |
| ADC-STAP | 27.11929 | |
| This paper | 3.6221 |
| PRF | Wind Speed Estimation Method | RMS Error (m/s) |
|---|---|---|
| 5000 Hz | STAP | 18.4618 |
| DW-STAP | 16.5961 | |
| ADC-STAP | 15.6833 | |
| This paper | 1.0402 | |
| 6000 Hz | STAP | 20.0491 |
| DW-STAP | 18.2206 | |
| ADC-STAP | 17.7085 | |
| This paper | 1.3193 | |
| 7000 Hz | STAP | 21.0683 |
| DW-STAP | 19.8742 | |
| ADC-STAP | 21.1224 | |
| This paper | 1.5196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zheng, L.; Meng, F. Low-Altitude Windshear Estimation Method Based on Four-Dimensional Frequency Domain Compensation for Fuselage Frustum Conformal Array. Sensors 2023, 23, 371. https://doi.org/10.3390/s23010371
Li H, Zheng L, Meng F. Low-Altitude Windshear Estimation Method Based on Four-Dimensional Frequency Domain Compensation for Fuselage Frustum Conformal Array. Sensors. 2023; 23(1):371. https://doi.org/10.3390/s23010371
Chicago/Turabian StyleLi, Hai, Lei Zheng, and Fanwang Meng. 2023. "Low-Altitude Windshear Estimation Method Based on Four-Dimensional Frequency Domain Compensation for Fuselage Frustum Conformal Array" Sensors 23, no. 1: 371. https://doi.org/10.3390/s23010371
APA StyleLi, H., Zheng, L., & Meng, F. (2023). Low-Altitude Windshear Estimation Method Based on Four-Dimensional Frequency Domain Compensation for Fuselage Frustum Conformal Array. Sensors, 23(1), 371. https://doi.org/10.3390/s23010371





