QCL Active Area Modeling with a View to Being Applied to Chemical Substance Detection Systems
Abstract
:1. Introduction
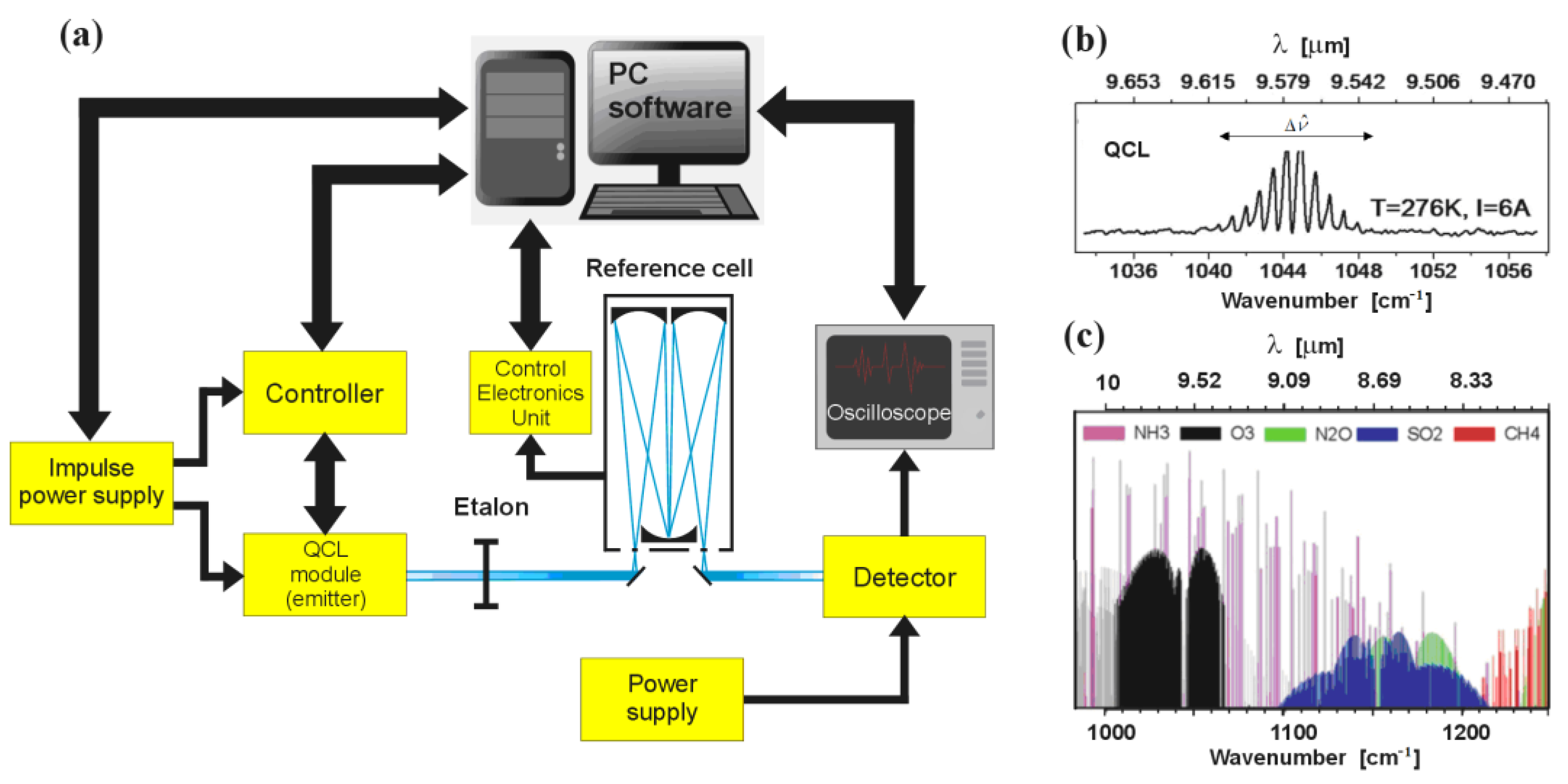
2. Numerical Models of QCL
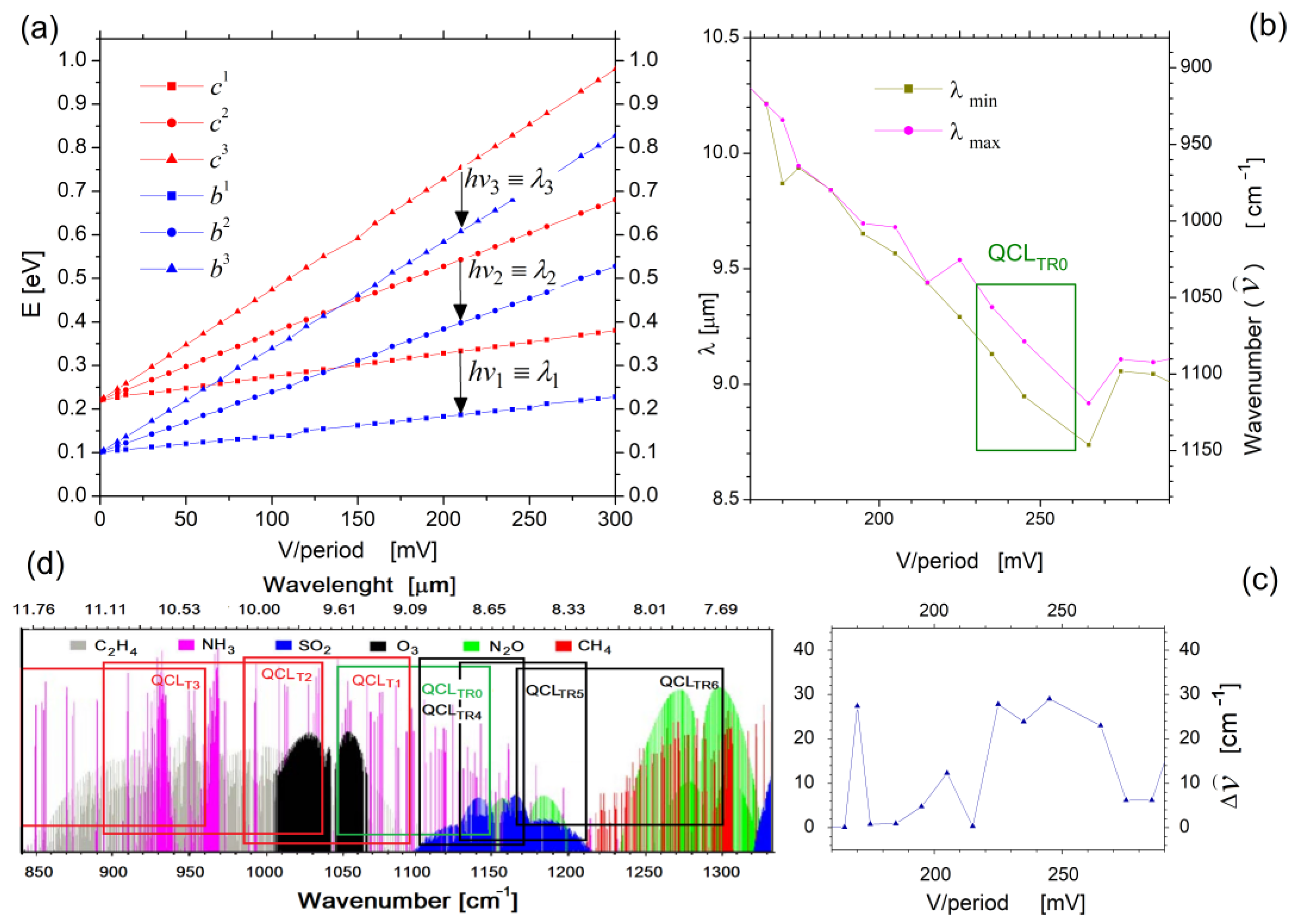
3. QCL Tuning
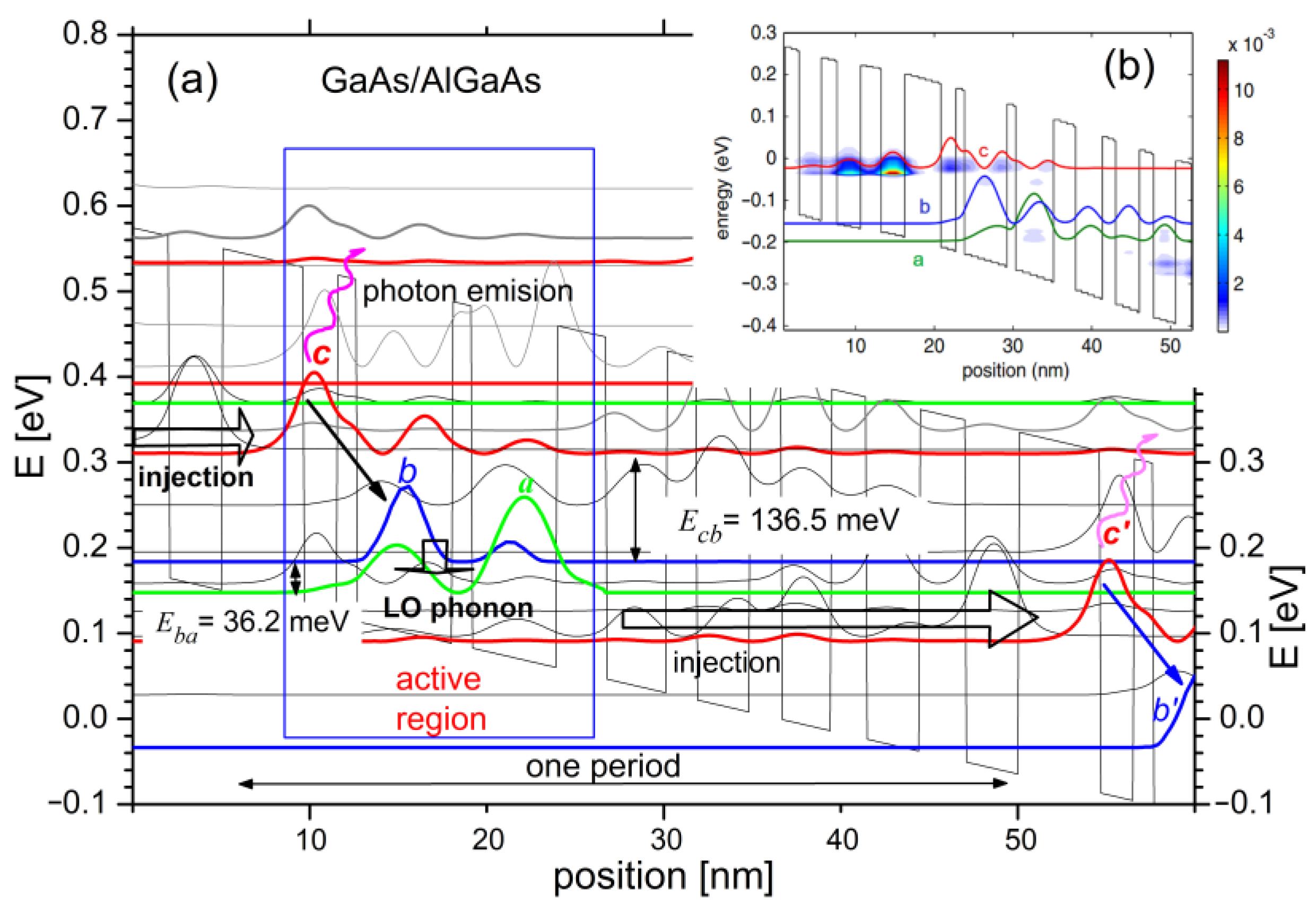
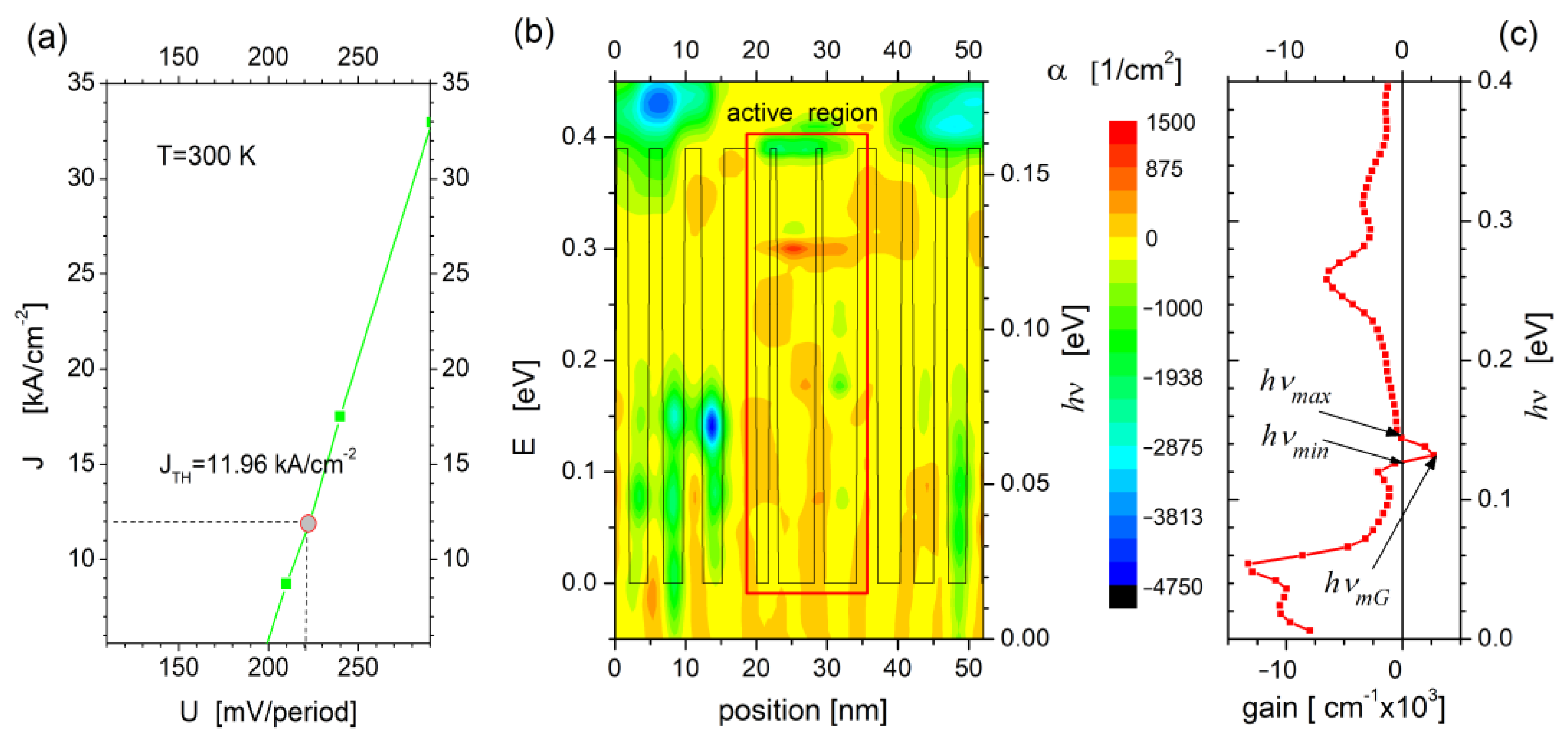
4. Modeling of QCL Active Region
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duxbury, G.; Normand, E.L.; Langford, N.; McCulloch, M.T.; Walker, S. Highly Sensitive detection of Trace Gases Using Pulsed Quantum Cascade Lasers. In Diode Lasers and Applications in Atmospheric Sensing; SPIE: Bellingham, WA, USA, 2002. [Google Scholar]
- Akhgar, C.K.; Ramer, G.; Żbik, M.; Trajnerowicz, A.; Pawluczyk, J.; Schwaighofer, A.; Lendl, B. The next generation of IR spectroscopy: EC-QCL-based mid-IR transmission spectroscopy of proteins with balanced detection. Anal. Chem. 2020, 92, 9901–9907. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ding, J.; Liu, N.; Yang, G.; Li, J. Detection of multiple chemicals based on external cavity quantum cascade laser spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 191, 532–538. [Google Scholar] [CrossRef] [PubMed]
- Lima, J.; Vargas, H.; Miklós, A.; Angelmahr, M.; Hess, P. Photoacoustic detection of NO2 and N2O using quantum cascade lasers. Appl. Phys. B. 2006, 85, 279–284. [Google Scholar] [CrossRef]
- Brown, A. Guied missile systems. Janes Int. Deffense Rev. 2001, 11, 40. [Google Scholar]
- Davis, C. Laser warners. Janes Electro-Opt. Syst. 2007, 101, 521–525. [Google Scholar]
- Spitz, O.; Herdt, A.; Wu, J.; Maisons, G.; Carras, M.; Wong, C.-W.; Elsäßer, W.; Grillot, F. Private communication with quantum cascade laser photonic chaos. Nat. Commun. 2021, 12, 3327. [Google Scholar] [CrossRef]
- Deng, Y.; Fan, Z.F.; Zhao, B.B.; Wang, X.-G.; Zhao, S.; Wu, J.; Grillot, F.; Wang, C. Mid-infrared hyperchaos of interband cascade lasers. Light Sci. Appl. 2022, 11, 7. [Google Scholar] [CrossRef]
- Kim, I.I.; Korevaar, E.J. Availability of free-space optics (FSO) and hybrid FSO/RF systems. In Proceedings of the ITCom 2001: International Symposium on the Convergence of IT and Communications, Denver, CO, USA, 27 November 2001. [Google Scholar] [CrossRef] [Green Version]
- Kosiel, K.; Szerling, A.; Karbownik, P.; Kubacka-Traczyk, J.; Sankowska, I.; Pierscinska, D.; Pierscinski, K.; Bugajski, M.; Miczuga, M.; Kopczynski, K.; et al. AlGaAs/GaAs quantum cascade lasers for gas detection systems. In Proceedings of the 2011 International Conference on Infrared, Millimeter, and Terahertz Waves, Houston, TX, USA, 2–7 October 2011; pp. 1–2. [Google Scholar] [CrossRef]
- Wysocki, G.; Lewicki, R.; Curl, R.; Tittel, F.; Diehl, L.; Capasso, F.; Troccoli, M.; Höfler, G.; Bour, D.; Corzine, S.; et al. Widely tunable mode-hop free external cavity quantum cascade lasers for high resolution spectroscopy and chemical sensing. Appl. Phys. B 2008, 92, 305–311. [Google Scholar] [CrossRef]
- Kwaśny, M.; Miczuga, M.Ł. Gas detection systems utilizing cascade lasers. Elektron.-Konstr. Technol. Zastos. 2009, 50, 86–90. [Google Scholar]
- Park, S.; Son, J.; Yu, J.; Lee, J. Standoff Detection and Identification of Liquid Chemicals on a Reflective Substrate Using a Wavelength-Tunable Quantum Cascade Laser. Sensors 2022, 22, 3172. [Google Scholar] [CrossRef]
- Lewicki, R.; Jahjah, M.; Ma, Y.; Stefanski, P.; Tarka, J.; Razeghi, M.; Tittel, F. Current Status of Mid-infrared Semiconductor-Laser-based Sensor Technologies for Trace-Gas Sensing Applications. In The Wonder of Nanotechnology: Quantum Optoelectronic Devices and Applications; Esaki, L., von Klitzing, K., Razeghi, M., Eds.; SPIE Digital Library: Bellingham, WA, USA, 2013. [Google Scholar] [CrossRef]
- McManus, J.B.; Nelson, D.D.; Shorter, J.H.; Jimenez, R.; Herndon, S.; Saleska, S.; Zahniser, M. A high precision pulsed quantum cascade laser spectrometer for measurement of stable isotopes of carbon dioxide. J. Mod. Opt. 2005, 52, 2309–2321. [Google Scholar] [CrossRef]
- McCulloch, M.T.; Erwan, L.; Langford, N.N.; Duxbury, G.; Newnham, D.A. Highly sensitive detection of trace gases using the time-resolved frequency downchirp from pulsed quantum-cascade lasers. J. Opt. Soc. Am. 2003, 20, 1761–1768. [Google Scholar] [CrossRef]
- Maulinia, R.; Mohan, A.; Giovannini, M.; Faist, J. External cavity quantum-cascade laser tunable from 8.2 to 10.4 µm using a gain element with a heterogeneous cascade. Appl. Phys. Lett. 2006, 88, 201113. [Google Scholar] [CrossRef]
- Wysocki, G.; Curl, R.; Tittel, F.; Maulini, R.; Bulliard, J.; Faist, J. Widely tunable mode-hop free external cavity quantum cascade laser for high resolution spectroscopic applications. Appl. Phys. B 2005, 81, 769–777. [Google Scholar] [CrossRef]
- Mohan, A.; Wittmann, A.; Hugi, A.; Blaser, S.; Giovannini, M.; Faist, J. Room-temperature continuous-wave operation of an external-cavity quantum cascade laser. Opt. Lett. 2007, 32, 2792–2794. [Google Scholar] [CrossRef]
- Pawłowski, S.; Mączka, M. Optimisation of QCL Structures Modelling by Polynomial Approximation. Materials 2022, 15, 5715. [Google Scholar] [CrossRef]
- Mączka, M.; Pawłowski, S. A Polynomial Approximation to Self Consistent Solution for Schrödinger–Poisson Equations in Superlattice Structures. Energies 2022, 15, 760. [Google Scholar] [CrossRef]
- Mączka, M.; Pawłowski, S. Efficient method for transport simulations in quantum cascade lasers. In Proceedings of the International Conference on Semiconductor Nanostructures for Optoelectronics and Biosensors (IC SeNOB), EPJ Web of Conferences, Rzeszow, Poland, 22–25 May 2016; p. 133. [Google Scholar]
- Mączka, M.; Hałdaś, G. Calculations of transport parameters in semiconductor superlattices based on the Green’s functions method in different Hamiltonian representations. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 631–641. [Google Scholar]
- Hałdaś, G. Implementation of non-uniform mesh in non-equilibrium Green’s function simulations of quantum cascade lasers. J. Comput. Electron. 2019, 18, 1400–1406. [Google Scholar] [CrossRef] [Green Version]
- Faist, J.; Capasso, F.; Sirtori, C.; Sivco, D.L.; Baillargeon, J.N.; Hutchinson, A.L.; Chu, S.N.G.; Cho, A.Y. High power mid-infrared (λ∼5 μm) quantum cascade lasers operating above room temperature. Appl. Phys. Lett. 1996, 68, 3680. [Google Scholar] [CrossRef]
- Lake, R.; Klimeck, G.; Bowen, R.C.; Jovanovic, D. Single and multiband modeling of quantum electron transport through layered semiconductor devices. J. Appl. Phys. 1997, 81, 7845–7869. [Google Scholar] [CrossRef]
- Kubis, T.; Yeh, C.; Vogl, P.; Benz, A.; Fasching, G.; Deutsch, C. Theory of nonequilibrium quantum transport and energy dissipation in terahertz quantum cascade lasers. Phys. Rev. B 2009, 79, 195323. [Google Scholar] [CrossRef] [Green Version]
- Pereira, M.; Lee, S.-C.; Wacker, A. Effect of Coulomb corrections and mean field on gain and absorption in Quantum Casscade Lasers. Phys. Status Solidi. C Curr. Top. Solid State Phys. 2005, 2, 3027–3030. [Google Scholar] [CrossRef]
- Hałdaś, G.; Kolek, A.; Tralle, I. Modeling of Mid-Infrared Quantum Cascade Laser by Means of Nonequilibrium Green’s Functions. IEEE J. Quantum Electron. 2011, 47, 878–885. [Google Scholar] [CrossRef]
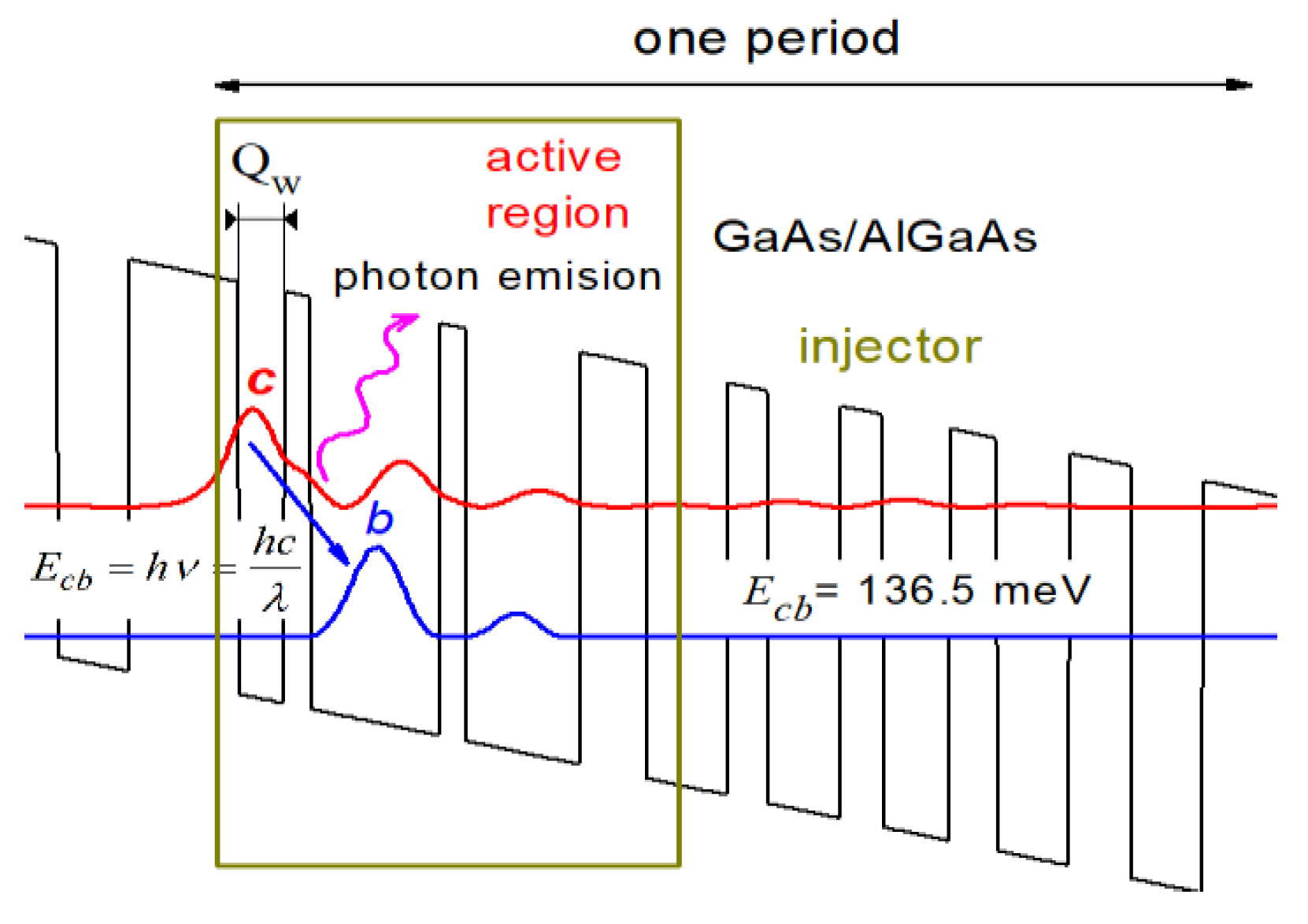
| GaAs/Al045Ga0,55As QCL | Well | Barrier | |
|---|---|---|---|
| m* | 0.067 | 0.10435 | |
| Eg [eV] | 0.84 | 1.84 | |
| εr | 12.85 | 13.8 | |
| Structure layers [nm] (barriers in bold) | 4.6, 1.9, 1.1, 5.4, 1.1, 4.8, 2.8, 3.4, 1.7, 3.0, 1.8, 2.8, 2.0, 3.0, 2.6, 3.0 | ||
| ∆EC [eV] | 0.39 | ||
| ndop [cm−3] | 2.29 × 1018 | ||
| LO-phonon energy | 0.036 | ||
| deformation potential [eV] | 5.89 | ||
| Screening length λDebye [nm] | 32 | ||
| Number of periods QCL | 30 | ||
| Temperature [K] | 300 |
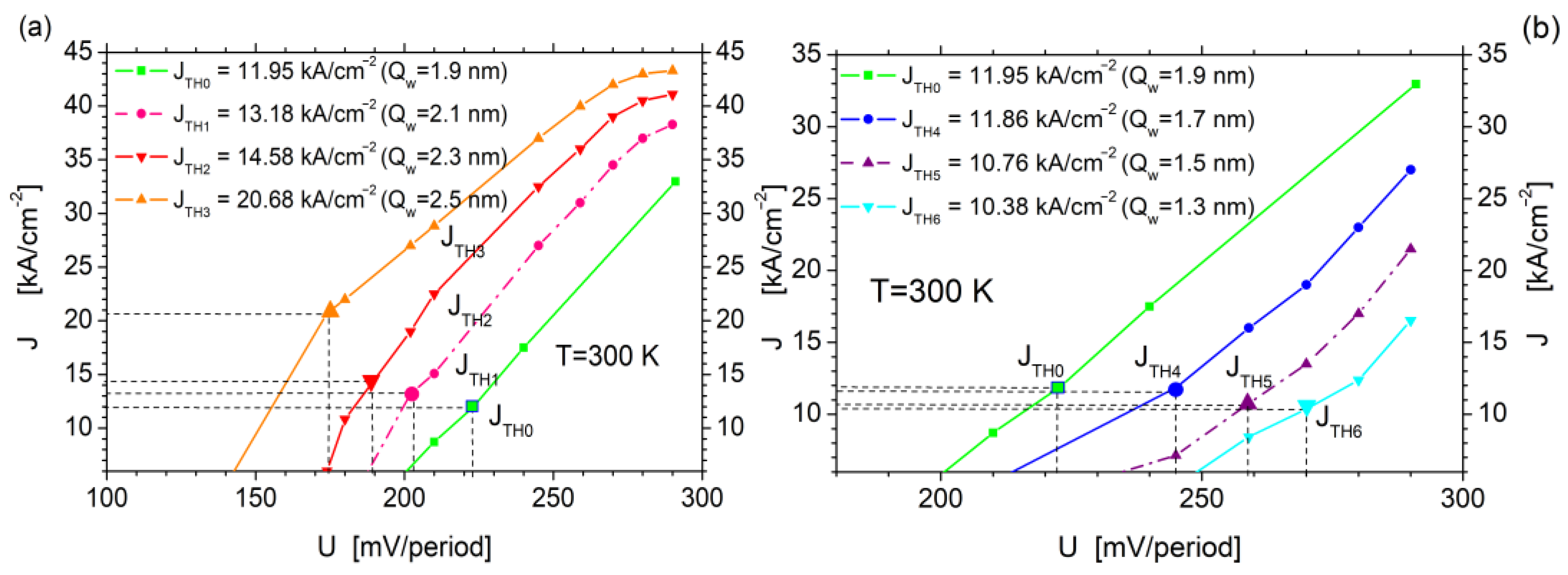
| Qw [nm] | 1.9 | |||||
|---|---|---|---|---|---|---|
| U [mV/Period] | 230 | 260 | QCLTR0 | |||
| Model | FMSL | RSM | FMSL | RSM | FMSL | RSM |
| hνmin [meV] | 129 | 126 | 138 | 129 | 9 | 3 |
| hνmax [meV] | 133 | 132 | 142 | 141 | 9 | 9 |
| hνmG [meV] | 130 | 135 | 5 | |||
| λmin [μm] | 9.31 | 9.38 | 8.72 | 8.78 | 0.59 | 0.6 |
| λmax [μm] | 9.52 | 9.83 | 8.97 | 9.59 | 0.55 | 0.24 |
| λmG [μm] | 9.52 | 9.17 | 0.35 | |||
| [cm−1] | 1074 | 1066 | 1146 | 1139 | 72 | 73 |
| [cm−1] | 1041 | 1018 | 1116 | 1042 | 75 | 24 |
| [cm−1] | 1050 | 1090 | 40 | |||
| ΔQw [nm] | +0.2 (2.1) | +0.4 (2.3) | +0.6 (2.5) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| U [mV] | 210 | 250 | QCLT1 | 200 | 250 | QCLT2 | 180 | 250 | QCLT3 |
| hνmax [meV] | 130 | 135 | 5 | 119 | 128 | 9 | 108 | 119 | 11 |
| hνmin [meV] | 122 | 131 | 9 | 111 | 122 | 11 | 99 | 114 | 15 |
| hνmG [meV] | 120 | 126 | 6 | 114 | 120 | 6 | 102 | 114 | 12 |
| λmin [μm] | 9.52 | 9.14 | 0.38 | 10.40 | 9.67 | 0.73 | 11.46 | 10.42 | 1.04 |
| λmax [μm] | 10.1 | 9.46 | 0.64 | 11.14 | 10.15 | 0.99 | 12.50 | 10.89 | 1.61 |
| λmG [μm] | 10.31 | 9.82 | 0.49 | 10.86 | 10.32 | 0.54 | 12.13 | 10.86 | 1.27 |
| [cm−1] | 1050 | 1094 | 44 | 902 | 1038 | 136 | 872 | 960 | 88 |
| [cm−1] | 985 | 1057 | 72 | 897 | 1007 | 110 | 799 | 918 | 119 |
| [cm−1] | 969 | 1017 | 48 | 920 | 969 | 49 | 824 | 921 | 97 |
| ΔQw [nm] | −0.2 (1.7) | −0.4 (1.5) | −0.6 (1.3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| U [mV] | 250 | 290 | QCLT4 | 260 | 290 | QCLT5 | 270 | 290 | QCLT6 |
| hνmax [meV] | 142 | 145 | 3 | 145 | 150 | 5 | 154 | 161 | 7 |
| hνmin [meV] | 137 | 141 | 4 | 140 | 148 | 8 | 144 | 156 | 12 |
| hνmG [meV] | 138 | 138 | 0 | 144 | 144 | 0 | 144 | 150 | 6 |
| λmin [μm] | 8.71 | 8.54 | 0.17 | 8.54 | 8.25 | 0.29 | 8.04 | 7.69 | 0.35 |
| λmax [μm] | 9.04 | 8.78 | 0.26 | 8.84 | 8.37 | 0.47 | 8.60 | 7.94 | 0.66 |
| λmG [μm] | 8.97 | 8.97 | 0 | 8.60 | 8.60 | 0 | 8.60 | 8.25 | 0.35 |
| [cm−1] | 1147 | 1171 | 24 | 1171 | 1211 | 40 | 1243 | 1300 | 57 |
| [cm−1] | 1106 | 1139 | 33 | 1131 | 1195 | 64 | 1163 | 1260 | 97 |
| [cm−1] | 1115 | 1115 | 0 | 1163 | 1163 | 0 | 1163 | 1211 | 48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mączka, M.; Hałdaś, G.; Pawłowski, S. QCL Active Area Modeling with a View to Being Applied to Chemical Substance Detection Systems. Sensors 2023, 23, 389. https://doi.org/10.3390/s23010389
Mączka M, Hałdaś G, Pawłowski S. QCL Active Area Modeling with a View to Being Applied to Chemical Substance Detection Systems. Sensors. 2023; 23(1):389. https://doi.org/10.3390/s23010389
Chicago/Turabian StyleMączka, Mariusz, Grzegorz Hałdaś, and Stanisław Pawłowski. 2023. "QCL Active Area Modeling with a View to Being Applied to Chemical Substance Detection Systems" Sensors 23, no. 1: 389. https://doi.org/10.3390/s23010389
APA StyleMączka, M., Hałdaś, G., & Pawłowski, S. (2023). QCL Active Area Modeling with a View to Being Applied to Chemical Substance Detection Systems. Sensors, 23(1), 389. https://doi.org/10.3390/s23010389






