TCAD Analysis of Leakage Current and Breakdown Voltage in Small Pitch 3D Pixel Sensors
Abstract
:1. Introduction
2. Experiment & Simulation Setup
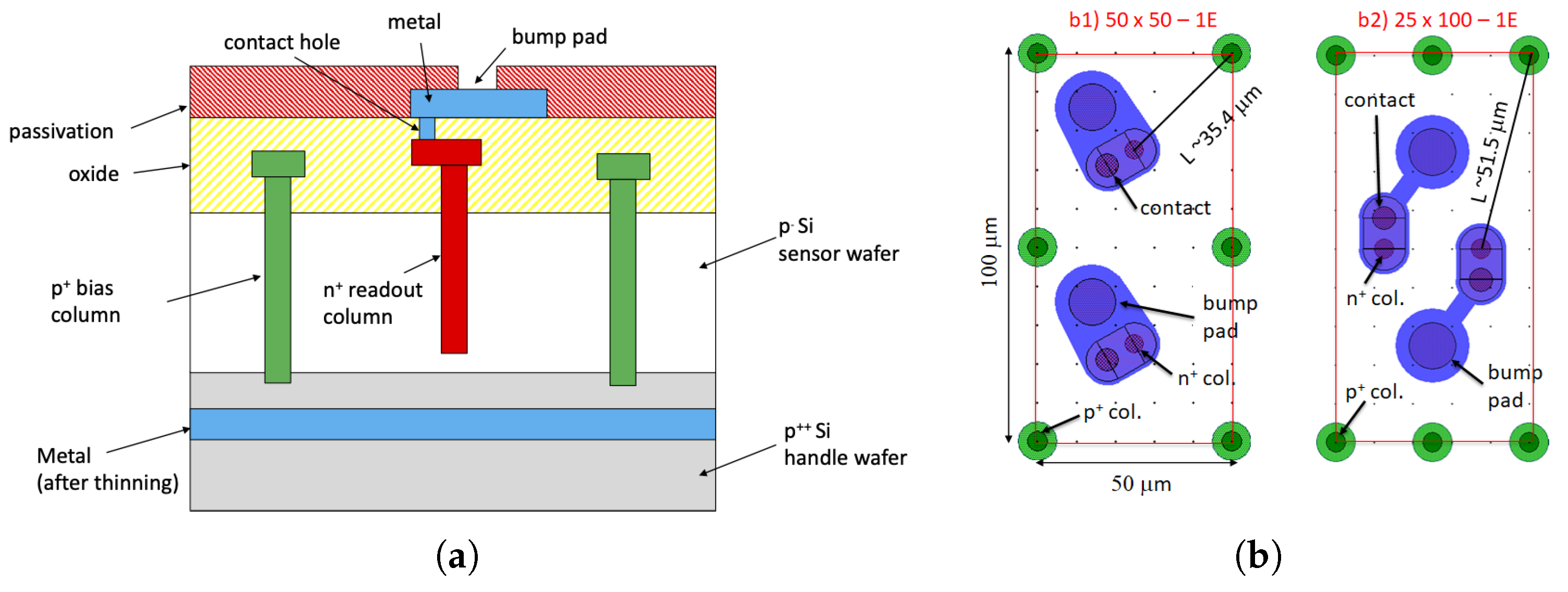
2.1. Device Description
2.2. Electrical Tests
2.3. TCAD Simulation Approach
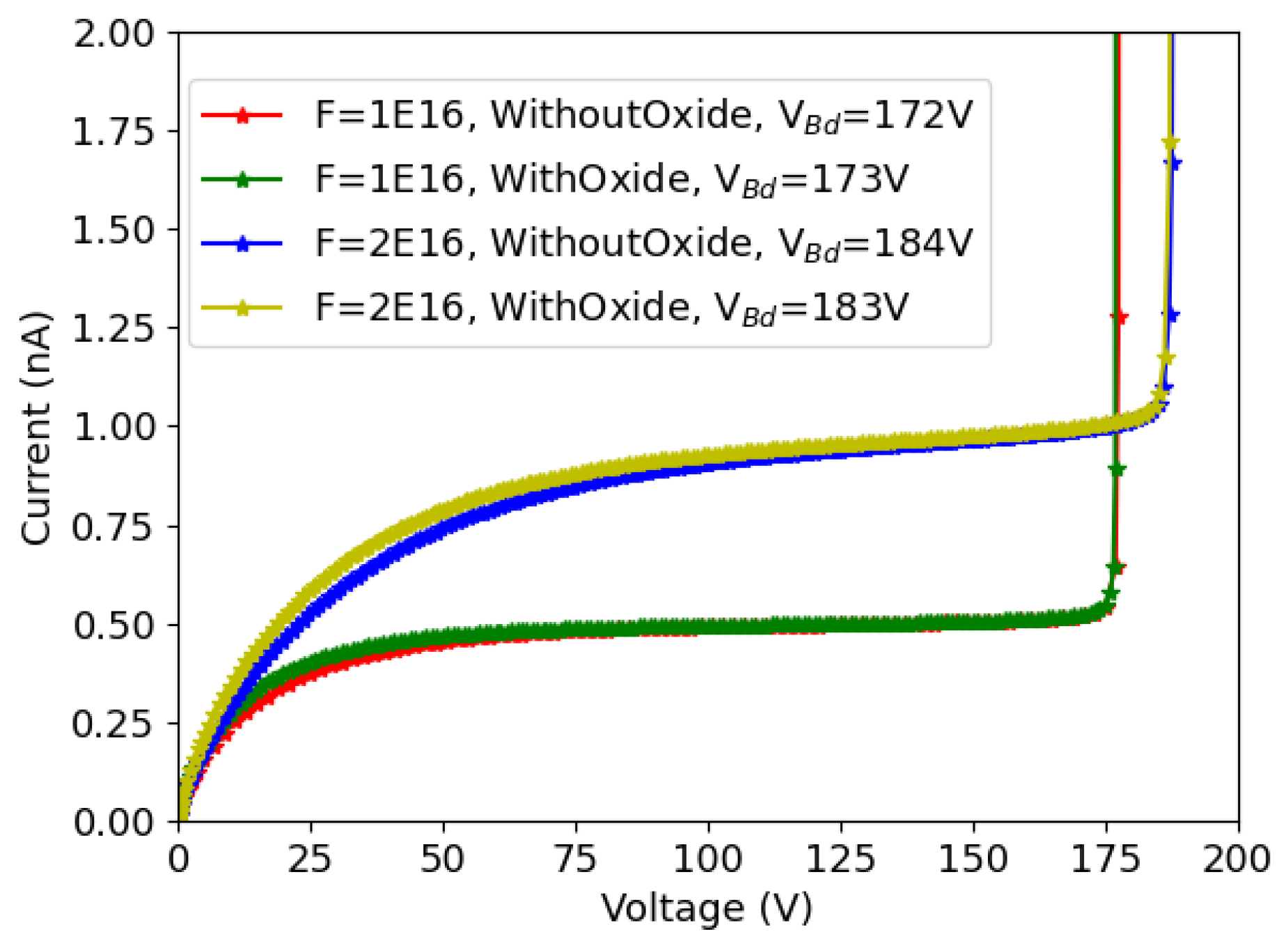
3. Comparison between Measurements and Simulations
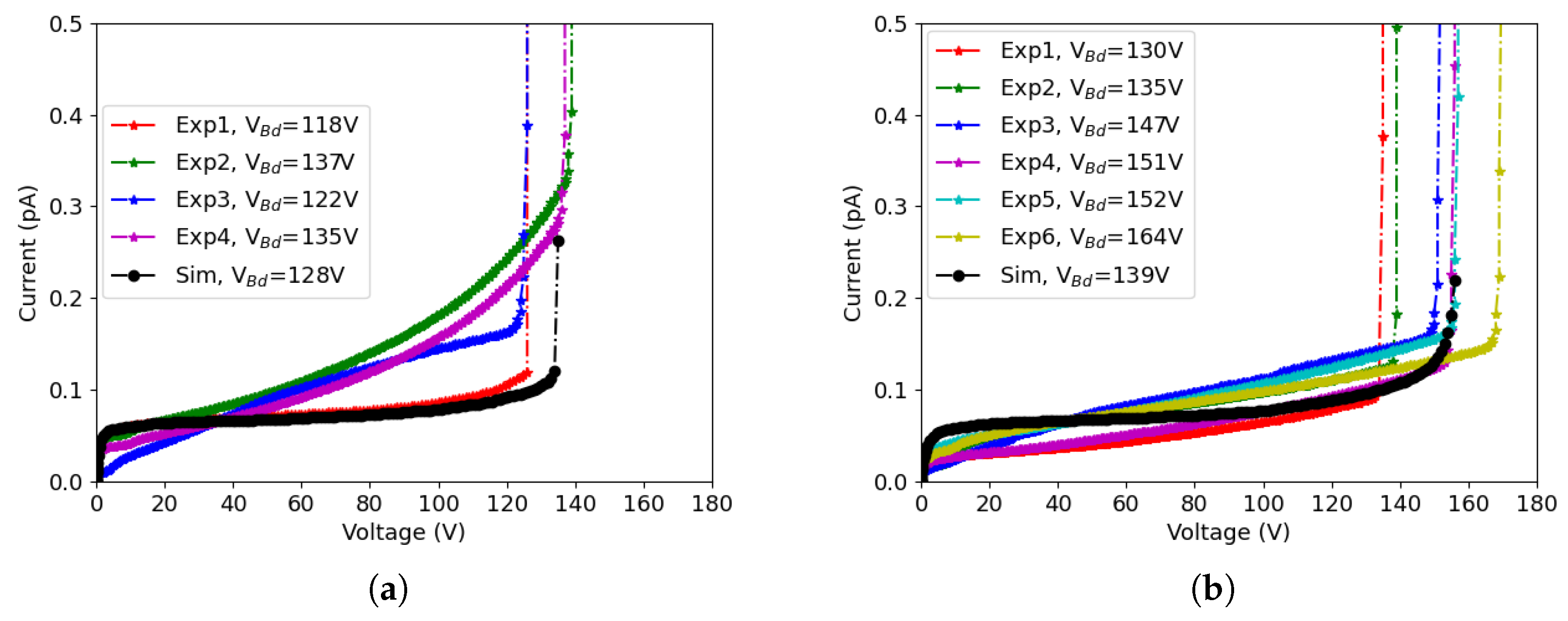
3.1. Pre-Irradiation
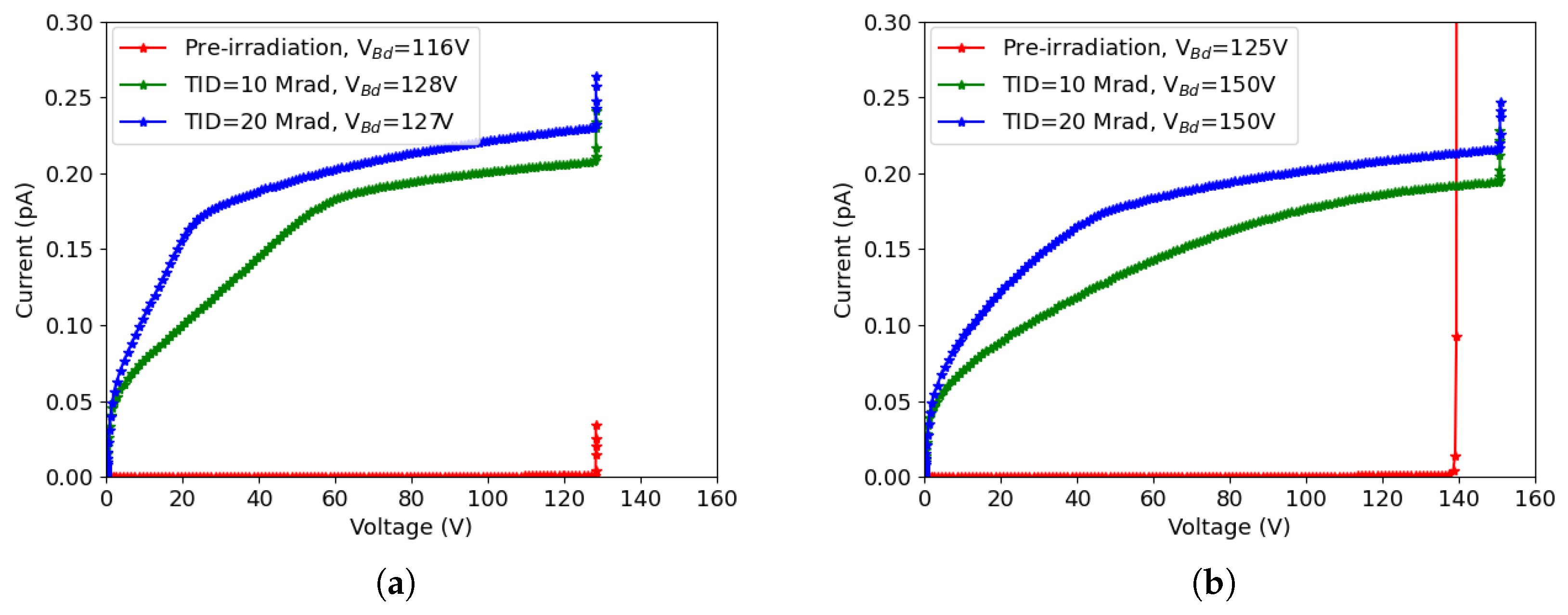
3.2. Surface Damage
3.3. Combined Effects
- -
- There is a relatively wide dispersion in the experimental curves, especially for devices irradiated at , possibly due to the uncertainties in the neutron fluence (within 10%) and in the measurement temperature (within 1 C, that corresponds to a 10% variation in the leakage current);
- -
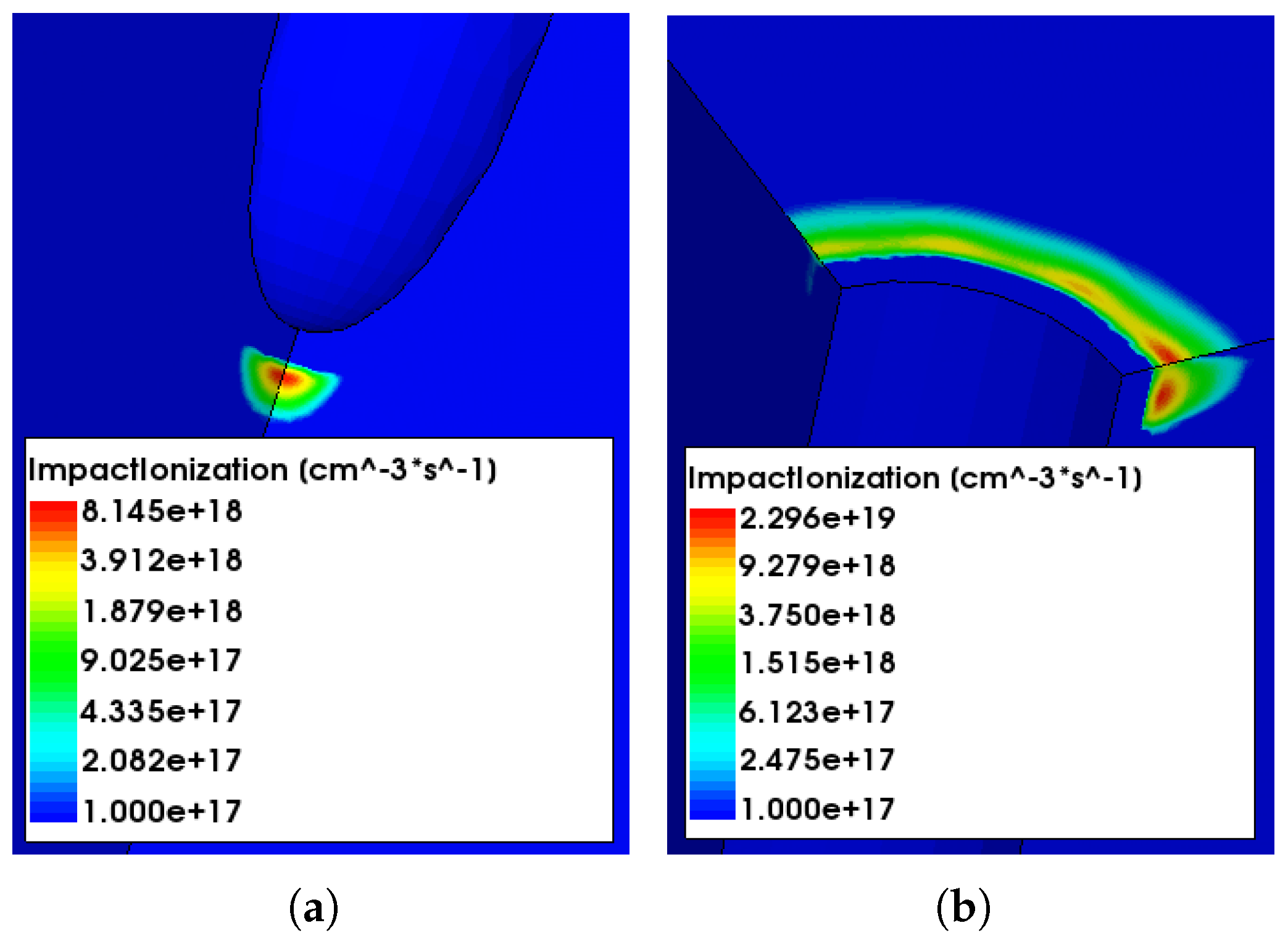
- Edge effects also play a role, as observed in [9], although to a lesser extent with respect to the pre-irradiation case, because the extension of the depletion region into the slim-edge region is much smaller after irradiation;
- -
- Both the Perugia and CERN model have been developed with reference to the characteristics of planar sensors, and so far no attempt has been made to tune their parameters for using them with 3D sensors; moreover, as far as the I-V curves are concerned, both models have been validated up to fluences smaller than those involved in our study, i.e., for the Perugia model and for the CERN model;
- -
- As far as the specific deficiencies in the two models, the Perugia model largely underestimates the depletion voltage, so the I-V curves rapidly saturate, leading to an overestimation of the leakage current, whereas the CERN model provides a better agreement with the shapes of the experimental I-V curves, but then does not properly describe the effects related to impact ionization, which are predicted to occur at a much larger voltage than that observed experimentally.
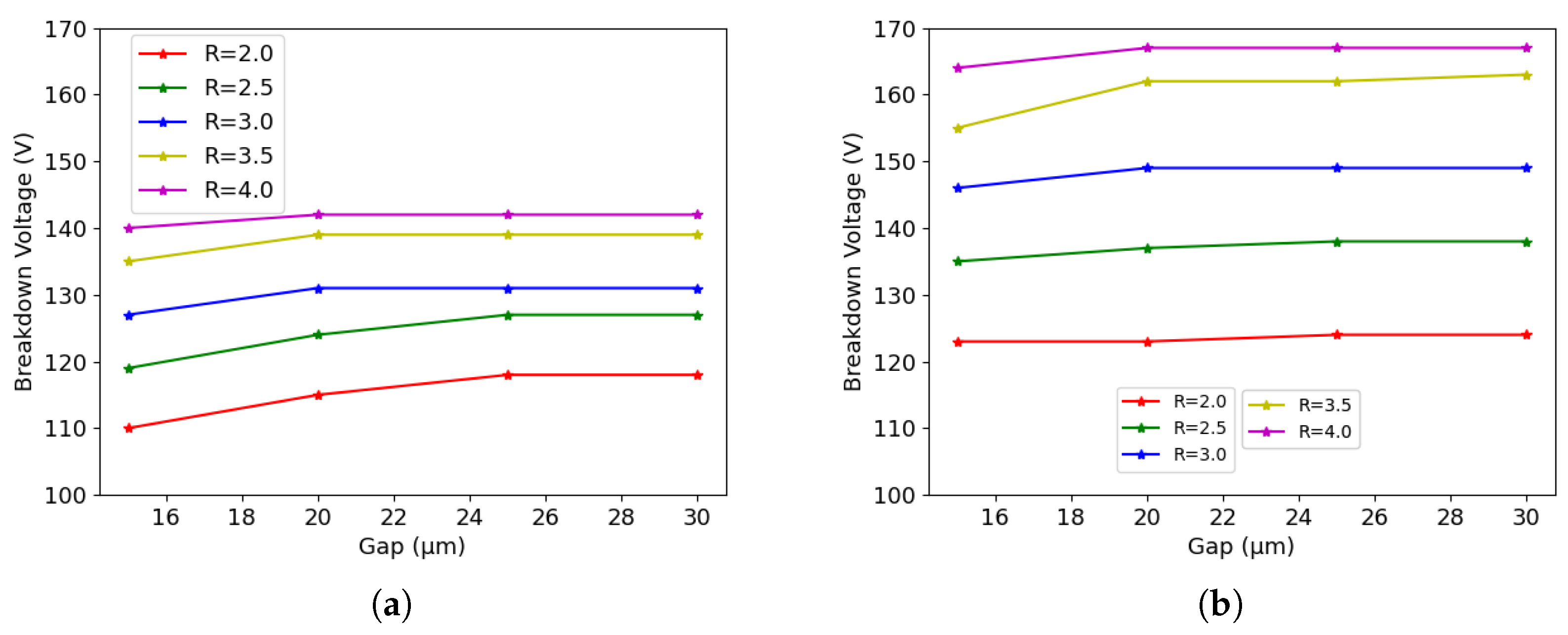
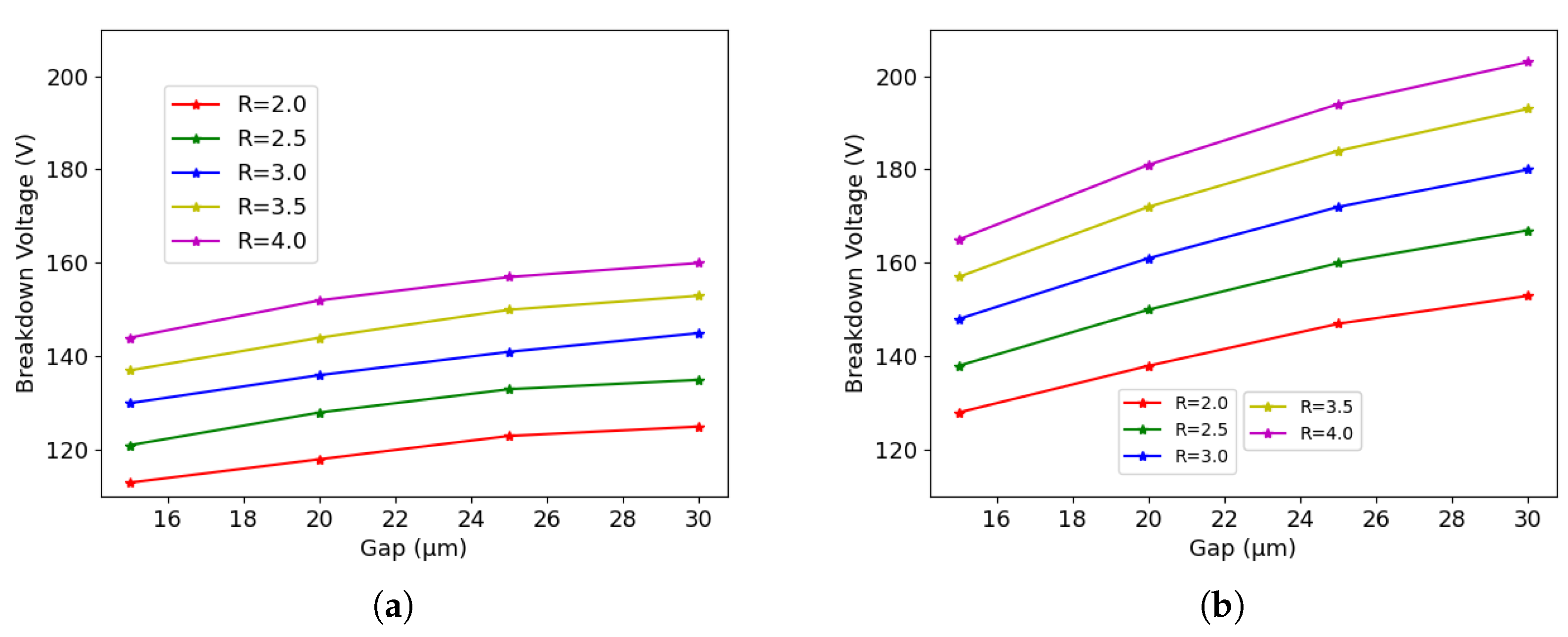
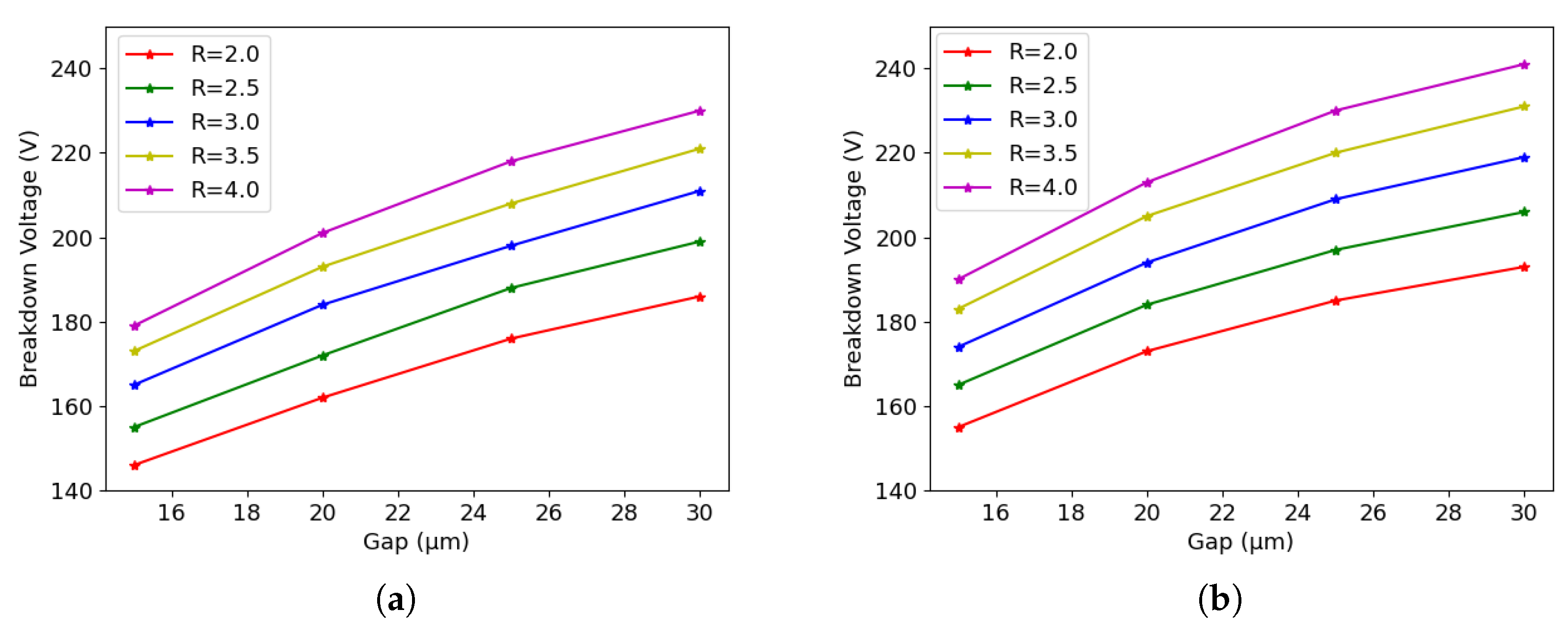
4. Influence of Geometrical Parameters
4.1. Pre-Irradiation
4.2. Surface Damage
4.3. Bulk Damage
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meng, L. ATLAS ITk Pixel Detector Overview. arXiv 2021, arXiv:2105.10367. [Google Scholar]
- Da Via, C.; Boscardin, M.; Dalla Betta, G.F.; Darbo, G.; Fleta, C.; Gemme, C.; Grenier, P.; Grinstein, S.; Hansen, T.E.; Hasi, J.; et al. 3D silicon sensors: Design, large area production and quality assurance for the ATLASIBL pixel detector upgrade. Nucl. Instrum. Methods A 2012, 694, 321–330. [Google Scholar] [CrossRef]
- Dalla Betta, G.-F.; Boscardin, M.; Mendicino, R.; Ronchin, S.; Sultan, D.; Zorzi, N. Development of new 3D pixel sensors for phase 2 upgrades at LHC. In Proceedings of the NSS/MIC Conference Record, San Diego, CA, USA, 31 October–7 November 2015; p. N3C3-5. [Google Scholar]
- Dalla Betta, G.-F.; Boscardin, M.; Darbo, G.; Mendicino, R.; Meschini, M.; Messineo, A.; Ronchin, S.; Sultan, D.M.S.; Zorzi, N. Development of a new generation of 3D pixel sensors for HL-LHC. Nucl. Instrum. Methods A 2016, 824, 386–387. [Google Scholar] [CrossRef]
- Sultan, D.; Dalla Betta, G.-F.; Mendicino, R.; Boscardin, M.; Ronchin, S.; Zorzi, N. First production of new thin 3D sensors for HL-LHC at FBK. Jinst 2017, 12, C01022. [Google Scholar] [CrossRef]
- Garcia-Sciveres, M. The RD53A Integrated Circuit; Technical Report CERN-RD53-PUB-17-001; CERN: Geneva, Switzerland, 2017. [Google Scholar]
- Oide, H.; Alimonti, G.; Boscardin, M.; Dalla Betta, G.-F.; Darbo, G.; Ficorella, F.; Fumagalli, E.; Gariano, G.; Gaudiello, A.; Gemme, C.; et al. INFN-FBK developments of 3D sensors for High-Luminosity LHC. Nucl. Instrum. Methods A 2019, 924, 73–77. [Google Scholar] [CrossRef]
- Alonso, A.G.; Currás, E.; Duarte-Campderrós, J.; Fernandez, M.; Gomez, G.; Gonzalez, J.; Silva, E.; Vila, I.; Jaramillo, R.; Meschini, M.; et al. Test beam characterization of irradiated 3D pixel sensors. Jinst 2020, 14, C03017. [Google Scholar] [CrossRef]
- Terzo, S.; Boscardin, M.; Carlotto, J.; Dalla Betta, G.-F.; Darbo, G.; Dorholt, O.; Ficorella, F.; Gariano, G.; Gemme, C.; Giannini, G.; et al. Novel 3D pixel sensors for the upgrade of the ATLAS Inner Tracker. Front. Phys. 2021, 9, 624668. [Google Scholar] [CrossRef]
- Ceccarelli, R. Performance of highly irradiated FBK planar and 3D pixel detectors. Nucl. Instrum. Methods A 2023, 1046, 167650. [Google Scholar] [CrossRef]
- Boscardin, M.; Ferrari, S.; Ficorella, F.; Lai, A.; Mendicino, R.; Meschini, M.; Ronchin, S.; Samy, A.A.; Dalla Betta, G.-F. Advances in 3D sensor technology by using stepper lithography. Front. Phys. 2021, 9, 625275. [Google Scholar] [CrossRef]
- Dalla Betta, G.F.; Boscardin, M.; Hoeferkamp, M.; Mendicino, R.; Seidel, S.; Sultan, D.M.S. Electrical characterization of FBK small-pitch 3D sensors after γ-ray, neutron and proton irradiations. Jinst 2017, 12, C11028. [Google Scholar] [CrossRef]
- Mandic, I.; Cindro, V.; Kramberger, G.; Kristof, E.; Mikuz, M.; Vrtacnik, D.; Ullan, M.; Anghinolfi, F. Bulk damage in DMILL npn bipolar transistors caused by thermal neutrons versus protons and fast neutrons. IEEE Trans. Nucl. Sci. 2004, 5, 1752–1758. [Google Scholar] [CrossRef]
- Povoli, M.; Bagolini, A.; Boscardin, M.; Dalla Betta, G.-F.; Giacomini, G.; Vianello, E.; Zorzi, N. Slim edges in double-sided silicon 3D detectors. Jinst 2012, 7, C01015. [Google Scholar] [CrossRef]
- Synopsys Inc. Sentaurus Device User Guide Version R-2020.09; Synopsys Inc.: San Jose, CA, USA, 2020. [Google Scholar]
- Morozzi, A.; Moscatelli, F.; Croci, T.; Passeri, D. TCAD modeling of surface radiation damage effects: A state-of-the-art review. Front. Phys. 2021, 9, 617322. [Google Scholar] [CrossRef]
- Moscatelli, F.; Passeri, D.; Morozzi, A.; Mendicino, R.; Dalla Betta, G.-F.; Bilei, G.M. Combined bulk and surface radiation damage effects at very high fluences in silicon detectors: Measurements and TCAD simulations. IEEE Trans. Nucl. Sci. 2016, 63, 2716–2723. [Google Scholar] [CrossRef]
- Folkestad, A.; Akiba, K.; van Beuzekom, M.; Buchanan, E.; Collins, P.; Dall’occo, E.; Di Canto, A.; Evans, T.; Lima, V.F.; Pardiñas, J.G.; et al. Development of a silicon bulk radiation damage model for Sentaurus TCAD. Nucl. Instrum. Methods A 2017, 874, 94–102. [Google Scholar] [CrossRef]
- Passeri, D.; Morozzi, A. TCAD Radiation Damage Model, AIDA-2020-D7.4 Deliverable Report. 2019. Available online: http://cds.cern.ch/search?p=AIDA-2020-D7.4 (accessed on 1 December 2022).
- Dalla Betta, G.-F.; Ayllon, N.; Boscardin, M.; Hoeferkamp, M.; Mattiazzo, S.; McDuff, H.; Mendicino, R.; Povoli, M.; Seidel, S.; Sultan, D.; et al. Investigation of leakage current and breakdown voltage in irradiated double-sided 3D silicon sensors. Jinst 2016, 11, P09006. [Google Scholar] [CrossRef]
- Moll, M. Displacement damage in silicon detectors for High Energy Physics. IEEE Trans. Nucl. Sci. 2018, 65, 1561–1582. [Google Scholar] [CrossRef]
- Chilingarov, A. Temperature dependence of the current generated in Si bulk. Jinst 2013, 8, P10003. [Google Scholar] [CrossRef]
- Boughedda, A.; Lakhdara, M.; Latreche, S.; Mendicino, R.; Dalla Betta, G.-F. Comparing different bulk radiation damage models in TCAD simulations of small-pitch 3D Si sensors. Jinst 2021, 16, C10006. [Google Scholar] [CrossRef]
- Wonsak, S.; Affolder, A.; Casse, G.; Dervan, P.; Tsurin, I.; Wormald, M. Measurements of the reverse current of highly irradiated silicon sensors. Nucl. Instrum. Methods A 2015, 796, 126–130. [Google Scholar] [CrossRef]
- Moll, M.; Fretwurst, E.; Kuhnke, M.; Lindström, G. Relation between microscopic defects and macroscopic changes in silicon detector properties after hadron irradiation. Nucl. Instrum. Methods B 2002, 186, 100–110. [Google Scholar] [CrossRef]





| Fluence | Structure | (V) Experiment | (V) Perugia Model | (V) CERN Model |
|---|---|---|---|---|
| 1.0 | 117 ± 14.5 | 145 | 277 | |
| 180 ± 8.5 | 169 | 399 | ||
| 1.5 | 120 ± 7.2 | 154 | 249 | |
| 186 ± 9.9 | 179 | 389 |
| Fluence | Structure | Experiment | Perugia Model | CERN Model |
|---|---|---|---|---|
| 1.0 | 6.92 ± 1.14 | 5.92 | 4.90 | |
| 4.25 ± 0.91 | 5.74 | 4.22 | ||
| 1.5 | 4.41 ± 0.36 | 5.91 | 5.14 | |
| 3.87 ± 0.43 | 5.54 | 4.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Boughedda, A.; Sultan, D.M.S.; Dalla Betta, G.-F. TCAD Analysis of Leakage Current and Breakdown Voltage in Small Pitch 3D Pixel Sensors. Sensors 2023, 23, 4732. https://doi.org/10.3390/s23104732
Ye J, Boughedda A, Sultan DMS, Dalla Betta G-F. TCAD Analysis of Leakage Current and Breakdown Voltage in Small Pitch 3D Pixel Sensors. Sensors. 2023; 23(10):4732. https://doi.org/10.3390/s23104732
Chicago/Turabian StyleYe, Jixing, Abderrezak Boughedda, D M S Sultan, and Gian-Franco Dalla Betta. 2023. "TCAD Analysis of Leakage Current and Breakdown Voltage in Small Pitch 3D Pixel Sensors" Sensors 23, no. 10: 4732. https://doi.org/10.3390/s23104732






