Abstract
This study proposed a novel adaptive interval Type-II fuzzy fault-tolerant control for constrained uncertain 2-DOF robotic multi-agent systems with an active fault-detection algorithm. This control method can realize the predefined-accuracy stability of multi-agent systems under input saturation constraint, complex actuator failure and high-order uncertainties. Firstly, a novel active fault-detection algorithm based on pulse-wave function was proposed to detect the failure time of multi-agent systems. To the best of our knowledge, this was the first time that an active fault-detection strategy had been used in multi-agent systems. Then, a switching strategy based on active fault detection was presented to design the active fault-tolerant control algorithm of the multi-agent system. In the end, based on the interval type-II fuzzy approximated system, a novel adaptive fuzzy fault-tolerant controller was proposed for multi-agent systems to deal with system uncertainties and redundant control inputs. Compared with other relevant fault-detection and fault-tolerant control methods, the proposed method can achieve predefinition of stable accuracy with smoother control input. The theoretical result was verified by simulation.
1. Introduction
In recent years, multi-agent systems have been widely used in robots, factories, laboratories and networks [1,2,3,4]. However, because of actuator failure and system uncertainty, intelligent fault-tolerant control of multiple agents has become a research hotspot [5,6].
The existing fault-tolerant control strategies are mainly divided into passive fault-tolerant control strategies and active ones [7,8,9]. Most passive fault-tolerant control methods are based on robust control strategy, but this control strategy is often conservative and requires prior fault information [7]. In order to solve the defect that the fault information in passive fault-tolerant control needs prior information, the active fault-tolerant control was proposed by adding a fault-detection and diagnosis module [10]. This strategy can realize the online reconstruction of the controller without prior fault information. An active fault-tolerant control method was proposed by integrating detection, diagnosis and controller reconstruction, but it may be unstable in the detection and diagnosis stages [11]. In order to solve this stability problem, an active fault-tolerant control method was proposed as a robust control idea to deal with the conflict between stabilization and restructuring [12]. After that, active fault-tolerant control has been widely used in various mechanical control systems. Active fault-tolerant control was applied to unmanned aerial vehicles (UAVs), which achieved the rapid stability of the control system under actuator failure [13]. In order to solve the stability problem of underwater robots under actuator fault conditions, an active fault-tolerant control was used to realize the stability of the closed-loop system [14,15]. In order to improve the fault-tolerant control performance of the manipulator, an active fault-tolerant control based on redundant motors was proposed to reduce the structural complexity [16]. In order to improve the performance of fault-tolerant controls under noisy conditions, fault detection was often used [17,18,19,20,21]. With the development of fault-detection technology, it was applied in many fields [22,23,24,25,26]. However, traditional active fault-tolerant controls mainly relied on a passive detection mechanism. In systems with complex uncertainties and faults, the passive detection mechanism may not be sensitive enough to detect faults. In order to improve the sensitivity of the detection stage, an active fault-detection algorithm was proposed by adding auxiliary input signals [27]. Since the active fault-detection algorithm can identify more complex and variable faults, it has been studied by some scholars [28,29,30]. However, the existing active detection algorithms are mainly for single-agent systems and few are for multi-agent systems. The subsystem faults of multi-agent systems are often different and the sensors are interfered with by multiple subsystems. As a result, the detection mechanism may be insensitive to faults and thus trigger incorrectly. Furthermore, the constraints of multi-agent controllers are also very complex [31] and the control input saturation is not considered in most fault-tolerant control methods for multi-agent systems. Hence, it is a challenge to detect complex faults in multi-agent systems.
The actual control system often contains complex and changeable uncertainties, and fuzzy logic systems are often used to approximate system uncertainty because of their good approximation performance [32,33,34,35]. It is often difficult to deal with high-order uncertainties with traditional fuzzy logic systems, so type-II fuzzy control was proposed to improve the approximation performance to complex uncertainties [36]. The calculation of traditional Type-II fuzzy logic systems is often slow, so an interval Type-II fuzzy logic system was applied to the design of the controller [37]. In order to make the fuzzy logic system approximate the rapidly changing uncertainty, an adaptive fuzzy control strategy was proposed based on the adaptive adjustment of weight parameters [38]. Based on that, the weight adaptive law was applied to interval Type-II fuzzy control to deal with high-order uncertainties and changeable uncertainties [39]. By considering the fault-tolerant control algorithm, an interval Type-II fuzzy fault-tolerant control was proposed to deal with system faults and system uncertainties at the same time [40]. However, most existing interval Type-II fuzzy fault-tolerant control methods are based on passive fault detection [40,41,42]. This passive detection has difficulty distinguishing between faults and the uncertainty of multi-agent systems, which is caused by the strong coupling of multiple subsystems. This problem may make it difficult for the fuzzy system to approximate the actual uncertainty and affect the system control performance. Meanwhile, the active fault-tolerant control strategy of the multi-agent system can also lead to fast changes in uncertainty. Therefore, it is valuable to study adaptive interval Type-II fuzzy fault-tolerant controls for multi-agent systems.
Motivated by the above-mentioned problem, we propose a novel adaptive interval Type-II fuzzy fault-tolerant control for the proposed multi-agent systems based on active fault detection. This control method can realize the predefined-accuracy stability of multi-agent systems under input saturation, complex actuator failure and high-order uncertainties. The main innovative contributions are listed in the following:
(1) To the best of our knowledge, active fault detection of multi-agent systems is realized for the first time. Compared with the existing passive fault-detection methods, the novel active detection algorithm can resist more topology communication interference than passive detection.
(2) An improved fault-tolerant control algorithm of multi-agent systems was designed by the novel active fault-detection switching strategy. Compared with the existing passive fault-tolerant control methods, the proposed method can handle more serious and complex actuator failures in multi-agent systems.
(3) Based on the interval Type-II fuzzy approximated system, a novel adaptive fuzzy fault-tolerant controller was proposed for multi-agent systems to deal with high-order uncertainties and redundant control inputs. Compared with other fault-tolerant control methods, the proposed method can achieve predefinition of stable accuracy.
2. Preliminaries
Assumption 1
([43,44,45]). Assume that only the failures given in Definition 2 occur during system operation and no additional failures occur. The soundness of the system can be ensured in this study.
Lemma 1
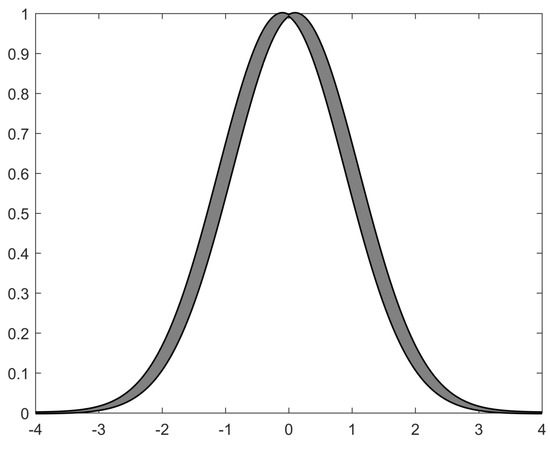
([32]). Consider a continuous function: and is the compact set. Then, can be approximated by an interval Type-II fuzzy logic system with arbitrary small error δ:
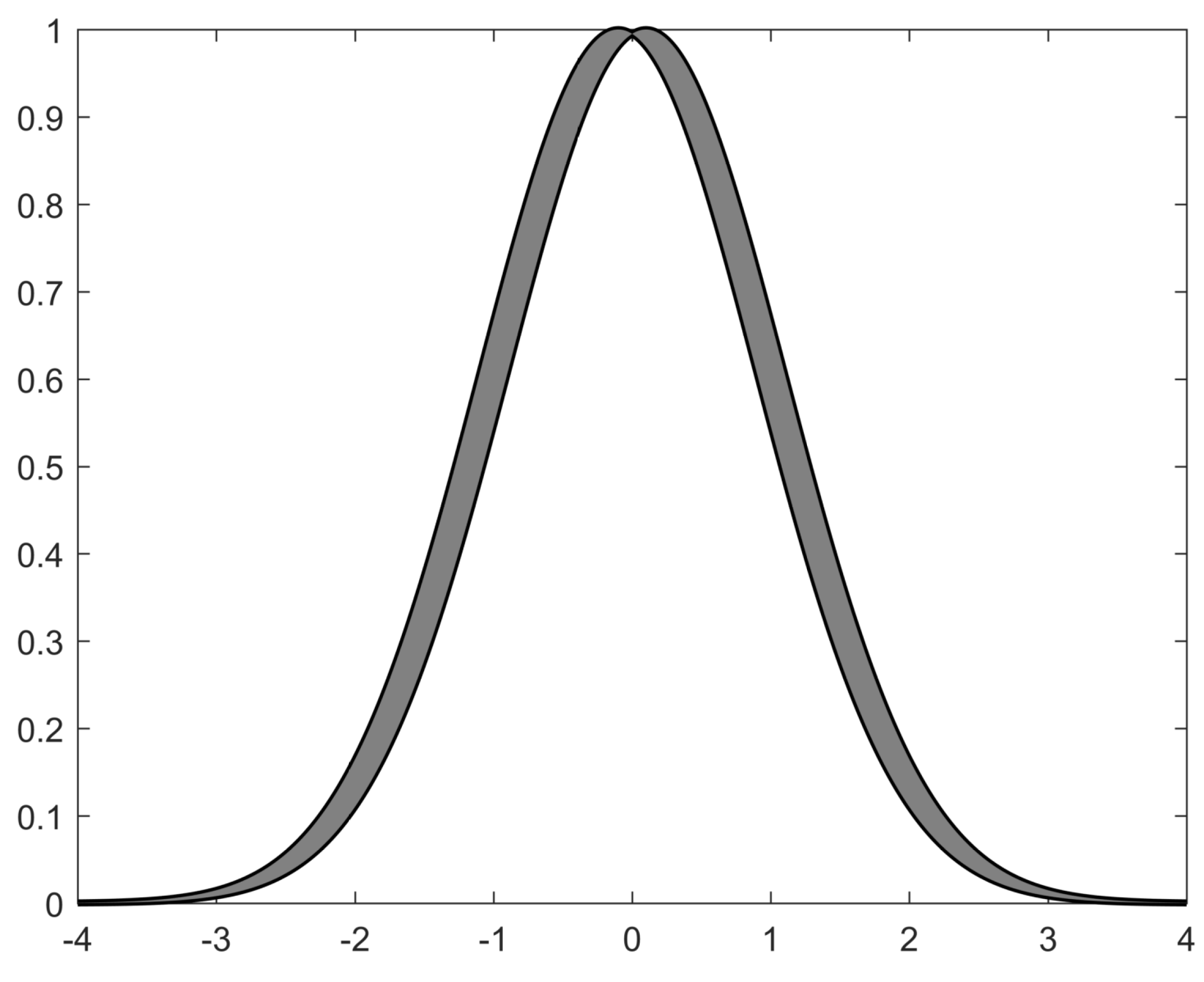
where is the adaptive weight parameter vector. is the expected weight parameter vector. is a basis function as shown in Figure 1, which can be expressed as:
in which
here, . and are the lower and upper membership grades:
with the following fuzzy rules:
Here, the fuzzy set is considered as the complete and continuous set [46,47,48,49,50,51].

Figure 1.
Interval Type-II fuzzy membership function.
3. Problem Description
Multi-agent systems are based on graph theory and the relevant background is described in Appendix A.
Definition 1.
A 2-DOF robotic multi-agent system is defined with a leader and N () followers:
and the dynamic model of the leader is described as follows ():
where and . represents the main control input and represents the redundant control input. , in which is the symmetric inertia matrix, is the centripetal and Coriolis torques matrix and is the gravitational torque. . and denote the unknown uncertainties caused by parameter perturbation and modeling uncertainty. When the subscript i is replaced by l, the symbolic meaning is that of the leader. Uncertainty from multiple sources can be called high-order uncertainty.
Condition 1.
The input constraint is , in which U is the known and bounded constant.
Lemma 2.
In order to achieve Condition 1, the actual control input can be designed by [52] as:
where . and E is a bounded unknown constant.
Definition 2.
The faults of sub-systems for multi-agent systems are often various, so their overall fault situation is complex. The actuator fault of subsystem [5] is considered as the following:
in which
where . and are the positive parameters. is the failure time of actuator. is considered to be zero in this paper.
The control objective is to make the tracking error of the system converge to the predefined accuracy † before and after the fault occurs.
4. Results
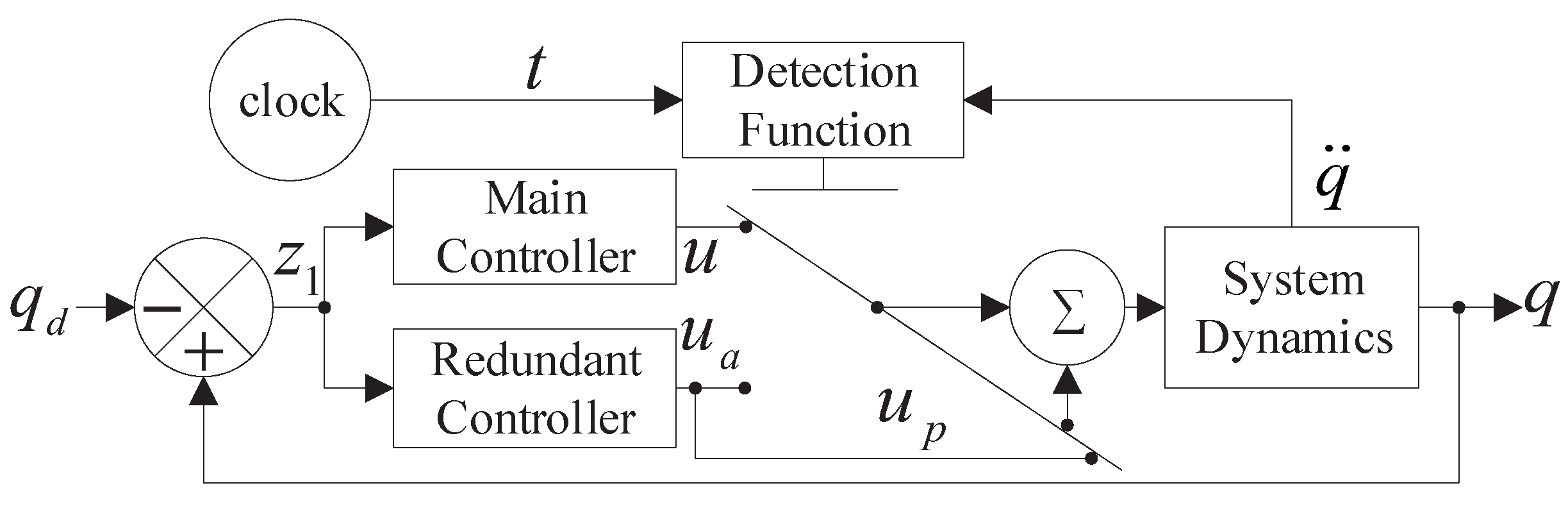
The design scheme of the proposed controller is shown in Figure 2. Assumption 1 is satisfied and the system is considered optimized [53,54,55,56,57].
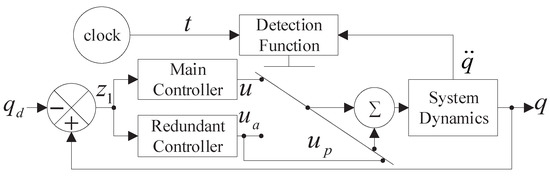
Figure 2.
The controller structure block diagram of the agent.
4.1. Active Fault Detection and Fault-Tolerant Control
The auxiliary input signal of redundant controller is considered as a pulse-wave function:
where . is the pulse amplitude vector. is the pulse repetition period. is the start time of detection. is the pulse width.
By observing (6) and (7), it is clear that observable information is more sensitive to the change of control input than other observable information and . Hence, a novel active detection algorithm is designed as follows.
When in Algorithm 1, the system is judged to be faulty. Then, the following improved active fault-tolerant control algorithm is activated:
| Algorithm 1 Active fault-detection algorithm () |
|
4.2. Main Controller Design
4.2.1. Main Controller Design of Leader
The virtual error can be designed as:
where is virtual control.
The uncertainty of the system can be approximated by a fuzzy logic system [58,59] and then an approximation-based controller can be designed as follows.
Theorem 1.
The leader system in Definition 1—(7) can be controlled by the following controller with a predefined accuracy :
and the adaptive law is
and the adaptive law is
where is the adaptive parameter vector. is an adaptive parameter and is a positive parameter. , and . † is the accuracy parameter.
The proof of Theorem 1 is given in Appendix B.
4.2.2. Main Controller Design of Follower
The virtual error can be designed as:
where is the virtual control.
Theorem 2.
The follower systems in Definition 1—(6) can be controlled by the following controller with a predefined accuracy :
and the adaptive law is
and the adaptive law is
where is the adaptive parameter vector. is an adaptive parameter and is a positive parameter. and . † is the accuracy parameter.
The proof of Theorem 2 is given in Appendix C.
4.3. Redundant Controller Design
Theorem 3.
According to Algorithm 2, the redundant controller can be designed as follows ():
where is from (12). When , the proof of Theorem 3 is similar to Theorems 1 and 2. The mathematical principle is that the value of and can be exchanged to obtain a symmetric stability result. According to (A10), (A21) and (21), it is clear that can converge to a neighborhood of zero after controller reconstruction.
| Algorithm 2 Active fault-tolerant control algorithm () |
|
4.4. Stability Analysis of the System
The Lyapunov functions in (A1) , (A3) , (A11) and (A14) are considered to verify the stability of system.
No-fault stage: According to Theorems 1 and 2, it can be deduced that , , and at . Hence, the system is predefined-accuracy stable.
Fault and no-switching stage: According to Algorithm 1, if , is small and bounded. Then, and are bounded if the operation time is finite. Next, by considering (8), (13), (14) and (18), and is bounded, it can be deduced that each virtual error is bounded. Then, the Lyapunov functions , , and are also bounded. Hence, according to the above-mentioned bounded inference and Barbalat stability theorem, the system is Lyapunov stable. The steady-state accuracy at this stage can be adjusted by a fault threshold parameter Y in Algorithm 1.
Switching stage: If the switching is considered as a momentary event [61] and Condition 1 is considered, (A4) can be rewritten as:
Since the virtual errors of the system in the fault and no-switching stage are bounded, is bounded. Assuming that the switching time is a very small constant . By considering that the Lyapunov functions V in the fault and no-switching stage are also bounded, then is bounded. Hence, the leader system is also Lyapunov stable by considering (22).
Redundant control stage: According to Theorem 3, the system is predefined-accuracy stable at .
Remark 1.
Based on the proposed active fault-detection and redundant fault-tolerance mechanism, the Lyapunov stability analysis of this system can be regarded as continuous. Hence, compared with other existing fault-tolerant control methods, the proposed method can achieve predefinition of stable accuracy.
5. Simulation
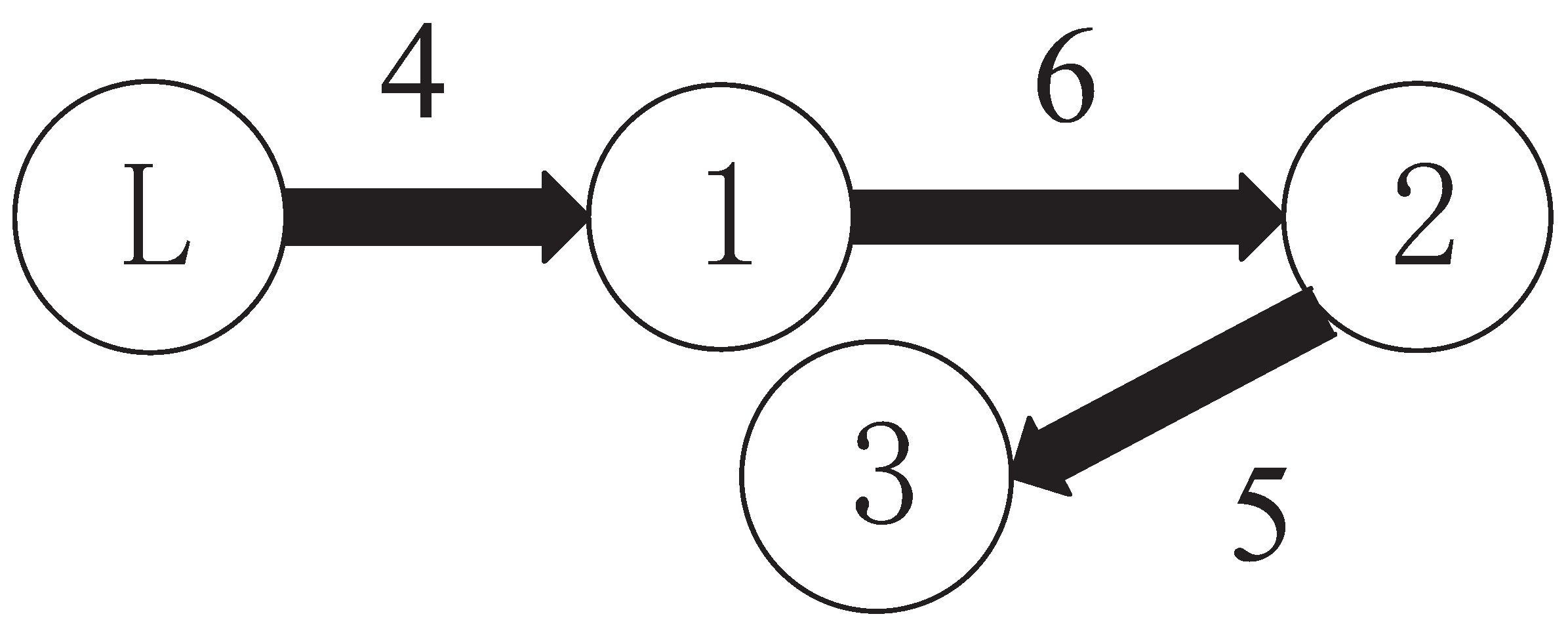
The following simulations are carried out on MATLAB R2016a with a variable simulation step of ode45, relative tolerance and auto other additional options. A small image embedded in a large image is a local magnification of a large image with the same time scale. Section 5.1 presents the validation simulations of the proposed controller for the single-agent system. Section 5.2 presents the validation simulations of the proposed controller for multi-agent systems with different actuator subsystem faults. Section 5.3 presents comparative simulations between the proposed method and recent passive fault-tolerant methods. Section 5.4 presents the comparative simulations between the proposed method and recent active fault-tolerant methods. This active fault-tolerant method adopts passive fault detection. The structure of multi-agent systems is shown in Figure 3; the subsystem is modeled as the following 2-DOF robot arm system. The advantages of the proposed method can be verified by comparative simulation.
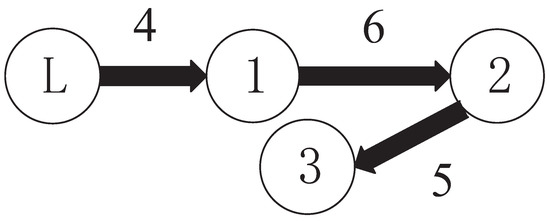
Figure 3.
The communication topology of MASs.
According to recent robot studies [62,63,64], the dynamics of simplified 2-DOF robot arm system are modeled as follows:
in which,
and parameter perturbation is expressed as:
where is disturbance. kg/m. Mass parameters are and . Link lengths are and .
The initial condition is and the joint angle command is .
The singularity problem of Jacobian matrix is solved by the DLS method [65]:
in which
where .
By considering one communication topology structure of MASs as shown in Figure 3, the weighted Laplacian matrix L and weighted adjacency matrix defined by [66] are shown in the following:
with a connected weight matrix of leader and followers
The auxiliary input signal is selected as
where , , , .
The interval type 2 membership function with is chosen as the Gaussian function:
where , , .
5.1. Validation Simulations of the Proposed Controller for Single-Agent Systems
In this section, the validation simulation of the proposed method for uncertain single-agent systems is carried out with Condition 1. The model of the single-agent system is based on the leader model of topology-free communication. The initial detector parameter is . The initial parameters are , , , , . The actuator fault parameters in Definition 2 are set as follows: , and .
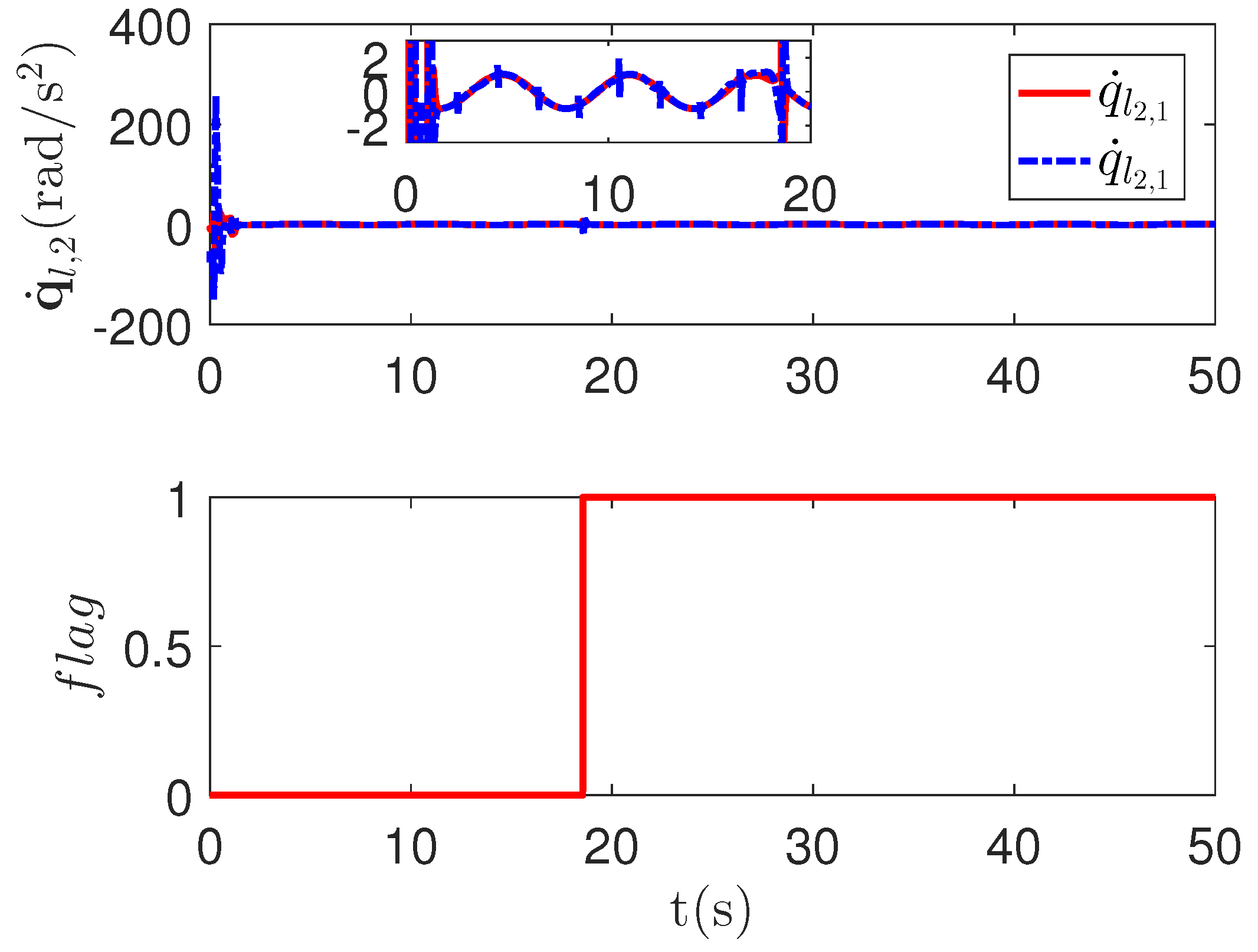
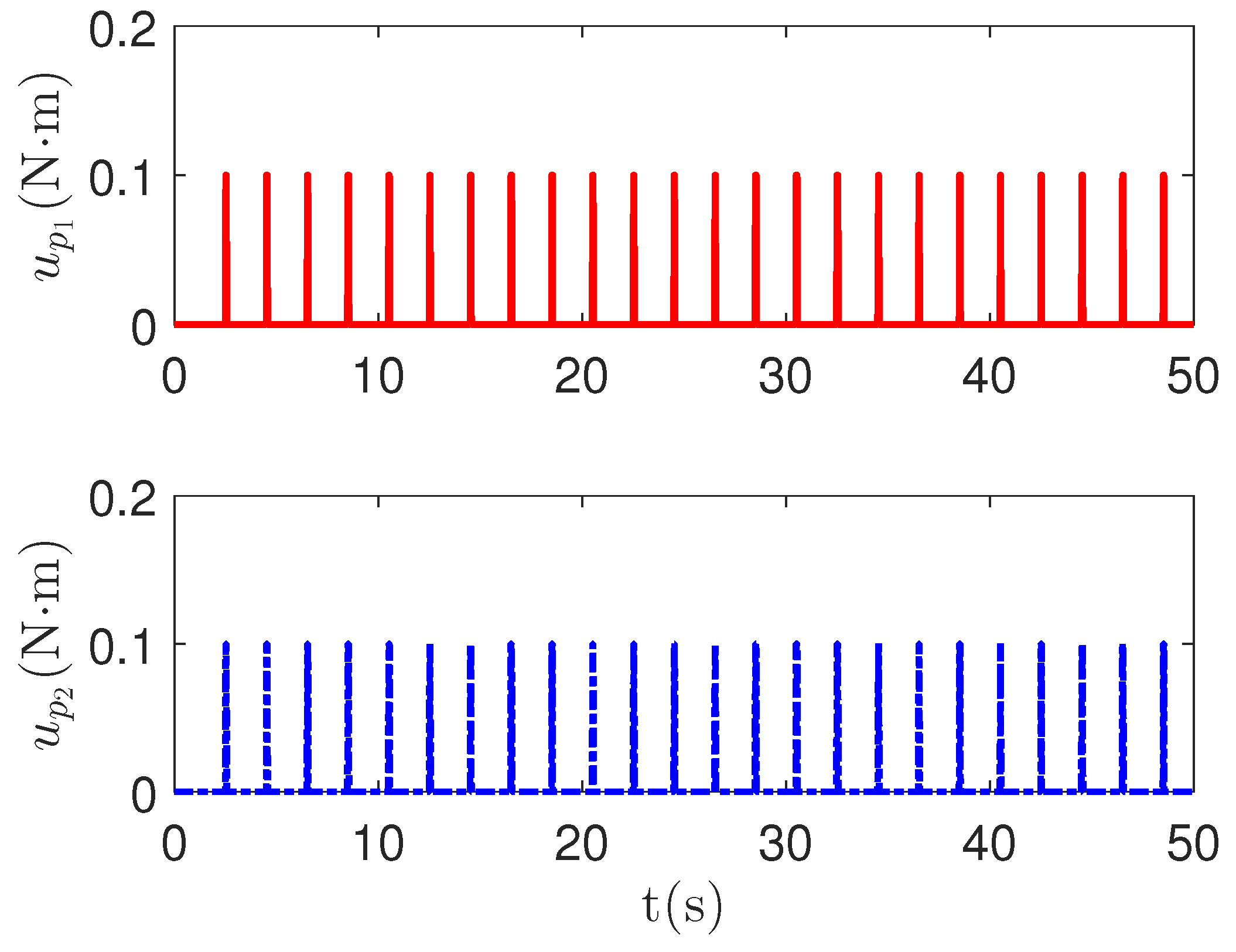
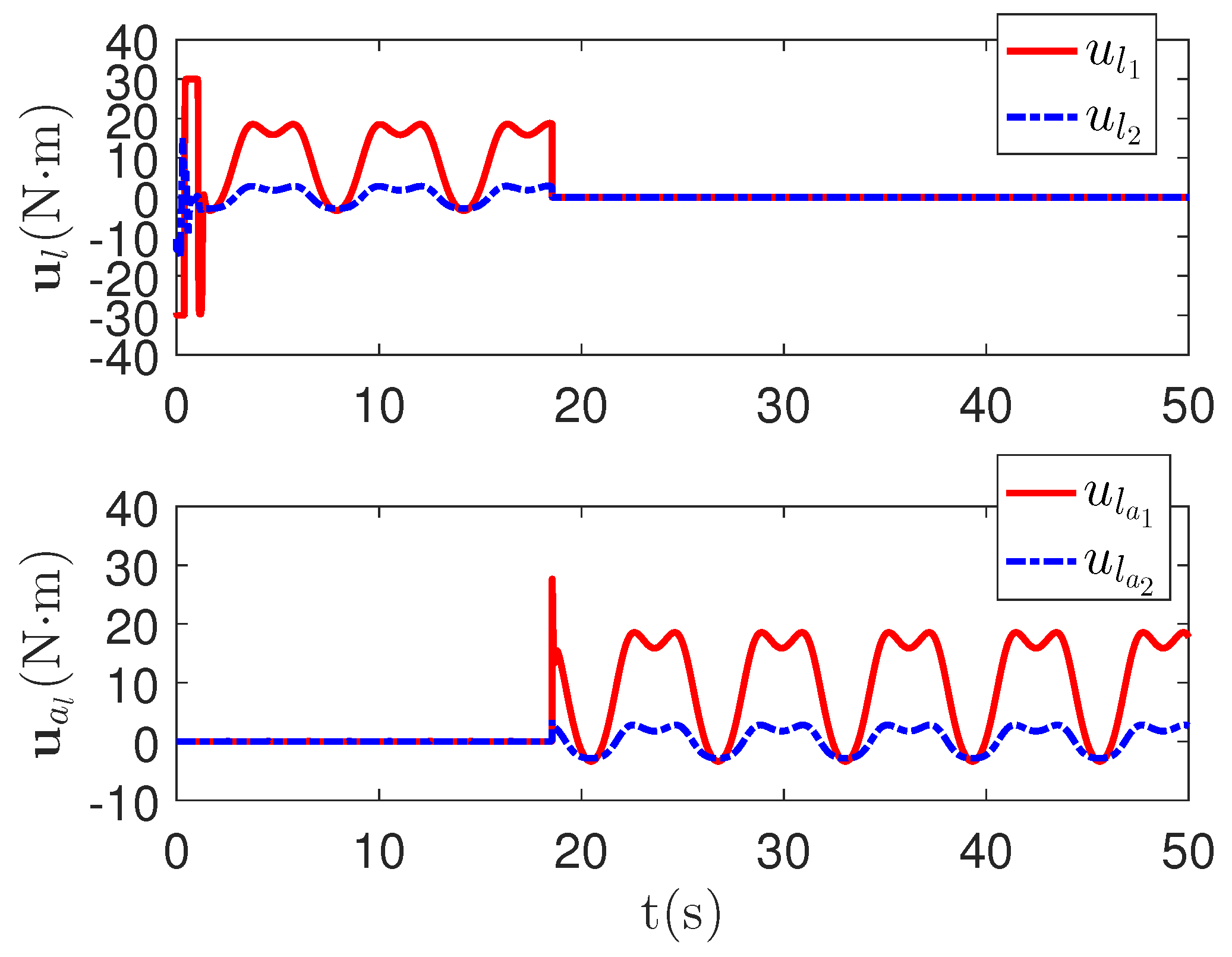
As shown in Figure 4, it is clear that the tracking error of the proposed method is about , which is less than the predefined accuracy . By considering the simulation results in Figure 4 and Figure 5, there is no significant change in system tracking performance when the fault occurs at 10 s. The reason is the robustness of the control system. Therefore, the auxiliary input in Figure 6 is considered to be added to the control system. According to the results in Figure 5, when the sensor detects the occurrence of acceleration-level abnormal phenomena, Algorithm 1 judges the system failure at about 18.55 s. Furthermore, as shown in Figure 7, the maximum absolute values of and are 30 and 27.63, respectively. This result verifies the validity of the constraint controller in Lemma 2.
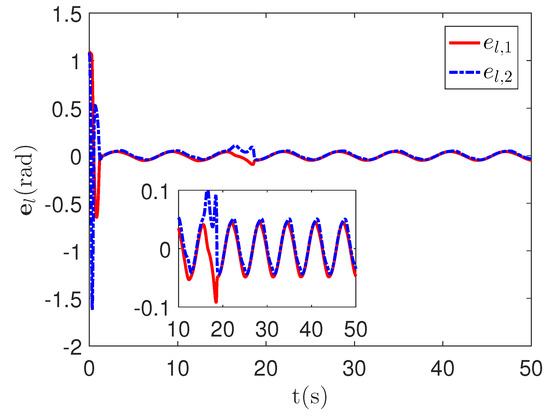
Figure 4.
The tracking error curves of the proposed method.
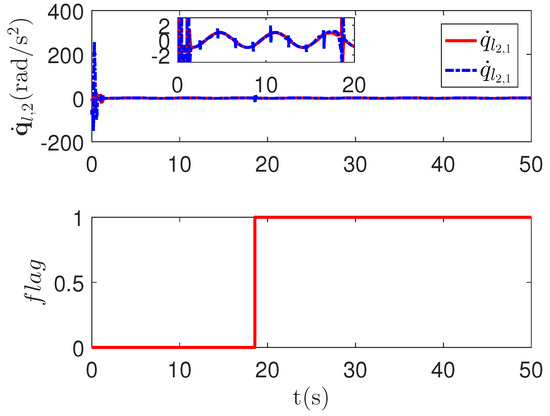
Figure 5.
The joint angular acceleration curves and fault-detection curve of the proposed method.
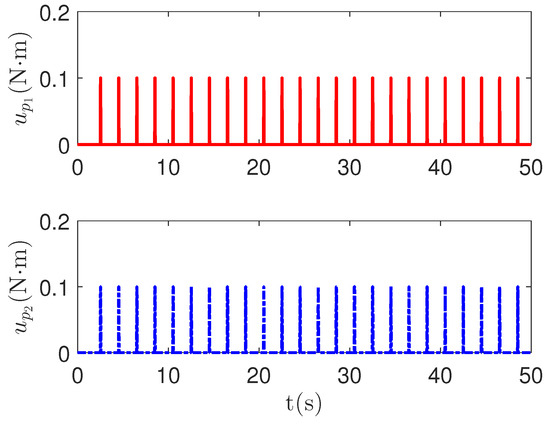
Figure 6.
The pulse-wave function curves of the redundant control input .
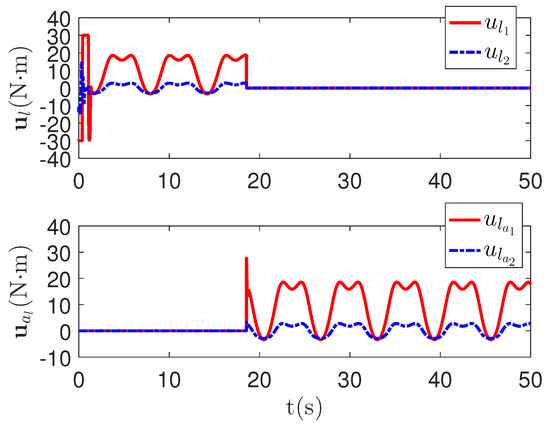
Figure 7.
The main control input curves and redundant control input curves of the proposed method.
5.2. Validation Simulations of the Proposed Controller for Multi-Agent Systems
In this section, the validation simulation of the proposed method for uncertain multi-agent systems is carried out with Condition 1. The initial detector parameter is . The initial parameters are , , , , . The actuator fault parameters in Definition 2 are set as follows: ; , , ; , , ; , , .
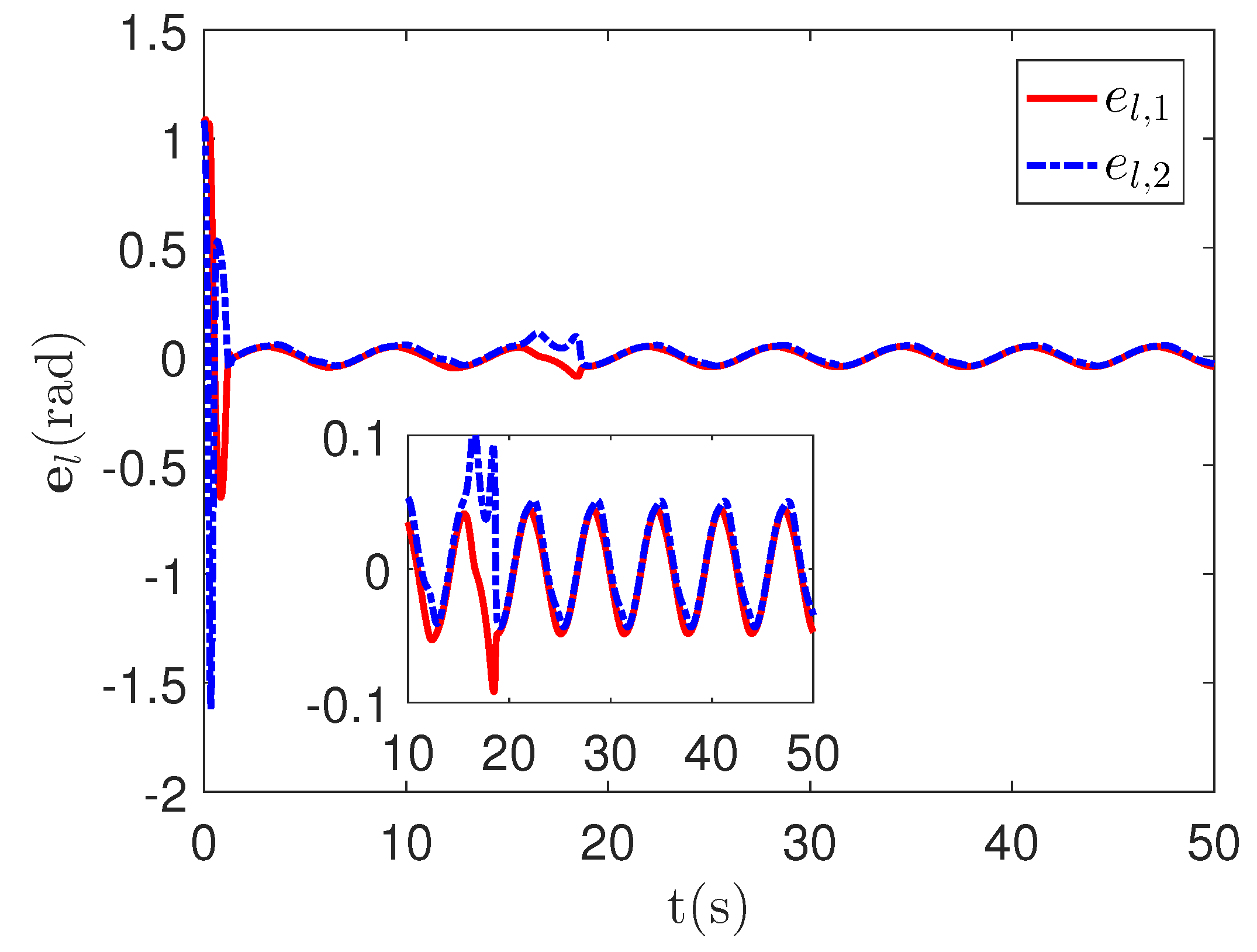
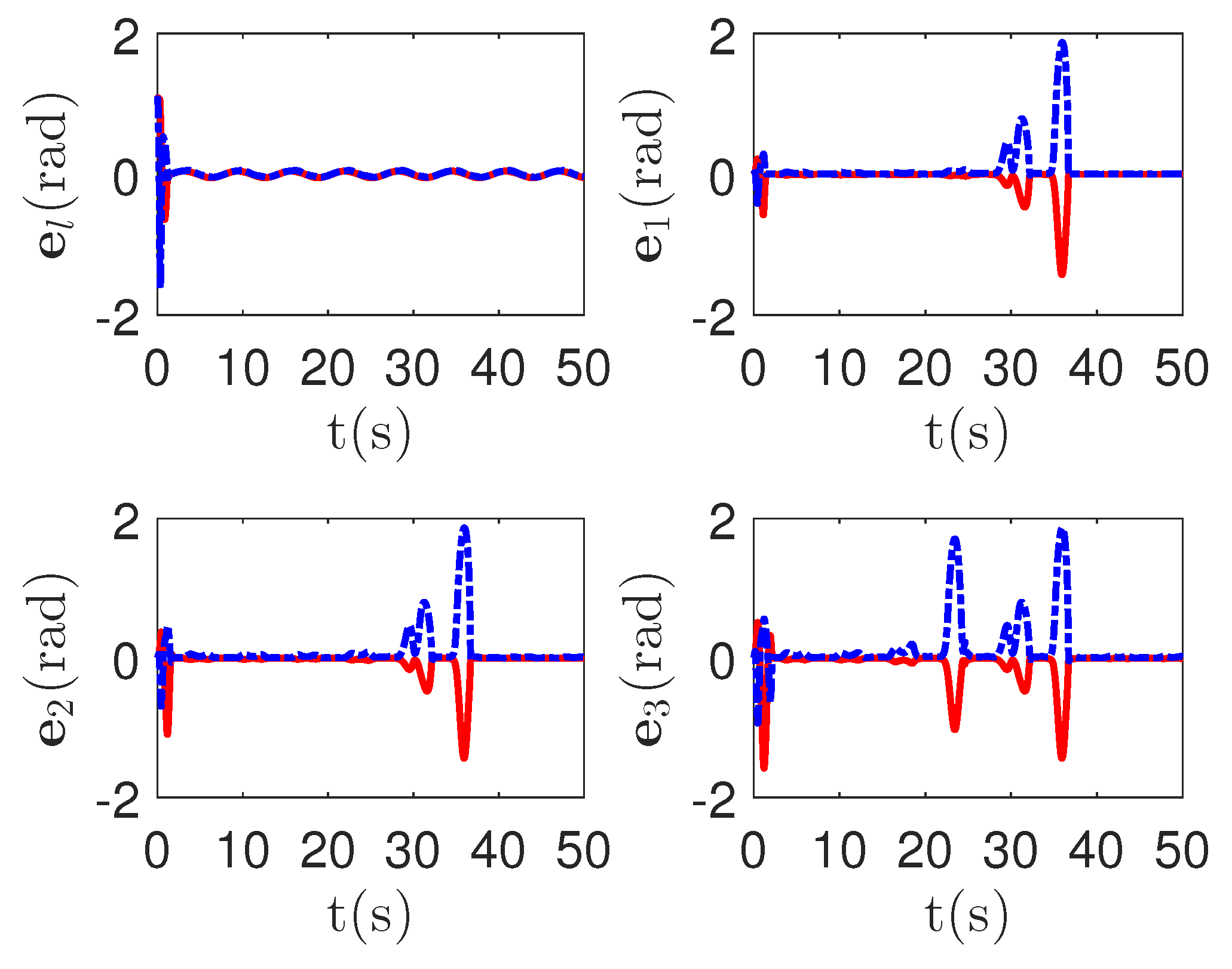
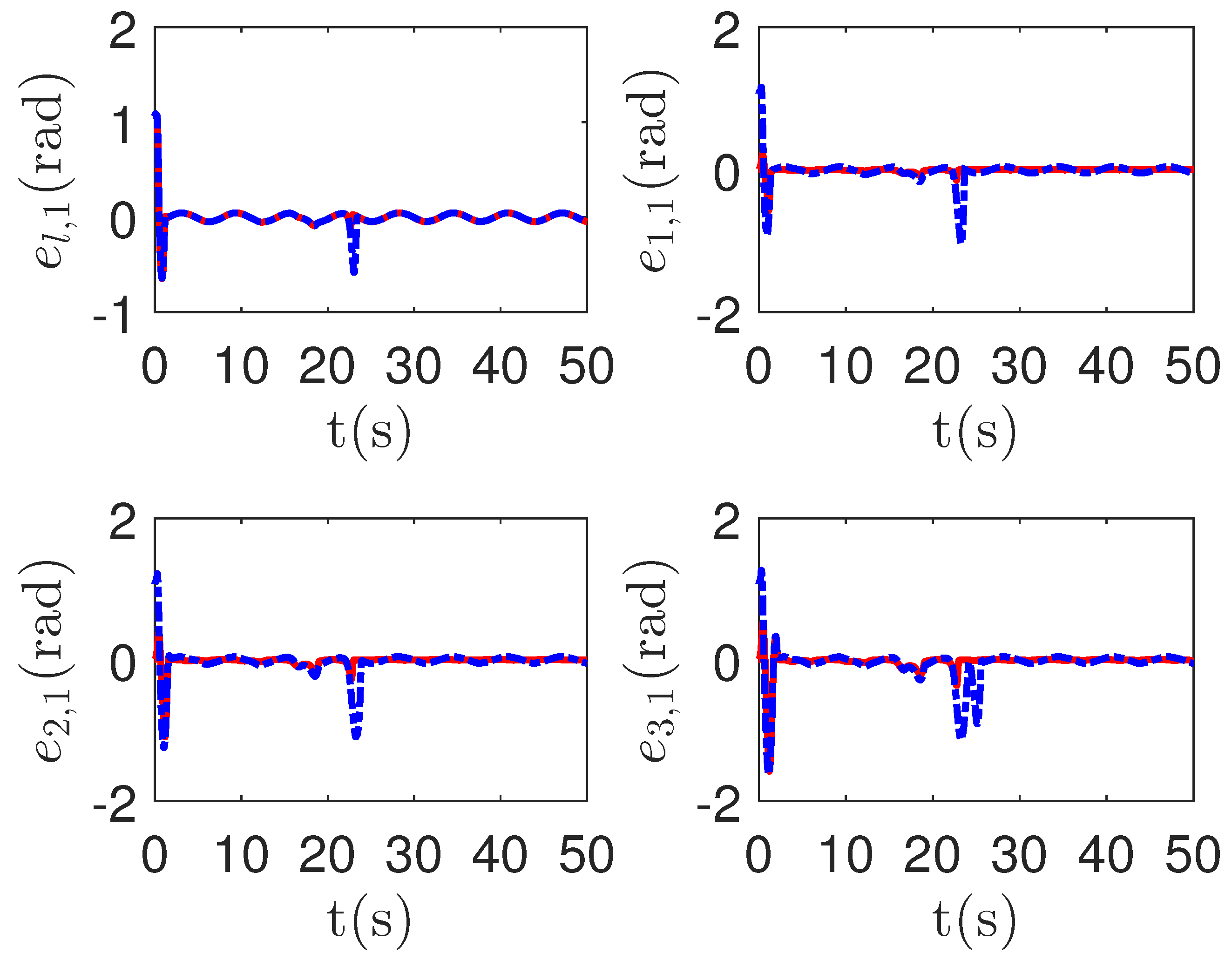
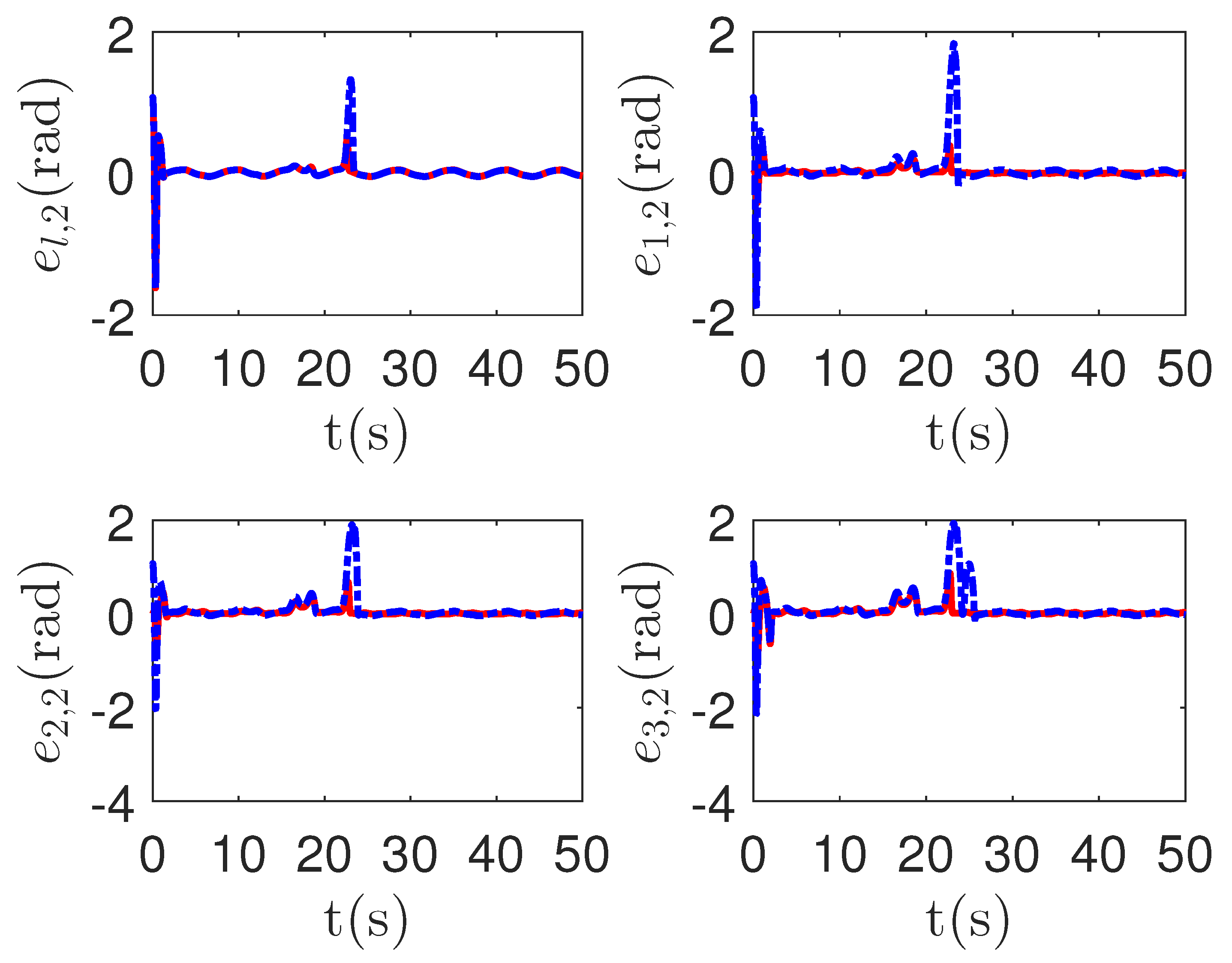
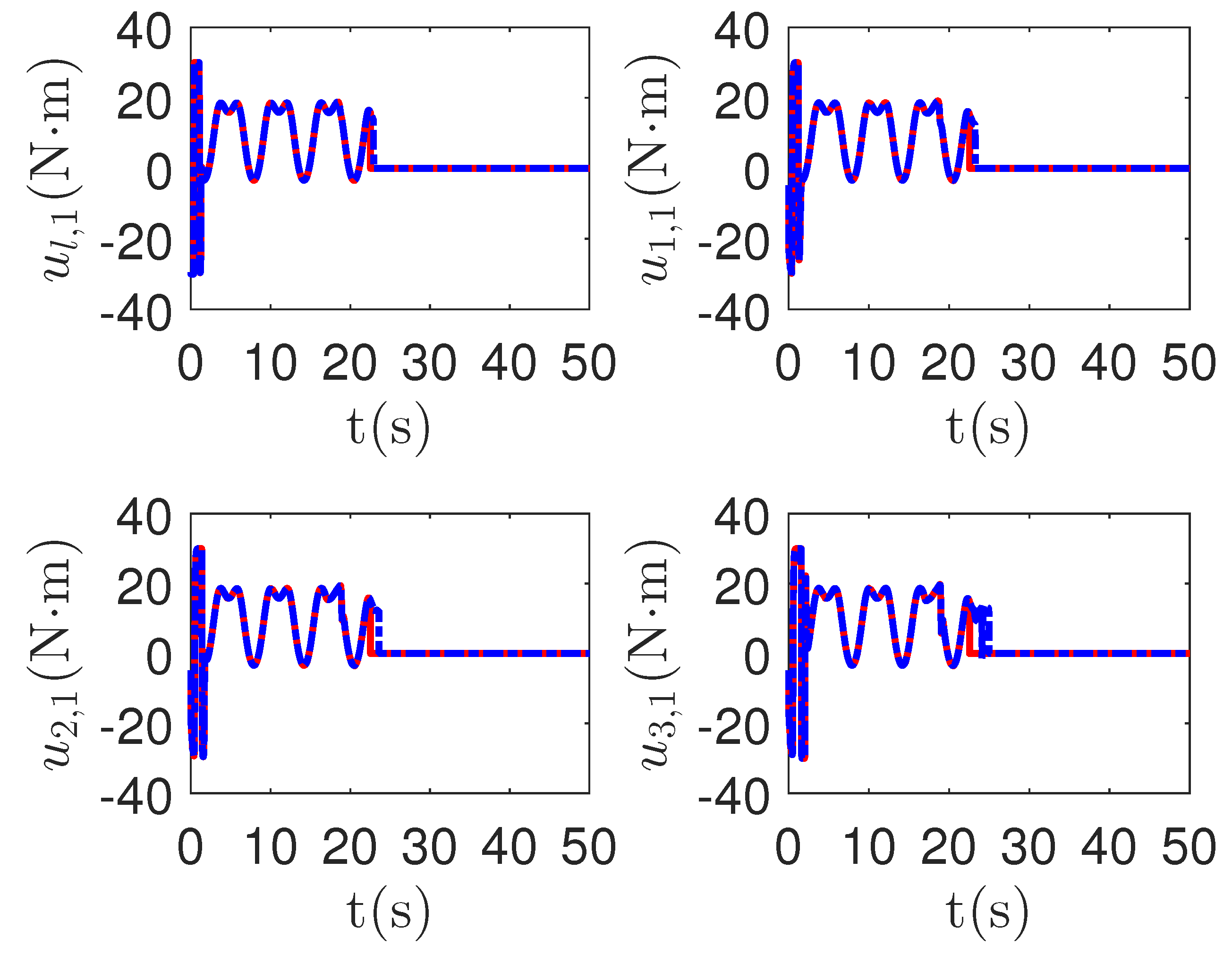
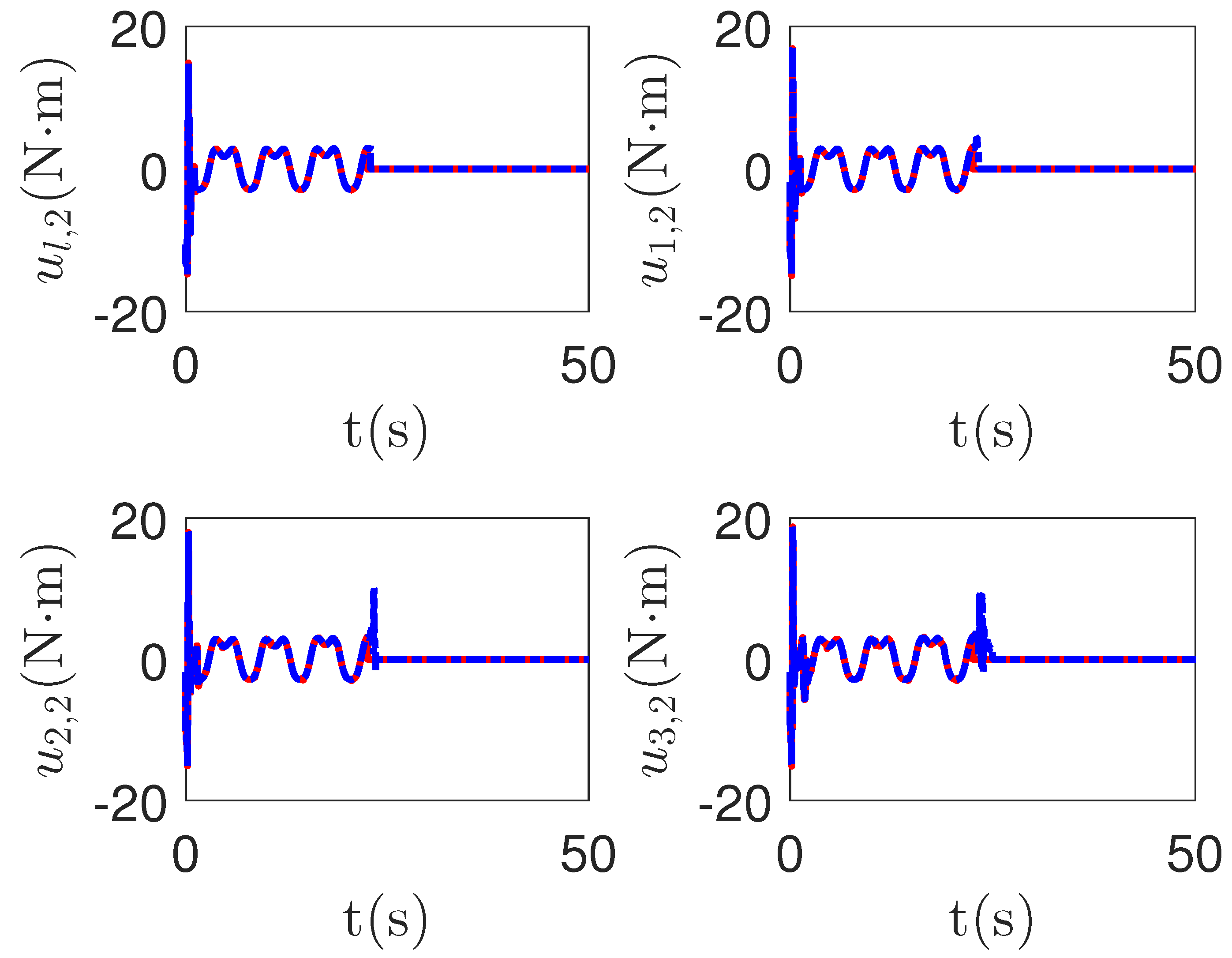
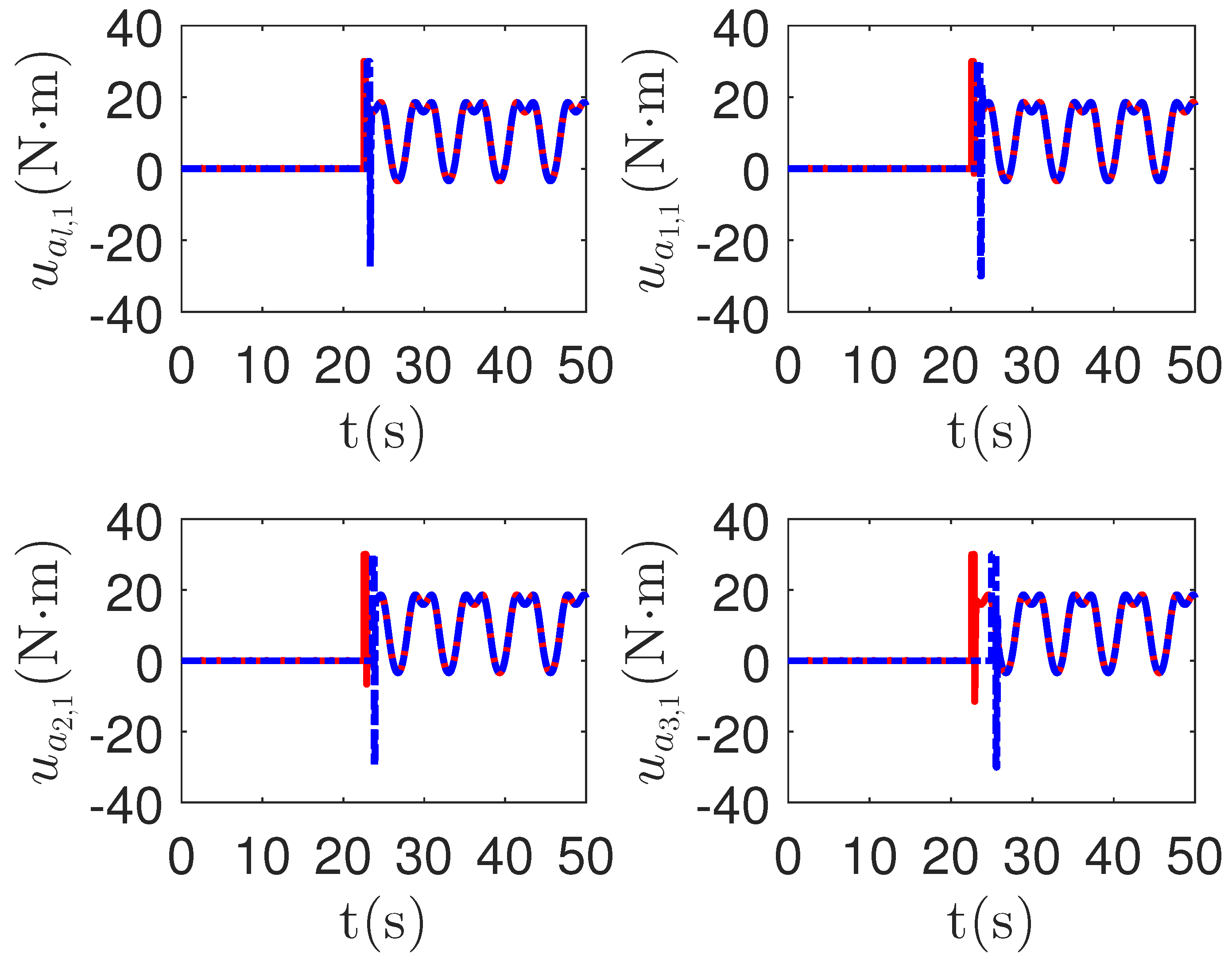
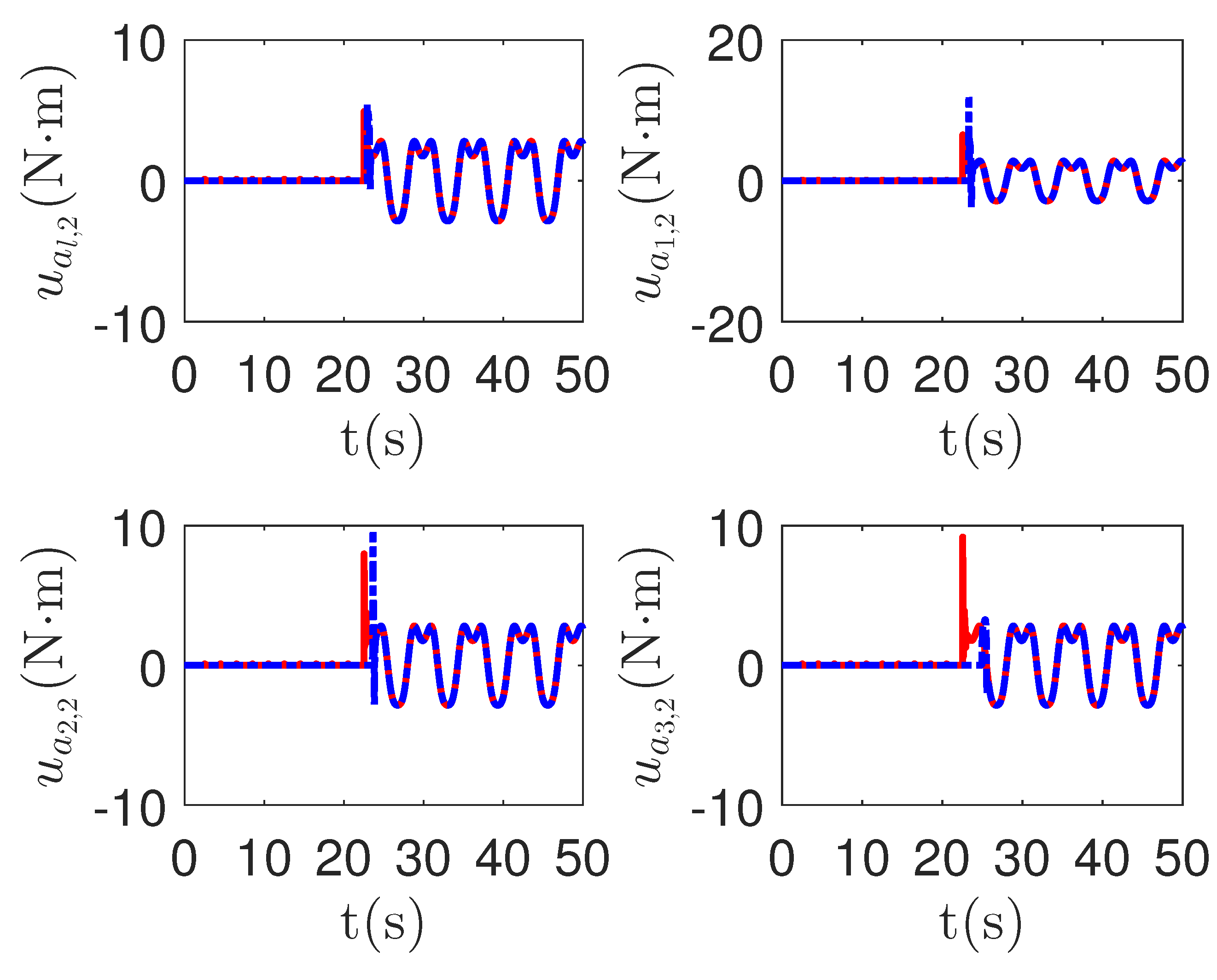
As shown in Figure 8, it is clear that the final tracking error of the proposed method is about 0.02 at 50 s, which is less than the predefined accuracy † = 0.1. According to the results in Figure 9 and Figure 10, under three different fault types, the proposed method successfully carries out the corresponding fault detection and controller reconstruction of three followers. When the sensor detects the occurrence of acceleration-level abnormal phenomena, Algorithm 1 judges the system failure at about 36.55 s, 36.55 s and 24.55 s, respectively. Meanwhile, the detector is not triggered by mistake for the leader . Furthermore, as shown in Figure 9 and Figure 10, the maximum absolute values of and are 30.00 and 30.00, respectively. This result verifies the validity of the constraint controller in Lemma 2.
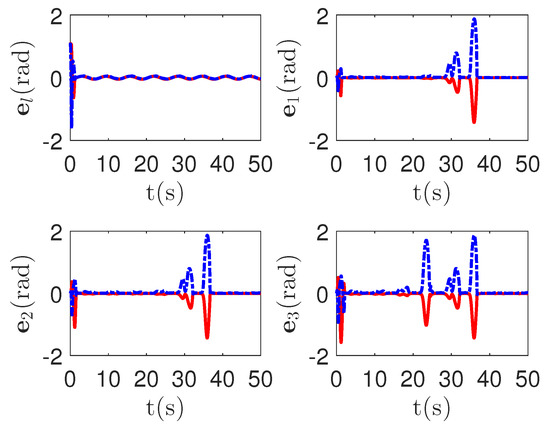
Figure 8.
The tracking error curves of leader and followers for the proposed method with different actuator faults of subsystems. Figure legends: : ;
: ; : .
: .
 : ;
: ; : .
: .
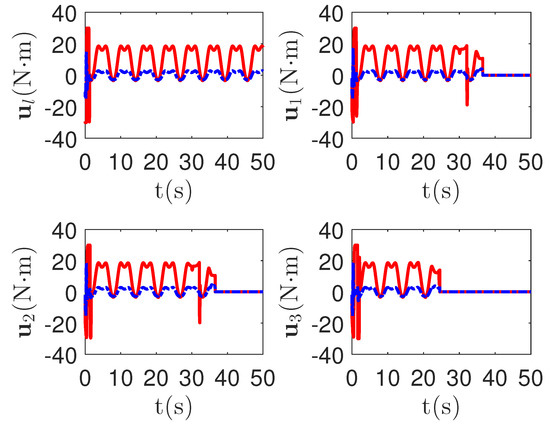
Figure 9.
The tracking error curves of leader and followers for the proposed method with different actuator faults of subsystems. Figure legends: : ;
: ; : .
: .
 : ;
: ; : .
: .
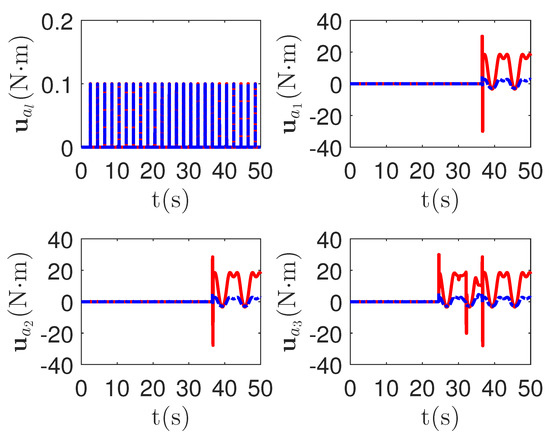
Figure 10.
The tracking error curves of leader and followers for the proposed method with different actuator faults of subsystems. Figure legends: : ;
: ; : .
: .
 : ;
: ; : .
: .
5.3. Comparative Simulations between the Proposed Method and the Passive Fault-Tolerant Method
In this section, comparative simulations between the proposed method and the passive fault-tolerant method [67] for uncertain multi-agent systems are carried out with Condition 1. In order to ensure the fairness of the comparison, we use the same fuzzy approximator; the only difference between them is the active detection strategy and passive fault-tolerant strategy. The initial detector parameter is . The initial parameters are , , , , . The actuator fault parameters in Definition 2 are set as follows: , , .
As shown in Figure 11 and Figure 12, it is clear that the final tracking error of the proposed method is about 0.05 at 50 s, which is less than the predefined accuracy † = 0.1. However, the tracking error of passive fault-tolerant control method is not convergent. The reason is that passive fault-tolerant controllers can only operate under minor actuator failures. If the fault function is too small, the more master control input is required. However, by considering the control input constraint in Condition 1, the control system can not be stable.
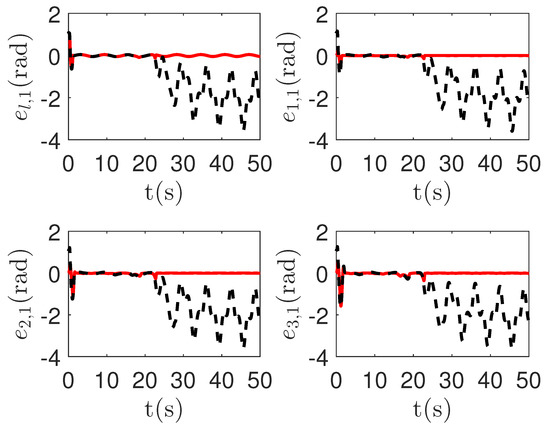
Figure 11.
The tracking error curves of leader and followers in the proposed method and passive fault-tolerant control method [67]. Figure legends: : The proposed method;
: The proposed method; : The passive fault-tolerant control method [67].
: The passive fault-tolerant control method [67].
 : The proposed method;
: The proposed method; : The passive fault-tolerant control method [67].
: The passive fault-tolerant control method [67].
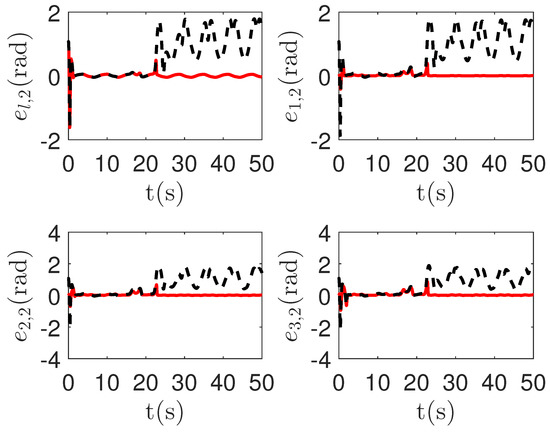
Figure 12.
The tracking error curves of leader and followers in the proposed method and passive fault-tolerant control method [67]. Figure legends: : The proposed method;
: The proposed method; : The passive fault-tolerant control method [67].
: The passive fault-tolerant control method [67].
 : The proposed method;
: The proposed method; : The passive fault-tolerant control method [67].
: The passive fault-tolerant control method [67].
5.4. The Comparative Simulations between the Proposed Method and Active Fault-Tolerant Method
In this section, the comparative simulations between the proposed method and active fault-tolerant method [68] for uncertain multi-agent systems is carried out with Condition 1. This active fault-tolerant method [68] adopts the passive fault-detection algorithm. In order to ensure the fairness of the comparison, we use the same main controller and adjust similar tracking accuracy. The only difference is that the active and passive detection mechanism. As shown in Figure 13 and Figure 14, the final tracking errors of the two algorithms are similar. The initial detector parameter is . The initial parameters are † = 0.1, U = 30, , , . The actuator fault parameters in Definition 2 are set as follows: , , .
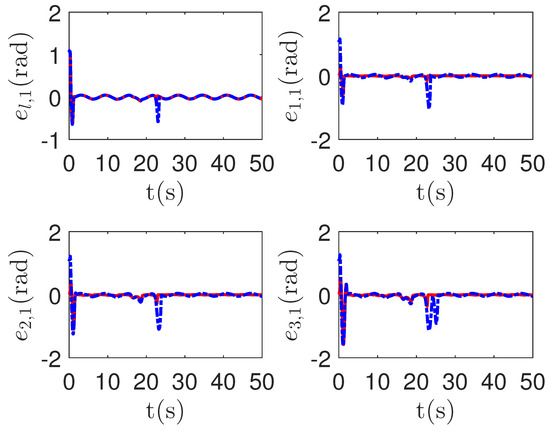
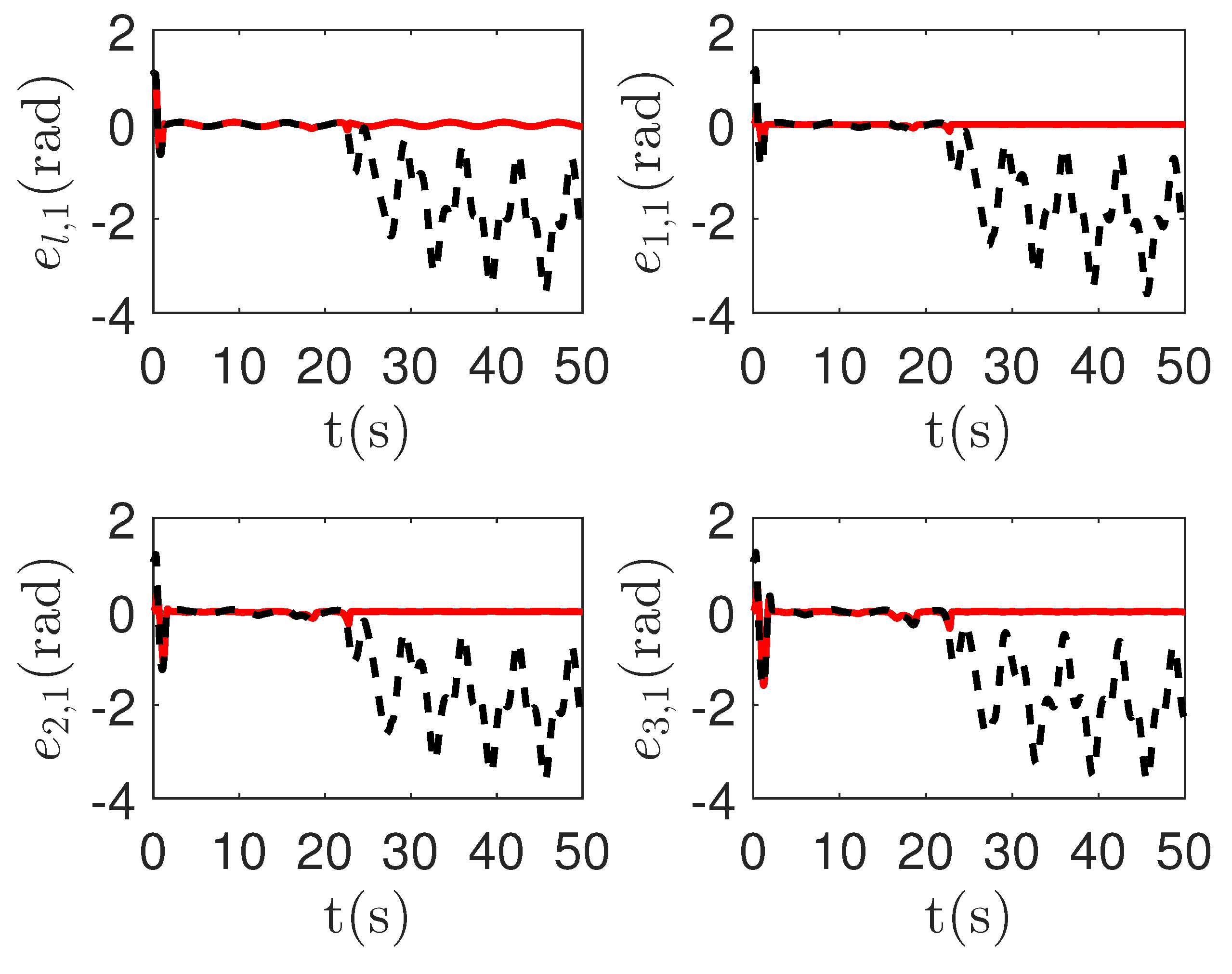
Figure 13.
The tracking error curves of leader and followers in the proposed method and passive fault-detection control method [68]. Figure legends: : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
 : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
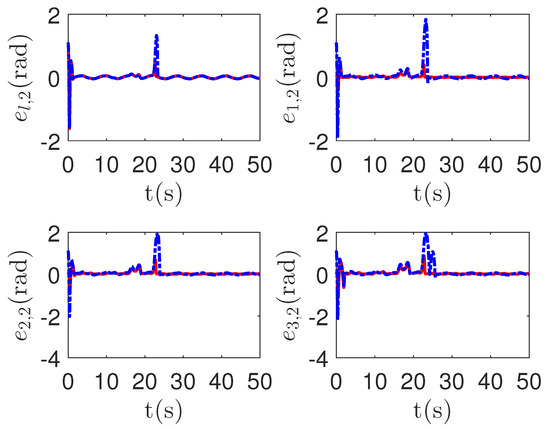
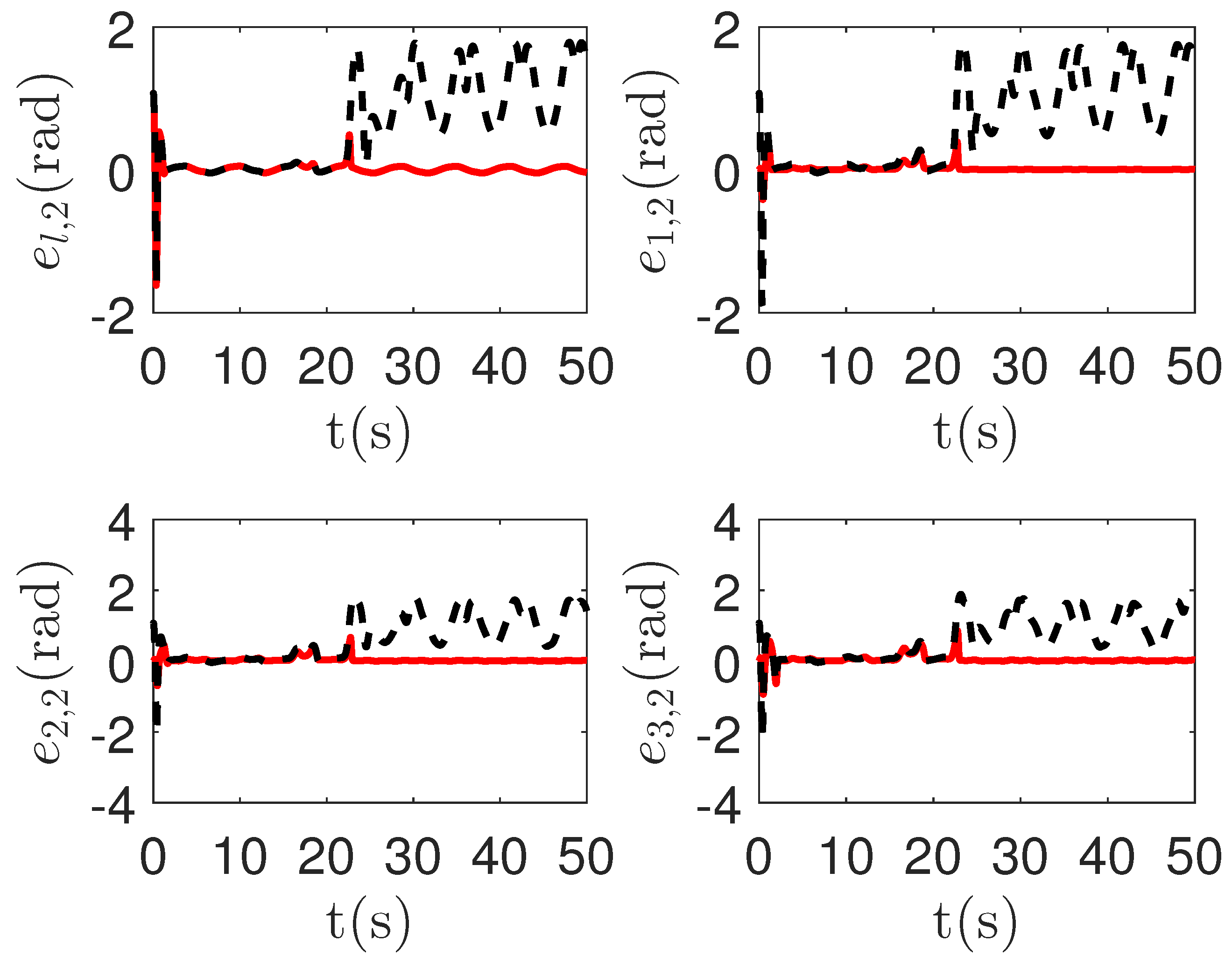
Figure 14.
The tracking error curves of leader and followers in the proposed method and passive fault-detection control method [68]. Figure legends: : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
 : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
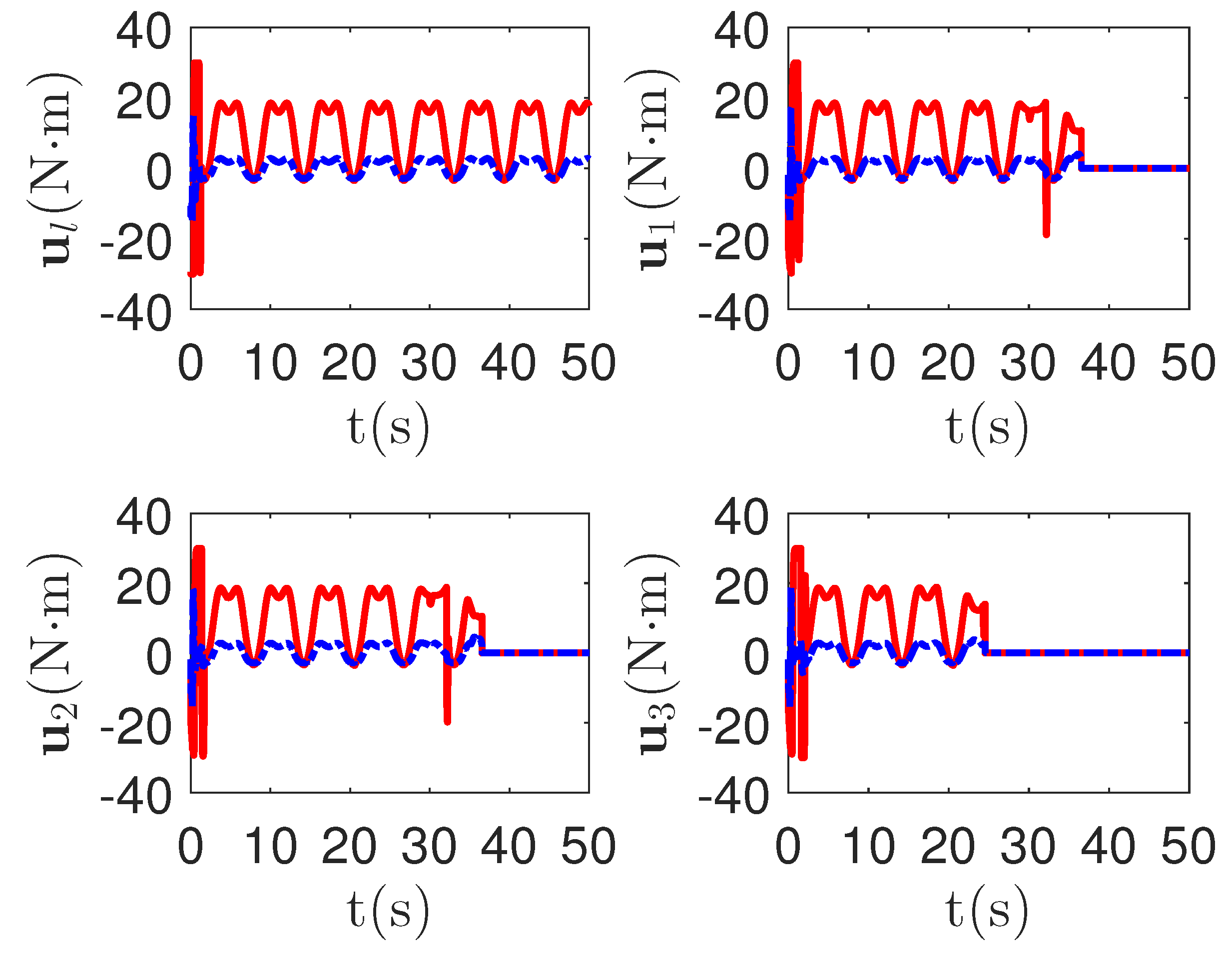
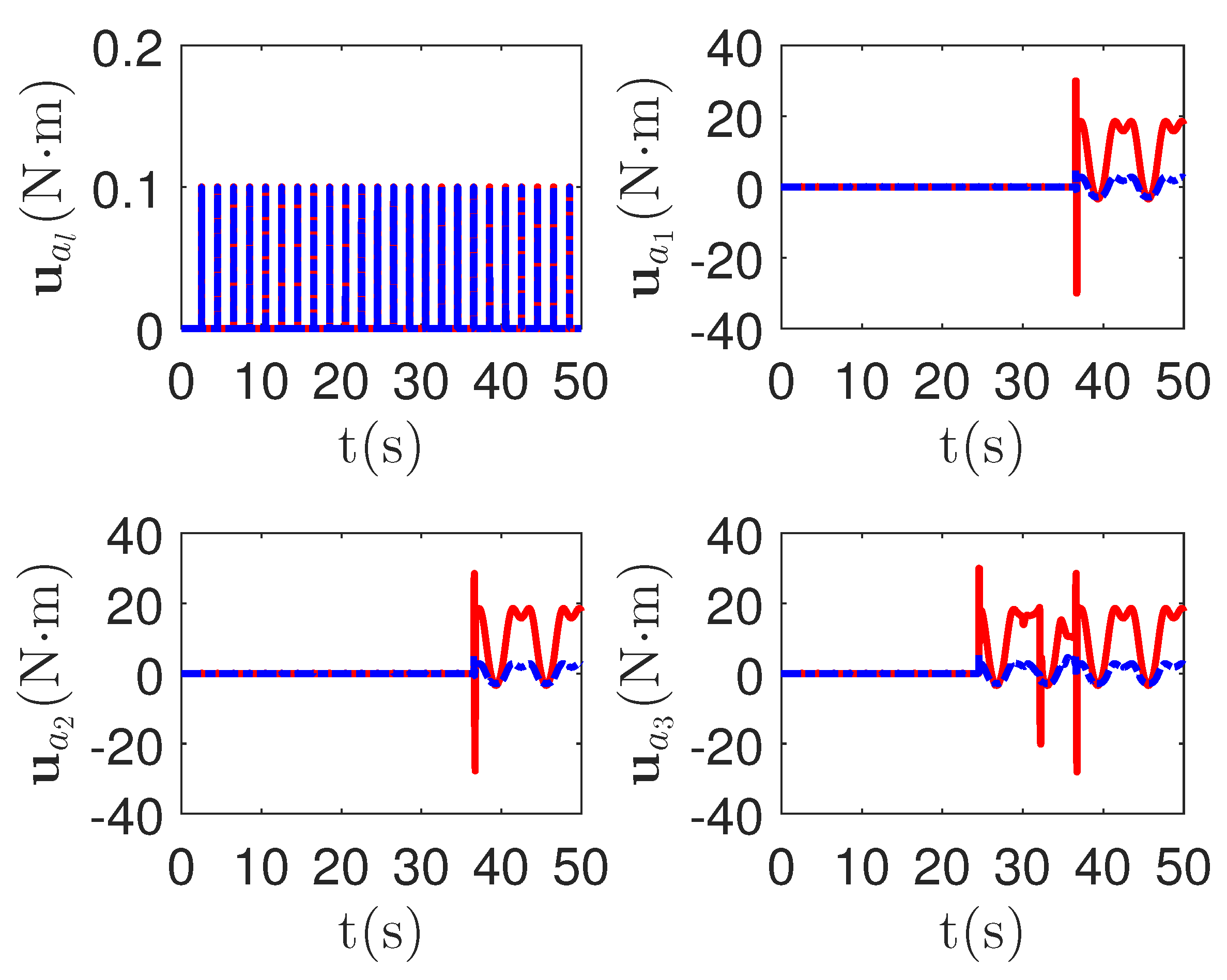
As shown in Figure 13 and Figure 14, when the switch happens, the maximum absolute values of tracking errors in the proposed control method are [0.12, 0.49]T, [0.15, 0.39]T, [0.27, 0.67]T and [0.36, 0.86]T, respectively. When the switch happens, the maximum absolute values of tracking errors in the compared control method [68] are [0.58, 1.33]T, [1.04, 1.84]T, [1.09, 1.91]T and [1.13, 1.94]T, respectively. It is clear that the system tracking performance of the proposed method is better than that of the passive detection method when switching occurs. According to the results in Figure 15 and Figure 16, the chattering of the proposed main controller is weaker than that of the compared control method during switching. In Figure 17 and Figure 18, the chattering of the proposed main controller is basically weaker than that of the compared control method during switching. Furthermore, according to Figure 15, Figure 16, Figure 17 and Figure 18, under the same fault, the proposed active fault detector basically detects the fault occurrence at 22.55 s. The compared passive fault detector detects the fault occurrence at 22.91 s, 23.25 s, 23.60 s and 24.90, respectively. This simulation result means that passive detection is more susceptible to topology communication interference of multi-agent systems than active detection.
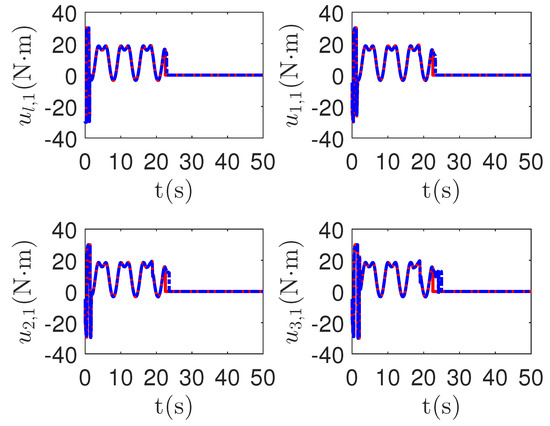
Figure 15.
The main control input curves of leader and followers in the proposed method and passive fault-detection control method [68]. Figure legends: : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
 : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
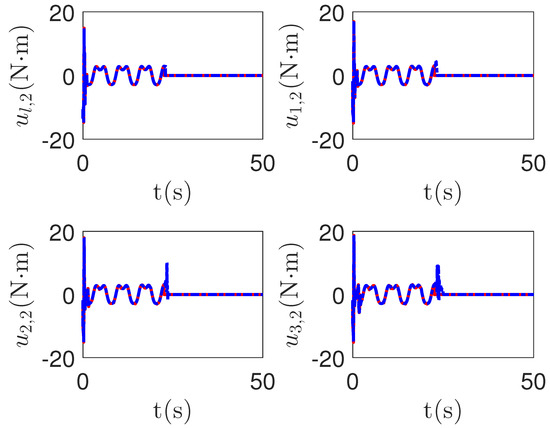
Figure 16.
The main control input curves of leader and followers in the proposed method and passive fault-detection control method [68]. Figure legends: : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
 : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
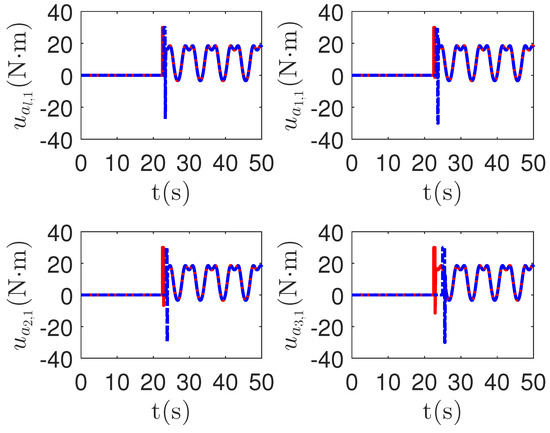
Figure 17.
The redundant control input curves of leader and followers in the proposed method and passive fault-detection control method [68]. Figure legends: : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
 : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
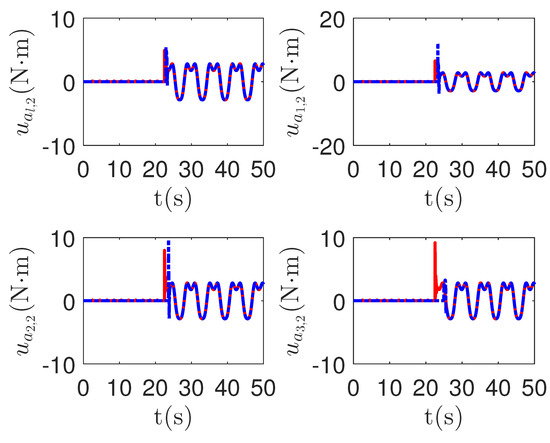
Figure 18.
The redundant control input curves of leader and followers in the proposed method and passive fault-detection control method [68]. Figure legends: : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
 : The proposed method;
: The proposed method; : The active fault-tolerant control method with passive fault detection [68].
: The active fault-tolerant control method with passive fault detection [68].
6. Conclusions
A novel adaptive interval Type-II fuzzy fault-tolerant control method was proposed for constrained uncertain 2-DOF robotic multi-agent systems by considering an active fault-detection algorithm. This control method can realize the predefined-accuracy stability of multi-agent systems under input saturation, complex actuator failure and high-order system uncertainties. Firstly, a novel active fault-detection algorithm based on pulse-wave function was proposed to detect the failure time of multi-agent systems for the first time. Compared with the existing passive fault-detection methods, the novel active detection algorithm can resist more topology communication interference than passive detection. Then, an improved fault-tolerant control algorithm was adopted to deal with more complex actuator failures. In the end, based on the interval Type-II fuzzy approximated system, a novel adaptive fuzzy fault-tolerant controller was proposed for constrained uncertain mechanical multi-agent systems to achieve predefined-accuracy stability. Compared with other fault-tolerant control methods, the proposed method can achieve predefined-accuracy stability of multi-agent systems under complex multi-agent faults. Meanwhile, the switching chattering of the controller was weaker. These theoretical results were verified by simulation.
Author Contributions
Conceptualization, W.Y. and H.T.; methodology, W.Y.; software, W.Y.; validation, W.Y., H.T. and P.Q.; investigation, W.Y.; resources, H.T.; writing—original draft preparation, W.Y.; writing—review and editing, W.Y., H.T., P.Q. and T.Z.; visualization, W.Y.; supervision, H.T.; funding acquisition, H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Department of Sichuan Province (No. 2020YFG0119).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Graph theory [66]: The topological structure of a multi-agent system is represented by one directed graph , where and . is a node which represents agent i. If only gets information from , can be true. represents the neighbor of . represents a collection of . If weights are considered, the proposed graph is a weighted graph. Adjacency matrix is also the weighted topology. if , otherwise . , where is in-degree of . The Laplacian matrix is . The communication topology is described by augmented graph . There are one leader and N followers.
Appendix B
Proof.
Step 1: Consider a candidate Lyapunov function:
Step 2: Consider a candidate Lyapunov function:
where . , in which is defined in (A7).
By considering Lemma 2, (7) and (13), the time derivative of Lyapunov function (A3) can be deduced as:
where .
By considering (14), (A4) can be deduced as:
in which
where stands for taking the absolute value of each element in the vector or matrix. and are constant vectors. .
According to Lemma 1, can be approximated by an interval Type-II fuzzy logic system:
where . . is an arbitrary small bounded parameter and the boundary is defined as: . .
Then, by considering AM–GM inequality, matrix transformation and (A7), (A5) can be written as:
where and .
According to (A10), it is clear that can converge to a neighborhood of zero if there is no actuator fault.
The proof is completed. □
Appendix C
Proof.
Step 1: Consider a candidate Lyapunov function:
Step 2: Consider a candidate Lyapunov function:
where . , in which is defined in (A18).
By considering Lemma 2, (6) and (17), the time derivative of Lyapunov function (A14) can be deduced as:
where .
By considering (18), (A15) can be deduced as:
in which
where stands for taking the absolute value of each element in the vector or matrix. and are the constant vectors. .
According to Lemma 1, can be approximated by an interval Type-2 fuzzy logic system:
where . . is an arbitrary small bounded parameter and the boundary is defined as: . .
Then, by considering AM–GM inequality, matrix transformation and (A18), (A16) can be written as:
where and .
According to (A21), it is clear that can converge to a neighborhood of zero if there is no actuator fault.
The proof is completed. □
References
- Wang, X.; Park, J.H.; Yang, H. An improved protocol to consensus of delayed MASs with UNMS and aperiodic DoS cyber-attacks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2506–2516. [Google Scholar] [CrossRef]
- Jiang, Y.; Niu, B.; Wang, X.; Zhao, X.; Wang, H.; Yan, B. Distributed finite-time consensus tracking control for nonlinear multi-agent systems with FDI attacks and application to single-link robots. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 1505–1509. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, T.; Dian, S. Dynamic output feedback control for nonlinear networked control systems with a two-terminal event-triggered mechanism. Nonlinear Dyn. 2020, 100, 2537–2555. [Google Scholar] [CrossRef]
- Zhao, T.; Li, H.; Dian, S. Multi-robot path planning based on improved artificial potential field and fuzzy inference system. J. Intell. Fuzzy Syst. 2020, 39, 7621–7637. [Google Scholar] [CrossRef]
- Chen, W.D.; Li, Y.X.; Liu, L.; Zhao, X.D.; Niu, B.; Han, L.M. Nussbaum-Based Adaptive Fault-Tolerant Control for Nonlinear CPSs With Deception Attacks: A New Coordinate Transformation Technology. IEEE Trans. Cybern. 2022. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ma, J.; Zhao, X.; Niu, B.; Chen, M.; Wang, W. Adaptive Fuzzy Fixed-Time Control for High-Order Nonlinear Systems With Sensor and Actuator Faults. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Amin, A.A.; Hasan, K.M. A review of fault tolerant control systems: Advancements and applications. Measurement 2019, 143, 58–68. [Google Scholar] [CrossRef]
- Wang, X.; Niu, B.; Song, X.; Zhao, P.; Wang, Z. Neural networks-based adaptive practical preassigned finite-time fault tolerant control for nonlinear time-varying delay systems with full state constraints. Int. J. Robust Nonlinear Control 2021, 31, 1497–1513. [Google Scholar] [CrossRef]
- Li, Q.; Wu, Q.; Tu, H.; Zhang, J.; Zou, X.; Huang, S. Ground Risk Assessment for Unmanned Aircraft Focusing on Multiple Risk Sources in Urban Environments. Processes 2023, 11, 542. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Active fault-tolerant control system against partial actuator failures. IEE Proc. Control Theory Appl. 2002, 149, 95–104. [Google Scholar] [CrossRef]
- Maki, M.; Jiang, J.; Hagino, K. A stability guaranteed active fault-tolerant control system against actuator failures. Int. J. Robust Nonlinear Control IFAC Affil. J. 2004, 14, 1061–1077. [Google Scholar] [CrossRef]
- Merheb, A.R.; Noura, H.; Bateman, F. Active fault tolerant control of quadrotor uav using sliding mode control. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 156–166. [Google Scholar]
- Hosseinnajad, A.; Loueipour, M. Design of finite-time active fault tolerant control system with real-time fault estimation for a remotely operated vehicle. Ocean Eng. 2021, 241, 110063. [Google Scholar] [CrossRef]
- Li, J.; Xiang, X.; Dong, D.; Yang, S. Prescribed time observer based trajectory tracking control of autonomous underwater vehicle with tracking error constraints. Ocean Eng. 2023, 274, 114018. [Google Scholar] [CrossRef]
- Zhang, J.; Niu, B.; Wang, D.; Wang, H.; Zhao, P.; Zong, G. Time-/event-triggered adaptive neural asymptotic tracking control for nonlinear systems with full-state constraints and application to a single-link robot. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6690–6700. [Google Scholar] [CrossRef]
- Tang, H.; Gao, S.; Wang, L.; Li, X.; Li, B.; Pang, S. A novel intelligent fault diagnosis method for rolling bearings based on Wasserstein generative adversarial network and Convolutional Neural Network under Unbalanced Dataset. Sensors 2021, 21, 6754. [Google Scholar] [CrossRef]
- Xiao, L.; Bajric, R.; Zhao, J.; Tang, J.; Zhang, X. An adaptive vibrational resonance method based on cascaded varying stable-state nonlinear systems and its application in rotating machine fault detection. Nonlinear Dyn. 2021, 103, 715–739. [Google Scholar] [CrossRef]
- Bzioui, S.; Channa, R. Estimation and fault diagnosis for non-linear system with time-varying faults and measurement noises: Application on two CSTRs in series. Can. J. Chem. Eng. 2023, 101, 1919–1930. [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, F.; Liu, J.; Wang, R. Distributed soft fault detection for interval type-2 fuzzy-model-based stochastic systems with wireless sensor networks. IEEE Trans. Ind. Inform. 2018, 15, 334–347. [Google Scholar] [CrossRef]
- Hebda-Sobkowicz, J.; Zimroz, R.; Pitera, M.; Wyłomańska, A. Informative frequency band selection in the presence of non-Gaussian noise—A novel approach based on the conditional variance statistic with application to bearing fault diagnosis. Mech. Syst. Signal Process. 2020, 145, 106971. [Google Scholar] [CrossRef]
- Zhang, G.; Shu, Y.; Zhang, T. Piecewise unsaturated multi-stable stochastic resonance under trichotomous noise and its application in bearing fault diagnosis. Results Phys. 2021, 30, 104907. [Google Scholar] [CrossRef]
- Stojanovic, V.; Prsic, D. Robust identification for fault detection in the presence of non-Gaussian noises: Application to hydraulic servo drives. Nonlinear Dyn. 2020, 100, 2299–2313. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y.; Zhang, T.; Mdsohel, R. Stochastic resonance in an asymmetric bistable system driven by multiplicative and additive Gaussian noise and its application in bearing fault detection. Chin. J. Phys. 2018, 56, 1173–1186. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, X.; Chen, B.; Chen, H.; Deng, W. Bearing fault diagnosis using transfer learning and optimized deep belief network. Meas. Sci. Technol. 2022, 33, 065009. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, P.; Zhang, R.; Yao, R.; Deng, W. A novel performance trend prediction approach using ENBLS with GWO. Meas. Sci. Technol. 2022, 34, 025018. [Google Scholar] [CrossRef]
- Andjelkovic, I.; Sweetingham, K.; Campbell, S.L. Active fault detection in nonlinear systems using auxiliary signals. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2142–2147. [Google Scholar]
- Ashari, A.E.; Nikoukhah, R.; Campbell, S.L. Effects of feedback on active fault detection. Automatica 2012, 48, 866–872. [Google Scholar] [CrossRef]
- Punčochář, I.; Širokỳ, J.; Šimandl, M. Constrained active fault detection and control. IEEE Trans. Autom. Control 2014, 60, 253–258. [Google Scholar] [CrossRef]
- Jia, F.; Cao, F.; Lyu, G.; He, X. A novel framework of cooperative design: Bringing active fault diagnosis into fault-tolerant control. IEEE Trans. Cybern. 2022, 53, 3301–3310. [Google Scholar] [CrossRef]
- Jiang, Y.; Niu, B.; Wang, X.; Wang, H.; Chen, W. Dynamic-estimator-based adaptive secure containment control for constrained nonlinear multi-agent systems under denial-of-service attacks. Int. J. Robust Nonlinear Control 2023, 33, 605–622. [Google Scholar] [CrossRef]
- Zhao, T.; Dian, S. State feedback control for interval type-2 fuzzy systems with time-varying delay and unreliable communication links. IEEE Trans. Fuzzy Syst. 2017, 26, 951–966. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; She, K.; Zhong, S.; Shi, L. Stabilization of chaotic systems with T–S fuzzy model and nonuniform sampling: A switched fuzzy control approach. IEEE Trans. Fuzzy Syst. 2018, 27, 1263–1271. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, T.; Dian, S. Interval type-2 fuzzy neural network-based adaptive compensation control for omni-directional mobile robot. Neural Comput. Appl. 2023, 1–15. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, T.; Liu, N. Fractional-Order Active Disturbance Rejection Control with Fuzzy Self-Tuning for Precision Stabilized Platform. Entropy 2022, 24, 1681. [Google Scholar] [CrossRef] [PubMed]
- Xiu, Z.; Wang, Y.; Cheng, Z. Stability analysis and design of Type-II fuzzy controllers. In Proceedings of the 2008 Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008; pp. 2054–2059. [Google Scholar]
- Mohagheghi, S.; Venayagamoorthy, G.K.; Harley, R.G. An interval Type-II robust fuzzy logic controller for a static compensator in a multimachine power system. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 2241–2248. [Google Scholar]
- Tang, F.; Niu, B.; Wang, H.; Zhang, L.; Zhao, X. Adaptive fuzzy tracking control of switched MIMO nonlinear systems with full state constraints and unknown control directions. IEEE Trans. Circuits Syst. Express Briefs 2022, 69, 2912–2916. [Google Scholar] [CrossRef]
- Dian, S.; Hu, Y.; Zhao, T.; Han, J. Adaptive backstepping control for flexible-joint manipulator using interval type-2 fuzzy neural network approximator. Nonlinear Dyn. 2019, 97, 1567–1580. [Google Scholar] [CrossRef]
- Tong, W.; Zhao, T.; Duan, Q.; Zhang, H.; Mao, Y. Non-singleton interval type-2 fuzzy PID control for high precision electro-optical tracking system. ISA Trans. 2022, 120, 258–270. [Google Scholar] [CrossRef]
- Wang, J.; Hu, L.; Chen, F.; Wen, C. Multiple-step fault estimation for interval type-II TS fuzzy system of hypersonic vehicle with time-varying elevator faults. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417699149. [Google Scholar] [CrossRef]
- Patel, H.; Shah, V. Actuator and system component fault tolerant control using interval type-2 Takagi-Sugeno fuzzy controller for hybrid nonlinear process. Int. J. Hybrid Intell. Syst. 2019, 15, 143–153. [Google Scholar] [CrossRef]
- Yeh, C.C.; Demerdash, N.A. Fault-tolerant soft starter control of induction motors with reduced transient torque pulsations. IEEE Trans. Energy Convers. 2009, 24, 848–859. [Google Scholar]
- Yang, L.; Ozay, N. Fault-tolerant output-feedback path planning with temporal logic constraints. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 4032–4039. [Google Scholar]
- Li, Z.; Jamshidian, M.; Mousavi, S.; Karimipour, A.; Tlili, I. Develop a numerical approach of fuzzy logic type-2 to improve the reliability of a hydraulic automated guided vehicles. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 1396–1409. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Xu, Z.; Chen, R. Evaluating IoT platforms using integrated probabilistic linguistic MCDM method. IEEE Internet Things J. 2020, 7, 11195–11208. [Google Scholar] [CrossRef]
- Huang, C.; Lin, M.; Xu, Z. Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: Its application in multicriteria decision making process. Knowl. Inf. Syst. 2020, 62, 4373–4406. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Xu, Z. TOPSIS method based on correlation coefficient and entropy measure for linguistic Pythagorean fuzzy sets and its application to multiple attribute decision making. Complexity 2019, 2019, 6967390. [Google Scholar] [CrossRef]
- Lin, M.; Wang, H.; Xu, Z. TODIM-based multi-criteria decision-making method with hesitant fuzzy linguistic term sets. Artif. Intell. Rev. 2020, 53, 3647–3671. [Google Scholar] [CrossRef]
- Lin, M.; Li, X.; Chen, R.; Fujita, H.; Lin, J. Picture fuzzy interactional partitioned Heronian mean aggregation operators: An application to MADM process. Artif. Intell. Rev. 2022, 55, 1171–1208. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Chen, R.; Fujita, H.; Wang, X. Directional correlation coefficient measures for Pythagorean fuzzy sets: Their applications to medical diagnosis and cluster analysis. Complex Intell. Syst. 2021, 7, 1025–1043. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, L.; Wu, C.; Li, H.; Du, H. Adaptive fuzzy control for nonstrict-feedback systems with input saturation and output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1–12. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.; Cao, H. Evolutionary self-organizing fuzzy system using fuzzy-classification-based social learning particle swarm optimization. Inf. Sci. 2022, 606, 92–111. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Song, J.; Li, Z.; Lu, S. A Clinical-Oriented Non-Severe Depression Diagnosis Method Based on Cognitive Behavior of Emotional Conflict. IEEE Trans. Comput. Soc. Syst. 2022, 10, 131–141. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.; Cao, H.; Dian, S.; Xie, X. Multiobjective Optimization design of interpretable evolutionary fuzzy systems with type self-organizing learning of fuzzy sets. IEEE Trans. Fuzzy Syst. 2022, 31, 1638–1652. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Liu, Y.; Deng, W.; Deng, W. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2023, 619, 2–18. [Google Scholar] [CrossRef]
- Zhao, T.; Cao, H.; Dian, S. A self-organized method for a hierarchical fuzzy logic system based on a fuzzy autoencoder. IEEE Trans. Fuzzy Syst. 2022, 30, 5104–5115. [Google Scholar] [CrossRef]
- Zhao, T.; Tong, W.; Mao, Y. Hybrid Non-singleton Fuzzy Strong Tracking Kalman Filtering for High Precision Photoelectric Tracking System. IEEE Trans. Ind. Inform. 2023, 19, 2395–2408. [Google Scholar] [CrossRef]
- Rudin, K.; Ducard, G.J.; Siegwart, R.Y. Active fault-tolerant control with imperfect fault detection information: Applications to UAVs. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2792–2805. [Google Scholar] [CrossRef]
- Liberzon, D.; Morse, A.S. Basic problems in stability and design of switched systems. IEEE Control Syst. Mag. 1999, 19, 59–70. [Google Scholar]
- Liu, Y.; Yan, W.; Yu, C.; Zhang, T.; Tu, H. Predefined-Time Trajectory Planning for a Dual-Arm Free-Floating Space Robot. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 2798–2803. [Google Scholar]
- Yan, W.; Liu, Y.; Lan, Q.; Zhang, T.; Tu, H. Trajectory planning and low-chattering fixed-time nonsingular terminal sliding mode control for a dual-arm free-floating space robot. Robotica 2022, 40, 625–645. [Google Scholar] [CrossRef]
- Yao, J.; Yan, W.; Lan, Q.; Liu, Y.; Zhao, Y. Parameter Optimization of dsRNA Splicing Evolutionary Algorithm Based Fixed-Time Obstacle-Avoidance Trajectory Planning for Space Robot. Appl. Sci. 2021, 11, 8839. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, W.; Zhang, T.; Yu, C.; Tu, H. Trajectory tracking for a dual-arm free-floating space robot with a class of general nonsingular predefined-time terminal sliding mode. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3273–3286. [Google Scholar] [CrossRef]
- Yan, B.; Niu, B.; Zhao, X.; Wang, H.; Chen, W.; Liu, X. Neural-network-based adaptive event-triggered asymptotically consensus tracking control for nonlinear nonstrict-feedback MASs: An improved dynamic surface approach. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Van, M.; Sun, Y.; Mcllvanna, S.; Nguyen, M.N.; Khyam, M.O.; Ceglarek, D. Adaptive Fuzzy Fault Tolerant Control for Robot Manipulators with Fixed-Time Convergence. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Ouyang, H.; Lin, Y. Adaptive fault-tolerant control and performance recovery against actuator failures with deferred actuator replacement. IEEE Trans. Autom. Control 2020, 66, 3810–3817. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).