GPR Clutter Removal Based on Weighted Nuclear Norm Minimization for Nonparallel Cases
Abstract
:1. Introduction
2. Methodology
2.1. GPR Clutter Removal via Low-Rank and Sparse Decomposition
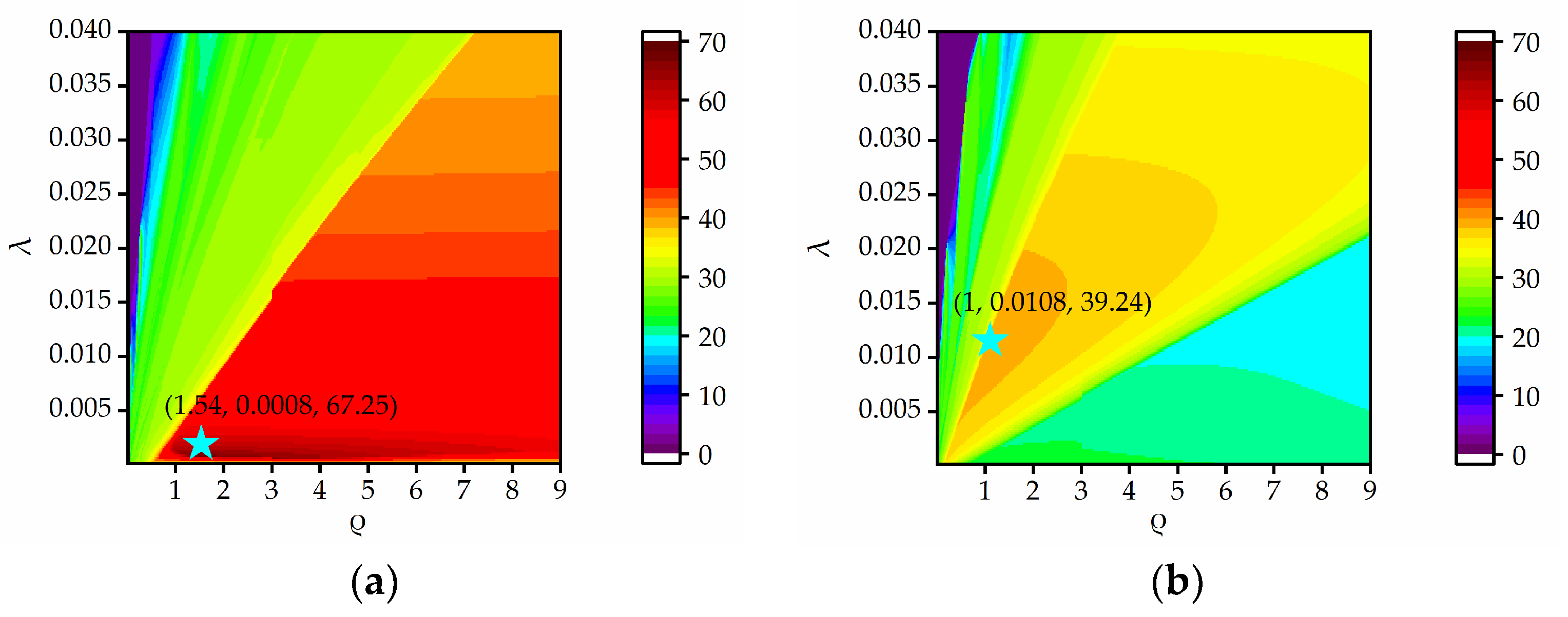
2.2. Proposed WNNM-Based Clutter Removal Method
| Algorithm 1: WNNM-based clutter removal method in GPR. |
| Input: X: Raw B-scan with size M × N; tmax: Maximum number of iterations; ε: Convergence error; λ: Regularization parameter; ρ: Weight parameter. Output: St (target response) and Lt (clutter response). Initialize Main iteration: 1. t = t + 1; 2. Calculate the singular value decomposition of X − St−1, ; 3. Calculate the singular diagonal weight matrix Wt−1 by Equation (6); 4. Fix S and update Lt by ; 5. Fix L and update St by ; Until convergence or t = tmax. |
3. Experimental Results
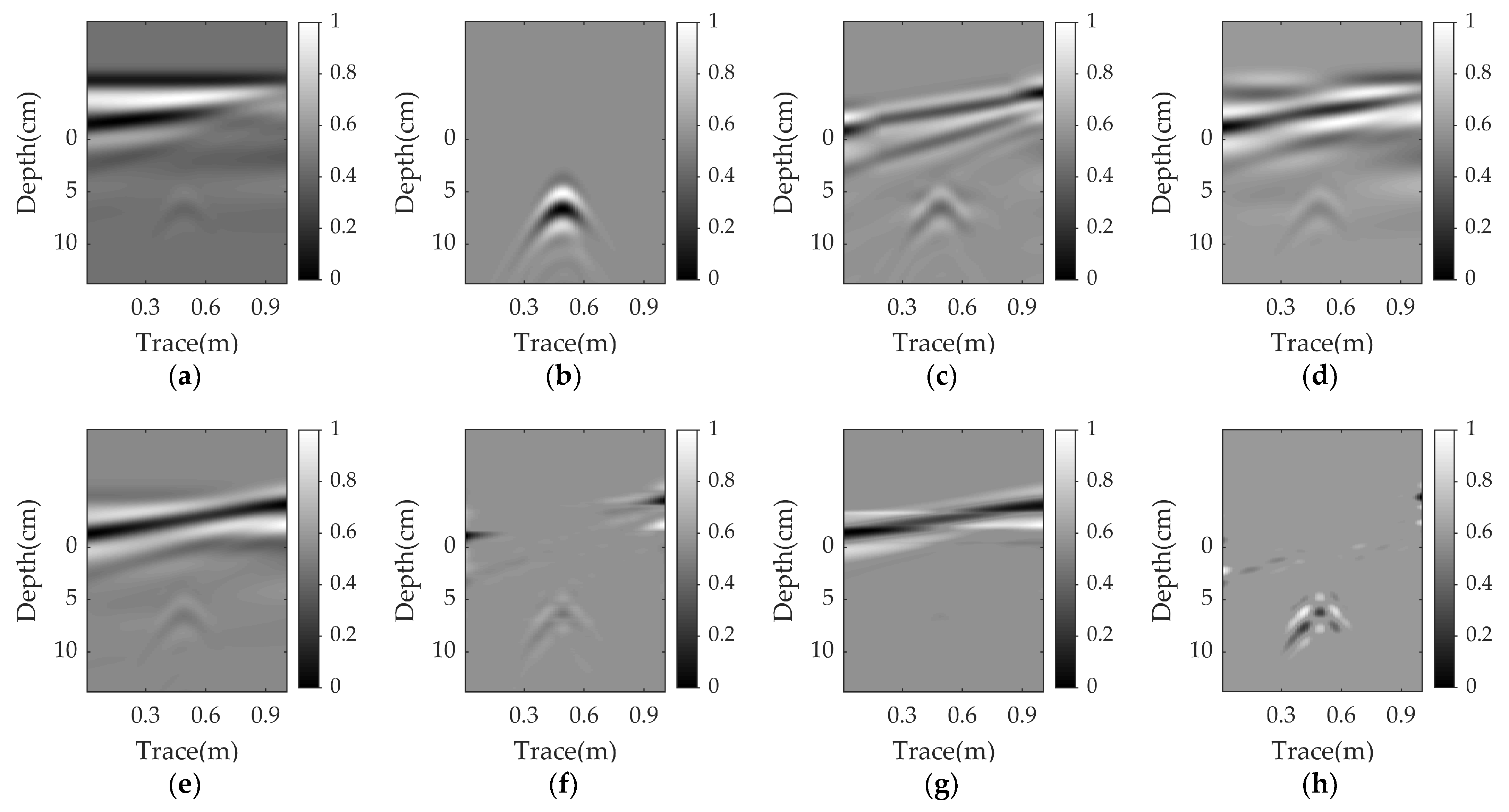
3.1. Simulation Data Results
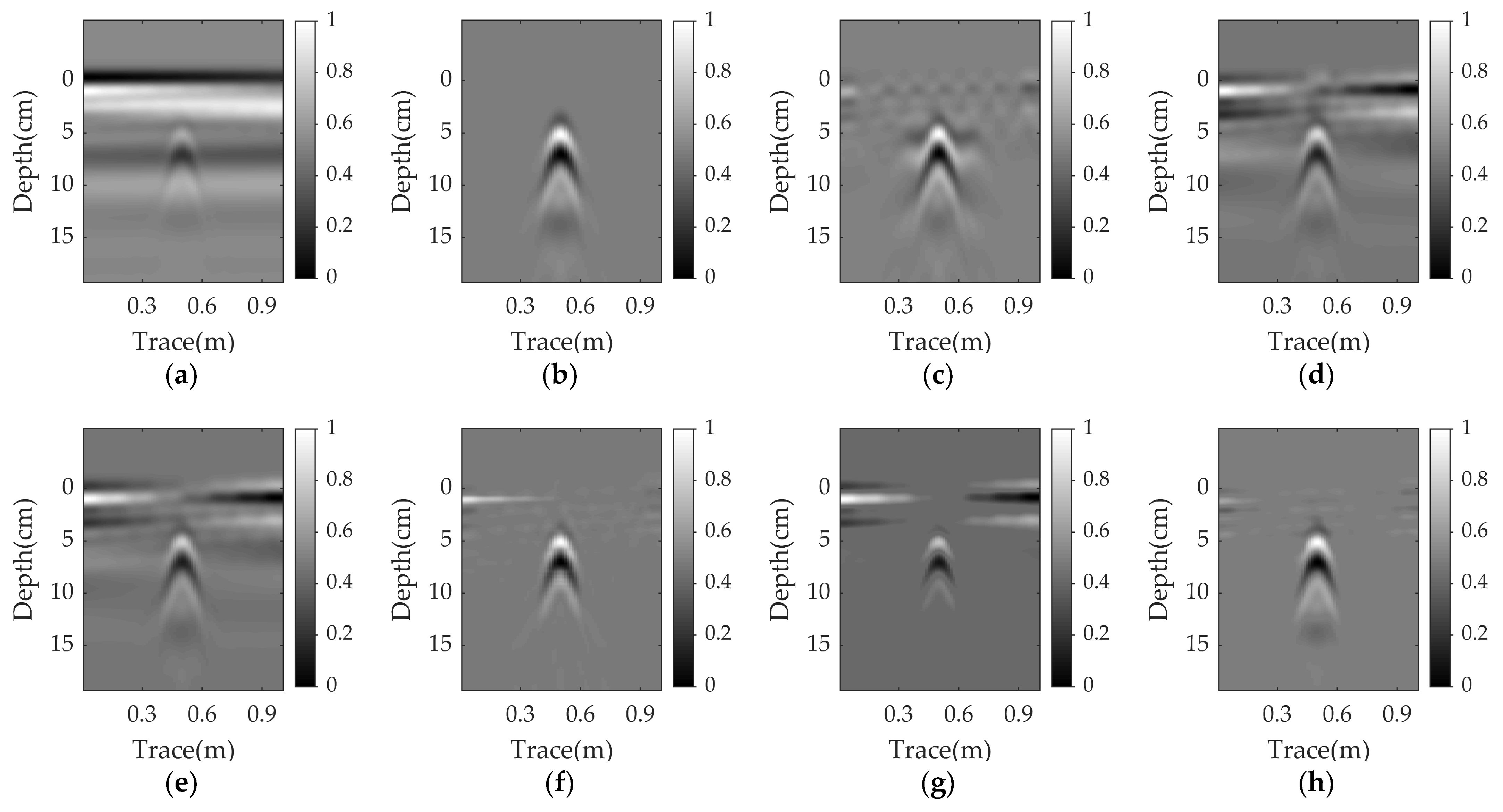
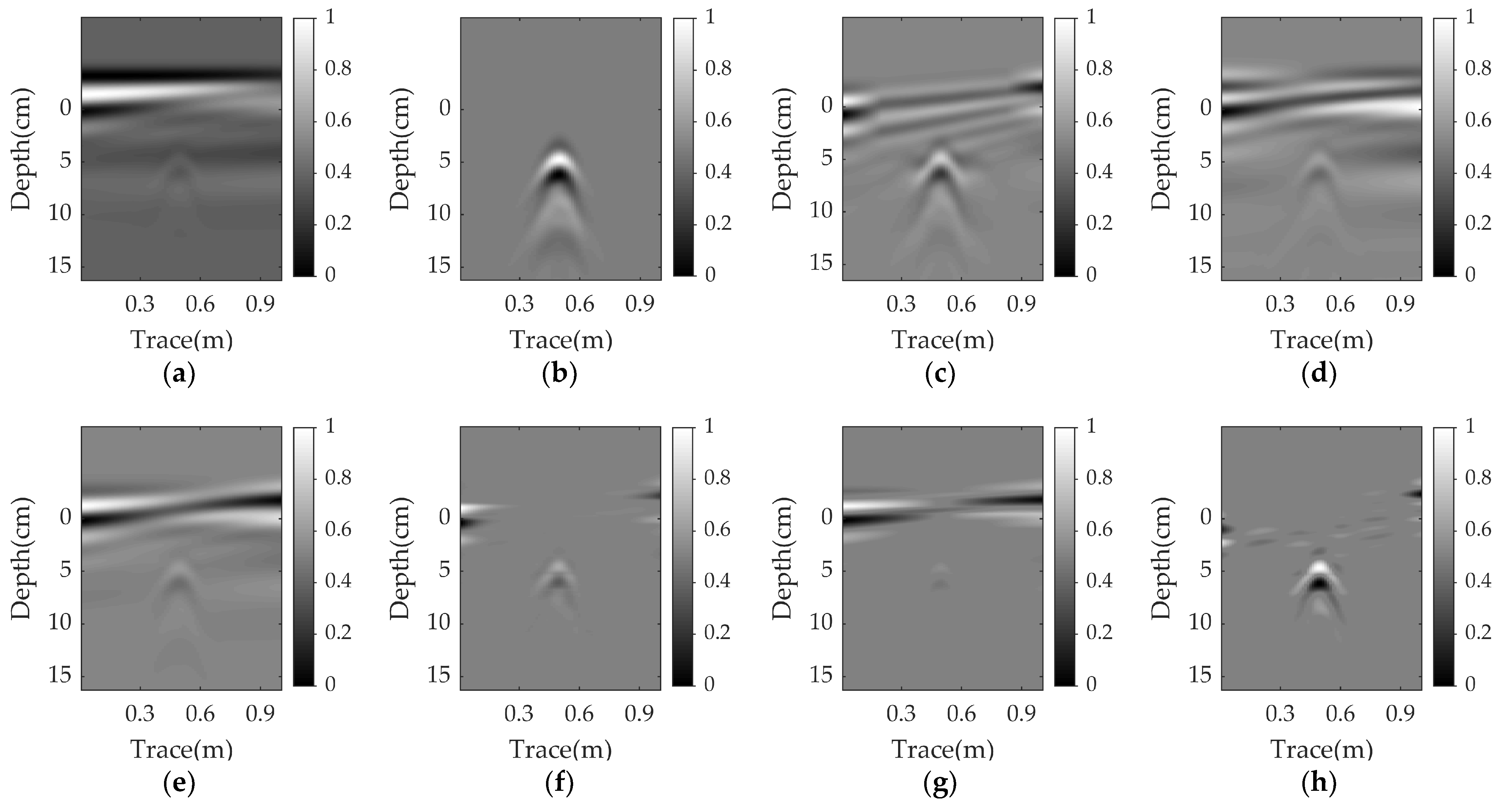
3.1.1. Clutter-Removal Results in the Nonparallel Case
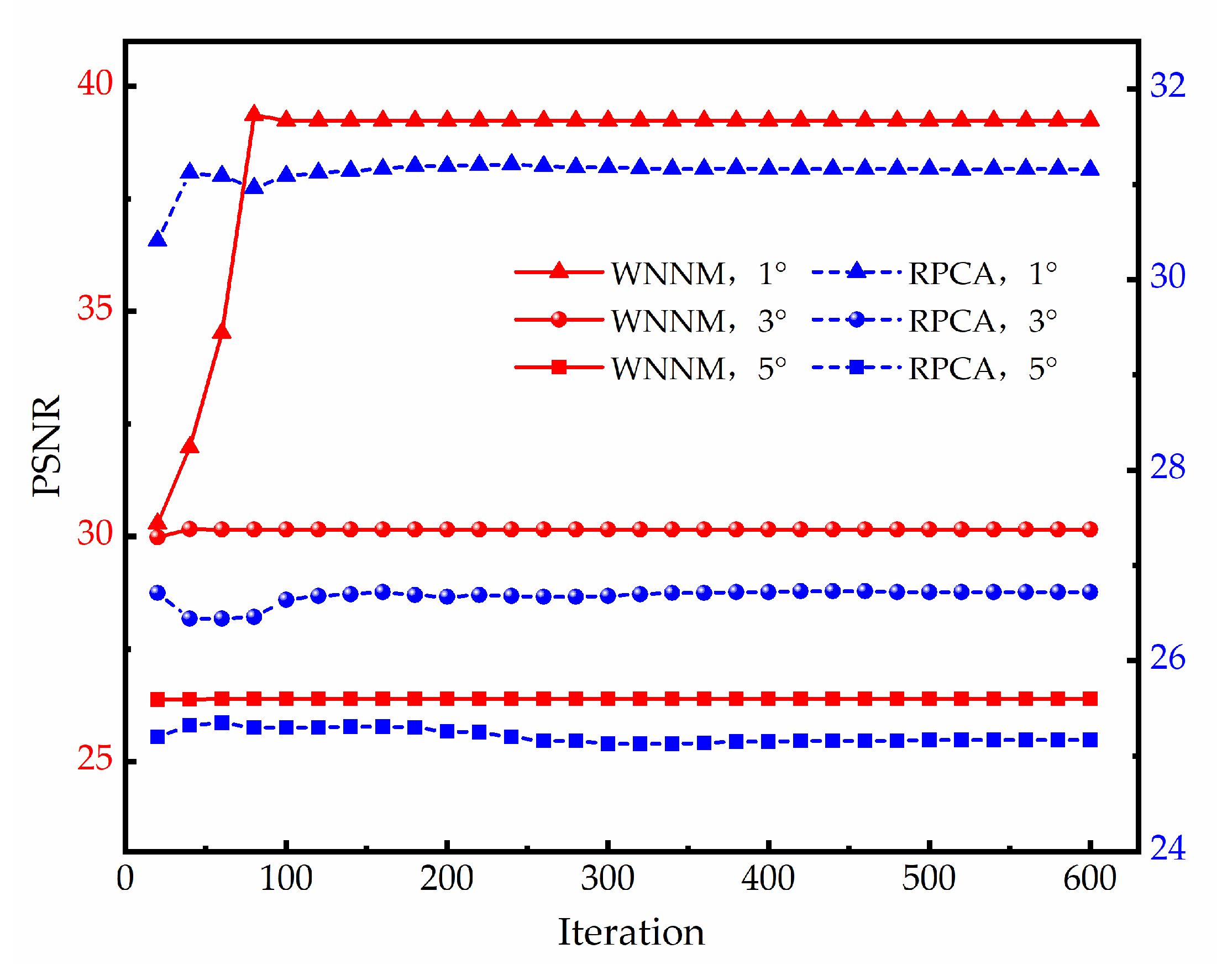
3.1.2. Running Time
3.2. Real Data Results
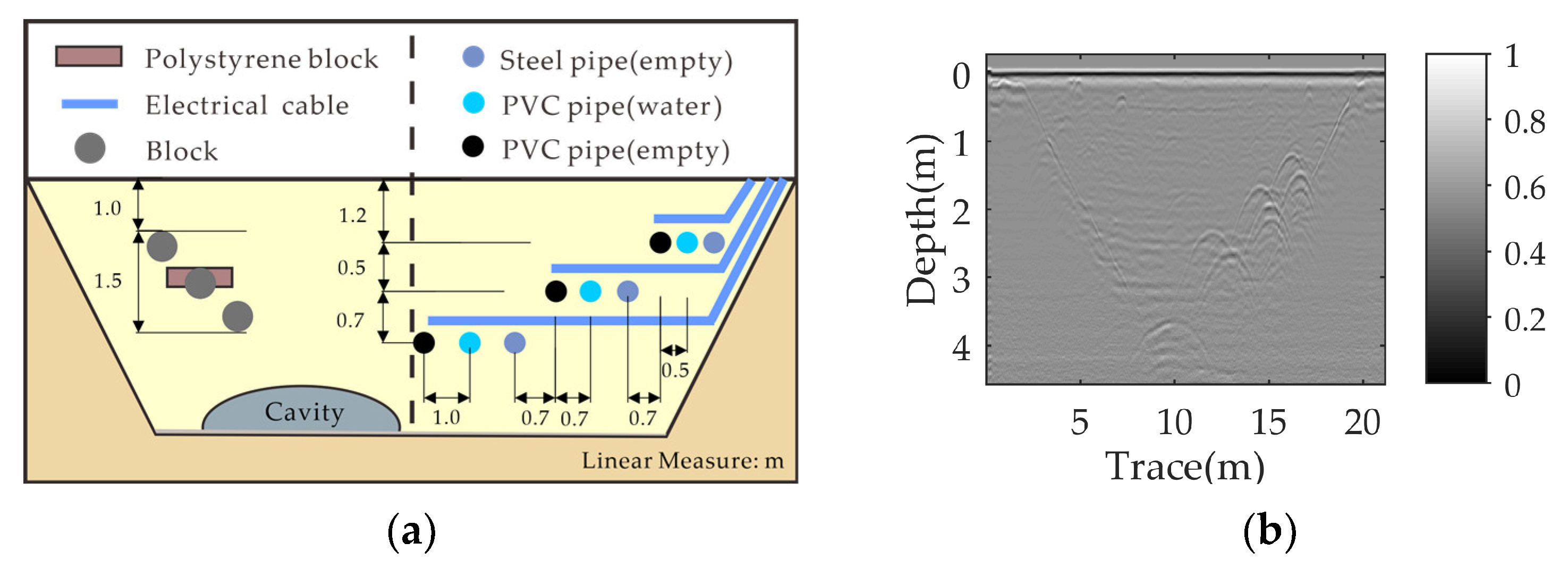
3.2.1. Real Data-I
3.2.2. Real Data-II
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Daniels, D.J. Ground Penetrating Radar; IET: London, UK, 2004. [Google Scholar]
- Lai, W.W.L.; Derobert, X.; Annan, P. A review of ground penetrating radar application in civil engineering: A 30-year journey from locating and testing to imaging and diagnosis. NDT E Int. 2018, 96, 58–78. [Google Scholar]
- Liu, H.; Zhong, J.Y.; Ding, F.; Meng, X.; Liu, C.; Cui, J. Detection of Early-stage Rebar Corrosion Using a Polarimetric Ground Penetrating Radar System. Constr. Build. Mater. 2022, 317, 125768. [Google Scholar] [CrossRef]
- Qin, H.; Tang, Y.; Wang, Z.; Xie, X.; Zhang, D. Shield tunnel grouting layer estimation using sliding window probabilistic inversion of GPR data. Tunn. Undergr. Space Technol. 2021, 112, 103913. [Google Scholar] [CrossRef]
- Liu, H.; Long, Z.J.; Han, F.; Fang, G.Y.; Liu, Q.H. Frequency-domain reverse-time migration of ground penetrating radar based on layered medium Green’s functions. IEEE J. Select. Topic Appl. Earth Observ. Rem. Sens. 2018, 11, 2957–2965. [Google Scholar] [CrossRef]
- Torrione, P.A.; Morton, K.D.; Sakaguchi, R.; Collins, L.M. Histograms of oriented gradients for landmine detection in ground-penetrating radar data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1539–1550. [Google Scholar] [CrossRef]
- Solimene, R.; Cuccaro, A.; Dell’Aversano, A.; Catapano, I.; Soldovieri, F. Ground clutter removal in GPR surveys. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 792–798. [Google Scholar] [CrossRef]
- Chen, J. Research on Signal Processing and Imaging of Ultra-Wideband Radar. Ph.D. Thesis, The Institute of Electronics, Chinese Academy of Sciences, Beijing, China, 2007; pp. 24–25. [Google Scholar]
- Chen, G.X.; Fu, L.Y.; Chen, K.F.; Boateng, C.D.; Ge, S.C. Adaptive ground clutter reduction in ground-penetrating radar data based on principal component analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3271–3282. [Google Scholar] [CrossRef]
- Abujarad, F.; Omar, A. GPR data processing using the component-separation methods PCA and ICA. In Proceedings of the IEEE International Workshop on Imagining Systems and Techniques (IST 2006), Minori, Italy, 28–29 April 2006. [Google Scholar]
- Abujarad, F.; Omar, A. Comparison of independent component analysis (ICA) algorithms for GPR detection of non-metallic land mines. In Proceedings of the Conference on Image and Signal Processing for Remote Sensing XII, Stockholm, Sweden, 13–14 September 2006. [Google Scholar]
- Abujarad, F.; Nadim, G.; Omar, A. Clutter reduction and detection of landmine objects in ground penetrating radar data using singular value decomposition (SVD). In Proceedings of the 3rd International Workshop on Advanced Ground Penetrating Radar, Delft, The Netherlands, 2–3 May 2005. [Google Scholar]
- Liu, C.; Song, C.; Lu, Q. Random noise de-noising and direct wave eliminating based on SVD method for ground penetrating radar signals. J. Appl. Geophys. 2017, 144, 125–133. [Google Scholar] [CrossRef]
- Su, Q.B.; Bi, B.Z.; Zhang, P.Y.; Shen, L.; Huang, X.T.; Xin, Q. GPR Image Clutter Suppression Using Gaussian Curvature Decomposition in the PCA Domain. Remote Sens. 2022, 14, 4879. [Google Scholar] [CrossRef]
- Temlioglu, E.; Erer, I. Clutter removal in ground-penetrating radar images using morphological component analysis. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1802–1806. [Google Scholar] [CrossRef]
- Ni, Z.K.; Pan, J.; Shi, C.; Ye, S.B.; Zhao, D.; Fang, G.Y. DL-based clutter removal in migrated GPR data for detection of buried target. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3507205. [Google Scholar] [CrossRef]
- Bao, Q.Z.; Li, Q.C.; Chen, W.C. GPR data noise attenuation on the curvelet transform. Appl. Geophys. 2014, 11, 301–310. [Google Scholar] [CrossRef]
- Terrasse, G.; Nicolas, J.M.; Trouvé, E.; Drouet, É. Application of the curvelet transform for clutter and noise removal in GPR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4280–4294. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I. The multiscale directional neighborhood filter and its application to clutter removal in GPR data. Signal Image Video Process. 2018, 12, 1237–1244. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I.; Kaplan, N.H. Low complexity clutter removal in GPR images via lattice filters. Digit. Signal Process. 2020, 101, 102724. [Google Scholar] [CrossRef]
- Candés, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2009, 58, 1–37. [Google Scholar] [CrossRef]
- Masarik, M.P.; Burns, J.; Thelen, B.T.; Kelly, J.; Havens, T.C. GPR anomaly detection with robust principal component analysis. In Proceedings of the Conference on Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XX, Baltimore, MD, USA, 20–23 April 2015. [Google Scholar]
- Zhang, Y.; Burns, D.; Orfeo, D.; Huston, D.R.; Xia, T. Rough ground surface clutter removal in air-coupled ground penetrating radar data using low-rank and sparse representation. In Proceedings of the Conference on Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure, Portland, OR, USA, 26–29 March 2017. [Google Scholar]
- Song, X.J.; Xiang, D.L.; Zhou, K.; Su, Y. Improving RPCA-based clutter suppression in GPR detection of antipersonnel mines. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1338–1342. [Google Scholar] [CrossRef]
- Song, X.J.; Xiang, D.L.; Zhou, K.; Su, Y. Fast prescreening for GPR Antipersonnel mine detection via go decomposition. IEEE Geosci. Remote Sens. Lett. 2019, 16, 15–19. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I. Clutter removal in GPR images using non-negative matrix factorization. J. Electromagn. Waves Appl. 2018, 32, 2055–2066. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I. Improved clutter removal in GPR by robust nonnegative matrix factorization. IEEE Geosci. Remote Sens. Lett. 2020, 17, 958–962. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I. Ground penetrating radar clutter removal via randomized low rank and sparse decomposition for missing data case. Int. J. Remote Sens. 2020, 41, 7680–7699. [Google Scholar] [CrossRef]
- Kumlu, D.; Erer, I. GPR clutter reduction by robust orthonormal subspace learning. IEEE Access 2020, 8, 74145–74156. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Z.Z.; Xu, H.; Wang, B.J.; Li, J.X. GPR Clutter Removal Based on Factor Group-Sparse Regularization. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3509305. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Liu, L.; Li, J.X.; Xu, H.; Wang, B.J. A novel 3D clutter removal for GPR pipe detection via tensor RPCA. In Proceedings of the 7th Asia Pacific Conference on Optics Manufacture (APCOM), Shanghai, China, 28–31 October 2021. [Google Scholar]
- Ni, Z.K.; Ye, S.B.; Shi, C.; Li, C.; Fang, G.Y. Clutter suppression in GPR B-scan images using robust autoencoder. IEEE Geosci. Remote Sens. Lett. 2020, 19, 3500705. [Google Scholar] [CrossRef]
- Temlioglu, E.; Erer, I. A Novel Convolutional Autoencoder-Based Clutter Removal Method for Buried Threat Detection in Ground-Penetrating Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5103313. [Google Scholar] [CrossRef]
- Zhou, H.L.; Wang, Y.; Liu, Q.G.; Wang, Y.H. RNMF-Guided Deep Network for Signal Separation of GPR without Labeled Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3507705. [Google Scholar] [CrossRef]
- Ni, Z.K.; Shi, C.; Pan, J.; Zheng, Z.J.; Ye, S.B.; Fang, G.Y. Declutter-GAN: GPR B-Scan Data Clutter Removal Using Conditional Generative Adversarial Nets. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023105. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Qin, H.; Tang, Y.; Zhang, D.H.; Yang, D.H.; Qu, C.X.; Geng, T.S. RCE-GAN: A rebar clutter elimination network to improve tunnel lining void detection from GPR images. Remote Sens. 2022, 14, 251. [Google Scholar] [CrossRef]
- Sun, H.H.; Cheng, W.X.; Fan, Z. Learning to remove clutter in real-world GPR images using hybrid data. IEEE Trans. on Geosci. Remote Sens. 2022, 60, 5113714. [Google Scholar] [CrossRef]
- Gu, S.H.; Zhang, L.; Zuo, W.M.; Feng, X.C. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Vaswani, N.; Bouwmans, T.; Javed, S.; Narayanamurthy, P. Robust subspace learning: Robust PCA, robust subspace tracking, and robust subspace recovery. IEEE Signal Process. Mag. 2018, 35, 32–55. [Google Scholar] [CrossRef]
- Gao, W.B.; Goldfarb, D.; Curtis, F.E. ADMM for multiaffine constrained optimization. Optim. Method Softw. 2018, 35, 257–303. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Giannakis, I.; Giannopoulos, A.; Warren, C. A realistic FDTD numerical modeling framework of ground penetrating radar for landmine detection. IEEE J. Sel. Topics Appl. Earth Observ. 2016, 9, 37–51. [Google Scholar] [CrossRef]
- Giannakis, I.; Giannopoulos, A.; Warren, C. Realistic FDTD GPR antenna models optimised using a novel linear/non-linear Full Waveform Inversion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1768–1778. [Google Scholar] [CrossRef]
- Dérobert, X.; Pajewski, L. TU1208 open database of radargrams: The dataset of the IFSTTAR geophysical test site. Remote Sens. 2018, 10, 530. [Google Scholar] [CrossRef]
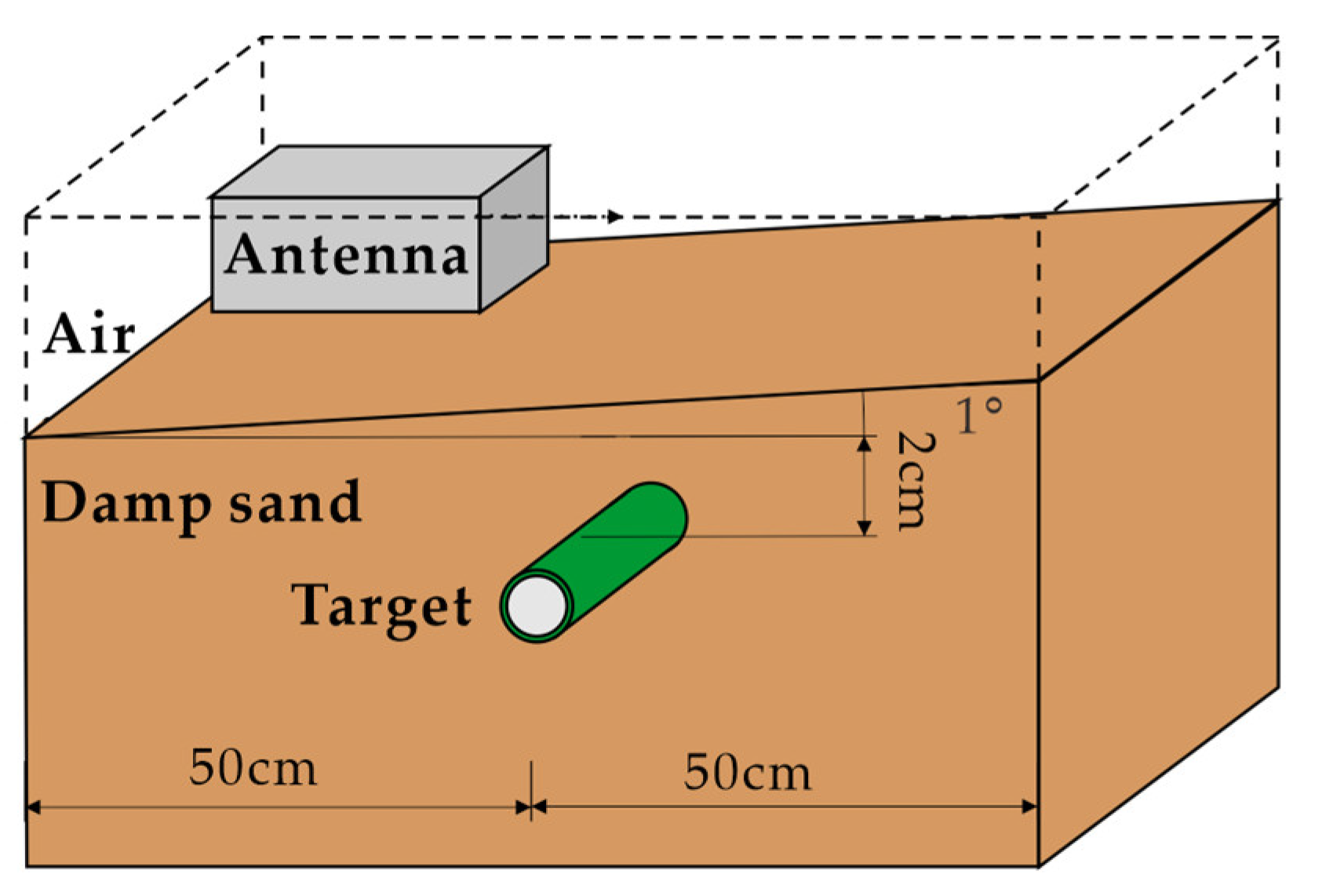

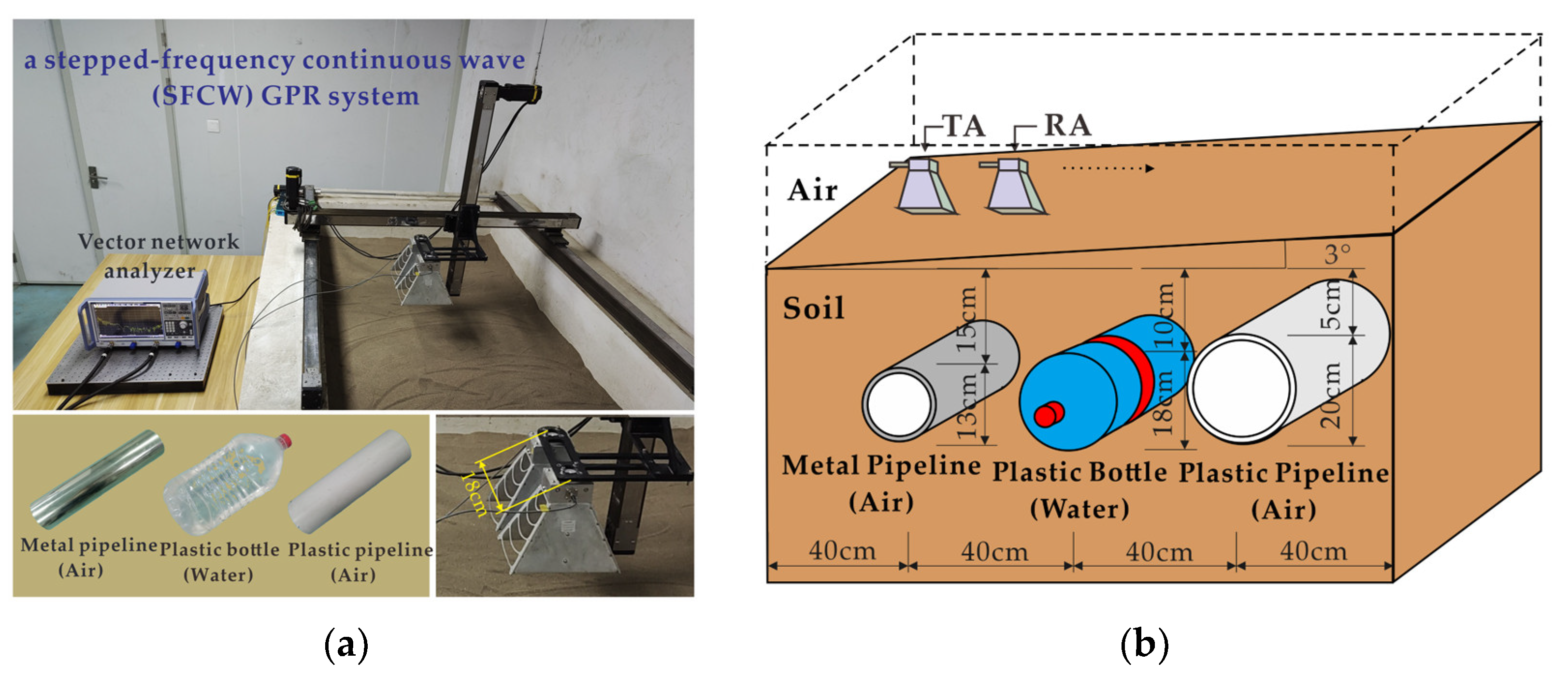



| Material | Dielectric Constant (F/m) | Conductivity (S/m) |
|---|---|---|
| Damp sand | 8.0 | 0.01 |
| Dry sand | 3.0 | 0.001 |
| Wet sand | 20.0 | 0.1 |
| Dry clay soil | 10.0 | 0.01 |
| Wet clay soil | 12.0 | 0.01 |
| Dry loam soil | 10.0 | 0.001 |
| Aluminum | 3.1 | 2.3 × 107 |
| Plastic | 3.0 | 0.01 |
| EMA | PCA | NMF | RPCA | RNMF | WNNM | |
|---|---|---|---|---|---|---|
| Aluminum target | ||||||
| 0° | 31.43 | 36.99 | 36.41 | 43.21 | 62.47 | 63.21 |
| 1° | 29.53 | 24.87 | 23.40 | 30.46 | 25.57 | 38.25 |
| 2° | 25.21 | 16.31 | 13.64 | 25.76 | 12.78 | 26.96 |
| 3° | 24.92 | 16.48 | 15.90 | 28.26 | 15.55 | 33.06 |
| 4° | 22.98 | 19.95 | 20.00 | 28.57 | 21.48 | 31.91 |
| 5° | 21.59 | 17.94 | 19.14 | 24.87 | 19.92 | 30.85 |
| Plastic target | ||||||
| 0° | 32.03 | 34.55 | 36.56 | 38.78 | 60.68 | 67.25 |
| 1° | 30.84 | 22.29 | 22.54 | 31.16 | 20.70 | 39.24 |
| 2° | 25.63 | 17.83 | 22.20 | 26.73 | 23.32 | 35.17 |
| 3° | 23.77 | 20.41 | 20.88 | 26.72 | 22.52 | 30.15 |
| 4° | 23.13 | 19.73 | 19.54 | 22.95 | 20.35 | 28.54 |
| 5° | 22.09 | 18.41 | 18.64 | 25.17 | 20.14 | 26.39 |
| EMA | PCA | NMF | RPCA | RNMF | WNNM | |
|---|---|---|---|---|---|---|
| Aluminum target | ||||||
| Damp sand | 29.53 | 24.87 | 23.40 | 30.46 | 25.57 | 38.25 |
| Dry sand | 31.29 | 28.17 | 30.00 | 38.24 | 32.24 | 41.13 |
| Wet sand | 29.01 | 12.89 | 13.12 | 17.03 | 11.26 | 32.87 |
| Dry clay soil | 29.22 | 20.64 | 19.80 | 27.53 | 19.71 | 38.79 |
| Wet clay soil | 29.16 | 17.48 | 17.49 | 27.51 | 17.20 | 38.54 |
| Dry loam soil | 29.14 | 21.09 | 20.35 | 27.49 | 20.30 | 38.64 |
| Plastic target | ||||||
| Damp sand | 30.84 | 22.29 | 22.54 | 31.16 | 20.70 | 39.24 |
| Dry sand | 30.03 | 22.57 | 22.57 | 33.00 | 22.04 | 40.23 |
| Wet sand | 27.57 | 22.72 | 22.94 | 21.26 | 22.01 | 32.18 |
| Dry clay soil | 30.35 | 22.44 | 22.59 | 31.23 | 20.39 | 35.47 |
| Wet clay soil | 30.40 | 22.70 | 22.73 | 30.17 | 20.66 | 37.29 |
| Dry loam soil | 30.45 | 22.41 | 22.56 | 31.43 | 20.34 | 36.17 |
| EMA | PCA | NMF | RPCA | RNMF | WNNM | |
|---|---|---|---|---|---|---|
| Aluminum target | ||||||
| 2 cm | 29.53 | 24.87 | 23.40 | 30.46 | 25.57 | 38.25 |
| 3 cm | 29.95 | 24.34 | 25.26 | 30.15 | 26.32 | 41.16 |
| 4 cm | 30.22 | 23.25 | 25.24 | 33.89 | 26.53 | 41.70 |
| 5 cm | 30.07 | 25.23 | 24.33 | 32.07 | 25.77 | 42.18 |
| 6 cm | 29.85 | 24.43 | 23.19 | 31.20 | 24.61 | 42.17 |
| Plastic target | ||||||
| 2 cm | 30.84 | 22.29 | 22.54 | 31.16 | 20.70 | 39.24 |
| 3 cm | 30.40 | 22.56 | 22.46 | 31.10 | 20.92 | 38.05 |
| 4 cm | 29.82 | 22.45 | 22.26 | 28.26 | 20.87 | 38.68 |
| 5 cm | 29.51 | 22.15 | 22.08 | 28.19 | 20.66 | 38.27 |
| 6 cm | 29.18 | 21.82 | 21.84 | 29.12 | 20.34 | 37.60 |
| EMA | PCA | NMF | RPCA | RNMF | WNNM | |
|---|---|---|---|---|---|---|
| 1° | 0.03 | 0.04 | 0.25 | 12.65 | 0.71 | 2.31 |
| 3° | 0.03 | 0.04 | 0.26 | 12.13 | 0.70 | 2.23 |
| 5° | 0.03 | 0.04 | 0.29 | 13.24 | 0.64 | 2.58 |
| EMA | PCA | NMF | RPCA | RNMF | WNNM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IF (dB) | RT (S) | IF (dB) | RT (S) | IF (dB) | RT (S) | IF (dB) | RT (S) | IF (dB) | RT (S) | IF (dB) | RT (S) | ||
| Data Ⅰ | 3° | 12.57 | 0.01 | 6.91 | 0.01 | 7.28 | 0.01 | 16.61 | 0.90 | 12.36 | 0.03 | 17.44 | 0.19 |
| 5° | 7.62 | 0.01 | 3.85 | 0.02 | 3.89 | 0.01 | 9.11 | 0.91 | 4.47 | 0.02 | 15.53 | 0.20 | |
| Data Ⅱ | 0° | 6.52 | 0.02 | 6.47 | 0.12 | 6.40 | 3.21 | 7.64 | 65.91 | 8.69 | 18.84 | 9.53 | 16.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Song, C.; Wu, Z.; Xu, H.; Li, J.; Wang, B.; Li, J. GPR Clutter Removal Based on Weighted Nuclear Norm Minimization for Nonparallel Cases. Sensors 2023, 23, 5078. https://doi.org/10.3390/s23115078
Liu L, Song C, Wu Z, Xu H, Li J, Wang B, Li J. GPR Clutter Removal Based on Weighted Nuclear Norm Minimization for Nonparallel Cases. Sensors. 2023; 23(11):5078. https://doi.org/10.3390/s23115078
Chicago/Turabian StyleLiu, Li, Chenyan Song, Zezhou Wu, Hang Xu, Jingxia Li, Bingjie Wang, and Jiasu Li. 2023. "GPR Clutter Removal Based on Weighted Nuclear Norm Minimization for Nonparallel Cases" Sensors 23, no. 11: 5078. https://doi.org/10.3390/s23115078
APA StyleLiu, L., Song, C., Wu, Z., Xu, H., Li, J., Wang, B., & Li, J. (2023). GPR Clutter Removal Based on Weighted Nuclear Norm Minimization for Nonparallel Cases. Sensors, 23(11), 5078. https://doi.org/10.3390/s23115078






