MVDR-LSTM Distance Estimation Model Based on Diagonal Double Rectangular Array
Abstract
:1. Introduction
2. Theory
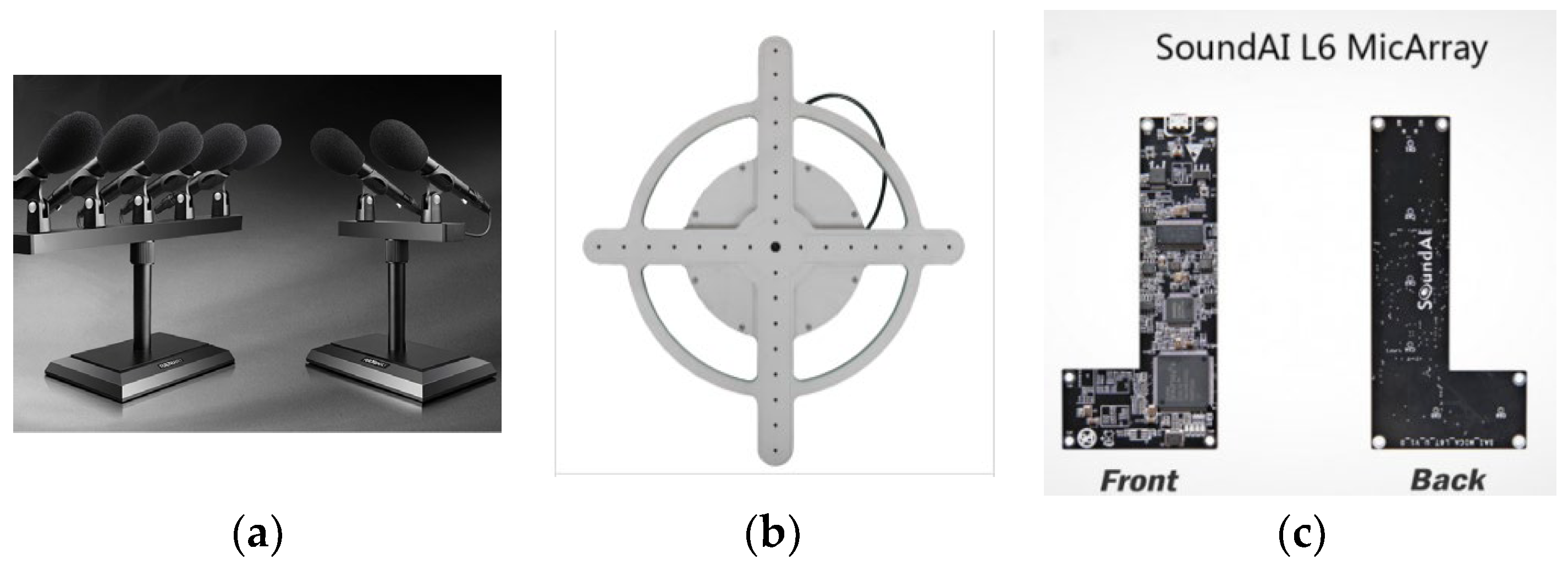
2.1. Microphone Array
2.2. MVDR
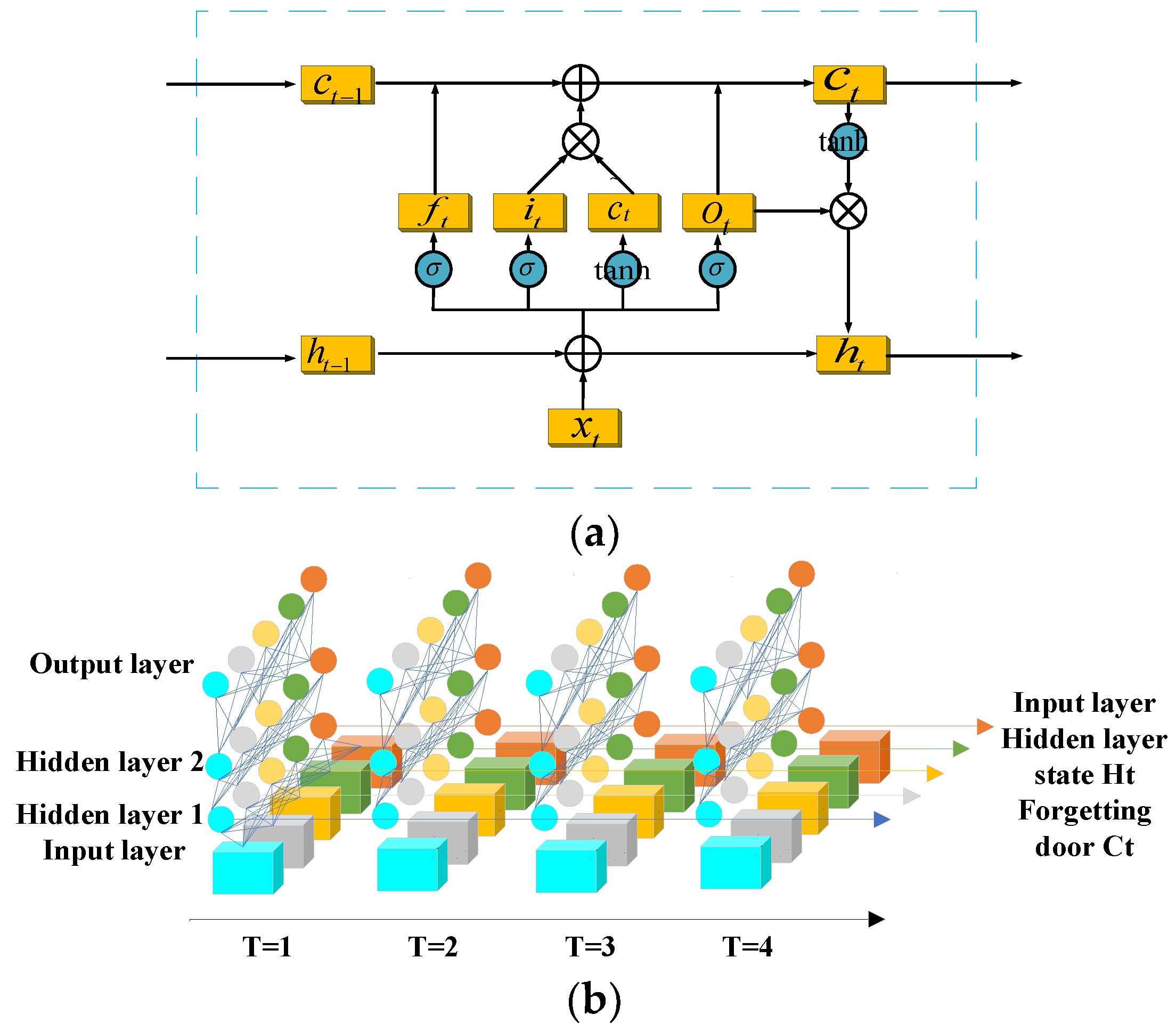
2.3. LSTM
3. Simulation
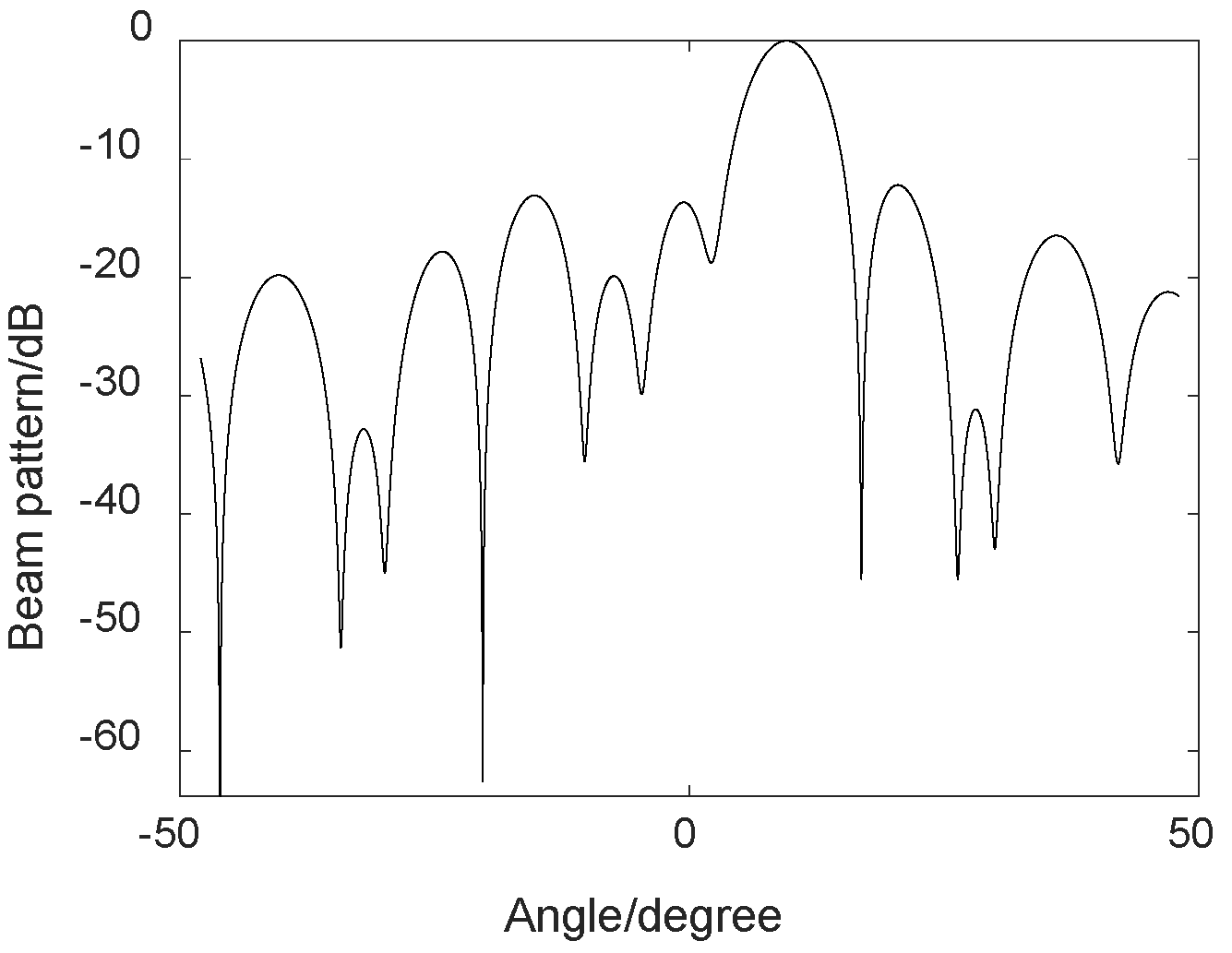
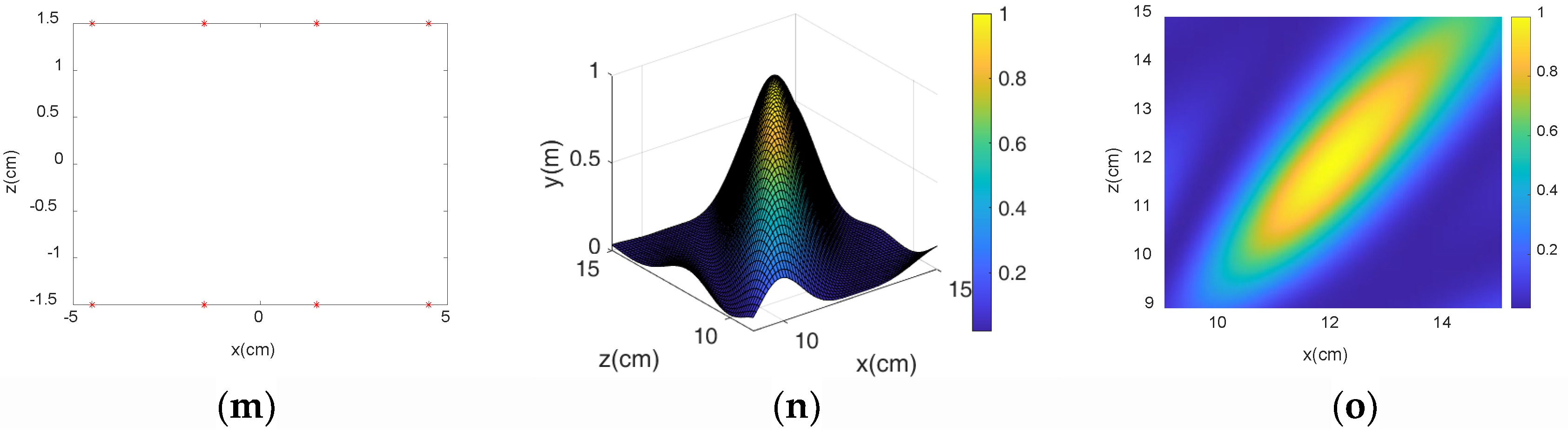
3.1. MVDR Algorithm Simulation
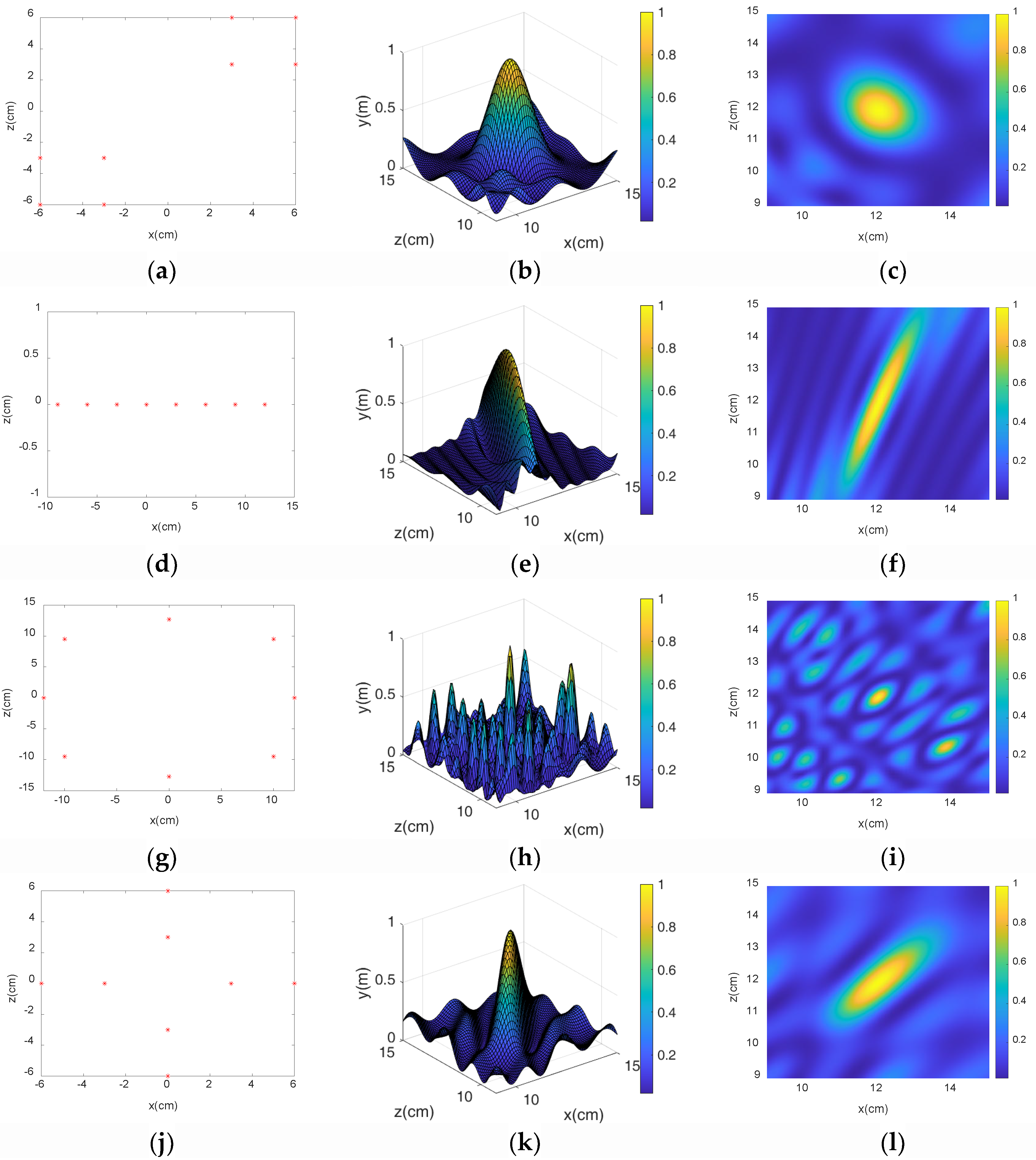
3.2. Microphone Array Formation Selection
4. Experiments
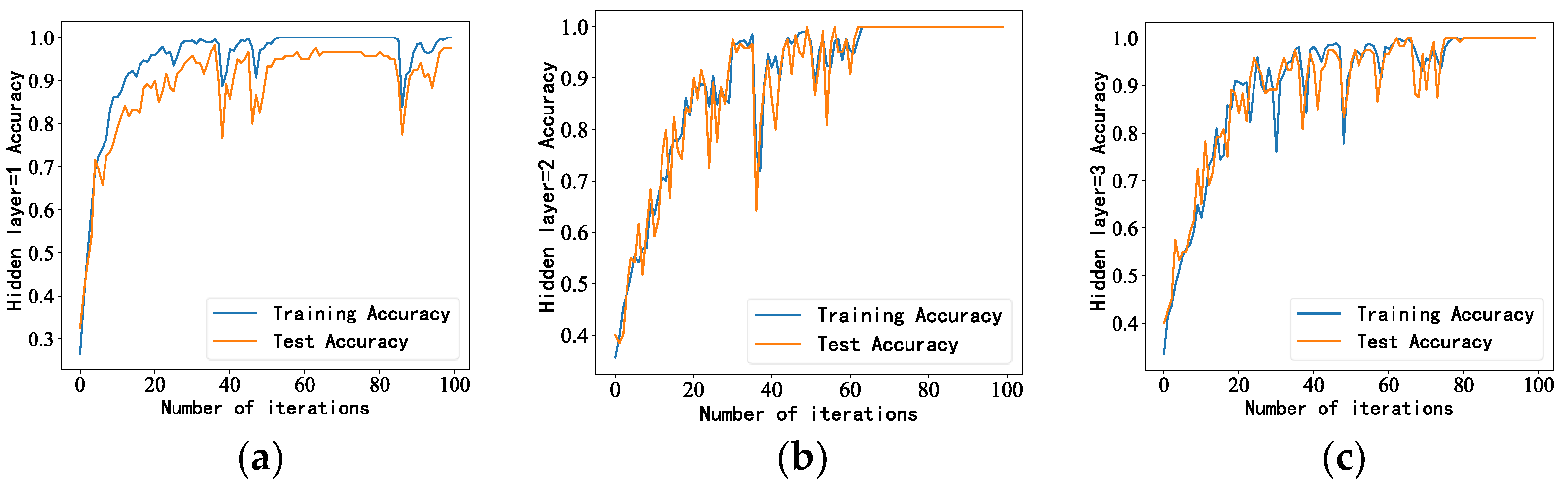
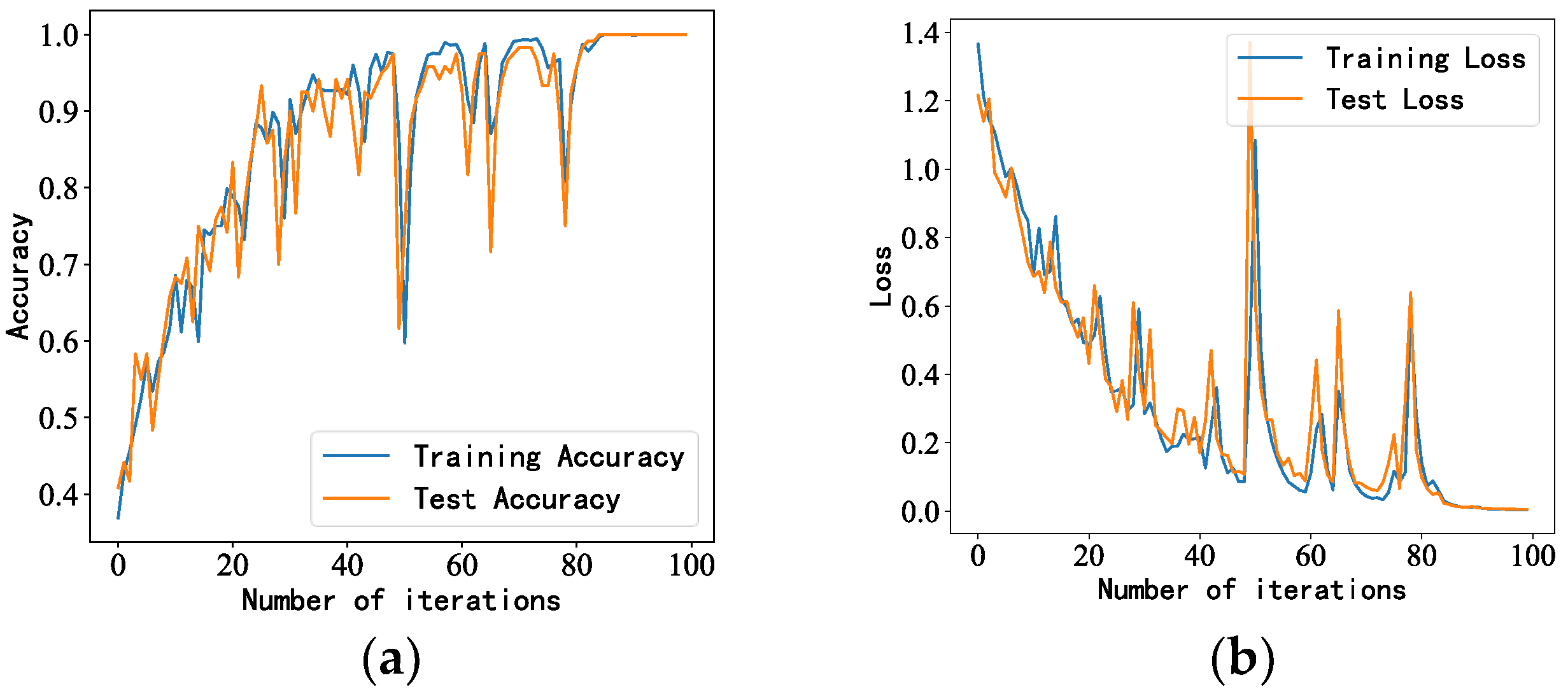
4.1. LSTM Model Parameter Settings
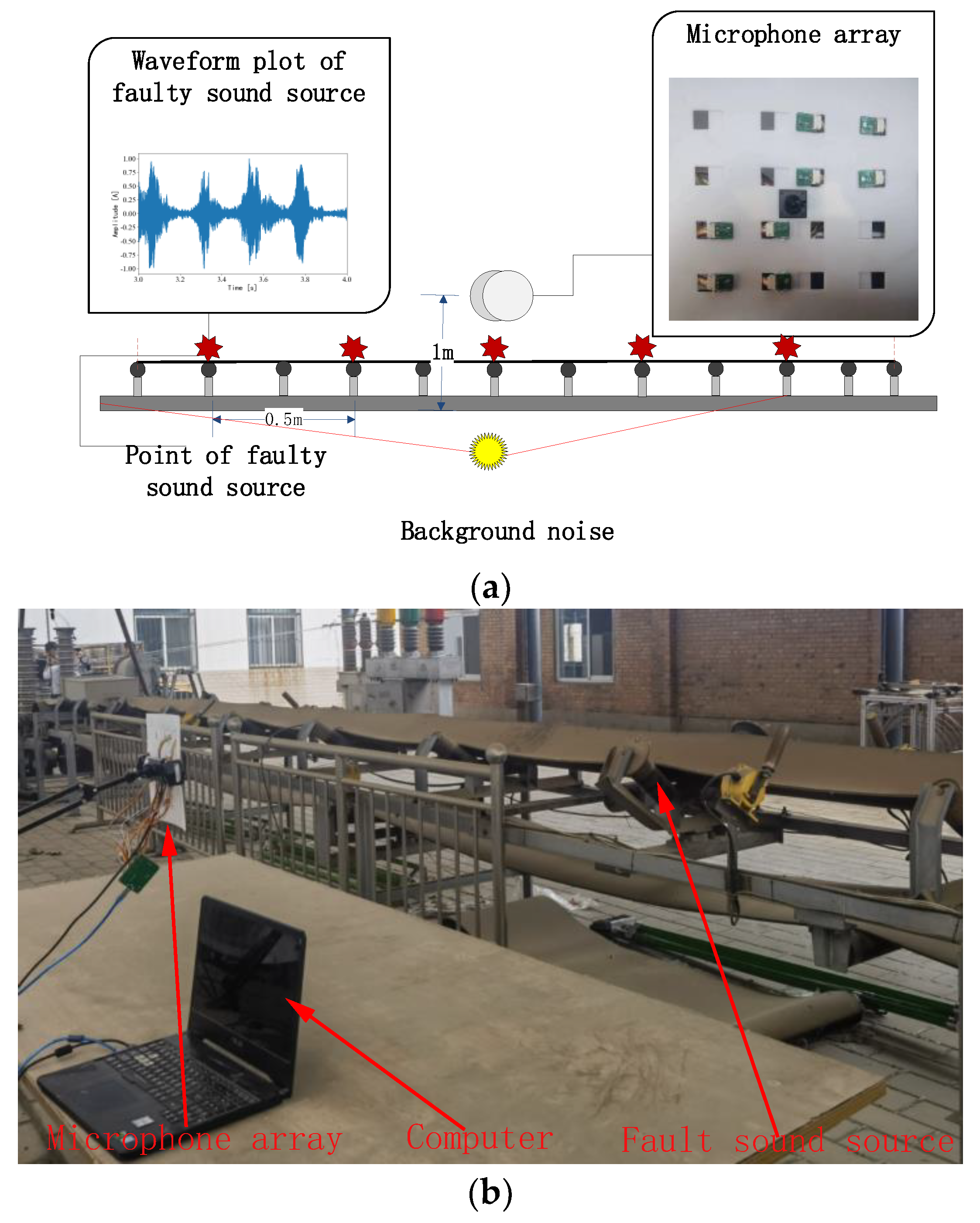
4.2. Experimental Setup
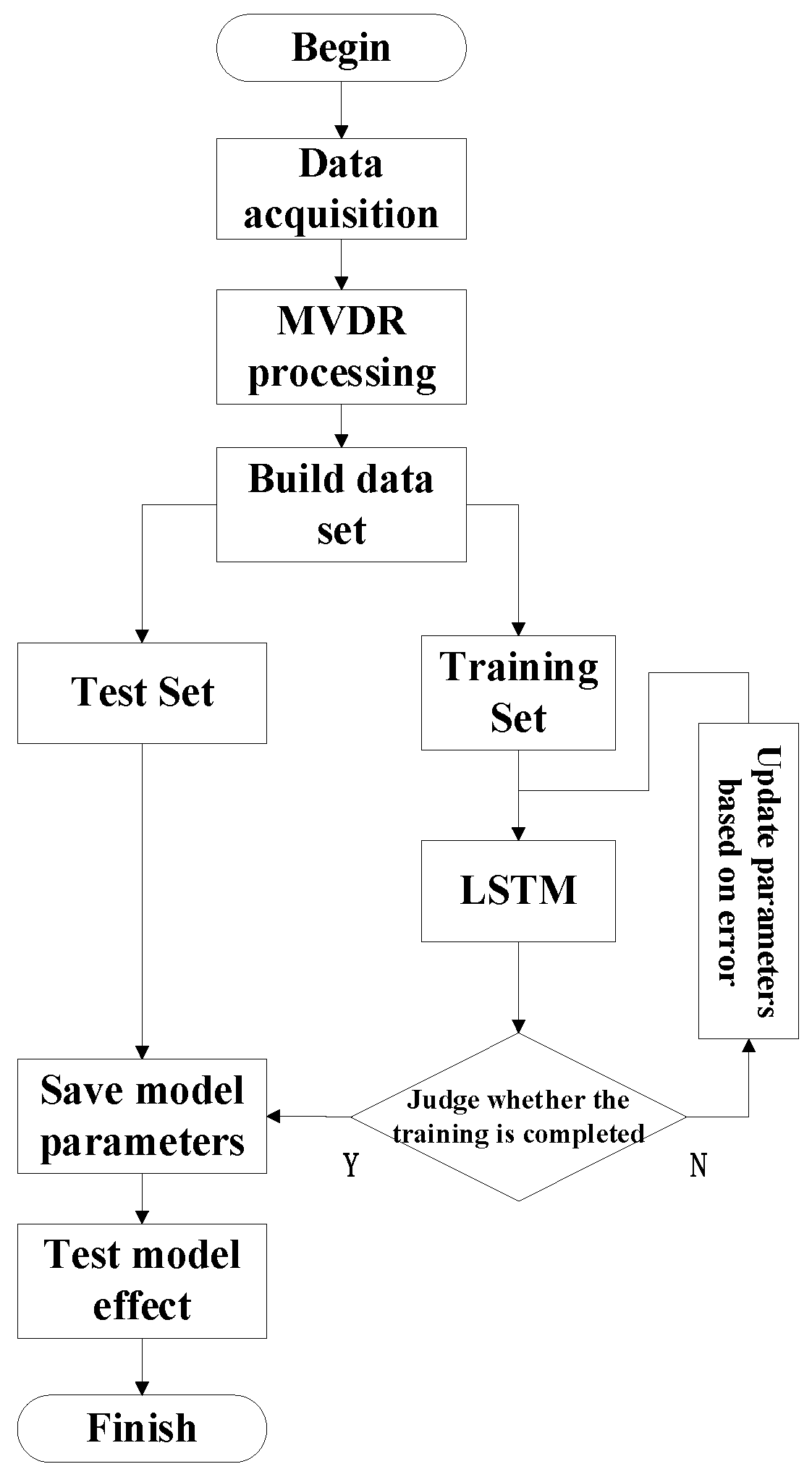
4.3. Experimental Process
- Step 1—The microphone array was used to collect the idler fault audio signal.
- Step 2—MVDR processing was performed on the collected signal to generate idler fault distance data.
- Step 3—We processed the data again to build the dataset.
- Step 4—We divided the data into the training set (90%) and testing set (10%).
- Step 5—We trained and tested the model to draw conclusions.
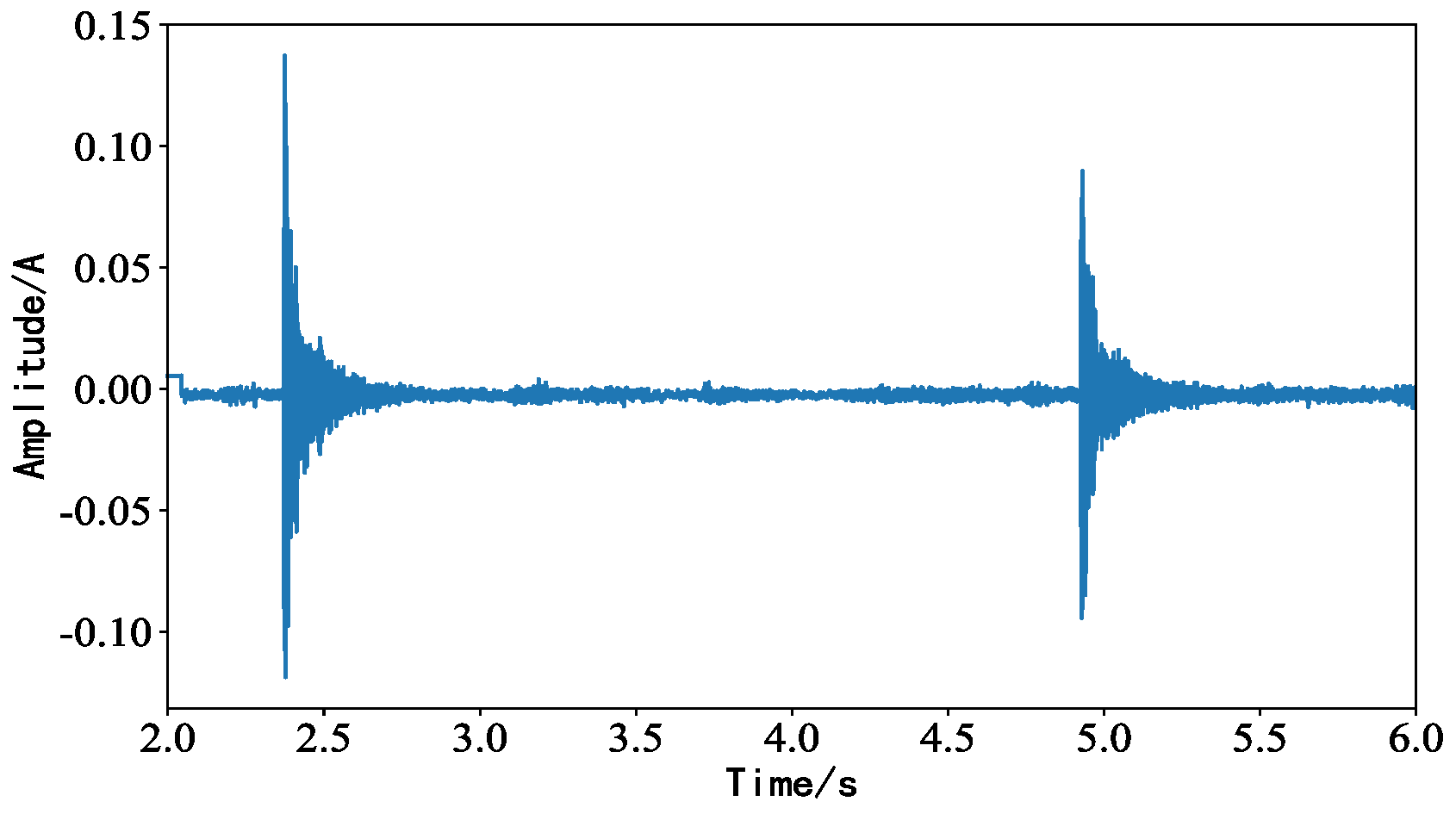
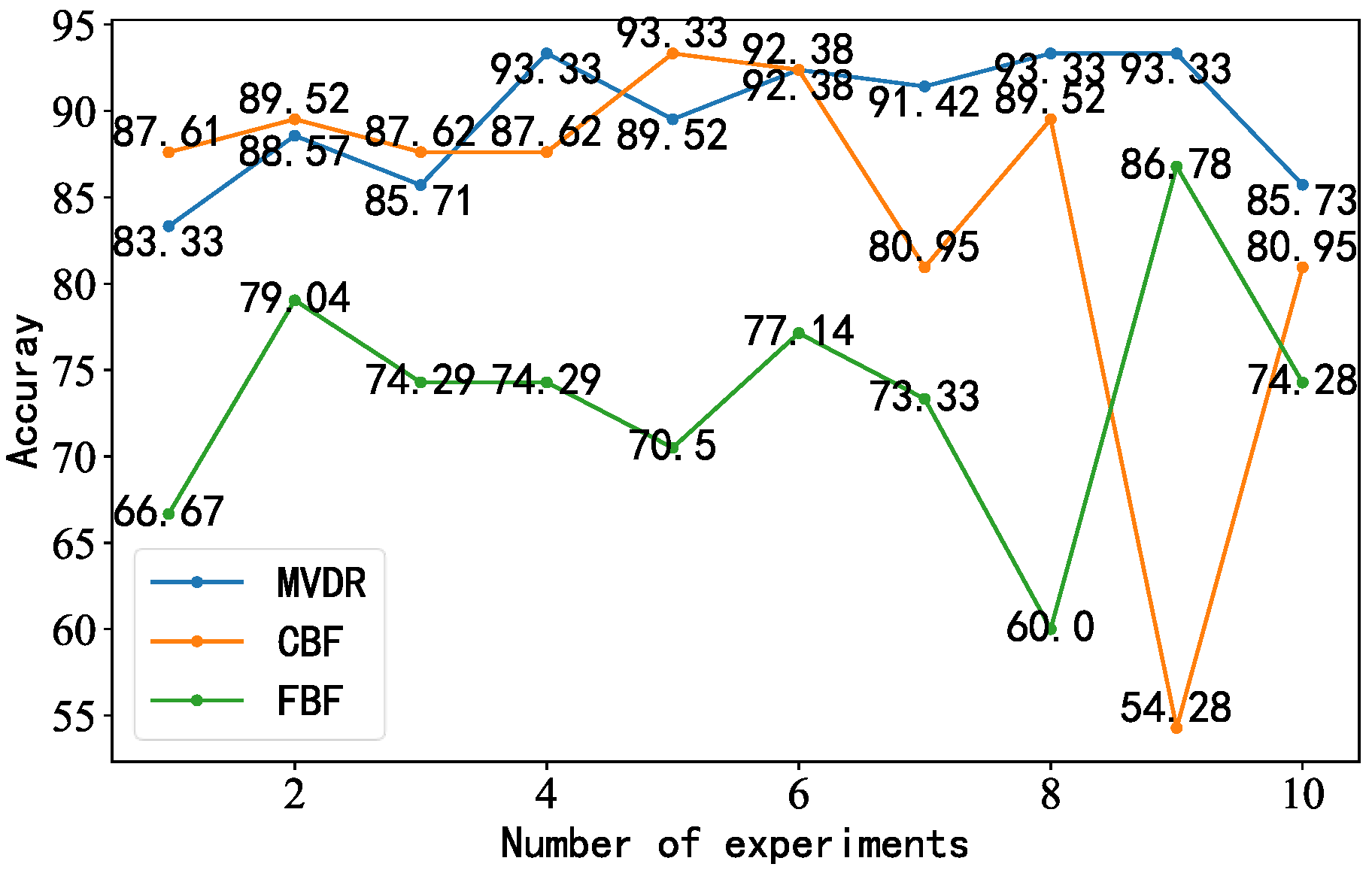
4.4. Background Noise Interference Experiment
4.5. Impact Noise Interference Experiment
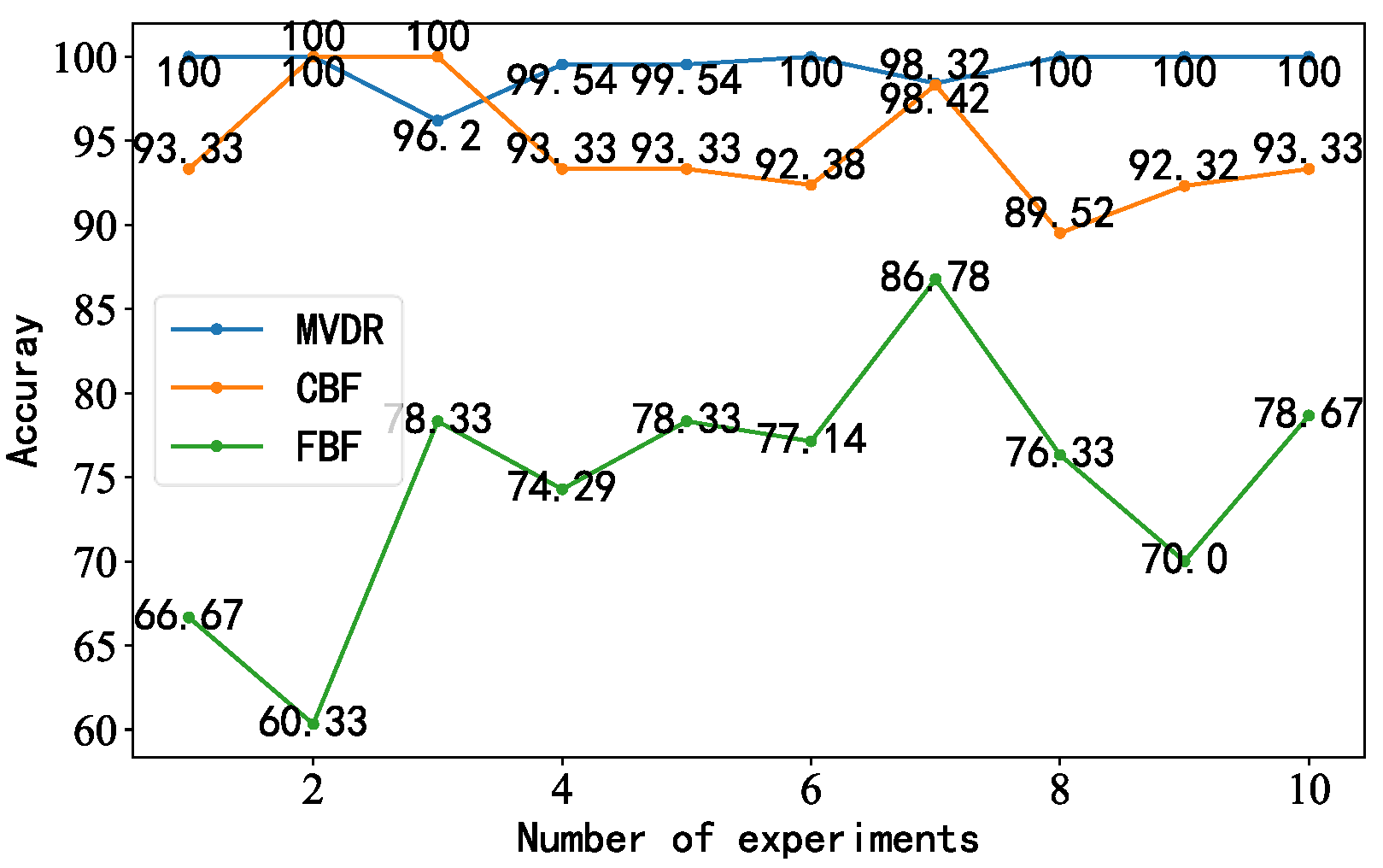
4.6. Evaluation Criteria and Comparison of Models
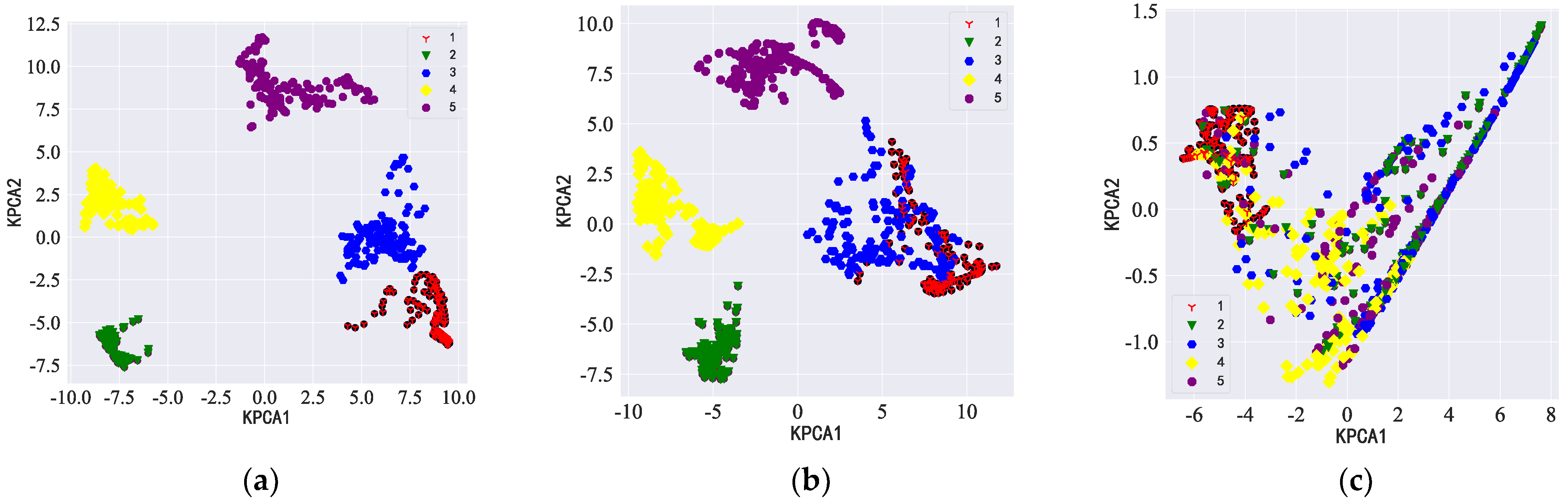
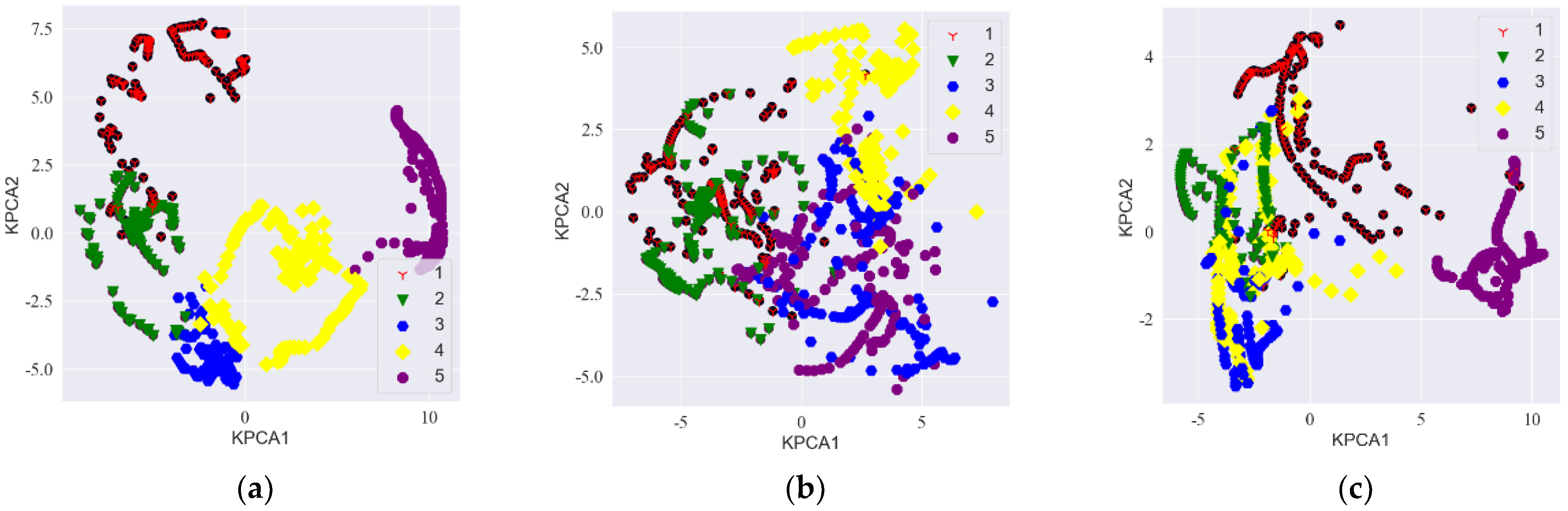
4.6.1. Data Comparison for Diagonal Double Rectangular Microphone Array
4.6.2. Data Comparison for Circular Microphone Array
5. Conclusions
- Due to the special structure of an idler, the human diagnosis steps are cumbersome and time is wasted. Based on deep learning, our model removed the tedious step of manually extracting idler fault features, which could greatly shorten the time required and improve the efficiency of idler fault diagnosis.
- Through simulation experiments, we found that the diagonal dual rectangular microphone array had higher resolution and noise resistance compared to the other microphone arrays and could be beneficial to the estimation of roller fault distance.
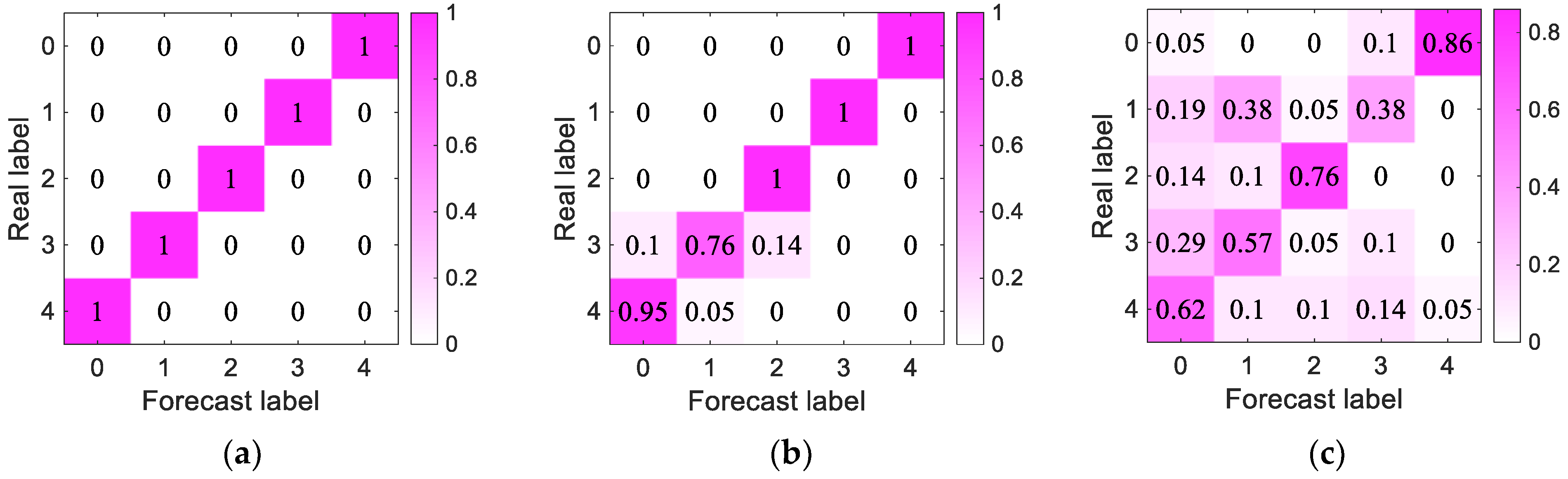
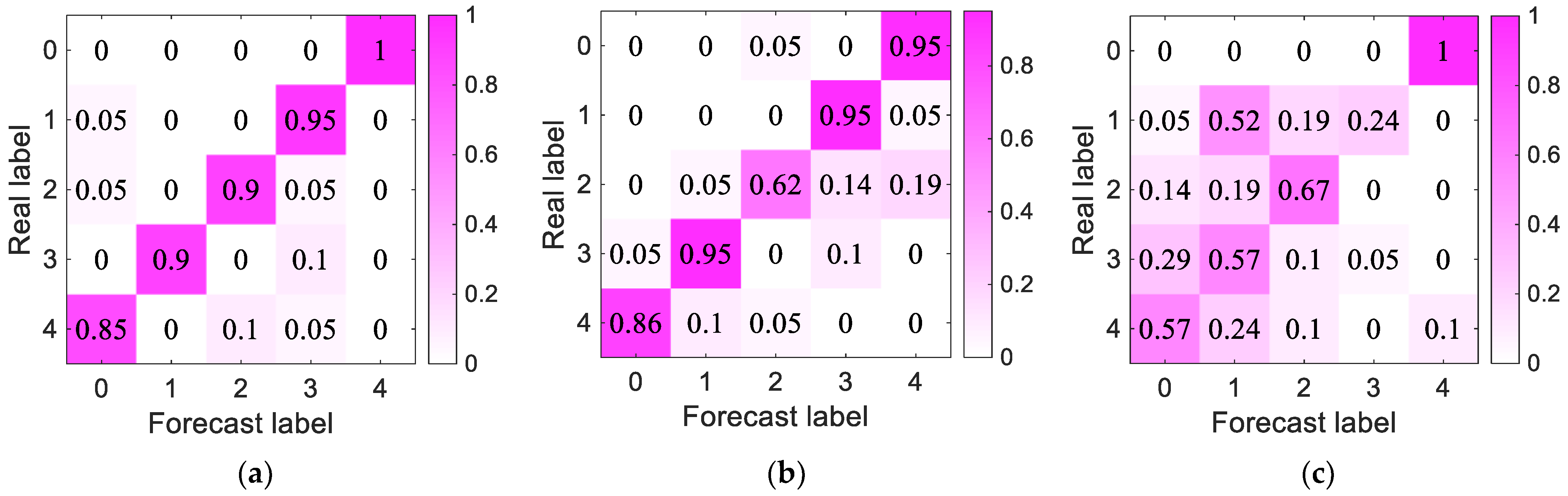
- After adjusting the model structure and parameters, we trained the generated idler fault distance samples. The accuracy of the proposed model was 100%, with better performance than the other models and results closer to the true values.
- Five fault locations during idler operation were analyzed, and the experimental results showed that the proposed model had the ability to estimate the fault distance and provide better robustness. It could be used as a standard for judging the fault distance of idlers and provide ideas for combining beamforming algorithms and deep learning with idler fault diagnosis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Zhang, F.; Qin, Z.; Han, Q.; Wang, T.; Chu, F. Piezoelectric energy harvester for rolling bearings with capability of self-powered condition monitoring. Energy 2022, 238, 121770. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Zhu, H.; Lei, Y. Design, modeling and experimental verification of circular Halbach electromagnetic energy harvesting from bearing motion. Energy Convers. Manag. 2019, 180, 811–821. [Google Scholar] [CrossRef]
- Zhou, Y.; Kumar, A.; Gandhi, C.P.; Vashishtha, G.; Tang, H.; Kundu, P.; Singh, M.; Xiang, J.W. Discrete entropy-based health indicator and LSTM for the forecasting of bearing health. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 12. [Google Scholar] [CrossRef]
- Aljemely, A.H.; Xuan, J.; Al-Azzawi, O.; Jawad, F.K. Intelligent fault diagnosis of rolling bearings based on LSTM with large margin nearest neighbor algorithm. Neural Comput. Appl. 2022, 34, 19401–19421. [Google Scholar] [CrossRef]
- Xie, W.; Li, Z.; Xu, Y.; Gardoni, P.; Li, W. Evaluation of Different Bearing Fault Classifiers in Utilizing CNN Feature Extraction Ability. Sensors 2022, 22, 3314. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, J.; Chen, L.; Wu, D.S. Fault diagnosis of motor bearing based on improved convolution neural network based on VMD. In Proceedings of the 31st Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 405–409. [Google Scholar]
- Yu, J.; Wen, Y.; Yang, L.; Zhao, Z.; Guo, Y.; Guo, X. Monitoring on triboelectric nanogenerator and deep learning method. Nano Energy 2021, 92, 106698. [Google Scholar] [CrossRef]
- Chen, L.; Choy, Y.S.; Wang, T.G.; Chiang, Y.K. Fault detection of wheel in wheel/rail system using kurtosis beamforming method. Struct. Health Monit. 2020, 19, 495–509. [Google Scholar] [CrossRef]
- Cabada, E.C.; Leclere, Q.; Antoni, J.; Hamzaoui, N. Fault detection in rotating machines with beamforming: Spatial visualization of diagnosis features. Mech. Syst. Signal Process. 2017, 97, 33–43. [Google Scholar] [CrossRef]
- Sun, S.L.; Wang, T.Y.; Yang, H.X.; Chu, F.L. Damage identification of wind turbine blades using an adaptive method for compressive beamforming based on the generalized minimax-concave penalty function. Renew. Energy 2022, 181, 59–70. [Google Scholar] [CrossRef]
- He, T.; Xiao, D.H.; Pan, Q.; Liu, X.D.; Shan, Y.C. Analysis on accuracy improvement of rotor–stator rubbing localization based on acoustic emission beamforming method. Ultrasonics 2014, 54, 318–329. [Google Scholar] [CrossRef]
- Subramanian, A.S.; Weng, C.; Watanabe, S.; Yu, M.; Yu, D. Deep learning based multi-source localization with source splitting and its effectiveness in multi-talker speech recognition. Comput. Speech Lang. 2022, 75, 101360. [Google Scholar] [CrossRef]
- Zhang, X.L. Deep ad-hoc beamforming. Comput. Speech Lang. 2021, 68, 101201. [Google Scholar] [CrossRef]
- Yang, Z.; Guan, S.; Zhang, X.L. Deep ad-hoc beamforming based on speaker extraction for target-dependent speech separation. Speech Communication 2022, 140, 87–97. [Google Scholar] [CrossRef]
- Ramezanpour, P.; Mosavi, M.-R. Two-Stage Beamforming for Rejecting Interferences Using Deep Neural Networks. IEEE Syst. Journal 2021, 15, 4439–4447. [Google Scholar] [CrossRef]
- Tao, T.; Zheng, H.; Yang, J.; Guo, Z.; Zhang, Y.; Ao, J.; Chen, Y.; Lin, W.; Tan, X. Sound Localization and Speech Enhancement Algorithm Based on Dual-Microphone. Sensors 2022, 22, 715. [Google Scholar] [CrossRef]
- Ahamed, P.S.S.; Duraiswamy, P. Virtual Sensing Active Noise Control System with 2D Microphone Array for Automotive Applications. In Proceedings of the International Conference on Signal Processing and Integrated Networks, Noida, India, 7–8 March 2019; pp. 151–155. [Google Scholar]
- Wakabayashi, Y.; Yamaoka, K.; Ono, N. Rotation-Robust Beamforming Based on Sound Field Interpolation with Regularly Circular Microphone Array. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 771–775. [Google Scholar]
- Kidav, J.U.; Sivamangai, N.M.; Pillai, M.P.; Sreejeesh, S.G. A broadband MVDR beamforming core for ultrasound imaging. Integration 2021, 81, 221–233. [Google Scholar] [CrossRef]
- Huang, Q.H.; Hu, R.; Fang, Y. Real-valued MVDR beamforming using spherical arrays with frequency invariant characteristic. Digit. Signal Process. 2016, 48, 239–245. [Google Scholar] [CrossRef]
- Li, J.; White, P.R.; Bull, J.M.; Leighton, T.G.; Roche, B.; Davis, J.W. Passive acoustic localisation of undersea gas seeps using beamforming. Int. J. Greenh. Gas Control. 2021, 108, 103316. [Google Scholar] [CrossRef]
- Ngoc, H.V.; Mayer JR, R.; Bitar-Nehme, E. Deep learning LSTM for predicting thermally induced geometric errors using rotary axes’powers as input parameters. CIRP J. Manuf. Sci. Technol. 2022, 37, 70–80. [Google Scholar] [CrossRef]
- Nemani, V.P.; Lu, H.; Thelen, A.; Hu, C.; Zimmerman, A.T. Ensembles of probabilistic LSTM predictors and correctors for bearing prognostics using industrial standards. Neurocomputing 2022, 491, 575–596. [Google Scholar] [CrossRef]
- Liu, J.; Pan, C.; Lei, F.; Hu, D.; Zuo, H. Fault prediction of bearings based on LSTM and statistical process analysis. Reliab. Eng. Syst. Saf. 2021, 214, 107646. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2014, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Yu, Y.; Ahmed, H.O.A.; Darwish, M.; Nandi, A.K. Open-Circuit Fault Detection and Classification of Modular Multilevel Converters in High Voltage Direct Current Systems (MMC-HVDC) with Long Short-Term Memory (LSTM) Method. Sensors 2021, 21, 4159. [Google Scholar] [CrossRef]
- Yin, A.; Yan, Y.; Zhang, Z.; Li, C.; Sánchez, R.-V. Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss. Sensors 2020, 20, 2339. [Google Scholar] [CrossRef]
- Zheng, J.; Liao, J.; Chen, Z. End-to-End Continuous/Discontinuous Feature Fusion Method with Attention for Rolling Bearing Fault Diagnosis. Sensors 2022, 22, 6489. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]


| Parameter Name | Parameter Value |
|---|---|
| Number of arrays | 18 |
| Desired signal angle | 10 |
| Interference signal angle | −30, 30 |
| SNR | 10 |
| INR | 10 |
| Number of stories | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, W.; Li, J.; Dong, F.; Wan, S. MVDR-LSTM Distance Estimation Model Based on Diagonal Double Rectangular Array. Sensors 2023, 23, 5094. https://doi.org/10.3390/s23115094
Zhang X, Wu W, Li J, Dong F, Wan S. MVDR-LSTM Distance Estimation Model Based on Diagonal Double Rectangular Array. Sensors. 2023; 23(11):5094. https://doi.org/10.3390/s23115094
Chicago/Turabian StyleZhang, Xiong, Wenbo Wu, Jialu Li, Fan Dong, and Shuting Wan. 2023. "MVDR-LSTM Distance Estimation Model Based on Diagonal Double Rectangular Array" Sensors 23, no. 11: 5094. https://doi.org/10.3390/s23115094
APA StyleZhang, X., Wu, W., Li, J., Dong, F., & Wan, S. (2023). MVDR-LSTM Distance Estimation Model Based on Diagonal Double Rectangular Array. Sensors, 23(11), 5094. https://doi.org/10.3390/s23115094






