Spectroscopic Microtomography in the Short-Wave Infrared Wavelength Range
Abstract
:1. Introduction
2. Materials and Methods
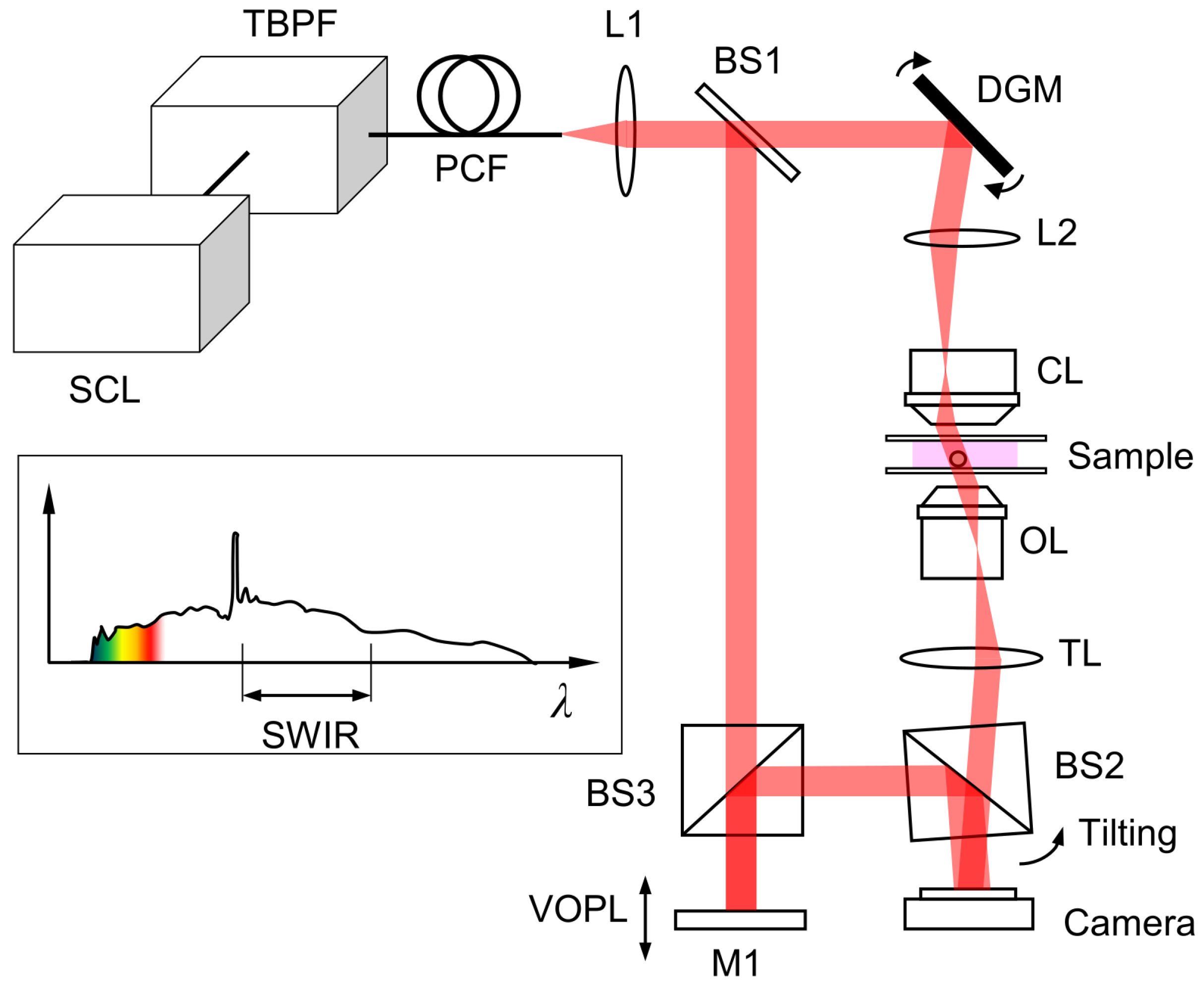
2.1. System Design
2.2. Sample Preparation
2.3. Data Acquisition
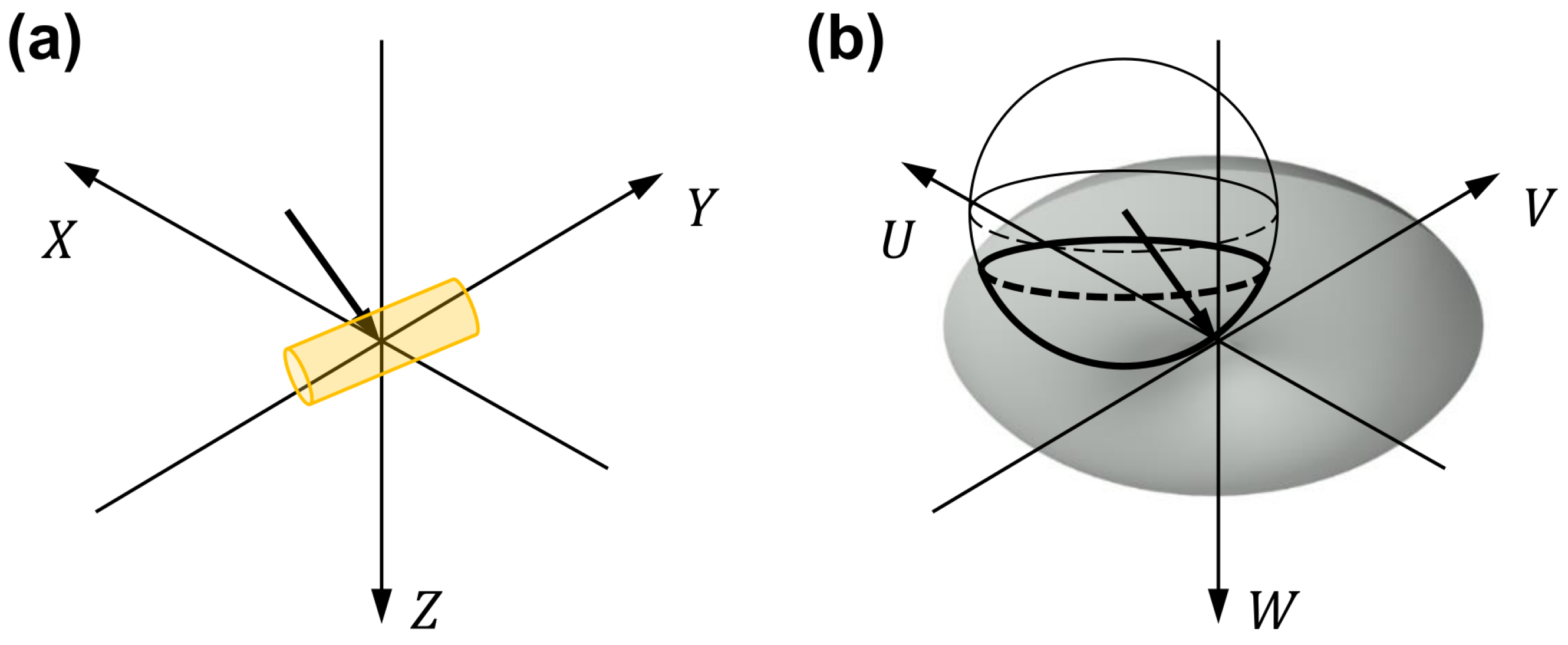
2.4. Data Processing
3. Results
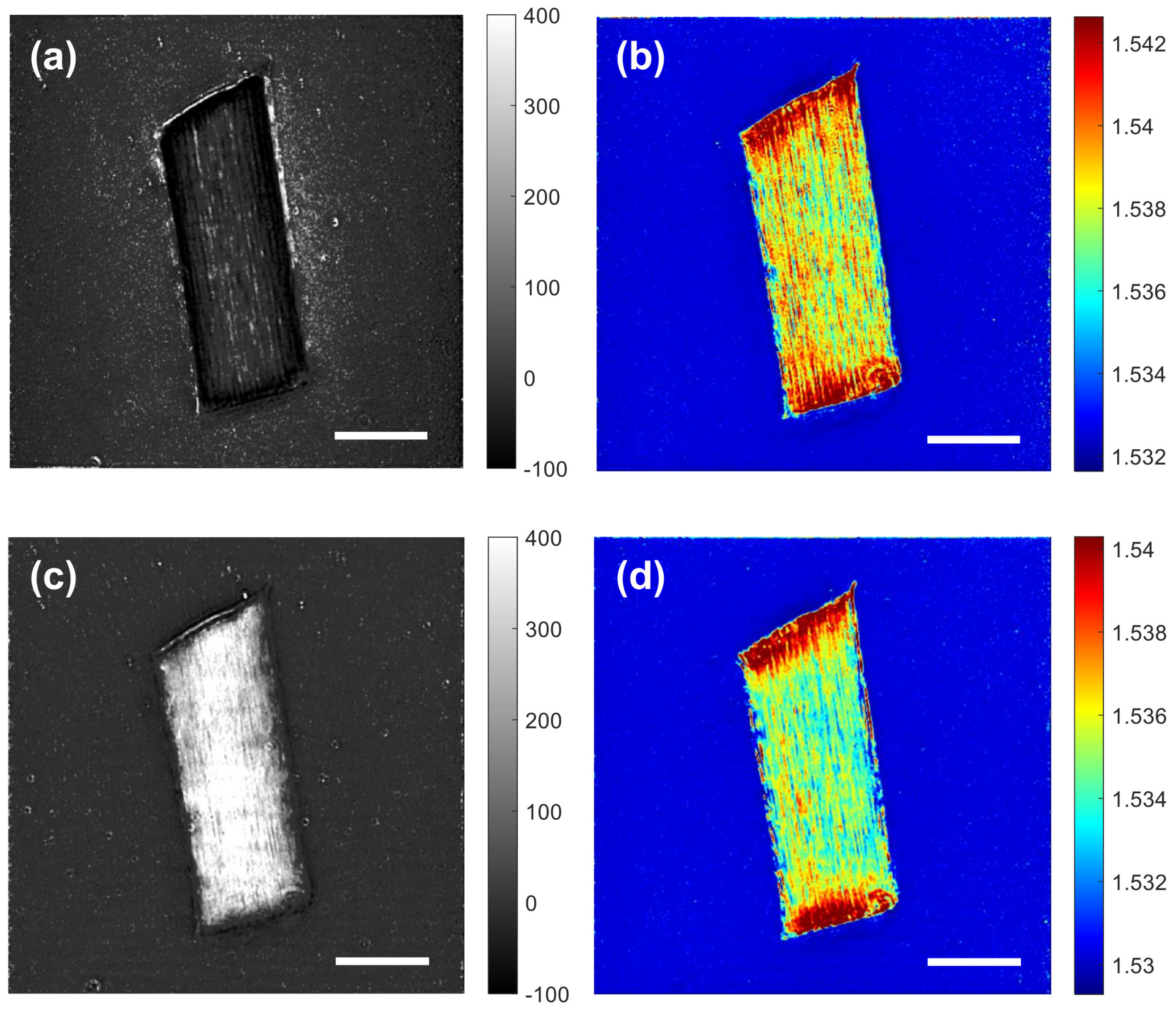
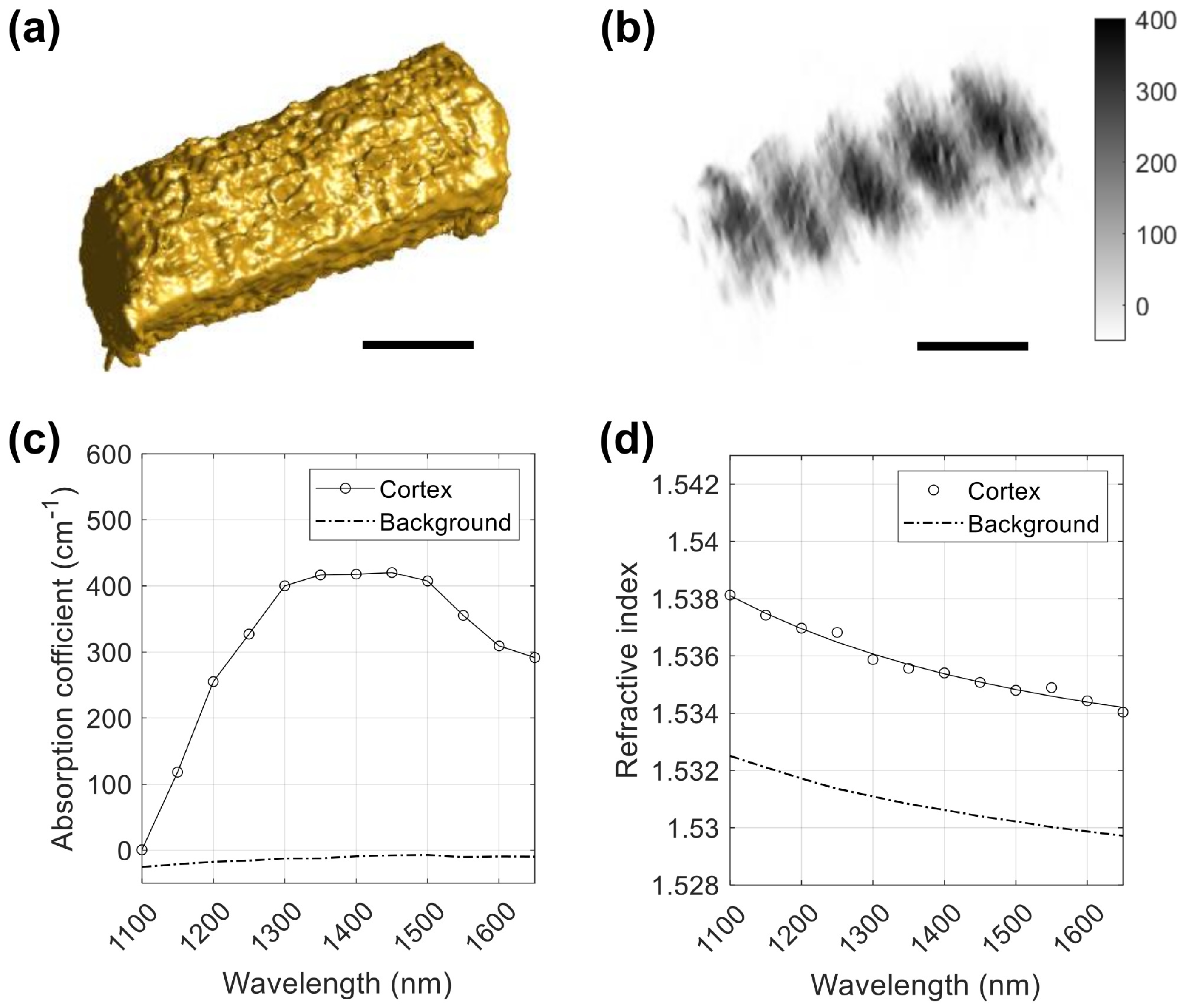
3.1. 3D Maps of the Absorption and Refractive Index of Human Hair
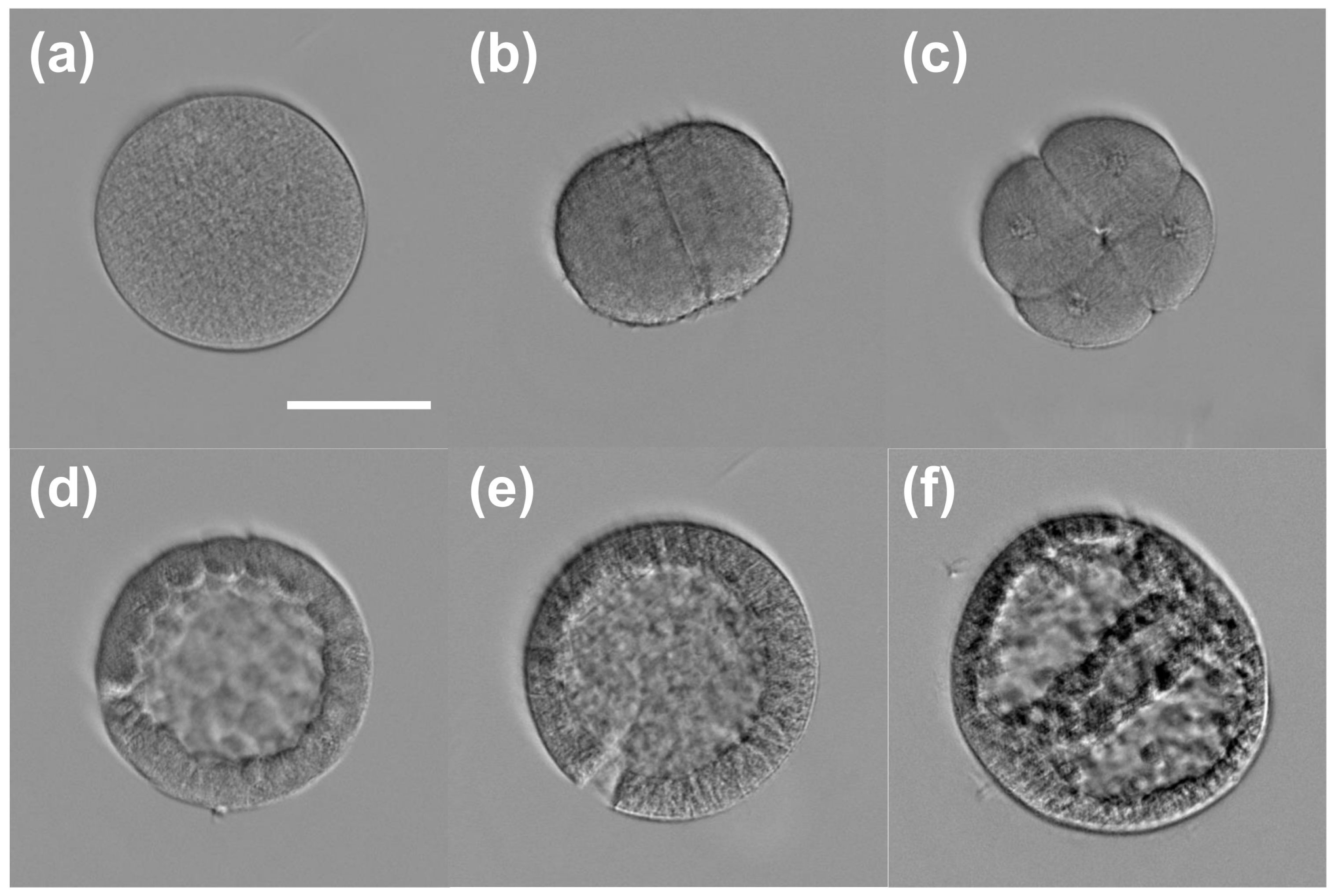
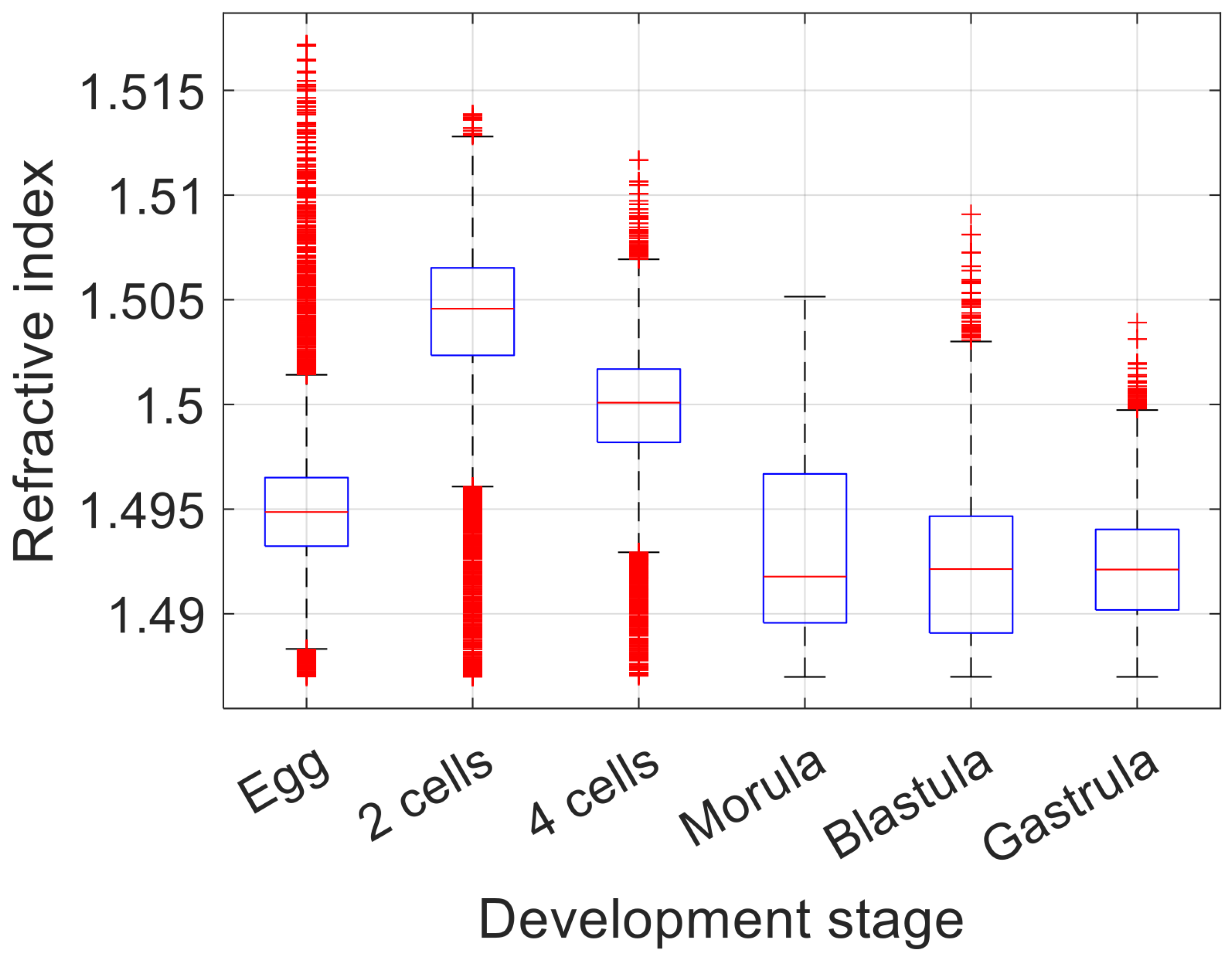
3.2. 3D Refractive Index Imaging of Sea Urchin Embryos in Different Developmental Stages
3.3. 3D Point Spread Function of the SWIR Digital Holographic Tomography System
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MIR | Mid-infrared |
| NIR | Near-infrared |
| SWIR | Short-wave infrared |
| DHT | Digital holographic tomography |
| TBPF | Tunable bandpass filter |
| OPD | Optical path difference |
| VOPL | Variable optical path length |
| LED | Light-emitting diode |
References
- Sung, Y. Spectroscopic microtomography in the visible wavelength range. Phys. Rev. Appl. 2018, 10, 054041. [Google Scholar] [CrossRef]
- Juntunen, C.; Abramczyk, A.R.; Woller, I.M.; Sung, Y. Hyperspectral three-dimensional absorption imaging using snapshot optical tomography. Phys. Rev. Appl. 2022, 18, 034055. [Google Scholar] [CrossRef]
- Martin, M.C.; Dabat-Blondeau, C.; Unger, M.; Sedlmair, J.; Parkinson, D.Y.; Bechtel, H.A.; Illman, B.; Castro, J.M.; Keiluweit, M.; Buschke, D.; et al. 3D spectral imaging with synchrotron Fourier transform infrared spectro-microtomography. Nat. Methods 2013, 10, 861. [Google Scholar] [CrossRef]
- Bobroff, V.; Chen, H.H.; Delugin, M.; Javerzat, S.; Petibois, C. Quantitative IR microscopy and spectromics open the way to 3D digital pathology. J. Biophotonics 2017, 10, 598–606. [Google Scholar] [CrossRef]
- Dudak, J.; Zemlicka, J.; Karch, J.; Hermanova, Z.; Kvacek, J.; Krejci, F. Microtomography with photon counting detectors: Improving the quality of tomographic reconstruction by voxel-space oversampling. J. Instrum. 2017, 12, C01060. [Google Scholar] [CrossRef]
- Obst, M.; Wang, J.; Hitchcock, A.P. Soft X-ray spectro-tomography study of cyanobacterial biomineral nucleation. Geobiology 2009, 7, 577–591. [Google Scholar] [CrossRef]
- Sathyanarayana, D.N. Vibrational Spectroscopy: Theory and Applications; New Age International: Delhi, India, 2015. [Google Scholar]
- Griffiths, P.R.; De Haseth, J.A. Fourier Transform Infrared Spectrometry; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 171. [Google Scholar]
- Ferraro, J.R. Introductory Raman Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Ozaki, Y.; Huck, C.; Tsuchikawa, S.; Engelsen, S.B. Near-Infrared Spectroscopy: Theory, Spectral Analysis, Instrumentation, and Applications; Springer: Singapore, 2021. [Google Scholar]
- Charriere, F.; Marian, A.; Montfort, F.; Kuehn, J.; Colomb, T.; Cuche, E.; Marquet, P.; Depeursinge, C. Cell refractive index tomography by digital holographic microscopy. Opt. Lett. 2006, 31, 178–180. [Google Scholar] [CrossRef] [PubMed]
- Lauer, V. New approach to Optical diffraction tomography yielding a vector equation of diffraction tomography and a novel tomographic microscope. J. Microsc. 2002, 205, 165–176. [Google Scholar] [CrossRef]
- Choi, W.; Fang-Yen, C.; Badizadegan, K.; Oh, S.; Lue, N.; Dasari, R.R.; Feld, M.S. Tomographic phase microscopy. Nat. Methods 2007, 4, 717. [Google Scholar] [CrossRef]
- Vertu, S.; Flügge, J.; Delaunay, J.J.; Haeberlé, O. Improved and isotropic resolution in tomographic diffractive microscopy combining sample and illumination rotation. Cent. Eur. J. Phys. 2011, 9, 969–974. [Google Scholar] [CrossRef]
- Simon, B.; Debailleul, M.; Houkal, M.; Ecoffet, C.; Bailleul, J.; Lambert, J.; Spangenberg, A.; Liu, H.; Soppera, O.; Haeberlé, O. Tomographic diffractive microscopy with isotropic resolution. Optica 2017, 4, 460–463. [Google Scholar] [CrossRef]
- Haeberlé, O.; Belkebir, K.; Giovaninni, H.; Sentenac, A. Tomographic diffractive microscopy: Basics, techniques and perspectives. J. Mod. Opt. 2010, 57, 686–699. [Google Scholar] [CrossRef]
- Creath, K. Phase-measurement interferometry techniques. Prog. Opt. 1988, 26, 349–393. [Google Scholar]
- Wolf, E. Three-dimensional structure determination of semi-transparent objects from holographic data. Opt. Commun. 1969, 1, 153–156. [Google Scholar] [CrossRef]
- Devaney, A. Inverse-scattering theory within the Rytov approximation. Opt. Lett. 1981, 6, 374–376. [Google Scholar] [CrossRef]
- Sung, Y.; Choi, W.; Fang-Yen, C.; Badizadegan, K.; Dasari, R.R.; Feld, M.S. Optical diffraction tomography for high resolution live cell imaging. Opt. Express 2009, 17, 266–277. [Google Scholar] [CrossRef]
- Sung, Y.; Dasari, R.R. Deterministic regularization of three-dimensional Optical diffraction tomography. J. Opt. Soc. Am. A 2011, 28, 1554–1561. [Google Scholar] [CrossRef]
- Zoccola, M.; Mossotti, R.; Innocenti, R.; Loria, D.I.; Rosso, S.; Zanetti, R. Near infrared spectroscopy as a tool for the determination of eumelanin in human hair. Pigment Cell Res. 2004, 17, 379–385. [Google Scholar] [CrossRef]
- Miyamae, Y.; Yamakawa, Y.; Ozaki, Y. Evaluation of physical properties of human hair by diffuse reflectance near-infrared spectroscopy. Appl. Spectrosc. 2007, 61, 212–217. [Google Scholar] [CrossRef]
- Egawa, M.; Hagihara, M.; Yanai, M. Near-infrared imaging of water in human hair. Skin Res. Technol. 2013, 19, 35–41. [Google Scholar] [CrossRef]
- Barer, R.; Tkaczyk, S. Refractive index of concentrated protein solutions. Nature 1954, 173, 821–822. [Google Scholar] [CrossRef]
- Sung, Y.; Tzur, A.; Oh, S.; Choi, W.; Li, V.; Dasari, R.R.; Yaqoob, Z.; Kirschner, M.W. Size homeostasis in adherent cells studied by synthetic phase microscopy. Proc. Natl. Acad. Sci. USA 2013, 110, 16687–16692. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Hadjur, C.; Daty, G.; Madry, G.; Corcuff, P. Cosmetic assessment of the human hair by confocal microscopy. Scanning J. Scanning Microsc. 2002, 24, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Ward, K.; Bertails, F.; Kim, T.Y.; Marschner, S.R.; Cani, M.P.; Lin, M.C. A survey on hair modeling: Styling, simulation, and rendering. IEEE Trans. Vis. Comput. Graph. 2007, 13, 213–234. [Google Scholar] [CrossRef] [PubMed]
- Brandes, S. Near-Infrared Spectroscopic Studies of Human Scalp Hair in a Forensic Context. Ph.D. Thesis, Queensland University of Technology, Brisbane City, QLD, Australia, 2009. [Google Scholar]
- Lasisi, T.; Ito, S.; Wakamatsu, K.; Shaw, C.N. Quantifying variation in human scalp hair fiber shape and pigmentation. Am. J. Phys. Anthropol. 2016, 160, 341–352. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.M.; Mancini, M.C.; Nie, S. Second window for in vivo imaging. Nat. Nanotechnol. 2009, 4, 710–711. [Google Scholar] [CrossRef]
- Bhowmik, M.K.; Saha, K.; Majumder, S.; Majumder, G.; Saha, A.; Sarma, A.N.; Bhattacharjee, D.; Basu, D.K.; Nasipuri, M. Thermal infrared face recognition—A biometric identification technique for robust security system. Rev. Refinements New Ideas Face Recognit. 2011, 7, 113–138. [Google Scholar]
- Serranti, S.; Fiore, L.; Bonifazi, G.; Takeshima, A.; Takeuchi, H.; Kashiwada, S. Microplastics characterization by hyperspectral imaging in the SWIR range. Spie Future Sens. Technol. 2019, 11197, 134–140. [Google Scholar]
- Lyon, R.C.; Lester, D.S.; Lewis, E.N.; Lee, E.; Yu, L.X.; Jefferson, E.H.; Hussain, A.S. Near-infrared spectral imaging for quality assurance of pharmaceutical products: Analysis of tablets to assess powder blend homogeneity. Aaps Pharmscitech 2002, 3, 17. [Google Scholar] [CrossRef]
- Popescu, G. Quantitative Phase Imaging of Cells and Tissues; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Bertero, M.; Boccacci, P.; De Mol, C. Introduction to Inverse Problems in Imaging; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juntunen, C.; Abramczyk, A.R.; Shea, P.; Sung, Y. Spectroscopic Microtomography in the Short-Wave Infrared Wavelength Range. Sensors 2023, 23, 5164. https://doi.org/10.3390/s23115164
Juntunen C, Abramczyk AR, Shea P, Sung Y. Spectroscopic Microtomography in the Short-Wave Infrared Wavelength Range. Sensors. 2023; 23(11):5164. https://doi.org/10.3390/s23115164
Chicago/Turabian StyleJuntunen, Cory, Andrew R. Abramczyk, Peter Shea, and Yongjin Sung. 2023. "Spectroscopic Microtomography in the Short-Wave Infrared Wavelength Range" Sensors 23, no. 11: 5164. https://doi.org/10.3390/s23115164
APA StyleJuntunen, C., Abramczyk, A. R., Shea, P., & Sung, Y. (2023). Spectroscopic Microtomography in the Short-Wave Infrared Wavelength Range. Sensors, 23(11), 5164. https://doi.org/10.3390/s23115164



