On the Consistency between a Classical Definition of the Geoid-to-Quasigeoid Separation and Helmert Orthometric Heights
Abstract
:1. Introduction
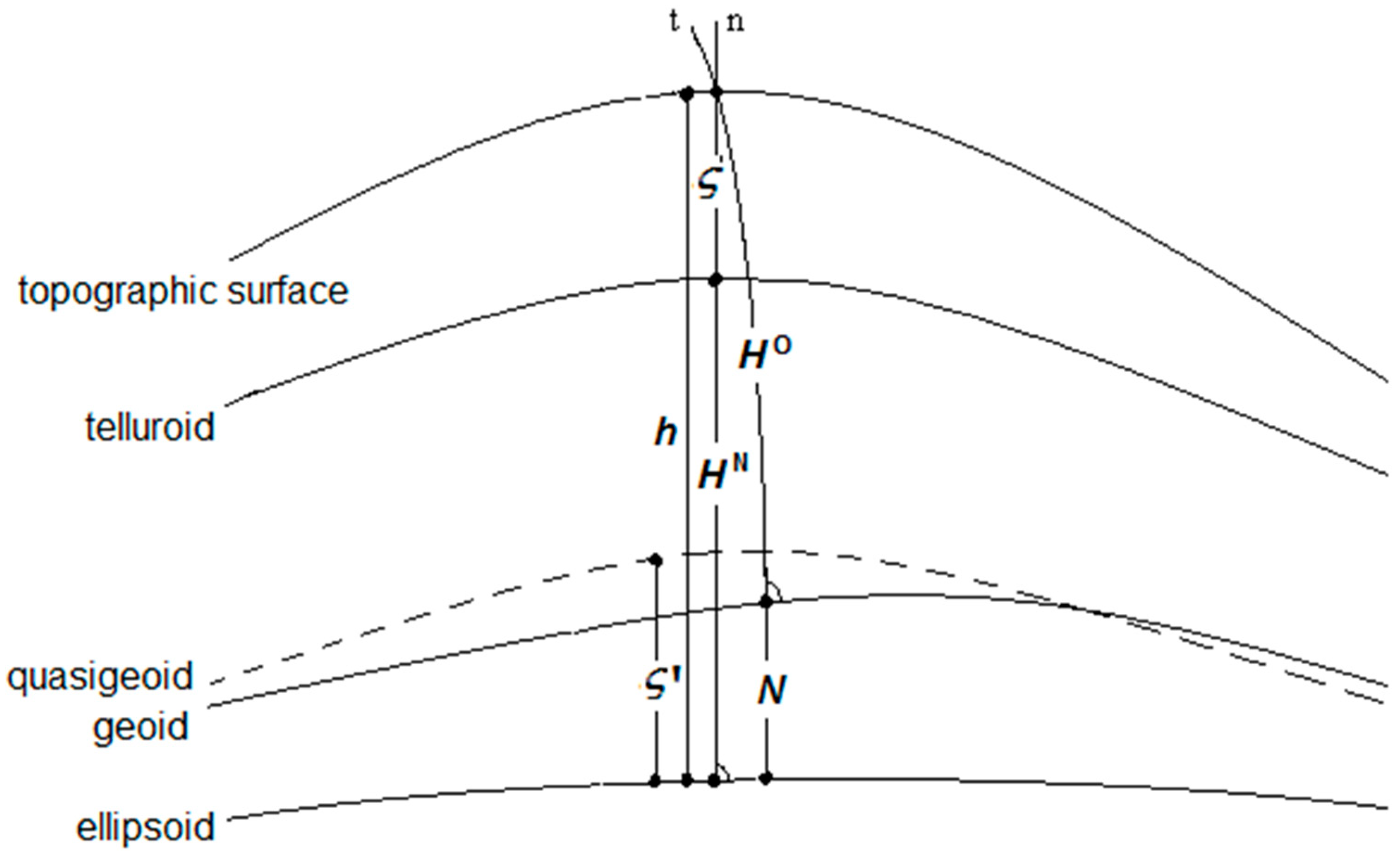
2. Theory
2.1. Normal and Orthometric Heights
2.2. Difference between the Normal and Orthometric Corrections
2.3. Geoid-to-Quasigeoid Separation Difference
2.4. Approximate Definition of the Geoid-to-Quasigeoid Separation
2.5. Approximate Definition of the Geoid-to-Quasigeoid Separation Difference
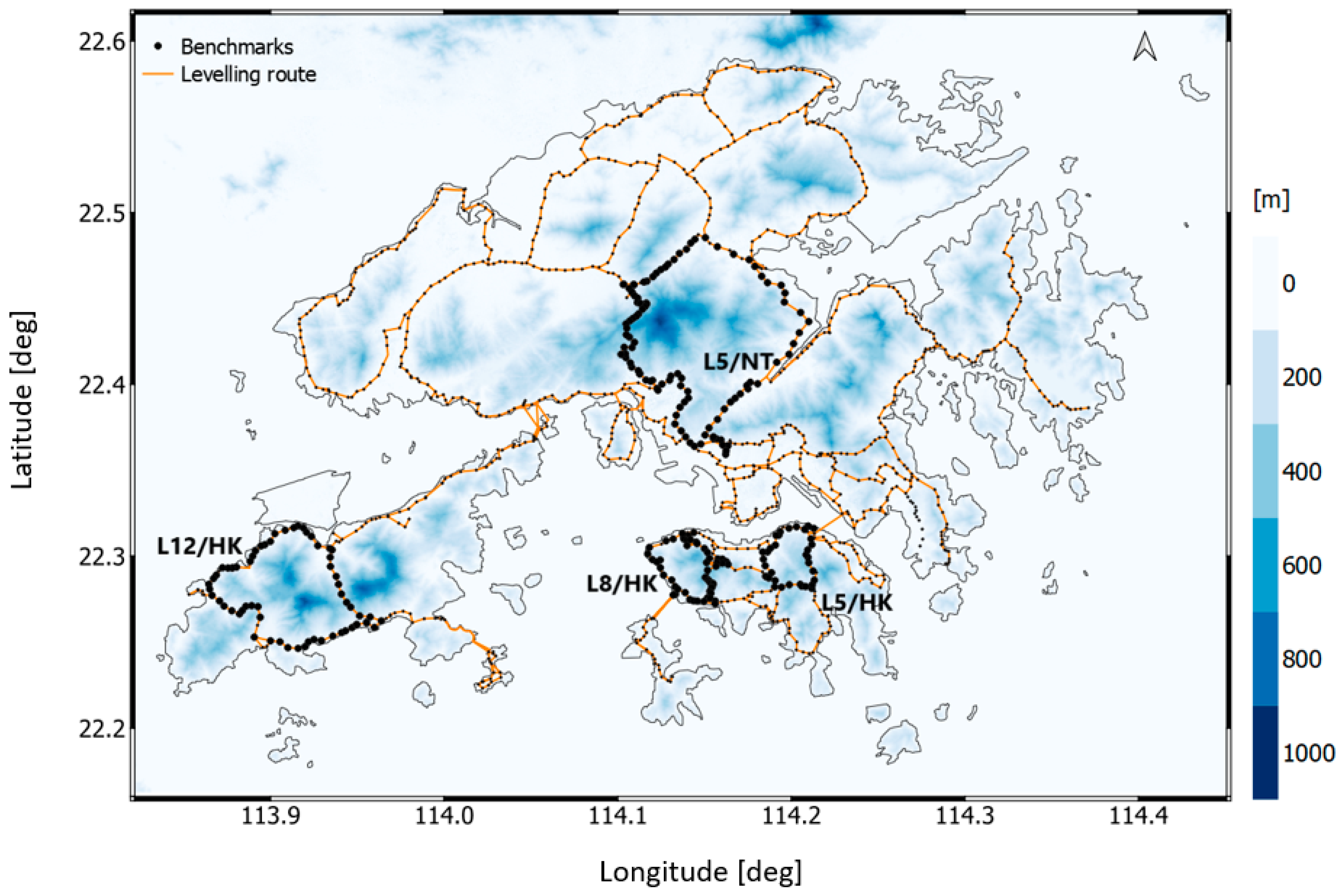
3. Numerical Procedures
3.1. Gravity Data Interpolation
3.2. Orthometric and Normal Heights
3.3. The Orthometric and Normal Correction Differences and the Geoid-to-Quasigeoid Separation Differences
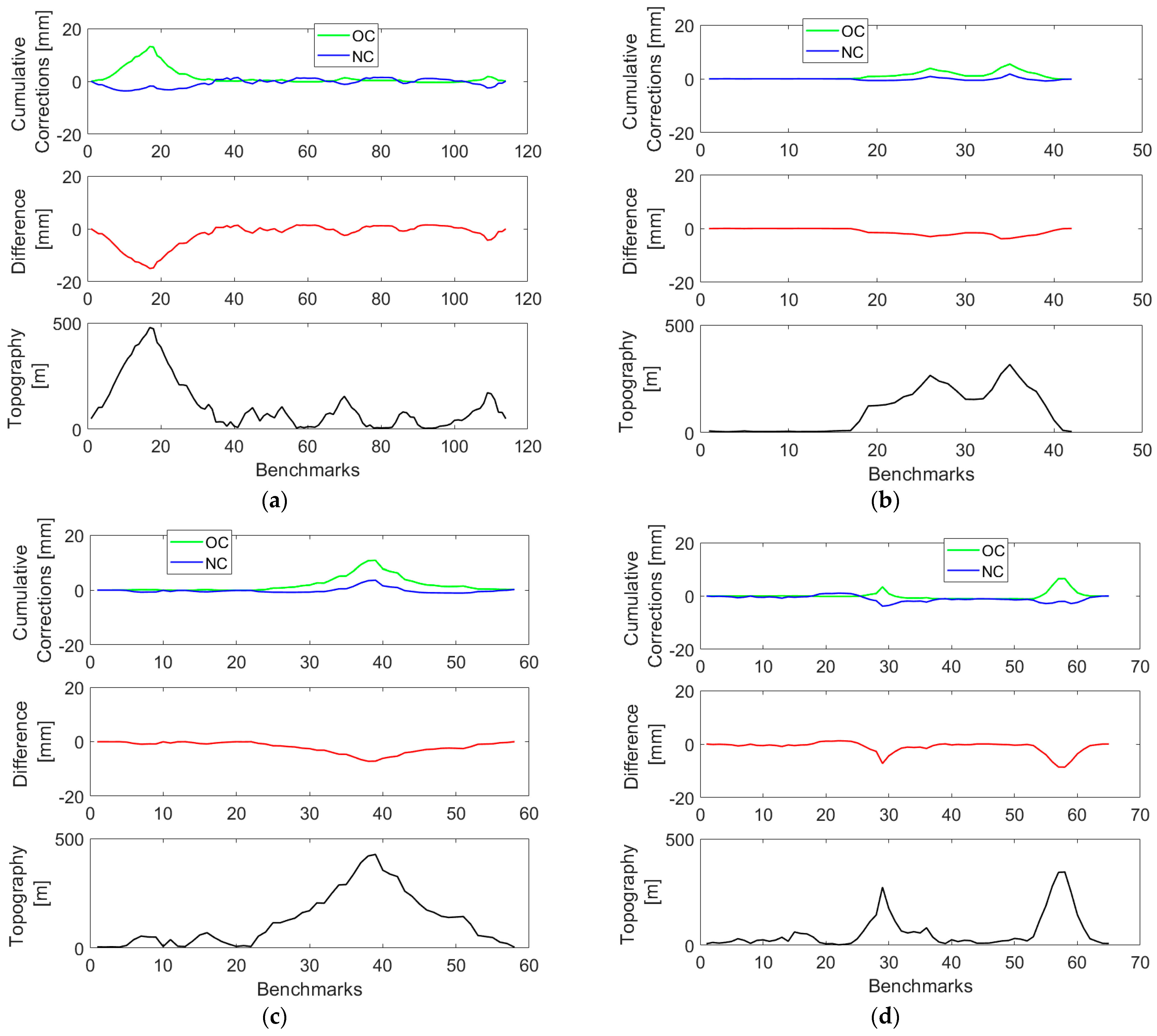
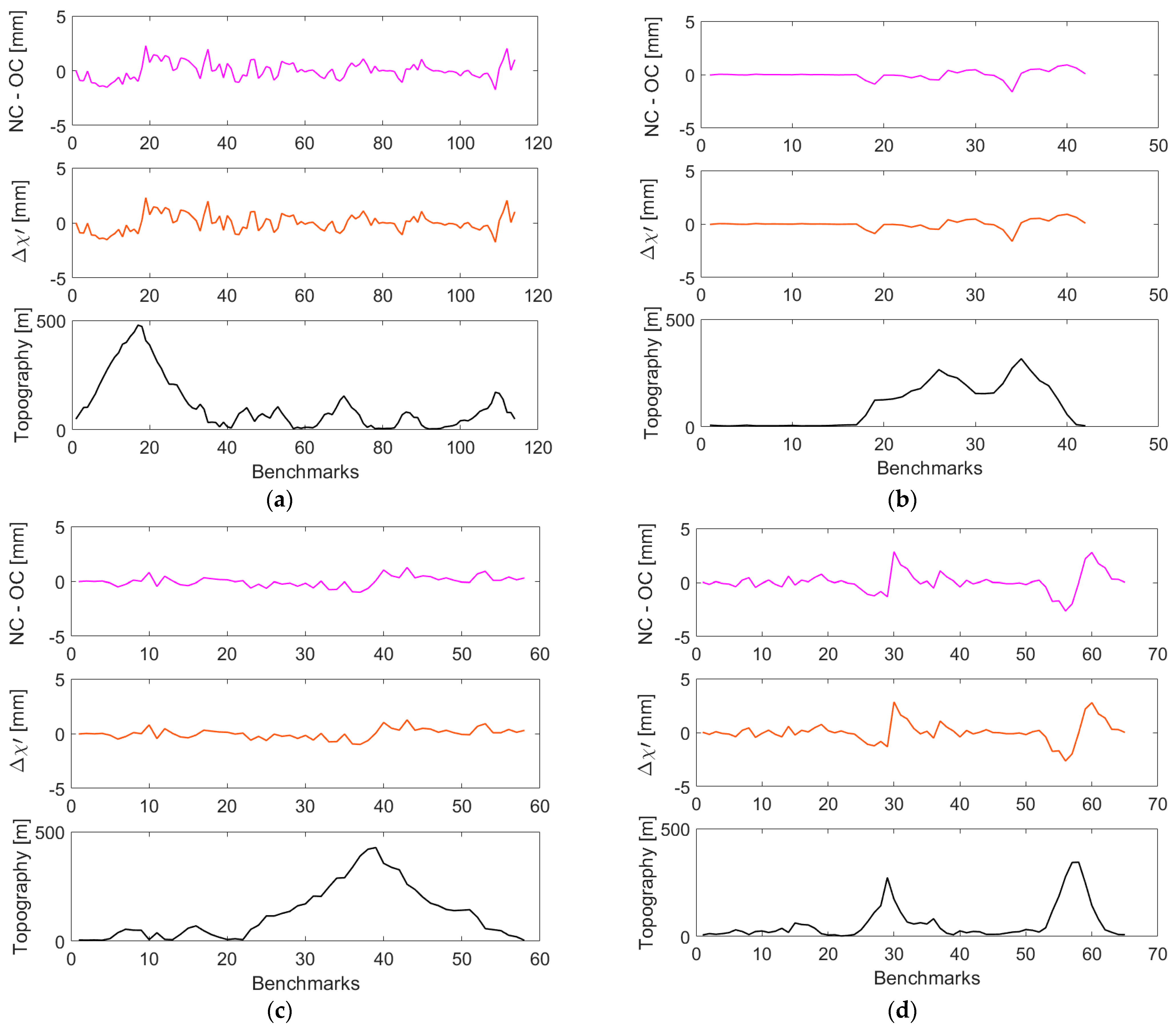
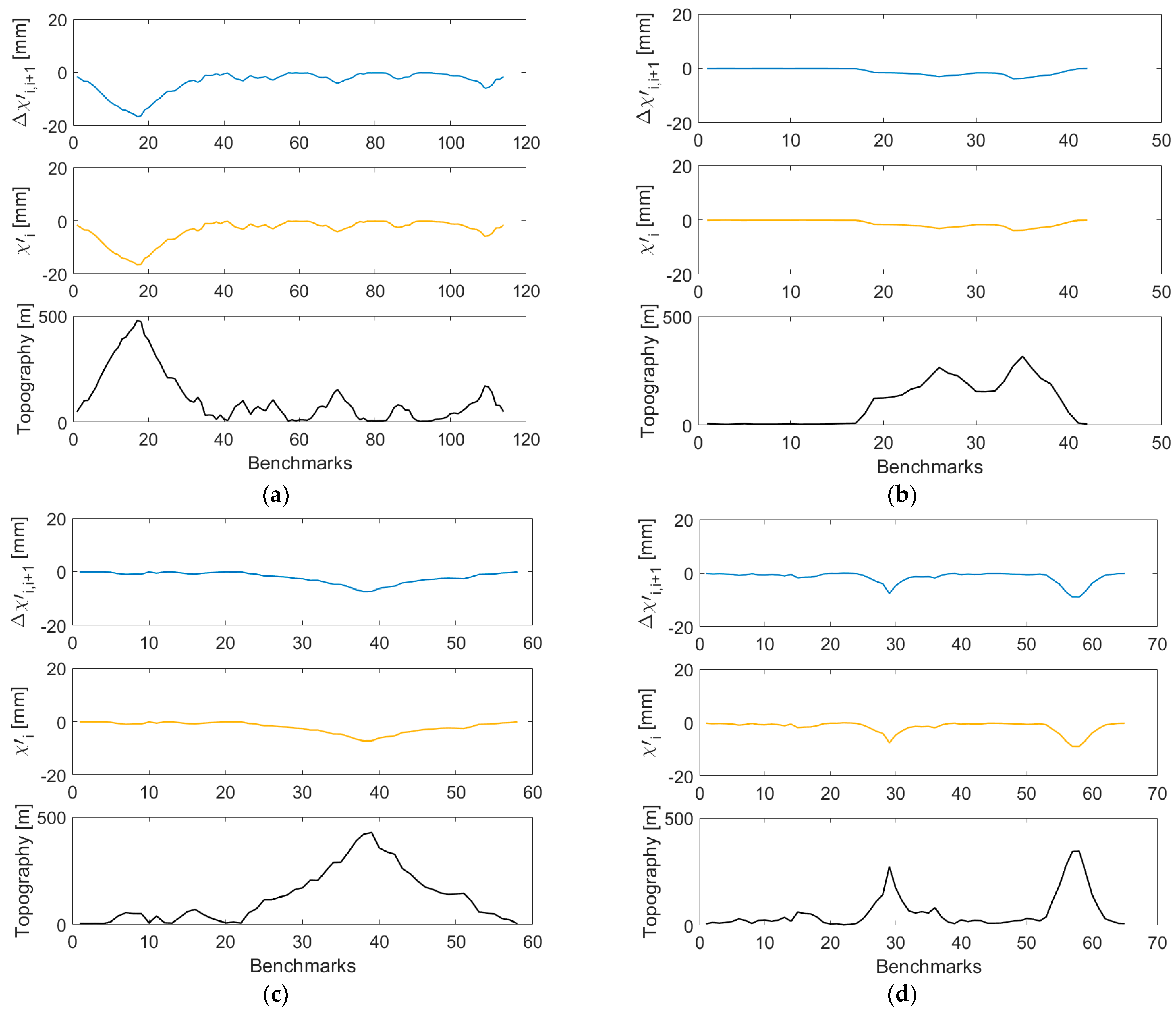
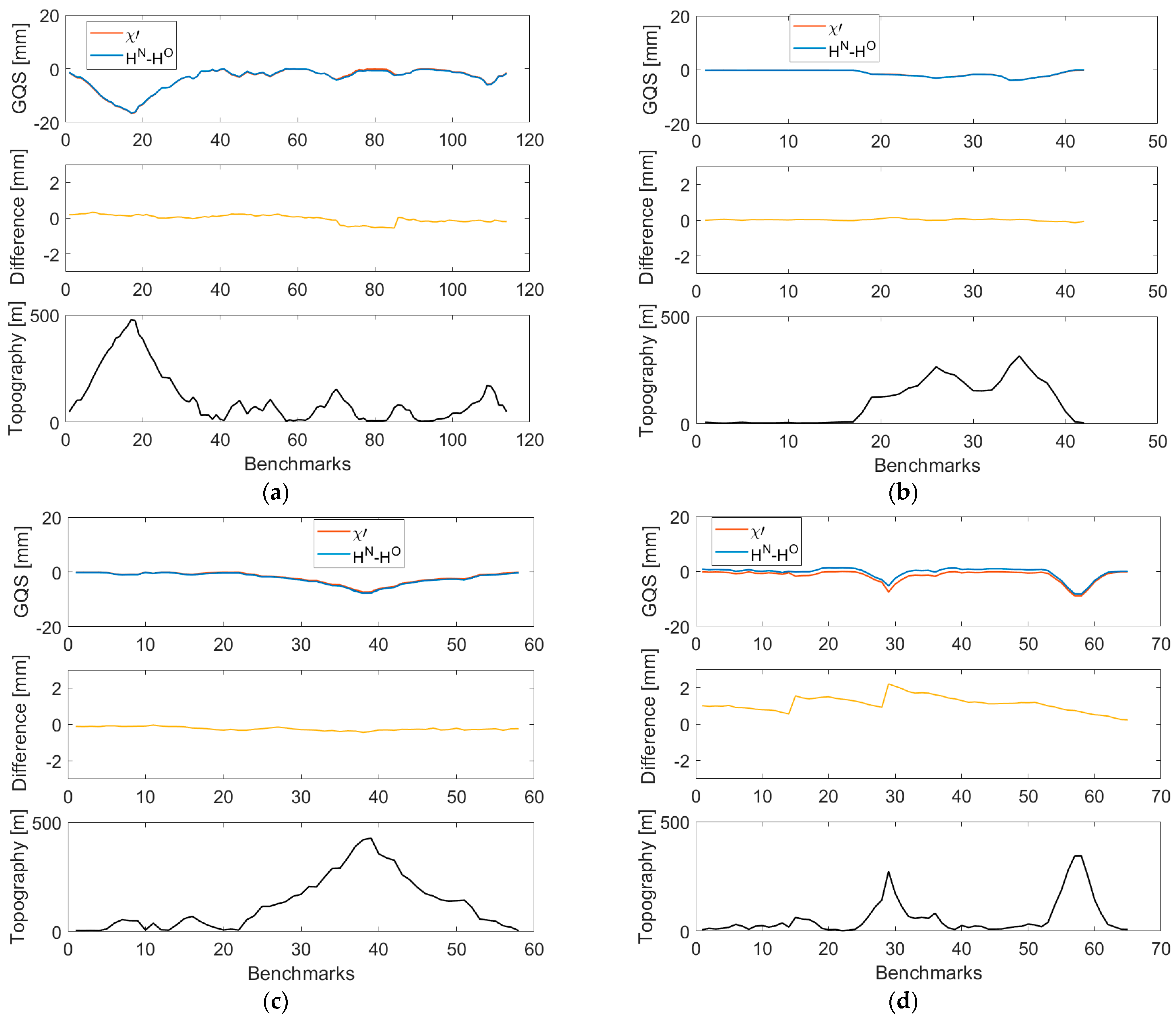
4. Results
5. Discussion
6. Summary and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Molodensky, M.S. Fundamental Problems of Geodetic Gravimetry; TRUDY Ts NIIGAIK, Geodezizdat: Moscow, Russia, 1945. (In Russian) [Google Scholar]
- Molodensky, M.S. External Gravity Field and the Shape of the Earth Surface; Izv CCCP: Moscow, Russia, 1948. (In Russian) [Google Scholar]
- Molodensky, M.S.; Yeremeev, V.F.; Yurkina, M.I. Methods for Study of the External Gravitational Field and Figure of the Earth; TRUDY Ts NIIGAiK, Geodezizdat: Moscow, Russia; Israel Program for Scientific Translation: Jerusalem, Israel, 1962; Volume 131. [Google Scholar]
- Helmert, F.R. Die Mathematischen und physikalischen Theorien der höheren Geodäsie; Teubner: Leipzig, Germany, 1884; Volume 2. [Google Scholar]
- Helmert, F.R. Die Schwerkraft im Hochgebirge, Insbesondere in den Tyroler Alpen; Veröff Königl Preuss Geod Inst: Berlin, Germany, 1890. [Google Scholar]
- Niethammer, T. Nivellement und Schwere als Mittel zur Berechnung Wahrer Meereshöhen; Schweizerische Geodätische Kommission: Zürich, Switzerland, 1932. [Google Scholar]
- Niethammer, T. Das astronomische nivellement Im Meridian des St Gotthard, Part II, Die berechneten Geoiderhebungen und der Verlauf des Geoidschnittes. In Astronomisch-Geodätische Arbeiten in der Schweiz; Swiss Geodetic Commission: Zürich, Switzerland, 1939; Volume 20, p. 47. [Google Scholar]
- Mader, K. Die Orthometrische Schwerekorrektion des Präzisions-Nivellements in den Hohen Tauern; Österreichische Zeitschrift für Vermessungswesen, Sonderheft 15: Wien, Austria, 1954. [Google Scholar]
- Ledersteger, K. Astronomische und Physikalische Geodäsie (Erdmessung). In Handbuch der Vermessungskunde; Jordan, W., Eggert, E., Kneissl, M., Eds.; Metzler: Stuttgart, Germany, 1968; Volume V. [Google Scholar]
- Sünkel, H.; Bartelme, N.; Fuchs, H.; Hanafy, M.; Schuh, W.D.; Wieser, M. The gravity field in Austria. In Geodätische Arbeiten Österreichs für Die Intenationale Erdmessung, Neue Folge; Austrian Geodetic Commission: Singapore, 1987; Volume IV, pp. 47–75. [Google Scholar]
- Wirth, B. Höhensysteme, Schwerepotentiale und Niveaufläachen. In Geodätisch-Geophysikalische Arbeiten in der Schweiz; Swiss Geodetic Commission: Zürich, Switzerland, 1990; Volume 42, p. 35. [Google Scholar]
- Marti, U. Comparison of high precision geoid models in Switzerland. In Dynamic Planet; Tregonig, P., Rizos, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Flury, J.; Rummel, R. On the geoid-quasigeoid separation in mountain areas. J. Geod. 2009, 83, 829–847. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Tenzer, R.; Vaníček, P. Correction to Helmert’s orthometric height due to actual lateral variation of topographical density. Rev. Bras. Cartogr. 2003, 55, 44–47. [Google Scholar]
- Ledersteger, K. Der Schwereverlauf in den Lotlinien und Die Berechnung der Wahren Geoidschwere; Publ Finn Geod Inst: Heiskanen, WA, USA, 1955; pp. 109–124. [Google Scholar]
- Rapp, R.H. The Orthometric Height. Master’s Thesis, Ohio State University, Department of Geodetic Science, Columbus, OH, USA, 1961; p. 117. [Google Scholar]
- Krakiwsky, E.J. Heights. Master’s Thesis, Ohio State University, Department of Geodetic Science, Columbus, OH, USA, 1965; p. 157. [Google Scholar]
- Strange, W.E. An evaluation of orthometric height accuracy using borehole gravimetry. Bull. Géod. 1982, 56, 300–311. [Google Scholar] [CrossRef]
- Sünkel, H. Digital Height and Density Model and Its Use for the Orthometric Height and Gravity Field Determination for Austria; Proc Int Symp on the Definition of the Geoid: Florence, Italy, 1986; pp. 599–604. [Google Scholar]
- Kao, S.P.; Rongshin, H.; Ning, F.S. Results of field test for computing orthometric correction based on measured gravity. Geom. Res. Aus. 2000, 72, 43–60. [Google Scholar]
- Allister, N.A.; Featherstone, W.E. Estimation of Helmert orthometric heights using digital barcode levelling, observed gravity and topographic mass-density data over part of Darling Scarp, Western Australia. Geom. Res. Aust. 2001, 75, 25–52. [Google Scholar]
- Drewes, H.; Dodson, A.H.; Fortes, L.P.; Sanchez, L.; Sandoval, P. (Eds.) Vertical Reference Systems. IAG Symposia 24; Springer: Berlin/Heidelberg, Germany, 2002; p. 353. [Google Scholar]
- Dennis, M.L.; Featherstone, W.E. Evaluation of orthometric and related height systems using a simulated mountain gravity field. In Gravity and Geoid 2002; Tziavos, I.N., Ed.; Department of Geodesy and Surveying, Aristotle University of Thessaloniki: Thessaloniki, Greece, 2003; pp. 389–394. [Google Scholar]
- Hwang, C.; Hsiao, Y.S. Orthometric height corrections from leveling, gravity, density and elevation data: A case study in Taiwan. J. Geod. 2003, 77, 292–302. [Google Scholar] [CrossRef]
- Tenzer, R. Discussion of mean gravity along the plumbline. Stud. Geoph. Geod. 2004, 48, 309–330. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Kuhn, M. Height systems and vertical datums: A review in the Australian context. J. Spatial. Sci. 2006, 51, 21–42. [Google Scholar] [CrossRef]
- Tenzer, R.; Vaníček, P.; Santos, M.; Featherstone, W.E.; Kuhn, M. The rigorous determination of orthometric heights. J. Geod. 2005, 79, 82–92. [Google Scholar] [CrossRef]
- Santos, M.C.; Vaníček, P.; Featherstone, W.E.; Kingdon, R.; Ellmann, A.; Martin, B.-A.; Kuhn, M.; Tenzer, R. The relation between rigorous and Helmert’s definitions of orthometric heights. J. Geod. 2006, 80, 691–704. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A strict formula for geoid-to-quasigeoid separation. J. Geod. 2010, 84, 699–702. [Google Scholar] [CrossRef]
- Foroughi, I.; Tenzer, R. Comparison of different methods for estimating the geoid-to-quasigeoid separation. Geophys. J. Int. 2017, 210, 1001–1020. [Google Scholar] [CrossRef]
- Heiskanen, W.H.; Moritz, H. Physical Geodesy; WH Freeman and Co.: San Francisco, NC, USA, 1967. [Google Scholar]
- Sjöberg, L.E. On the quasigeoid to geoid separation. Manuscr. Geod. 1995, 20, 182–192. [Google Scholar]
- Sjöberg, L.E. On the Downward Continuation Error at the Earth’s Surface and the Geoid of Satellite Derived Geopotential Models. Boll. Geod. Sci. Affin. 1999, 58, 215–229. [Google Scholar]
- Sjöberg, L.E. A refined conversion from normal height to orthometric height. Stud. Geophys. Geod. 2006, 50, 595–606. [Google Scholar] [CrossRef]
- Sjöberg, L.E. The topographical bias by analytical continuation in physical geodesy. J. Geod. 2007, 81, 345–350. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Rigorous geoid-from-quasigeoid correction using gravity disturbances. J. Geod. Sci. 2015, 5, 115–118. [Google Scholar] [CrossRef]
- Rapp, R.H. Use of potential coefficient models for geoid undulation determinations using a spherical harmonic representation of the height anomaly/geoid undulation difference. J. Geod. 1997, 71, 282–289. [Google Scholar] [CrossRef]
- Tenzer, R.; Moore, P.; Novák, P.; Kuhn, M.; Vaníček, P. Explicit formula for the geoid-to-quasigeoid separation. Stud. Geoph. Geod. 2006, 50, 607–618. [Google Scholar] [CrossRef]
- Tenzer, R.; Hirt, C.; Claessens, S.; Novák, P. Spatial and spectral representations of the geoid-to-quasigeoid correction. Surv. Geophys. 2015, 36, 627. [Google Scholar] [CrossRef]
- Tenzer, R.; Hirt, C.; Novák, P.; Pitoňák, M.; Šprlák, M. Contribution of mass density heterogeneities to the geoid-to-quasigeoid separation. J. Geod. 2016, 90, 65–80. [Google Scholar] [CrossRef]
- Tenzer, R.; Foroughi, I.; Sjöberg, L.E.; Bagherbandi, M.; Hirt, C.; Pitoňák, M. Definition of physical height systems for telluric planets and moons. Surv. Geophys. 2018, 39, 313–335. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W.; Rathnayake, S.; Pitoňák, M. The effect of anomalous global lateral topographic density on the geoid-to-quasigeoid separation. J. Geod. 2020, 95, 12. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. Quasigeoid-to-geoid determination by EGM08. Earth Sci. Inform. 2012, 5, 87–91. [Google Scholar] [CrossRef]
- Bagherbandi, M.; Tenzer, R. Geoid-to-quasigeoid separation computed using the GRACE/GOCE global geopotential model GOCO02S—A case study of Himalayas, Tibet and central Siberia. Terr. Atmo. Ocean Sci. 2013, 24, 59–68. [Google Scholar] [CrossRef]
- Tenzer, R.; Foroughi, I. Effect of the mean dynamic topography on the geoid-to-quasigeoid separation offshore. Mar. Geod. 2018, 41, 368–381. [Google Scholar] [CrossRef]
- Tenzer, R.; Foroughi, I. On the applicability of Molodensky’s concept of heights in planetary sciences. Special Issue: Gravity Field Determination and Its Temporal Variation. Geosciences 2018, 8, 239. [Google Scholar] [CrossRef]
- Bruns, H. Die Figur der Erde; Published Preuss Geod Inst: Berlin, Germany, 1878. [Google Scholar]
- Pizzetti, P. Sopra il calcolo teorico delle deviazioni del geoide dall` ellissoide. Atti. R Accad. Sci. Torino 1911, 46, 331–350. [Google Scholar]
- Somigliana, C. Teoria Generale del Campo Gravitazionale dell’Ellisoide di Rotazione; Memoire della Societa Astronomica Italiana: Milano, Italy, 1929; p. 425. [Google Scholar]
- Filmer, M.S.; Featherstone, W.E.; Kuhn, M. The effect of EGM2008-based normal, normal-orthometric and Helmert orthometric height systems on the Australian levelling network. J. Geod. 2010, 84, 501–513. [Google Scholar] [CrossRef]
- Tenzer, R.; Vatrt, V.; Abdalla, A.; Dayoub, N. Assessment of the LVD offsets for the normal-orthometric heights and different permanent tide systems—A case study of New Zealand. Appl. Geomat. 2011, 3, 1–8. [Google Scholar] [CrossRef]
- Tenzer, R.; Vatrt, V.; Luzi, G.; Abdalla, A.; Dayoub, N. Combined approach for the unification of levelling networks in New Zealand. J. Geod. Sci. 2011, 1, 324–332. [Google Scholar] [CrossRef]
- Hinze, W.J. Bouguer reduction density, why 2.67? Geophysics 2003, 68, 1559–1560. [Google Scholar] [CrossRef]
- Nsiah Ababio, A.; Tenzer, R. The use of gravity data to determine orthometric heights at the Hong Kong territories. J. Appl. Geod. 2022, 16, 401–416. [Google Scholar] [CrossRef]
- Vaníček, P.; Tenzer, R.; Sjöberg, L.E.; Martinec, Z.; Featherstone, W.E. New views of the spherical Bouguer gravity anomaly. Geophys. J. Int. 2005, 159, 460–472. [Google Scholar] [CrossRef]
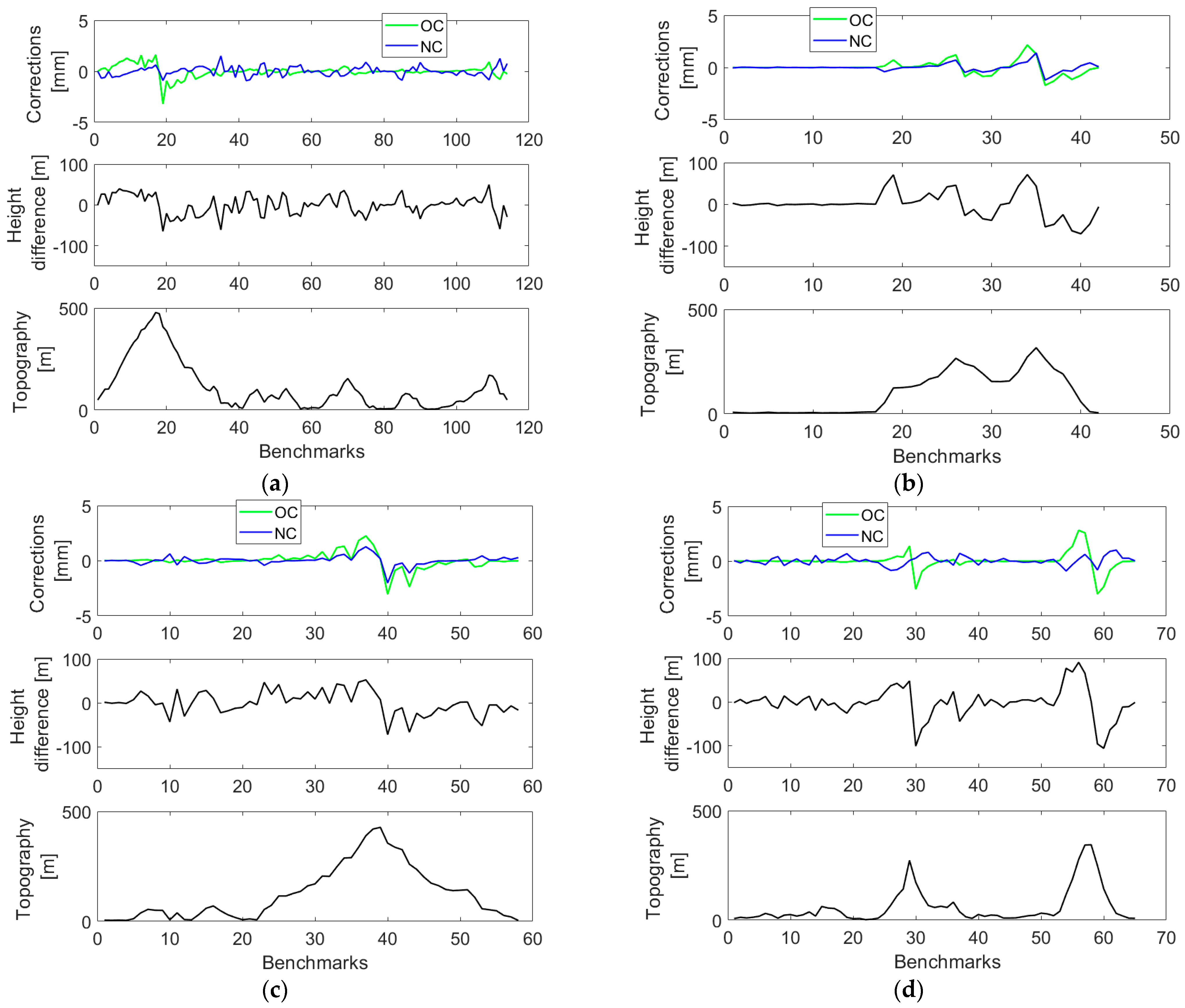
| Orthometric Corrections | ||||
| LOOPS | MIN [mm] | MAX [mm] | MEAN [mm] | STD [mm] |
| L5/NT | −3.2 | 1.6 | 0.0 | 0.6 |
| L5/HK | −1.7 | 2.2 | 0.0 | 0.7 |
| L8/HK | −3.1 | 2.2 | 0.0 | 0.8 |
| L12/HK | −3.0 | 2.8 | 0.0 | 0.8 |
| Normal Corrections | ||||
| L5/NT | −0.9 | 1.5 | 0.0 | 0.4 |
| L5/HK | −1.2 | 1.4 | 0.0 | 0.4 |
| L8/HK | −2.0 | 1.3 | 0.0 | 0.4 |
| L12/HK | −0.9 | 1.0 | 0.0 | 0.4 |
| Height differences | ||||
| LOOPS | MIN [m] | MAX [m] | MEAN [m] | STD [m] |
| L5/NT | −64.565 | 49.667 | −0.036 | 23.642 |
| L5/HK | −70.247 | 71.207 | 0.000 | 31.656 |
| L8/HK | −71.900 | 52.568 | 0.000 | 26.868 |
| L12/HK | −105.580 | 90.796 | −1.829 | 35.269 |
| Topography | ||||
| L5/NT | 4.109 | 478.233 | 110.541 | 118.707 |
| L5/HK | 3.850 | 316.242 | 102.053 | 100.755 |
| L8/HK | 3.844 | 427.394 | 125.350 | 121.717 |
| L12/HK | 2.150 | 344.152 | 60.358 | 80.841 |
| Cumulative Orthometric Correction | ||||
| LOOPS | MIN [mm] | MAX [mm] | MEAN [mm] | STD [mm] |
| L5/NT | −0.4 | 13.2 | 1.5 | 3.0 |
| L5/HK | −0.1 | 5.5 | 1.1 | 1.4 |
| L8/HK | −0.1 | 10.8 | 1.8 | 2.8 |
| L12/HK | −1.0 | 6.6 | 0.1 | 1.5 |
| Cumulative normal correction | ||||
| L5/NT | −3.6 | 1.5 | −0.5 | 1.5 |
| L5/HK | −0.8 | 1.8 | −0.1 | 0.5 |
| L8/HK | −1.1 | 3.6 | −0.2 | 1.0 |
| L12/HK | −3.8 | 1.1 | −1.0 | 1.1 |
| Differences in cumulative corrections | ||||
| L5/NT | −15.0 | 1.5 | −2.1 | 4.2 |
| L5/HK | −3.8 | 0.0 | −1.2 | 1.2 |
| L8/HK | −7.2 | 0.0 | −2.0 | 2.1 |
| L12/HK | −8.6 | 1.2 | −1.1 | 2.2 |
| Normal and Orthometric Correction Differences (NC–OC) | ||||
| LOOPS | MIN [mm] | MAX [mm] | MEAN [mm] | STD [mm] |
| L5/NT | −1.8 | 2.3 | 0.0 | 0.8 |
| L5/HK | −1.6 | 0.9 | 0.0 | 0.4 |
| L8/HK | −1.0 | 1.3 | 0.0 | 0.5 |
| L12/HK | −2.6 | 2.8 | 0.1 | 0.9 |
| Geoid-to-quasigeoid separation differences | ||||
| L5/NT | −1.8 | 2.3 | 0.0 | 0.8 |
| L5/HK | −1.6 | 0.9 | 0.0 | 0.4 |
| L8/HK | −1.0 | 1.3 | 0.0 | 0.5 |
| L12/HK | −2.6 | 2.8 | 0.1 | 0.9 |
| Cumulatively Computed Values of the Geoid-to-Quasigeoid Separation | ||||
| LOOPS | MIN [mm] | MAX [mm] | MEAN [mm] | STD [mm] |
| L5/NT | −16.6 | −0.1 | −3.7 | 4.2 |
| L5/HK | −3.9 | −0.1 | −1.2 | 1.2 |
| L8/HK | −7.3 | −0.1 | −2.1 | 2.1 |
| L12/HK | −8.9 | −0.1 | −1.6 | 2.1 |
| Pointwise computed values of the geoid-to-quasigeoid separation | ||||
| L5/NT | −16.6 | −0.1 | −3.7 | 4.2 |
| L5/HK | −3.9 | −0.1 | −1.2 | 1.2 |
| L8/HK | −7.3 | −0.1 | −2.1 | 2.1 |
| L12/HK | −8.9 | −0.1 | −1.6 | 2.1 |
| Pointwise Geoid-to-Quasigeoid Separation | ||||
| LOOPS | MIN [mm] | MAX [mm] | MEAN [mm] | STD [mm] |
| L5/NT | −16.615 | −0.122 | −3.667 | 4.231 |
| L5/HK | −3.881 | −0.054 | −1.239 | 1.220 |
| L8/HK | −7.272 | −0.069 | −2.050 | 2.058 |
| L12/HK | −8.857 | −0.060 | −1.571 | 2.105 |
| Differences between Molodensky normal heights and Helmert orthometric heights | ||||
| L5/NT | −16.500 | 0.000 | −3.689 | 4.146 |
| L5/HK | −3.900 | 0.000 | −1.257 | 1.230 |
| L8/HK | −7.700 | −0.200 | −2.279 | 2.123 |
| L12/HK | −8.200 | 1.300 | −0.466 | 2.149 |
| Differences | ||||
| L5/NT | −0.552 | 0.326 | −0.020 | 0.227 |
| L5/HK | −0.142 | 0.144 | 0.018 | 0.053 |
| L8/HK | −0.428 | −0.034 | −0.230 | 0.096 |
| L12/HK | 0.226 | 2.196 | 1.105 | 0.422 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tenzer, R.; Nsiah Ababio, A. On the Consistency between a Classical Definition of the Geoid-to-Quasigeoid Separation and Helmert Orthometric Heights. Sensors 2023, 23, 5185. https://doi.org/10.3390/s23115185
Tenzer R, Nsiah Ababio A. On the Consistency between a Classical Definition of the Geoid-to-Quasigeoid Separation and Helmert Orthometric Heights. Sensors. 2023; 23(11):5185. https://doi.org/10.3390/s23115185
Chicago/Turabian StyleTenzer, Robert, and Albertini Nsiah Ababio. 2023. "On the Consistency between a Classical Definition of the Geoid-to-Quasigeoid Separation and Helmert Orthometric Heights" Sensors 23, no. 11: 5185. https://doi.org/10.3390/s23115185






