A Smart Active Phase-Change Micropump Based on CMOS-MEMS Technology
Abstract
1. Introduction
2. Materials and Methods
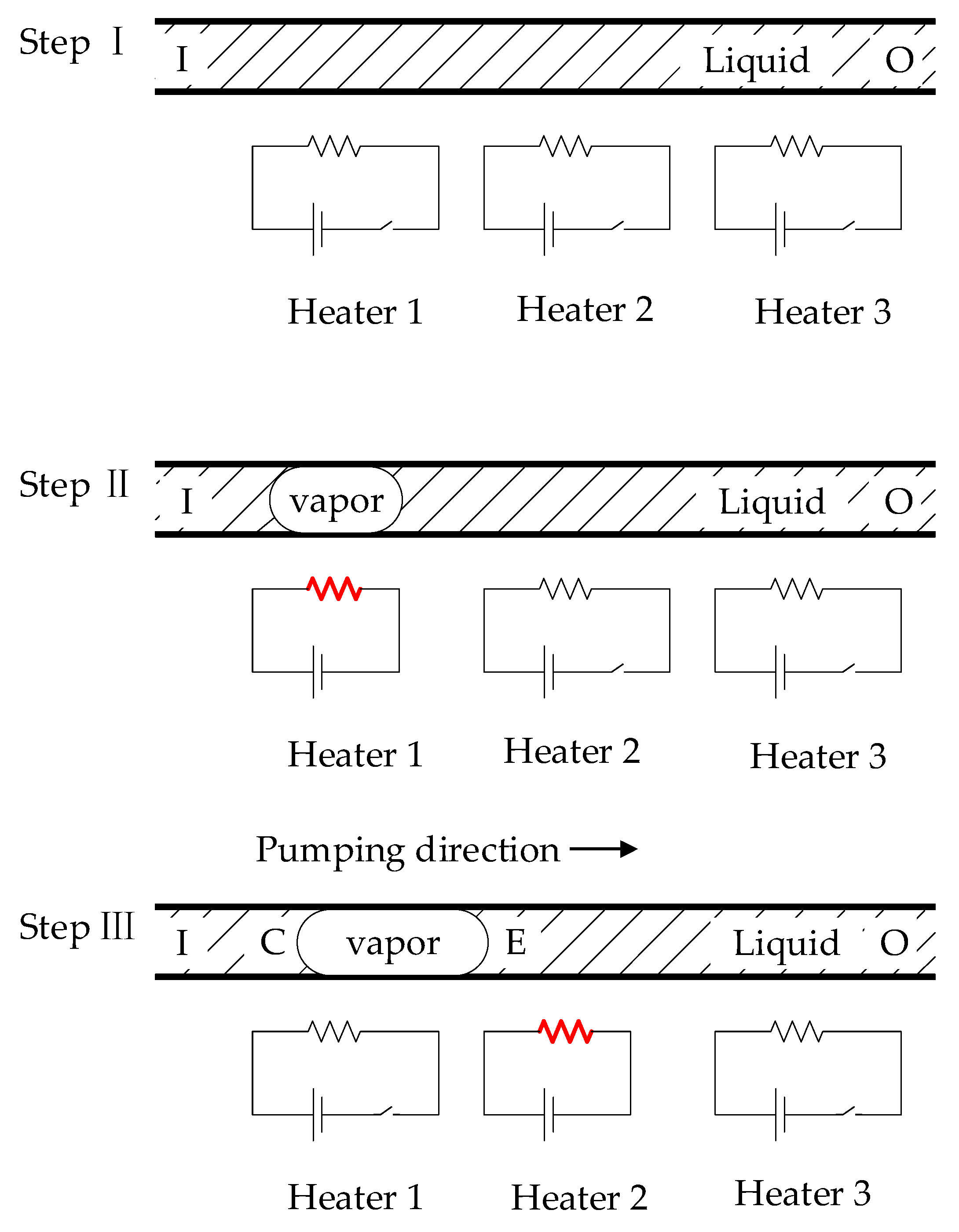
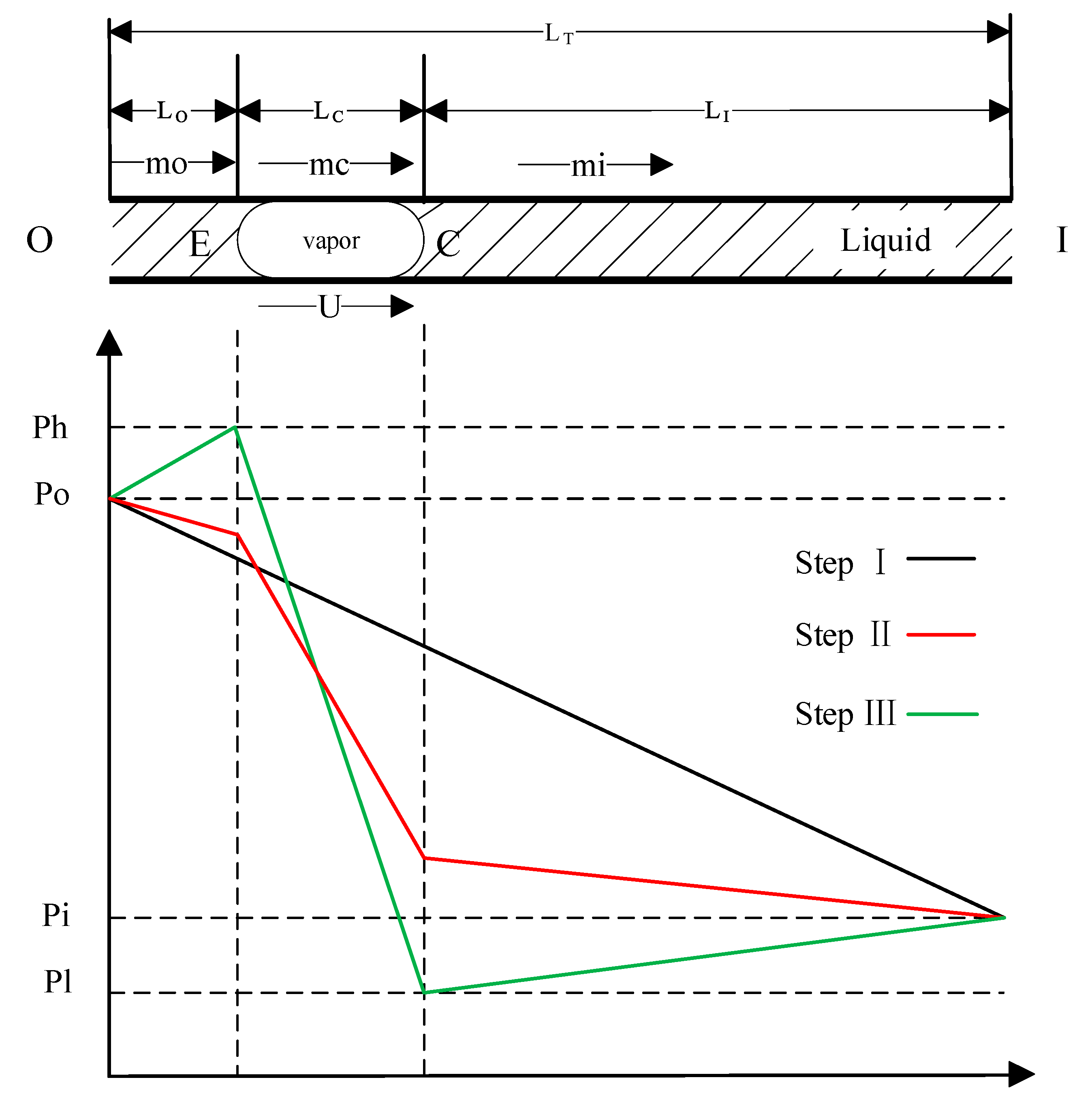
2.1. Principle of Pumping
2.2. Micropump CMOS Design
2.3. Micropump MEMS Design
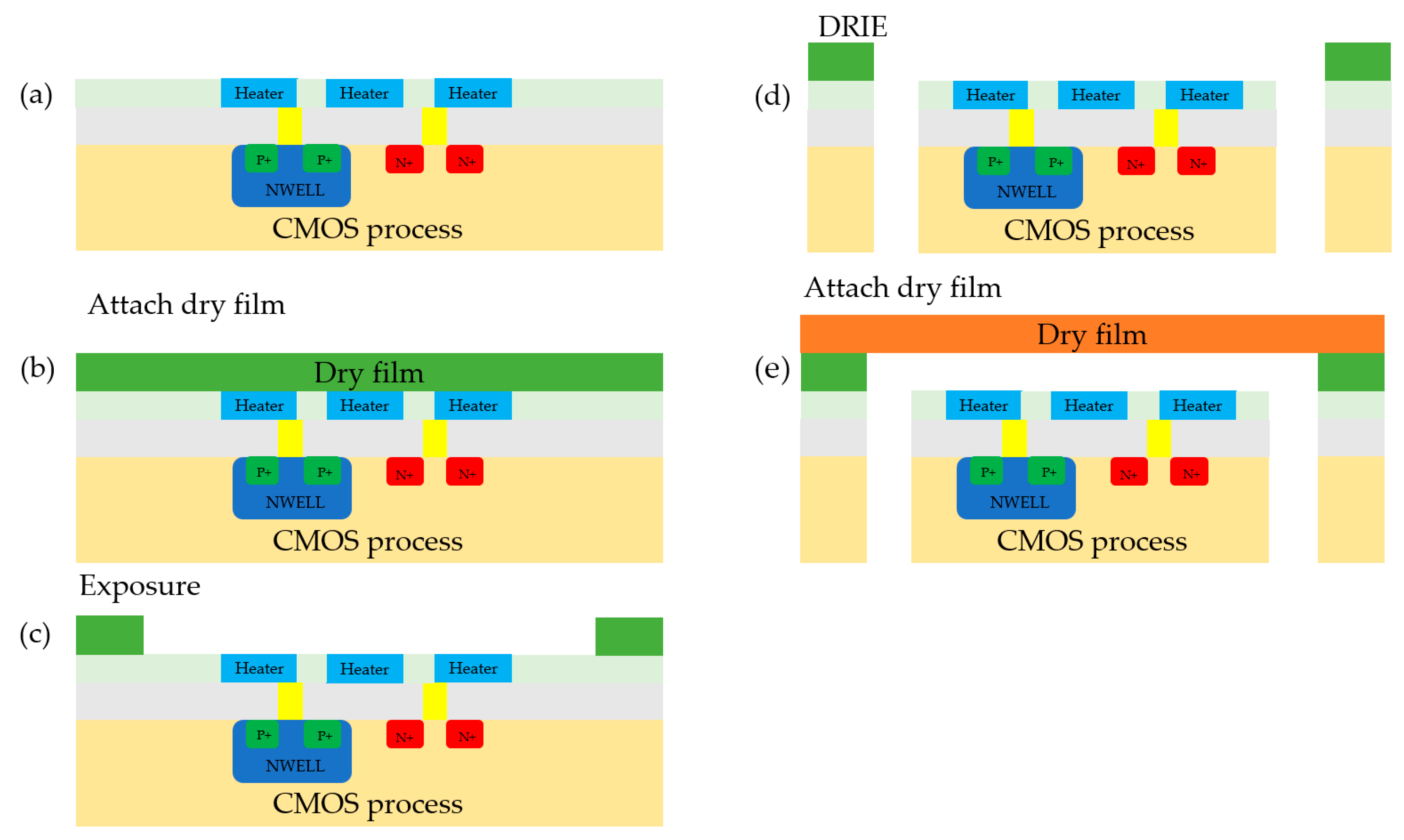
2.4. Micropump Fabrication
- A high signal-to-noise ratio is possible while reducing the interference between external leads and sensitive positions and minimizing parasitic and cross-coupling effects.
- By integrating internal sensors and control signals, it is possible to achieve the integration of large array units and effectively reduce the number of external leads in these large arrays. This enables better integration of even larger arrays and facilitates the realization of an intelligent system.
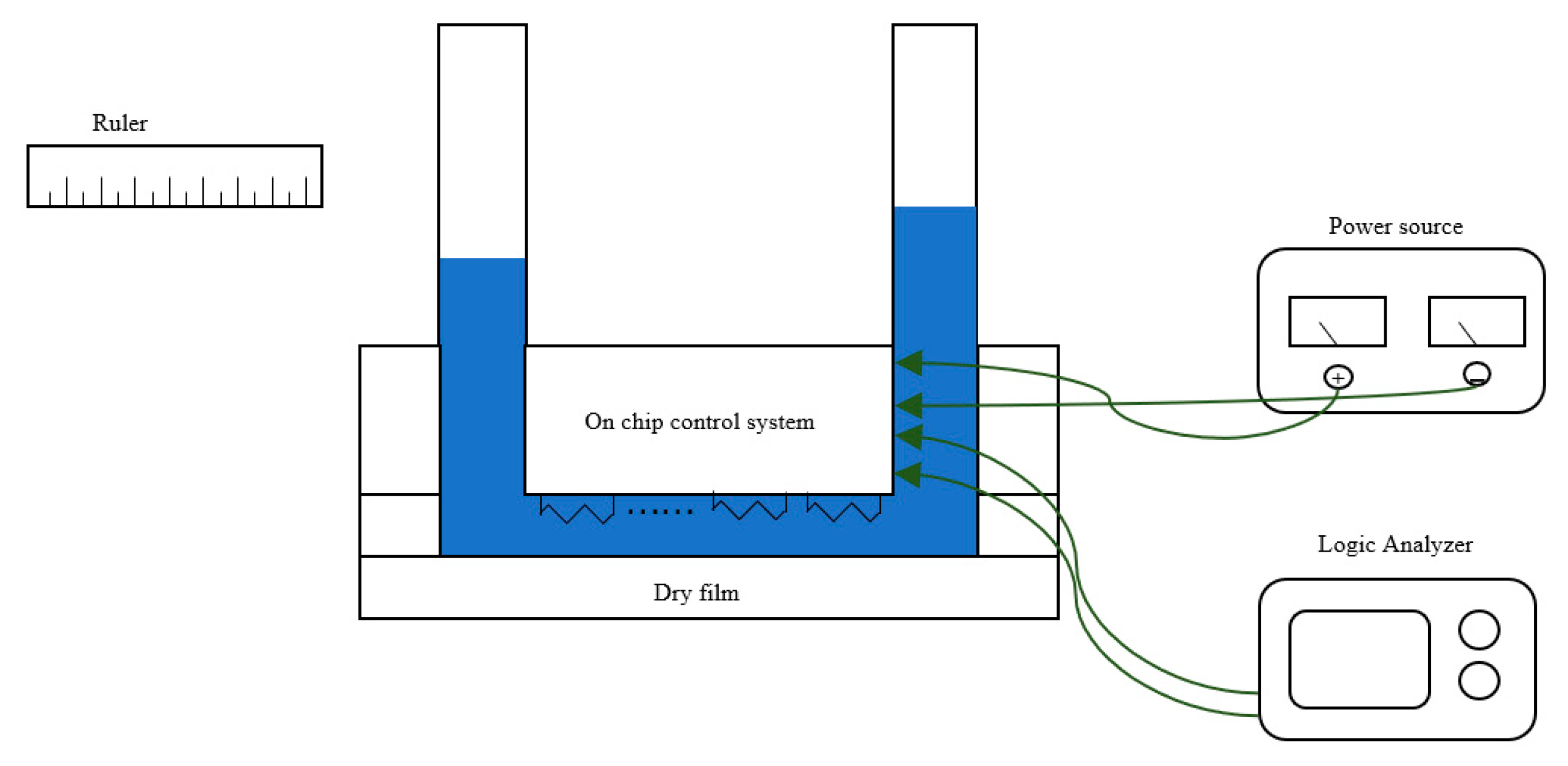
2.5. Experimental System
3. Results
3.1. Bubble Nucleation
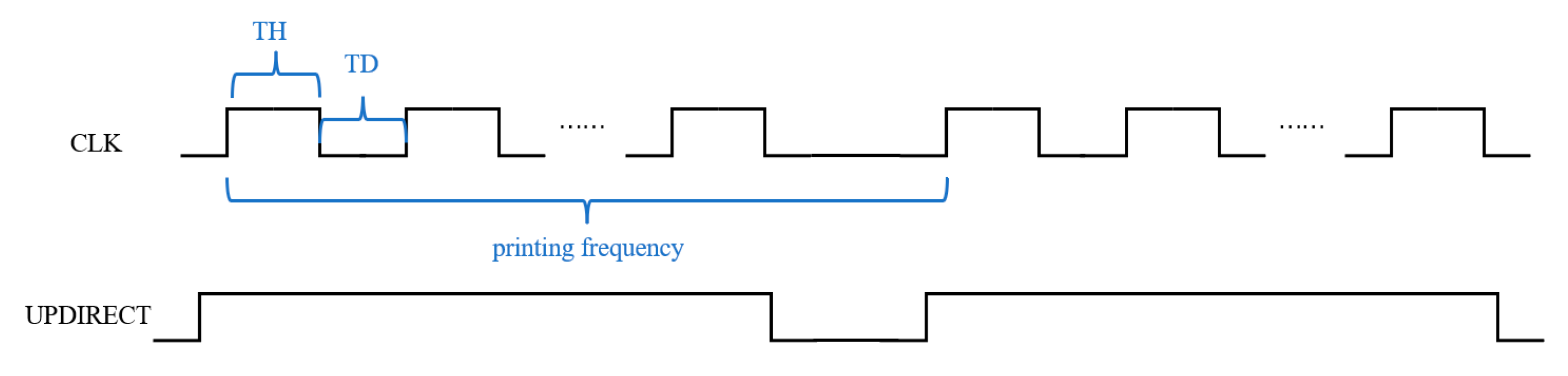
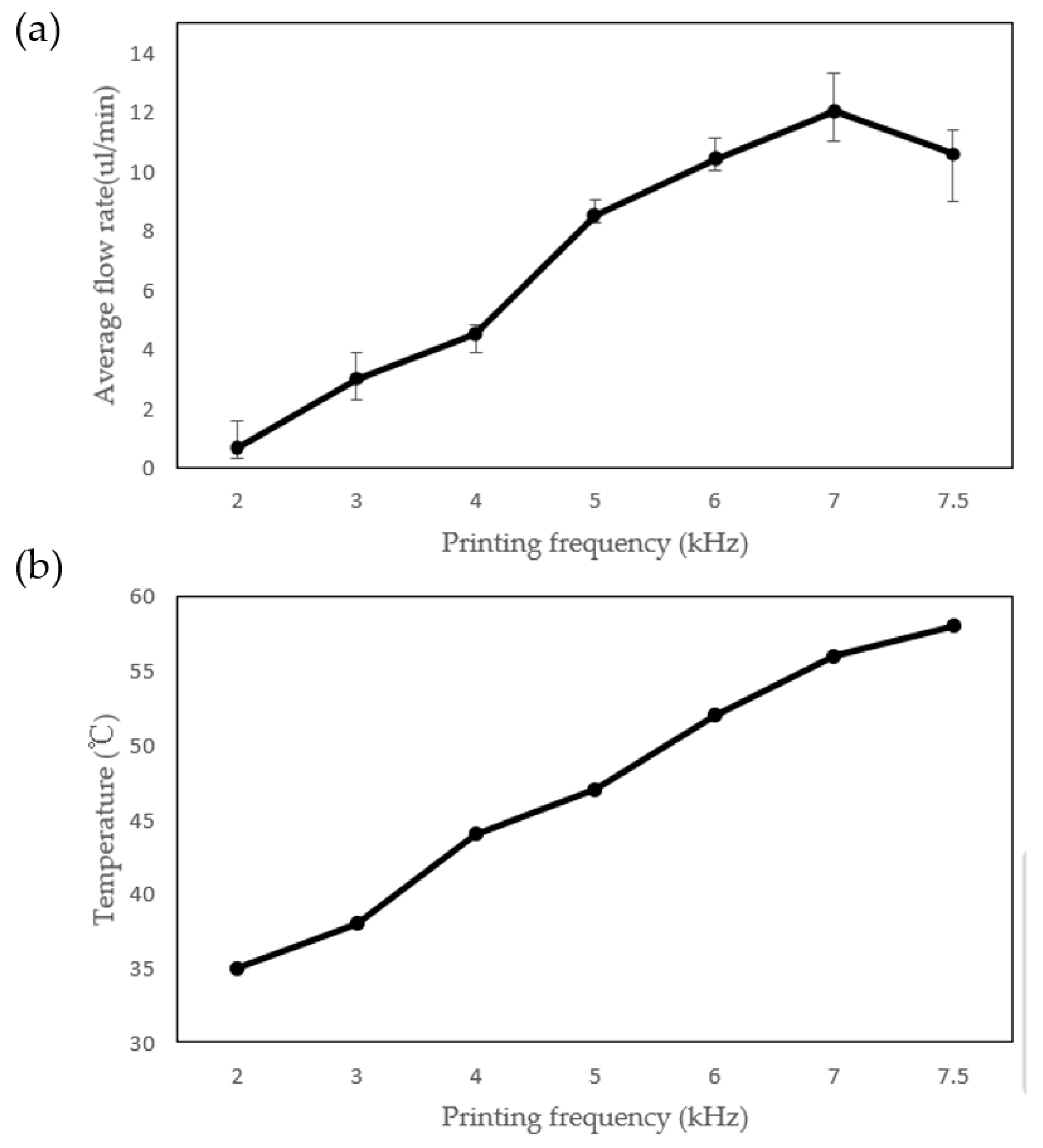
3.2. Optimization of Printing Frequency
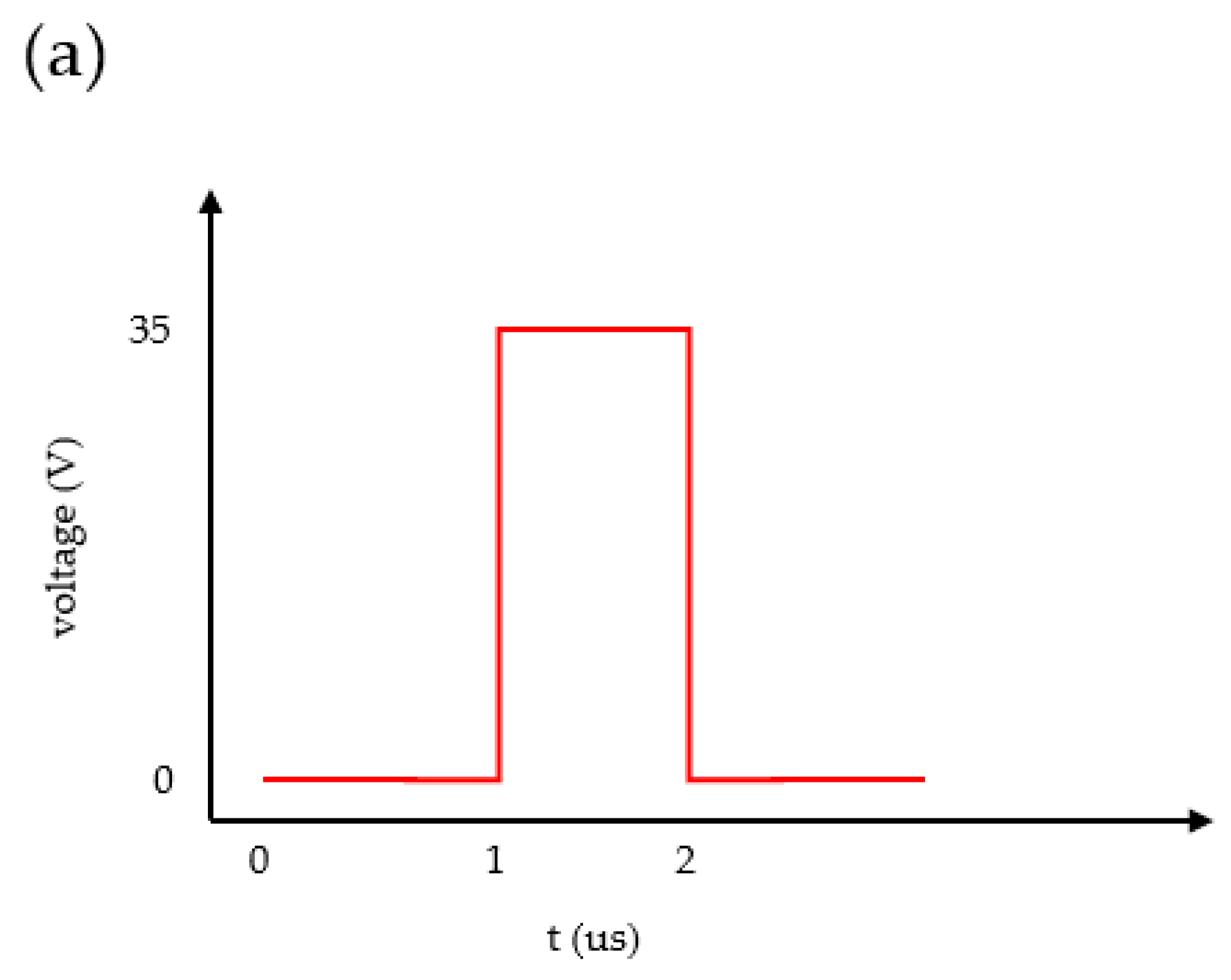
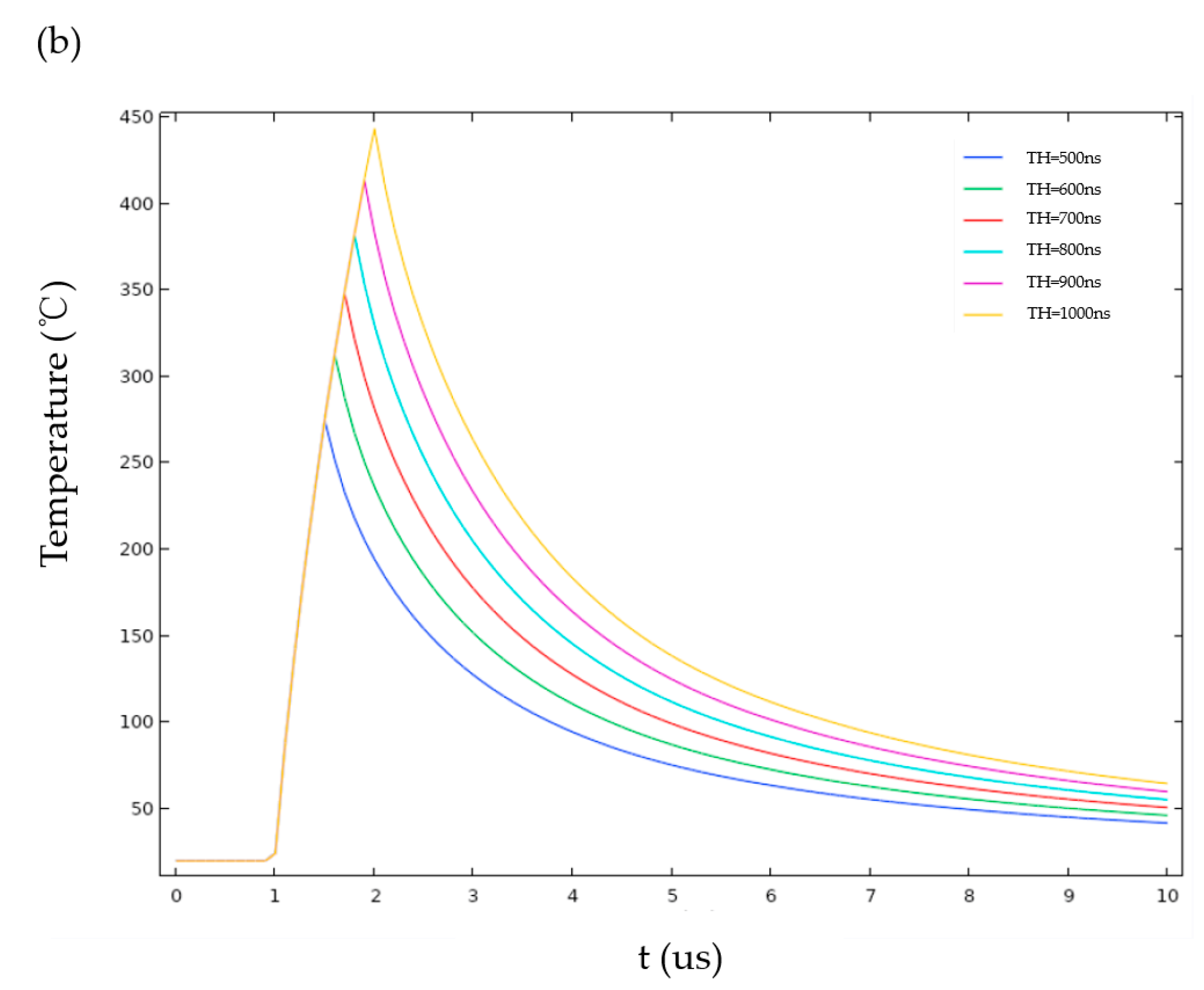
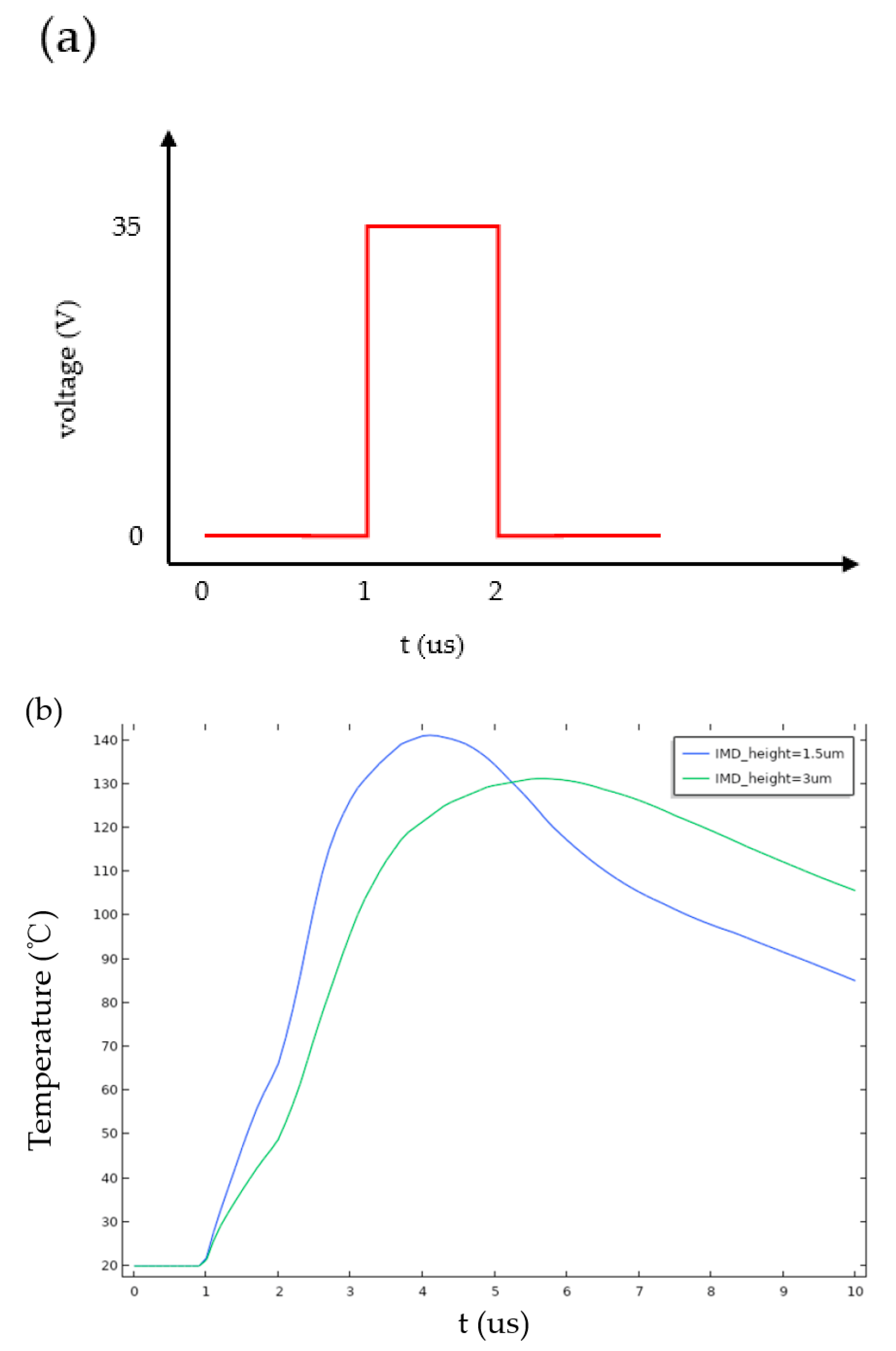
3.3. Thermal Effect
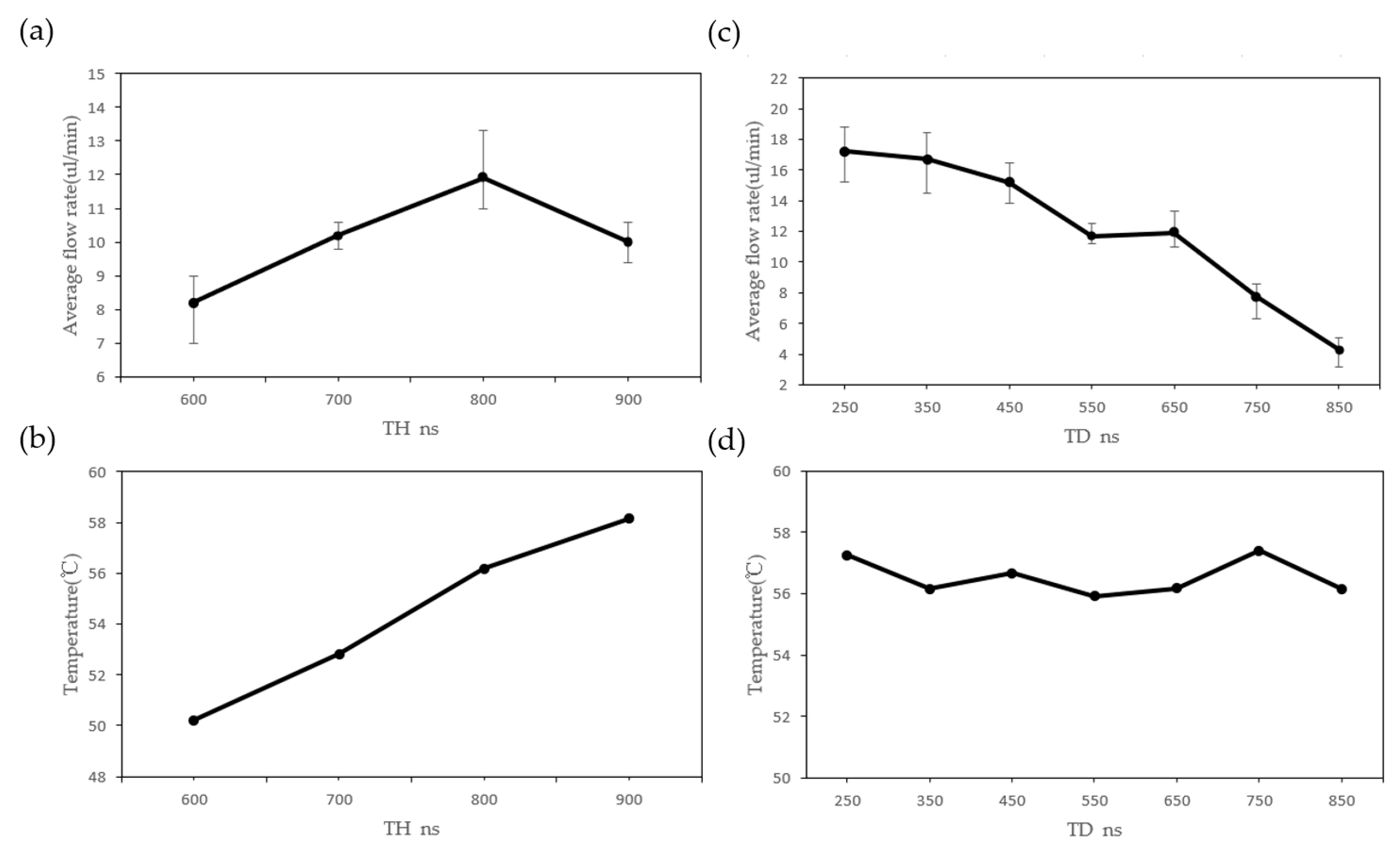
3.4. Optimization of Pumping Conditions
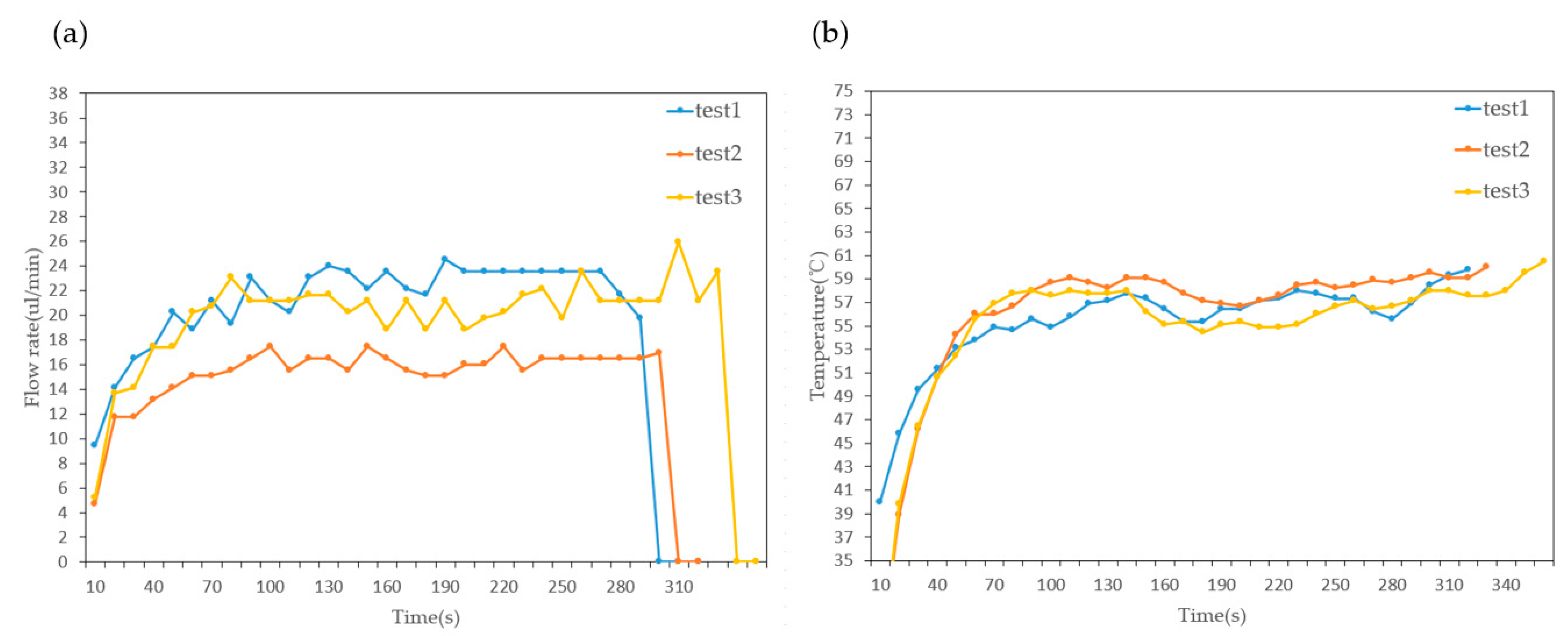
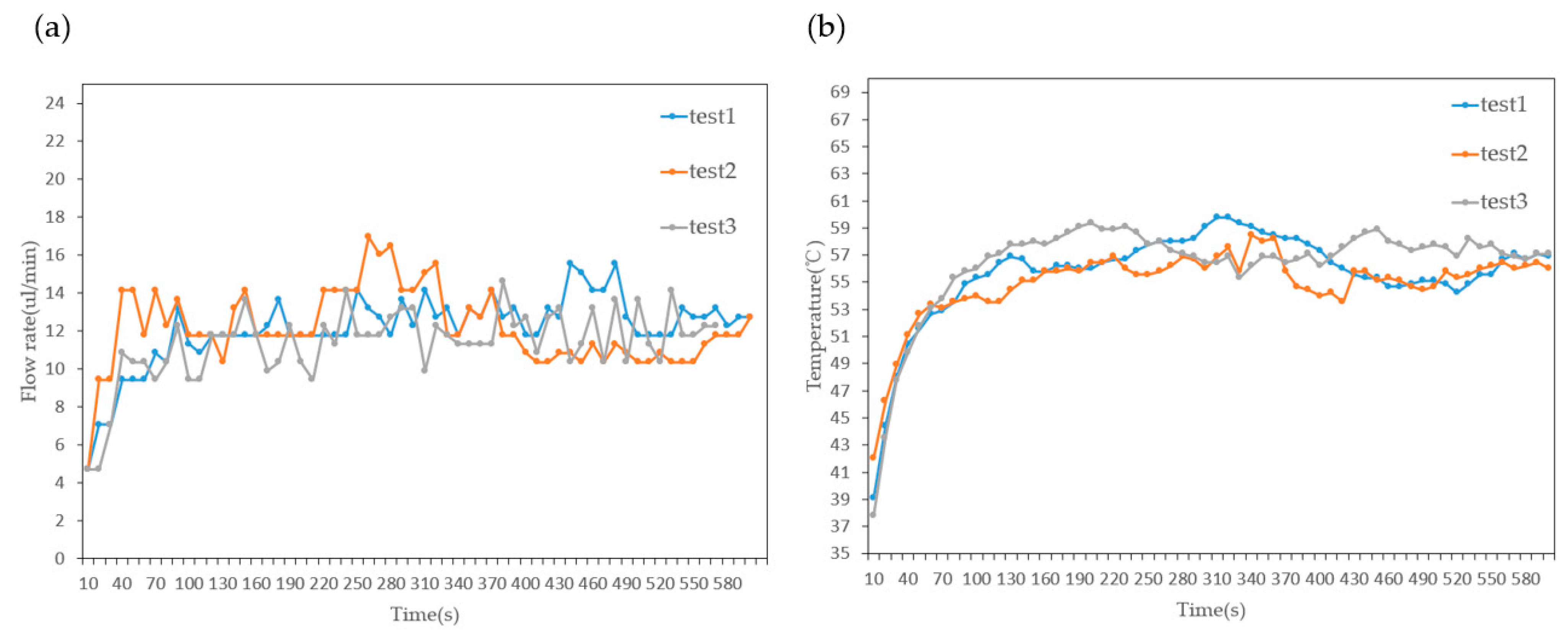
3.5. Optimization of Pumping Stability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, N.; Huang, X.; Chuan, T.K. MEMS-Micropumps: A Review. ASME J. Fluids Eng. 2002, 124, 384–392. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid Physics at the Nanoliter Scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Takagi, H.; Maeda, R.; Ozaki, K.; Parameswaran, M.; Mehta, M. Phase Transformation Type Micro Pump. In Proceedings of the 1994 5th International Symposium on Micro Machine and Human Science Proceedings; IEEE: Nagoya, Japan, 1994; p. 199. [Google Scholar]
- Mao, Z.; Asai, Y.; Wiranata, A.; Kong, D.; Man, J. Eccentric Actuator Driven by Stacked Electrohydrodynamic Pumps. J. Zhejiang Univ. Sci. A 2022, 23, 329–334. [Google Scholar] [CrossRef]
- Manz, A.; Effenhauser, C.S.; Burggraf, N.; Harrison, D.J.; Seiler, K.; Fluri, K. Electroosmotic Pumping and Electrophoretic Separations for Miniaturized Chemical Analysis Systems. J. Micromech. Microeng. 1994, 4, 257–265. [Google Scholar] [CrossRef]
- Azimi-Boulali, J.; Zakeri, M.; Shoaran, M. A Study on the 3D Fluid Flow of MHD Micropump. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 478. [Google Scholar] [CrossRef]
- Singhal, V.; Garimella, S.V.; Raman, A. Microscale Pumping Technologies for Microchannel Cooling Systems. Appl. Mech. Rev. 2004, 57, 191–221. [Google Scholar] [CrossRef]
- Saidi, M.H.; Sadjadi, B.; Safaei, H.; Pirouzpanah, S. Experimental and Analytical Modeling of Phase Change Micropump. In Proceedings of the ASME 8th Biennial Conference on Engineering Systems Design and Analysis, Turin, Italy, 4–7 July 2006. [Google Scholar]
- Xu, W.; Wang, X.; Wang, R.; Izhar; Xu, J.; Lee, Y.-K. CMOS MEMS Thermal Flow Sensor With Enhanced Sensitivity for Heating, Ventilation, and Air Conditioning Application. IEEE Trans. Ind. Electron. 2021, 68, 4468–4476. [Google Scholar] [CrossRef]
- Tsukada, T.; Takigawa, R.; Hasegawa, Y.; Al Farisi, M.S.; Shikida, M. Sensitivity Enhancement of Tube-Integrated MEMS Flow Sensor Using Flexible Copper on Polyimide Substrate. Micromachines 2022, 14, 42. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, K. Pumping Mechanism Using Periodic Phase Changes of a Fluid. In Proceedings IEEE Micro Electro Mechanical Systems; IEEE: Amsterdam, The Netherlands, 1995; p. 31. [Google Scholar]
- Yuan, H.; Oguz, H.; Prosperetti, A. Growth and collapse of a vapor bubble in a small tube. Int. J. Heat Mass Transf. 1999, 42, 3643–3657. [Google Scholar] [CrossRef]
- Yuan, H.; Prosperetti, A. The pumping effect of growing and collapsing bubbles in a tube. J. Micromech. Microeng. 1999, 9, 402–413. [Google Scholar] [CrossRef]
- Jun, T.K.; Kim, C.-J. “CJ” Valveless Pumping Using Traversing Vapor Bubbles in Microchannels. J. Appl. Phys. 1998, 83, 5658–5664. [Google Scholar] [CrossRef]
- Yousefzadeh, B.; Shalmany, S.H.; Makinwa, K.A. A BJT-Based Temperature-to-Digital Converter With ±60 mK (3σ) Inaccuracy From −55 °C to +125 °C in 0.16-μm CMOS. IEEE J. Solid State Circuits 2017, 52, 1044–1052. [Google Scholar] [CrossRef]
- Yousefzadeh, B.; Shalmany, S.H.; Makinwa, K. A BJT-Based Temperature-to-Digital Converter with ±60mK (3σ) Inaccuracy from −70 °C to 125 °C in 160 nm CMOS. In Proceedings of the 2016 IEEE Symposium on VLSI Circuits (VLSI-Circuits), Honolulu, HI, USA, 15–17 June 2016; IEEE: Honolulu, HI, USA, 2016; pp. 1–2. [Google Scholar]
- Torniainen, E.D.; Govyadinov, A.N.; Markel, D.P.; Kornilovitch, P.E. Bubble-Driven Inertial Micropump. Phys. Fluids 2012, 24, 122003. [Google Scholar] [CrossRef]
- Song, Y.J.; Zhao, T.S. Modelling and Test of a Thermally-Driven Phase-Change Nonmechanical Micropump. J. Micromech. Microeng. 2001, 11, 713–719. [Google Scholar] [CrossRef]
- Li, Z.; Wang, M.; Tan, L. Experimental investigation on phase transformation type micropump. Chin. Sci. Bull. 2002, 47, 519–523. [Google Scholar]
- Cornell, R. A Theoretical and Experimental Examination of Thermal Inkjet Nucleation Criteria. Recent Prog. Ink Jet Technol. 1999, 12, 108–113. [Google Scholar]
- Guo, G.; Wu, X.; Liu, D.; Liao, L.; Zhang, D.; Zhang, Y.; Mao, T.; He, Y.; Huang, P.; Wang, W.; et al. A Self-Regulated Microfluidic Device with Thermal Bubble Micropumps. Micromachines 2022, 13, 1620. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Korolj, A.; Lai, B.F.L.; Radisic, M. Advances in Organ-on-a-Chip Engineering. Nat. Rev. Mater. 2018, 3, 257–278. [Google Scholar] [CrossRef]
- Beckwitt, C.H.; Clark, A.M.; Wheeler, S.; Taylor, D.L.; Stolz, D.B.; Griffith, L.; Wells, A. Liver ‘Organ on a Chip’. Exp. Cell Res. 2018, 363, 15–25. [Google Scholar] [CrossRef] [PubMed]




| Parameter | Phase-Change Micropump [3] | Electrohydrodynamic Micropump | Electroosmotic Micropump [7] | Magnetohydrodynamic Micropump [7] |
|---|---|---|---|---|
| Bidirectional | Yes | Yes | Yes | Yes |
| Miniaturization potential | High | High | Medium | Medium |
| Moving parts | No | No | No | No |
| Fabrication (ease of alignment) | Silicon micromachining; heating alignment required | Silicon micromachining; no alignment | Not compatible with silicon micromachining | Silicon micromachining |
| Advantages and disadvantages | Simple structure; low cost | Large electric field close to the chip | Difficult to integrate into a pump | Low voltage; continuous flow |
| Parameter | Reference [18] | Reference [19] | Reference [7] | This Work |
|---|---|---|---|---|
| Cross-sectional area of the microchannel (µm2) | 3.14 × 106 | 1.256 × 105 | 1.96 × 105 | 1.2 × 103 |
| Length of microchannel (mm) | 372 | 300 | 104 | 1.47 |
| Flow rate (µL/min) | 300 | 33 | 63 | 22 |
| Control system | PLC | PLC | PLC | On-chip |
| Fabrication | Silicon micromachining | Silicon micromachining | Silicon micromachining | CMOS-MEMS |
| Parameter | Reference [21] | This Work |
|---|---|---|
| Insulating layer (µm) | 1.5 | 3 |
| Average flow rate (µL/min) | 8.6 | 8.57 |
| Printing frequency (kHz) | 24.5 | 5 |
| Coefficient of variation in the average flow rate | 6% | 3% |
| Temperature (°C) | 66 | 47 |
| Parameter | Constant Heating Conditions | Optimized Heating Conditions |
|---|---|---|
| Average flow rate (µL/min) | 18.8 | 12 |
| Coefficient of variation in the average flow rate | 13% | 3% |
| TH/TD (ns) | 800/250 | 800–700–600–500/250 |
| Printing frequency (kHz) | 7 | 7 |
| Temperature (°C) | 58 | 57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, W.; Guan, Y.; Wang, Q.; Huang, P.; Zhou, Q.; Wang, K.; Liu, D. A Smart Active Phase-Change Micropump Based on CMOS-MEMS Technology. Sensors 2023, 23, 5207. https://doi.org/10.3390/s23115207
Jin W, Guan Y, Wang Q, Huang P, Zhou Q, Wang K, Liu D. A Smart Active Phase-Change Micropump Based on CMOS-MEMS Technology. Sensors. 2023; 23(11):5207. https://doi.org/10.3390/s23115207
Chicago/Turabian StyleJin, Wenzui, Yimin Guan, Qiushi Wang, Peng Huang, Qin Zhou, Kun Wang, and Demeng Liu. 2023. "A Smart Active Phase-Change Micropump Based on CMOS-MEMS Technology" Sensors 23, no. 11: 5207. https://doi.org/10.3390/s23115207
APA StyleJin, W., Guan, Y., Wang, Q., Huang, P., Zhou, Q., Wang, K., & Liu, D. (2023). A Smart Active Phase-Change Micropump Based on CMOS-MEMS Technology. Sensors, 23(11), 5207. https://doi.org/10.3390/s23115207





