Continuous Structural Displacement Monitoring Using Accelerometer, Vision, and Infrared (IR) Cameras
Abstract
1. Introduction
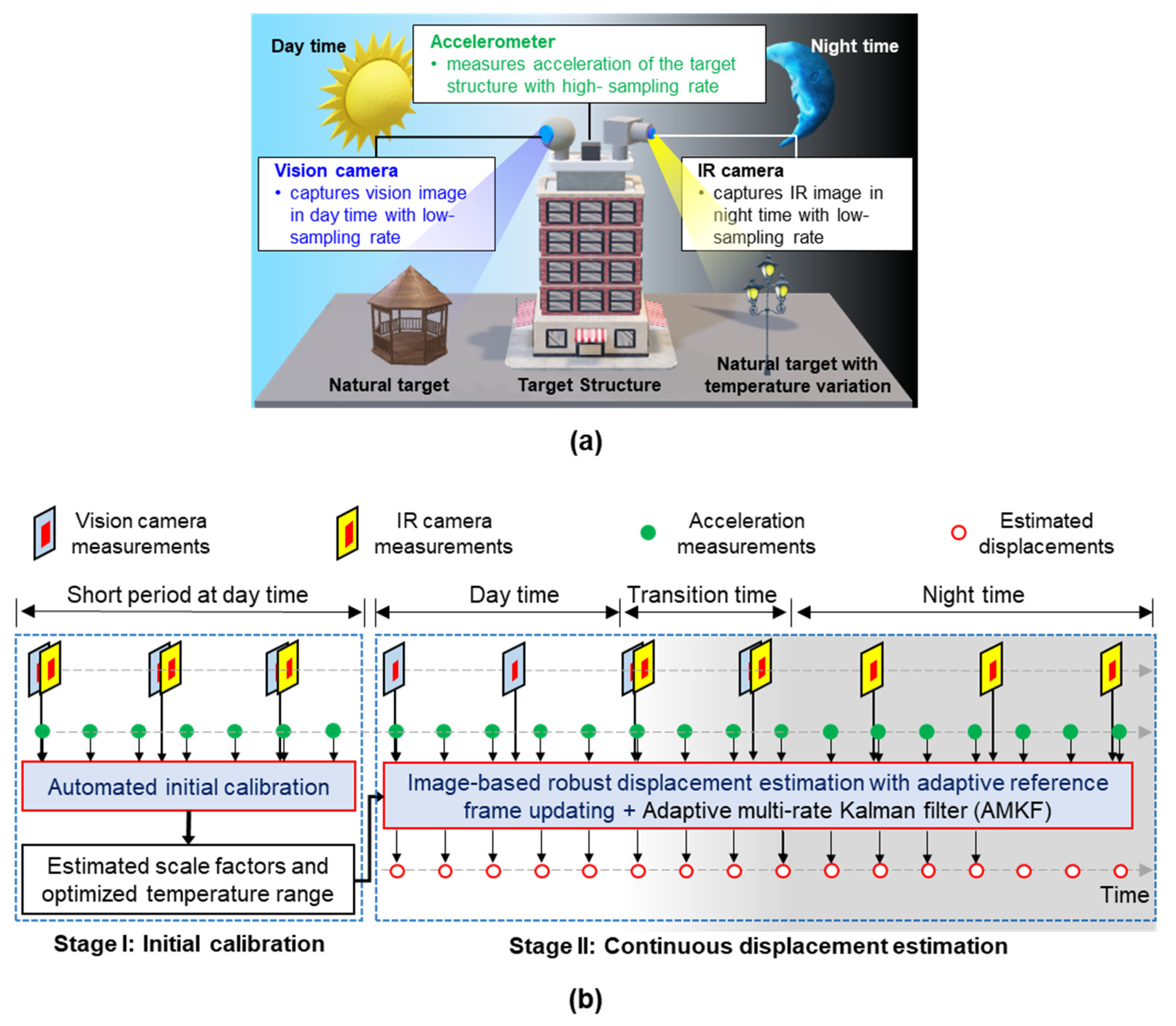
2. Development of Structural Displacement Estimation Technique by Fusing Accelerometer, Vision, and IR Cameras
2.1. Stage I: Automated Initial Calibration
2.1.1. Scale Factor Estimation for Vision and IR Cameras
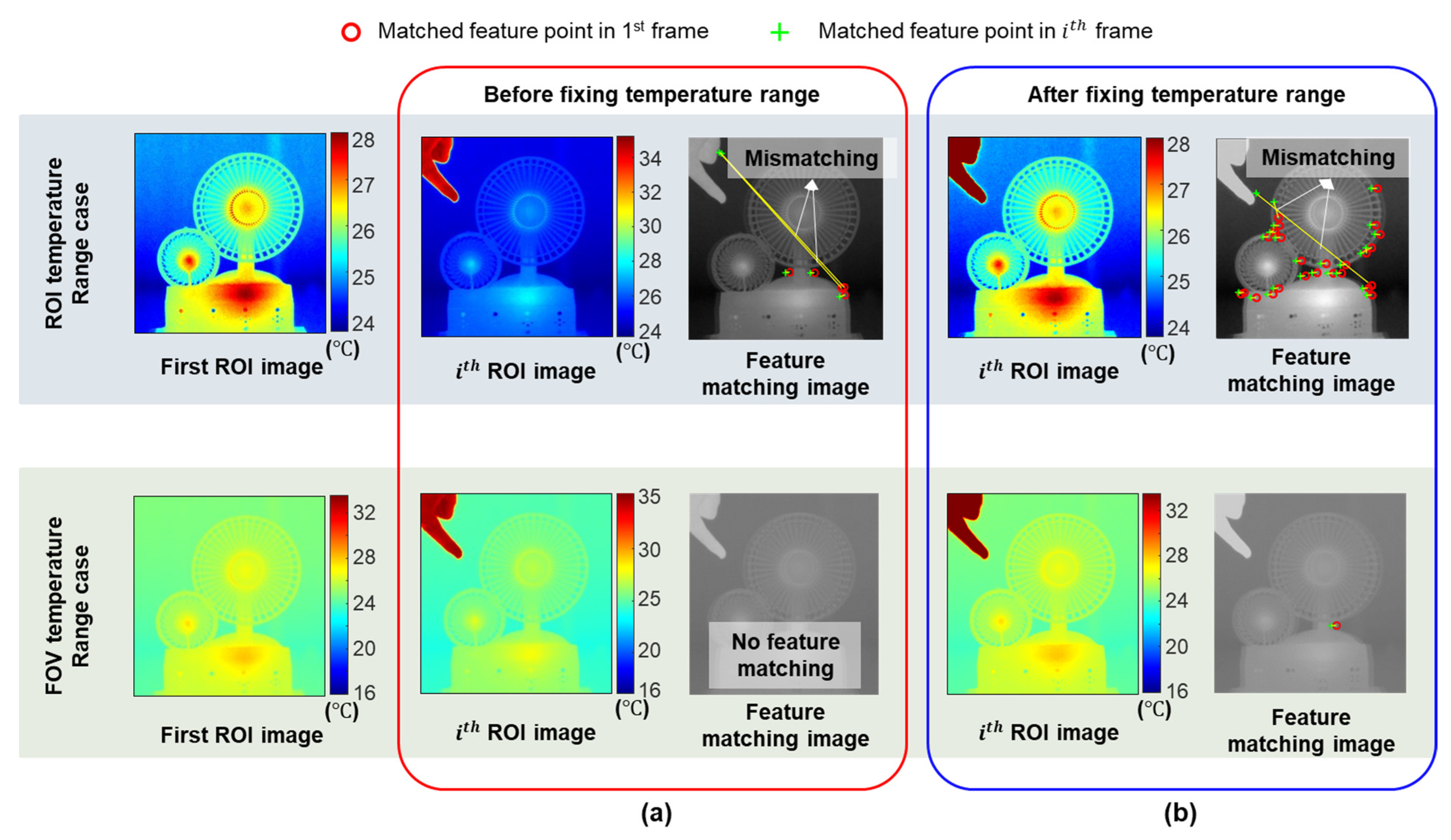
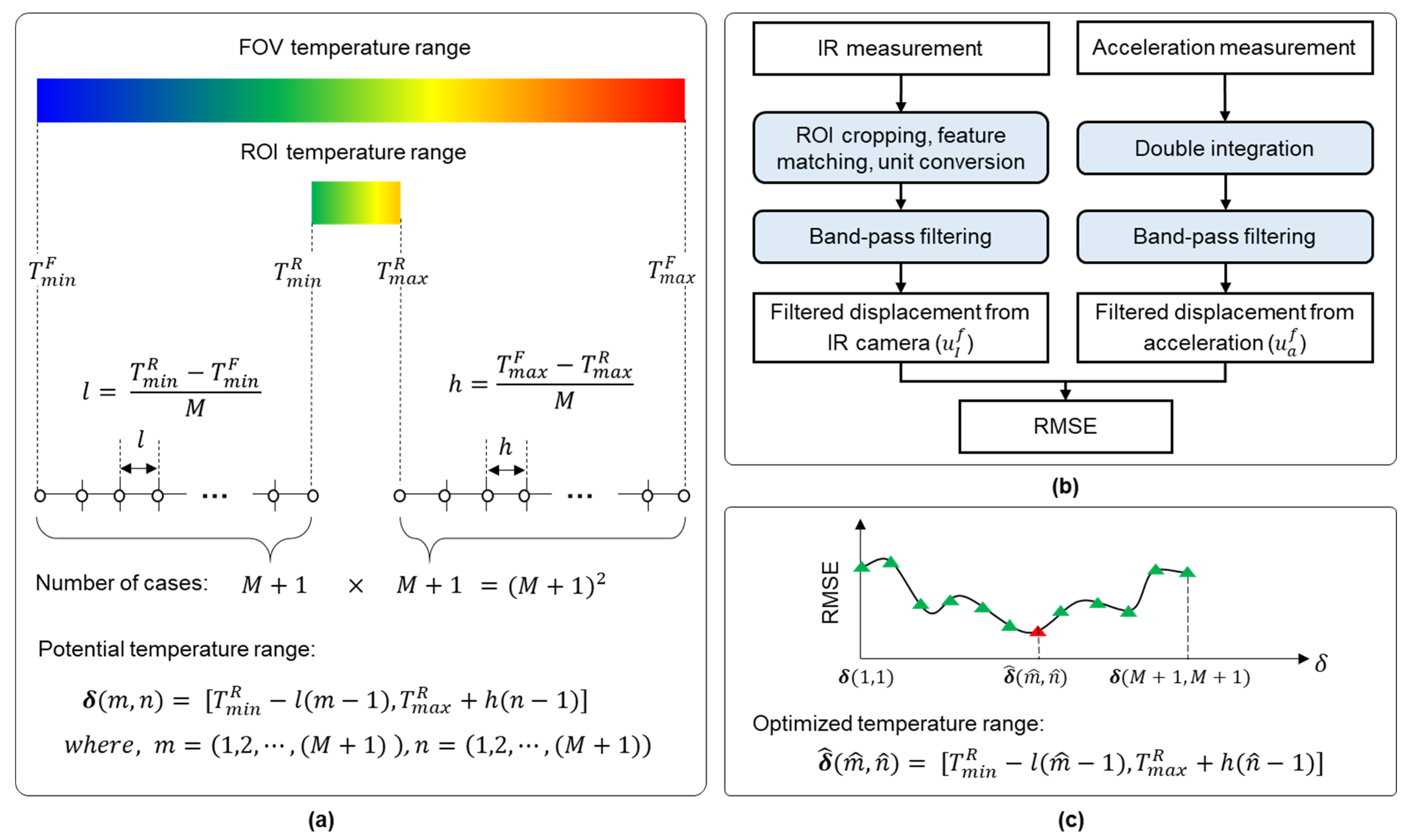
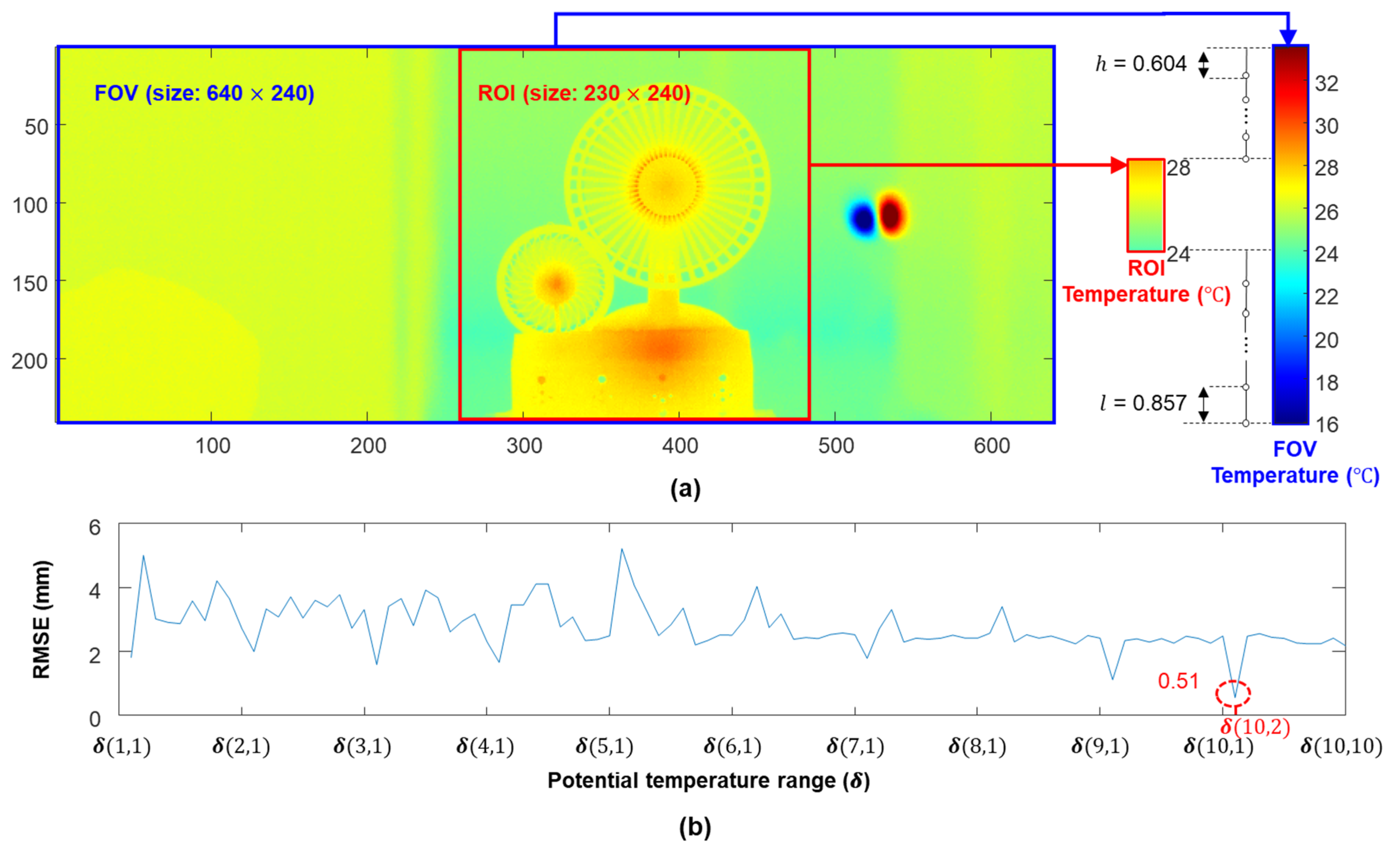
2.1.2. Optimization of the Temperature Range for IR Camera
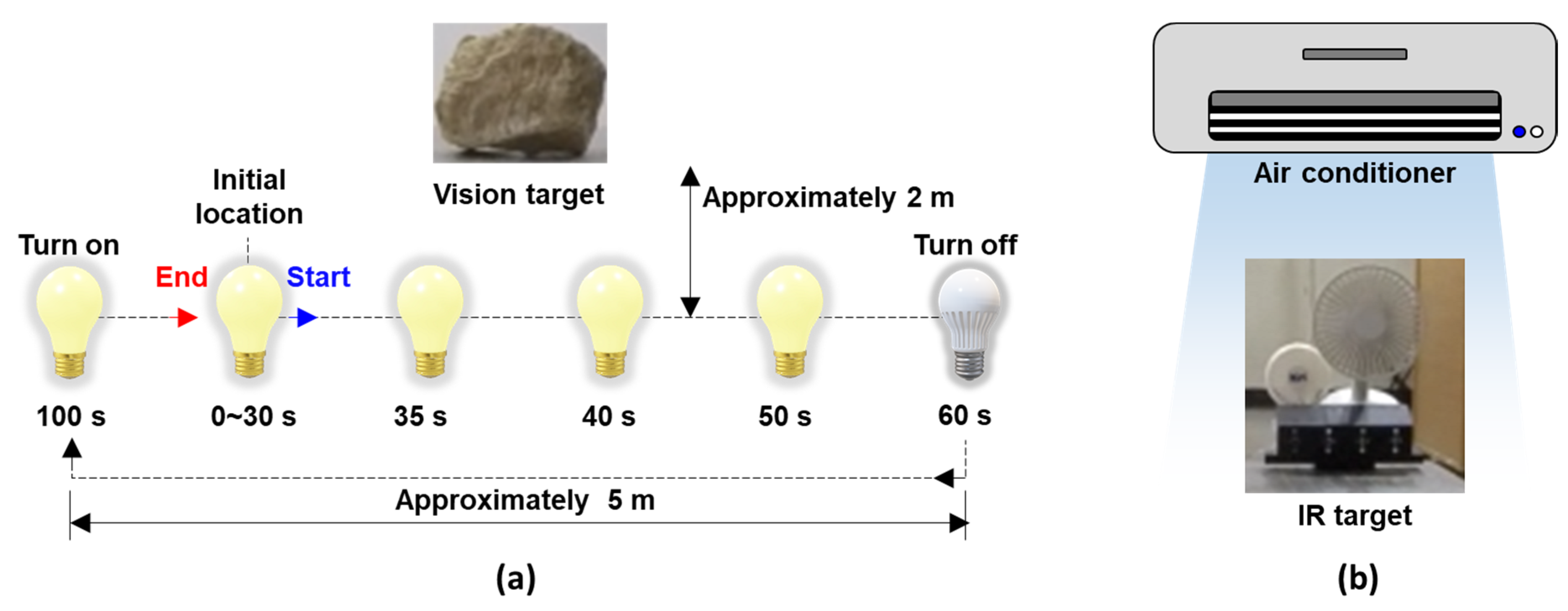
- (a)
- Necessity of fixing and optimizing the temperature range
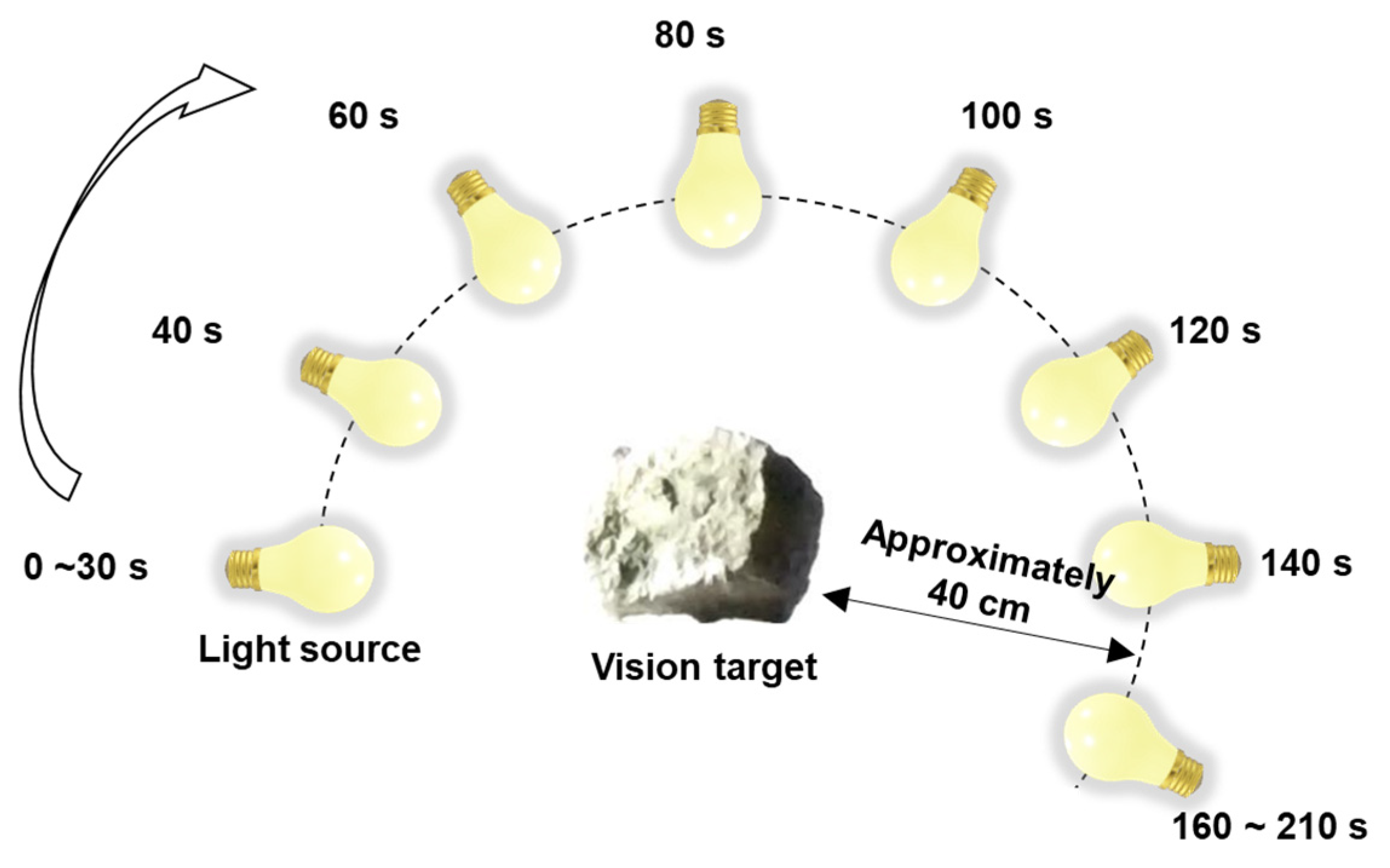
- (b)
- Working principle of automated optimization of the temperature range
2.2. Stage II: Continuous Displacement Estimation Using Image-Based Robust Displacement Estimation Algorithm and Adaptive Multirate Kalman Filter (AMKF)
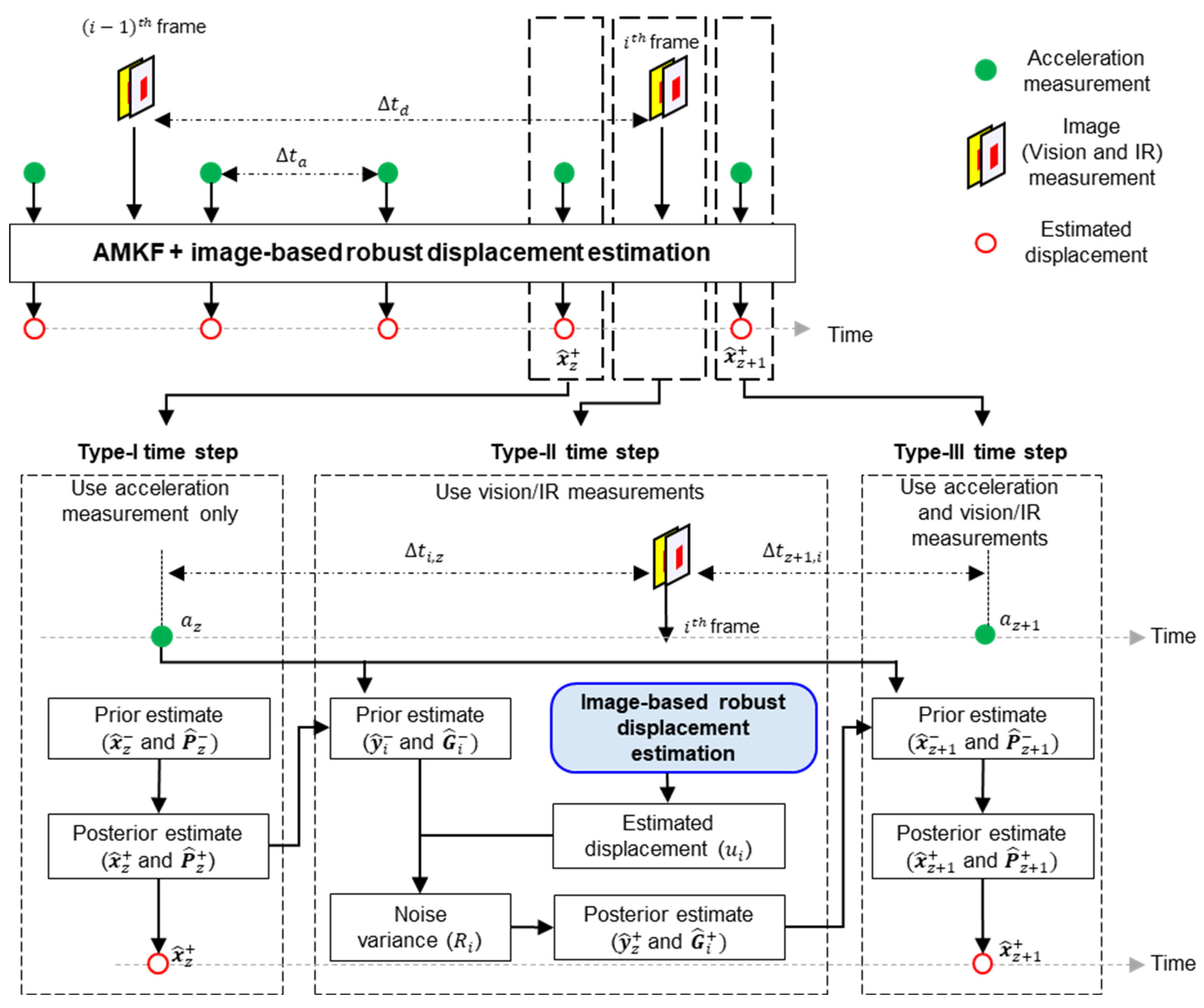
2.2.1. AMKF-Based Fusion of Asynchronous Image and Acceleration Measurement
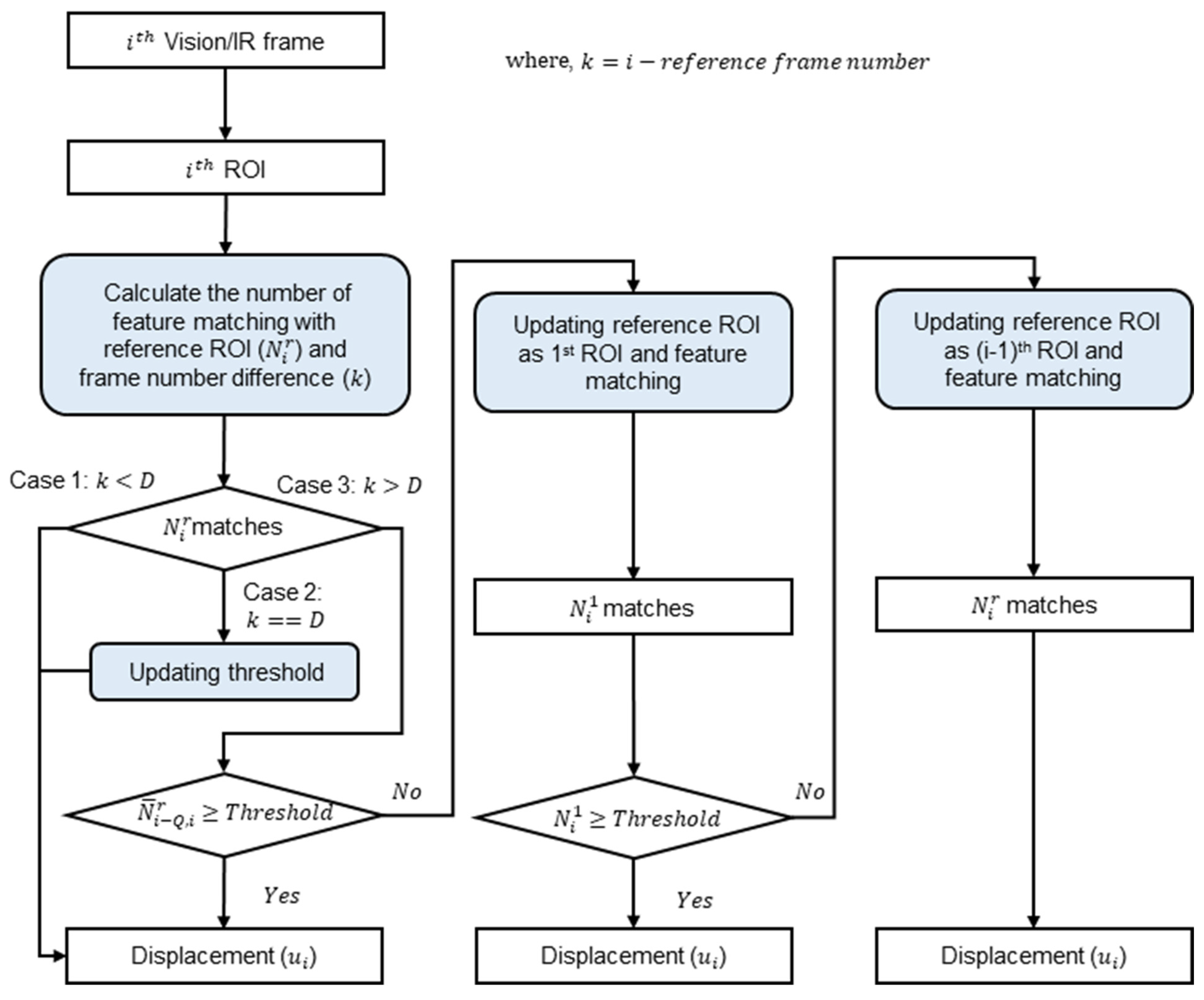
2.2.2. Image-Based Robust Displacement Estimation with Adaptive Reference Frame Updating
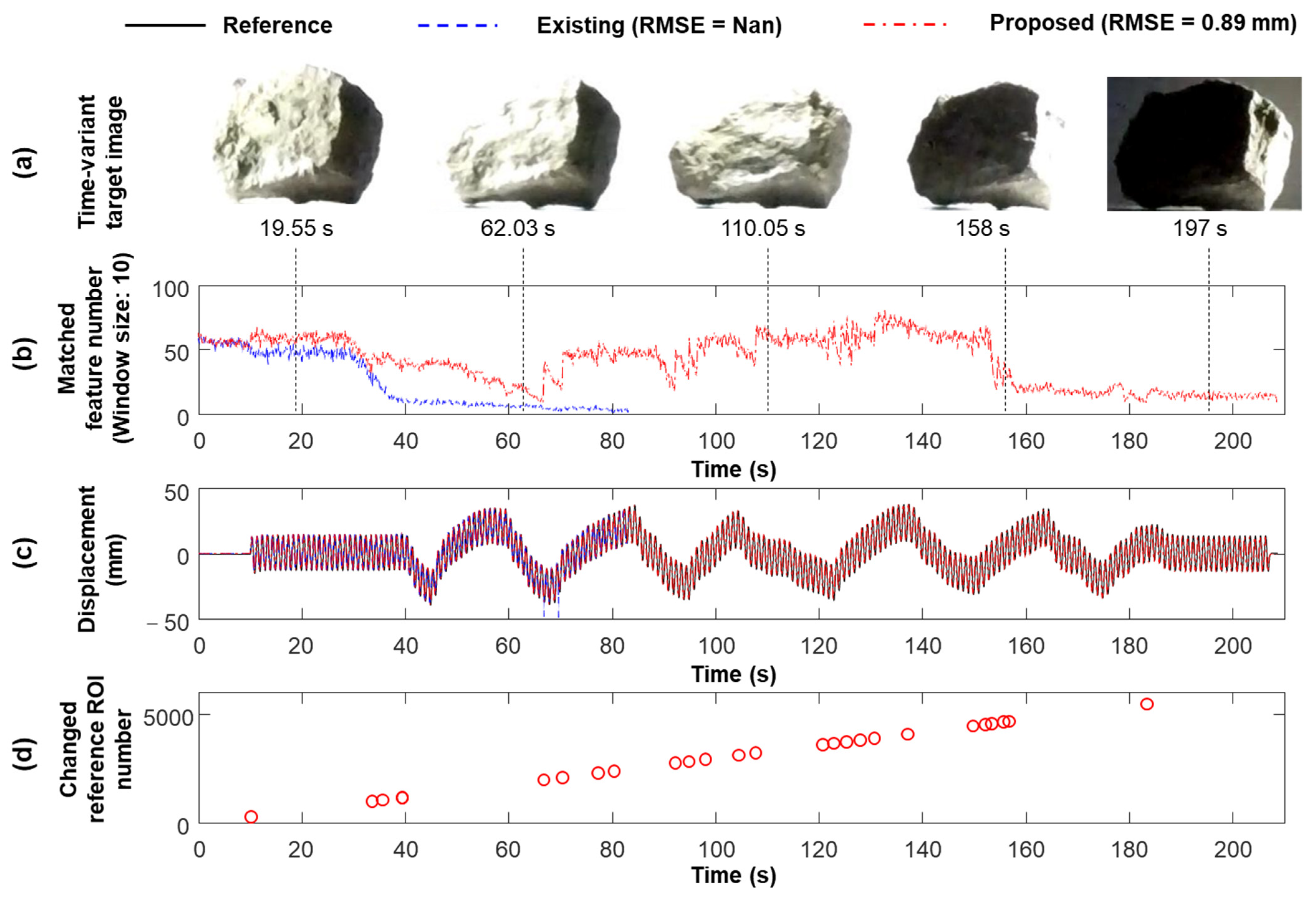
- (a)
- A brief review of the existing algorithm with a fixed reference frame and its limitations
- (b)
- Working principle of adaptive reference frame updating
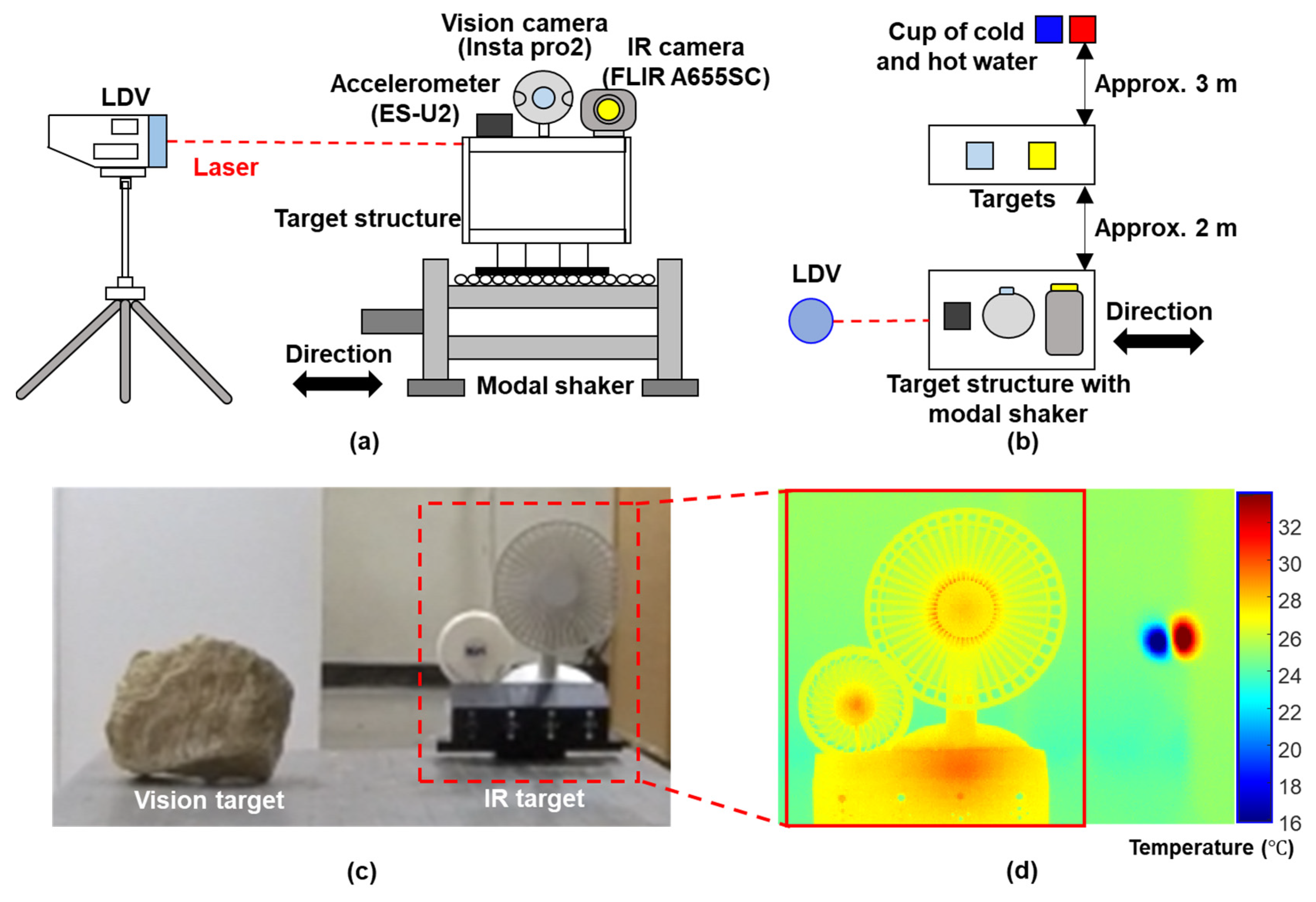
3. Experimental Validation
3.1. Lab-Scale Test Using Single-Story Building Model Test
3.1.1. Initial Calibration Results (Case 1)
3.1.2. Displacement Estimation Results
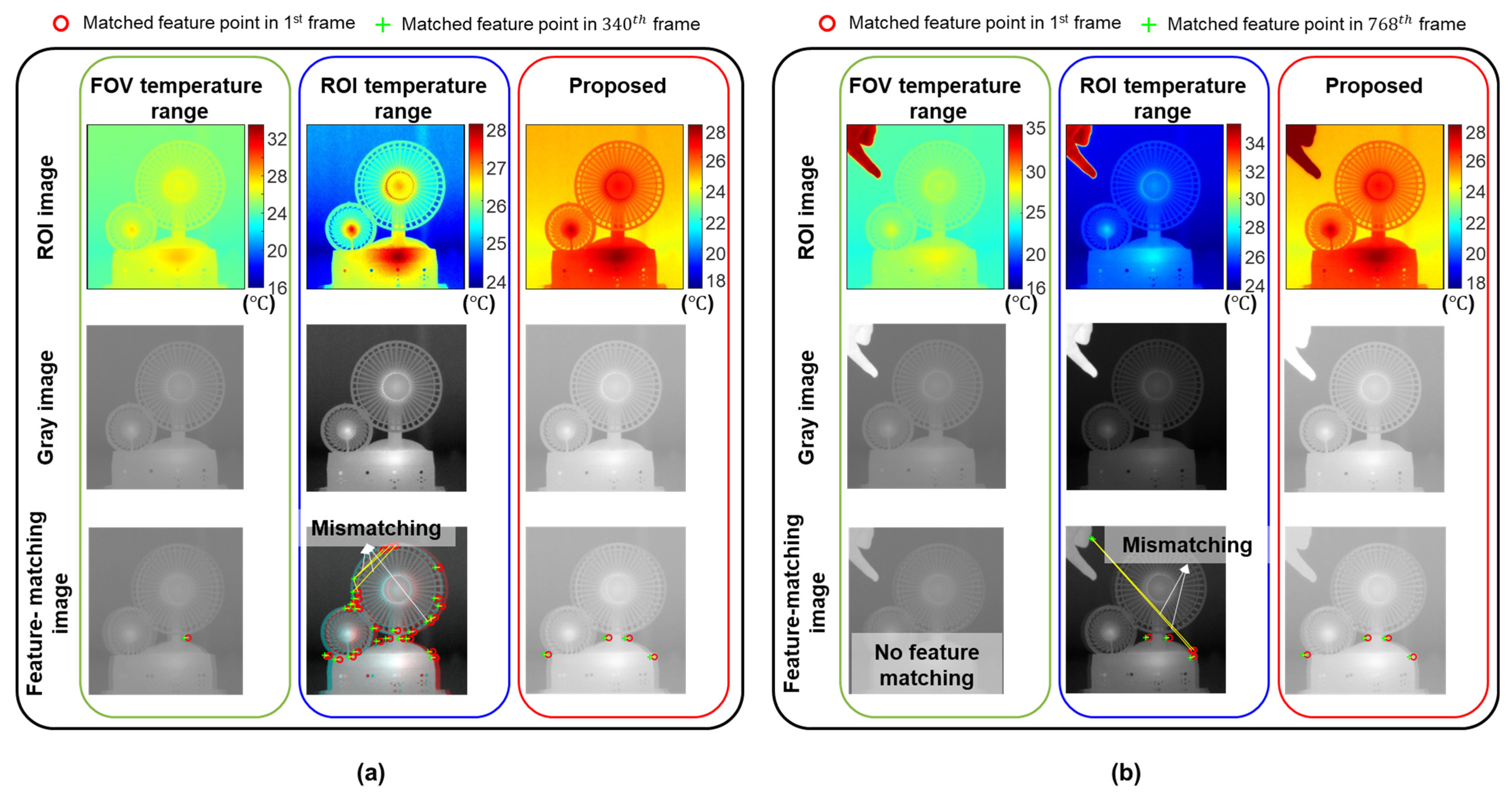
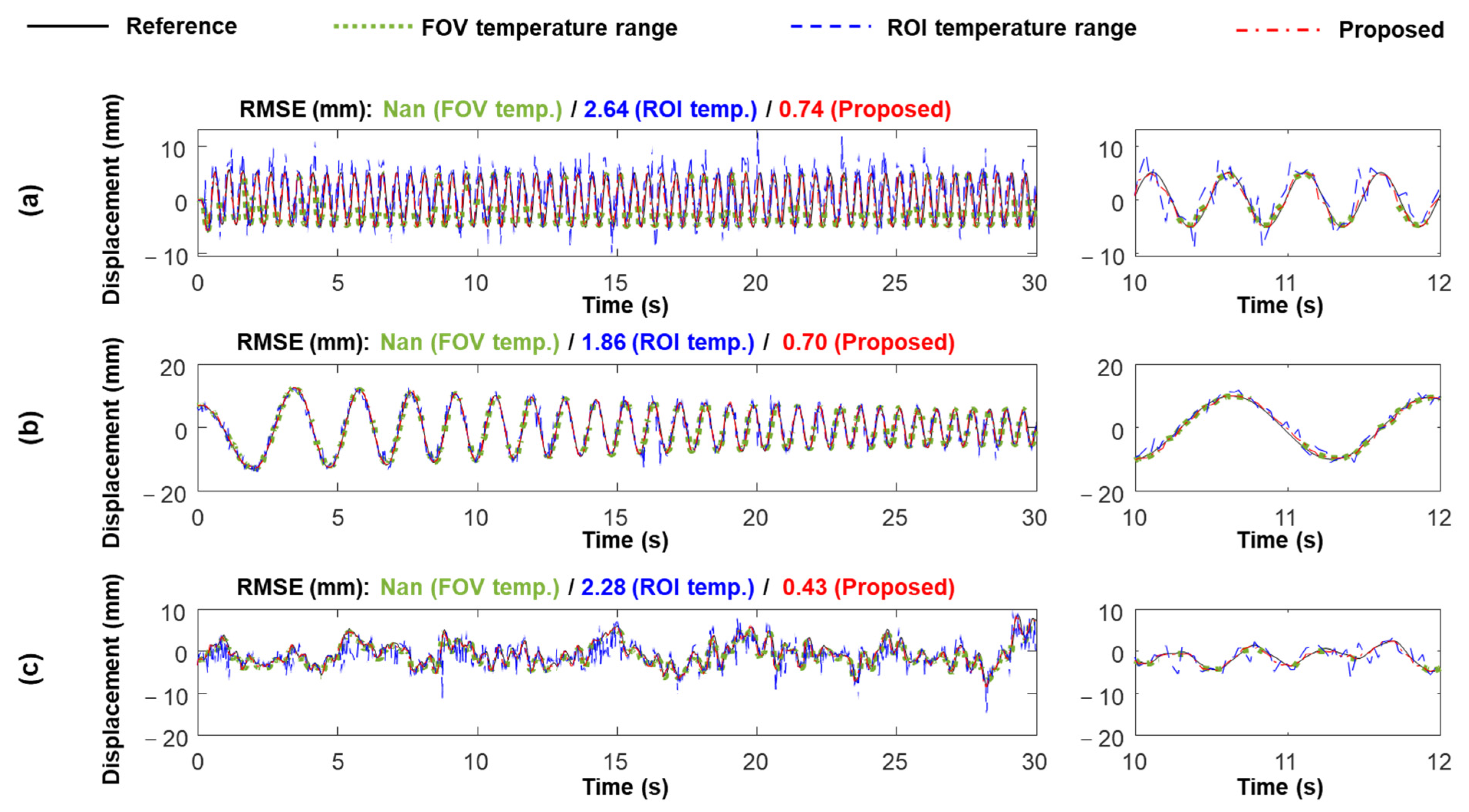
- (a)
- IR-based displacement estimation using optimized temperature range (Cases 2–5)
- (b)
- Vision-based displacement estimation using adaptive reference frame updating (Case 6)
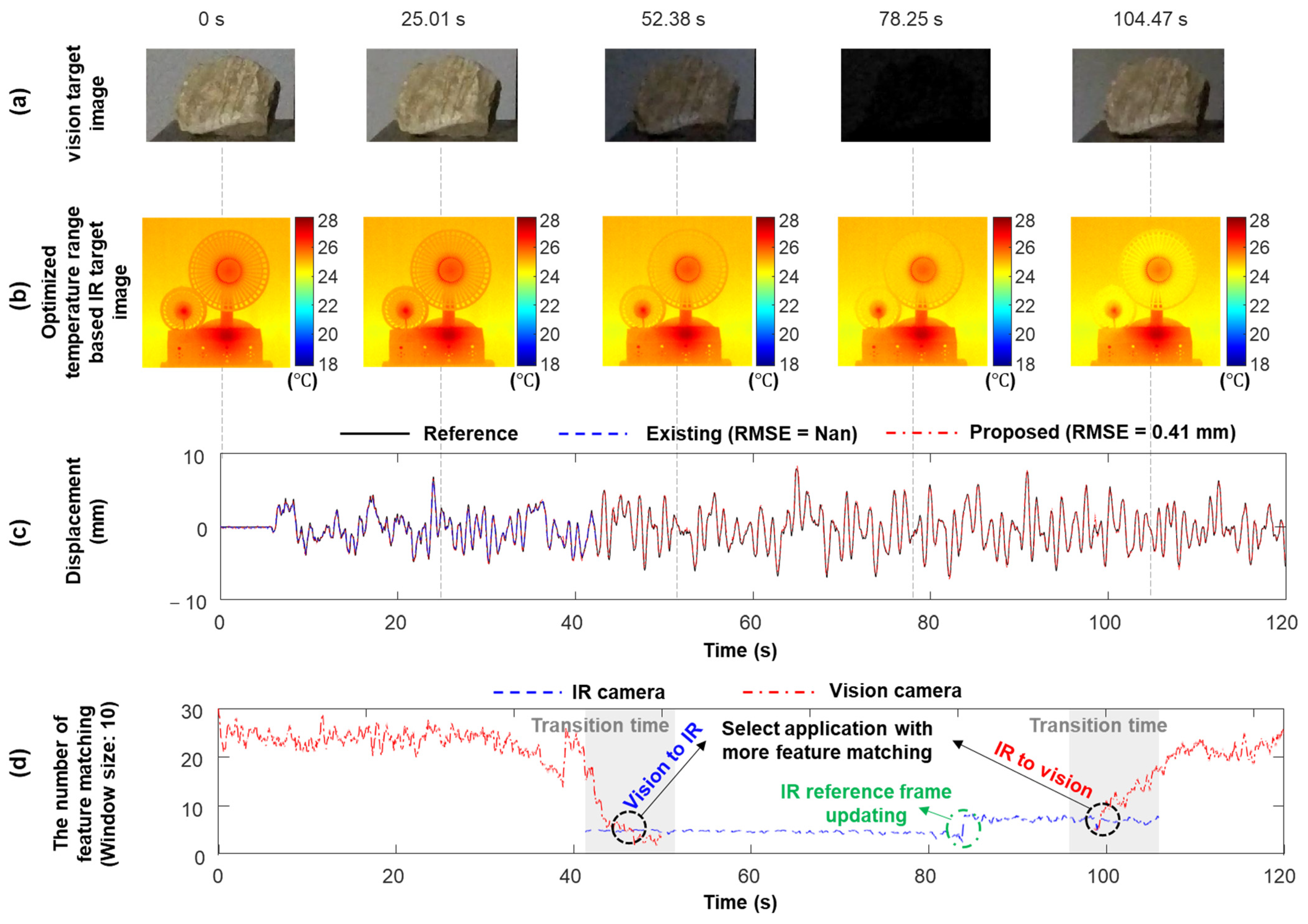
- (c)
- Continuous displacement estimation (Case 7).
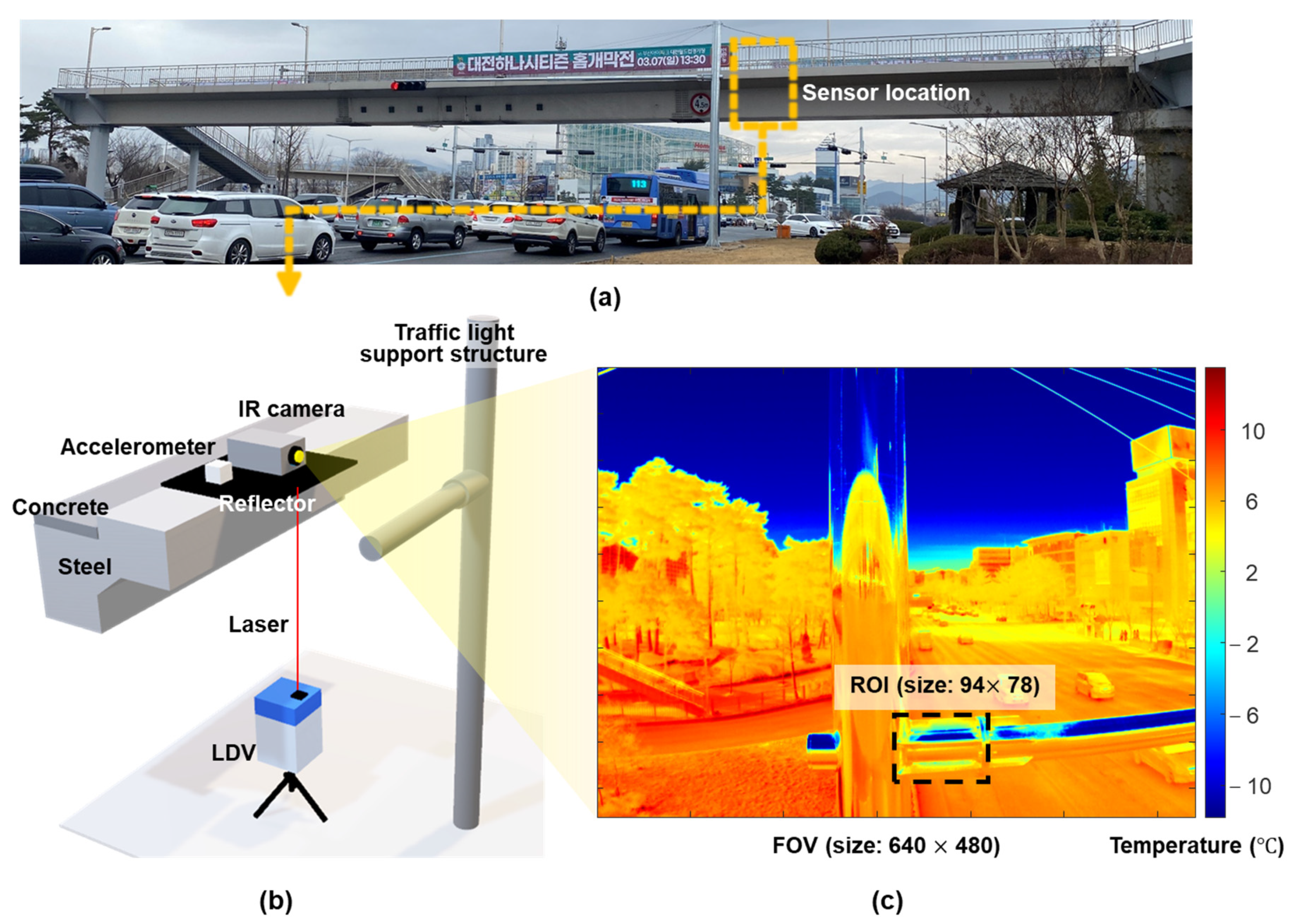
3.2. Field Test
3.2.1. Experimental Setup
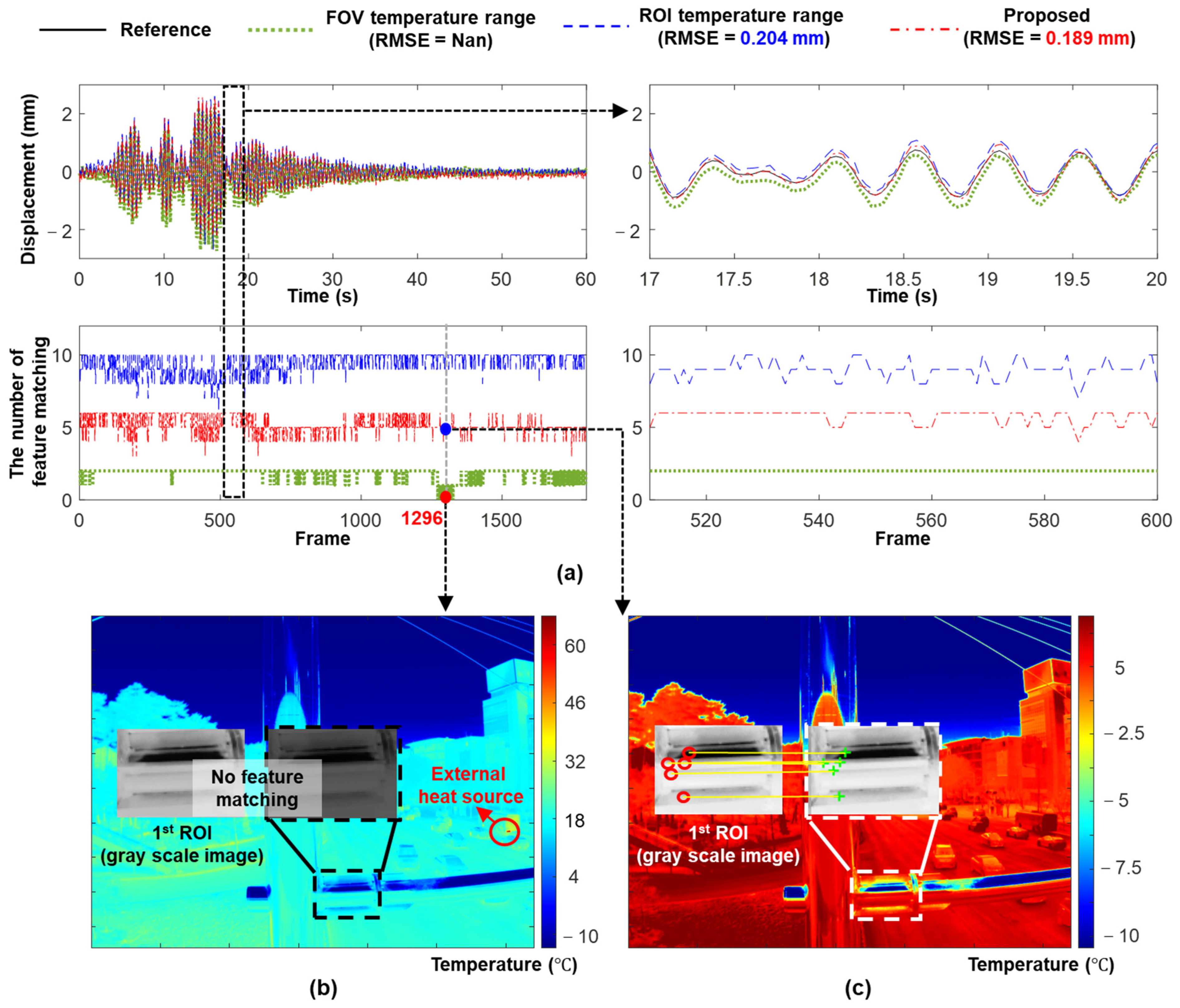
3.2.2. IR-Displacement Estimation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Catbas, F.N.; Aktan, A.E. Condition and damage assessment: Issues and some promising indices. J. Struct. Eng. 2002, 128, 1026–1036. [Google Scholar] [CrossRef]
- Mau, S. Introduction to Structural Analysis: Displacement and Force Methods; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Nassif, H.H.; Gindy, M.; Davis, J. Comparison of laser Doppler vibrometer with contact sensors for monitoring bridge deflection and vibration. NDT E Int. 2005, 38, 213–218. [Google Scholar] [CrossRef]
- Nakamura, S.-I. GPS measurement of wind-induced suspension bridge girder displacements. J. Struct. Eng. 2000, 126, 1413–1419. [Google Scholar] [CrossRef]
- Xiong, C.; Wang, M.; Chen, W. Data analysis and dynamic characteristic investigation of large-scale civil structures monitored by RTK-GNSS based on a hybrid filtering algorithm. J. Civ. Struct. Health Monit. 2022, 12, 857–874. [Google Scholar] [CrossRef]
- Infante, D.; Di Martire, D.; Confuorto, P.; Tessitore, S.; Tòmas, R.; Calcaterra, D.; Ramondini, M. Assessment of building behavior in slow-moving landslide-affected areas through DInSAR data and structural analysis. Eng. Struct. 2019, 199, 109638. [Google Scholar] [CrossRef]
- Nettis, A.; Massimi, V.; Nutricato, R.; Nitti, D.O.; Samarelli, S.; Uva, G. Satellite-based interferometry for monitoring structural deformations of bridge portfolios. Autom. Constr. 2023, 147, 104707. [Google Scholar] [CrossRef]
- Gomez, F.; Park, J.W.; Spencer, B.F., Jr. Reference-free structural dynamic displacement estimation method. Struct. Control Health Monit. 2018, 25, e2209. [Google Scholar] [CrossRef]
- Park, J.-W.; Sim, S.-H.; Jung, H.-J.; Spencer, B.F., Jr. Development of a wireless displacement measurement system using acceleration responses. Sensors 2013, 13, 8377–8392. [Google Scholar] [CrossRef] [PubMed]
- Reu, P.L.; Rohe, D.P.; Jacobs, L.D. Comparison of DIC and LDV for practical vibration and modal measurements. Mech. Syst. Signal Process. 2017, 86, 2–16. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, Y.; Luzi, G.; Crosetto, M.; Monserrat, O.; Jiang, J.; Zhao, H.; Ding, Y. Ground-based radar interferometry for monitoring the dynamic performance of a multitrack steel truss high-speed railway bridge. Remote Sens. 2020, 12, 2594. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Y.; Zhao, W.; Zhang, J. Radar-based multipoint displacement measurements of a 1200-m-long suspension bridge. ISPRS J. Photogramm. Remote Sens. 2020, 167, 71–84. [Google Scholar] [CrossRef]
- Jeong, J.H.; Jo, H. Real-time generic target tracking for structural displacement monitoring under environmental uncertainties via deep learning. Struct. Control Health Monit. 2022, 29, e2902. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Computer vision-based displacement and vibration monitoring without using physical target on structures. Struct. Infrastruct. Eng. 2017, 13, 505–516. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Sim, S.-H. Equation Chapter 1 Section 1 nontarget-based displacement measurement using LiDAR and camera. Autom. Constr. 2022, 142, 104493. [Google Scholar] [CrossRef]
- Nasimi, R.; Moreu, F. A methodology for measuring the total displacements of structures using a laser–camera system. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 421–437. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Measurement of the dynamic displacements and of the modal frequencies of a short-span pedestrian bridge using GPS and an accelerometer. Eng. Struct. 2011, 33, 10–17. [Google Scholar] [CrossRef]
- Ozdagli, A.; Gomez, J.; Moreu, F. Real-time reference-free displacement of railroad bridges during train-crossing events. J. Bridge Eng. 2017, 22, 04017073. [Google Scholar] [CrossRef]
- Park, J.W.; Moon, D.S.; Yoon, H.; Gomez, F.; Spencer, B.F., Jr.; Kim, J.R. Visual–inertial displacement sensing using data fusion of vision-based displacement with acceleration. Struct. Control Health Monit. 2018, 25, e2122. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Q.-S.; Han, X.-L.; Wan, J.-W.; Xu, K. Horizontal displacement estimation of high-rise structures by fusing strain and acceleration measurements. J. Build. Eng. 2022, 57, 104964. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.; Huseynov, F. Accurate deformation monitoring on bridge structures using a cost-effective sensing system combined with a camera and accelerometers: Case study. J. Bridge Eng. 2019, 24, 05018014. [Google Scholar] [CrossRef]
- Ma, Z.; Choi, J.; Sohn, H. Real-time structural displacement estimation by fusing asynchronous acceleration and computer vision measurements. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 688–703. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. Surf: Speeded up Robust Features. In Proceedings of the 9th European Conference on Computer Vision (ECCV 2006), Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Brandt, A. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Akhlaghi, S.; Zhou, N.; Huang, Z. Adaptive Adjustment of Noise Covariance in Kalman Filter for Dynamic State Estimation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Scaramuzza, D.; Martinelli, A.; Siegwart, R. A Toolbox for Easily Calibrating Omnidirectional Cameras. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5695–5701. [Google Scholar]





| # of Cases | Test Duration (s) | Illumination Variation | Temperature Variation | Purposes |
|---|---|---|---|---|
| 1 | 30 | No | No | Initial calibration |
| 2 | 30 | No | Yes | Robustness of the proposed technique to external heat source |
| 3 | 30 | No | No | Performance of displacement estimation using optimized temperature range |
| 4 | ||||
| 5 | ||||
| 6 | 210 | Yes (Extreme) | No | Robustness of the proposed technique to extreme variations in illumination |
| 7 | 120 | Yes | Yes | Application selection of transition time for continuous displacement estimation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Ma, Z.; Kim, K.; Sohn, H. Continuous Structural Displacement Monitoring Using Accelerometer, Vision, and Infrared (IR) Cameras. Sensors 2023, 23, 5241. https://doi.org/10.3390/s23115241
Choi J, Ma Z, Kim K, Sohn H. Continuous Structural Displacement Monitoring Using Accelerometer, Vision, and Infrared (IR) Cameras. Sensors. 2023; 23(11):5241. https://doi.org/10.3390/s23115241
Chicago/Turabian StyleChoi, Jaemook, Zhanxiong Ma, Kiyoung Kim, and Hoon Sohn. 2023. "Continuous Structural Displacement Monitoring Using Accelerometer, Vision, and Infrared (IR) Cameras" Sensors 23, no. 11: 5241. https://doi.org/10.3390/s23115241
APA StyleChoi, J., Ma, Z., Kim, K., & Sohn, H. (2023). Continuous Structural Displacement Monitoring Using Accelerometer, Vision, and Infrared (IR) Cameras. Sensors, 23(11), 5241. https://doi.org/10.3390/s23115241







