Optimized Unilateral Magnetic Resonance Sensor with Constant Gradient and Its Applications in Composite Insulators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Magnet Optimization
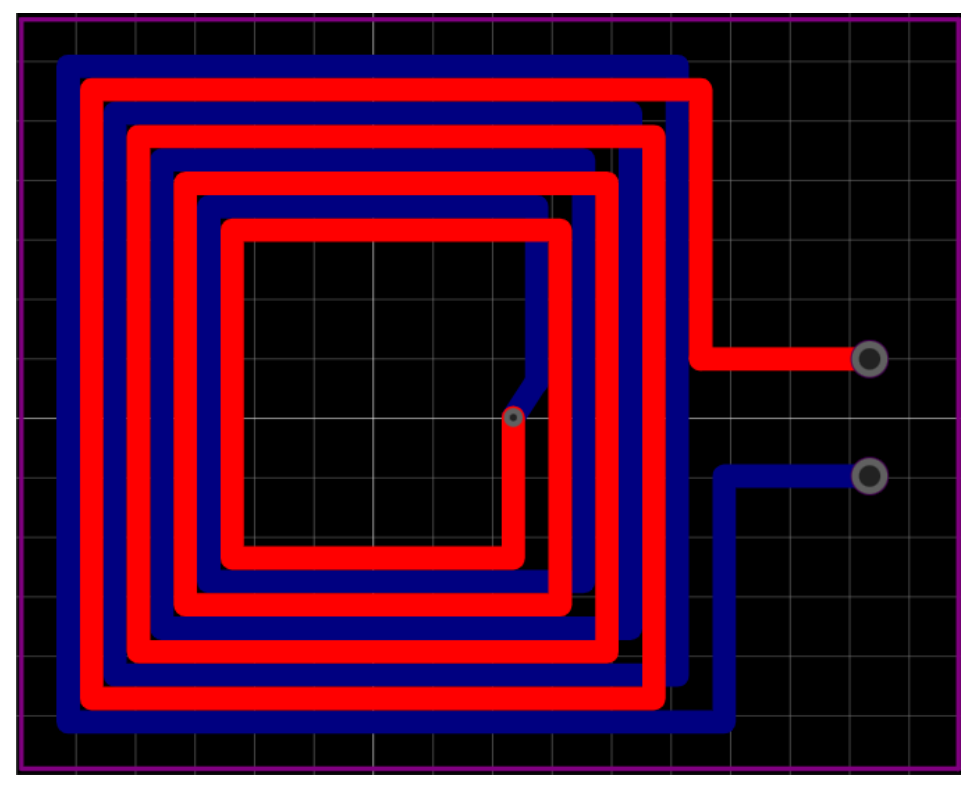
2.2. RF Coil Optimization
2.3. Eddy Current Effect Optimization
3. Results and Discussion
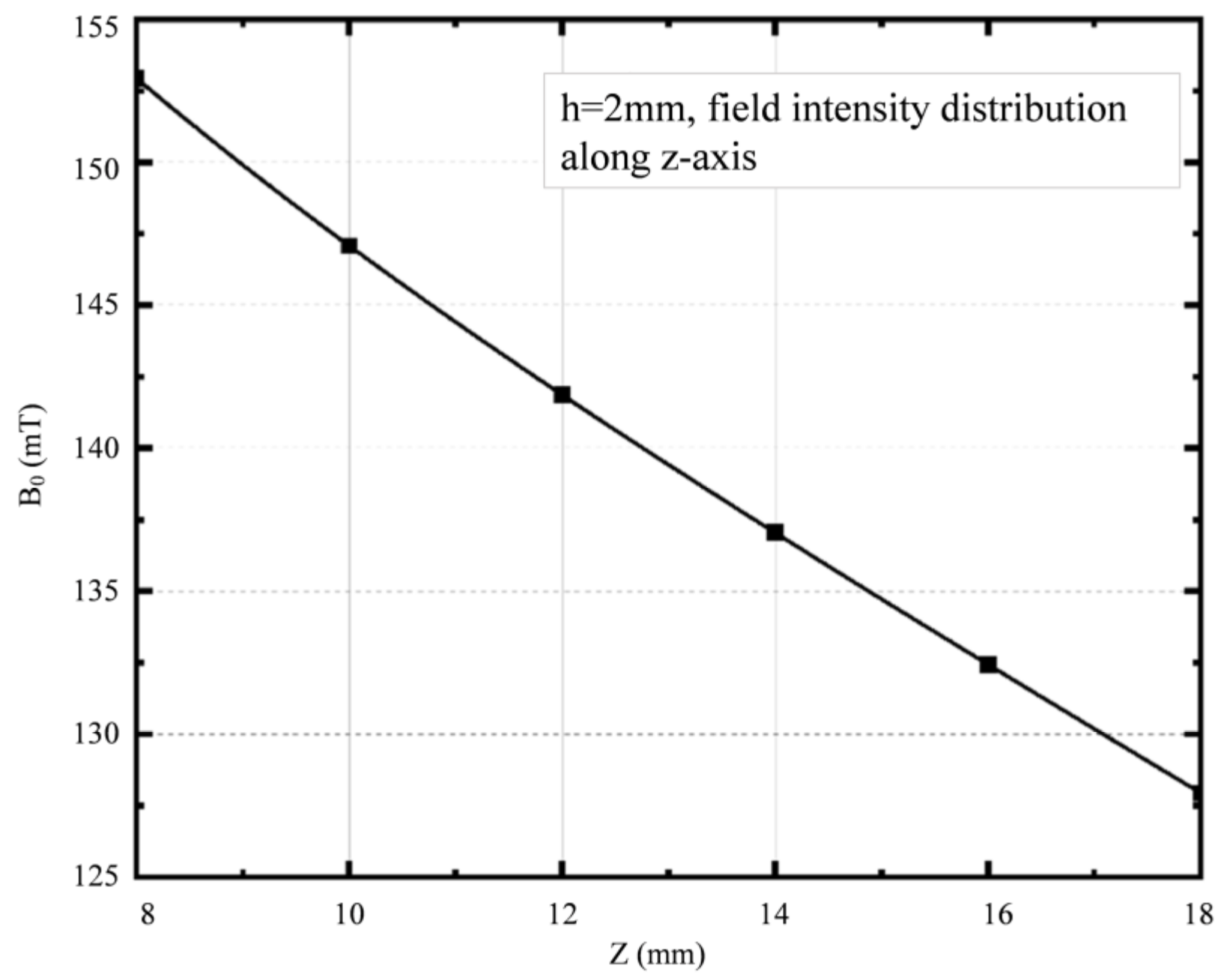
3.1. Field Measurements
3.2. Sensitivity Map
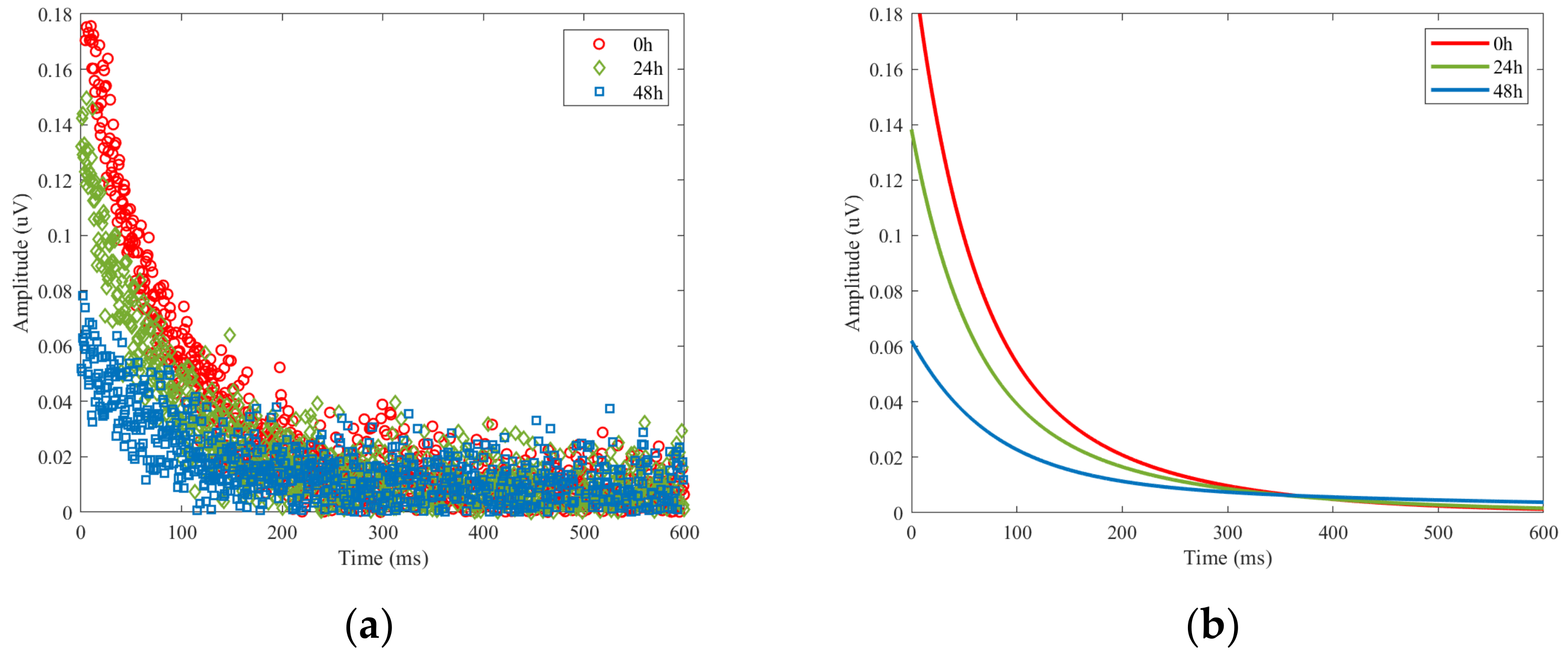
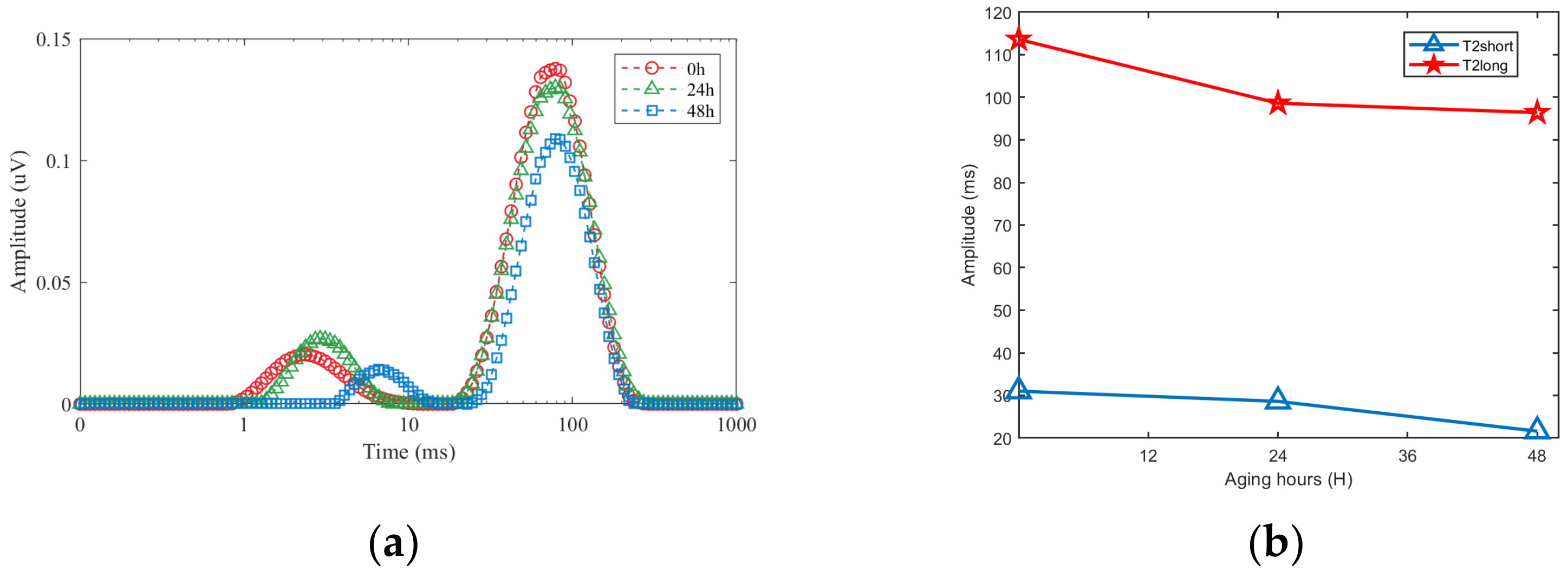
3.3. Aging Assessment of Composite Insulators
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mavrikakis, N.C.; Mikropoulos, P.N.; Siderakis, K. Evaluation of Field-ageing Effects on Insulating Materials of Composite Suspension Insulators. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 490–498. [Google Scholar] [CrossRef]
- Jiang, H.; Li, B.; Zhao, B.; Sun, Q.; Gao, C.; Chen, L. Evaluation of aging process of silicone rubber composite insulators with photothermal radiometry. J. Phys. D Appl. Phys. 2018, 51, 425304. [Google Scholar] [CrossRef]
- Vosloo, W.; Davey, R. Power utility perspective on natural ageing and pollution performance of outdoor insulators. IEEE Electr. Insul. Mag. 2020, 36, 56–66. [Google Scholar] [CrossRef]
- He, W.; Zhang, F.; Zhang, F.; He, Q. Effect of CeO2 on UV aging of composite insulators prepared by template-spraying method. J. Appl. Polym. Sci. 2022, 140, e53274. [Google Scholar]
- Blümich, B.; Casanova, F.; Perlo, J.; Anferova, S.; Anferov, V.; Kremer, K.; Goga, N.; Kupferschläger, K.; Adams, M. Advances of unilateral mobile NMR in nondestructive materials testing. Magn. Reson. Imaging 2005, 23, 197–201. [Google Scholar] [CrossRef]
- Marble, A.E.; Mastikhin, I.V.; Colpitts, B.G.; Balcom, B.J. An analytical methodology for magnetic field control in unilateral NMR. J. Magn. Reson. 2005, 174, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Proietti, N.; Capitani, D.; Lamanna, R.; Presciutti, F.; Rossi, E.; Segre, A. Fresco paintings studied by unilateral NMR. J. Magn. Reson. 2005, 177, 111–117. [Google Scholar] [CrossRef] [PubMed]
- Proietti, N.; Capitani, D.; Pedemonte, E.; Blümich, B.; Segre, A. Monitoring degradation in paper: Non-invasive analysis by unilateral NMR. Part II. J. Magn. Reson. 2004, 170, 113–120. [Google Scholar] [CrossRef]
- Manz, B.; Coy, A.; Dykstra, R.; Eccles, C.; Hunter, M.; Parkinson, B.; Callaghan, P. A mobile one-sided NMR sensor with a homogeneous magnetic field: The NMR-MOLE. J. Magn. Reson. 2006, 183, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Liberman, A.; Bergman, E.; Sarda, Y.; Nevo, U. Faster imaging with a portable unilateral NMR device. J. Magn. Reson. 2013, 231, 72–78. [Google Scholar] [CrossRef]
- Kehlet, C.; Catalano, A.; Dittmer, J. Degradation of natural rubber in works of art studied by unilateral NMR and high field NMR spectroscopy. Polym. Degrad. Stab. 2014, 107, 270–276. [Google Scholar] [CrossRef]
- Xu, Z.; Morris, R.H.; Bencsik, M.; Newton, M.I. Detection of Virgin Olive Oil Adulteration Using Low Field Unilateral NMR. Sensors 2014, 14, 2028–2035. [Google Scholar] [CrossRef] [Green Version]
- Blümich, B.; Blümler, P.; Eidmann, G.; Guthausen, A.; Haken, R.; Schmitz, U.; Saito, K.; Zimmer, G. The NMR-mouse: Construction, excitation, and applications. Magn. Reson. Imaging 1998, 16, 479–484. [Google Scholar] [CrossRef]
- Balibanu, Hailu, Eymael, Demco, and Blumich, Nuclear magnetic resonance in inhomogeneous magnetic fields. J. Magn. Reson. 2000, 145, 246–258. [CrossRef] [PubMed]
- Perlo, J.; Casanova, F.; Blümich, B. Profiles with microscopic resolution by single-sided NMR. J. Magn. Reson. 2005, 176, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Oligschläger, D.; Glöggler, S.; Watzlaw, J.; Brendel, K.; Jaschtschuk, D.; Colell, J.; Zia, W.; Vossel, M.; Schnakenberg, U.; Blümich, B. A Miniaturized NMR-MOUSE with a High Magnetic Field Gradient (Mini-MOUSE). Appl. Magn. Reson. 2014, 46, 181–202. [Google Scholar] [CrossRef]
- García-Naranjo, J.C.; Mastikhin, I.V.; Colpitts, B.G.; Balcom, B.J. A unilateral magnet with an extended constant magnetic field gradient. J. Magn. Reson. 2010, 207, 337–344. [Google Scholar] [CrossRef]
- Morin, D.M.; Yan, P.; Augustine, M.P.; Balcom, B.J. An Optimized 2 MHz Unilateral Magnet with a Large Homogeneous Sensitive Spot. Appl. Magn. Reson. 2022, 53, 401–415. [Google Scholar] [CrossRef]
- Perlo, J.; Danieli, E.; Perlo, J.; Blümich, B.; Casanova, F. Optimized slim-line logging NMR tool to measure soil moisture in situ. J. Magn. Reson. 2013, 233, 74–79. [Google Scholar] [CrossRef]
- Shen, S.; Guo, P.; Wu, J.; Ding, Y.; Chen, F.; Meng, F.; Xu, Z. Optimized inside-out magnetic resonance probe for soil moisture measuring in situ. J. Magn. Reson. 2019, 307, 106565. [Google Scholar] [CrossRef]
- Nakashima, Y.; Sawatsubashi, T.; Fujii, S. Nondestructive quantification of moisture in powdered low-rank coal by a unilateral nuclear magnetic resonance scanner. Int. J. Coal Prep. Util. 2020, 42, 1421–1434. [Google Scholar] [CrossRef] [Green Version]
- Cooley, C.Z.; Stockmann, J.P.; Witzel, T.; LaPierre, C.; Mareyam, A.; Jia, F.; Zaitsev, M.; Wenhui, Y.; Zheng, W.; Stang, P.; et al. Design and implementation of a low-cost, tabletop MRI scanner for education and research prototyping. J. Magn. Reson. 2020, 310, 106625. [Google Scholar] [CrossRef] [PubMed]
- Ross, M.M.B.; Wilbur, G.R.; Barrita, P.F.J.C.; Balcom, B.J. A portable, submersible, MR sensor—The Proteus magnet. J. Magn. Reson. 2021, 326, 106964. [Google Scholar] [CrossRef]
- He, Z.; He, W. Calculating Temperature Distribution of Uniplanar Gradient Coils for Unilateral NMR Magnet Based on Fourier Analysis. Appl. Magn. Reson. 2016, 47, 613–626. [Google Scholar] [CrossRef]
- Utsuzawa, S.; Tang, Y.; Song, Y.-Q. Inside-out NMR with two concentric ring magnets. J. Magn. Reson. 2021, 333, 107082. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Guo, P.; Lu, M.; Zhao, S.; Xu, Z. Optimized Portable Unilateral Magnetic Resonance Sensor for Assessing the Aging Status of Silicon Rubber Insulators. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]


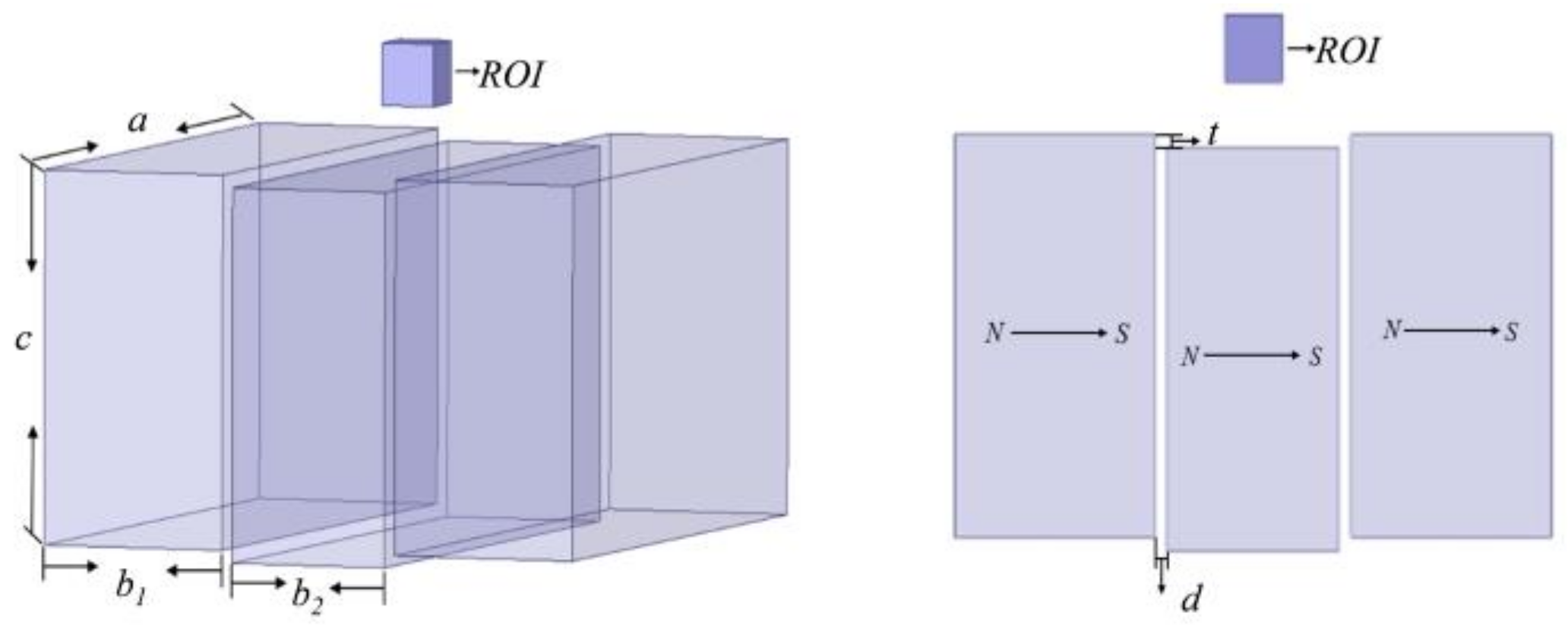
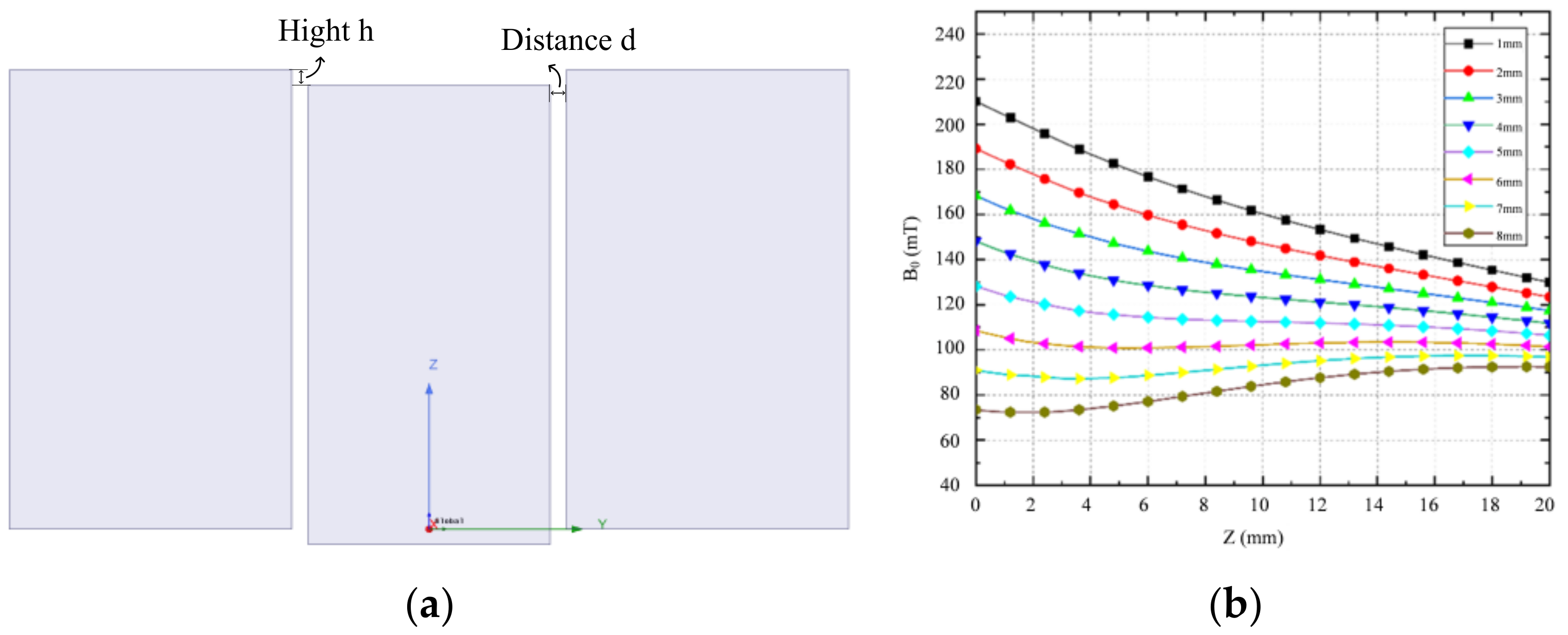


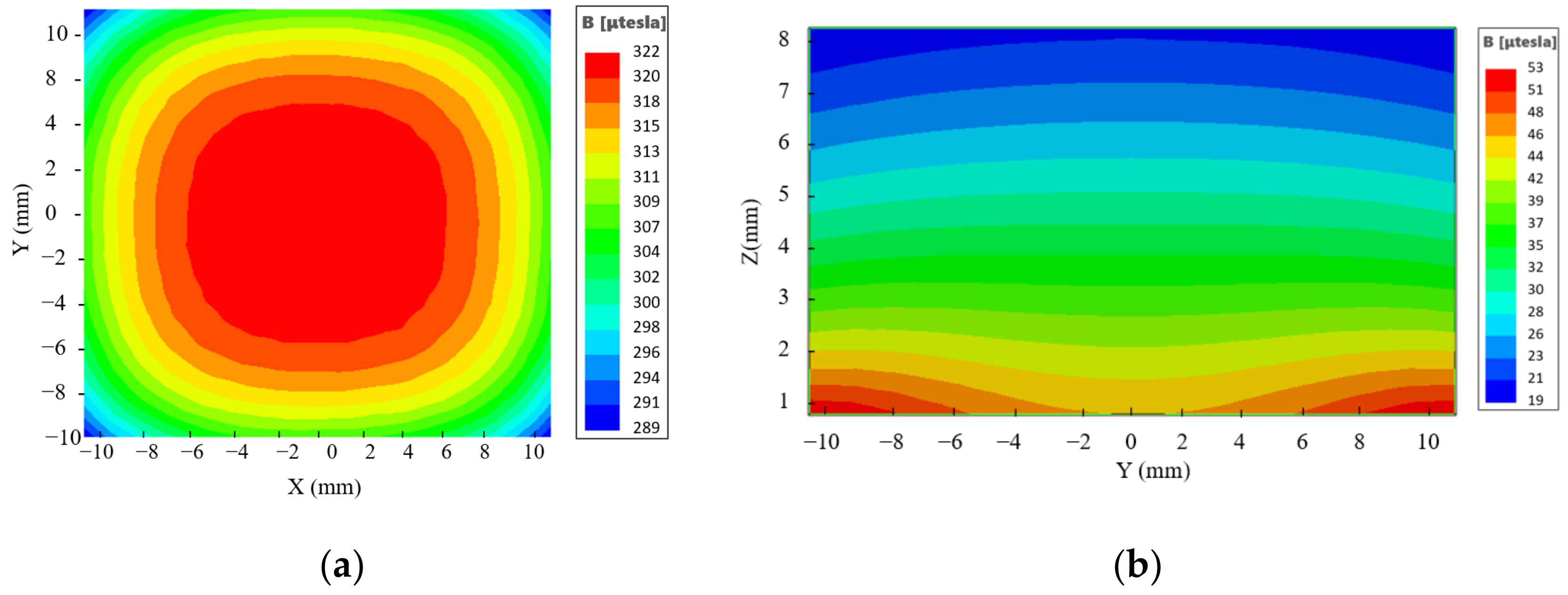
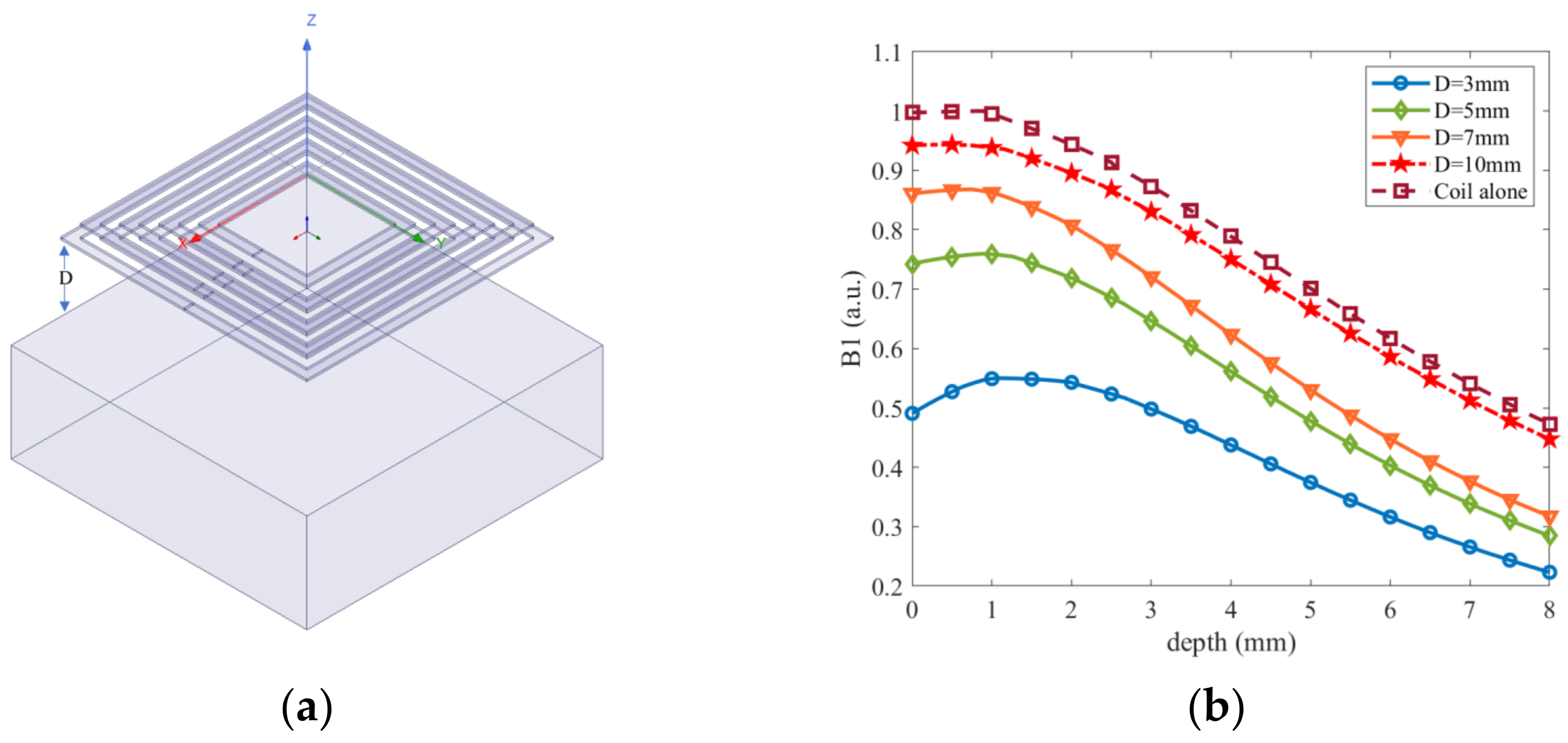

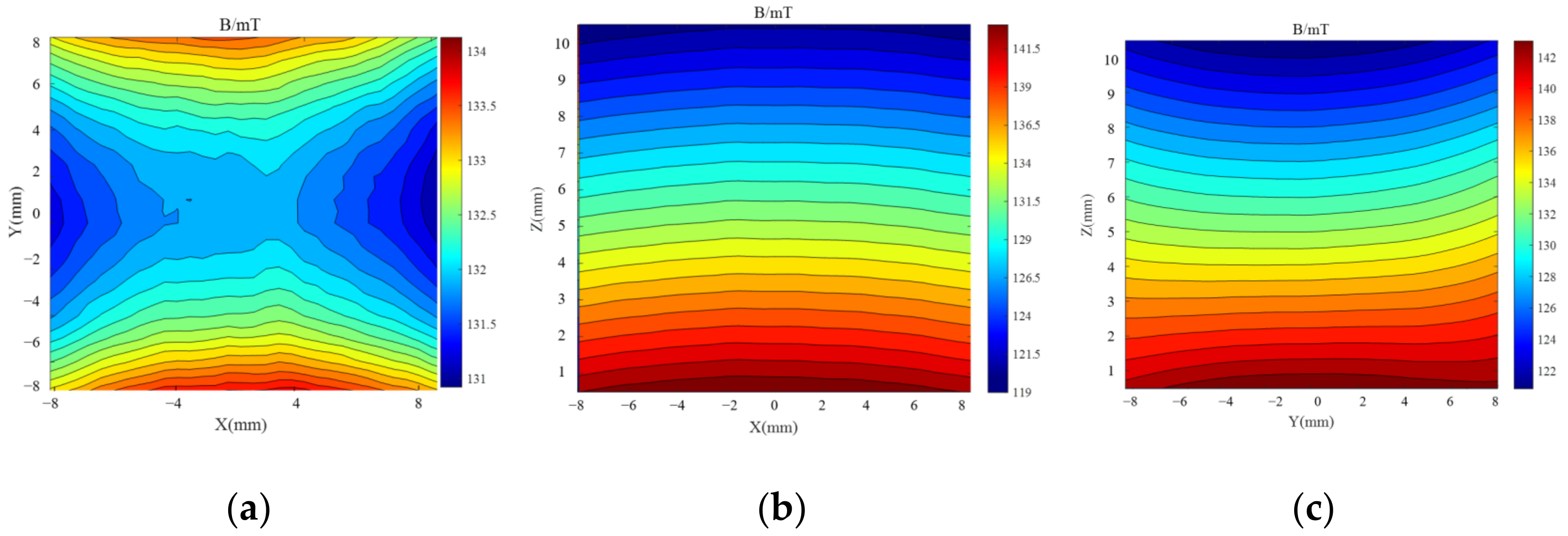
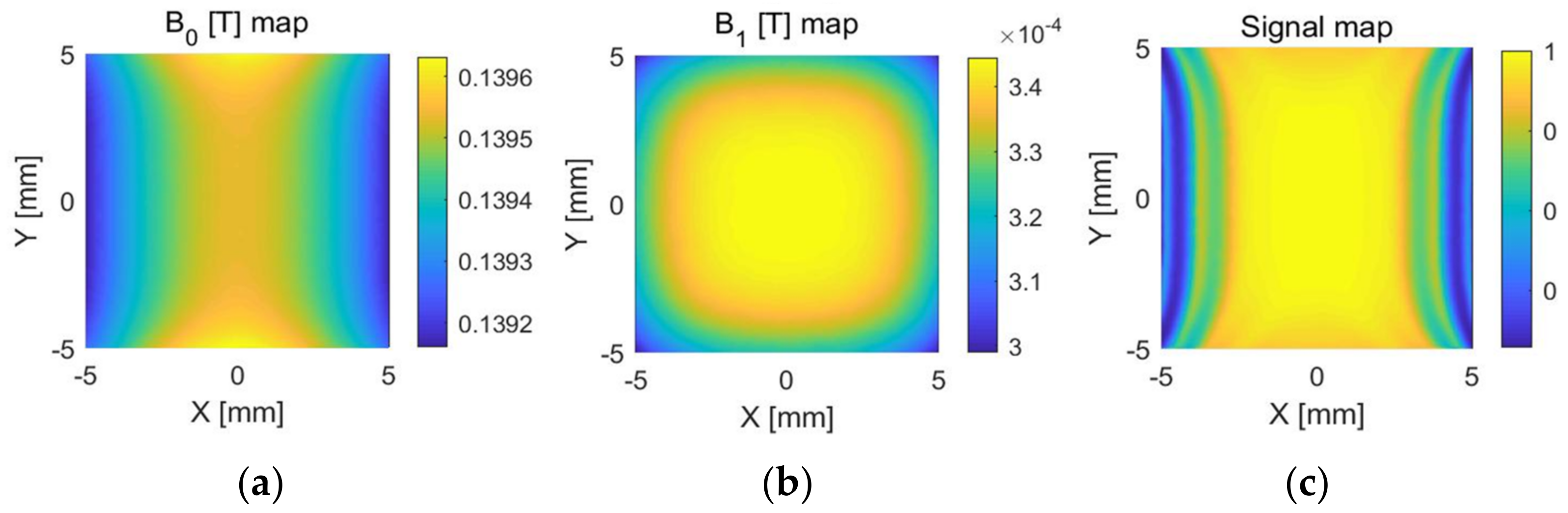

| Sensors | Frequency (MHz) | Gradient (T/m) | Dimension (cm) | Magnet Materials |
|---|---|---|---|---|
| NMR-MOUSE | 17 | 20 | 20 × 20 × 10 | Na2Fe14B |
| Mini-NMR-MOUSE | 17.14 | 67.8 | 7 × 5 × 7 | Na2Fe14B |
| Three-magnet array | 4.26 | 2 | 10 × 8 × 5 | N48NaFeB |
| The sensor in this work | 5.95 | 2.318 | 12 × 13.05 × 7.6 | (SmGd)2(CoFeCuZr)17 |
| Turns | U | ||
|---|---|---|---|
| 3 | 111 | 109 | 99.05% |
| 4 | 151 | 134 | 94.04% |
| 5 | 184 | 144 | 87.80% |
| 6 | 191 | 143 | 85.63% |
| Thickness (mm) | |||
|---|---|---|---|
| 0.2 | 322 | 289 | 94.50% |
| 0.4 | 318 | 284 | 94.30% |
| 0.8 | 313 | 278 | 94.08% |
| 1.6 | 309 | 274 | 93.94% |
| Model | Remanence | Coercivity | Intrinsic Coercivity | Maximum Magnetic Energy Product | Temperature Coefficient of Remanence |
|---|---|---|---|---|---|
| XYG-32 | 1.10–1.13 | 812–860 | ≥1433 | 230–255 | −0.035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, P.; Yang, C.; Wu, J.; Xu, Z. Optimized Unilateral Magnetic Resonance Sensor with Constant Gradient and Its Applications in Composite Insulators. Sensors 2023, 23, 5476. https://doi.org/10.3390/s23125476
Guo P, Yang C, Wu J, Xu Z. Optimized Unilateral Magnetic Resonance Sensor with Constant Gradient and Its Applications in Composite Insulators. Sensors. 2023; 23(12):5476. https://doi.org/10.3390/s23125476
Chicago/Turabian StyleGuo, Pan, Chenjie Yang, Jiamin Wu, and Zheng Xu. 2023. "Optimized Unilateral Magnetic Resonance Sensor with Constant Gradient and Its Applications in Composite Insulators" Sensors 23, no. 12: 5476. https://doi.org/10.3390/s23125476
APA StyleGuo, P., Yang, C., Wu, J., & Xu, Z. (2023). Optimized Unilateral Magnetic Resonance Sensor with Constant Gradient and Its Applications in Composite Insulators. Sensors, 23(12), 5476. https://doi.org/10.3390/s23125476







