Terrain Characterization via Machine vs. Deep Learning Using Remote Sensing
Abstract
:1. Introduction
2. Materials and Methods
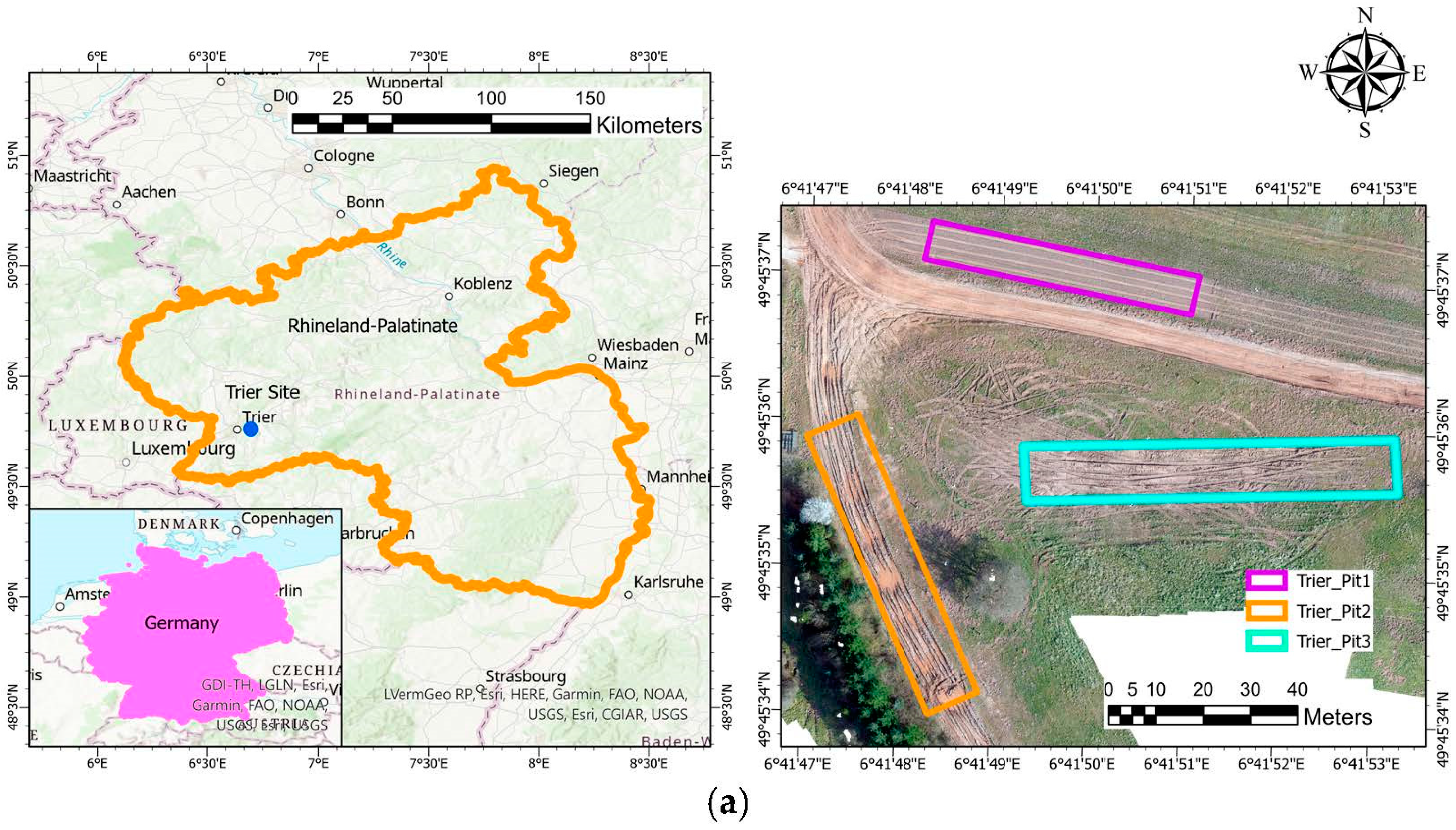
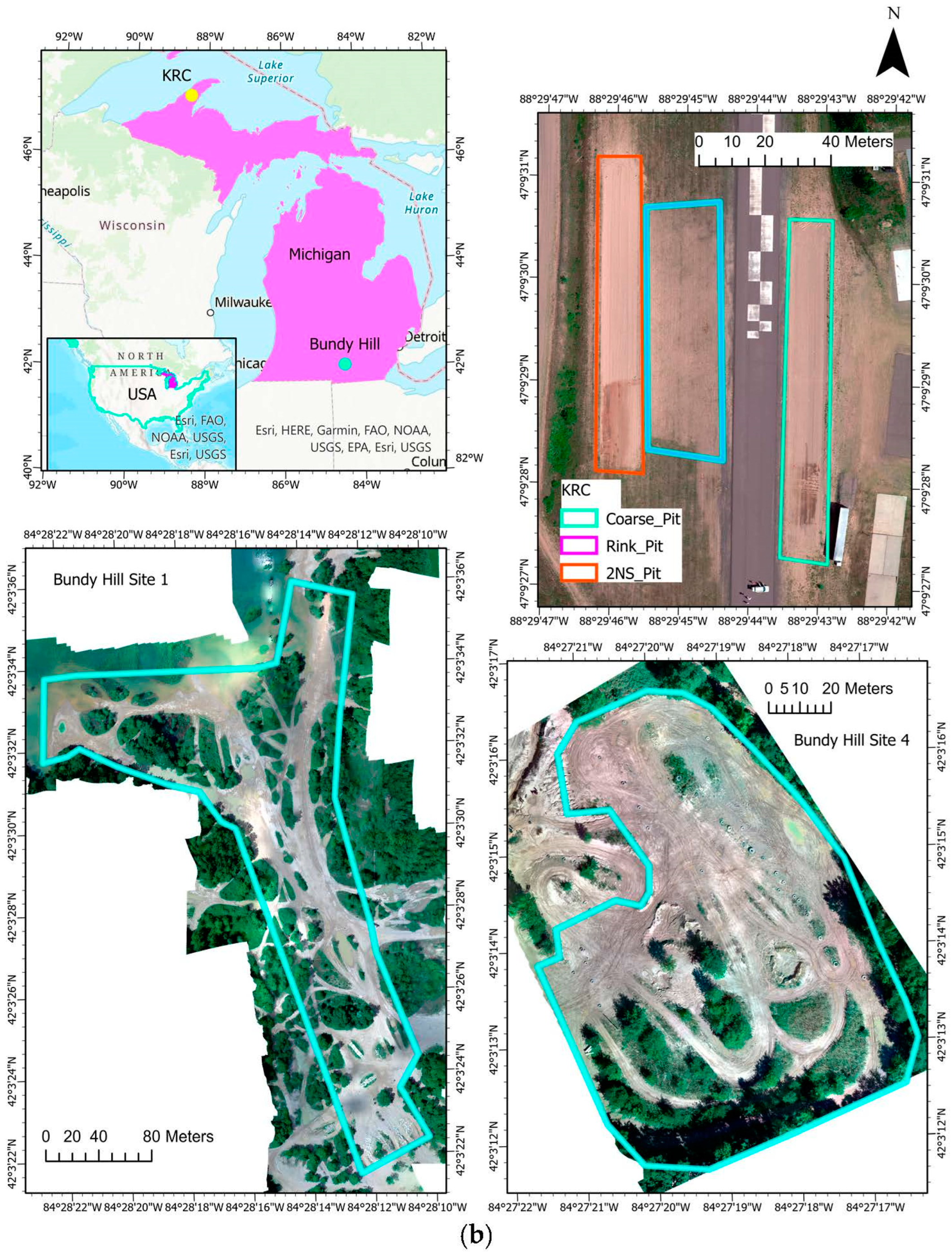
2.1. Field Sites and Soil Characteristics
2.2. Remote Sensing Data Collection
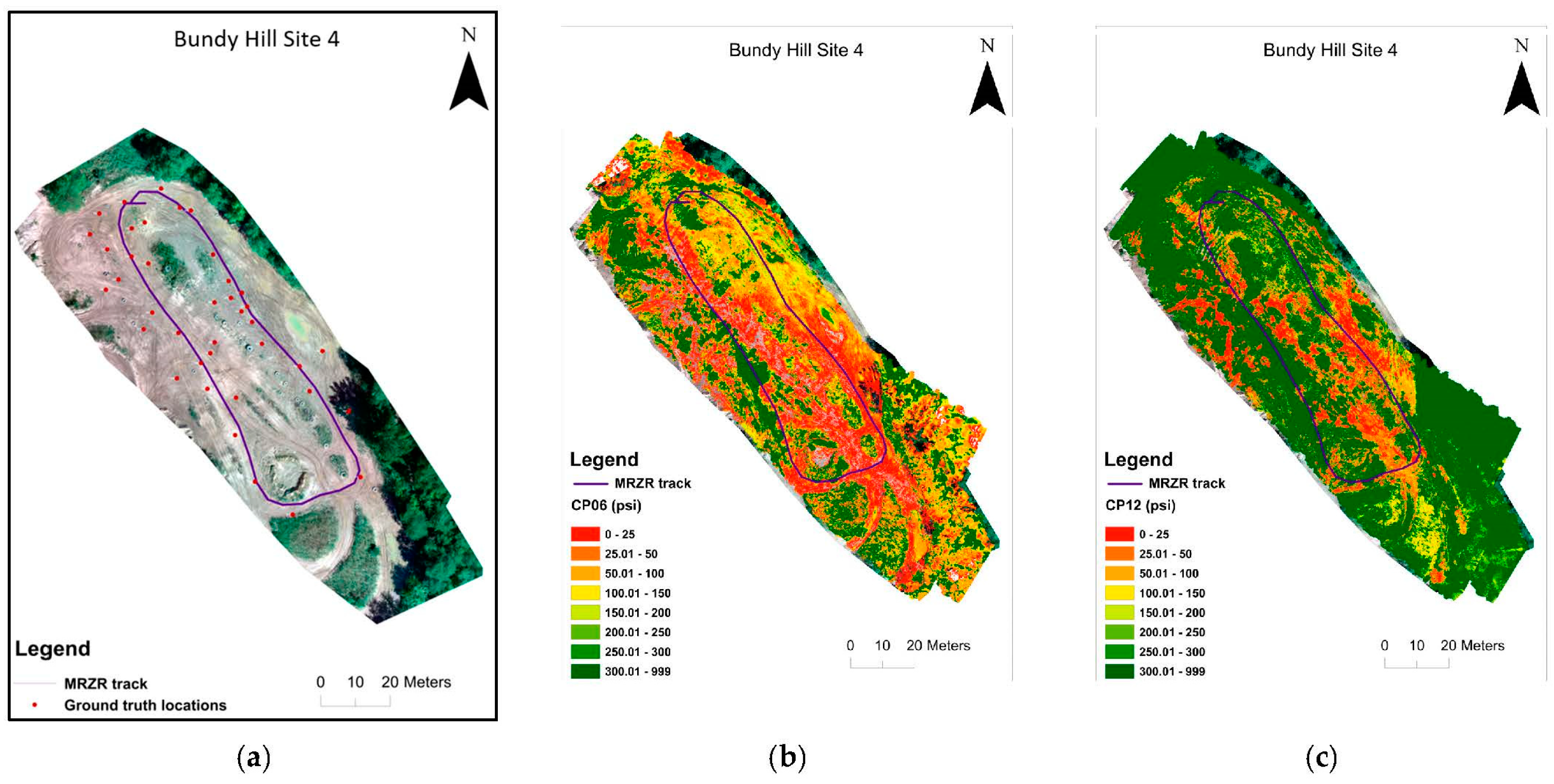
2.3. In-Situ Data Collection
2.4. ML and DL Modeling
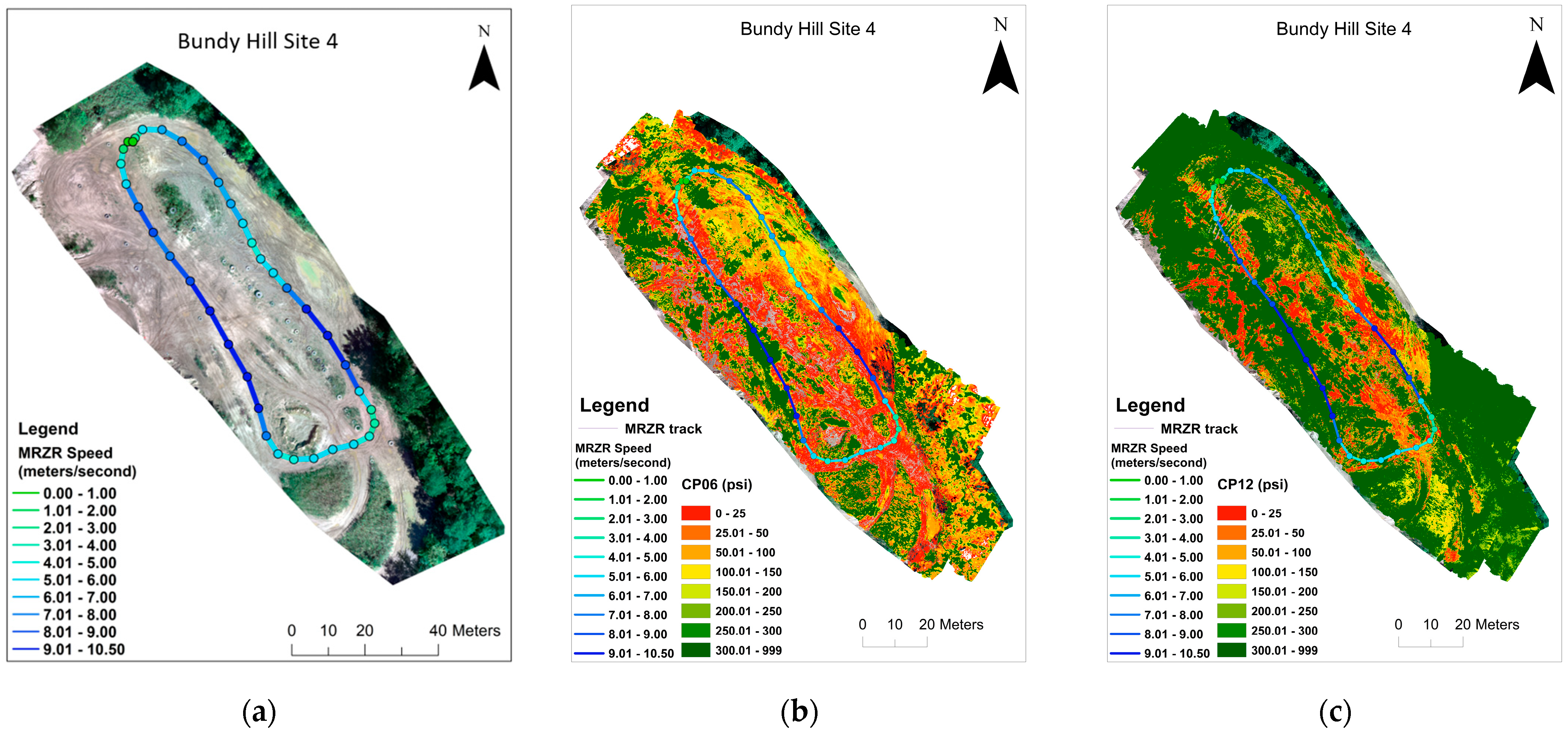
2.5. Field Validation
2.6. Predictors and Data Cleaning
2.6.1. Predictor Variables
2.6.2. Thermal Inertia/Apparent Thermal Inertia
2.6.3. Data Pre-Processing
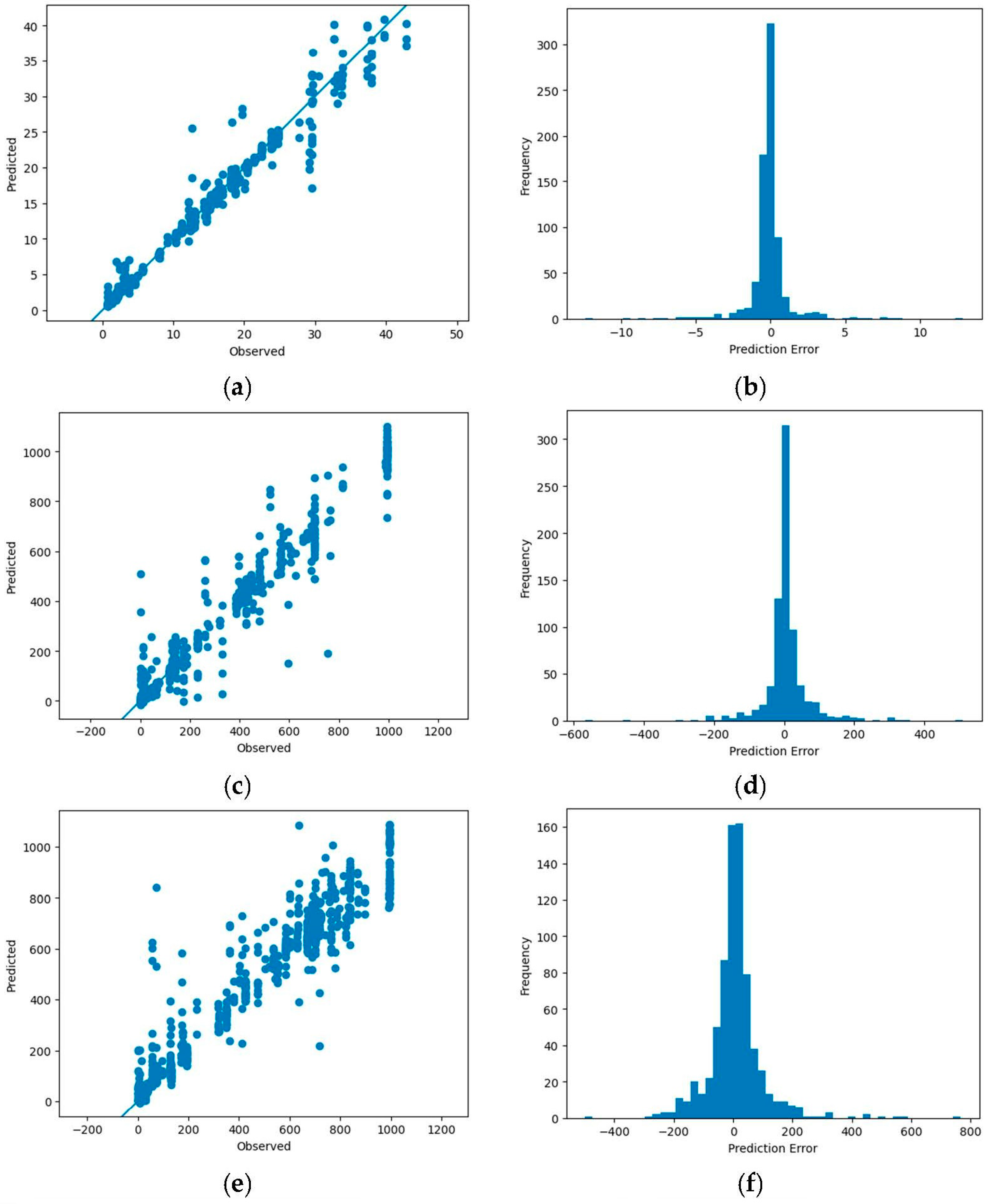
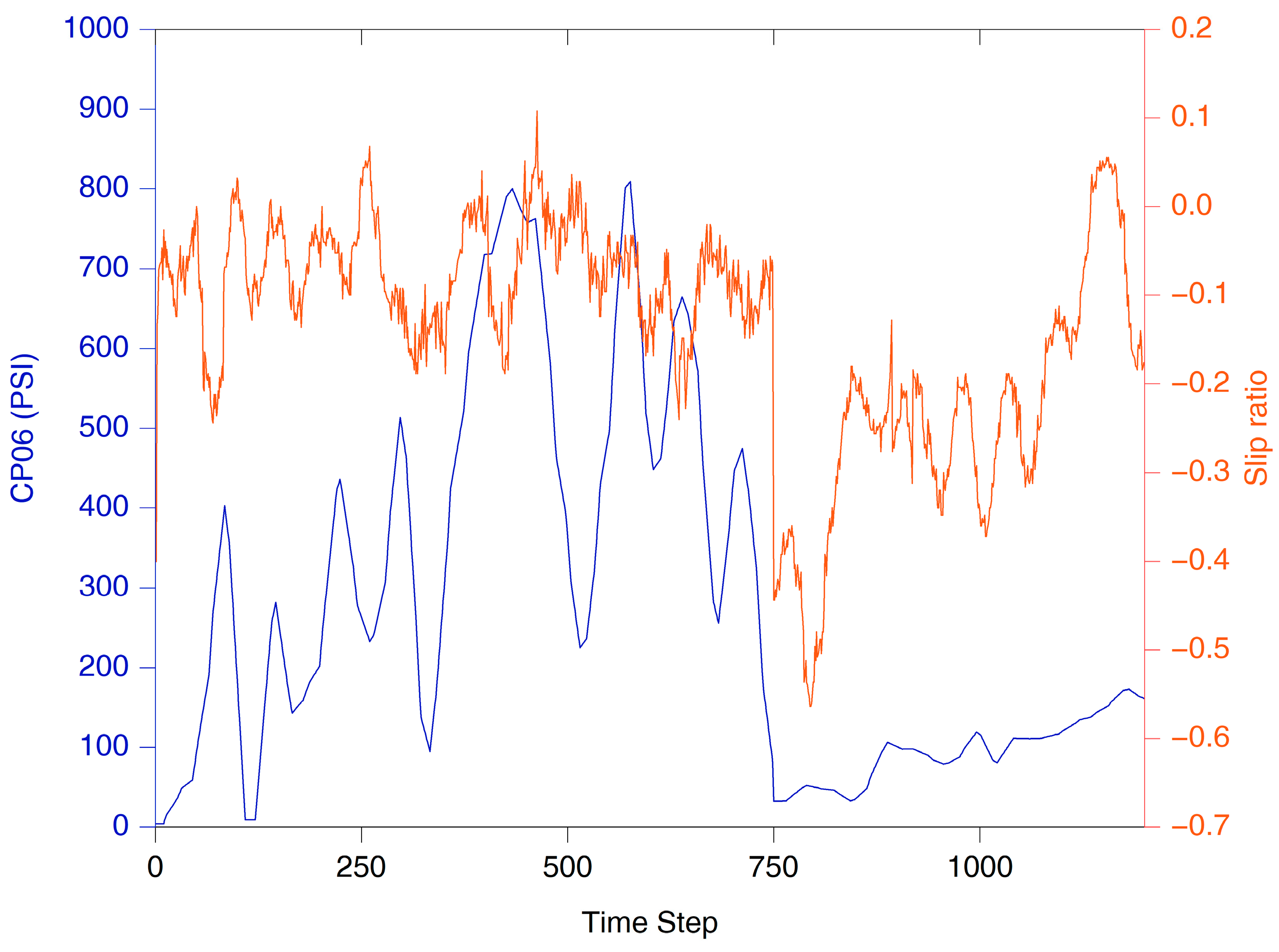
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Distribution Statement
References
- McCullough, M.; Jayakumar, P.; Dasch, J.; Gorsich, D. Developing the Next Generation NATO Reference Mobility Model. In Proceedings of the 2016 Ground Vehicle Systems Engineering and Technology Symposium (GVSETS), Novi, MI, USA, 2–4 August 2016. [Google Scholar]
- Mechergui, D.; Jayakumar, P. Efficient Generation of Accurate Mobility Maps Using Machine Learning Algorithms. J. Terramechanics 2020, 88, 53–63. [Google Scholar] [CrossRef]
- Pandey, V.; Bos, J.P.; Ewing, J.; Kysar, S.; Oommen, T.; Smith, W.; Jayakumar, P.; Gorsich, D. Decision-Making for Autonomous Mobility Using Remotely Sensed Terrain Parameters in Off-Road Environments. SAE 2021, 3, 1682–1689. [Google Scholar]
- Cole, M.; Lucas, C.; Kulkarni, K.; Carruth, D.; Hudson, C.; Jayakumar, P.; Gorsich, D. Quantitative assessment of modelling and simulation tools for autonomous navigation of military vehicles over off-road terrains. Int. J. Veh. Perform. 2020, 6, 327–355. [Google Scholar] [CrossRef]
- Okello, J.A. A Review of Soil Strength Measurement Techniques for Prediction of Terrain Vehicle Performance. J. Agric. Eng. Res. 1991, 50, 129–155. [Google Scholar] [CrossRef]
- Shoop, S.A. Terrain Characterization for Trafficability; US Army Corps of Engineers Cold Regions Research & Engineering Laboratory: Hanover, NH, USA, 1993. [Google Scholar]
- Huang, W.; Wong, J.Y.; Preston-Thomas, J.; Jayakumar, P. Predicting terrain parameters for physics-based vehicle mobility models from cone index data. J. Terramechanics 2020, 88, 29–40. [Google Scholar] [CrossRef]
- Riese, F.M.; Keller, S.; Hinz, S. Supervised and Semi-Supervised Self-Organizing Maps for Regression and Classification Focusing on Hyperspectral Data. Remote Sens. 2019, 12, 7. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Tang, R.; Zhao, W.; Tang, B.; Wu, H.; Shao, K.; Li, Z.-L. Surface Soil Water Content Estimation from Thermal Remote Sensing based on the Temporal Variation of Land Surface Temperature. Remote Sens. 2014, 6, 3170–3187. [Google Scholar] [CrossRef] [Green Version]
- Tasora, A.; Mangoni, D.; Negrut, D.; Serban, R.; Jayakumar, P. Deformable soil with adaptive level of detail for tracked and wheeled vehicles. Int. J. Veh. Perform. 2019, 5, 17. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital soil mapping: A brief history and some lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Shahriari, M.; Delbari, M.; Afrasiab, P.; Pahlavan-Rad, M.R. Predicting regional spatial distribution of soil texture in floodplains using remote sensing data: A case of southeastern Iran. CATENA 2019, 182, 104149. [Google Scholar] [CrossRef]
- Müller, B.; Bernhardt, M.; Jackisch, C.; Schulz, K. Estimating spatially distributed soil texture using time series of thermal remote sensing—A case study in central Europe. Hydrol. Earth Syst. Sci. 2016, 20, 3765–3775. [Google Scholar] [CrossRef] [Green Version]
- Dyson, J.; Mancini, A.; Frontoni, E.; Zingaretti, P. Deep Learning for Soil and Crop Segmentation from Remotely Sensed Data. Remote Sens. 2019, 11, 1859. [Google Scholar] [CrossRef] [Green Version]
- Rahimzadeh-Bajgiran, P.; Berg, A.A.; Champagne, C.; Omasa, K. Estimation of soil moisture using optical/thermal infrared remote sensing in the Canadian Prairies. ISPRS J. Photogramm. Remote Sens. 2013, 83, 94–103. [Google Scholar] [CrossRef]
- Zwissler, B.; Oommen, T.; Vitton, S.; Seagren, E.A. Thermal Remote Sensing For Moisture Content Monitoring of Mine Tailings: Laboratory Study. Environ. Eng. Geosci. 2017, 23, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Scheidt, S.; Ramsey, M.; Lancaster, N. Determining soil moisture and sediment availability at White Sands Dune Field, New Mexico, from apparent thermal inertia data. J. Geophys. Res. Earth Surf. 2010, 115, F2. [Google Scholar] [CrossRef]
- Lei, S.-g.; Bian, Z.-f.; Daniels, J.L.; Liu, D.-l. Improved spatial resolution in soil moisture retrieval at arid mining area using apparent thermal inertia. Trans. Nonferrous Met. Soc. China 2014, 24, 1866–1873. [Google Scholar] [CrossRef]
- Sohrabinia, M.; Rack, W.; Zawar-Reza, P. Soil moisture derived using two apparent thermal inertia functions over Canterbury, New Zealand. J. Appl. Remote Sens. 2014, 8, 083624. [Google Scholar] [CrossRef] [Green Version]
- Taktikou, E.; Bourazanis, G.; Papaioannou, G.; Kerkides, P. Prediction of Soil Moisture from Remote Sensing Data. Procedia Eng. 2016, 162, 309–316. [Google Scholar] [CrossRef] [Green Version]
- Van doninck, J.; Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E.C. The potential of multitemporal Aqua and Terra MODIS apparent thermal inertia as a soil moisture indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar] [CrossRef]
- Soliman, A.; Heck, R.; Brenning, A.; Brown, R.; Miller, S. Remote Sensing of Soil Moisture in Vineyards Using Airborne and Ground-Based Thermal Inertia Data. Remote Sens. 2013, 5, 3729–3748. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Yang, K.; Lu, N.; Chen, Y.; Zhao, L.; Han, M. Spatial upscaling of in-situ soil moisture measurements based on MODIS-derived apparent thermal inertia. Remote Sens. Environ. 2013, 138, 1–9. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, G. Estimation of Soil Moisture from Optical and Thermal Remote Sensing: A Review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef] [Green Version]
- Stark, N.; McNinch, J.; Wadman, H.; Graber, H.C.; Albatal, A.; Mallas, P.A. Friction angles at sandy beaches from remote imagery. Géotechnique Lett. 2017, 7, 292–297. [Google Scholar] [CrossRef]
- Ewing, J.; Oommen, T.; Jayakumar, P.; Alger, R. Characterizing Soil Stiffness Using Thermal Remote Sensing and Machine Learning. Remote Sens. 2021, 13, 2306. [Google Scholar] [CrossRef]
- Gao, Y.; Spiteri, C.; Li, C.-L.; Zheng, Y.-C. Lunar soil strength estimation based on Chang’E-3 images. Adv. Space Res. 2016, 58, 1893–1899. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A hybrid MLP-CNN classifier for very fine resolution remotely sensed image classification. ISPRS J. Photogramm. Remote Sens. 2018, 140, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Yamaç, S.S.; Şeker, C.; Negiş, H. Evaluation of machine learning methods to predict soil moisture constants with different combinations of soil input data for calcareous soils in a semi arid area. Agric. Water Manag. 2020, 234, 106121. [Google Scholar] [CrossRef]
- Khaledian, Y.; Miller, B.A. Selecting appropriate machine learning methods for digital soil mapping. Appl. Math. Model. 2020, 81, 401–418. [Google Scholar] [CrossRef]
- Hughes, I.; Verdugo, J.L.; Carcamo, A.; Mark, E.; Larenas, J.M.; Jayakumar, P. Self-Supervised Mobility Assessment from Unsupervised Proprioceptive Feature Learning on Simulated Environment; U.S. Army Combat Capabilities Development Command Ground Vehicle Systems Center, US ARMY DEVCOM GVSC: Warren, MI, USA, 2022; p. 25. [Google Scholar]
- Reina, G.; Milella, A.; Galati, R. Terrain assessment for precision agriculture using vehicle dynamic modelling. Biosyst. Eng. 2017, 162, 124–139. [Google Scholar] [CrossRef]
- Liu, J.; Jayakumar, P.; Stein, J.L.; Ersal, T. Combined speed and steering control in high-speed autonomous ground vehicles for obstacle avoidance using model predictive control. IEEE Trans. Veh. Technol. 2017, 66, 8746–8763. [Google Scholar] [CrossRef]
- Xue, L.; Li, J.; Zou, M.; Zong, W.; Huang, H. In situ identification of shearing parameters for loose lunar soil using least squares support vector machine. Aerosp. Sci. Technol. 2016, 53, 154–161. [Google Scholar] [CrossRef]
- Dallas, J.; Cole, M.P.; Jayakumar, P.; Ersal, T. Terrain Adaptive Trajectory Planning and Tracking on Deformable Terrains. IEEE Trans. Veh. Technol. 2021, 70, 11255–11268. [Google Scholar] [CrossRef]
- González, R.; López, A.; Iagnemma, K. Thermal vision, moisture content, and vegetation in the context of off-road mobile robots. J. Terramechanics 2017, 70, 35–48. [Google Scholar] [CrossRef]
- Pundir, S.K.; Garg, R.D. Development of mapping techniques for off road trafficability to support military operation. Spat. Inf. Res. 2020, 28, 495–506. [Google Scholar] [CrossRef]
- MicaSense, Inc. User Guide for MicaSense Sensors; MicaSense, Inc.: Seattle, WA, USA, 2021. [Google Scholar]
- MicaSense, Inc. MicaSense RedEdge-MX™ and DLS 2 Integration Guide; MicaSense, Inc.: Seattle, WA, USA, 2020. [Google Scholar]
- BaySpec, Inc. OCI-F Ultra-Compact Hyperspectral Imager User Manual; BaySpec Inc.: San Jose, CA, USA, 2018; p. 66. [Google Scholar]
- FLIR. FLIR Vue Pro and Vue Pro R User Guide; Teledyne FLIR LLC: Wilsonville, OR, USA, 2016; p. 36. [Google Scholar]
- DJI. Mavic 2 Enterprise Advanced User Manual; DJI: Los Angeles, CA, USA, 2021; p. 68. [Google Scholar]
- Propellor. AeroPoints Manual; Propellor: Denver, CO, USA, 2021; p. 20. [Google Scholar]
- Spectrum Technologies, Inc. FieldScout SC 900 Soil Compaction Meter User Manual; Spectrum Technologies, Inc.: Aurora, IL, USA, 2009; p. 28. [Google Scholar]
- Spectrum Technologies, Inc. FieldScout TDR 150 Soil Moisture Meter; Spectrum Technologies, Inc.: Aurora, IL, USA, 2017; p. 36. [Google Scholar]
- Trimble. Trimble GeoXH6000 User Manual; Trimble Navigation Limited: Westminster, CO, USA, 2012; p. 137. [Google Scholar]
- Trimble. Trimble Geo 7X Handheld User Guide; Trimble Navigation Limited: Westminster, CO, USA, 2013; p. 133. [Google Scholar]
- Guilkey, D.K.; Murphy, J.L. Directed Ridge Regression Techniques in Cases of Multicollinearity. J. Am. Stat. Assoc. 1975, 70, 769–775. [Google Scholar] [CrossRef]
- Marquardt, D.W.; Snee, R.D. Ridge Regression in Practice. Am. Stat. 1975, 29, 3–20. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R.; Johnstone, I.; Hastie, T.; Efron, B. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Burges, C.J.C. A Tutorial On Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Cristianini, N. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Mũnoz-Marí, J.; Bovolo, F.; Gómez-Chova, L.; Bruzzone, L.; Camp-Valls, G. Semisupervised One-Class Support Vector Machines for Classification of Remote Sensing Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3188–3197. [Google Scholar] [CrossRef] [Green Version]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Ramchoun, H.; Amine, M.; Idrissi, J.; Ghanou, Y.; Ettaouil, M. Multilayer Perceptron: Architecture Optimization and Training. Int. J. Interact. Multimed. Artif. Intell. 2016, 4, 26–30. [Google Scholar] [CrossRef] [Green Version]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Mura, M.D. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef] [Green Version]
- Ewing, J.; Oommen, T.; Jayakumar, P.; Alger, R. Utilizing Hyperspectral Remote Sensing for Soil Gradation. Remote Sens. 2020, 12, 3312. [Google Scholar] [CrossRef]
- Minacapilli, M.; Cammalleri, C.; Ciraolo, G.; D’Asaro, F.; Iovino, M.; Maltese, A. Thermal Inertia Modeling for Soil Surface Water Content Estimation: A Laboratory Experiment. Soil Sci. Soc. Am. J. 2012, 76, 92–100. [Google Scholar] [CrossRef]
- Al Bodour, W.; Hanandeh, S.; Hajij, M.; Murad, Y. Development of Evaluation Framework for the Unconfined Compressive Strength of Soils Based on the Fundamental Soil Parameters Using Gene Expression Programming and Deep Learning Methods. J. Mater. Civ. Eng. 2022, 34, 1–12. [Google Scholar] [CrossRef]



| # | Site | Pit | %Gravel | %Sand | %Fine |
|---|---|---|---|---|---|
| 1 | KRC | 2NS | 3.3 | 95.6 | 1.1 |
| 2 | KRC | 2NS | 1.7 | 97.4 | 0.9 |
| 3 | KRC | Rink | 7.2 | 86.6 | 6.2 |
| 4 | KRC | Rink | 4.7 | 90.4 | 4.9 |
| 5 | KRC | Coarse | 3.0 | 95.7 | 1.3 |
| 6 | KRC | Coarse | 1.8 | 97.3 | 0.9 |
| 7 | Bundy Hill | S1 | 0.4 | 25.4 | 74.2 |
| 8 | Bundy Hill | S1 | 0.0 | 48.3 | 51.7 |
| 9 | Bundy Hill | S1 | 2.0 | 92.3 | 5.7 |
| 10 | Bundy Hill | S1 | 6.9 | 79.3 | 13.8 |
| 11 | Bundy Hill | S1 | 3.0 | 94.7 | 2.3 |
| 12 | Bundy Hill | S4 | 2.6 | 26.5 | 70.9 |
| 13 | Bundy Hill | S4 | 8.9 | 38.4 | 52.7 |
| 14 | Bundy Hill | S4 | 19.1 | 44.7 | 36.2 |
| 15 | Bundy Hill | S4 | 1.3 | 68.8 | 29.9 |
| 16 | Trier | Pit 1 | 6.9 | 38.2 | 54.9 |
| 17 | Trier | Pit 1 | 4.0 | 48.4 | 47.6 |
| 18 | Trier | Pit 1 | 7.2 | 43.2 | 49.6 |
| 19 | Trier | Pit 2 | 7.4 | 40.8 | 51.8 |
| 20 | Trier | Pit 2 | 6.2 | 41.1 | 52.7 |
| 21 | Trier | Pit 3 | 8.1 | 36.9 | 55.0 |
| 22 | Trier | Pit 3 | 4.9 | 42.6 | 52.5 |
| Location (Pit) | Moisture Range | Moisture Mean | CP12 Range | CP12 Mean | CP06 Range | CP06 Mean |
|---|---|---|---|---|---|---|
| Trier (Pit1) | 10.3–14.7 | 12.3 | 37–195 | 109 | 11–116 | 46 |
| Trier (Pit2) | 14.7–24.8 | 19.9 | 58–995 | 436 | 0–995 | 264 |
| Trier (Pit3) | 14.7–16.4 | 15.8 | 7–837 | 512 | 13–701 | 294 |
| KRC (Coarse) | 1.0–2.9 | 1.9 | 0–702 | 148 | 0–451 | 71 |
| KRC (Rink) | 1.1–2.1 | 1.6 | 175–995 | 489 | 0–995 | 251 |
| KRC (2NS) | 0.8–4.6 | 2.3 | 0–812 | 112 | 0–655 | 66 |
| BH (S1) | 4.9–27.8 | 14.2 | 77–821 | 640 | 44–671 | 416 |
| BH (S4) | 0.8–42.9 | 19.2 | 73–995 | 740 | 15–995 | 586 |
| R2/RMSE for Each Regression Model | |||
|---|---|---|---|
| Algorithms | Moisture Content (%) | CP06 (PSI) | CP12 (PSI) |
| Linear | 0.508/6.00 | 0.478/231 | 0.524/229 |
| Ridge | 0.510/5.99 | 0.483/230 | 0.527/229 |
| Lasso | 0.508/6.01 | 0.489/229 | 0.531/228 |
| PLS | 0.044/8.37 | 0.140/297 | 0.109/314 |
| SVM | 0.351/6.90 | 0.197/287 | 0.539/226 |
| KNN | 0.614/5.32 | 0.662/186 | 0.647/197 |
| MLP (All predictors) | 0.967/1.55 | 0.953/67 | 0.917/94 |
| CNN_(All predictors) | 0.895/2.78 | 0.895/100 | 0.852/126 |
| MLP (No RGB) | 0.951/1.89 | 0.934/79 | 0.940/80 |
| CNN_(No RGB) | 0.860/3.21 | 0.906/95 | 0.867/119 |
| MLP_(PCA 10) | 0.929/2.21 | 0.932/86 | 0.944/80 |
| CNN_(PCA 10) | 0.913/2.44 | 0.918/94 | 0.902/106 |
| MLP (Single flight predictors) | 0.932/2.23 | 0.906/95 | 0.924/90 |
| CNN (Single flight predictors) | 0.862/3.18 | 0.866/113 | 0.846/128 |
| MLP (Single flight predictors with PCA 10) | 0.887/3.01 | 0.877/110 | 0.903/104 |
| CNN (Single flight predictors with PCA 10) | 0.874/3.18 | 0.863/116 | 0.858/126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ewing, J.; Oommen, T.; Thomas, J.; Kasaragod, A.; Dobson, R.; Brooks, C.; Jayakumar, P.; Cole, M.; Ersal, T. Terrain Characterization via Machine vs. Deep Learning Using Remote Sensing. Sensors 2023, 23, 5505. https://doi.org/10.3390/s23125505
Ewing J, Oommen T, Thomas J, Kasaragod A, Dobson R, Brooks C, Jayakumar P, Cole M, Ersal T. Terrain Characterization via Machine vs. Deep Learning Using Remote Sensing. Sensors. 2023; 23(12):5505. https://doi.org/10.3390/s23125505
Chicago/Turabian StyleEwing, Jordan, Thomas Oommen, Jobin Thomas, Anush Kasaragod, Richard Dobson, Colin Brooks, Paramsothy Jayakumar, Michael Cole, and Tulga Ersal. 2023. "Terrain Characterization via Machine vs. Deep Learning Using Remote Sensing" Sensors 23, no. 12: 5505. https://doi.org/10.3390/s23125505
APA StyleEwing, J., Oommen, T., Thomas, J., Kasaragod, A., Dobson, R., Brooks, C., Jayakumar, P., Cole, M., & Ersal, T. (2023). Terrain Characterization via Machine vs. Deep Learning Using Remote Sensing. Sensors, 23(12), 5505. https://doi.org/10.3390/s23125505







