Distributed Poloidal Magnetic Field Measurement in Tokamaks Using Polarization-Sensitive Reflectometric Fiber Optic Sensor
Abstract
:1. Introduction
2. Polarization-Sensitive Reflectometry for Distributed Magnetic Field Measurement: Theory and Sensor Modeling
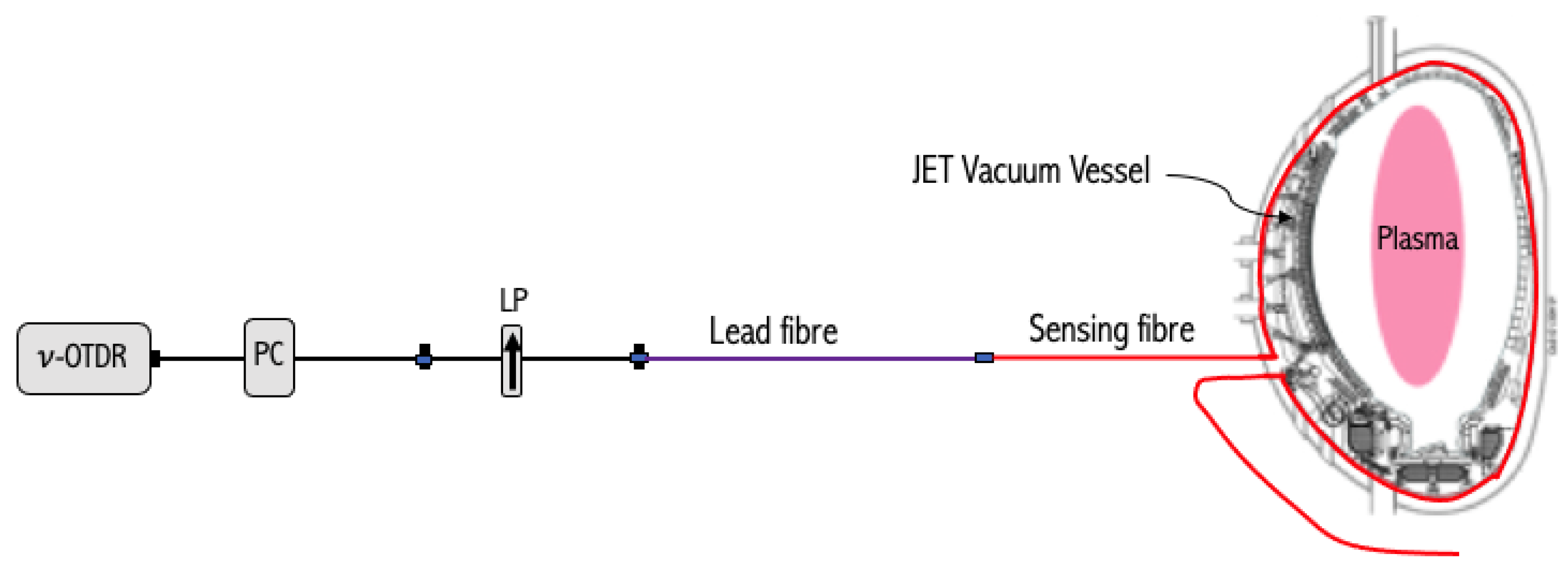
3. Experimental Results
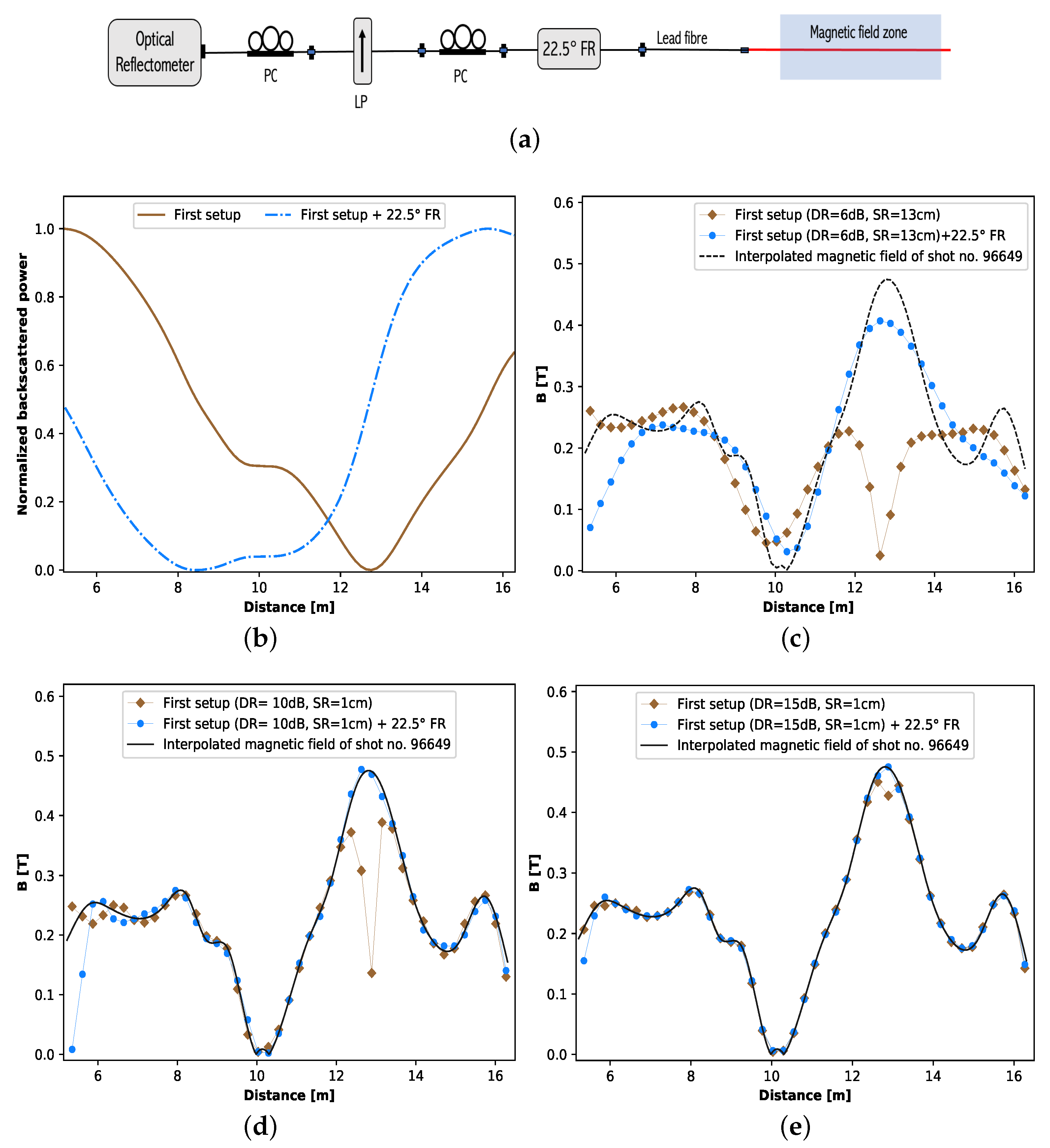
4. Approach for Avoiding the Issue Due to Reflectometer’s Noise Level
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Equipe, T.F.R. Tokamak plasma diagnostics. Nucl. Fusion 1978, 18, 647. [Google Scholar] [CrossRef]
- Strait, E.J. Magnetic diagnostic system of the DIII-D tokamak. Rev. Sci. Instrum. 2006, 77, 023502. [Google Scholar] [CrossRef]
- Biel, W.; Albanese, R.; Ambrosino, R.; Ariola, M.; Berkel, M.; Bolshakova, I.; Brunner, K.; Cavazzana, R.; Cecconello, M.; Conroy, S.; et al. Diagnostics for plasma control–From ITER to DEMO. Fusion Eng. Des. 2019, 146, 465–472. [Google Scholar] [CrossRef]
- Moreau, P.; Bolshakova, I.; Brichard, B.; Chitarin, G.; Delogu, R.; Duran, I.; Encheva, A.; Fournier, Y.; Galo, A.; Le-Luyer, A.; et al. Development of a magnetic diagnostic suitable for the ITER radiation environment. In Proceedings of the 2009 1st International Conference on Advancements in Nuclear Instrumentation, Measurement Methods and Their Applications, Marseille, France, 7–10 June 2009; pp. 1–8. [Google Scholar]
- Vayakis, G.; Bertalot, L.; Encheva, A.; Walker, C.; Brichard, B.; Cheon, M.; Chitarin, G.; Hodgson, E.; Ingesson, C.; Ishikawa, M.; et al. Nuclear technology aspects of ITER vessel-mounted diagnostics. J. Nucl. Mater. 2011, 417, 780–786. [Google Scholar] [CrossRef] [Green Version]
- Girard, S.; Kuhnhenn, J.; Gusarov, A.; Brichard, B.; Van Uffelen, M.; Ouerdane, Y.; Boukenter, A.; Marcandella, C. Radiation effects on silica-based optical fibers: Recent advances and future challenges. IEEE Trans. Nucl. Sci. 2013, 60, 2015–2036. [Google Scholar] [CrossRef]
- Gusarov, A.; Leysen, W.; Wuilpart, M.; Mégret, P. Status and future developments of R&D on fiber optics current sensor for ITER. Fusion Eng. Des. 2018, 136, 477–480. [Google Scholar]
- Gusarov, A.; Leysen, W.; Kim, S.M.; Dandu, P.; Wuilpart, M.; Danisi, A.; Vayakis, G.; Danisi, A.; Barbero, J.L. Recent achievements in R&D on fibre optics current sensor for ITER. Fusion Eng. Des. 2023, 192, 113626. [Google Scholar]
- Palmieri, L.; Schenato, L. Distributed optical fiber sensing based on Rayleigh scattering. Open Opt. J. 2013, 7, 104–127. [Google Scholar] [CrossRef]
- Aerssens, M.; Gusarov, A.; Moreau, P.; Malard, P.; Massaut, V.; Mégret, P.; Wuilpart, M. Development of a Jones vector based model for the measurement of a plasma current in a thermonuclear fusion reactor with a POTDR setup. In Proceedings of the Optical Sensing and Detection II, Belgium, 21 May 2012; Volume 8439, pp. 91–102. [Google Scholar]
- Wuilpart, M.; Aerssens, M.; Gusarov, A.; Moreau, P.; Mégret, P. Plasma current measurement in thermonuclear fusion reactors using a photon-counting POTDR. IEEE Photonics Technol. Lett. 2017, 29, 547–550. [Google Scholar] [CrossRef]
- Ross, J. Measurement of magnetic field by polarisation optical time-domain reflectometry. Electron. Lett. 1981, 17, 596–597. [Google Scholar] [CrossRef]
- Rogers, A.J. Polarization-optical time domain reflectometry: A technique for the measurement of field distributions. Appl. Opt. 1981, 20, 1060–1074. [Google Scholar] [CrossRef] [PubMed]
- Galtarossa, A.; Palmieri, L. Mapping of intense magnetic fields based on polarization sensitive reflectometry in single mode optical fibers. In Proceedings of the 2013 Africon, Pointe aux Piments, Mauritius, 9–12 September 2013; pp. 1–5. [Google Scholar]
- Palmieri, L.; Galtarossa, A. Reflectometric fiber optic sensor for distributed measurement of intense magneto-static fields. In Proceedings of the SENSORS, 2011 IEEE, Limerick, Ireland, 28–31 October 2011; pp. 117–120. [Google Scholar]
- Laming, R.I.; Payne, D.N. Electric current sensors employing spun highly birefringent optical fibers. J. Light. Technol. 1989, 7, 2084–2094. [Google Scholar] [CrossRef] [Green Version]
- Wegmuller, M.; Scholder, F.; Gisin, N. Photon-counting OTDR for local birefringence and fault analysis in the metro environment. J. Light. Technol. 2004, 22, 390. [Google Scholar] [CrossRef]
- Masoudi, A.; Newson, T.P. Distributed optical fiber dynamic magnetic field sensor based on magnetostriction. Appl. Opt. 2014, 53, 2833–2838. [Google Scholar] [CrossRef]
- Ding, Z.; Du, Y.; Liu, T.; Liu, K.; Feng, B.; Jiang, J. Distributed optical fiber current sensor based on magnetostriction in OFDR. IEEE Photonics Technol. Lett. 2015, 27, 2055–2058. [Google Scholar] [CrossRef]
- Veeser, L.R.; Chandler, G.I.; Day, G.W. Fiber optic sensing of pulsed currents. In Proceedings of the Photonics: High Bandwidth Analog Applications, Proceedings of the SPIE, Hamburg, Germany, 13 August 1986; Volume 648, pp. 197–212. [Google Scholar]
- Rappé, G. The JET (joint European torus) vacuum vessel. Rev. De Phys. Appl. 1977, 12, 1735–1741. [Google Scholar] [CrossRef]
- Buckingham, A.; Stephens, P. Magnetic optical activity. Annu. Rev. Phys. Chem. 1966, 17, 399–432. [Google Scholar] [CrossRef]
- Haider, T. A review of magneto-optic effects and its application. Int. J. Electromagn. Appl. 2017, 7, 17–24. [Google Scholar]
- Piller, H. Faraday rotation. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 1972; Volume 8, pp. 103–179. [Google Scholar]
- Kim, B.; Park, D.; Choi, S. Use of polarization-optical time domain reflectometry for observation of the Faraday effect in single-mode fibers. IEEE J. Quantum Electron. 1982, 18, 455–456. [Google Scholar]
- Cruz, J.; Andres, M.; Hernandez, M. Faraday effect in standard optical fibers: Dispersion of the effective Verdet constant. Appl. Opt. 1996, 35, 922–927. [Google Scholar] [CrossRef]
- Faraday, M. XXVII. On the magnetic affection of light, and on the distinction between the ferromagnetic and diamagnetic conditions of matter. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1846, 29, 153–156. [Google Scholar] [CrossRef] [Green Version]
- Palmieri, L.; Galtarossa, A. Distributed polarization-sensitive reflectometry in nonreciprocal single-mode optical fibers. J. Light. Technol. 2011, 29, 3178–3184. [Google Scholar] [CrossRef]
- Noda, J.; Hosaka, T.; Sasaki, Y.; Ulrich, R. Dispersion of Verdet constant in stress-birefringent silica fibre. Electron. Lett. 1984, 22, 906–908. [Google Scholar] [CrossRef]
- Rose, A.; Etzel, S.M.; Wang, C.M. Verdet constant dispersion in annealed optical fiber current sensors. J. Light. Technol. 1997, 15, 803–807. [Google Scholar] [CrossRef] [Green Version]
- Simon, A.; Ulrich, R. Evolution of polarization along a single-mode fiber. Appl. Phys. Lett. 1977, 31, 517–520. [Google Scholar] [CrossRef]
- Chen, H.c.; Wen, J.x.; Huang, Y.; Dong, W.l.; Pang, F.f.; Luo, Y.h.; Peng, G.d.; Chen, Z.y.; Wang, T.y. Influence of linear birefringence on Faraday effect measurement for optical fibers. Optoelectron. Lett. 2017, 13, 147–150. [Google Scholar] [CrossRef]
- Aerssens, M.; Descamps, F.; Gusarov, A.; Mégret, P.; Moreau, P.; Wuilpart, M. Influence of the optical fiber type on the performances of fiber-optics current sensor dedicated to plasma current measurement in ITER. Appl. Opt. 2015, 54, 5983–5991. [Google Scholar] [CrossRef]
- Rashleigh, S.; Ulrich, R. Magneto-optic current sensing with birefringent fibers. Appl. Phys. Lett. 1979, 34, 768–770. [Google Scholar] [CrossRef]
- Barlow, A.; Ramskov-Hansen, J.; Payne, D. Birefringence and polarization mode-dispersion in spun single-mode fibers. Appl. Opt. 1981, 20, 2962–2968. [Google Scholar] [CrossRef]
- Li, L.; Qian, J.; Payne, D.N. Miniature multi-turn fibre current sensors. Int. J. Opt. Sens. 1987, 2, 25–31. [Google Scholar]
- Li, L.; Qian, J.R.; Payne, D. Current sensors using highly birefringent bow-tie fibres. Electron. Lett. 1986, 21, 1142–1144. [Google Scholar] [CrossRef] [Green Version]
- Payne, D.N.; Barlow, A.J.; Hansen, J.R. Development of low-and high-birefringence optical fibers. IEEE Trans. Microw. Theory Tech. 1982, 30, 323–334. [Google Scholar] [CrossRef]
- Barlow, A.; Ramskov-Hansen, J.; Payne, D.N. Anisotropy in spun single-mode fibres. Electron. Lett. 1982, 18, 200–202. [Google Scholar] [CrossRef] [Green Version]
- Przhiyalkovsky, Y.V.; Vasiliev, S.; Medvedkov, O.; Morshnev, S.; Dianov, E. Polarization state evolution in spun birefringent optical fibers. J. Appl. Phys. 2017, 122, 123104. [Google Scholar] [CrossRef]
- Morshnev, S.K.; Gubin, V.P.; Vorob’ev, I.; Starostin, I.; Sazonov, A.I.; Chamorovsky, Y.K.; Korotkov, N. Spun optical fibres: A helical structure of linear birefringence or circular birefringence? Quantum Electron. 2009, 39, 287. [Google Scholar] [CrossRef]
- Kim, S.M.; Dandu, P.; Gusarov, A.; Danisi, A.; Vayakis, G.; Wuilpart, M. Assessment of the Structural Vibration Effect on Plasma Current Measurement Using a Fiber Optic Current Sensor in ITER. Sensors 2023, 23, 1460. [Google Scholar] [CrossRef] [PubMed]
- Dandu, P.; Goussarov, A.; Moreau, P.; Leysen, W.; Kim, S.; Mégret, P.; Wuilpart, M. Polarization-OTDR-based optical fibre sensor for plasma current measurement in ITER: Effect of fibre bending, twisting and temperature dependence of Verdet constant on the measurement accuracy. In Proceedings of the Optical Sensors 2021, Online Only (Czech Republic), 19–23 April 2021; Volume 11772, pp. 312–322. [Google Scholar]
- Jones, R.C. A new calculus for the treatment of optical systems I. Description and discussion of the calculus. Josa 1941, 31, 488–493. [Google Scholar] [CrossRef]
- Hurwitz, H.; Jones, R. A new calculus for the treatment of optical systems II. Proof of three general equivalence theorems. J. Opt. Soc. Am. 1941, 31, 493–499. [Google Scholar] [CrossRef]
- Jones, R.C. A new calculus for the treatment of optical systems. VII. Properties of the N-matrices. Josa 1948, 38, 671–685. [Google Scholar] [CrossRef]
- Dandu, P.; Gusarov, A.; Moreau, P.; Leysen, W.; Kim, S.; Mégret, P.; Wuilpart, M. Plasma current measurement in ITER with a polarization-OTDR: Impact of fiber bending and twisting on the measurement accuracy. Appl. Opt. 2022, 61, 2406–2416. [Google Scholar] [CrossRef]
- Rogers, A.; Zhou, Y.; Handerek, V. Computational polarization-optical time domain reflectometry for measurement of the spatial distribution of PMD in optical fibers. In Proceedings of the 4th Optical Fiber Measurement Conference, Teddington, UK, 1 January 1997; pp. 126–129. [Google Scholar]
- Ross, J.N. Birefringence measurement in optical fibers by polarization-optical time-domain reflectometry. Appl. Opt. 1982, 21, 3489–3495. [Google Scholar] [CrossRef]
- Wuilpart, M. Rayleigh scattering in optical fibers and applications to distributed measurements. In Advanced Fiber Optics: Concepts and Technology; EPFL Press: Lausanne, Switzerland, 2011; pp. 207–260. [Google Scholar]
- Pistoni, N.C. Simplified approach to the Jones calculus in retracing optical circuits. Appl. Opt. 1995, 34, 7870–7876. [Google Scholar] [CrossRef]
- VanWiggeren, G.D.; Roy, R. Transmission of linearly polarized light through a single-mode fiber with random fluctuations of birefringence. Appl. Opt. 1999, 38, 3888–3892. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J. Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements; University Science Books: New York, NY, USA, 1997. [Google Scholar]
- Healey, P. Optical time domain reflectometry—a performance comparison of the analogue and photon counting techniques. Opt. Quantum Electron. 1984, 16, 267–276. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Schafer, R.W. What is a Savitzky-Golay filter?[lecture notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay smoothing filters. Comput. Phys. 1990, 4, 669–672. [Google Scholar] [CrossRef]
- King, R.L.; Ruffin, C.; LaMastus, F.; Shaw, D. The analysis of hyperspectral data using Savitzky-Golay filtering-practical issues. 2. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium. IGARSS’99 (Cat. No. 99CH36293), Hamburg, Germany, 28 June–2 July 1999; Volume 1, pp. 398–400. [Google Scholar]
- Chan, S.; Leong, L. Analysis of least squares smoothing operators in the frequency domain. Geophys. Prospect. 1972, 20, 892–900. [Google Scholar] [CrossRef]
- Proctor, A.; Sherwood, P.M. Smoothing of digital X-ray photoelectron spectra by an extended sliding least-squares approach. Anal. Chem. 1980, 52, 2315–2321. [Google Scholar] [CrossRef]
- Bromba, M.U.; Ziegler, H. Application hints for Savitzky-Golay digital smoothing filters. Anal. Chem. 1981, 53, 1583–1586. [Google Scholar] [CrossRef]
- Hecht, E. Electromagnetic Theory, Photons, and Light. In Proceedings of the Optics, 5th ed.; Pearson Education: New York, NY, USA, 2017; pp. 45–95. [Google Scholar]
- Grexa, M.; Hermann, G.; Lasnitschka, G.; Scharmann, A. Faraday rotation in a single-mode fiber with controlled birefringence. Appl. Phys. B 1984, 35, 145–148. [Google Scholar] [CrossRef]
- Anderson, D.R.; Bell, F.G. Optical Time-Domain Reflectometry; Tektronix. Inc.: Wilsonville, OR, USA, 1997. [Google Scholar]
- Motuz, R.; Leysen, W.; Moreau, P.; Gusarov, A.; Drexler, P.; Wuilpart, M. Theoretical assessment of the OTDR detector noise on plasma current measurement in tokamaks. Appl. Opt. 2019, 58, 2795–2802. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dandu, P.; Gusarov, A.; Leysen, W.; Beaumont, P.; Wuilpart, M.; JET Contributors. Distributed Poloidal Magnetic Field Measurement in Tokamaks Using Polarization-Sensitive Reflectometric Fiber Optic Sensor. Sensors 2023, 23, 5923. https://doi.org/10.3390/s23135923
Dandu P, Gusarov A, Leysen W, Beaumont P, Wuilpart M, JET Contributors. Distributed Poloidal Magnetic Field Measurement in Tokamaks Using Polarization-Sensitive Reflectometric Fiber Optic Sensor. Sensors. 2023; 23(13):5923. https://doi.org/10.3390/s23135923
Chicago/Turabian StyleDandu, Prasad, Andrei Gusarov, Willem Leysen, Perry Beaumont, Marc Wuilpart, and JET Contributors. 2023. "Distributed Poloidal Magnetic Field Measurement in Tokamaks Using Polarization-Sensitive Reflectometric Fiber Optic Sensor" Sensors 23, no. 13: 5923. https://doi.org/10.3390/s23135923
APA StyleDandu, P., Gusarov, A., Leysen, W., Beaumont, P., Wuilpart, M., & JET Contributors. (2023). Distributed Poloidal Magnetic Field Measurement in Tokamaks Using Polarization-Sensitive Reflectometric Fiber Optic Sensor. Sensors, 23(13), 5923. https://doi.org/10.3390/s23135923





