Algorithms Research and Precision Comparison of Different Frequency Combinations of BDS-3\GPS\Galileo for Precise Point Positioning in Asia-Pacific Region
Abstract
1. Introduction
2. Mathematical Model
3. Experimental Analysis
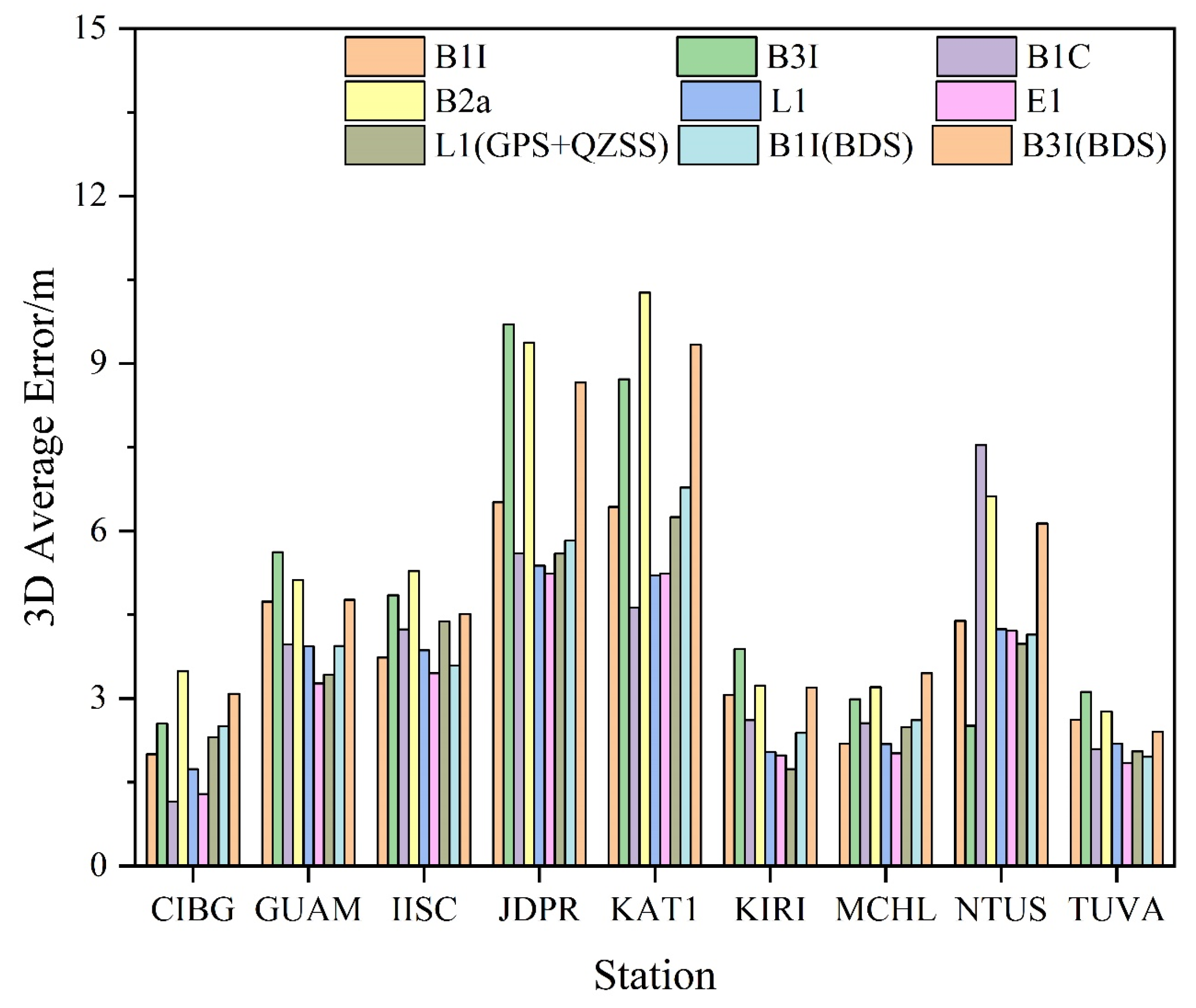
3.1. SPP Location Analysis
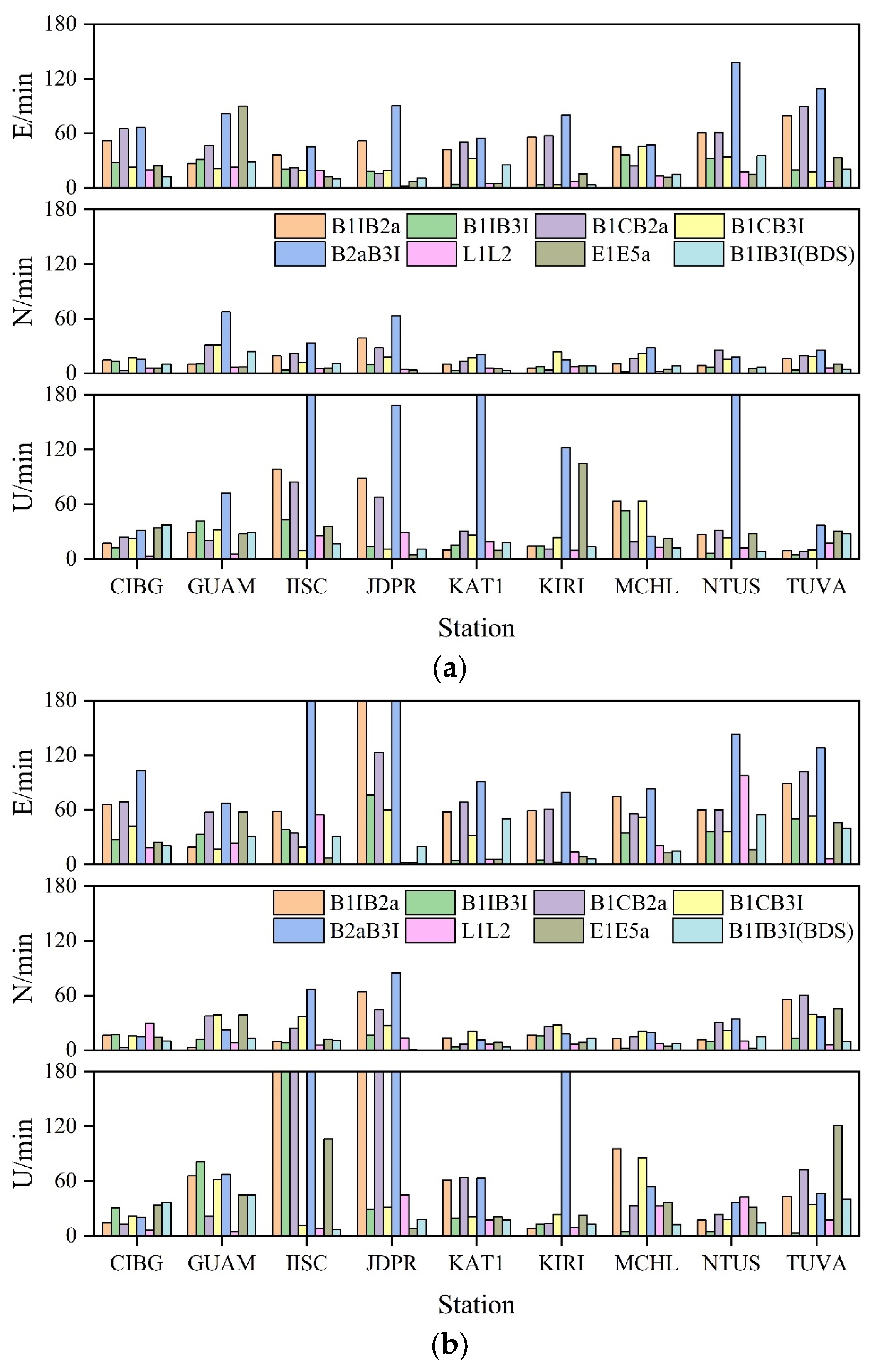
3.2. PPP Convergence Analysis
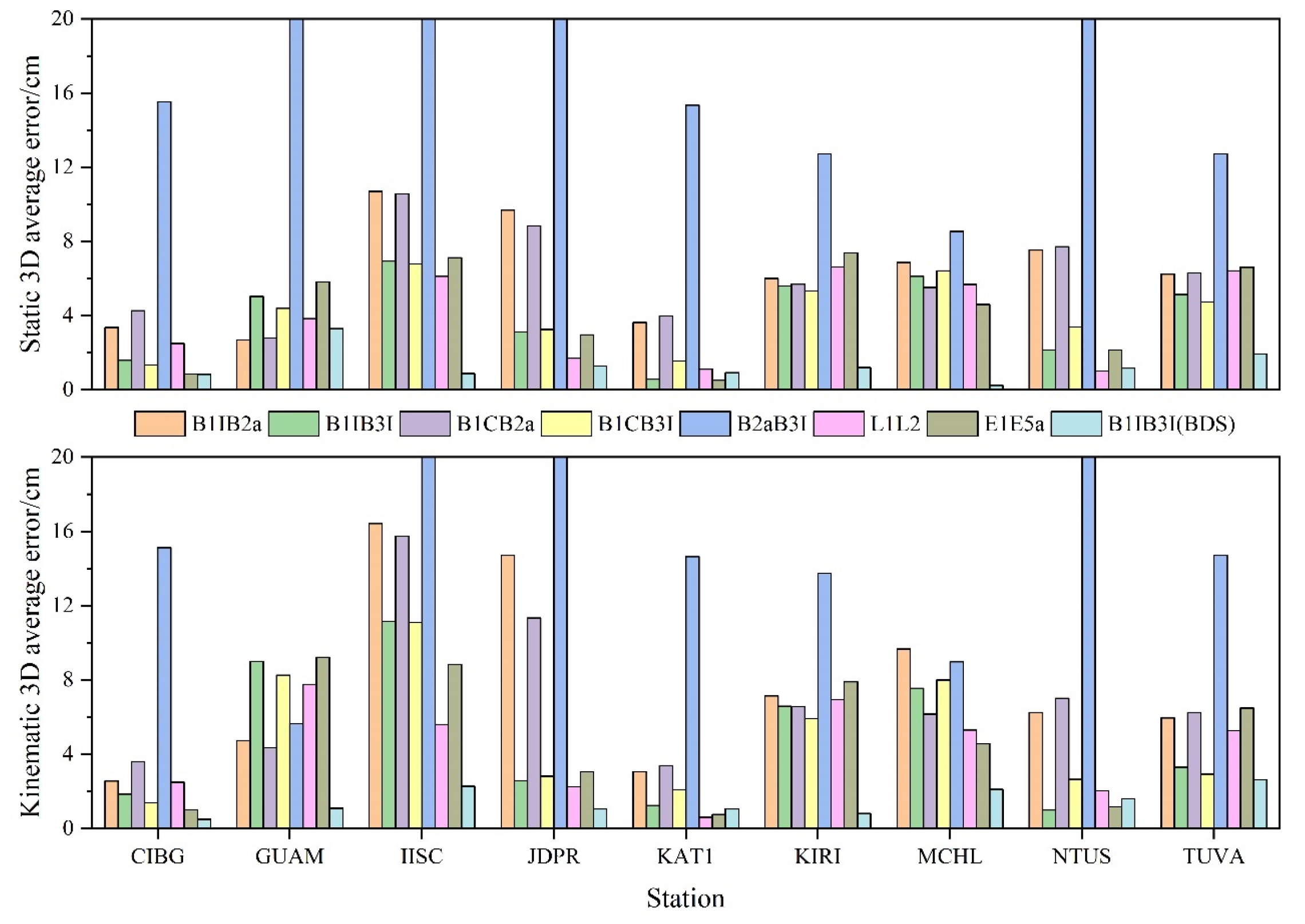
3.3. PPP Precision Analysis
4. Conclusions
- (1)
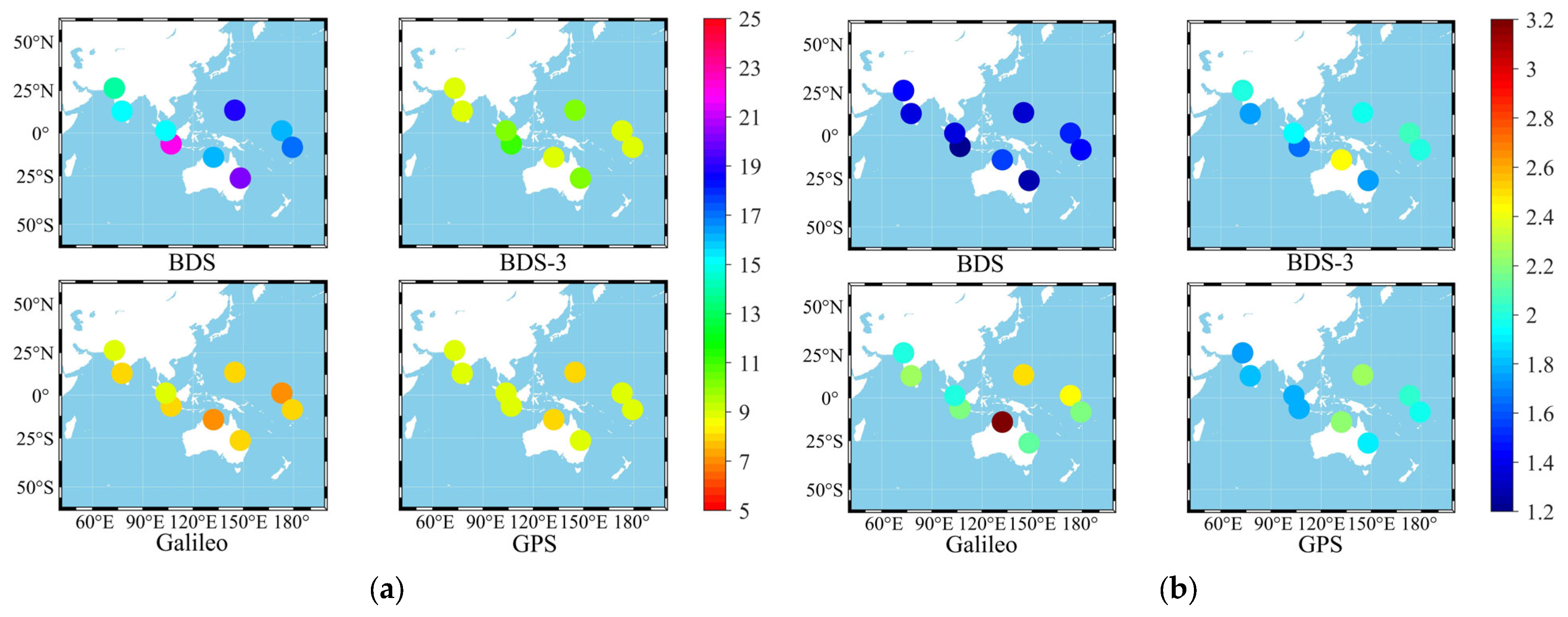
- BDS-3 is better than GPS and Galileo in terms of both the number of satellites and the PDOP. The average number of visible satellites of BDS-3 is around 13, and the average PDOP can reach around 1.7. The average number of visible satellites of GPS is around 10 and the average PDOP can reach around 1.9. In contrast, the average number of visible satellites of Galileo is around 7 and the average PDOP is around 2.2. After adding BDS-2, the number of visible satellites of BDS can reach around 21, and the PDOP can reach around 1.3, which corresponds to a significant improvement.
- (2)
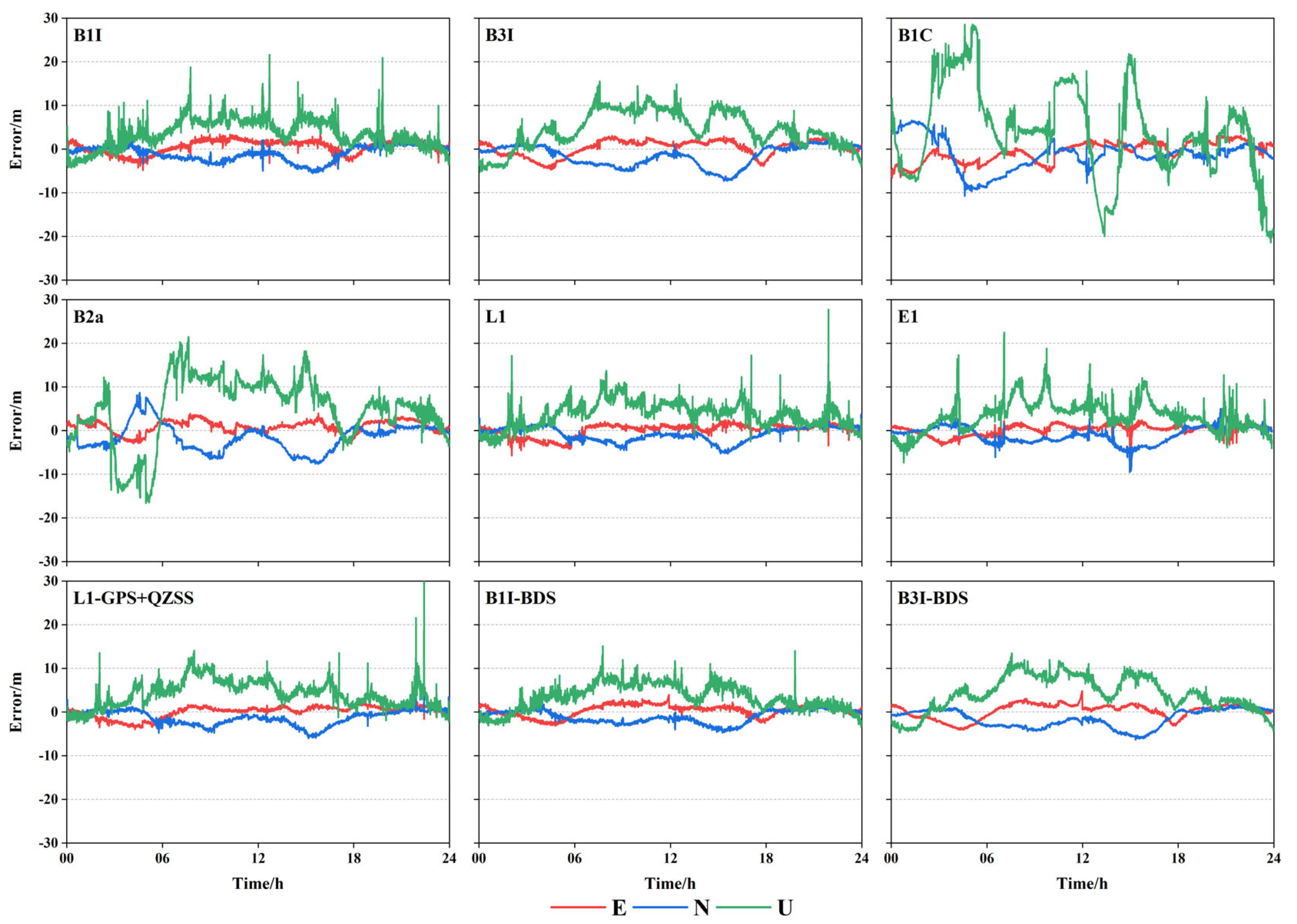
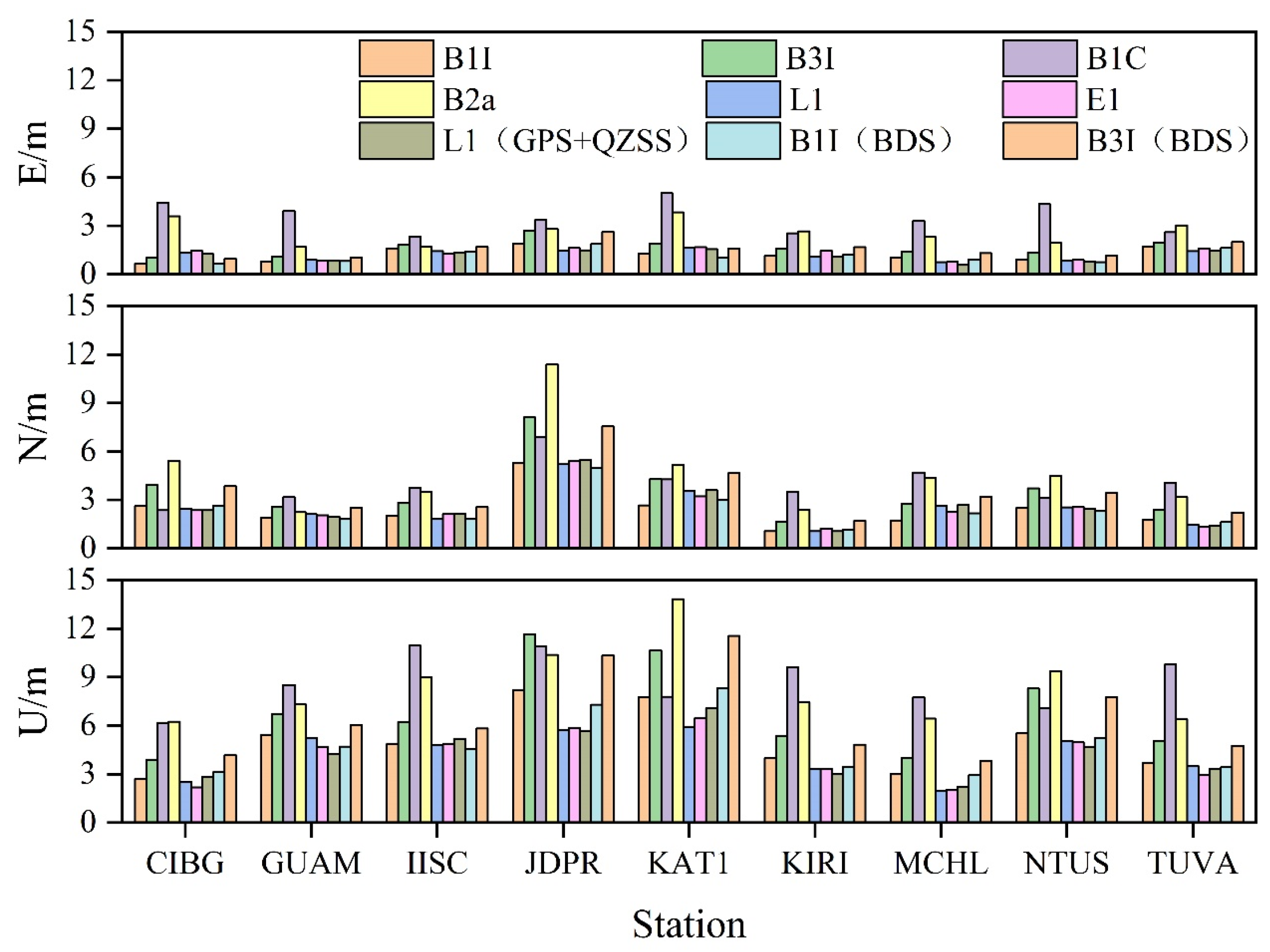
- In terms of SPP precision, the positioning precision of each frequency in the E direction is the best, with most of the stations having a positioning precision of around 1.5 m. The positioning precision of each frequency in the N direction is mostly below 3 m, while that of each frequency in the U direction is around 6 m. After adding BDS-2 and QZSS, the positioning precision does not improve significantly. Overall, the positioning precision is in the following order: B1C > E1 > L1 > B1I > B3I > B2a.
- (3)
- In terms of PPP convergence time, L1L2 shows the convergence time of about 11 min in static mode and 19 min in kinematic mode, while B1IB3I shows about 20 min in static mode and 28 min in kinematic mode, and the convergence time of other frequency combinations is slightly slower. After adding BDS-2, the convergence time of B1IB3I is reduced to 15 min in static mode and 21 min in kinematic mode, respectively, being improved by 11% and 27%, respectively. Overall, the convergence time is as follows: L1L2 > B1IB3I > E1E5a > B1CB3I > B1CB2a > B1IB2a > B2aB3I. After BDS-2 is added, the convergence times of B1IB3I and L1L2 are similar.
- (4)
- In terms of PPP precision, the N direction is better than the E direction. In static mode, the positioning precision of the N direction is mostly within 2 cm, and that of only part of the frequency combination in the E direction can be within 2 cm. However, in kinematic mode, the positioning precision of the N direction is mostly within 3 cm, and most frequency combinations in the E direction are within 6 cm. In the 3D direction, most of the frequency combinations in the static mode are within 6 cm, and only some of them can reach 3 cm, while most of the frequency combinations in the kinematic mode are within 8 cm, and only a few can reach 4 cm. After adding BDS-2, the plane direction of B1IB3I in static mode is not significantly improved, the elevation direction is improved by about 61%, and the 3D direction is improved by about 67%. In kinematic mode, the E direction is improved by about 16%, the N direction does not change significantly, the U direction is improved by about 38%, and the 3D direction is improved by about 70%, which is significantly better than those of GPS and Galileo in terms of positioning precision. Overall, the order of positioning precision is as follows: B1IB3I > B1CB3I > L1L2 > E1E5a > B1B2a > B1CB2a > B2aB3I.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, G.; Zhang, L. The BeiDou leads the world and its wisdom shines on the world. China Sci. Technol. Award. 2020, 8, 16–19. [Google Scholar]
- Li, R.; Zheng, S.; Wang, E.; Chen, J.; Feng, S.; Wang, D.; Dai, L. Advances in BeiDou Navigation Satellite System (BDS) and satellite navigation augmentation technologies. Satell. Navig. 2020, 1, 12. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to Beidou-3 Navigation Satellite System. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Sun, B. Basic performance and future developments of Beidou global navigation satellite system. Satell. Navig. 2020, 1, 1. [Google Scholar] [CrossRef]
- Sun, D.W.; Ai, X.J.; Jia, X.L. Assessment of BDS/GNSS Precise Point Positioning Performance. J. Geod. Geodyn. 2022, 42, 1111–1116+1127. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Maciuk, K. Different approaches in GLONASS orbit computation from broadcast ephemeris. Geod. Vestn. 2016, 3, 455–466. [Google Scholar] [CrossRef]
- Farah, A. Kinematic-PPP using Single/Dual Frequency Observations from (GPS, GLONASS and GPS/GLONASS) Constellations for Hydrography. Artif. Satell. 2018, 53, 37–46. [Google Scholar] [CrossRef]
- Yalvac, S. Investigating the historical development of accuracy and precision of Galileo by means of relative GNSS analysis technique. Earth Sci. Inform. 2021, 14, 193–200. [Google Scholar] [CrossRef]
- Karutin, S. The Status of GLONASS System. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Virtual, 21–25 September 2020; pp. 938–949. [Google Scholar]
- Cai, H.; Meng, Y.; Geng, C.; Gao, W.; Zhang, T.; Li, G.; Lou, Y. BDS-3 performance assessment; PNT, SBAS, PPP, SMC and SAR. Acta Geod. Cartogr. Sin. 2021, 50, 427–435. [Google Scholar]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning. GPS Solut. 2018, 22, 11. [Google Scholar] [CrossRef]
- Yan, X.; Huang, G.; Zhang, Q.; Wang, L.; Qin, Z.; Xie, S. Estimation of the Antenna Phase Center Correction Model for the BeiDou-3 MEO Satellites. Remote Sens. 2019, 11, 2850. [Google Scholar] [CrossRef]
- Song, W.; Zhao, X.; Lou, Y.; Sun, W.; Zhao, Z. Performance Evaluation of BDS-3 PPP-B2b Service. Geomat. Inf. Sci. Wuhan Univ. 2023, 48, 408–415. [Google Scholar]
- Gu, J.C.; Song, C.F.; Tian, K.J. Precision Single Point Positioning Accuracy Analysis of BDS-3ew Frequencies Based on OSB Correction. J. Geod. Geodyn. 2023, 43, 5. [Google Scholar]
- Shen, P.; Cheng, F.; Lu, X.; Xiao, X.; Ge, Y. An Investigation of Precise Orbit and Clock Products for BDS-3 from Different Analysis Centers. Sensors 2021, 21, 1596. [Google Scholar] [CrossRef]
- Bu, J.; Yu, K.; Qian, N.; Zuo, X.; Chang, J. Performance Assessment of Positioning Based on Multi-Frequency Multi-GNSS Ob-servations: Signal Quality, PPP and Baseline Solution. IEEE Access 2020, 9, 5845–5861. [Google Scholar] [CrossRef]
- Malik, J.S. Performance Evaluation of Precise Point Positioning Using Dual Frequency Multi-GNSS Observations. Artif. Satell. 2020, 55, 150–170. [Google Scholar] [CrossRef]
- Zhang, X.H.; Hu, J.H.; Ren, X.D. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP. Acta Geod. Cartogr. Sin. 2020, 49, 1084–1100. [Google Scholar]
- Zhang, Q.; Zhu, Y.; Chen, Z. An In-Depth Assessment of the New BDS-3 B1C and B2a Signals. Remote Sens. 2021, 13, 788. [Google Scholar] [CrossRef]
- Shi, J.; Ouyang, C.; Huang, Y.; Peng, W. Assessment of BDS-3 Global Positioning Service: Ephemeris, SPP, PPP, RTK, and New Signal. GPS Solut. 2020, 24, 81. [Google Scholar] [CrossRef]
- Hu, J.; Li, P.; Zhang, X.; Bisnath, S.; Pan, L. Precise Point Positioning with BDS-2 and BDS-3 constellations: Ambiguity resolution and positioning comparison. Adv. Space Res. 2022, 70, 1830–1846. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, K.; Cui, X.; Zhang, Q.; Jia, X.; Zhang, M.; Fan, S. Preliminary Analysis of the Quality and Positioning Performance of BDS-3 Global Interoperable Signal B1C&B2a. Adv. Space Res. 2021, 67, 2483–2490. [Google Scholar]
- Liu, W.; Jiao, B.; Hao, J.; Lv, Z.; Xie, J.; Liu, J. Signal-in-space range error and positioning accuracy of BDS-3. Sci. Rep. 2022, 12, 8181. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Yang, T.; Wang, Z.; Zhang, Y.; Guo, J.; Shu, W.; Qu, P. Performance Evaluation of Precise Point Positioning for BeiDou-3 B1c/B2a Signals in the Global Range. Sensors 2021, 21, 5780. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Wang, C.; Yang, Z.; Yang, X. Assessment of GPS/BDS Precise Point Positioning Performance with BDS-3 New Signals. In China Satellite Navigation Conference (CSNC 2021) Proceedings; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Shi, C.; Wu, X.; Zheng, F.; Wang, X.; Wang, J. Modeling of BDS-2/BDS-3 Single-Frequency PPP with B1I and B1C Signals and Positioning Performance Analysis. Measurement 2021, 178, 109355. [Google Scholar] [CrossRef]
- Cheng, Q.R.; Zhang, Y.Z.; Chen, J.P. Evaluation of BDS-2/BDS-3 Precise Point Positioning Performance in Polar Region. In Proceedings of the China Satellite Navigation Conference (CSNC 2022), Beijing, China, 25−27 May 2022; pp. 161–172. [Google Scholar]
- Li, J.; Yang, Y.; He, H.; Guo, H. Benefits of BDS 3 B1C/B1I/B2a Triple Frequency Signals on Precise Positioning and Ambiguity Resolution. GPS Solut. 2020, 24, 100. [Google Scholar] [CrossRef]
- Li, B.; Mi, J.; Zhu, H.; Gu, S.; Xu, Y.; Wang, H.; Pang, Y. BDS-3/GPS/Galileo OSB estimation and PPP-AR positioning analysis of different positioning models. Remote Sens. 2022, 14, 4207. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Q.; Li, G.; Zhang, K. Assessment of Multi-Frequency PPP Ambiguity Resolution Using Galileo and BeiDou-3 Signals. Remote Sens. 2021, 13, 4746. [Google Scholar] [CrossRef]
- Ren, Z.; Gong, H.; Lyu, D.; Peng, J.; Guo, Y.; Sun, G. Time transfer with BDS-3 signals: CV, PPP and IPPP. Meas. Sci. Technol. 2023, 34, 045007. [Google Scholar] [CrossRef]
- Chen, H.; Liu, X.; Jiang, W.; Yuan, P.; Ju, B.; Chen, Y. Preliminary analysis and evaluation of BDS-2/BDS-3 precise point positioning. Adv. Space Res. 2021, 68, 4113–4128. [Google Scholar] [CrossRef]
- Zhao, W. Research on Key Technology of Combined BeiDou-2 and BeiDou-3 Precise Point Positioning. Ph.D. Thesis, Wuhan University, Wuhan, China, 2020. [Google Scholar]


| Station | Longitude | Latitude | Receiver Type | Antenna Type | Frequency |
|---|---|---|---|---|---|
| CIBG | 106.849 | −6.49 | TRIMBLE ALLOY | LEIAR25.R4 | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| GUAM | 144.868 | 13.589 | SEPT POLARX5 | JAVRINGANT_DM | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| IISC | 77.57 | 13.021 | SEPT POLARX5 | ASH701945E_M | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| JDPR | 73.024 | 26.207 | TRIMBLE ALLOY | TWIVC6050 | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| KAT1 | 132.153 | −14.376 | SEPT POLARX5 | LEIAR25.R3 | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| KIRI | 172.923 | 1.355 | SEPT POLARX5 | TRM59800 | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| MCHL | 148.145 | −26.359 | TRIMBLE ALLOY | TRM59800 | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| NTUS | 103.68 | 1.346 | LEICA GR50 | LEIAR20 | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| TUVA | 179.197 | −8.525 | SEPT POLARX5 | JAVRINGANT_DM | B1I/B1C/B2a/B3I/L1/L2/E1/E5a |
| Options | Processing Strategies |
|---|---|
| Observation | Carrier phase and pseudo-range |
| Model | Ionosphere-free |
| Solution model | Single frequency pseudo-distance, static/kinematic |
| Observation interval | 30 s |
| Frequency | BDS:B1I/B1C/B2a/B3I;QZSS:L1 GPS:L1/L2;Galileo:E1/E5a |
| satellite orbit and clock | WHU precision orbits and clock |
| Elevation cut off | 10° |
| Parameter estimation method | Kalman filtering |
| Satellite phase center | igs20.atx |
| Cycle slip detection | GF + MW |
| Weighting scheme | Elevation dependent weight |
| Tropospheric delay | Saastamoinen |
| Tropospheric mapping function | VMF1 |
| Ambiguity | Float |
| Receiver coordinates | Parameters estimation |
| Receiver clock error | Parameters estimation |
| Intersystem bias | WHU-BIA |
| B1IB2a | B1IB3I | B1CB2a | B1CB3I | B2aB3I | L1L2 | E1E5a | B1IB3I(BDS) | |
|---|---|---|---|---|---|---|---|---|
| Static | 35 | 17 | 33 | 23 | 115 | 11 | 21 | 15 |
| Kinematic | 58 | 29 | 56 | 32 | 107 | 19 | 27 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Cao, Z.; Meng, Z.; Tan, C.; Zhu, H.; Huang, L. Algorithms Research and Precision Comparison of Different Frequency Combinations of BDS-3\GPS\Galileo for Precise Point Positioning in Asia-Pacific Region. Sensors 2023, 23, 5935. https://doi.org/10.3390/s23135935
Gao M, Cao Z, Meng Z, Tan C, Zhu H, Huang L. Algorithms Research and Precision Comparison of Different Frequency Combinations of BDS-3\GPS\Galileo for Precise Point Positioning in Asia-Pacific Region. Sensors. 2023; 23(13):5935. https://doi.org/10.3390/s23135935
Chicago/Turabian StyleGao, Meng, Zhihua Cao, Ziheng Meng, Chunbo Tan, Huizhong Zhu, and Lu Huang. 2023. "Algorithms Research and Precision Comparison of Different Frequency Combinations of BDS-3\GPS\Galileo for Precise Point Positioning in Asia-Pacific Region" Sensors 23, no. 13: 5935. https://doi.org/10.3390/s23135935
APA StyleGao, M., Cao, Z., Meng, Z., Tan, C., Zhu, H., & Huang, L. (2023). Algorithms Research and Precision Comparison of Different Frequency Combinations of BDS-3\GPS\Galileo for Precise Point Positioning in Asia-Pacific Region. Sensors, 23(13), 5935. https://doi.org/10.3390/s23135935






