Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel
Abstract
1. Introduction
2. Hybrid Inverse Finite Element Method
2.1. 1D Inverse Finite Element Method
2.1.1. Kinematic Relations
2.1.2. Experimental Sectional Strains
2.1.3. Least-Squares Error Functional
2.2. 2D Inverse Finite Element Method
2.2.1. Kinematic Relations
2.2.2. Experimental Strain Measures
2.2.3. Least-Squares Error Functional
2.3. Hybrid Formulation
3. Experimental Test Specimen
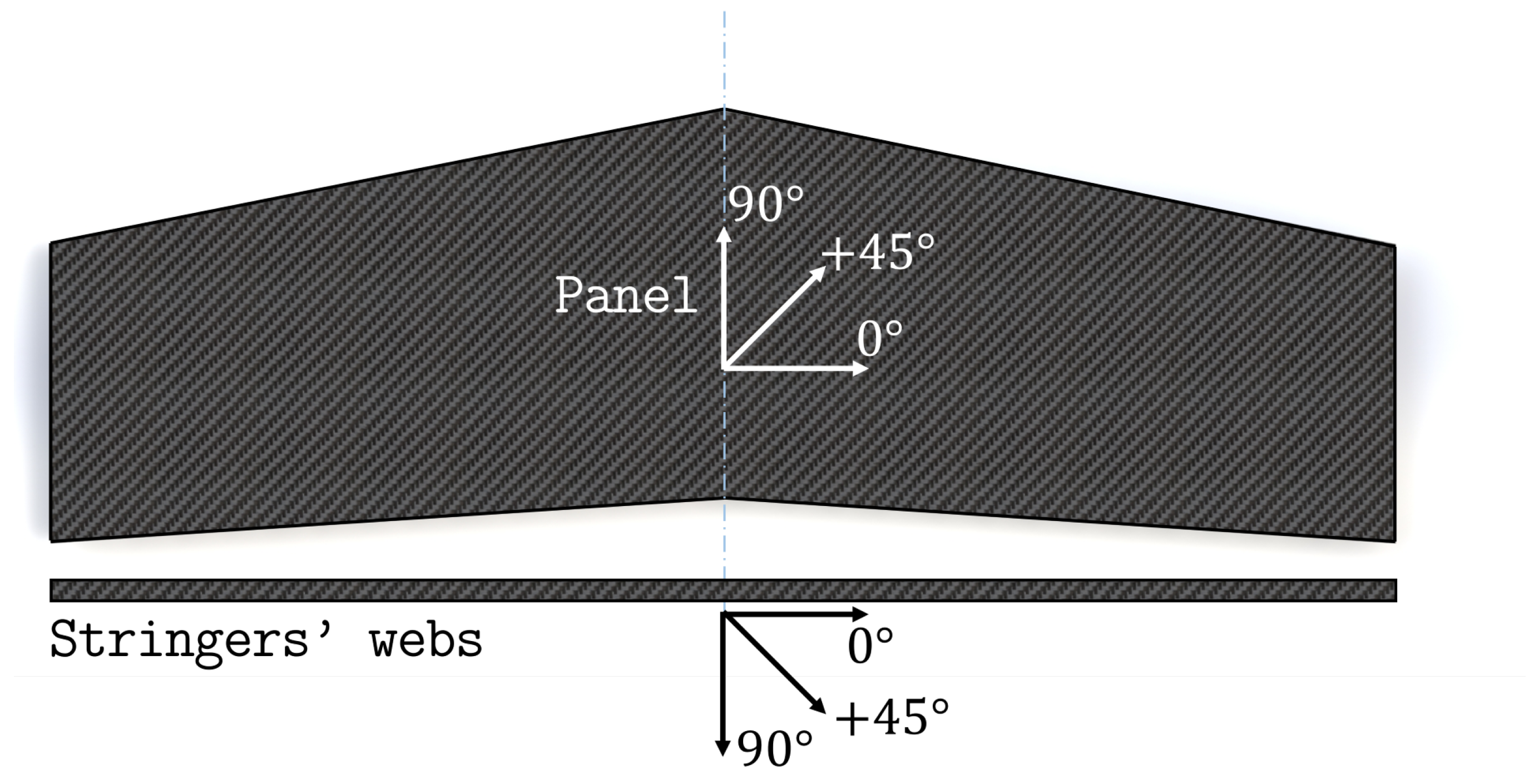
3.1. Composite Wing Panel
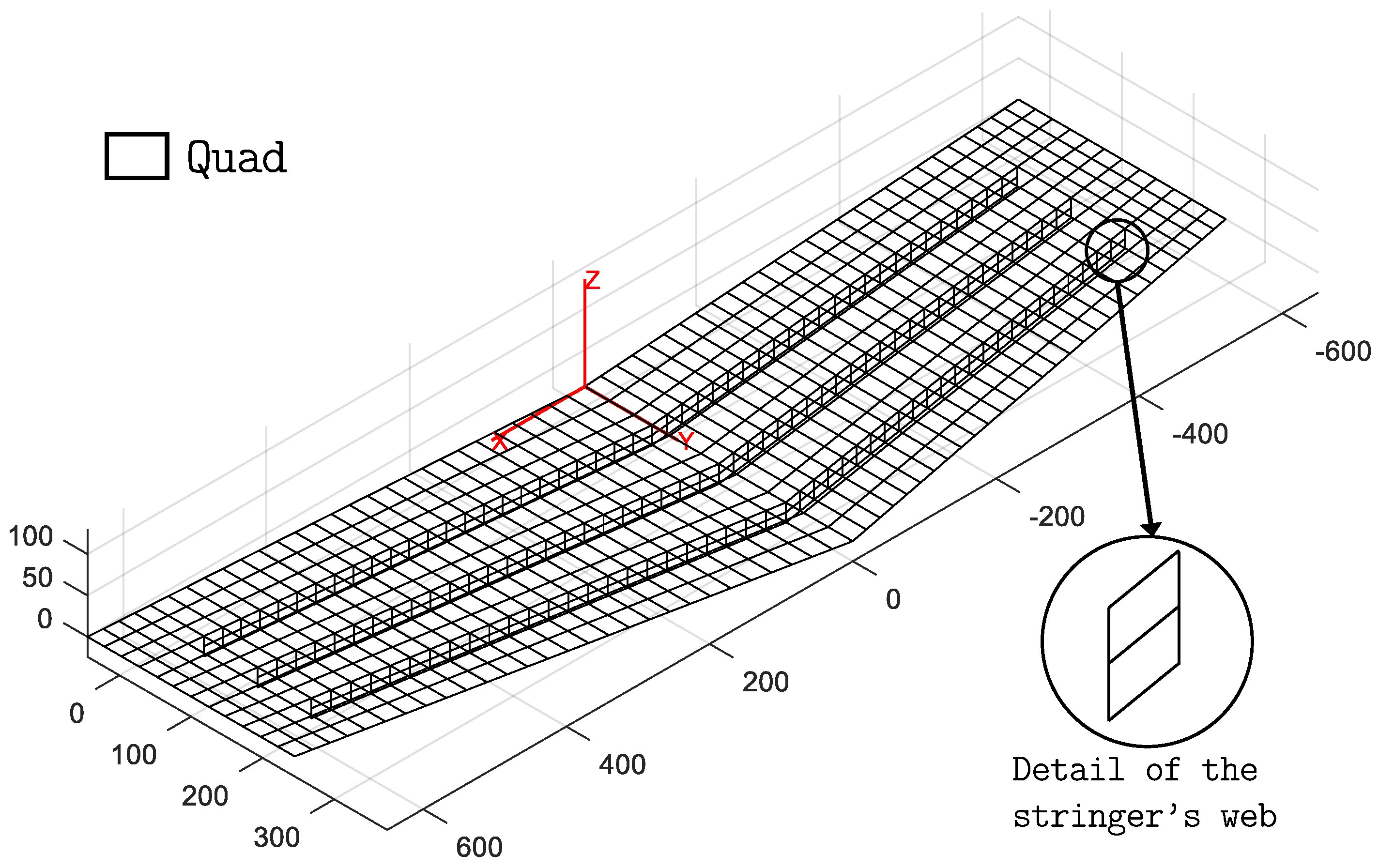
3.2. Inverse Element Models
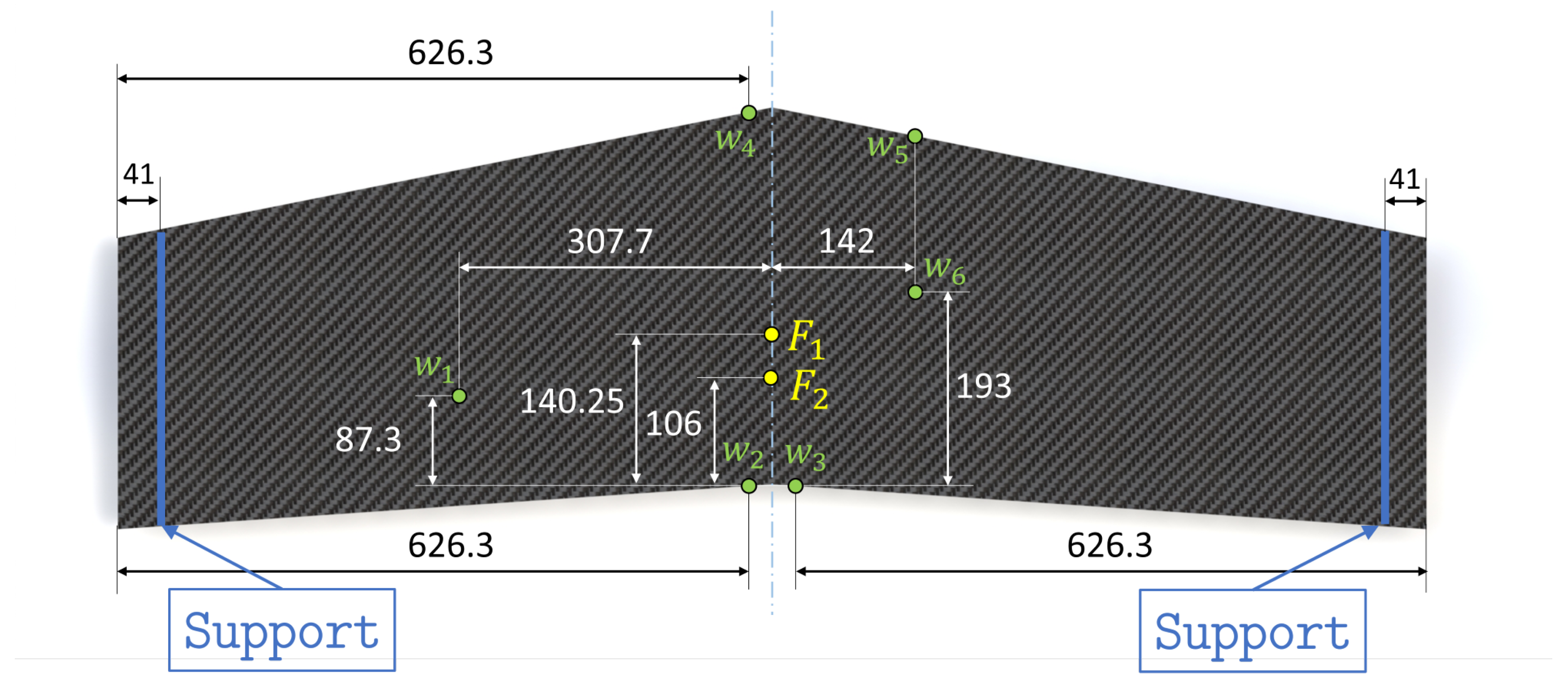
3.3. Test Configuration
3.4. Strain Sensors
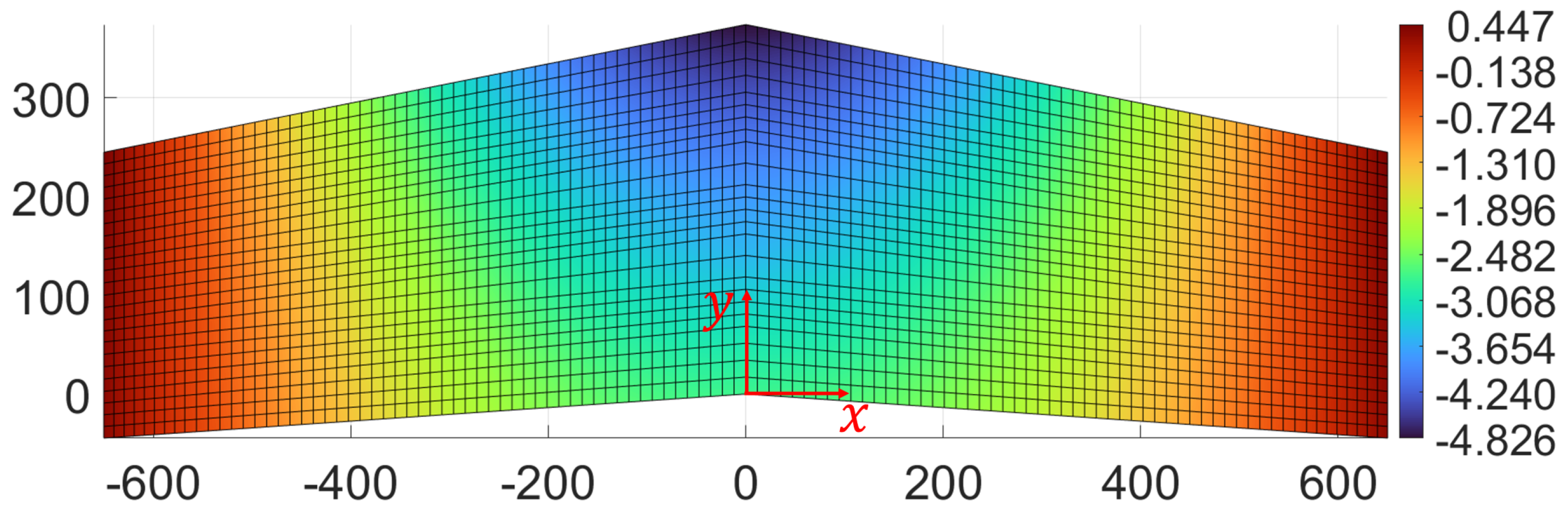
4. Experimental Setup and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farrar, C.R.; Worden, K. An Introduction to Structural Health Monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Farrar, C.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons Ltd.: West Sussex, UK, 2013. [Google Scholar]
- Staszewski, W.J.; Boller, C.; Tomlinson, G.R. Health Monitoring of Aerospace Structures; John Wiley & Sons: West Sussex, UK, 2003. [Google Scholar]
- Tessler, A. Structural analysis methods for structural health management of future aerospace vehicles. Key Eng. Mater. 2007, 347, 57–66. [Google Scholar] [CrossRef]
- Sofla, A.Y.N.; Meguid, S.A.; Tan, K.T.; Yeo, W.K. Shape morphing of aircraft wing: Status and challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape sensing methods: Review and experimental comparison on a wing-shaped plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Ko, W.L.; Richards, W.L.; Tran, V.T. Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures; NASA/TP-2007-214612; NASA: Washington, DC, USA, 2007.
- Ko, W.L.; Richards, W.L.; Fleischer, V.T. Applications of Ko Displacement Theory to the Deformed Shape Predictions of the Doubly-Tapered Ikhana Wing; NASA/TP-2009-214652; NASA: Washington, DC, USA, 2009.
- Akl, W.; Poh, S.; Baz, A. Wireless and distributed sensing of the shape of morphing structures. Sens. Actuators A Phys. 2007, 140, 94–102. [Google Scholar] [CrossRef]
- Smoker, J.; Baz, A. Monitoring the bending and twist of morphing structures. Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2008, 6932, 69321X. [Google Scholar] [CrossRef]
- Heaney, P.S.; Ivanco, T.G.; Bilgen, O. Distributed sensing of a cantilever beam and plate using a fiber optic sensing system. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; pp. 1–28. [Google Scholar] [CrossRef]
- Bogert, P.B.; Haugse, E.; Works, B.P.; Gehrki, R.E.; Martin, L. Structural shape identification from experimental strains using a modal transformation technique. In Proceedings of the 44th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics and Materials Conference, Norfolk, UV, USA, 7–10 April 2003; pp. 1–18. [Google Scholar]
- Kim, N.S.; Cho, N.S. Estimating deflection of a simple beam model using fiber optic Bragg-grating sensors. Exp. Mech. 2004, 44, 433–439. [Google Scholar] [CrossRef]
- Rapp, S.; Kang, L.H.; Han, J.H.; Mueller, U.C.; Baier, H. Displacement field estimation for a two-dimensional structure using fiber Bragg grating sensors. Smart Mater. Struct. 2009, 18, 025006. [Google Scholar] [CrossRef]
- Glaser, R.; Caccese, V.; Shahinpoor, M. Shape Monitoring of a Beam Structure from Measured Strain or Curvature. Exp. Mech. 2012, 52, 591–606. [Google Scholar] [CrossRef]
- Kang, L.H.; Kim, D.K.; Han, J.H. Estimation of dynamic structural displacements using fiber Bragg grating strain sensors. J. Sound Vib. 2007, 305, 534–542. [Google Scholar] [CrossRef]
- Pak, C.G. Wing shape sensing from measured strain. AIAA J. 2016, 54, 1064–1073. [Google Scholar] [CrossRef]
- Davis, M.A.; Kersey, A.D.; Sirkis, J.; Friebele, E.J. Shape and vibration mode sensing using a fiber optic Bragg grating array. Smart Mater. Struct. 1996, 5, 759–765. [Google Scholar] [CrossRef]
- Bruno, R.; Toomarian, N.; Salama, M. Shape estimation from incomplete measurements: A neural-net approach. Smart Mater. Struct. 1994, 3, 92–97. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A Variational Principle for Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells; NASA/TM-2003-212445; NASA: Washington, DC, USA, 2003.
- Tessler, A.; Spangler, J.L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J. Inverse FEM for Full-Field Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells. Proceedings of Second European Workshop on Structural Health Monitoring, Munich, Germany, 7–9 July 2004; pp. 83–90. [Google Scholar]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A quadrilateral inverse-shell element with drilling degrees of freedom for shape sensing and structural health monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Kefal, A. An efficient curved inverse-shell element for shape sensing and structural health monitoring of cylindrical marine structures. Ocean. Eng. 2019, 188, 106262. [Google Scholar] [CrossRef]
- Mindlin, R. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 1951, 12, 31–38. [Google Scholar] [CrossRef]
- Tessler, A.; Hughes, T.J.R. A three-node mindlin plate element with improved transverse shear. Comput. Methods Appl. Mech. Eng. 1985, 50, 71–101. [Google Scholar] [CrossRef]
- Kefal, A.; Tessler, A.; Oterkus, E. An enhanced inverse finite element method for displacement and stress monitoring of multilayered composite and sandwich structures. Compos. Struct. 2017, 179, 514–540. [Google Scholar] [CrossRef]
- Kefal, A.; Tabrizi, I.E.; Tansan, M.; Kisa, E.; Yildiz, M. An experimental implementation of inverse finite element method for real-time shape and strain sensing of composite and sandwich structures. Compos. Struct. 2021, 258, 113431. [Google Scholar] [CrossRef]
- Miller, E.J.; Manalo, R.; Tessler, A. Full-Field Reconstruction of Structural Deformations and Loads from Measured Strain Data on a Wing Test Article Using the Inverse Finite Element Method; NASA/TM-2016-219407; NASA: Washington, DC, USA, 2016.
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Shape Sensing of a Complex Aeronautical Structure with Inverse Finite Element Method. Sensors 2021, 21, 1388. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Tessler, A. Real-time displacement monitoring of a composite stiffened panel subjected to mechanical and thermal loads. Meccanica 2015, 50, 2487–2496. [Google Scholar] [CrossRef]
- Esposito, M.; Mattone, M.; Gherlone, M. Experimental Shape Sensing and Load Identification on a Stiffened Panel: A Comparative Study. Sensors 2022, 22, 1064. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Gherlone, M. Material and strain sensing uncertainties quantification for the shape sensing of a composite wing box. Mech. Syst. Signal Process. 2021, 160, 107875. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean. Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Kefal, A.; Mayang, J.B.; Oterkus, E.; Yildiz, M. Three dimensional shape and stress monitoring of bulk carriers based on iFEM methodology. Ocean. Eng. 2018, 147, 256–267. [Google Scholar] [CrossRef]
- Tessler, A.; Roy, R.; Esposito, M.; Surace, C.; Gherlone, M. Shape Sensing of Plate and Shell Structures Undergoing Large Displacements Using the Inverse Finite Element Method. Shock Vib. 2018, 2018, 8076085. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Ali, H.; Yildiz, M.; Kefal, A. Experimental and numerical investigation on large deformation reconstruction of thin laminated composite structures using inverse finite element method. Thin-Walled Struct. 2022, 178, 109485. [Google Scholar] [CrossRef]
- Colombo, L.; Sbarufatti, C.; Giglio, M. Definition of a load adaptive baseline by inverse finite element method for structural damage identification. Mech. Syst. Signal Process. 2019, 120, 584–607. [Google Scholar] [CrossRef]
- Roy, R.; Gherlone, M.; Surace, C. Damage Localisation in Thin Plates Using the Inverse Finite Element Method. In Lecture Notes in Mechanical Engineering, Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019; Wahab, M., Ed.; Springer: Singapore, 2020. [Google Scholar]
- Kefal, A.; Tessler, A. Delamination damage identification in composite shell structures based on Inverse Finite Element Method and Refined Zigzag Theory. In Developments in the Analysis and Design of Marine Structures; CRC PRESS: Boca Raton, FL, USA, 2021; pp. 354–363. [Google Scholar] [CrossRef]
- Colombo, L.; Oboe, D.; Sbarufatti, C.; Cadini, F.; Russo, S.; Giglio, M. Shape sensing and damage identification with iFEM on a composite structure subjected to impact damage and non-trivial boundary conditions. Mech. Syst. Signal Process. 2021, 148, 107163. [Google Scholar] [CrossRef]
- Ganjdoust, F.; Kefal, A.; Tessler, A. A novel delamination damage detection strategy based on inverse finite element method for structural health monitoring of composite structures. Mech. Syst. Signal Process. 2023, 192, 110202. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Jia, D.; Qiu, S.; He, W. Structural damage identification using strain mode differences by the iFEM based on the convolutional neural network (CNN). Mech. Syst. Signal Process. 2022, 165, 108289. [Google Scholar] [CrossRef]
- Kefal, A.; Diyaroglu, C.; Yildiz, M.; Oterkus, E. Coupling of peridynamics and inverse finite element method for shape sensing and crack propagation monitoring of plate structures. Comput. Methods Appl. Mech. Eng. 2022, 391, 114520. [Google Scholar] [CrossRef]
- Kefal, A.; Yildiz, M. Modeling of sensor placement strategy for shape sensing and structural health monitoring of a wing-shaped sandwich panel using inverse finite element method. Sensors 2017, 17, 2775. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Bao, H.; Xu, Q. Optimal Sensor Placement for Inverse Finite Element Reconstruction of Three-Dimensional Frame Deformation. Int. J. Aerosp. Eng. 2018, 18, 6121293. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Bao, H.; Xu, Q. Optimal sensor placement based on eigenvalues analysis for sensing deformation of wing frame using iFEM. Sensors 2018, 18, 2424. [Google Scholar] [CrossRef]
- Kefal, A.; Emami, I.; Yildiz, M.; Tessler, A. A smoothed iFEM approach for efficient shape-sensing applications: Numerical and experimental validation on composite structures. Mech. Syst. Signal Process. 2021, 152, 107486. [Google Scholar] [CrossRef]
- Oboe, D.; Colombo, L.; Sbarufatti, C.; Giglio, M. Comparison of strain pre-extrapolation techniques for shape and strain sensing by iFEM of a composite plate subjected to compression buckling. Compos. Struct. 2021, 262, 113587. [Google Scholar] [CrossRef]
- Roy, R.; Tessler, A.; Surace, C.; Gherlone, M. Efficient shape sensing of plate structures using the inverse Finite Element Method aided by strain pre-extrapolation. Thin-Walled Struct. 2022, 180, 109798. [Google Scholar] [CrossRef]
- Roy, R.; Esposito, M.; Surace, C.; Gherlone, M.; Tessler, A. Shape Sensing of Stiffened Plates Using Inverse FEM Aided by Virtual Strain Measurements. In European Workshop on Structural Health Monitoring; Rizzo, P., Milazzo, A., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 454–463. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Shape sensing of 3D frame structures using an inverse Finite Element Method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Savino, P.; Gherlone, M.; Tondolo, F. Shape sensing with inverse Finite Element Method for slender structures. Struct. Eng. Mech. 2019, 72, 217–227. [Google Scholar] [CrossRef]
- Roy, R.; Gherlone, M.; Surace, C. A shape sensing methodology for beams with generic cross-sections: Application to airfoil beams. Aer. Sci. Tech. 2021, 110, 106484. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, L.; Bao, H.; Du, J. Shape sensing of variable cross-section beam using the inverse finite element method and isogeometric analysis. Meas. J. Int. Meas. Confed. 2020, 158, 107656. [Google Scholar] [CrossRef]
- Zhao, F.; Bao, H.; Liu, J.; Li, K. Shape sensing of multilayered composite and sandwich beams based on Refined Zigzag Theory and inverse finite element method. Compos. Struct. 2021, 261, 113321. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Beam shape sensing using inverse finite element method: Theory and experimental validation. In Structural Health Monitoring 2011: Condition-Based Maintenance and Intelligent Structures, Proceedings of the 8th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 13–15 September 2011; Destech Pubns Inc.: Lancaster, PA, USA, 2011; Volume 1, pp. 578–585. [Google Scholar]
- Zhao, Y.; Du, J.; Xu, Q.; Bao, H. Real-time monitoring of the position and orientation of a radio telescope sub-reflector with fiber bragg grating sensors. Sensors 2019, 19, 619. [Google Scholar] [CrossRef] [PubMed]
- Dong, T.; Yuan, S.; Huang, T. Beam Element-Based Inverse Finite Element Method for Shape Reconstruction of a Wing Structure; Volume 4 Advances in Aerospace Technology. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Online, 1–5 November 2021. V004T04A020. [Google Scholar] [CrossRef]
- Zhu, H.; Du, Z.; Tang, Y. Numerical study on the displacement reconstruction of subsea pipelines using the improved inverse finite element method. Ocean. Eng. 2022, 248, 110763. [Google Scholar] [CrossRef]
- Zhao, F.; Kefal, A.; Bao, H. Nonlinear deformation monitoring of elastic beams based on isogeometric iFEM approach. Int. J. Non-Linear Mech. 2022, 147, 104229. [Google Scholar] [CrossRef]
- Li, X.; Niu, S.; Bao, H.; Hu, N. Improved Adaptive Multi-Objective Particle Swarm Optimization of Sensor Layout for Shape Sensing with Inverse Finite Element Method. Sensors 2022, 22, 5203. [Google Scholar] [CrossRef] [PubMed]
- Deb, K. Multiobjective Optimization Using Evolutionary Algorithms; Jhon Wiley & Sons, Inc.: West Sussex, UK, 2001. [Google Scholar]
- Di Sante, R. Fibre Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]









| [GPa] | [GPa] | [GPa] | Thickness [mm] | |
|---|---|---|---|---|
| 59.7 | 59.7 | 0.09 | 3.8 | 0.25 |
| Torsional Load Case | Primarily Bending Load Case | |||||
|---|---|---|---|---|---|---|
| Experimental | Hybrid iFEM | Shell-Only iFEM | Experimental | Hybrid iFEM | Shell-Only iFEM | |
| F [N] | 200 | 200 | ||||
| [mm] | 2.42 | 2.52 | 2.50 | 2.44 | 2.56 | 2.55 |
| () | (+4.3%) | (+3.5%) | (+5.0%) | (+4.2%) | ||
| [mm] | 2.98 | 3.14 | 3.14 | 3.72 | 3.89 | 3.89 |
| () | (+5.2%) | (+5.4%) | (+4.5%) | (+4.5%) | ||
| [mm] | 2.98 | 3.13 | 3.14 | 3.72 | 3.89 | 3.90 |
| () | (+5.3%) | (+5.4%) | (+4.7%) | (+4.8%) | ||
| [mm] | 5.18 | 5.07 | 4.84 | 3.77 | 3.70 | 3.51 |
| () | (−2.0%) | (−6.5%) | (−1.9%) | (−7.0%) | ||
| [mm] | 4.72 | 4.54 | 4.35 | 3.42 | 3.35 | 3.19 |
| () | (−3.9%) | (−8.0%) | (−2.2%) | (−6.8%) | ||
| [mm] | 3.75 | 3.90 | 3.82 | 3.29 | 3.42 | 3.36 |
| () | (+3.9%) | (+1.8%) | (+3.9%) | (+1.9%) | ||
| 4.1% | 5.1% | 3.7% | 4.9% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esposito, M.; Roy, R.; Surace, C.; Gherlone, M. Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel. Sensors 2023, 23, 5962. https://doi.org/10.3390/s23135962
Esposito M, Roy R, Surace C, Gherlone M. Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel. Sensors. 2023; 23(13):5962. https://doi.org/10.3390/s23135962
Chicago/Turabian StyleEsposito, Marco, Rinto Roy, Cecilia Surace, and Marco Gherlone. 2023. "Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel" Sensors 23, no. 13: 5962. https://doi.org/10.3390/s23135962
APA StyleEsposito, M., Roy, R., Surace, C., & Gherlone, M. (2023). Hybrid Shell-Beam Inverse Finite Element Method for the Shape Sensing of Stiffened Thin-Walled Structures: Formulation and Experimental Validation on a Composite Wing-Shaped Panel. Sensors, 23(13), 5962. https://doi.org/10.3390/s23135962









