Safe and Robust Map Updating for Long-Term Operations in Dynamic Environments †
Abstract
:1. Introduction
Paper Contribution
2. Related Works
2.1. Occupancy Grid
2.2. Lifelong Mapping
2.3. Lifelong Localisation
2.4. Conventional Lifelong SLAM
3. List of Variables
4. Problem Formulation
Ideal Scenario vs. Real Scenario
5. Method

| Algorithm 1 Safe and robust map updating. |
| Algorithm 2 Beam classifier function. |
| Algorithm 3 Map-updating function |
|
5.1. Beam Classifier
5.2. Localisation Check
5.3. Changed Cells Evaluator
| Algorithm 4 Changed cells evaluator function. |
5.3.1. Change Detection of Cells in
5.3.2. Change Detection of
5.4. Unchanged Cells Evaluator
| Algorithm 5 Unchanged cells evaluator function. |
|
5.5. Cells Update
| Algorithm 6 Cells update function. |
|
5.6. Pose Updating
| Algorithm 7 Pose-updating function |
|
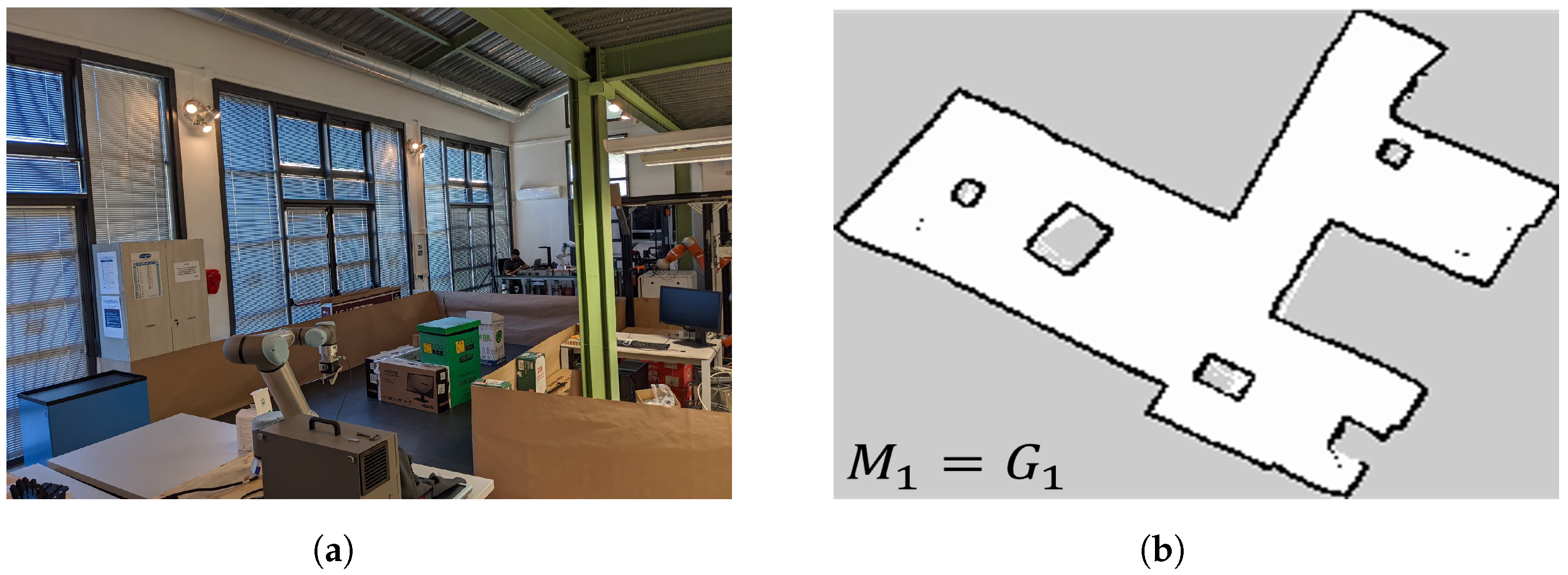
6. Experiments and Simulations
6.1. Map Benchmarking Metrics
6.2. Simulation Design
- The robot is immersed in an initial world, usually denoted with , and it is teleoperated to build an initial static map through the ROS Slam Toolbox package. Given , the proposed map update procedure starts from 2.
- The world is changed to create similar to the previous world .
- The robot autonomously navigates in the new environment by localising itself with adaptive Monte Carlo localisation (AMCL) [33] using the previous static map , while our approach provides a new updated map .
- We increase i by one and restart from 2.
6.3. Simulation Results
6.3.1. Localisation Check
6.3.2. System Evaluation
6.3.3. Pose Updating
6.4. System Validation
6.4.1. Updating Performance
6.4.2. Localisation Performances
6.4.3. Hardware Resource Consumption
7. Discussion
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2. Change Detection of c(p i ) Integration



Appendix A.3. Continue Map Updating vs. Localisation Check On


| Old / | New / | |
|---|---|---|
| CC (%) | 66.86 | 70.03 |
| MS (%) | 55.11 | 61.24 |
| OPDF (%) | 90.40 | 95.87 |


Appendix A.4. Case of Compromised Localisation

Appendix A.5. Pose-Updating Algorithm in Best-Case Scenario

Appendix A.6. Localisation Performance Results in the Simulated World W 4

References
- Chong, T.; Tang, X.; Leng, C.; Yogeswaran, M.; Ng, O.; Chong, Y. Sensor Technologies and Simultaneous Localization and Mapping (SLAM). Procedia Comput. Sci. 2015, 76, 174–179. [Google Scholar] [CrossRef] [Green Version]
- Dymczyk, M.; Gilitschenski, I.; Siegwart, R.; Stumm, E. Map summarization for tractable lifelong mapping. In Proceedings of the RSS Workshop, Ann Arbor, MI, USA, 16–19 June 2016. [Google Scholar]
- Sousa, R.B.; Sobreira, H.M.; Moreira, A. A Systematic Literature Review on Long-Term Localization and Mapping for Mobile Robots. J. Field Robot. 2023, 1–78. [Google Scholar] [CrossRef]
- Meyer-Delius, D.; Hess, J.; Grisetti, G.; Burgard, W. Temporary maps for robust localization in semi-static environments. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5750–5755. [Google Scholar]
- Shaik, N.; Liebig, T.; Kirsch, C.; Müller, H. Dynamic map update of non-static facility logistics environment with a multi-robot system. In Proceedings of the KI 2017: Advances in Artificial Intelligence: 40th Annual German Conference on AI, Dortmund, Germany, 25–29 September 2017; Proceedings 40. Springer: Berlin/Heidelberg, Germany, 2017; pp. 249–261. [Google Scholar]
- Abrate, F.; Bona, B.; Indri, M.; Rosa, S.; Tibaldi, F. Map updating in dynamic environments. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; pp. 1–8. [Google Scholar]
- Stefanini, E.; Ciancolini, E.; Settimi, A.; Pallottino, L. Efficient 2D LIDAR-Based Map Updating For Long-Term Operations in Dynamic Environments. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 832–839. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A. ROS: An Open-Source Robot Operating System. 2009. Volume 3. Available online: http://robotics.stanford.edu/~ang/papers/icraoss09-ROS.pdf (accessed on 15 January 2021).
- Banerjee, N.; Lisin, D.; Lenser, S.R.; Briggs, J.; Baravalle, R.; Albanese, V.; Chen, Y.; Karimian, A.; Ramaswamy, T.; Pilotti, P.; et al. Lifelong mapping in the wild: Novel strategies for ensuring map stability and accuracy over time evaluated on thousands of robots. Robot. Auton. Syst. 2023, 164, 104403. [Google Scholar] [CrossRef]
- Amigoni, F.; Yu, W.; Andre, T.; Holz, D.; Magnusson, M.; Matteucci, M.; Moon, H.; Yokotsuka, M.; Biggs, G.; Madhavan, R. A Standard for Map Data Representation: IEEE 1873–2015 Facilitates Interoperability Between Robots. IEEE Robot. Autom. Mag. 2018, 25, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Thrun, S. Robotic Mapping: A Survey. In Exploring Artificial Intelligence in the New Millennium; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2003. [Google Scholar]
- Sodhi, P.; Ho, B.J.; Kaess, M. Online and consistent occupancy grid mapping for planning in unknown environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; pp. 7879–7886. [Google Scholar]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Meyer-Delius, D.; Beinhofer, M.; Burgard, W. Occupancy Grid Models for Robot Mapping in Changing Environments. In Proceedings of the AAAI, Toronto, ON, Canada, 22–26 July 2012. [Google Scholar]
- Baig, Q.; Perrollaz, M.; Laugier, C. A Robust Motion Detection Technique for Dynamic Environment Monitoring: A Framework for Grid-Based Monitoring of the Dynamic Environment. IEEE Robot. Autom. Mag. 2014, 21, 40–48. [Google Scholar] [CrossRef]
- Nuss, D.; Reuter, S.; Thom, M.; Yuan, T.; Krehl, G.; Maile, M.; Gern, A.; Dietmayer, K. A random finite set approach for dynamic occupancy grid maps with real-time application. Int. J. Rob. Res. 2018, 37, 841–866. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Demir, M.; Lian, T.; Fujimura, K. An online multi-lidar dynamic occupancy mapping method. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 517–522. [Google Scholar]
- Llamazares, A.; Molinos, E.J.; Ocana, M. Detection and Tracking of Moving Obstacles (DATMO): A Review. Robotica 2020, 38, 761–774. [Google Scholar] [CrossRef]
- Biber, P.; Duckett, T. Dynamic Maps for Long-Term Operation of Mobile Service Robots. In Proceedings of the Robotics: Science and Systems, Cambridge, MA, USA, 8–11 June 2005. [Google Scholar]
- Banerjee, N.; Lisin, D.; Briggs, J.; Llofriu, M.; Munich, M.E. Lifelong mapping using adaptive local maps. In Proceedings of the 2019 European Conference on Mobile Robots (ECMR), Prague, Czech Republic, 4–6 September 2019; pp. 1–8. [Google Scholar]
- Tsamis, G.; Kostavelis, I.; Giakoumis, D.; Tzovaras, D. Towards life-long mapping of dynamic environments using temporal persistence modeling. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 10480–10485. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Wang, J. Long-term localization with time series map prediction for mobile robots in dynamic environments. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 1–7. [Google Scholar]
- Sun, D.; Geißer, F.; Nebel, B. Towards effective localization in dynamic environments. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4517–4523. [Google Scholar] [CrossRef]
- Hu, X.; Wang, J.; Chen, W. Long-term Localization of Mobile Robots in Dynamic Changing Environments. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 384–389. [Google Scholar] [CrossRef]
- Pitschl, M.L.; Pryor, M.W. Obstacle Persistent Adaptive Map Maintenance for Autonomous Mobile Robots using Spatio-temporal Reasoning*. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 1023–1028. [Google Scholar] [CrossRef]
- Lázaro, M.T.; Capobianco, R.; Grisetti, G. Efficient long-term mapping in dynamic environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2018), Madrid, Spain, 1–5 October 2018; pp. 153–160. [Google Scholar]
- Zhao, M.; Guo, X.; Song, L.; Qin, B.; Shi, X.; Lee, G.H.; Sun, G. A General Framework for Lifelong Localization and Mapping in Changing Environment. In Proceedings of the2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3305–3312. [Google Scholar]
- Amanatides, J.; Woo, A. A Fast Voxel Traversal Algorithm for Ray Tracing. In Proceedings of the 8th European Computer Graphics Conference and Exhibition, Eurographics 1987, Amsterdam, The Netherlands, 24–28 August 1987. [Google Scholar]
- Zhang, Z. Iterative Closest Point (ICP). In Computer Vision: A Reference Guide; Ikeuchi, K., Ed.; Springer: Boston, MA, USA, 2014; pp. 433–434. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point Set Registration: Coherent Point Drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 20 September 2021).
- Macenski, S.; Jambrecic, I. SLAM Toolbox: SLAM for the dynamic world. J. Open Source Softw. 2021, 6, 2783. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Dellaert, F.; Thrun, S. Monte Carlo Localization: Efficient Position Estimation for Mobile Robots. In Proceedings of the 16th National Conference on Artificial Intelligence (AAAI ’99), Orlando, FL, USA, 18–22 July 1999; pp. 343–349. [Google Scholar]
- Robotics, A.W.S. aws-robomaker-small-house-world. Available online: https://github.com/aws-robotics/aws-robomaker-small-house-world (accessed on 20 September 2021).
- Koenig, N.; Howard, A. Design and use paradigms for Gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar] [CrossRef] [Green Version]





















| Variable Name | Description |
|---|---|
| Robot | |
| Robot pose | |
| Robot position at time k | |
| Robot orientation at time k | |
| Robot estimated pose | |
| Robot estimated position at time k | |
| Robot estimated orientation at time k | |
| Robot pose displacement threshold | |
| i-th Robot World | |
| Occupancy grid map of | |
| j-th map’s cell associated to a Cartesian position q | |
| Origin of the grid coordinates | |
| Grid coordinates of a point | |
| Laser range measurement at time k | |
| i-th laser beam in | |
| n | Number of laser beams in a laser measurement |
| Point cloud associated to | |
| i-th hit point at time k belongs to . | |
| Cartesian coordinates of | |
| Angular offset of the first laser beam with respect to the orientation of the laser scanner | |
| Angular rate between adjacent beams | |
| The set of cells passed through by the measurement associated to | |
| The cell associated to . | |
| point in the centre of the cell | |
| Rolling buffer of | |
| Size of | |
| Expected value for the i-th laser beam | |
| Expected hit point associated with | |
| Cartesian coordinates of | |
| Set of expected hit points | |
| Perturbation | |
| Distance threshold, function of | |
| Number of the “detected change” measurements | |
| Min threshold related to localisation error to suspend the map-updating process, function of n | |
| Max threshold related to localisation error to update robot pose, function of n | |
| Threshold point belonging to a laser beam. | |
| Distance threshold, function of | |
| Counter of “changed” flag in | |
| Expected point cloud computed from the last updated map | |
| Rigid transformation between and | |
| i-th ground truth map |
| Parameter Name | Description | Value |
|---|---|---|
| Size of | 10 | |
| Design parameter | 1 | |
| Number of points in | 3 | |
| l | Design parameter | [−1, 0, 1] |
| Minimum fraction of acceptable changed measurements with respect to the number of laser beams that allows a good localisation performance | 0.75 | |
| Maximum fraction of acceptable changed measurements with respect to the number of laser beams, in addition to which the robot has definitively lost its localisation. | 0.90 | |
| Threshold for | 7 | |
| Robot linear displacement threshold | 0.05 [m] | |
| Robot angular displacement threshold | 20 |
| CC (%) | 69.69 | 78.95 | 63.77 | 68.80 | 60.87 | 67.14 |
| MS (%) | 54.63 | 74.57 | 51.44 | 72.58 | 50.45 | 70.26 |
| OPDF (%) | 84.61 | 97.25 | 78.92 | 95.37 | 82.18 | 94.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanini, E.; Ciancolini, E.; Settimi, A.; Pallottino, L. Safe and Robust Map Updating for Long-Term Operations in Dynamic Environments. Sensors 2023, 23, 6066. https://doi.org/10.3390/s23136066
Stefanini E, Ciancolini E, Settimi A, Pallottino L. Safe and Robust Map Updating for Long-Term Operations in Dynamic Environments. Sensors. 2023; 23(13):6066. https://doi.org/10.3390/s23136066
Chicago/Turabian StyleStefanini, Elisa, Enrico Ciancolini, Alessandro Settimi, and Lucia Pallottino. 2023. "Safe and Robust Map Updating for Long-Term Operations in Dynamic Environments" Sensors 23, no. 13: 6066. https://doi.org/10.3390/s23136066
APA StyleStefanini, E., Ciancolini, E., Settimi, A., & Pallottino, L. (2023). Safe and Robust Map Updating for Long-Term Operations in Dynamic Environments. Sensors, 23(13), 6066. https://doi.org/10.3390/s23136066







