Adaptively Lightweight Spatiotemporal Information-Extraction-Operator-Based DL Method for Aero-Engine RUL Prediction
Abstract
:1. Introduction
- Introducing InvGRU: We propose a novel operator called InvGRU, which replaces the connection operator in GRU and allows for adaptive capture of spatiotemporal information based on the input itself. InvGRU demonstrates the ability to extract spatiotemporal information with fewer parameters compared with other models.
- Constructing a deep learning framework: Building upon InvGRU, we construct a deep learning framework that achieves higher prediction accuracy.
- Experimental validation: The experimental results on aircraft engine RUL prediction validate the effectiveness and superiority of the proposed InvGRU-based deep learning framework. It outperforms other models in terms of prediction accuracy and showcases the potential for improved RUL estimation in practical applications.
2. Theoretical Basis
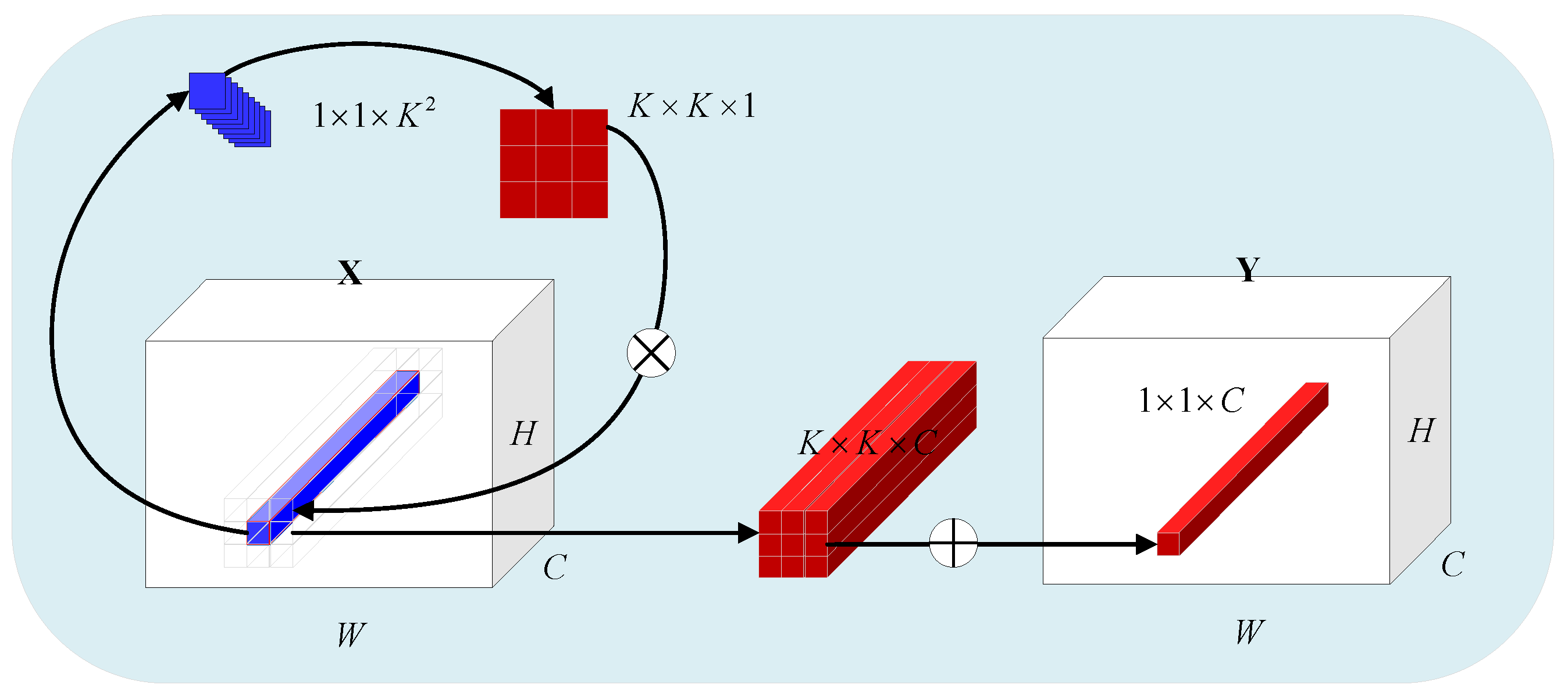
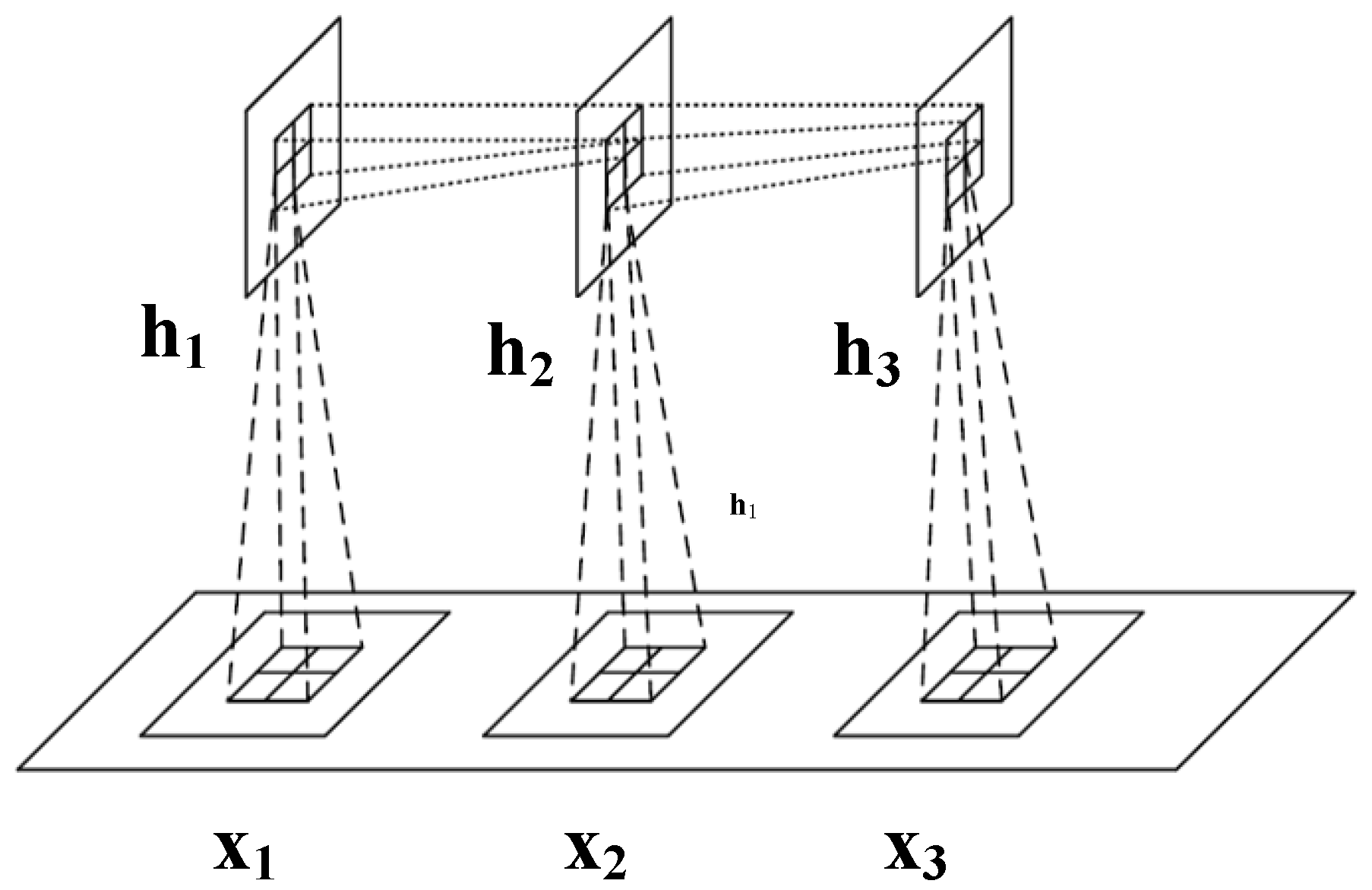
2.1. Inverse Convolution
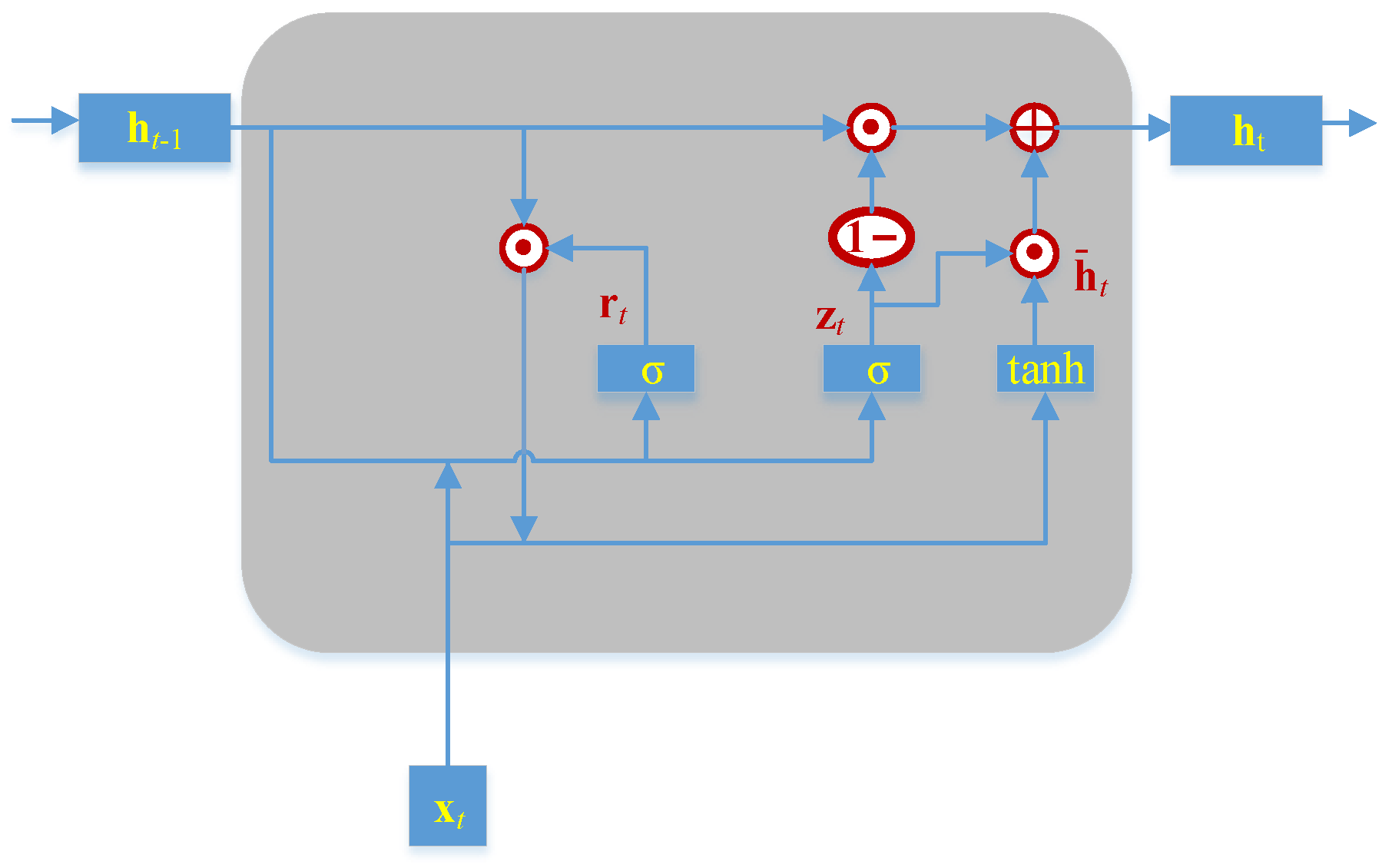
2.2. GRU
3. Proposed Methodology
3.1. Proposed InvGRU
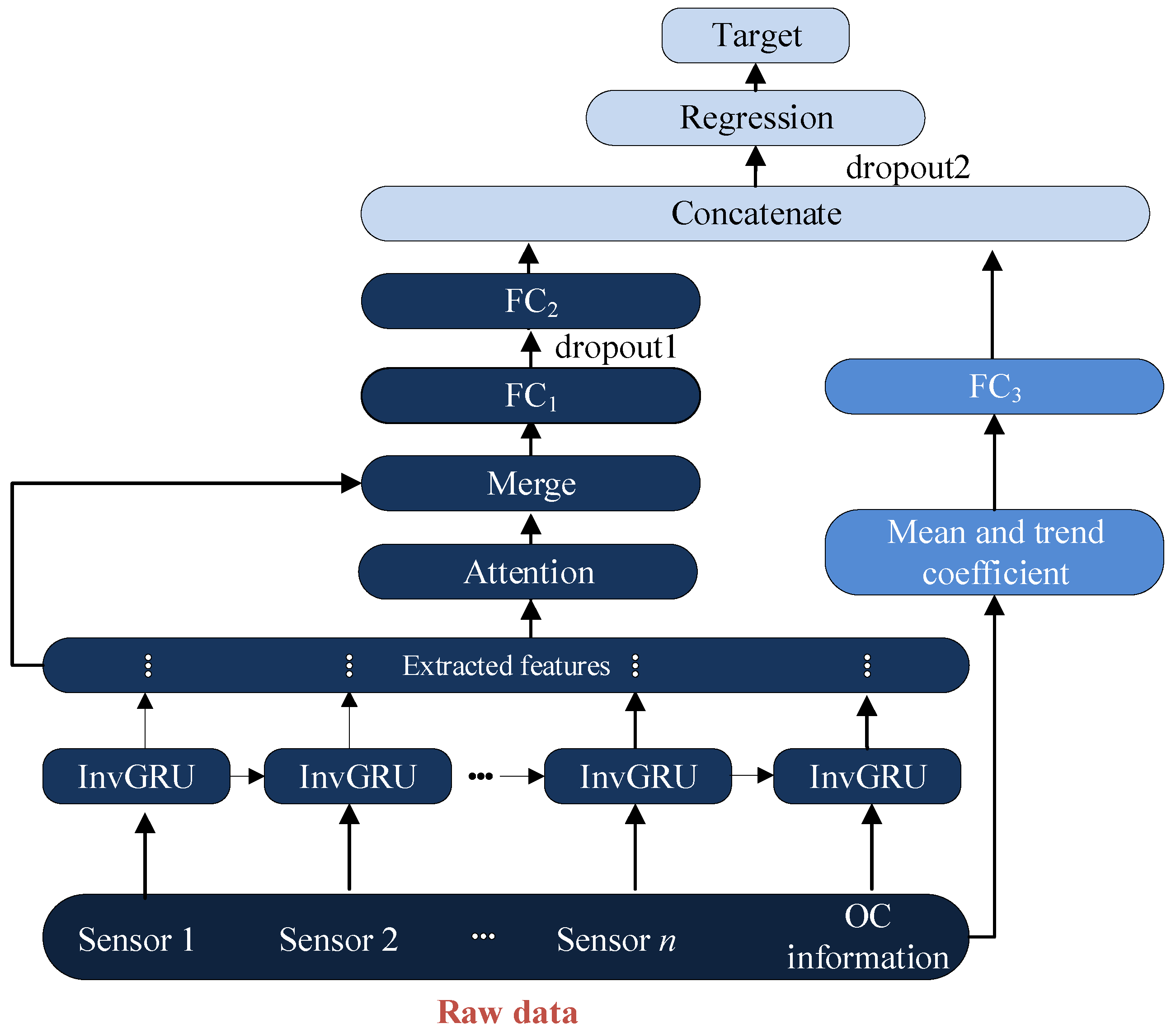
3.2. The Adopted DL Framework
4. Experimental Analysis
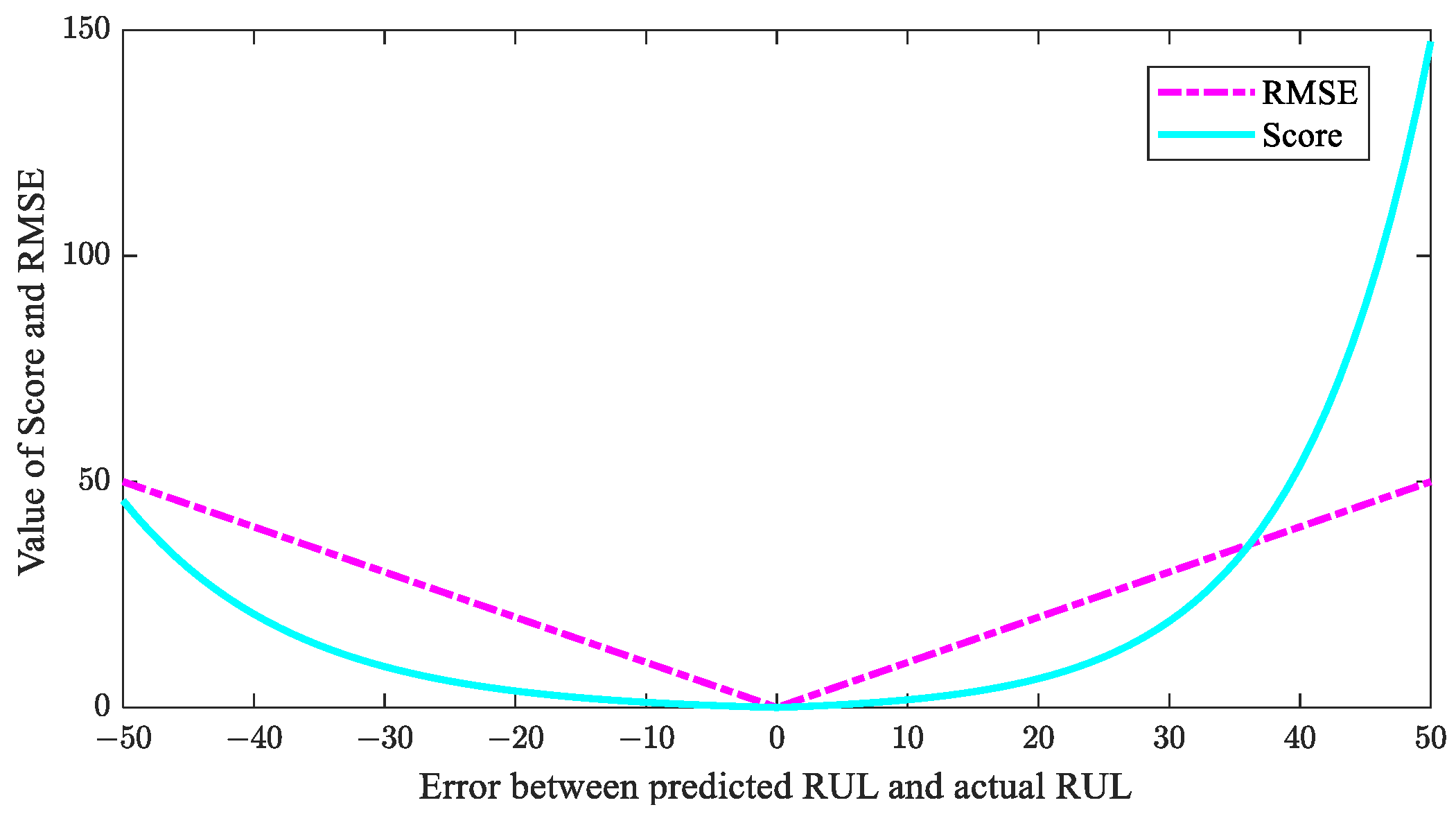
4.1. Evaluation Indexes
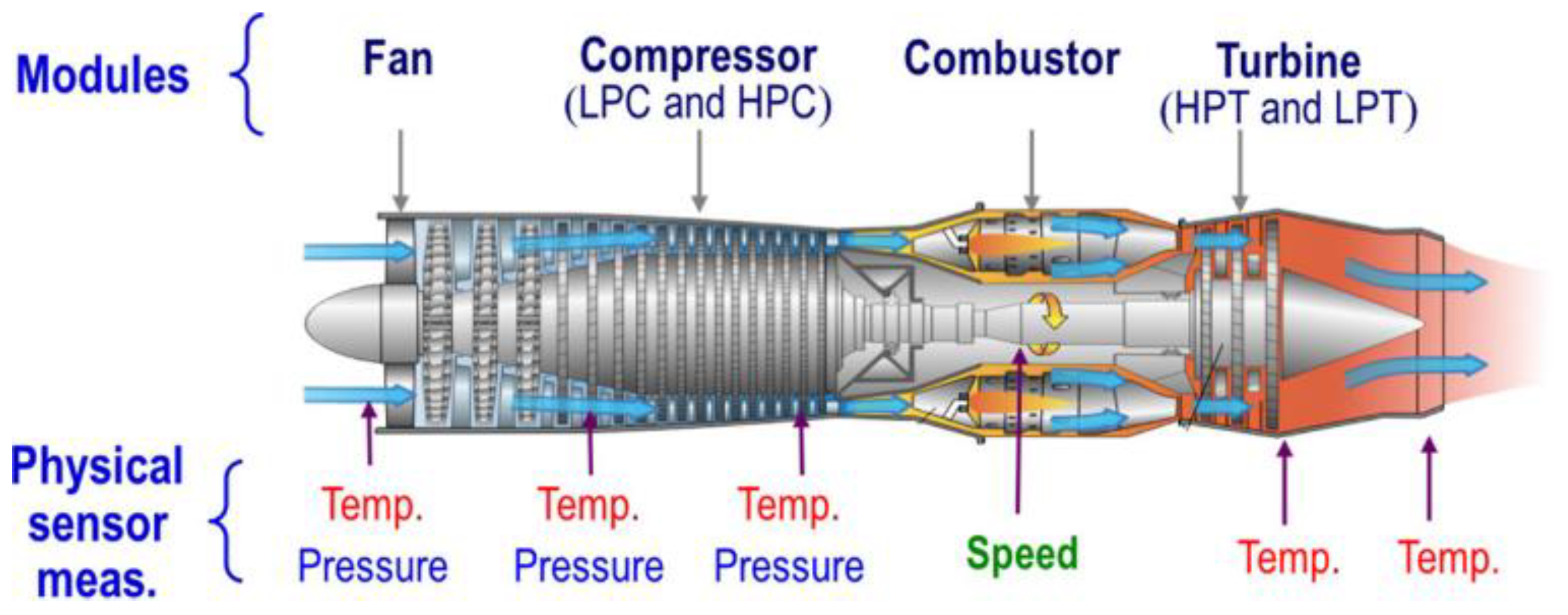
4.2. The Details of the C-MAPSS Dataset
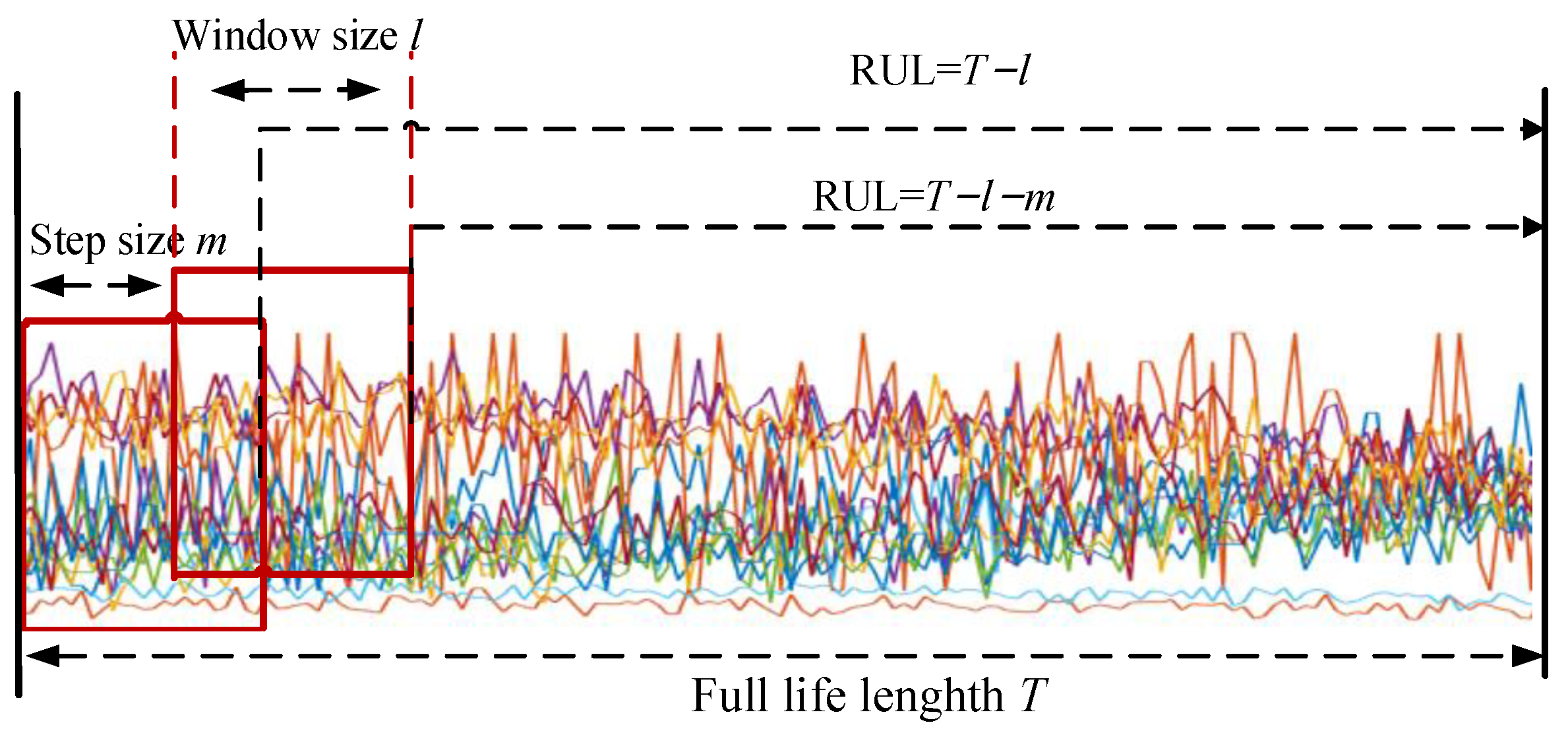
4.3. Data Preprocessing
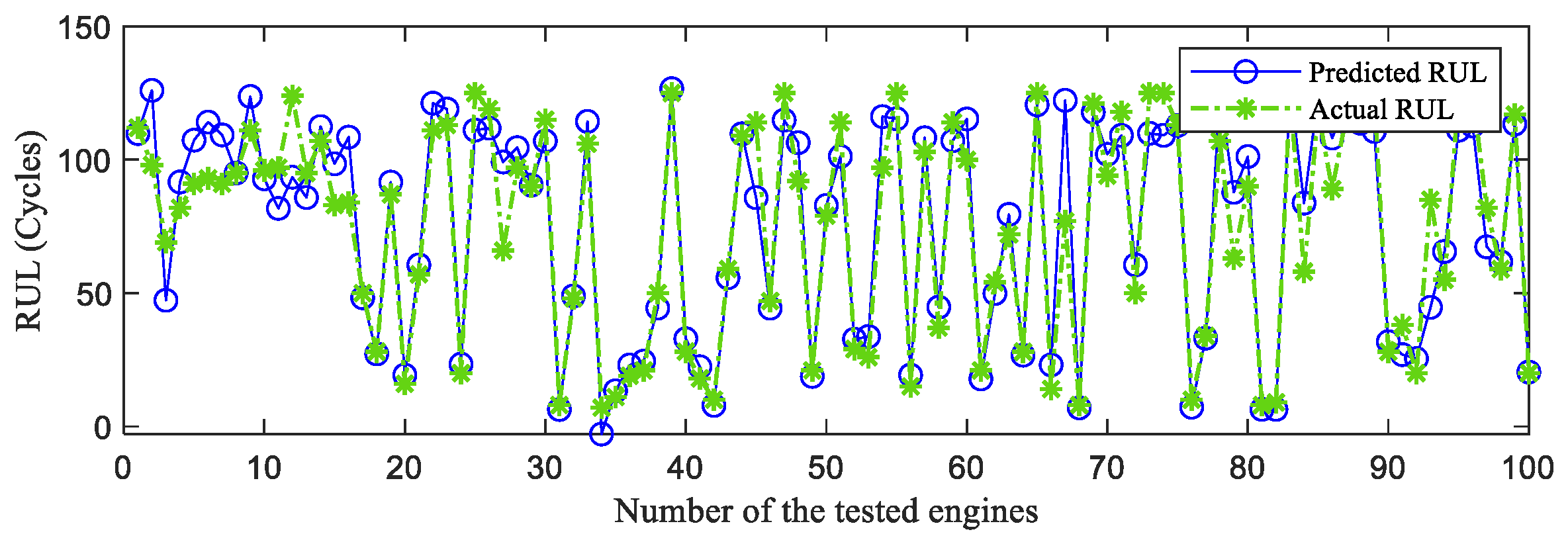
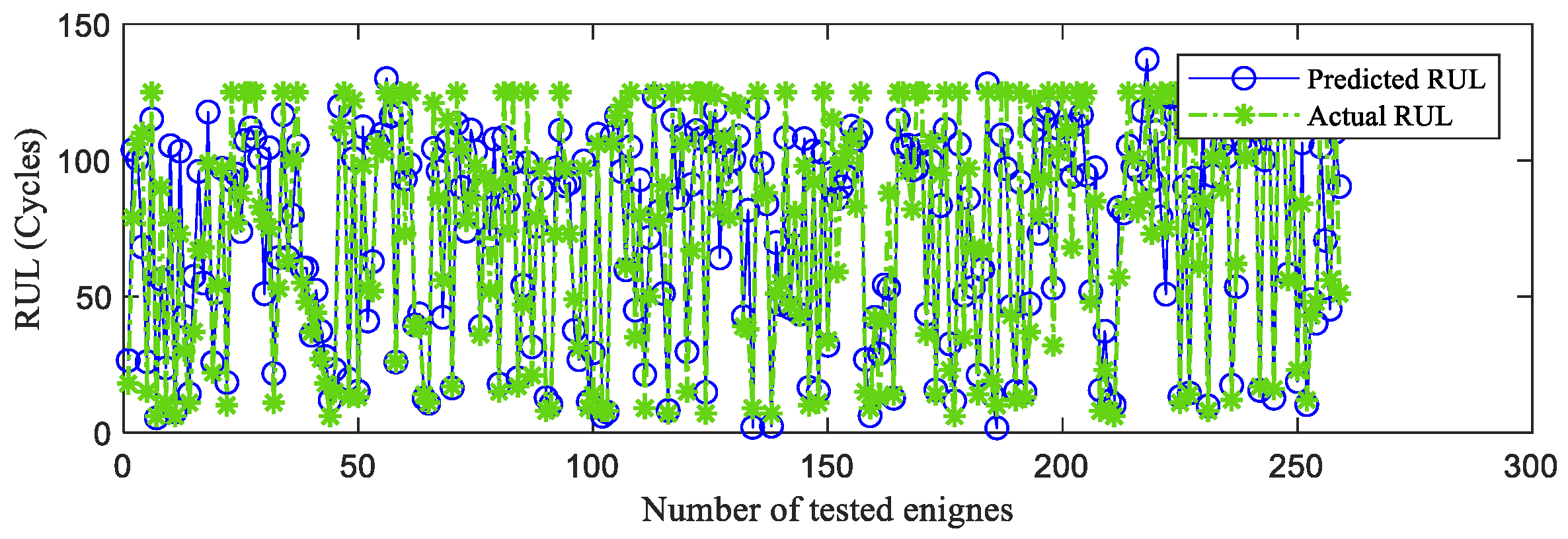
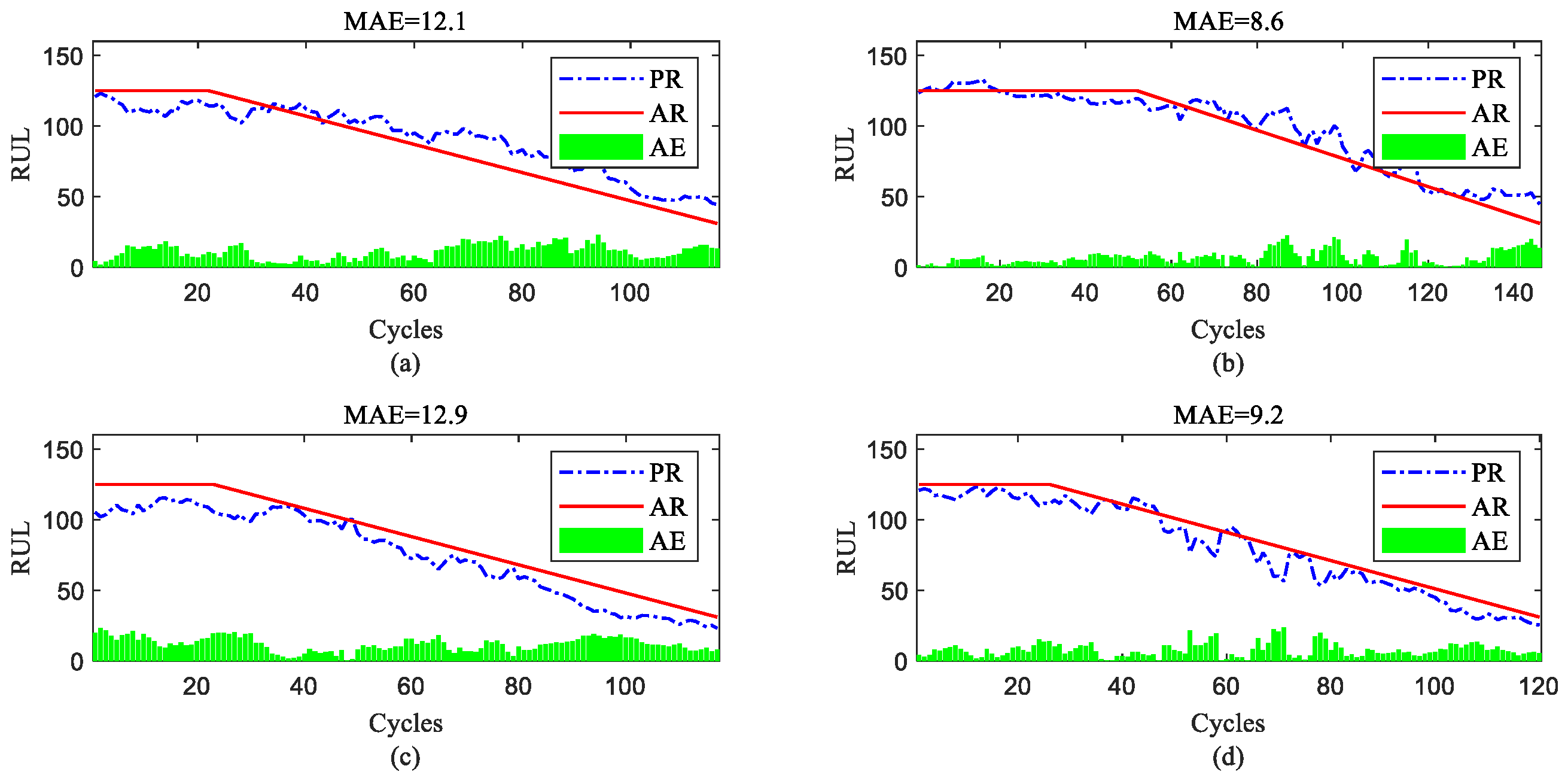
4.4. The Analysis and Comparison of RUL Prediction Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Luo, J.; Pu, H.; Tang, B. Multicellular LSTM-based deep learning model for aero-engine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 216, 107927. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Liu, R.; Parmeshwaran, V. Residual life predictions from vibration-based degradation signals: A neural network approach. IEEE Trans. Ind. Electron. 2004, 51, 694–700. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, T.; Zhao, Z.; Sun, C.; Chen, X.; Yan, R.; Jia, J. Time-varying trajectory modeling via dynamic governing network for remaining useful life prediction. Mech. Syst. Signal Process. 2023, 182, 109610. [Google Scholar] [CrossRef]
- Herzog, M.A.; Marwala, T.; Heyns, P.S. Machine and component residual life estimation through the application of neural networks. Reliab. Eng. Syst. Saf. 2009, 94, 479–489. [Google Scholar] [CrossRef] [Green Version]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Xu, D.; Xiao, X.; Liu, J.; Sui, S. Spatio-temporal degradation modeling and remaining useful life prediction under multiple operating conditions based on attention mechanism and deep learning. Reliab. Eng. Syst. Saf. 2023, 229, 108886. [Google Scholar] [CrossRef]
- Yu, W.; Kim, I.Y.; Mechefske, C. An improved similarity-based prognostic algorithm for RUL estimation using an RNN autoencoder scheme. Reliab. Eng. Syst. Saf. 2020, 199, 106926. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Liu, F.; Gryllias, K. Automatic multi-differential deep learning and its application to machine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2022, 223, 108531. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Luo, J.; Pu, H. Spatiotemporally multidifferential processing deep neural network and its application to equipment remaining useful life prediction. IEEE Trans. Ind. Inf. Inform. 2021, 18, 7230–7239. [Google Scholar] [CrossRef]
- Yuan, M.; Wu, Y.; Lin, L. Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 135–140. [Google Scholar]
- Wang, J.; Peng, B.; Zhang, X. Using a stacked residual LSTM model for sentiment intensity prediction. Neurocomputing 2018, 322, 93–101. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, J.; Yan, R.; Mao, K. Machine health monitoring with LSTM networks. In Proceedings of the 2016 10th International Conference on Sensing Technology (ICST), Nanjing, China, 11–13 November 2016; pp. 1–6. [Google Scholar]
- Wu, J.; Hu, K.; Cheng, Y.; Zhu, H.; Shao, X.; Wang, Y. Data-driven remaining useful life prediction via multiple sensor signals and deep long short-term memory neural network. ISA Trans. 2020, 97, 241–250. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2017, 65, 1539–1548. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, Y.; Chen, D.; Liu, F.; Qian, Q. Remaining useful life prediction of bearings by a new reinforced memory GRU network. Adv. Eng. Inform. 2022, 53, 101682. [Google Scholar] [CrossRef]
- He, X.; Wang, Z.; Li, Y.; Khazhina, S.; Du, W.; Wang, J.; Wang, W. Joint decision-making of parallel machine scheduling restricted in job-machine release time and preventive maintenance with remaining useful life constraints. Reliab. Eng. Syst. Saf. 2022, 222, 108429. [Google Scholar] [CrossRef]
- Que, Z.; Jin, X.; Xu, Z. Remaining useful life prediction for bearings based on a gated recurrent unit. IEEE Trans. Instrum. Meas. 2021, 70, 3511411. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Liu, Y.; Wang, T.; Li, Z. An integrated deep multiscale feature fusion network for aeroengine remaining useful life prediction with multisensor data. Knowl. Based Syst. 2022, 235, 107652. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.; Feng, K. Data-driven prognostic scheme for bearings based on a novel health indicator and gated recurrent unit network. IEEE Trans. Ind. Inf. Inform. 2022, 19, 1301–1311. [Google Scholar] [CrossRef]
- Zhang, Y.; Xin, Y.; Liu, Z.-W.; Chi, M.; Ma, G. Health status assessment and remaining useful life prediction of aero-engine based on BiGRU and MMoE. Reliab. Eng. Syst. Saf. 2022, 220, 108263. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep wavelet sequence-based gated recurrent units for the prognosis of rotating machinery. Struct. Health Monit. 2021, 20, 1794–1804. [Google Scholar] [CrossRef]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Dong, S.; Pecht, M. Deep residual networks with adaptively parametric rectifier linear units for fault diagnosis. IEEE Trans. Ind. Electron. 2020, 68, 2587–2597. [Google Scholar] [CrossRef]
- Ren, L.; Dong, J.; Wang, X.; Meng, Z.; Zhao, L.; Deen, M.J. A data-driven auto-CNN-LSTM prediction model for lithium-ion battery remaining useful life. IEEE Trans. Ind. Inf. Inform. 2020, 17, 3478–3487. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, X.; Li, Y.; Iqbal, M.Y. A double-channel hybrid deep neural network based on CNN and BiLSTM for remaining useful life prediction. Sensors 2020, 20, 7109. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Yan, T.; Li, N.; Guo, L. Recurrent convolutional neural network: A new framework for remaining useful life prediction of machinery. Neurocomputing 2020, 379, 117–129. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep-convolution-based LSTM network for remaining useful life prediction. IEEE Trans. Ind. Inf. Inform. 2020, 17, 1658–1667. [Google Scholar] [CrossRef]
- Li, B.; Tang, B.; Deng, L.; Zhao, M. Self-attention ConvLSTM and its application in RUL prediction of rolling bearings. IEEE Trans. Instrum. Meas. 2021, 70, 3518811. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, K.; Wu, J.; Zhu, H.; Shao, X. Autoencoder quasi-recurrent neural networks for remaining useful life prediction of engineering systems. IEEE ASME Trans. Mechatron. 2021, 27, 1081–1092. [Google Scholar] [CrossRef]
- Al-Dulaimi, A.; Zabihi, S.; Asif, A.; Mohammadi, A. A multimodal and hybrid deep neural network model for remaining useful life estimation. Comput. Ind. 2019, 108, 186–196. [Google Scholar] [CrossRef]
- Xia, T.; Song, Y.; Zheng, Y.; Pan, E.; Xi, L. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation. Comput. Ind. 2020, 115, 103182. [Google Scholar] [CrossRef]
- Xue, B.; Xu, Z.-B.; Huang, X.; Nie, P.-C. Data-driven prognostics method for turbofan engine degradation using hybrid deep neural network. J. Mech. Sci. Technol. 2021, 35, 5371–5387. [Google Scholar] [CrossRef]
- Li, D.; Hu, J.; Wang, C.; Li, X.; She, Q.; Zhu, L.; Zhang, T.; Chen, Q. Involution: Inverting the inherence of convolution for visual recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12321–12330. [Google Scholar]
- Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine remaining useful life prediction via an attention-based deep learning approach. IEEE Trans. Ind. Electron. 2020, 68, 2521–2531. [Google Scholar] [CrossRef]
- Sateesh Babu, G.; Zhao, P.; Li, X.-L. Deep. convolutional neural network based regression approach for estimation of remaining useful life. In Proceedings of the Database Systems for Advanced Applications: 21st International Conference, DASFAA 2016, Dallas, TX, USA, 16–19 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 214–228. [Google Scholar]
- Zhang, C.; Lim, P.; Qin, A.K.; Tan, K.C. Multiobjective deep belief networks ensemble for remaining useful life estimation in prognostics. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2306–2318. [Google Scholar] [CrossRef]
- Zheng, S.; Ristovski, K.; Farahat, A.; Gupta, C. Long. short-term memory network for remaining useful life estimation. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Detroit, MI, USA, 19–21 June 2017; pp. 88–95. [Google Scholar]
- Li, J.; Li, X.; He, D. A directed acyclic graph network combined with CNN and LSTM for remaining useful life prediction. IEEE Access 2019, 7, 75464–75475. [Google Scholar] [CrossRef]





| Sub Layer | Hyperparameter Value | Sub Layer | Hyperparameter Value |
|---|---|---|---|
| InvGRU | 70 | Regression (Linear) | 1 |
| FC1 (Relu) | 30 | Learning rate | 0.005 |
| FC2 (Relu) | 30 | Dropout1 | 0.5 |
| FC3 (Relu) | 10 | Dropout2 | 0.3 |
| Subset | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Total number of engines | 100 | 260 | 100 | 249 |
| Operating condition | 1 | 6 | 1 | 6 |
| Type of fault | 1 | 1 | 2 | 2 |
| Maximum cycles | 362 | 378 | 525 | 543 |
| Minimum cycles | 128 | 128 | 145 | 128 |
| Number | Symbol | Description | Unit | Trend | Number | Symbol | Description | Unit | Trend |
|---|---|---|---|---|---|---|---|---|---|
| 1 | T2 | Total fan inlet temperature | ºR | ~ | 12 | Phi | Fuel flow ratio to Ps30 | pps/psi | ↓ |
| 2 | T24 | Total exit temperature of LPC | ºR | ↑ | 13 | NRf | Corrected fan speed | rpm | ↑ |
| 3 | T30 | HPC total outlet temperature | ºR | ↑ | 14 | NRc | Modified core velocity | rpm | ↓ |
| 4 | T50 | Total LPT outlet temperature | ºR | ↑ | 15 | BPR | Bypass ratio | -- | ↑ |
| 5 | P2 | Fan inlet pressure | psia | ~ | 16 | farB | Burner gas ratio | -- | ~ |
| 6 | P15 | Total pressure of culvert pipe | psia | ~ | 17 | htBleed | Exhaust enthalpy | -- | ↑ |
| 7 | P30 | Total outlet pressure of HPC | psia | ↓ | 18 | NF_dmd | Required fan speed | rpm | ~ |
| 8 | Nf | Physical fan speed | rpm | ↑ | 19 | PCNR_dmd | Modify required fan speed | rpm | ~ |
| 9 | Nc | Physical core velocity | rpm | ↑ | 20 | W31 | HPT coolant flow rate | lbm/s | ↓ |
| 10 | Epr | Engine pressure ratio | -- | ~ | 21 | W32 | LPT coolant flow rate | lbm/s | ↓ |
| 11 | Ps30 | HPC outlet static pressure | psia | ↑ |
| Model | FD001 | FD002 | ||
|---|---|---|---|---|
| Score | RMSE | Score | RMSE | |
| Cox’s regression [34] | 28,616 | 45.10 | N/A | N/A |
| SVR [39] | 1382 | 20.96 | 58,990 | 41.99 |
| RVR [39] | 1503 | 23.86 | 17,423 | 31.29 |
| RF [39] | 480 | 17.91 | 70,456 | 29.59 |
| CNN [40] | 1287 | 18.45 | 17,423 | 30.29 |
| LSTM [42] | 338 | 16.14 | 4450 | 24.49 |
| DBN [41] | 418 | 15.21 | 9032 | 27.12 |
| MONBNE [41] | 334 | 15.04 | 5590 | 25.05 |
| LSTM+attention+ handscraft feature [20] | 322 | 14.53 | N/A | N/A |
| Acyclic Graph Network [43] | 229 | 11.96 | 2730 | 20.34 |
| AEQRNN [34] | N/A | N/A | 3220 | 19.10 |
| MCLSTM-based [4] | 260 | 13.21 | 1354 | 19.82 |
| SMDN [14] | 240 | 13.72 | 1464 | 16.77 |
| Proposed | 238 | 12.34 | 1205 | 15.59 |
| Model | FD003 | FD004 | ||
|---|---|---|---|---|
| Score | RMSE | Score | RMSE | |
| Cox’s regression [34] | N/A | N/A | 1,164,590 | 54.29 |
| SVR [39] | 1598 | 21.04 | 371,140 | 45.35 |
| RVR [39] | 17,423 | 22.36 | 26,509 | 34.34 |
| RF [39] | 711 | 20.27 | 46,568 | 31.12 |
| CNN [40] | 1431 | 19.81 | 7886 | 29.16 |
| LSTM [42] | 852 | 16.18 | 5550 | 28.17 |
| DBN [41] | 442 | 14.71 | 7955 | 29.88 |
| MONBNE [41] | 422 | 12.51 | 6558 | 28.66 |
| LSTM+attention+ handscraft feature [20] | N/A | N/A | 5649 | 27.08 |
| Acyclic Graph Network [43] | 535 | 12.46 | 3370 | 22.43 |
| AEQRNN [34] | N/A | N/A | 4597 | 20.60 |
| MCLSTM-based [4] | 327 | 13.45 | 2926 | 22.10 |
| SMDN [14] | 305 | 12.70 | 1591 | 18.24 |
| Proposed | 292 | 13.12 | 1020 | 13.25 |
| Model | Mean Performance | |
|---|---|---|
| RMSE | Score | |
| Cox’s regression [34] | 49.70 | 596,603 |
| SVR [39] | 32.335 | 108,277 |
| RVR [39] | 27.96 | 11,716 |
| RF [39] | 24.72 | 29,553 |
| CNN [40] | 24.42 | 7006 |
| LSTM [42] | 21.25 | 2797 |
| DBN [41] | 21.73 | 4461 |
| MONBNE [41] | 20.32 | 3225 |
| LSTM+attention+ handscraft feature [20] | 20.80 | 2985 |
| Acyclic Graph Network [43] | 16.80 | 1716 |
| AEQRNN [34] | 19.85 | 3908 |
| MCLSTM-based [4] | 17.40 | 1216 |
| SMDN [14] | 15.36 | 900 |
| Proposed | 13.58 | 689 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Gao, J.; Xiang, S. Adaptively Lightweight Spatiotemporal Information-Extraction-Operator-Based DL Method for Aero-Engine RUL Prediction. Sensors 2023, 23, 6163. https://doi.org/10.3390/s23136163
Shi J, Gao J, Xiang S. Adaptively Lightweight Spatiotemporal Information-Extraction-Operator-Based DL Method for Aero-Engine RUL Prediction. Sensors. 2023; 23(13):6163. https://doi.org/10.3390/s23136163
Chicago/Turabian StyleShi, Junren, Jun Gao, and Sheng Xiang. 2023. "Adaptively Lightweight Spatiotemporal Information-Extraction-Operator-Based DL Method for Aero-Engine RUL Prediction" Sensors 23, no. 13: 6163. https://doi.org/10.3390/s23136163
APA StyleShi, J., Gao, J., & Xiang, S. (2023). Adaptively Lightweight Spatiotemporal Information-Extraction-Operator-Based DL Method for Aero-Engine RUL Prediction. Sensors, 23(13), 6163. https://doi.org/10.3390/s23136163






