Abstract
Federated learning (FL) is a distributed training method for machine learning models (ML) that maintain data ownership on users. However, this distributed training approach can lead to variations in efficiency due to user behaviors or characteristics. For instance, mobility can hinder training by causing a client dropout when a device loses connection with other devices on the network. To address this issue, we propose a FL coordination algorithm, MoFeL, to ensure efficient training even in scenarios with mobility. Furthermore, MoFeL evaluates multiple networks with different central servers. To evaluate its effectiveness, we conducted simulation experiments using an image classification application that utilizes machine models trained by a convolutional neural network. The simulation results demonstrate that MoFeL outperforms traditional training coordination algorithms in FL, with more training cycles, in scenarios with high mobility compared to an algorithm that does not consider mobility aspects.
1. Introduction
Machine learning (ML) is increasingly used in various research areas, including computer vision, decision-making, natural language processing, computer graphics, and intelligent control [1]. In the context of the Internet of Things (IoT), ML-based solutions are developed to address network challenges such as traffic engineering, network management, security, internet traffic classification, and computational resource allocation [1]. ML is also widely applied in other domains, such as intelligent transportation for optimizing routes and parking [2], human health monitoring [3], and industrial processes [4,5].
Mobile devices have become widespread in the healthcare sector and can store users’ health data [6]. Integrating ML-based applications into mobile devices makes it possible to estimate energy expenditure, detect vital signs, and predict sleep quality based on physical activity data collected during waking hours [7,8].
A dataset is essential for effectively training some ML applications and algorithms. Additionally, some applications require that data be exclusively accessible to their owners. In healthcare applications, for instance, the sharing of patient data is legally and ethically restricted, posing challenges in data availability [9,10,11].
Another ML application scenario that requires data privacy and IoT is autonomous vehicle applications, where ML models can be used to perform autonomous driving tasks, and collaboration between vehicles can improve the performance of ML algorithms [12,13]. Such collaboration allows autonomous vehicles to exchange sensor data to improve the accuracy of the results for the ML [14]. Data security and privacy concerns pose a significant challenge in sharing data between connected vehicles. Without proper protection, there is a risk of malicious interception and unauthorized access to private information [15,16]. Consequently, ensuring data security and privacy becomes crucial for enabling vehicle ML techniques. It is essential to develop strategies that guarantee the privacy of shared data, mitigate potential attacks, and establish a robust framework for the safe implementation of ML techniques in vehicles [5,12,17,18].
The FL techniques arise to solve the data privacy requirements in machine learning applications. In FL, there are two essential roles for learning: the client and the central server. Clients train ML models locally, allocating computational resources to do so. In this sense, clients are usually applications’ users [19]. Therefore, in this work, we adopt the term clients to specify application users and the devices that perform local training in FL. The central server coordinates the FL, selecting the clients to perform local training and aggregating their training results into a single global model. The first FL coordination algorithm was named FedAvg [20,21]. This paper uses the term network to define the clients connected to a central server, sharing the same global model.
In FedAvg, the central server randomly chooses a group of clients and shares the global model with them so that they can perform local training to update and improve the global model. Furthermore, rather than clients sharing the input data for training, as in other distributed ML techniques, the clients’ training result is shared with the central server, ensuring clients’ data privacy [22].
A dropout problem can occur during the FL training because of the clients’ mobility in the network. This problem can happen if a client is requested to contribute to the model training but does not finish the local training tasks or send its results to the central application. A possible cause for this problem is the clients’ mobility, which can interrupt the communication between the FL’s central server and clients, interfering in the training coordination and interrupting the training results sharing.
In a local training cycle, clients can compromise the performance of other tasks when employing computing resources for the training. Thus, the performed processing is useless and lost if there is no communication with the central device. The global model is relatively unaffected from the central server perspective, given that other clients satisfy its requirements by contributing to their local training results. This way, the dropout of a single client only affects the global model once most of the other clients carry out their contributions successfully.
Nevertheless, as the clients’ dropout number increases, the learning of the global model starts to be impacted, decreasing the learning accuracy and convergence. Thus, usual issues of the conventional ML techniques, such as overfitting and underfitting, can also occur in the FL scenarios [23]. In the worst case, if the number of clients available in the network for training the model is too small, the learning can become impossible or skewed.
In this paper, based on the traditional FL algorithm, FedAvg [24], we propose the new MoFeL algorithm for multiple central servers simultaneously. MoFel differs from FedAvg in two steps: the training initialization strategy and the clients’ selection. During the beginning of the model training, MoFeL imposes a procedure, initiating a training cycle, while FedAvg does not specify what should be adopted. For the clients’ selection, MoFeL considers clients with fewer chances to drop out of the training, while FedAvg selects clients randomly.
Furthermore, in our new proposal, MoFeL evaluates multiple networks with different central servers simultaneously, ensuring that all of them can run the training, which is essential, especially in scenarios with mobility. As far as we know, this is the first FL algorithm in the literature that simultaneously addresses the evaluation of multiple networks.
In prior studies, we examined clients’ mobility in FL applications as they migrated to different central servers. However, each central server independently solved an optimization problem to select clients, resulting in a solution not coordinated with other central servers. We observed that solving the optimization problem for client selection required significant computational resources, which could pose challenges for central servers with limited computational capabilities [25]. In the current version of MoFeL, we consider another profile for the FL coordination, named the central station. The central station evaluates a group of central servers simultaneously to guarantee an evenly satisfactory solution for all central servers.
Client selection, including the optimization problem, is the responsibility of the central station. Transferring responsibility for selecting clients from the central server to the central station facilitates allocating computational resources specifically to that single device. This ensures the optimization in choosing clients and reduces resource allocation at the selection of clients in central servers.
The central station receives information from all central servers and clients (e.g., computational resources for local training, clients’ routes, and clients’ time connected to each central server). Based on this information and considering the application requirements, the central station establishes an optimization problem to select the clients for the central servers. This optimization problem can consider the minimum accuracies of global models or other application requirements in this context.
Thus, MoFeL is especially important for applications with the following features:
- The clients are mobile;
- The application does not oppose the disclosure of their routes;
- The models need training frequently to update;
- The trained models are different for each central server.
To evaluate the efficiency of MoFeL, we carried out experiments through simulations. In this paper, it is essential to note that the term efficiency refers to the capability of the FL algorithm to ensure the completion of training cycles while minimizing the computational resources allocated to clients. Additionally, it aims to meet the minimum required model training accuracy specified by the application. The results indicate that MoFeL can perform federated training even in scenarios with intense client mobility, while other traditional algorithms for training coordination cannot.
The main contributions of this work are summarized as follows:
- We propose a mobility-aware FL algorithm with multiple central servers analysis simultaneously;
- We formalize an optimization model that serves as a benchmark for new proposals;
- We evaluate the proposed technique comparing it with the FedAvg.
The remainder of this paper is organized as follows: Section 2 presents related work; Section 3 addresses an example scenario for applying MoFeL, highlighting the architecture and motivation for using the MoFeL; Section 4 describes the MoFeL algorithm and the optimization problem; Section 5 describes the experimental simulations; Section 6 presents and discusses the simulation results; lastly, Section 7 concludes this paper.
2. Related Work
Zhang et al. [26] proposed an FL algorithm, named CSFedAvg, that alleviates the accuracy degradation caused by clients’ non-IID (non-Independent, Identically Distribute) data. Their proposal considers a heterogeneous weight divergence present among the clients’ data. Thus, the algorithm chooses the clients with a lower degree of non-IID data to train the models with higher frequency. The authors conducted simulations, showing that the proposal improves the training performance compared to other FL algorithms. Nishio and Yonetani [27] proposed an FL algorithm that mitigates clients’ problems with limited computational resources, demanding higher training times, and poor wireless communications requiring longer upload times. Their proposal, named FedCS, considers the clients’ resource constraints for selecting the training participants. Additionally, the central server aggregates many updates at once to accelerate performance. The authors performed an experimental evaluation with public image datasets, training deep neural networks in a MEC (Multi-access Edge Computing) environment. The results demonstrate that FedCS can reduce the time to complete the training process compared to an original FL algorithm.
Although these two works consider mobile applications, they do not consider mobility aspects for client selection procedures.
In this sense, Wang et al. [28] proposed a client selection algorithm with mobility support for vehicular networks, where vehicles have high mobility and frequently switch between regions with different traffic characteristics. The proposal considered an architecture with edge computing, in which vehicles assume the role of clients and edge servers assume the role of a central server coordinating the FL. Besides, the authors also proposed another algorithm for allocating multidimensional communication resources to optimize the cost of FL after selecting participants for the training. In this work, the clients’ selection starts with the sharing of vehicle information with the central server, referring to the travelers’ distance within the central server’s domain, vehicle speed in free flow, as well as information about the environment, such as the volume of traffic in the area.
Still, in vehicular scenarios, Li et al. [29] identified that the limited computational resources for training the models locally and the locomotion of the vehicles could lead to low accuracy and high training delays of local models. Thus, the authors proposed a joint optimization scheme in selecting clients to train and allocate resources for the FL. This work uses FL in a high-precision FL-based cooperative map caching application to achieve dynamic edge caching while protecting clients’ privacy. In the selection stage, the authors proposed an optimization model considering the communication link, the computational processing capacity, and energy availability. In the solution, if the vehicle has not uploaded information within an established period, the central device does not wait for the training completion of this vehicle, aggregating the local parameters of other vehicles. Even though the work recognizes mobility as an essential factor in its application, it does not consider the mobility characteristics of the vehicles in the clients’ selection. Furthermore, considering the constraint of computational resources, running local training without leveraging its results in the aggregation is frustrating for the client who has committed the computational resources.
Xiao et al. [30] proposed a greedy algorithm to select vehicles for FL local training, considering their positions and velocities. The authors described a min-max optimization algorithm that optimizes the computation capability, transmission power, and local model accuracy, achieving the minimum cost for the FL. The simulation results demonstrated that the proposal presented good convergence with an acceptable cost. Deveaux et al. [31] considered vehicular mobility to propose an orchestration mechanism for data distribution-aware FL. The authors described protocols exchanging training requirements among the entities to improve the model training speed and accuracy. Experiments performed with the MNIST dataset presented improvements in the training speed and model accuracy compared to traditional FL algorithms.
Considering the impact of client mobility on learning performance, Feng et al. [32] proposed a mobility-aware cluster federated learning for hierarchical federated learning (HFL) in wireless networks. In this proposal, the clients move, causing the connection change between edge servers, preventing the conclusion and sharing of the local training results to the central server. The proposed algorithm, called MACFL, enables a new technique for updating the local training and aggregating the global model since the existing aggregation schemes consider the weighted average [20,33], which becomes the bottleneck of performance due to divergences in non-IID data distribution and client mobility.
The studies indicated that the mobility evaluation in FL techniques is recent, despite being a decisive factor for their success, including some studies that already consider the client’s mobility. However, these works still do not consider the clients’ routes and destinations. Thus, in the studies presented, the client’s path during migration does not add information for the clients’ selection in the central servers. However, the client route information can be used to improve FL if not confidential. The definition of which data must have restricted access to clients is unique to the application.
Thus, this work addresses applications that enable the sharing of client mobility information and is a pioneer in evaluating the selection of clients in FL considering several central servers simultaneously. In this way, it is possible to meet the needs of central servers without overloading clients and enabling the selection of clients capable of executing local training, even if the application has mobile clients.
3. Background and Motivation
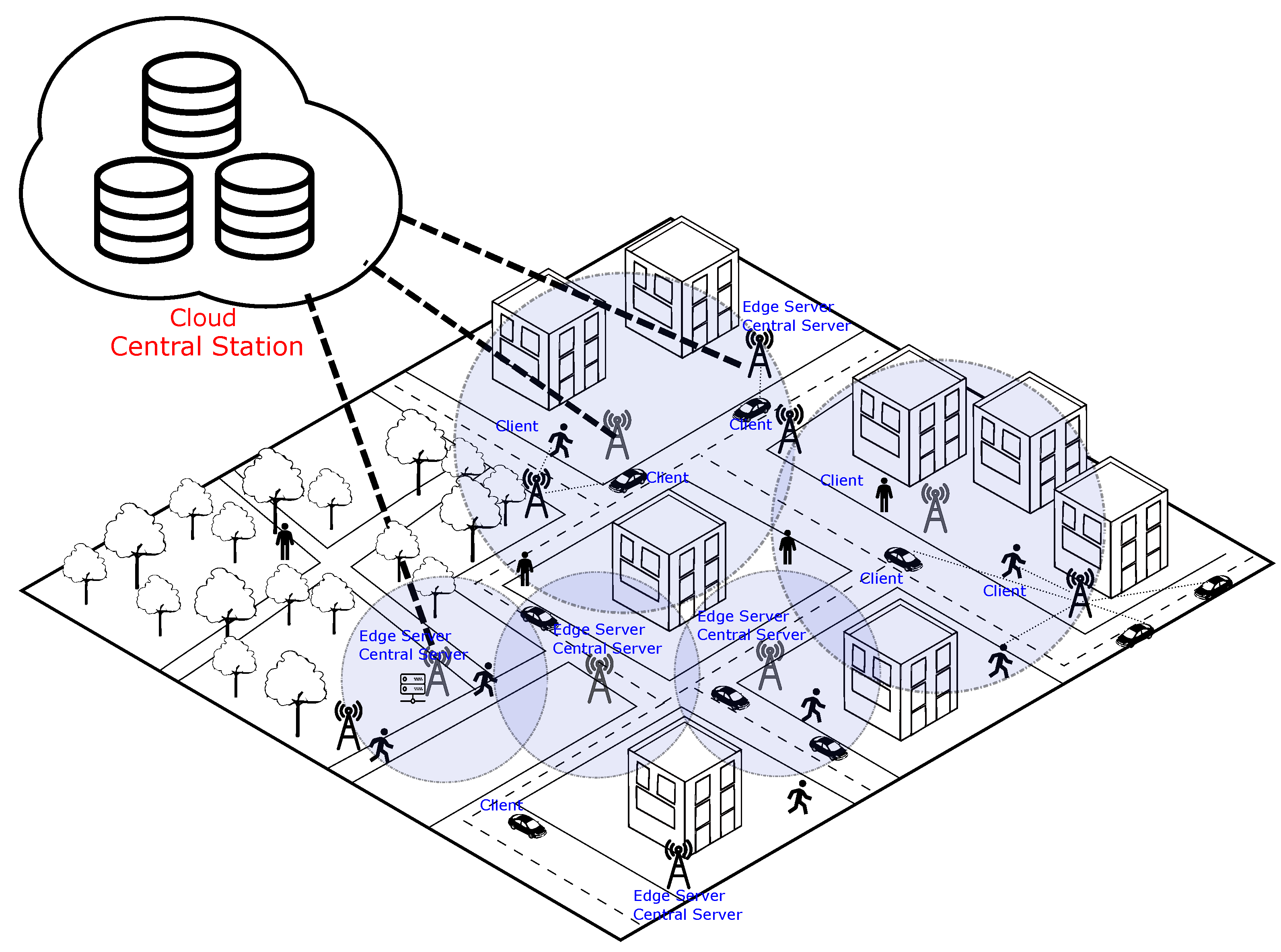
To explain the proposed FL coordination technique, we present in Figure 1 a smart city scenario based on an edge and cloud computing architecture. The proposed FL coordination technique aims to optimize resource usage in a smart city scenario. Figure 1 illustrates an architecture where IoT devices are deployed in vehicles and carried by people in the city. These devices establish wireless connections with various base stations to maintain connectivity with central servers and meet the application’s quality of service requirements.
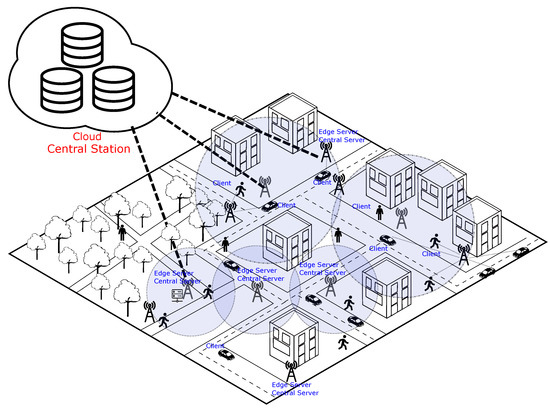
Figure 1.
A smart city scenario based on an edge and cloud computing architecture.
In the proposed scenario where FL is used in edge applications, edge servers allocate central servers, and each central server defines its own global FL model. When a device connects to the edge server in the FL application, the corresponding client connects to a specific central server. Each central server has its distinct global model independent of the others. Respecting the data confidentiality and ownership principles of FL, client data used in local training and the global models within each network cannot be shared among central servers.
A central station in the cloud is connected to all edge servers in the scenario. This central station assists the coordination of FL, particularly in the client selection stage. The central station can access information from all clients, such as their displacement routes, speeds, and available computational resources for local model processing. Additionally, the central station is aware of the territorial reach of each central server, precisely defining the geographic area through which clients move when connecting to a particular central server until they switch connections to a new central server.
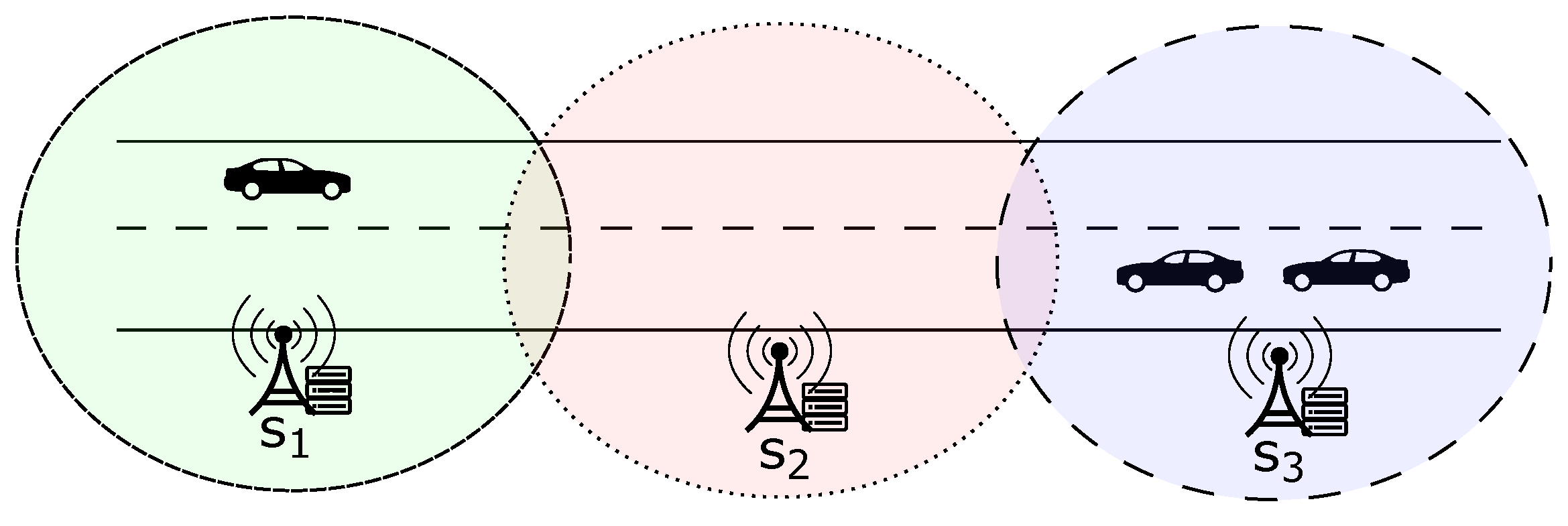
To understand the migration of clients among central servers, Figure 2 presents a scenario of vehicle traffic on a highway within a micro-region of the larger smart city depicted in Figure 1, where intelligent vehicles are clients who move between different central servers (, , ). In order to model the client migration between central servers, a graph representation can be utilized. In this work, we use the migration term to refer to changing a client’s connection between central servers.
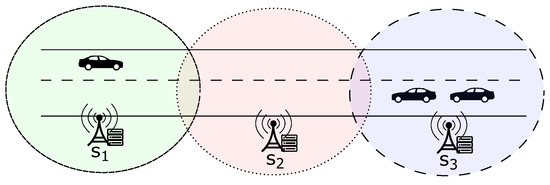
Figure 2.
Example of clients traveling between central servers.
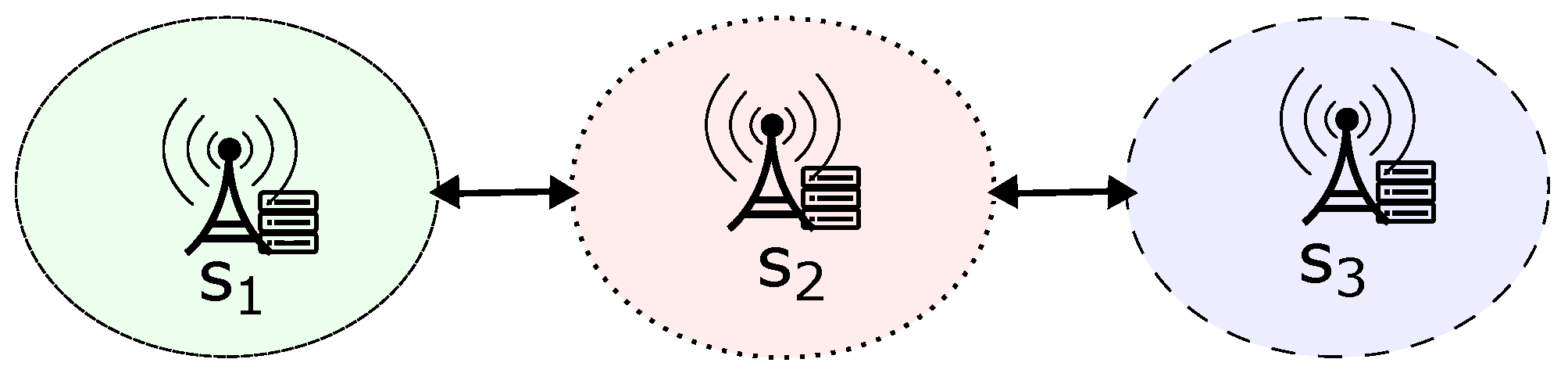
For this purpose, we can consider an undirected graph that simulates the traffic of clients between networks. In this graph, V represents a set of finite vertices that correspond to the domains of central servers, while E represents a finite set of edges defined as , where and . Thus, an edge indicates a pathway for a client to migrate from node v to node u within the graph. It is important to note that each client belongs to a single central server’s domain at any time. As a result, only one graph node can include a client at any particular moment. Thus, the scenario described by Figure 2 can be mapped in the graph of Figure 3.
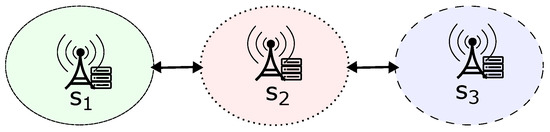
Figure 3.
Example of graph referring to Figure 2.
In specific applications, it is beneficial to maintain different models on central servers to optimize user access based on their connection to a particular server. For instance, vessels exhibit different mobility behaviors in maritime traffic depending on the region they navigate. Each region has fixed obstacles that directly influence navigation, alongside dynamic factors such as moving obstacles (e.g., animals) and changes in environmental conditions like tides, currents, and wind behavior. Machine learning models have been developed to enhance the safety of maritime transport systems by proactively preventing collisions based on region-specific training [34,35,36].
Similar challenges arise in air traffic involving Unmanned Aerial Vehicles (UAVs), particularly when flying over cities. Mobility control applications for UAVs must account for mobile obstacles, fixed obstacles, and ever-changing environmental conditions that directly impact their flight paths [37].
To address the need for frequent training, the MoFeL algorithm continuously evaluates clients, including their mobility patterns, to facilitate training and model updates. If frequent training is not required, the traditional FedAvg technique can be used, with the understanding that the model will be trained over the long term, even in challenging scenarios.
Training different models specific to territorial regions and regularly retraining them to adapt to dynamic scenarios is crucial in these contexts. The proposed architecture (refer to Figure 1) caters directly to such applications. Each coverage area can have an edge server deployed, which assigns a central server responsible for training a unique model tailored to the specific characteristics of that coverage area.
Additionally, in scenarios where frequent training is necessary, MoFeL is a practical algorithm that continuously evaluates clients, including their mobility patterns, to enable regular training and model updates. However, for applications where frequent training is not required, the traditional FedAvg technique can be used, ensuring that the model is trained in the long term, even in challenging conditions. For example, in urban environments where traffic conditions change over time, continuously updating models ensures the efficiency of public transportation systems [38].
4. MoFeL
This section provides an overview of the MoFeL algorithm, emphasizing the roles of clients, central servers, and the central station. The symbols frequently used in this paper are summarized in Table 1.

Table 1.
Symbols and description.
In the MoFeL design, we consider a set N of clients that move within a network and connect with central servers grouped in the set S. Each client n () has a specific time requirement for local training and moves at a certain speed (). It is important to note that the client’s speed () and the time required for training () are inherent characteristics of the client that remain constant regardless of its connection to a central server or geolocation.
On the other hand, each central server s () covers a specific territorial area (). A central server’s territorial reach () is a characteristic unique to that server, constant, and independent of client connections. Whenever a client n connects to a central server, it must traverse the corresponding territorial area until changing its connection. Therefore, a client n loses connection with a central server s after staying connected time units.
Consequently, a client n can only perform local training within the network managed by a specific central server s if and only if . The problem formulation and mathematical modeling can be further expanded by incorporating more complexity in variables , , and . For simplicity in understanding the optimization problem’s modeling, we assume constant values for these variables in this work.
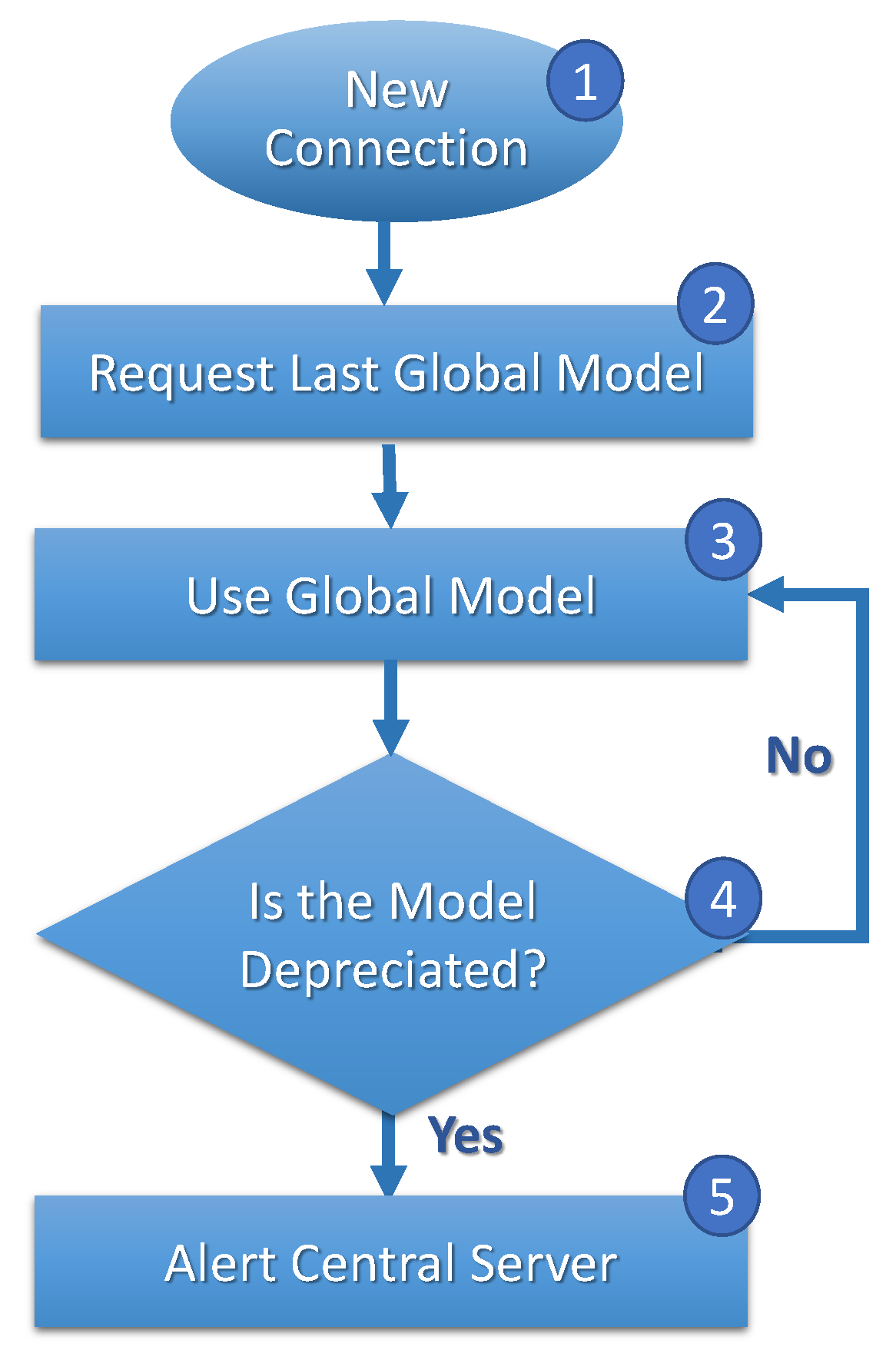
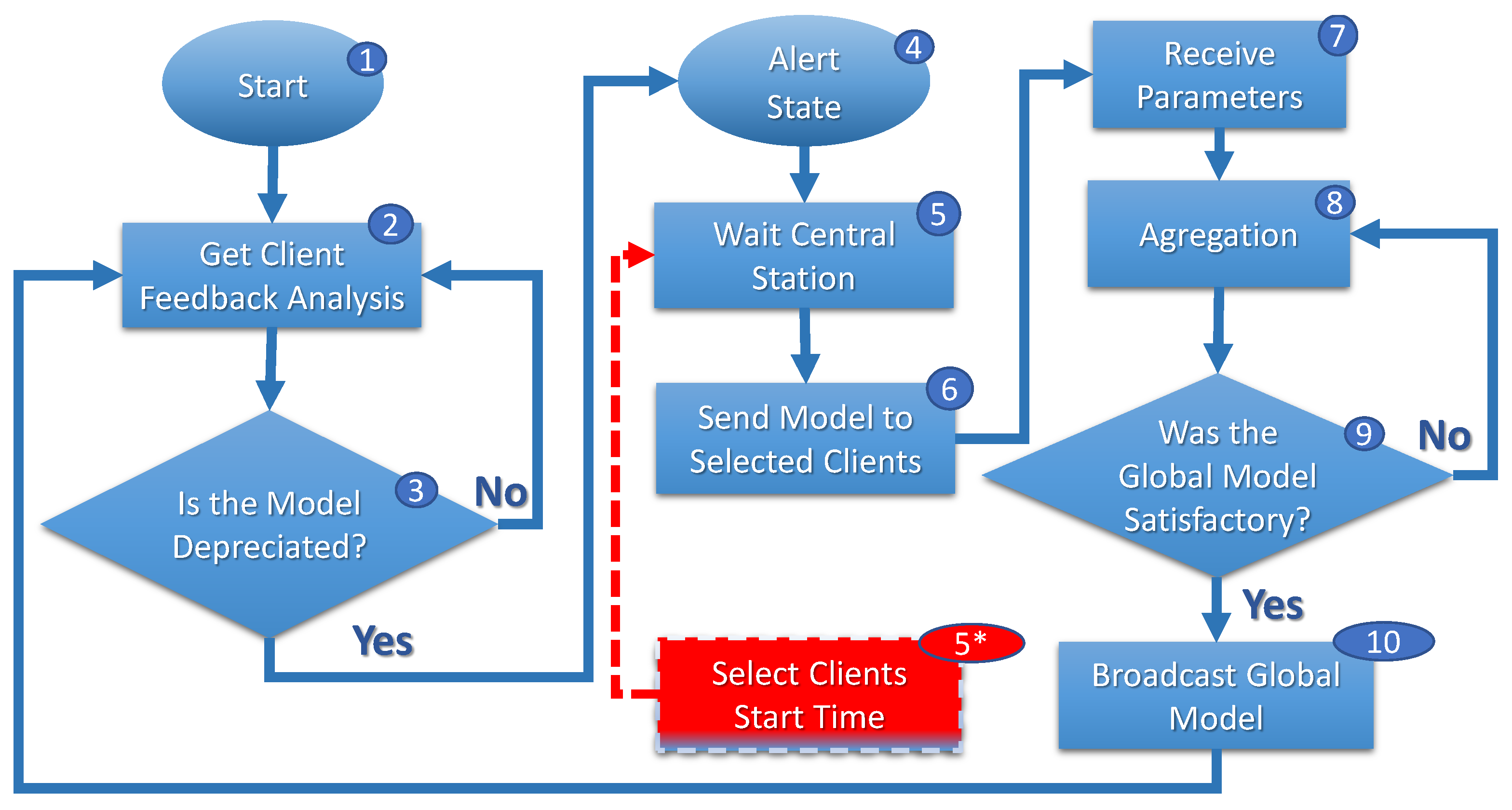
Figure 4, Figure 5 and Figure 6 show FL execution cycles on clients, central servers, and the central station. In Figure 4, when migrating and connecting a new central server (step 1), the client requests a current global model (step 2) from the central server. The client evaluates the model frequently (step 3), and if the client evaluates that the model is deprecated (step 4), the client reports to the central server (step 5).
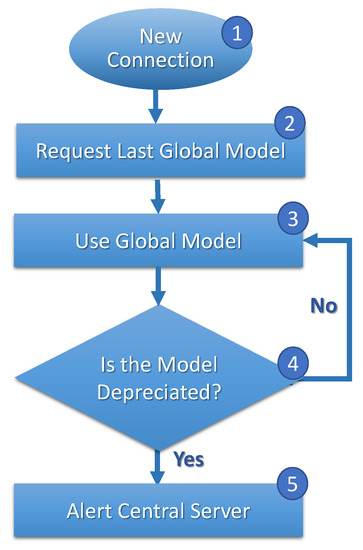
Figure 4.
Clients’ FL cycle.
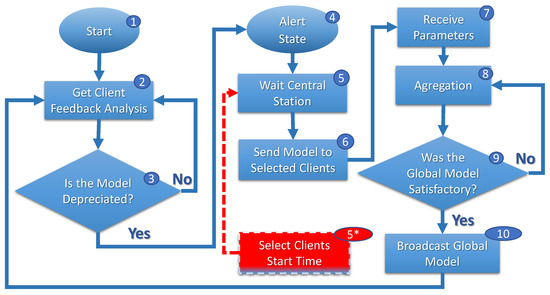
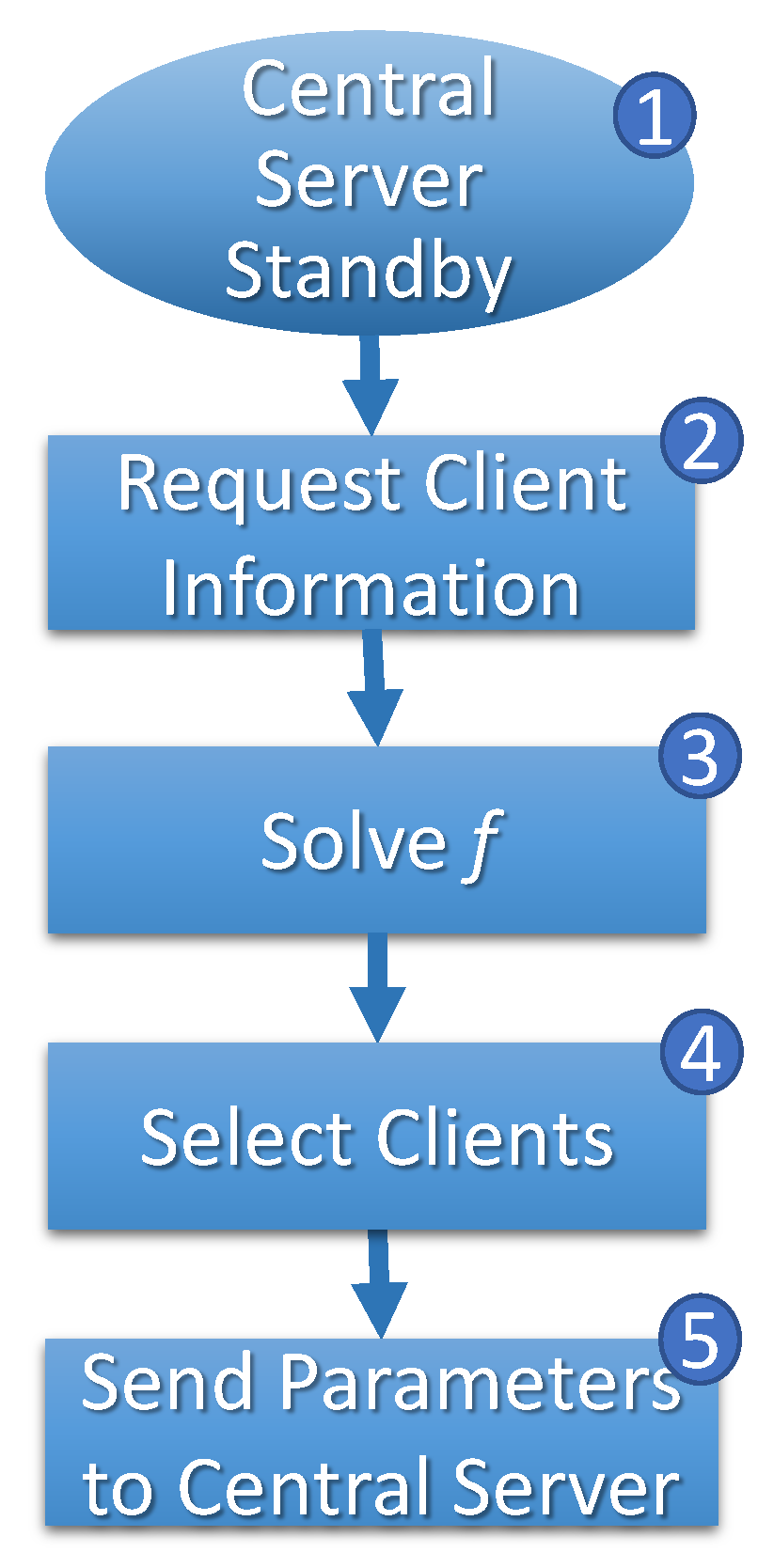
Figure 5.
Central servers’ FL cycle.
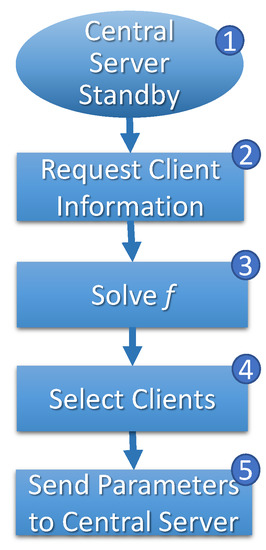
Figure 6.
Central station’ FL cycle.
The model’s inefficacy can be evaluated from sensitivity, specificity, accuracy, precision, and others [39]. For example, it is possible for applications to consider the average and the standard deviation of the accuracies in the model training evaluation, analyzing a maximum threshold for the standard deviation and a minimum threshold for the average value. In this way, a central server requests the accuracy values from the clients to calculate the mean and standard deviation and decides whether to update the model training if it does not meet the established condition. The definition of the minimum threshold for the average accuracy and the maximum threshold for the standard deviation depends on application requirements.
In any case, the central server enters an alert state (step 4, Figure 5) to start training the FL, waiting for information about selected clients by central stations (step 5, Figure 5). When a central server requires model retraining in the alert state, it notifies the central station accordingly. As illustrated in Figure 6, the central station awaits requests from other central servers within a predefined interval (step 1). Once all requests are received, the central station gathers information from all clients (step 2), including their respective routes and speeds (). Utilizing this information, the optimization problem, represented by Equation (1), is initiated (steps 3 and 4) to determine the optimal solution.
The evaluation process is conducted in a predictive manner, considering a future time interval denoted as . This interval begins when the central servers enter an alert state () and extends until time . The solution to Equation (1) determines when and which clients participate in the local training process for each central server that has requested to update its global model.
Once the selection is determined, the central station promptly notifies the respective central servers (step 5, Figure 6). In turn, the central server awaits the definition of the selection of clients by the central station (steps 5 and 5*, Figure 5). With the report, the central server waits when the selected clients connect to its network to start training.
Each central server’s training cycle is scheduled to begin once all designated clients have connected to its domain, as depicted in steps 7, 8, 9, and 10 of Figure 5. The central station assesses an objective function (Equation (1)) to identify a result that is deemed minimally satisfactory. This analysis helps to determine the optimal moment to initiate the training process.
The selection of clients to participate in the local training is based on the following criteria:
In Equation (1), is the global model error function aggregated by the central server s. Thus, the objective of Equation (1) is minimizing the sum of all error functions for the models aggregated by each central server. In detriment of the panoramic evaluation of all the networks’ models, restrictions can be attributed in this equation solution to direct the focus of fairness to it, depending on the application, such as controlling the number of training executed individually by the clients, controlling the number of clients participating in training, and minimizing the training time or another application constraint.
The value of is defined with a complete training of the model. Therefore, the solution to the proposed optimization problem must predict before the final decision on the selection of clients. The prediction of is analyzed based on the characteristics of the application, the database, and the training technique used in the application. In this work, based on the simulation and application in the following sections, we adopted the inference of through the number of clients that will contribute to the local training. In future works, we will analyze how the prediction of interferes with the solution of the optimization problem.
Equation (1) has mandatory constraints, by the Equations (2), (4), (5), (7) and (8), that are detailed as follows. Equation (2) is a logical constraint and defines that if a client n is selected for the central server s for local training, at least one time in interval , n participates in the training cycle of s. Equation (2) is given as follows:
where is a binary variable, such as , with denoting that the client n was chosen for local training and otherwise. t is the time step, such that . is a binary variable, such as , and indicates whether the client n is participating in the local training at the instant t. As with , the variable is the result of the Equation (1) solution and takes on the values:
The constraint in Equation (4) collaborates with the definition that all selected clients must remain connected and available computational resources during the FL cycle. The Equation (4) must be applied when condition is true. The Equation (4) and the Equation (2) define together that , thus
The constraint in Equation (5) guarantees that a client n can only participate in a training cycle in central server s while n is connected to s, i.e., .
where is a binary variable, such as . is inherent to the client’s mobility and defines whether client n is connected to the central server s. Therefore, is defined by the route and speed of each client, in addition to of the central servers belonging to the client’s route. So, is defined as:
The constraint in Equation (7) defines the execution of local training to be continuous, i.e., without interruptions. Therefore, Equation (7) is directly related to the Equation (4).
Equation (8) defines a constraint that guarantees that a client n, selected by s, must be available during the time required to complete all training cycles. MoFeL requires the aggregation of results of all local training. Therefore, the time required for completion is defined by the slowest client running the local training ().
After determining the starting point of training, the clients with are selected, while the remaining steps (7, 8, 9, and 10) of the algorithm are depicted in Figure 5 follow a similar approach to the FedAvg algorithm.
Besides the previously defined restrictions, it is possible to expand the modeling of the solution presented in Equation (1) by incorporating additional constraints to promote fairness requirements based on the specific application. For instance, Equation (9) introduces the constraint that the standard deviation of the error functions between the models defined in the central servers must be smaller than a threshold value (), ensuring that the data remains close to a predetermined average. By including such restrictions, the optimization process can be tailored to meet fairness objectives in distributing the global model’s accuracy among the central servers.
where is a constant defined in the optimization problem based on application requirements and is the average of all .
Another example of a restriction is presented in Equation (10). This restriction limits the number of training sessions (n) that each client can perform, ensuring that it does not exceed a certain threshold (). This constraint is implemented to prevent training overload and excessive allocation of computational resources to specific clients. By setting this restriction, a more balanced allocation of training tasks can be achieved to avoid client overload when selecting the same clients multiple times to run local training on different central servers.
It is crucial to emphasize that as restrictions are added to modeling an optimization problem, the feasibility of finding a solution may be compromised due to the reduction in the set of potential solutions. Balancing the incorporation of necessary constraints while maintaining a feasible solution space becomes a significant challenge in modeling the problem to meet the application’s specific requirements. Striking the right balance is essential to ensure the optimization problem remains solvable and effectively addresses the application’s constraints.
5. Experimental Evaluation
For the experimental evaluation, we constructed a simulated FL edge computing environment comprising central servers and clients and defined a network with a set of clients and a central server. In the FL process, we implemented the on-device training using the TensorFlow Federated framework [40], a widely used machine learning library. The simulation utilized the MNIST dataset, commonly used for handwritten digit recognition tasks, with images and corresponding labels for training and testing machine learning models [41].
In the simulation, each client is assigned a unique subset of the handwriting database from MNIST. Initially, the client does not have immediate access to its dataset slice, and the samples are uniformly distributed during the simulation. As the simulation progresses, the client’s database gradually increases in size.
Additionally, clients have the ability to migrate randomly within the network, based on a uniform distribution. The simulated application focuses on classifying images.
In the following subsections, we discuss the methodology used in the execution of the simulation experiment (Section 5.1) and the simulation parameters (Section 5.2).
5.1. Experimental Methodology
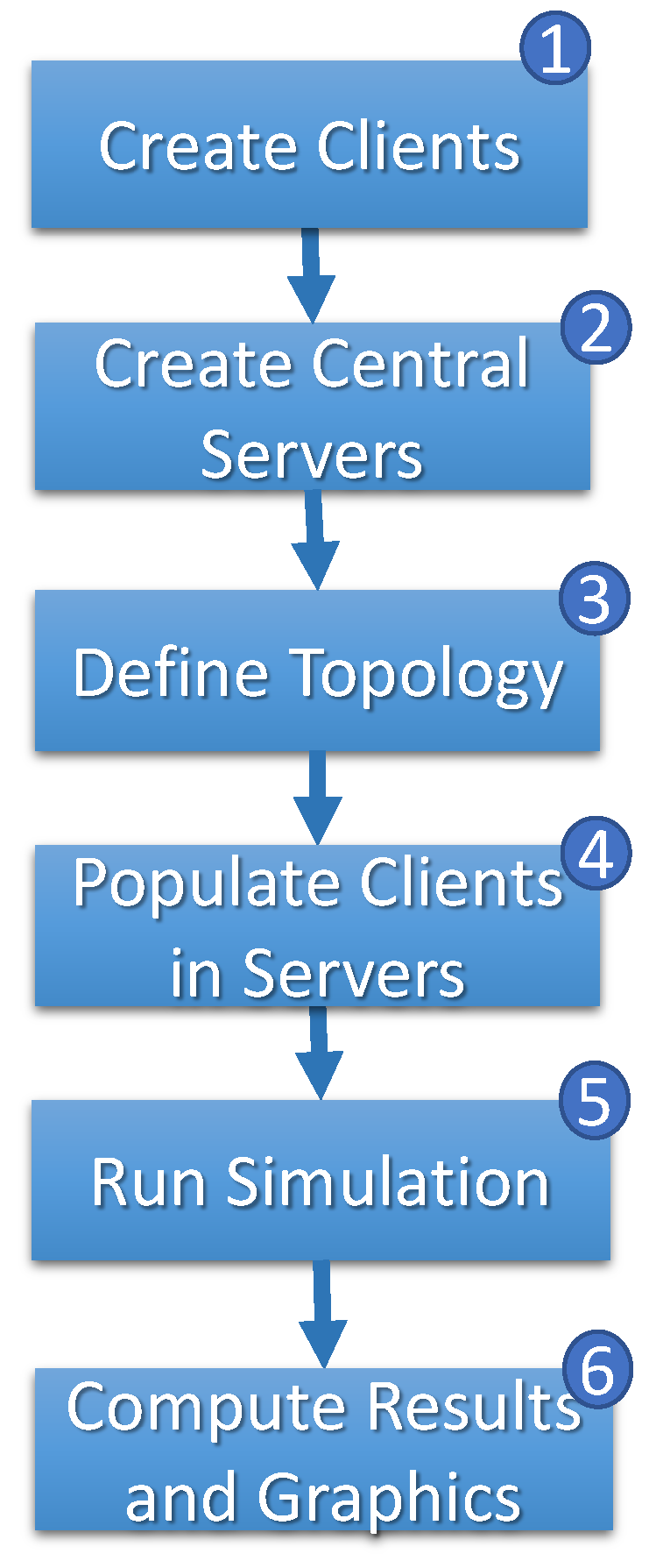
Figure 7 shows the simulation flowchart. The first step (step 1) generates clients. For each client, the speed () and the time required () are randomly chosen, respectively, between and . The combination between and of each client represents the system’s heterogeneity.
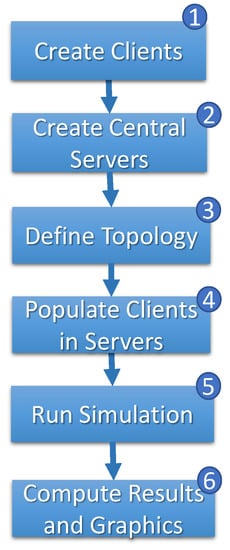
Figure 7.
Simulation flow.
In step 2, central servers are generated, and each central server randomly receives the length of the path to be traversed in the network between . With the clients and central servers created, the simulation receives the graph’s structure topology (step 3) as a parameter and randomly connects the clients to the central servers (step 4). When the simulation starts, a timer is initiated on step 5 to track the discrete progression of time t () throughout the simulation period . The duration of the simulation, T, is a required parameter to provide.
5.2. Experimental Evaluation
The evaluation of MoFeL is based on comparing two other proposals for simpler algorithms. The two algorithms are described as follows.
Algorithm randomly defines clients’ participation in a training cycle. The selection step does not consider features of the device’s mobility aspects or computational capacity. Thus, it is similar to FedAvg. A cycle starts considering fixed time intervals.
Algorithm selects clients that can complete the training before they migrate. Therefore, considers mobility aspects. However, each central server only evaluates connected clients at the beginning of the training cycle. In turn, the MoFeL algorithm takes a different approach. It assesses all clients through the central station to determine the most suitable set of clients for each central server. In MoFeL, the central station can select a client for a central server even if the client is not currently connected to that server. The only requirement is that the client establishes a connection with the server at the beginning of the training. This ability to anticipate client selection is made possible by MoFeL’s knowledge of the client’s route, allowing it to predict future migrations.
Finally, we evaluated two metrics. First, the number of training cycles (NTC) performed. Second, the number of frustrated clients (NFC), i.e., the total number of clients who initiated training but failed to complete it. Additionally, we evaluated the training accuracy average and the standard deviation of accuracy graphically.
5.3. Experimental Setup
For this simulation, we considered a scenario with 4 central servers connected through a mesh topology and 100 clients. In the simulation, = 1 m/min, the minimum accuracy that each central server wants to achieve is , and the FL process is requested by the central server until the global model reaches the minimum accuracy in training.
This experiment changes the value of , and the other simulation parameters are constant. The other simulation parameters are = 50 m, = 100 m, = 1 min, = 20 min, and T = 2000 min. The simulator generates new clients by changing the value of because each client can assume other speeds (). Increasing the value of increases the number of clients with greater mobility migrating between networks more frequently.
We simulated an image classification application using a Convolutional Neural Network, specifically the standard LeNet-5 [42]. Arbitrarily, we adopted the execution of 10 epochs in local training. All the simulations are performed on a computer with 32 GB RAM memory and a Intel i7-7700 3.60 GHz processor.
6. Experimental Results and Discussion
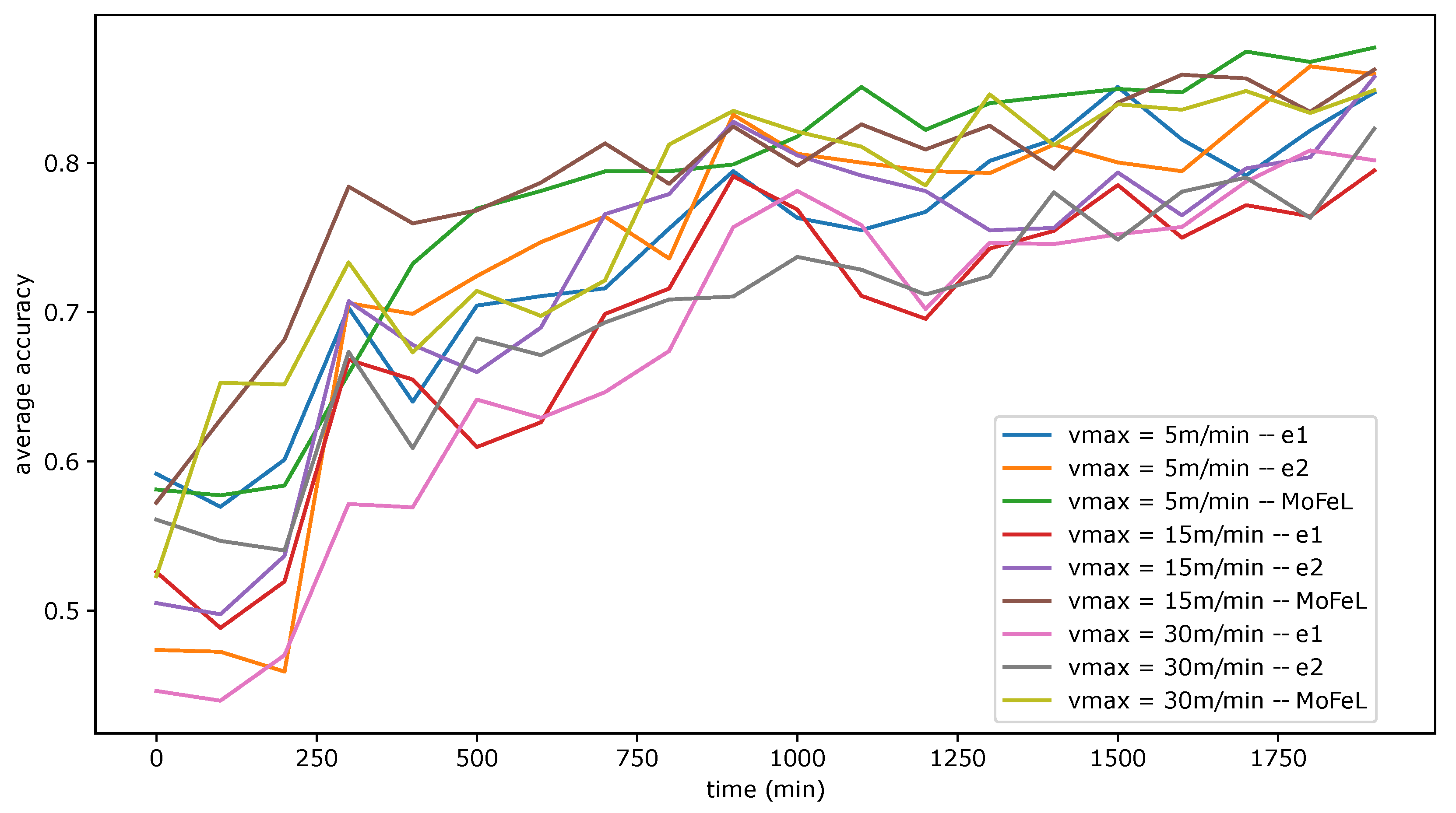
In this experiment, we evaluated three scenarios: = 5 m/min, = 15 m/min, and = 30 m/min. Figure 8 shows the progress of the average training accuracy across central servers by the number of FL simulation steps for each algorithm. Each curve represents the average training accuracy for the combination of an algorithm and a scenario.
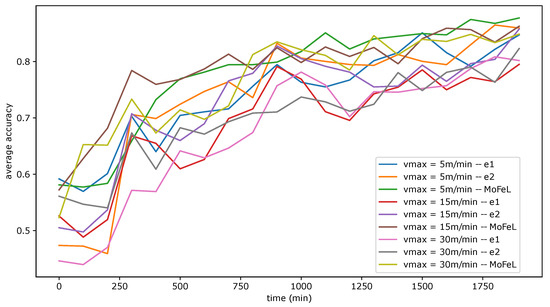
Figure 8.
Average between the training accuracies of the central servers.
Analyzing Figure 8, we can verify that all the algorithms suffered impacts with the increase in the system mobility level, resulting in the worsening of the global models training. This analysis alone supports the importance of evaluating mobility in FL since this fact can make model training unfeasible, especially when the mobility level is high. Furthermore, algorithms and MoFeL suffered losses in accuracy during training as increases. However, MoFeL was more robust to change scenarios, achieving training with more satisfactory results. In this sense, the experiment corroborates other studies by concluding that a biased client selection brings benefits to FL or that the client selection process can consider mobility aspects [26,27,28,29,30,31]. There are two reasons why this happens:
- Increased likelihood of choosing unsuitable clients for training, i.e., unable to complete training before changing their central server connection;
- The lack of clients capable of performing the full training.
Regarding the first reason, as increases, the speed average of devices also increases. Thus, algorithms that arbitrarily select clients are more likely to choose clients with greater mobility. In this context, as the level of mobility increases, the number of clients who follow the expression increases. The absence of clients capable of training on any central server, i.e., , makes FL completely unfeasible.
For algorithm , it is possible to identify a significant worsening in the model’s accuracy as the speed increases. Considering the graphical analysis, clients’ mobility can make the FL unfeasible if the training strategies do not consider the mobility aspect during the client selection.
Table 2 summarizes the experiment’s and results for each combination between mobility scenarios and algorithms. Through the values and the graph in Figure 8, it is possible to conclude that the algorithm wrongly chose many clients in the scenario with less mobility, causing damage to the application and the clients who made resources available for this training.

Table 2.
NFC and NTC of experiment. The dimension of the variable is m/min.
Algorithm achieved satisfactory results with the variable = 5 m/min. However, increasing decreases the number of complete training cycles. Even so, the technique ensures that clients unable to complete the training are not selected and, therefore, in all scenarios, like MoFeL. Although no client has unnecessarily allocated resources, the application is compromised by inadequate training and model accuracy due to the inability of the central servers to analyze a longer time interval to evaluate clients that will connect to the central servers in the future, i.e., the algorithm limits itself to querying the clients connected to it at the query instant. MoFeL and are biased in client selection strategies. However, in MoFeL, a central station analyzes all the clients and all central servers.
Furthermore, the limited view of the central servers in the algorithms and makes it challenging to adopt equality criteria among clients. In this way, clients with less mobility may be overwhelmed by running more training cycles. MoFeL solves this problem by adopting more restrictions in Equation (1). It is possible to propose that, in algorithms and , clients notify the central server of their history of local training so that the central server considers this in selecting clients. However, this proposal would still be ineffective compared to MoFeL since the view of the algorithms and are limited only to clients connected to the central server.
Results in Table 2 show that all algorithms were successful in executing training cycles in at least one of the central servers (). However, the number of trained cycles was not the same. Also, when the experiment increased the mobility, MoFeL was more robust. Between extreme scenarios, = 5 m/min and = 30 m/min, the decreased significantly. In algorithm , the decreased , and in algorithm , it decreased . In addition, there was an increase of of in the algorithm, that is, an increase in dissatisfied clients for having committed their resources unnecessarily. In turn, the of MoFeL remained practically constant.
In Table 2, it is possible to observe an increase in NTC in MoFeL between = 5 m/min and = 30 m/min. Despite the increase in mobility between scenarios, MoFeL performed more training cycles to achieve a more accurate model. However, with the decrease in available clients to complete the training, the model’s training did not obtain a satisfactory result, as shown in Figure 8. The increase in the NTC also occurred in algorithm . However, this increase was not able to improve the result of training and provoked an increase in NFC.
Regarding the number of training cycles, in the scenario with = 30 m/min, the MoFeL algorithm performed training cycles more than and more than , demonstrating the efficiency of MoFeL in defining instants and clients to execute the training in scenarios with high mobility. In scenarios with less mobility ( = 5 m/min), there was an increase of in the execution of training cycles compared to and compared to . Thus, MoFeL could perform more training in scenarios with less mobility.
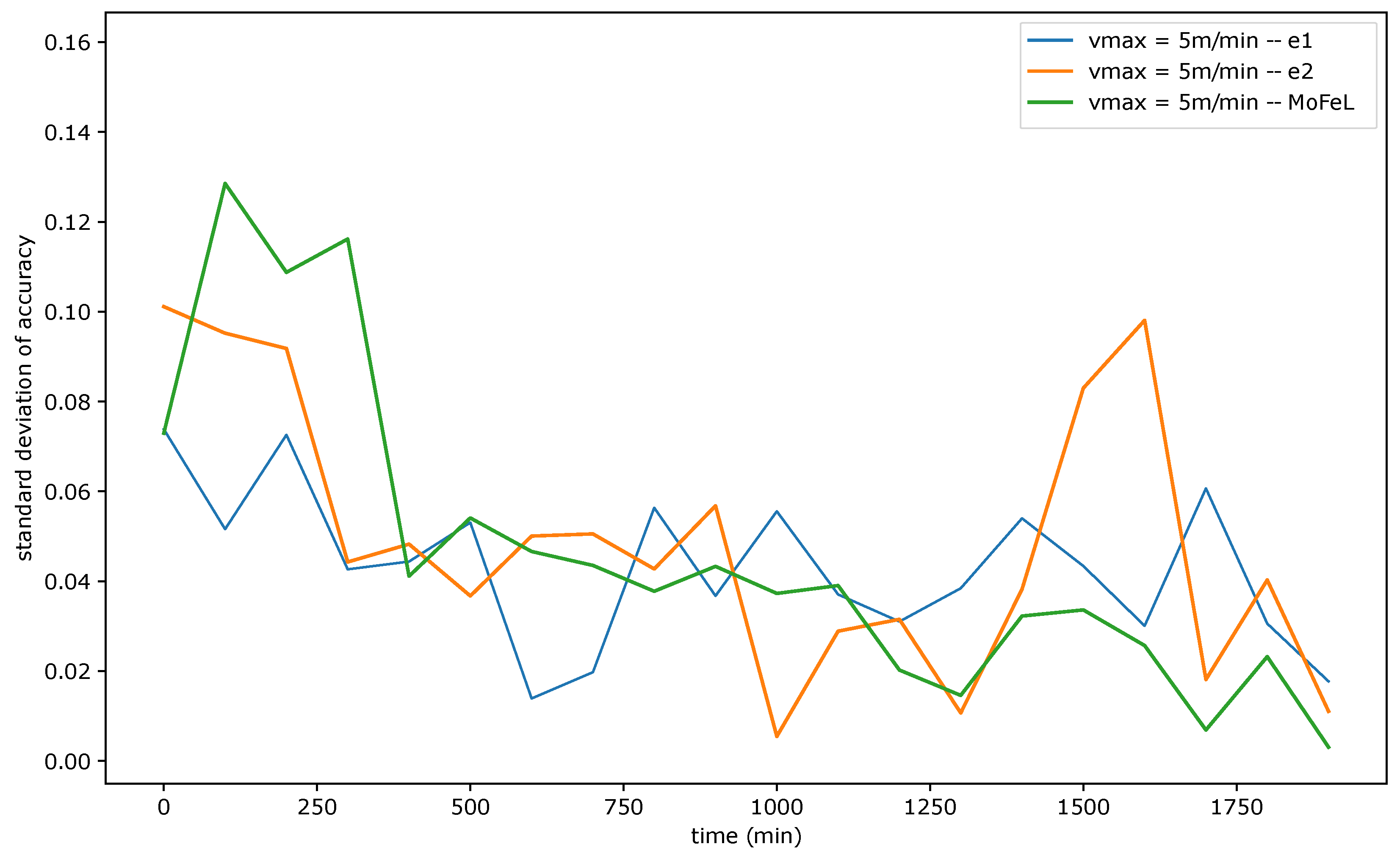
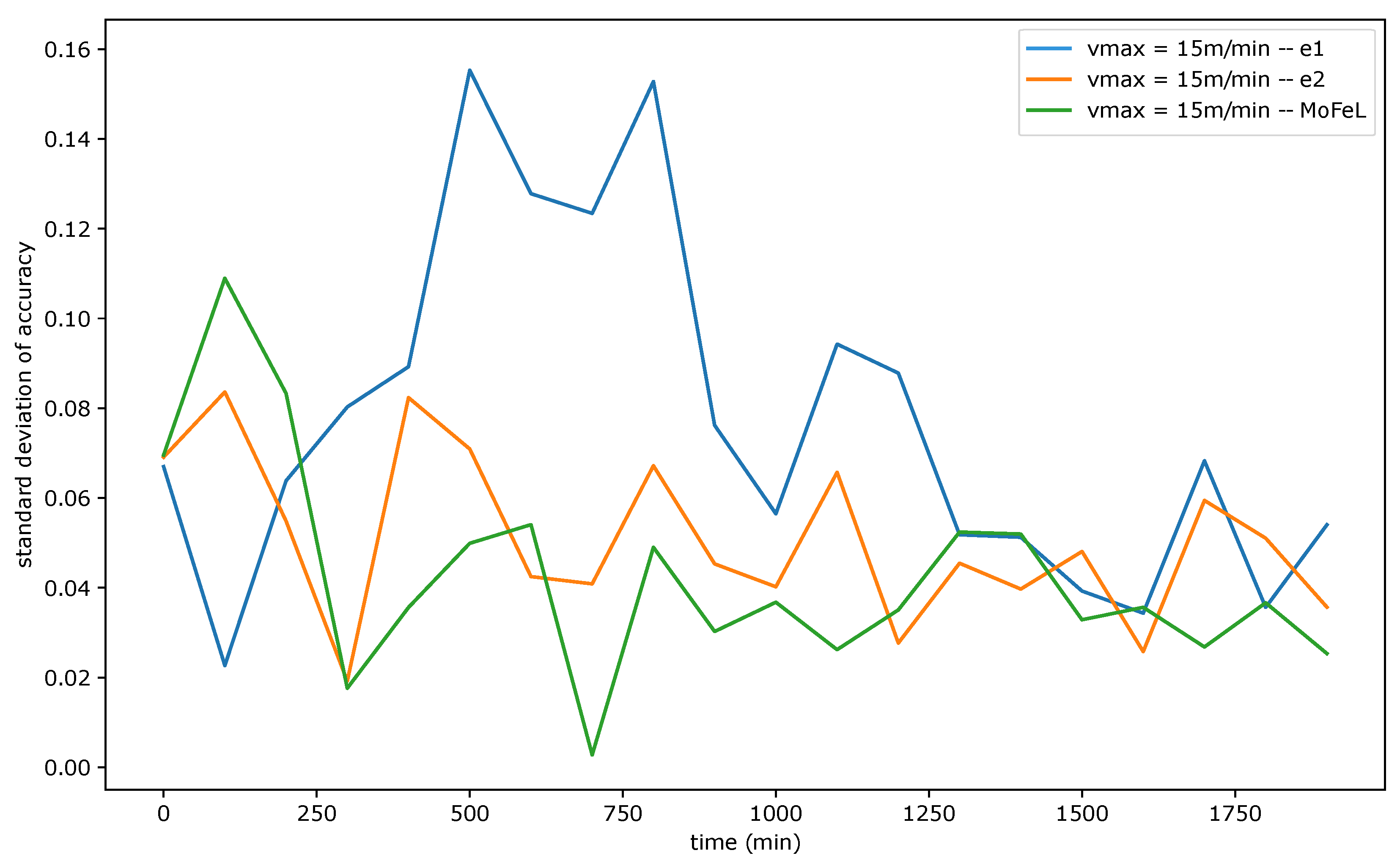
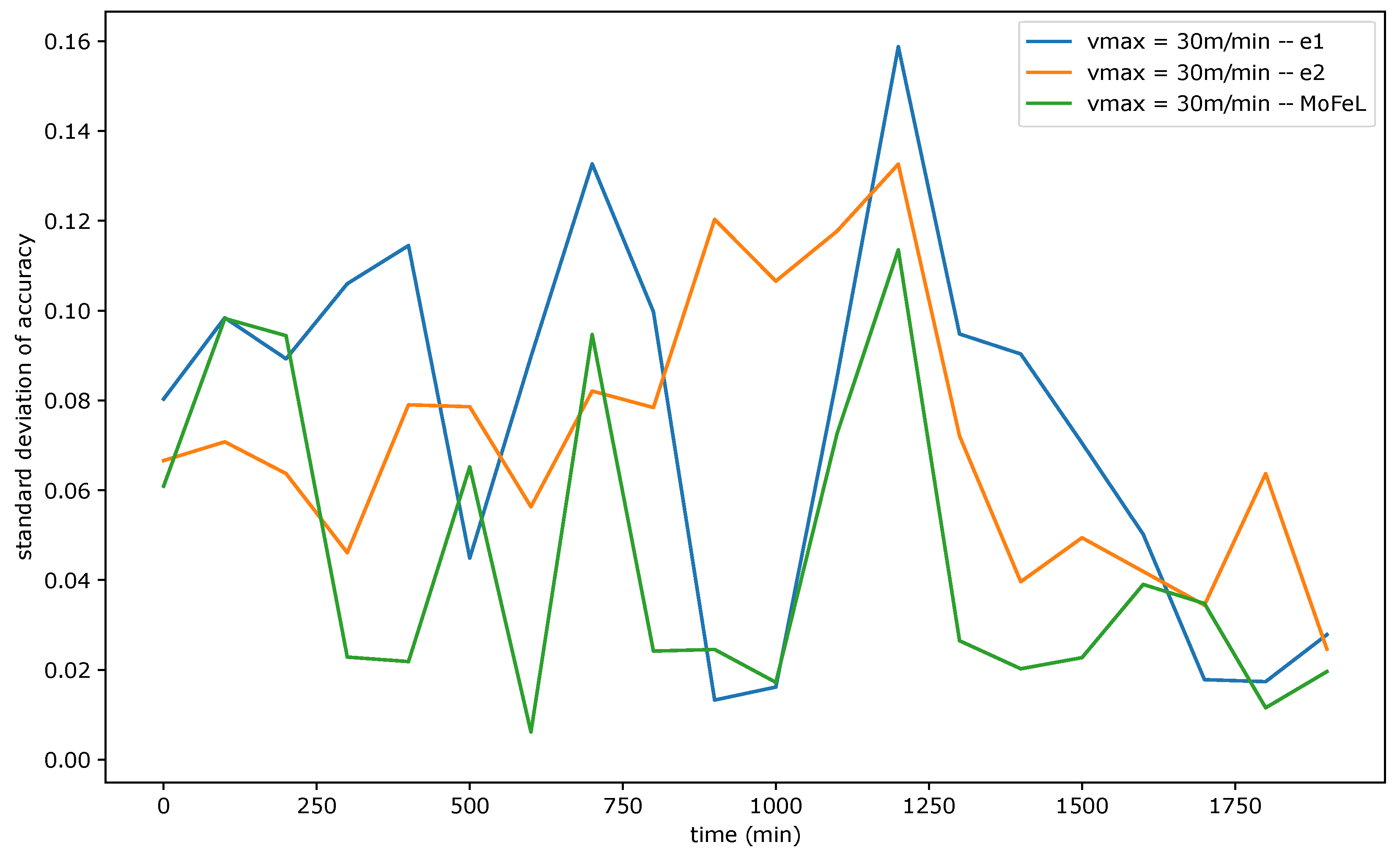
Figure 9, Figure 10 and Figure 11 show the standard deviation of training accuracy over time for each algorithm and each mobility scenario. Specifically, Figure 9 represents the scenario with = 5 m/min, Figure 10 represents the scenario with = 15 m/min, and Figure 11 represents the scenario = 30 m/min.
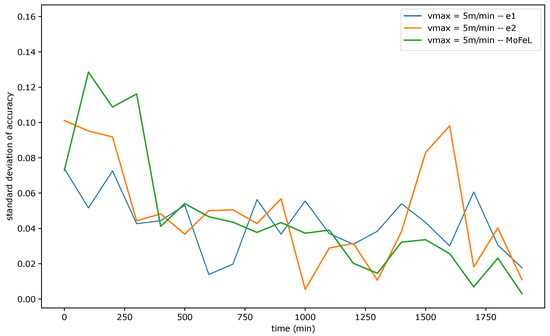
Figure 9.
Standard deviation of accuracy for = 5 m/min.
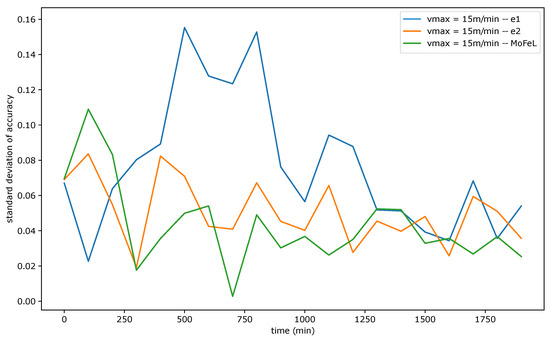
Figure 10.
Standard deviation of accuracy for = 15 m/min.
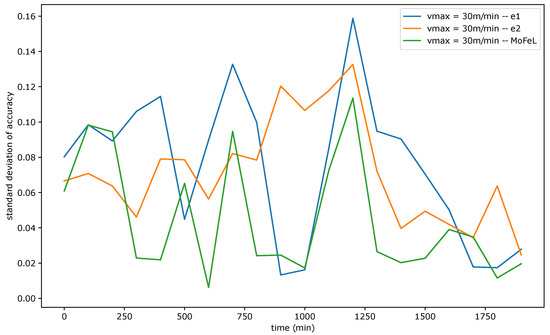
Figure 11.
Standard deviation of accuracy for = 30 m/min.
The standard deviation analysis assesses the degree of variation in training accuracy results among different models. When the standard deviation is slight, and the average accuracy is close to the application requirement, the accuracy values are tightly clustered around the average, and most central servers successfully train the global model. However, if the standard deviation is low and the mean accuracy is low, it implies that the training of most servers was not efficient.
Upon analyzing Figure 9, Figure 10 and Figure 11, it is evident that the standard deviation of MoFeL is lower than that of the other algorithms for the majority of the simulation duration. Additionally, in Figure 8, it can be observed that the average accuracy of MoFeL is higher compared to the other algorithms, indicating that the training results of MoFeL are more reliable and effective for most of the servers involved in the simulation. The standard deviation for algorithms and remained higher than that of MoFeL in most mobility scenarios, as indicated by the graphs, indicating that these algorithms favor specific central servers while hindering the training of others. Consequently, algorithms and proved inefficient for multiple edges and mobility scenarios.
In all scenarios, it is evident that during the initial stages of the simulation (from 0 min to 250 min), the MoFeL algorithm exhibits a more substantial variation in standard deviation compared to the rest of the simulation. The variation observed can be attributed to the fact that the global model of each central server is freshly trained and has undergone only a few training cycles and to the fact the central servers wait for the determined instant by the central station to execute the first training. Consequently, the accuracy of the models trained on each central server may experience more oscillations initially. However, this initial variation is eventually overcome as time advances.
Finally, all algorithms consistently exhibited similar standard deviation results across various mobility scenarios, indicating convergence. This convergence occurs because, over an extended simulation period, mobile clients capable of completing local training on each central server have already contributed to the global model definition at some point. Moreover, in the specified simulation methodology, the client database is continually expanded. Consequently, when clients train the data model locally, the older training data continues to be utilized, although its significance diminishes as the simulation progresses. This phenomenon contributes to the convergence of models, as the growing client database in the simulated scenario promotes the stabilization of local training.
The efficiency of MoFeL depends on the time interval , where , for evaluating the solution to Equation (1). A larger allows for a broader search range to find a solution, but it also delays the start of training by the central servers. Consequently, clients dissatisfied with the central server model may have already migrated, leading to inconsistencies in model retraining. Increasing also increases computational costs for solving Equation (1). Conversely, decreasing reduces computational costs but provides a smaller time window for a more suitable solution. Therefore, future work will focus on analyzing and proposing solutions to address these issues.
The solution of Equation (1) presents a challenge to implementing MoFeL due to its computational complexity. As the number of clients () or the number of central servers () increases, the feasibility of solving Equation (1) becomes impractical. Initially, this work assumes that the central station installed in the cloud can handle the client selection process, making MoFeL viable. However, alternative strategies can be employed to overcome this challenge besides relying on sufficient computing resources in the cloud:
- Adoption of optimization techniques that find viable and approximate solutions instead of seeking only the exact solution. For this, the use of techniques, such as genetic algorithms, can approximate the resolution of Equation (1);
- Analysis of mobility behavior patterns can decrease the number of calculations in route inference, as they store repetitive behaviors of clients [43].
Adopting the listed strategies can directly affect the efficiency of the FL coordination algorithm since they will bring approximate solutions to Equation (1). In this sense, the application requirements will define whether the error of the solution found is feasible or not, considering the computational gain in solving the problem.
Another disadvantage of MoFeL is the dependence on client information, such as computing resource capacity, mobility characteristics, and individual routes. Applications or clients may restrict access and disclosure of this information to the central station as privacy constraints.
Again, it is possible to evaluate strategies to bypass these barriers in the implementation of MoFel, giving up an optimal solution to find a viable solution for the requirements and constraints of the application. Some proposed strategies are
- Mobility data evaluation only from a subset of clients who are willing to collaborate with the algorithm or who are interested in application rewards [44,45];
- Approximate and infer the clients’ routes through the observatory perspective of the central server, exempting the client from providing its route with precision.
Despite the implementation’s challenges, the MoFel can serve as a benchmark for future improvements and tailoring the algorithm to meet specific application requirements.
7. Conclusions
In this work, we presented an FL algorithm named MoFeL that uses clients’ mobility data at the client selection stage to mitigate damages in the model learning process when dropouts occur during training. In MoFeL, the client selection stage is based on the computing resources available and mobility features. Unlike the other algorithms, MoFeL simultaneously evaluates different central servers, enabling all central servers to run FL in scenarios with mobility.
MoFeL’s simultaneous view of multiple central servers allows the application to impose requirements to ensure adequate training based on its criteria. For example, the mathematical model of MoFeL can be expanded to minimize the difference between the amount of training performed by each client. Furthermore, the approach of MoFeL presents a mathematical optimization model, which can be helpful as a benchmark for other solutions.
The experimental evaluation in this study showed that, in scenarios with high mobility, MoFeL had training results with better accuracy when compared to the other techniques ( and ). Furthermore, an advantage of MoFeL is the guarantee not to select unable clients. Thus, clients do not spend computational resources unnecessarily on training since they will not participate in the global model.
The implementation of the MoFeL algorithm faces challenges, particularly in dealing with the computational complexity of solving Equation 1. Thus, future research will explore the computational complexity of the MoFeL to ensure a more robust implementation. The computational analysis of MoFeL will be evaluated, and the simulation methodology will be expanded to examine the relationship between the overhead of client selection and the algorithm’s ability to meet the application requirements. Additionally, the methodology will be extended to include other databases and various ML methods to assess the impact of different models on FL in mobile scenarios.
Another challenge arises when applications require information about clients’ routes who consider these data confidential or refuse to provide it in advance. Some proposals suggest inferring clients’ mobility information solely from the perception of central servers observing their connected clients. Alternatively, offering incentives to clients who willingly share their information can also be considered. Future research will focus on studying the feasibility of these proposals and analyzing their impact on FL.
Author Contributions
Conceptualization, D.M., D.S., A.P. and D.C.G.V.; methodology, D.M., D.S. and A.P.; software, D.M.; validation, D.M., D.S. and A.P.; formal analysis, D.M., D.S. and A.P.; investigation, D.M., D.S. and A.P.; resources, D.M., D.S. and A.P.; data curation, D.M., D.S. and A.P.; writing—original draft preparation, D.M., D.S., A.P. and D.C.G.V.; writing—review and editing, D.M., D.S., A.P. and D.C.G.V.; visualization, D.M., D.S., A.P. and D.C.G.V.; supervision, D.M., D.S. and A.P.; project administration, D.M.; funding acquisition, D.S. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to Virtus Research, Development and Innovation Center (Virtus), Programa de Pós-Graduação em Engenharia Elétrica (PPGEE), Federal University of Campina Grande, and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brazil (CAPES) for supporting this research.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cui, L.; Yang, S.; Chen, F.; Ming, Z.; Lu, N.; Qin, J. A survey on application of machine learning for Internet of Things. Int. J. Mach. Learn. Cybern. 2018, 9, 1399–1417. [Google Scholar] [CrossRef]
- Zantalis, F.; Koulouras, G.; Karabetsos, S.; Kandris, D. A review of machine learning and IoT in smart transportation. Future Internet 2019, 11, 94. [Google Scholar] [CrossRef]
- Durga, S.; Nag, R.; Daniel, E. Survey on Machine Learning and Deep Learning Algorithms used in Internet of Things (IoT) Healthcare. In Proceedings of the 2019 3rd International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 27–29 March 2019; pp. 1018–1022. [Google Scholar] [CrossRef]
- Ambika, P. Chapter Thirteen-Machine learning and deep learning algorithms on the Industrial Internet of Things (IIoT). In The Digital Twin Paradigm for Smarter Systems and Environments: The Industry Use Cases; Advances in Computers; Raj, P., Evangeline, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 117, pp. 321–338. [Google Scholar] [CrossRef]
- Khan, L.U.; Saad, W.; Han, Z.; Hossain, E.; Hong, C.S. Federated Learning for Internet of Things: Recent Advances, Taxonomy, and Open Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 1759–1799. [Google Scholar] [CrossRef]
- Ramkumar, P.N.; Haeberle, H.S.; Bloomfield, M.R.; Schaffer, J.L.; Kamath, A.F.; Patterson, B.M.; Krebs, V.E. Artificial Intelligence and Arthroplasty at a Single Institution: Real-World Applications of Machine Learning to Big Data, Value-Based Care, Mobile Health, and Remote Patient Monitoring. J. Arthroplast. 2019, 34, 2204–2209. [Google Scholar] [CrossRef]
- Miotto, R.; Wang, F.; Wang, S.; Jiang, X.; Dudley, J.T. Deep learning for healthcare: Review, opportunities and challenges. Briefings Bioinform. 2017, 19, 1236–1246. [Google Scholar] [CrossRef]
- Zhang, C.; Patras, P.; Haddadi, H. Deep Learning in Mobile and Wireless Networking: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 2224–2287. [Google Scholar] [CrossRef]
- Abouelmehdi, K.; Beni-Hssane, A.; Khaloufi, H.; Saadi, M. Big data security and privacy in healthcare: A Review. Procedia Comput. Sci. 2017, 113, 73–80. [Google Scholar] [CrossRef]
- Abouelmehdi, K.; Beni-Hessane, A.; Khaloufi, H. Big healthcare data: Preserving security and privacy. J. Big Data 2018, 5, 1. [Google Scholar] [CrossRef]
- Dayan, I.; Roth, H.R.; Zhong, A.; Harouni, A.; Gentili, A.; Abidin, A.Z.; Liu, A.; Costa, A.B.; Wood, B.J.; Tsai, C.S.; et al. Federated learning for predicting clinical outcomes in patients with COVID-19. Nat. Med. 2021, 27, 1735–1743. [Google Scholar] [CrossRef]
- Balkus, S.V.; Wang, H.; Cornet, B.D.; Mahabal, C.; Ngo, H.; Fang, H. A Survey of Collaborative Machine Learning Using 5G Vehicular Communications. IEEE Commun. Surv. Tutor. 2022, 24, 1280–1303. [Google Scholar] [CrossRef]
- Ye, H.; Liang, L.; Ye Li, G.; Kim, J.; Lu, L.; Wu, M. Machine Learning for Vehicular Networks: Recent Advances and Application Examples. IEEE Veh. Technol. Mag. 2018, 13, 94–101. [Google Scholar] [CrossRef]
- Xiong, J.; Bi, R.; Tian, Y.; Liu, X.; Wu, D. Toward Lightweight, Privacy-Preserving Cooperative Object Classification for Connected Autonomous Vehicles. IEEE Internet Things J. 2022, 9, 2787–2801. [Google Scholar] [CrossRef]
- Xiong, J.; Bi, R.; Zhao, M.; Guo, J.; Yang, Q. Edge-Assisted Privacy-Preserving Raw Data Sharing Framework for Connected Autonomous Vehicles. IEEE Wirel. Commun. 2020, 27, 24–30. [Google Scholar] [CrossRef]
- Qu, Y.; Uddin, M.P.; Gan, C.; Xiang, Y.; Gao, L.; Yearwood, J. Blockchain-enabled federated learning: A survey. ACM Comput. Surv. 2022, 55, 1–35. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, W.; Han, Q.; Cai, Z. Privacy-Preserving Auto-Driving: A GAN-Based Approach to Protect Vehicular Camera Data. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 668–677. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Vincent Poor, H. Federated Learning for Internet of Things: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 1622–1658. [Google Scholar] [CrossRef]
- Lim, W.Y.B.; Luong, N.C.; Hoang, D.T.; Jiao, Y.; Liang, Y.C.; Yang, Q.; Niyato, D.; Miao, C. Federated learning in mobile edge networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 2031–2063. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Yu, R.; Li, P. Toward Resource-Efficient Federated Learning in Mobile Edge Computing. IEEE Netw. 2021, 35, 148–155. [Google Scholar] [CrossRef]
- Islam, M.; Reza, M.; Kaosar, M.; Parvez, M.Z. Effectiveness of Federated Learning and CNN Ensemble Architectures for Identifying Brain Tumors Using MRI Images. Neural Process. Lett. 2022, 1–31. [Google Scholar] [CrossRef]
- Dietterich, T. Overfitting and undercomputing in machine learning. ACM Comput. Surv. (CSUR) 1995, 27, 326–327. [Google Scholar] [CrossRef]
- Yang, T.; Andrew, G.; Eichner, H.; Sun, H.; Li, W.; Kong, N.; Ramage, D.; Beaufays, F. Applied Federated Learning: Improving Google Keyboard Query Suggestions. arXiv 2018, arXiv:1812.02903. [Google Scholar]
- Macedo, D.; Santos, D.; Perkusich, A.; Valadares, D. A mobility-aware federated learning coordination algorithm. J. Supercomput. 2023, 1–15. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.; Zhou, P.; Wu, W.; Zhang, X. Client Selection for Federated Learning with Non-IID Data in Mobile Edge Computing. IEEE Access 2021, 9, 24462–24474. [Google Scholar] [CrossRef]
- Nishio, T.; Yonetani, R. Client selection for federated learning with heterogeneous resources in mobile edge. In Proceedings of the ICC 2019–2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar]
- Wang, G.; Xu, F.; Zhang, H.; Zhao, C. Joint resource management for mobility supported federated learning in Internet of Vehicles. Future Gener. Comput. Syst. 2022, 129, 199–211. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Luo, Y. A federated learning-based edge caching approach for mobile edge computing-enabled intelligent connected vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 24, 3360–3369. [Google Scholar] [CrossRef]
- Xiao, H.; Zhao, J.; Pei, Q.; Feng, J.; Liu, L.; Shi, W. Vehicle Selection and Resource Optimization for Federated Learning in Vehicular Edge Computing. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11073–11087. [Google Scholar] [CrossRef]
- Deveaux, D.; Higuchi, T.; Uçar, S.; Wang, C.H.; Härri, J.; Altintas, O. On the Orchestration of Federated Learning through Vehicular Knowledge Networking. In Proceedings of the 2020 IEEE Vehicular Networking Conference (VNC), New York, NY, USA, 16–18 December 2020; pp. 1–8. [Google Scholar]
- Feng, C.; Yang, H.H.; Hu, D.; Zhao, Z.; Quek, T.Q.S.; Min, G. Mobility-Aware Cluster Federated Learning in Hierarchical Wireless Networks. IEEE Trans. Wirel. Commun. 2022, 21, 8441–8458. [Google Scholar] [CrossRef]
- Bonawitz, K.; Eichner, H.; Grieskamp, W.; Huba, D.; Ingerman, A.; Ivanov, V.; Kiddon, C.; Konečnỳ, J.; Mazzocchi, S.; McMahan, H.B.; et al. Towards federated learning at scale: System design. arXiv 2019, arXiv:1902.01046. [Google Scholar]
- Murray, B.; Perera, L.P. An AIS-based deep learning framework for regional ship behavior prediction. Reliab. Eng. Syst. Saf. 2021, 215, 107819. [Google Scholar] [CrossRef]
- Bedriñana-Romano, L.; Hucke-Gaete, R.; Viddi, F.A.; Johnson, D.; Zerbini, A.N.; Morales, J.; Mate, B.; Palacios, D.M. Defining priority areas for blue whale conservation and investigating overlap with vessel traffic in Chilean Patagonia, using a fast-fitting movement model. Sci. Rep. 2021, 11, 2709. [Google Scholar] [CrossRef]
- Womersley, F.C.; Humphries, N.E.; Queiroz, N.; Vedor, M.; da Costa, I.; Furtado, M.; Tyminski, J.P.; Abrantes, K.; Araujo, G.; Bach, S.S.; et al. Global collision-risk hotspots of marine traffic and the world’s largest fish, the whale shark. Proc. Natl. Acad. Sci. USA 2022, 119, e2117440119. [Google Scholar] [CrossRef]
- Kalidas, A.P.; Joshua, C.J.; Md, A.Q.; Basheer, S.; Mohan, S.; Sakri, S. Deep Reinforcement Learning for Vision-Based Navigation of UAVs in Avoiding Stationary and Mobile Obstacles. Drones 2023, 7, 245. [Google Scholar] [CrossRef]
- Xu, C.; Qu, Y.; Luan, T.H.; Eklund, P.W.; Xiang, Y.; Gao, L. An Efficient and Reliable Asynchronous Federated Learning Scheme for Smart Public Transportation. IEEE Trans. Veh. Technol. 2023, 72, 6584–6598. [Google Scholar] [CrossRef]
- Zhang, J.M.; Harman, M.; Ma, L.; Liu, Y. Machine Learning Testing: Survey, Landscapes and Horizons. IEEE Trans. Softw. Eng. 2022, 48, 1–36. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Deng, L. The mnist database of handwritten digit images for machine learning research. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Dhar, S.; Shamir, L. Evaluation of the benchmark datasets for testing the efficacy of deep convolutional neural networks. Vis. Inform. 2021, 5, 92–101. [Google Scholar] [CrossRef]
- Zhao, M.; Li, J.; Tang, F.; Asif, S.; Zhu, Y. Learning Based Massive Data Offloading in the IoV: Routing Based on Pre-RLGA. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2330–2340. [Google Scholar] [CrossRef]
- Zhan, Y.; Li, P.; Guo, S.; Qu, Z. Incentive Mechanism Design for Federated Learning: Challenges and Opportunities. IEEE Netw. 2021, 35, 310–317. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhang, J.; Hong, Z.; Wu, L.; Li, P.; Guo, S. A Survey of Incentive Mechanism Design for Federated Learning. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1035–1044. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).