Hierarchical Network-Based Tracklets Data Association for Multiple Extended Target Tracking with Intermittent Measurements
Abstract
:1. Introduction
2. Problem Formulations
3. Hierarchical Network-Based Data Association for Multiple Extended Target Tracking
3.1. Pre-Processing
3.2. Hierarchical Association
- a.
- Low-level association network
- b.
- High-level association network
3.3. Trajectory Smoothness
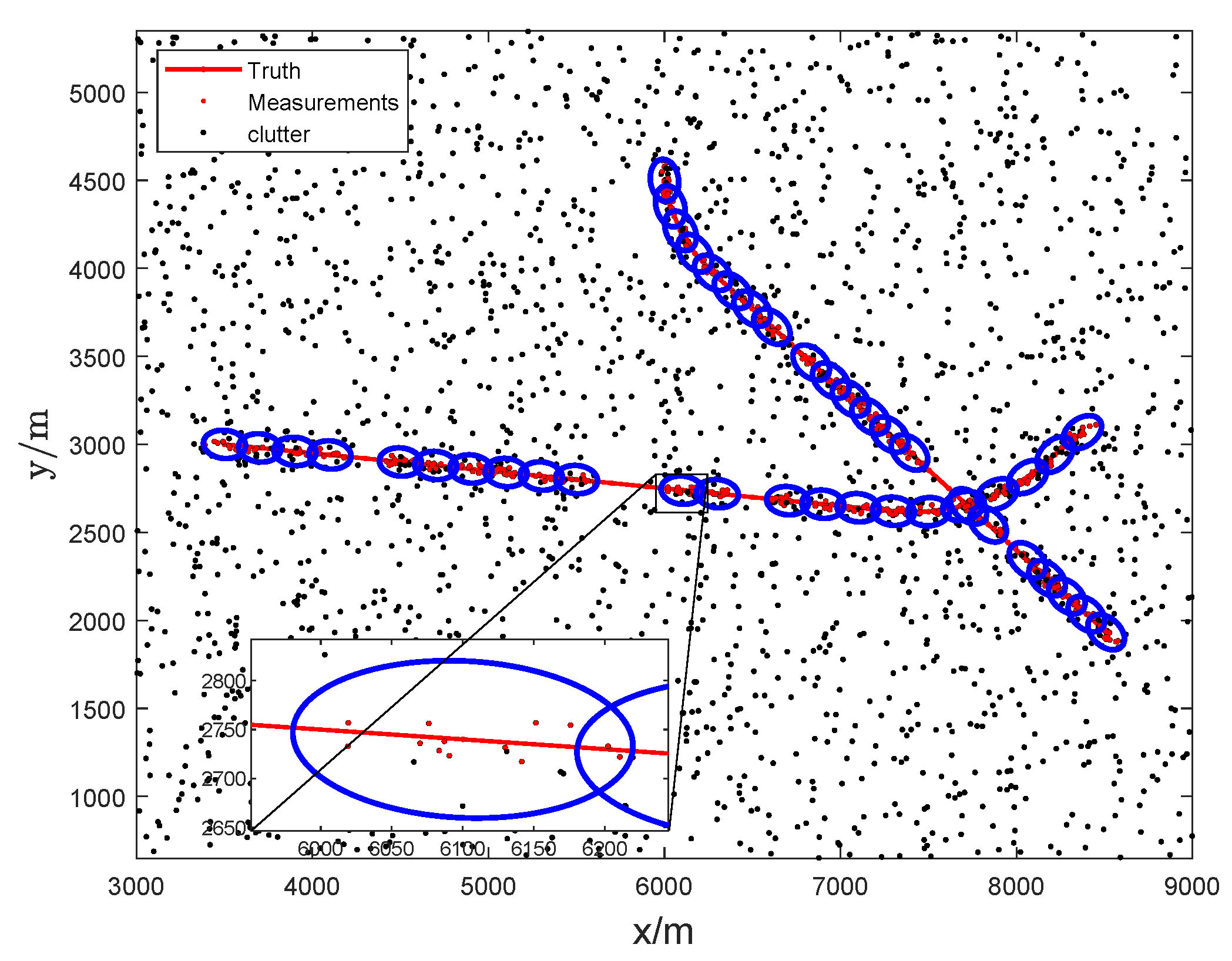
4. Numerical Simulation and Experiments
4.1. Case 1: Numerical Simulation
4.2. Time Complexity
4.3. Case 2: Real Data Verification
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahler, R.P.S. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2014; Volume 10, pp. 142–149. [Google Scholar]
- Lan, J.; Li, X.R. Tracking of extended object or target group using random matrix: New model and approach. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2973–2989. [Google Scholar] [CrossRef]
- Stateczny, A.; Kazimierski, W. Multisensor Tracking of Marine Targets—Decentralized Fusion of Kalman and Neural Filters. Int. J. Electron. Telecommun. 2011, 57, 65–70. [Google Scholar] [CrossRef]
- Morelande, M.R.; Kreucher, C.M.; Kastella, K. A Bayesian Approach to Multiple Target Detection and Tracking. IEEE Trans. Signal Process. 2007, 55, 1589–1604. [Google Scholar] [CrossRef]
- Vivone, G.; Braca, P. Joint Probabilistic Data Association Tracker for Extended Target Tracking Applied to X-Band Marine Radar Data. IEEE J. Ocean. Eng. 2016, 41, 1007–1019. [Google Scholar] [CrossRef]
- Habtemariam, B.; Tharmarasa, R.; Thayaparan, T. A Multiple-Detection Joint Probabilistic Data Association Filter. IEEE J. Sel. Top. Signal Process. 2013, 7, 461–471. [Google Scholar] [CrossRef]
- Schuster, M.; Reuter, J.; Wanielik, G. Multi- detection joint integrated probabilistic data association using random matrices with applications to radar-based multi object tracking. IEEE J. Adv. Inf. Fusion 2013, 12, 175–188. [Google Scholar]
- Xie, Y.; Huang, Y.; Song, T.L. Iterative joint integrated probabilistic data association filter for multiple-detection multiple-target tracking. Digit. Signal Process. 2018, 72, 232–243. [Google Scholar] [CrossRef]
- Yang, S.; Wolf, L.M.; Baum, M. Marginal Association Probabilities for Multiple Extended Objects without Enumeration of Measurement Partitions. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion, Rustenburg, South Africa, 6–9 July 2020; pp. 1–8. [Google Scholar]
- Li, P.; Ge, H.W.; Yang, J.L.; Wang, W. Modified Gaussian inverse Wishart PHD filter for tracking multiple non-ellipsoidal extended targets. Signal Process. 2018, 150, 191–203. [Google Scholar] [CrossRef]
- Peng, M.S.; Linares, R.; Bageshwar, V.L. Extended Target Tracking and Shape Estimation via Random Finite Sets. In Proceedings of the 2019 American Control Conference, Milwaukee, WI, USA, 10–12 July 2019; Volume 72, pp. 232–243. [Google Scholar]
- Zhibin, Z.; Liping, S.; Xuan, C. Labeled box-particle CPHD filter for multiple extended targets tracking. J. Syst. Eng. Electron. 2019, 30, 57–67. [Google Scholar]
- Liang, Z.; Liu, F.; Li, L. Improved generalized labeled multi-Bernoulli filter for non-ellipsoidal extended targets or group targets tracking based on random sub-matrices. Digit. Signal Process. 2020, 99, 102669–102682. [Google Scholar] [CrossRef]
- Granstrom, K.; Svensson, L.; Reuter, S.; Xia, Y.; Fatemi, M. Likelihood-Based Data Association for Extended Object Tracking Using Sampling Methods. IEEE Trans. Intell. Veh. 2018, 3, 30–45. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, L.; Xu, M.; Wang, Y. An improved probability hypothesis density filter for multi-target tracking. Optik 2019, 182, 23–31. [Google Scholar] [CrossRef]
- Su, Z.Z.; Ji, H.B.; Zhang, Y. Data association for extended target tracking by BP. IET Radar Sonar Navig. 2018, 12, 1484–1492. [Google Scholar] [CrossRef]
- Su, Z.Z.; Ji, H.B.; Zhang, Y. Loopy belief propagation based data association for extended target tracking. Chin. J. Aeronaut. 2020, 33, 2212–2223. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, S.; Wen, C.; Yu, Y. Structure modeling and estimation of multiple resolvable group targets via graph theory and multi-Bernoulli filter. Automatica 2018, 89, 274–289. [Google Scholar] [CrossRef]
- Yazdian, D.M.; Azimifar, Z. An improvement on GM-PHD filter for target tracking in presence of subsequent miss-detection. In Proceedings of the 2015 23rd Iranian Conference on Electrical Engineering, Tehran, Iran, 10–14 May 2015. [Google Scholar]
- Ma, T.L.; Wang, X.M.; Li, T. Multiple-model multiple hypothesis probability hypothesis density filter with blind zone. Int. J. Ind. Syst. Eng. 2017, 27, 180–195. [Google Scholar] [CrossRef]
- Wu, W.; Sun, H.; Cai, Y.; Jiang, S.; Xiong, J. Tracking multiple maneuvering targets hidden in the DBZ based on the MM-GLMB filter. IEEE Trans. Signal Process. 2020, 68, 2912–2924. [Google Scholar] [CrossRef]
- Yang, S.; Teich, F.; Baum, M. Network flow labeling for extended target tracking PHD filters. IEEE Trans. Ind. Inform. 2019, 15, 4164–4171. [Google Scholar] [CrossRef]
- You, K.Y.; Fu, M.Y.; Xie, L.H. Mean Square Stability for Kalman Filtering with Markovian Packet Losses. Automatica 2011, 47, 1247–1257. [Google Scholar] [CrossRef]
- Liu, Z.; Ji, L.; Yang, F.; Qu, X.; Yang, Z.; Qin, D. Cubature information Gaussian mixture probability hypothesis density approach for multi extended target tracking. IEEE Access 2019, 7, 103678–103692. [Google Scholar] [CrossRef]
- Guo, P.; Liu, Z.; Wang, J.J. HRRP multi-target recognition in a beam using prior-independent DBSCAN clustering algorithm. IET Radar Sonar Navig. 2019, 13, 1366–1372. [Google Scholar] [CrossRef]
- Xi, Z.; Liu, H. Multiple Object Tracking Using the Shortest Path Faster Association Algorithm. Sci. World J. 2014, 2014, 481719–481730. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; He, Z. An in-coordinate interval adaptive Kalman filtering algorithm for INS/GPS/SMNS. In Proceedings of the IEEE 10th International Conference on Industrial Informatics, Beijing, China, 25–27 July 2012; pp. 41–44. [Google Scholar]
- Aravkin, A.; Burke, J.; Ljung, L.; Lozano, A.; Pillonetto, G. Generalized Kalman smoothing: Modeling and algorithms. Automatica 2017, 86, 63–86. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, H.; Liu, Y.; Wang, X. Collaborative penalized Gaussian mixture PHD tracker for close target tracking. Signal Process. 2014, 102, 1–15. [Google Scholar] [CrossRef]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- Ma, T.; Gao, S.; Chen, C.; Song, X. Multitarget Tracking Algorithm Based on Adaptive Network Graph Segmentation in the Presence of Measurement Origin Uncertainty. Sensors 2018, 18, 3791. [Google Scholar] [CrossRef] [PubMed]
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1627–1645. [Google Scholar] [CrossRef]









| Filter | ET-HT | ET-PHD | ET-PMBM | ET-JPDA | ET-NFPHD |
|---|---|---|---|---|---|
| Time (t/s) | 10.1369 | 2232.9 | 96.3917 | 1.1254 | 411.9493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, K.; Li, Y.; Ma, T.; Li, L. Hierarchical Network-Based Tracklets Data Association for Multiple Extended Target Tracking with Intermittent Measurements. Sensors 2023, 23, 6372. https://doi.org/10.3390/s23146372
Jiang K, Li Y, Ma T, Li L. Hierarchical Network-Based Tracklets Data Association for Multiple Extended Target Tracking with Intermittent Measurements. Sensors. 2023; 23(14):6372. https://doi.org/10.3390/s23146372
Chicago/Turabian StyleJiang, Kaiyi, Yiguo Li, Tianli Ma, and Lin Li. 2023. "Hierarchical Network-Based Tracklets Data Association for Multiple Extended Target Tracking with Intermittent Measurements" Sensors 23, no. 14: 6372. https://doi.org/10.3390/s23146372






