Inner-Frame Time Division Multiplexing Waveform Design of Integrated Sensing and Communication in 5G NR System
Abstract
:1. Introduction
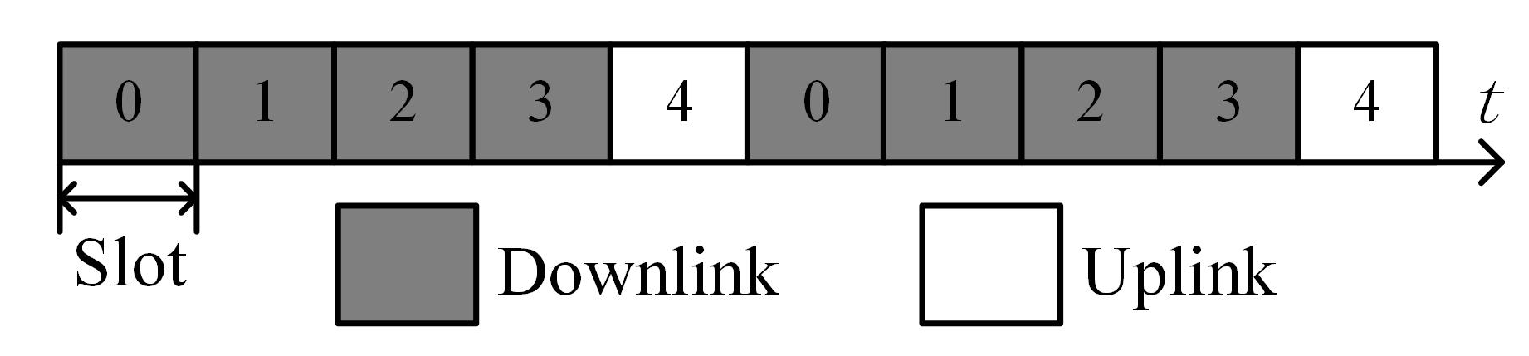
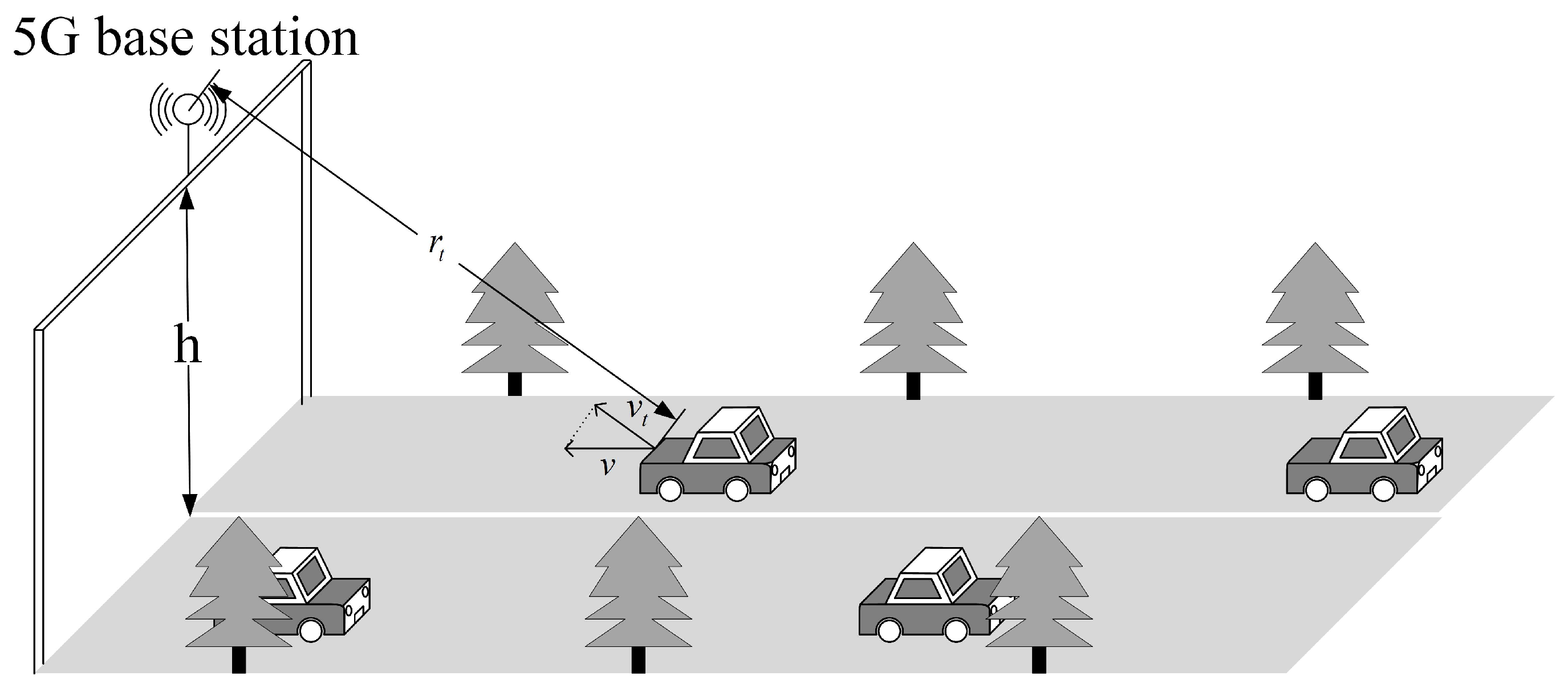
2. Signal Model in the 5G NR System
3. Proposed Sensing Waveform
3.1. Proposed Waveform Design Strategy
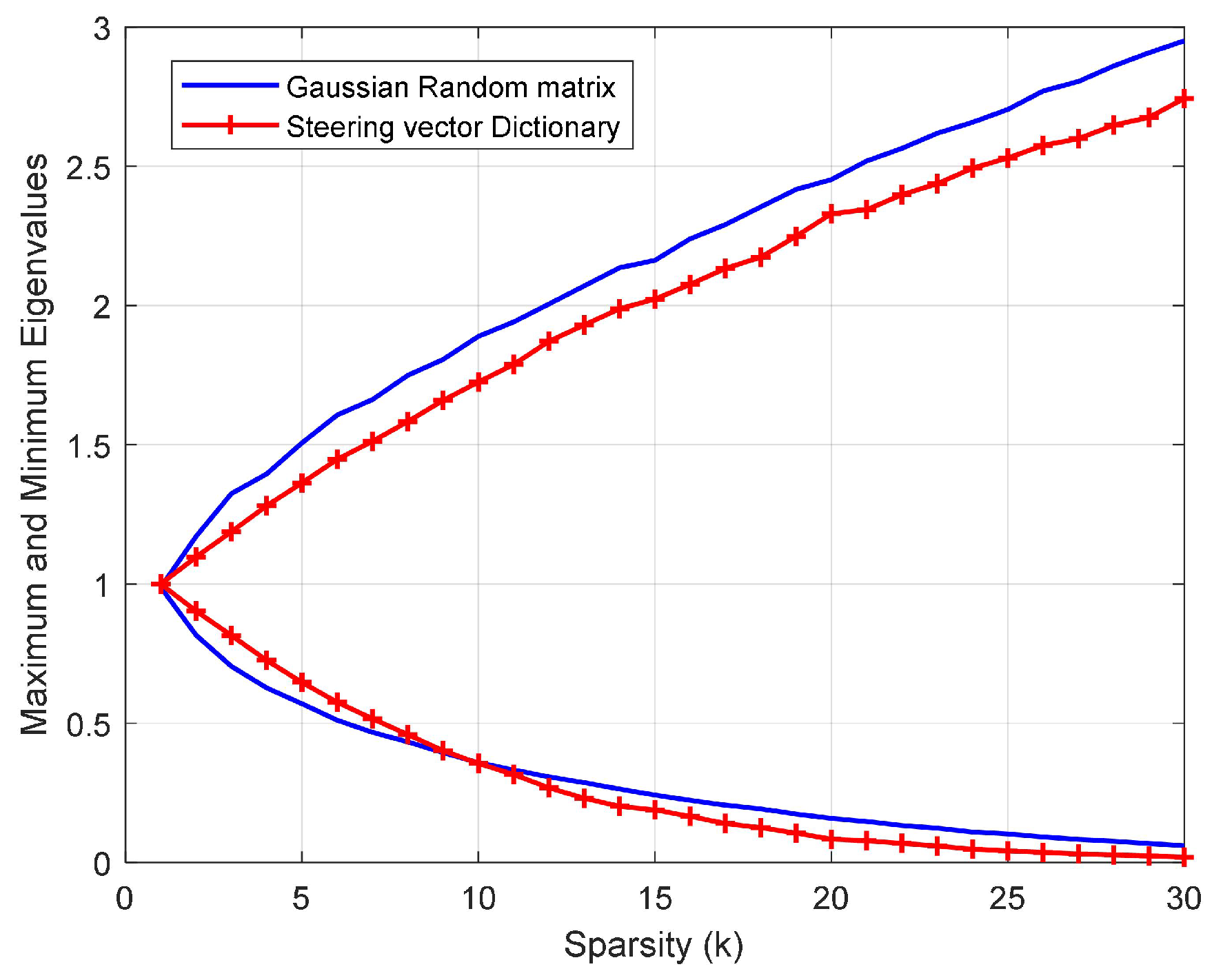
3.2. Waveform Solution Based on the Simulated Annealing Algorithm
| Algorithm 1 The simulated annealing algorithm. |
Initialization: Generate a randomly according to (10) to obtain ; ; Repeat: Generate a new according to (9), and to obtain ; ; If Then , ; Else Accept and with a probability ; ; Until ; Output: ; |
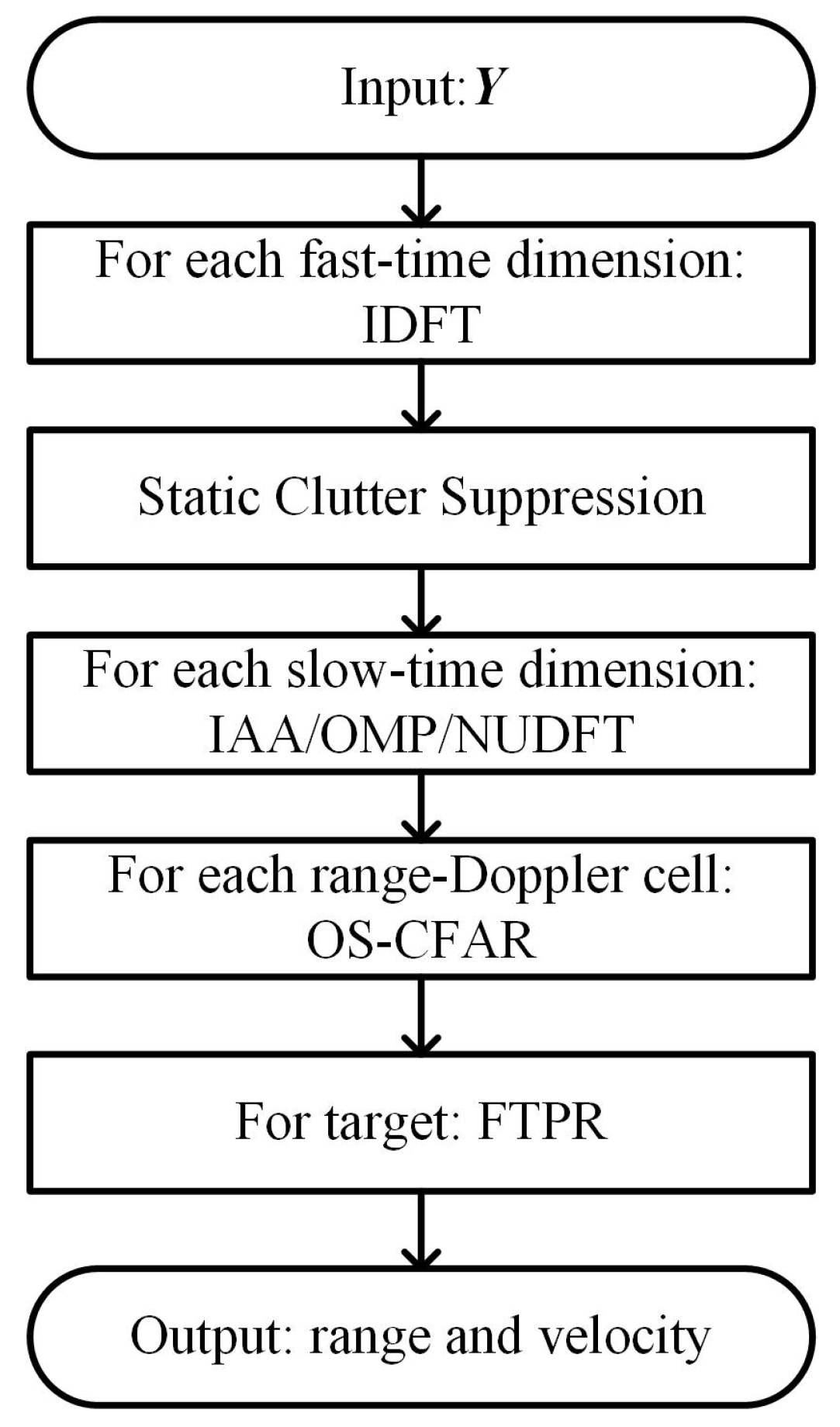
3.3. Signal Detection and Estimation
| Algorithm 2 The IAA algorithm. |
Initialization: , IAA covariance matrix , , . Repeat: , For , , End Until a certain number of iterations is reached. Output: . |
| Algorithm 3 The OMP algorithm. |
Initialization: , , , Residual vector , Stopping parameter , Selected index subset . While , , , , Update the residual vector , , End Compute the Doppler profile . |
4. Numerical Examples
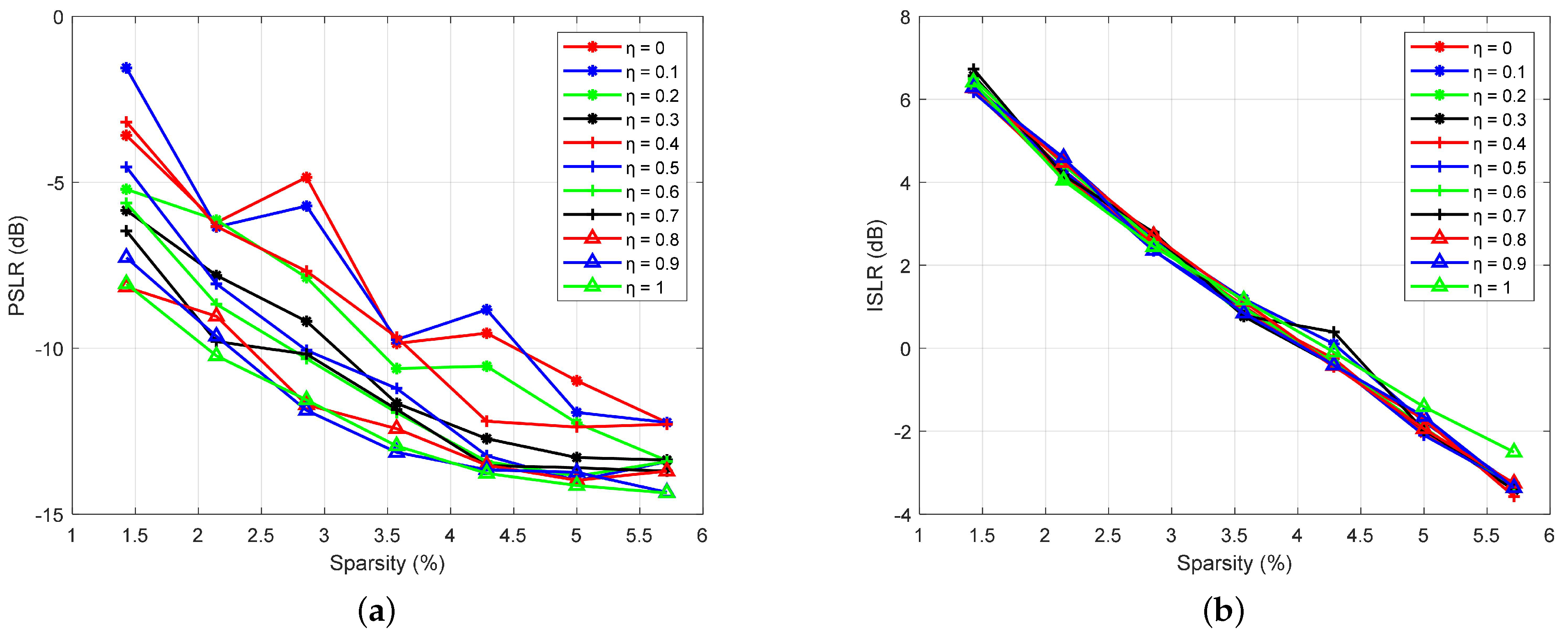
4.1. Waveform Parameters Impacts
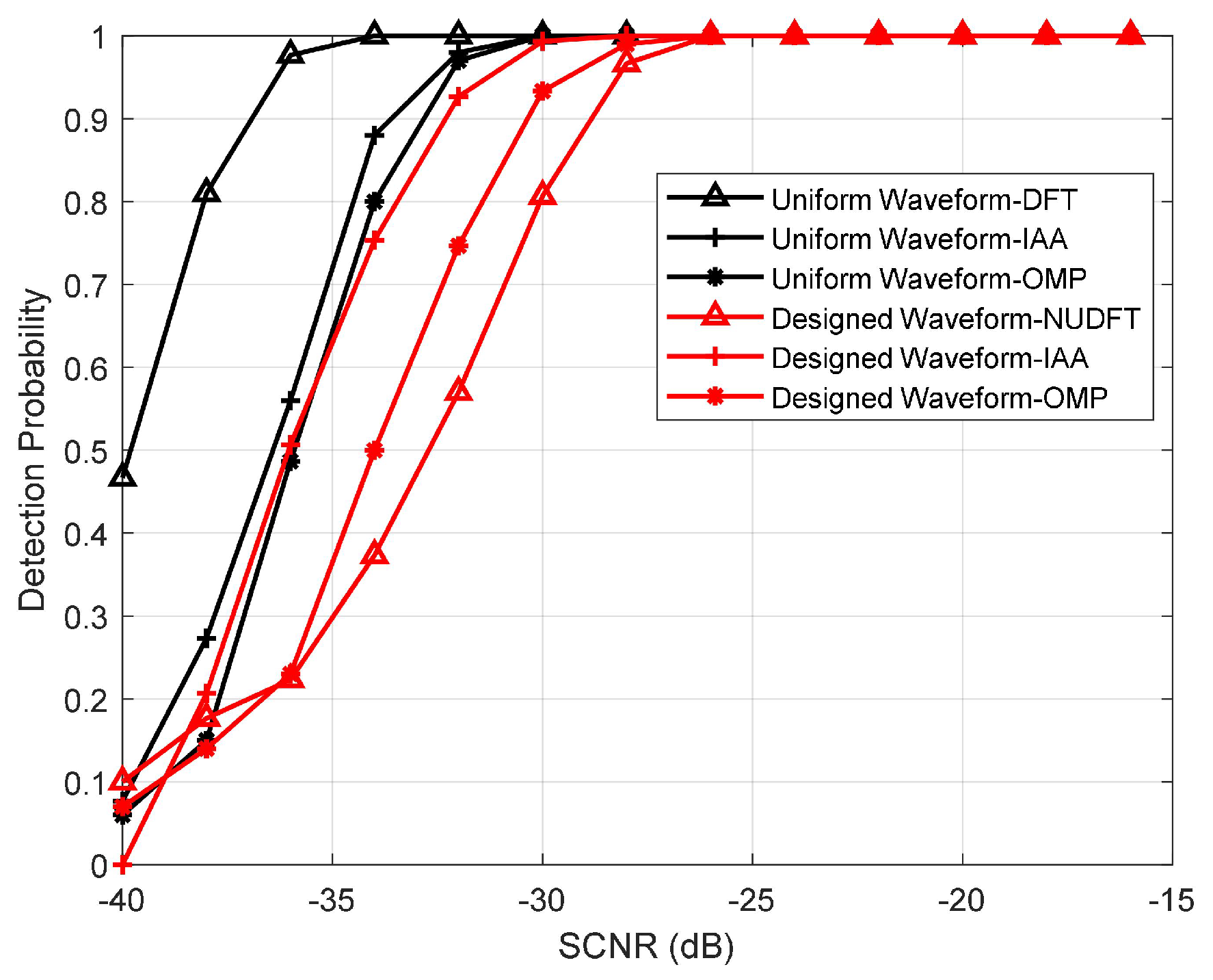
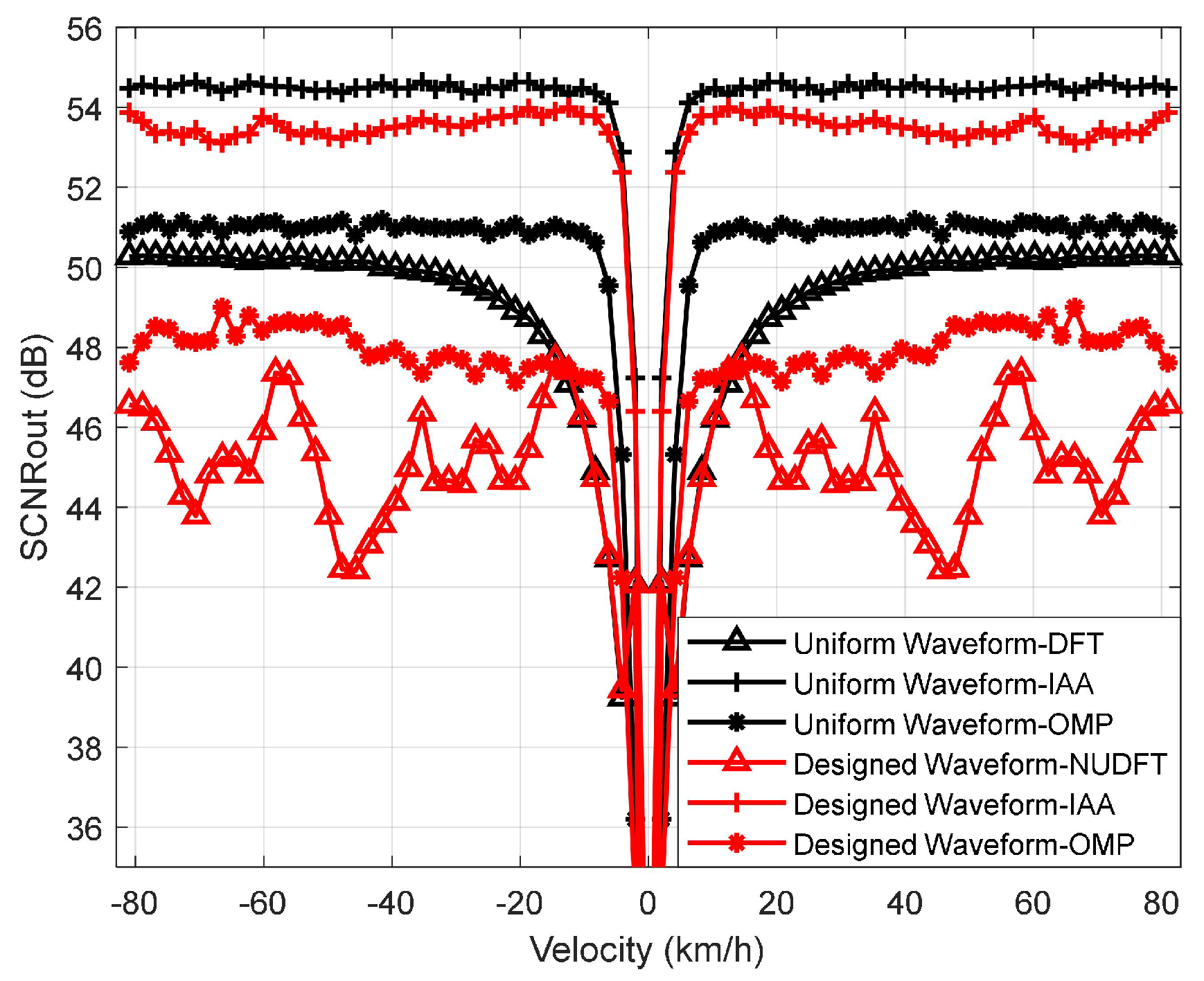
4.2. Detection Performance
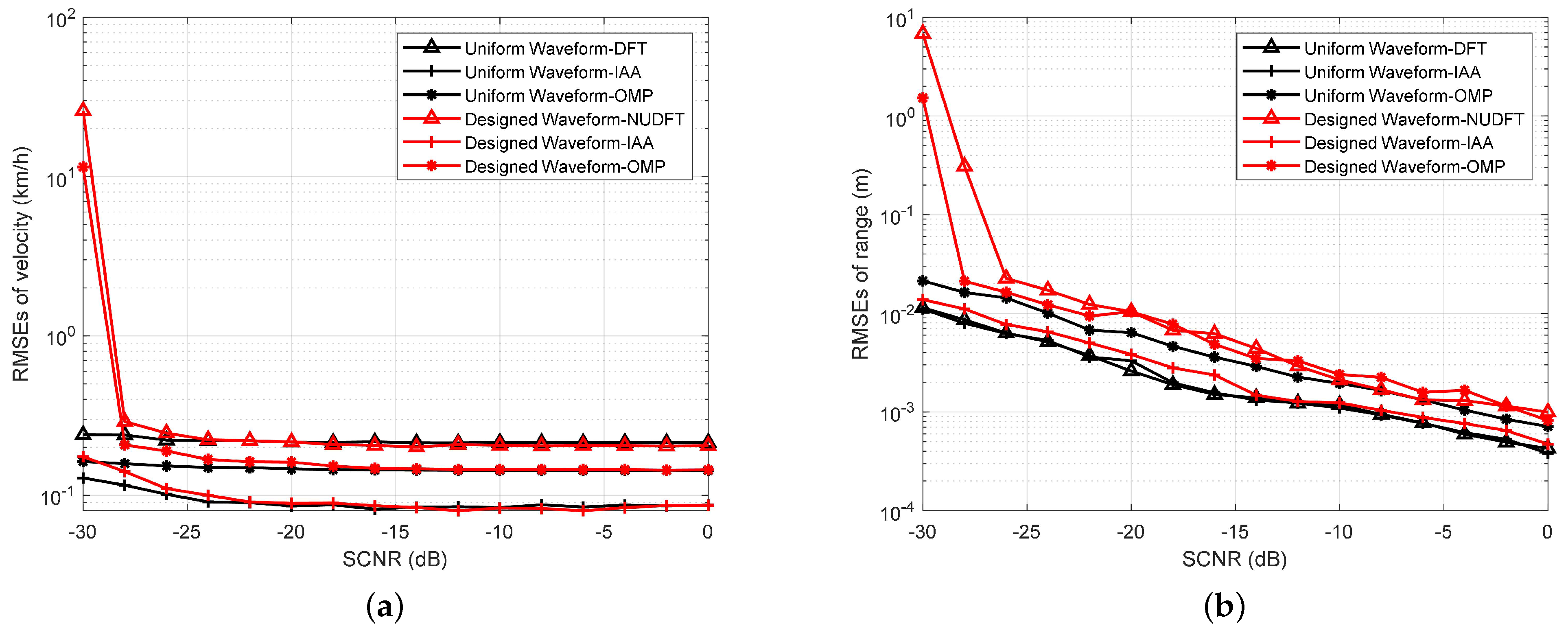
4.3. Estimation Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, B.; Liu, Y.; Huo, K.; Zhao, J.; Zhang, Z. OFDM integration waveform design for radar and communication application. In Proceedings of the International Conference on Radar Systems, Belfast, UK, 23–26 October 2017; pp. 1–5. [Google Scholar]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated sensing and communications: Towards dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar]
- Wei, Z.; Wang, Y.; Ma, L.; Yang, S.; Feng, Z.; Pan, C.; Zhang, Q.; Wang, Y.; Wu, H.; Zhang, P. 5G PRS-based sensing: A sensing reference signal approach for joint sensing and communication system. IEEE Trans. Veh. Technol. 2023, 72, 3250–3263. [Google Scholar] [CrossRef]
- Cui, Y.; Jing, X.; Mu, J. Integrated sensing and communications via 5G NR waveform: Performance analysis. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 23–27 May 2022; pp. 8747–8751. [Google Scholar]
- Cui, Y.; Liu, F.; Jing, X.; Mu, J. Integrating sensing and communications for ubiquitous IoT: Applications, trends, and challenges. IEEE Netw. 2021, 35, 158–167. [Google Scholar] [CrossRef]
- Han, L.; Wu, K. Multifunctional transceiver for future intelligent transportation systems. IEEE Trans. Microw. Theory Tech. 2011, 59, 1879–1892. [Google Scholar] [CrossRef]
- Moghaddasi, J.; Wu, K. Multifunctional transceiver for future radar sensing and radio communicating data-fusion platform. IEEE Access 2016, 4, 818–838. [Google Scholar] [CrossRef]
- Huang, T.; Shlezinger, N.; Xu, X.; Liu, Y.; Eldar, Y.C. MAJoRCom: A dual-function radar communication system using index modulation. IEEE Trans. Signal Process. 2020, 68, 3423–3438. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, J.A.; Huang, X.; Guo, Y.J.; Heath, R.W. Waveform design and accurate channel estimation for frequency-hopping MIMO radar-based communications. IEEE Trans. Commun. 2021, 69, 1244–1258. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar] [CrossRef]
- Xu, S.; Chen, B.; Zhang, P. Radar-communication integration based on DSSS techniques. In Proceedings of the 8th International Conference on Signal Processing, Guilin, China, 16–20 November 2006; pp. 2872–2875. [Google Scholar]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Signaling strategies for dual-function radar communications: An overview. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 36–45. [Google Scholar] [CrossRef]
- Zhang, J.A.; Liu, F.; Masouros, C.; Heath, R.W.; Feng, Z.; Zheng, L.; Petropulu, A. An overview of signal processing techniques for joint communication and radar sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1295–1315. [Google Scholar] [CrossRef]
- Mealey, R.M. A method for calculating error probabilities in a radar communication system. IEEE Trans. Space Electron. Telem. 1963, 9, 37–42. [Google Scholar] [CrossRef]
- Cook, C.E. Linear FM signal formats for beacon and communication systems. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 471–478. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Xu, S.; Zhang, J. A novel radar waveform compatible with communication. In Proceedings of the 2011 International Conference on Computational Problem-Solving, Chengdu, China, 21–23 October 2011; pp. 177–181. [Google Scholar]
- Barrenechea, P.; Elferink, F.; Janssen, J. FMCW radar with broadband communication capability. In Proceedings of the 2007 European Radar Conference, Munich, Germany, 10–12 October 2007; pp. 130–133. [Google Scholar]
- Liu, Y.; Liao, G.; Chen, Y.; Xu, J.; Yin, Y. Super-resolution range and velocity estimations with OFDM integrated radar and communications waveform. IEEE Trans. Veh. Technol. 2020, 69, 11659–11672. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Yang, Z. Robust OFDM integrated radar and communications waveform design based on information theory. Signal Process. 2019, 162, 317–329. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Du, Z.; Yu, W. Mutual-information-based OFDM waveform design for integrated radar-communication system in Gaussian mixture clutter. IEEE Sens. Lett. 2020, 4, 7000204. [Google Scholar] [CrossRef]
- Ahmed, A.; Zhang, Y.D.; Hassanien, A. Joint radar-communications exploiting optimized OFDM waveforms. Remote Sens. 2021, 13, 4376. [Google Scholar] [CrossRef]
- Keskin, M.F.; Koivunen, V.; Wymeersch, H. Limited feedforward waveform design for OFDM dual-functional radar-communications. IEEE Trans. Signal Process. 2021, 69, 2955–2970. [Google Scholar] [CrossRef]
- Ozkaptan, C.D.; Ekici, E.; Altintas, O. Adaptive waveform design for communication-enabled automotive radars. IEEE Trans. Wirel. Commun. 2022, 21, 3965–3978. [Google Scholar] [CrossRef]
- Temiz, M.; Alsusa, E.; Baidas, M.W. Optimized precoders for massive MIMO OFDM dual radar-communication systems. IEEE Trans. Commun. 2021, 69, 4781–4794. [Google Scholar] [CrossRef]
- Xu, Z.; Petropulu, A. A bandwidth efficient dual-function radar communication system based on a MIMO radar using OFDM waveforms. IEEE Trans. Signal Process. 2023, 71, 401–416. [Google Scholar] [CrossRef]
- Wu, Y.; Lemic, F.; Han, C.; Chen, Z. Sensing integrated DFT-spread OFDM waveform and deep learning-powered receiver design for terahertz integrated sensing and communication systems. IEEE Trans. Commun. 2023, 71, 595–610. [Google Scholar] [CrossRef]
- Shi, Q.; Zhang, T.; Yu, X.; Liu, X.; Lee, I. Waveform designs for joint radar-communication systems with OQAM-OFDM. Signal Process. 2022, 195, 108462. [Google Scholar] [CrossRef]
- Liyanaarachchi, S.D.; Riihonen, T.; Barneto, C.B.; Valkama, M. Optimized waveforms for 5G–6G communication with sensing: Theory, simulations and experiments. IEEE Trans. Wirel. Commun. 2021, 20, 8301–8315. [Google Scholar] [CrossRef]
- Shi, S.; Cheng, Z.; Wu, L.; He, Z.; Shankar, B. Distributed 5G NR-based integrated sensing and communication systems: Frame structure and performance analysis. In Proceedings of the 2022 30th European Signal Processing Conference, Belgrade, Serbia, 29 August–2 September 2022; pp. 1062–1066. [Google Scholar]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO communications with MIMO radar: From co-existence to joint transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- 3GPP. 5G New Radio-Physical Channels and Modulation (V17.4.0). Available online: https://www.3gpp.org/ftp/Specs/archive/38_series/38.211/38211-h40.zip (accessed on 10 June 2022).
- Wang, L.; Wang, H.; Wang, M.; Li, X. An overview of radar waveform optimization for target detection. J. Radars 2016, 5, 487–498. [Google Scholar]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, X.; Li, X. Aliasing-free moving target detection in random pulse repetition interval radar based on compressed sensing. IEEE Sens. J. 2013, 13, 2523–2534. [Google Scholar] [CrossRef]
- Quan, G.; Yang, Z.; Huang, J.; Huang, J. Sparsity-based space-time adaptive processing in random pulse repetition frequency and random arrays radar. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing, Chengdu, China, 6–10 November 2016; pp. 1642–1646. [Google Scholar]
- Applebaum, L.; Howard, S.D.; Searle, S.; Calderbank, R. Chirp sensing codes: Deterministic compressed sensing measurements for fast recovery. Appl. Comput. Harmon. Anal. 2009, 26, 283–290. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Li, X.; Wang, H.; Jiang, W. Adaptive clutter suppression based on iterative adaptive approach for airborne radar. Signal Process. 2013, 93, 3567–3577. [Google Scholar] [CrossRef]
- Davis, G.; Mallat, S.; Avellaneda, M. Adaptive greedy approximations. Constr. Approx. 1997, 13, 57–98. [Google Scholar] [CrossRef]
- Blake, S. OS-CFAR theory for multiple targets and nonuniform clutter. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 785–790. [Google Scholar] [CrossRef]
- Nosrati, M.; Tavassolian, N. High-accuracy heart rate variability monitoring using Doppler radar based on Gaussian pulse train modeling and FTPR algorithm. IEEE Trans. Microw. Theory Tech. 2017, 66, 556–567. [Google Scholar] [CrossRef]
- Ward, J. Space-time adaptive processing for airborne radar. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, London, UK, 6 April 1998; pp. 2809–2812. [Google Scholar]




| Slot | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Designed waveform | 3 | 0 | null | 13 | null | null | 13 | 13 |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Designed waveform | 12 | null | null | 0 | 13 | 11 | null | null |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Designed waveform | 3 | 1 | 0 | null | null | 1 | 0 | 0 |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| Designed waveform | null | 1 | null | 13 | 12 | null | 0 | null |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| Designed waveform | 13 | 13 | null | 0 | null | 1 | 0 | null |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| Designed waveform | 1 | 0 | null | 0 | null | null | 3 | 1 |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 |
| Designed waveform | 0 | null | null | 5 | 3 | 3 | null | null |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
| Designed waveform | 5 | 4 | 3 | null | 3 | 2 | null | 0 |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 |
| Designed waveform | null | null | 11 | 12 | 10 | null | 12 | 11 |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Slot | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| Designed waveform | null | 11 | null | 11 | null | 13 | 10 | null |
| Uniform waveform | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Chu, P.; Wang, X.; Yang, Z. Inner-Frame Time Division Multiplexing Waveform Design of Integrated Sensing and Communication in 5G NR System. Sensors 2023, 23, 6855. https://doi.org/10.3390/s23156855
Zheng J, Chu P, Wang X, Yang Z. Inner-Frame Time Division Multiplexing Waveform Design of Integrated Sensing and Communication in 5G NR System. Sensors. 2023; 23(15):6855. https://doi.org/10.3390/s23156855
Chicago/Turabian StyleZheng, Jian, Ping Chu, Xiaoye Wang, and Zhaocheng Yang. 2023. "Inner-Frame Time Division Multiplexing Waveform Design of Integrated Sensing and Communication in 5G NR System" Sensors 23, no. 15: 6855. https://doi.org/10.3390/s23156855





