Underwater Wireless Sensor Networks with RSSI-Based Advanced Efficiency-Driven Localization and Unprecedented Accuracy
Abstract
:1. Introduction
1.1. Problem Statement
1.2. Motivation
- ➢
- Investigation of Scaling Effect: The manuscript explores how object localization changes as the number of UWSNs grows. This analysis helps in understanding the impact of network size on the accuracy and effectiveness of object localization in UWSNs.
- ➢
- Evaluation of Distance-based Localization Algorithms: The manuscript examines distance-based localization algorithms in the context of UWSNs. By evaluating these algorithms, the study provides insights into their suitability, performance, and limitations for underwater localization scenarios.
- ➢
- Proposal of an Effective Localization Strategy: The manuscript proposes and recommends an acceptable localization strategy based on the desired RSSI data. This strategy aims to optimize object localization in UWSNs, taking into account the specific requirements and characteristics of the underwater environment.
2. Related Works
3. Proposed Network Design and Simulation Settings
4. Results and Discussion
4.1. Analysis of Angle-Based MEEs
4.2. Analysis of Distance-Based MEEs
4.3. Analysis of RSSI-Based MEEs
4.4. Comparative Analysis
5. Conclusions and Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Underwater wireless sensor networks (UWSNs) |
| TDOA majorization-minimization (T-MM) |
| Majorization-minimization (MM) |
| Squared position error bound (SPEB) |
| Global positioning system (GPS) |
| Infrared (IR) |
| Changeable transmission power-based sparsity-conscious energy-efficient clustering (CTP-SEEC) |
| Angle of arrival (AOA) |
| Time difference of arrival (TDoA) |
| Received signal strength indicator (RSSI) |
| Mean estimation error (MEE) |
| Equivalent Fisher information matrix (EFIM) |
| Line-of-sight (LOS) |
| Wireless sensor network (WSN) |
| Autonomous underwater vehicles (AUVs) |
| Transmission power level (TPL) |
References
- Sathish, K.; Ravikumar, C.V.; Rajesh, A.; Pau, G. Underwater Wireless Sensor Network Performance Analysis Using Diverse Routing Protocols. J. Sens. Actuator Netw. 2022, 11, 64. [Google Scholar] [CrossRef]
- Heidemann, J.; Ye, W.; Wills, J.; Syed, A.; Li, Y. Research challenges and applications for underwater sensor networking. In Proceedings of the Wireless Communications and Networking Conference (WCNC 2006), Las Vegas, NV, USA, 3–6 April 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 1, pp. 228–235. [Google Scholar]
- Ravikumar, C.V.; Kala, P.B. Design of MC-CDMA receiver using RBF network to mitigate MAI and nonlinear distortion. Neural Comput. Appl. 2019, 31, 1263–1273. [Google Scholar]
- Chuku, N.; Nasipuri, A. RSSI-Based Localization Schemes for Wireless Sensor Networks Using Outlier Detection. J. Sens. Actuator Netw. 2021, 10, 10. [Google Scholar] [CrossRef]
- Park, M.K.; Rodoplu, V. UWAN-MAC: An energy-efficient MAC protocol for underwater acoustic wireless sensor networks. IEEE J. Ocean. Eng. 2007, 32, 710–720. [Google Scholar] [CrossRef]
- Rani, S.; Talwar, R.; Malhotra, J.; Ahmed, S.H.; Sarkar, M.; Song, H. A novel scheme for an energy-efficient Internet of Things based on wireless sensor networks. Sensors 2015, 15, 28603–28626. [Google Scholar] [CrossRef] [Green Version]
- Manjula, S.H.; Abhilash, C.N.; Shaila, K.; Venugopal, K.R.; Patnaik, L.M. Performance of AODV routing protocol using group and entity mobility models in wireless sensor networks. In Proceedings of the International Multi-Conference of Engineers and Computer Scientist, Hong Kong, 19–21 March 2008; Volume 2, pp. 1212–1217. [Google Scholar]
- Sathish, K.; Ravikumar, C.V.; Asadi Srinivasulu, A.; Rajesh, A.; Oyerinde, O.O. Performance and Improvement Analysis of the Underwater WSN Using a Diverse Routing Protocol Approach. J. Comput. Netw. Commun. 2022, 2022, 9418392. [Google Scholar] [CrossRef]
- Bhattacharjya, K.; Alam, S.; De, D. Performance analysis of DYMO, ZRP and AODV routing protocols in a multi-hop grid based underwater wireless scensor network. In Proceedings of the 2nd International Conference on Computational Intelligence, Communications and Business Analytics (CICBA), Kalyani, India, 27–28 July 2018; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Alkindi, Z.; Alzeidi, N.; Touzene, B.A.A. Performance evolution of grid-based routing protocol for underwater wireless sensor networks under different mobile models. Int. J. Wirel. Mob. Netw. (IJWMN) 2018, 10, 13–25. [Google Scholar]
- Liu, L.; Zhou, Z.; Han, G.; Martínez-García, M. Boundary Tracking of Continuous Objects Based on Feasible Region Search in Underwater Acoustic Sensor Networks. IEEE Trans. Mob. Comput. 2022. [Google Scholar] [CrossRef]
- Saeed, K.; Khalil, W.; Al-Shamayleh, A.S.; Ahmad, I.; Akhunzada, A.; ALharethi, S.Z.; Gani, A. Analyzing the Impact of Active Attack on the Performance of the AMCTD Protocol in Underwater Wireless Sensor Networks. Sensors 2023, 23, 3044. [Google Scholar] [CrossRef]
- Sathish, K.; Ravikumar, C.V.; Srinivasulu, A.; Gupta, A.K. Performance Analysis of Underwater Wireless Sensor Network by Deploying FTP, CBR, and VBR as Applications. J. Comput. Netw. Commun. 2022, 2022, 7143707. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Du, J.; Hou, X.; Ren, Y.; Han, Z. Stochastic Optimization-Aided Energy-Efficient Information Collection in Internet of Underwater Things Networks. IEEE Internet Things J. 2022, 9, 1775–1789. [Google Scholar] [CrossRef]
- Bagadi, K.; Pavikumar, C.V.; Sathish, K.; Alibakhshikenari, M.; Virdee, B.S.; Kouhalvandi, L.; Olan-Nunez, K.N.; Pau, G.; See, C.H.; Dayoub, I.; et al. Detection of Signals in MC–CDMA Using a Novel Iterative Block Decision Feedback Equalizer. IEEE Access 2022, 10, 105674–105684. [Google Scholar] [CrossRef]
- Sathish, K.; Venkata, R.C.; Anbazhagan, R.; Pau, G. Review of Localization and Clustering in USV and AUV for Underwater Wireless Sensor Networks. Telecom 2023, 4, 43–64. [Google Scholar] [CrossRef]
- Xu, T.; Wang, J.; Shi, W.; Wang, J.; Chen, Z. A localization algorithm using a mobile anchor node based on region determination in underwater wireless sensor networks. J. Ocean. Univ. China 2019, 18, 394–402. [Google Scholar] [CrossRef]
- Sathish, K.; Hamdi, M.; Chinthaginjala, R.; Pau, G.; Ksibi, A.; Anbazhagan, R.; Abbas, M.; Usman, M. Reliable Data Transmission in Underwater Wireless Sensor Networks Using a Cluster-Based Routing Protocol Endorsed by Member Nodes. Electronics 2023, 12, 1287. [Google Scholar] [CrossRef]
- Yan, J.; Li, X.; Lu, X.; Guan, X. Virtual-lattice based intrusion detection algorithm over actuator-assisted underwater wireless sensor networks. Sensors 2017, 17, 1168. [Google Scholar] [CrossRef] [Green Version]
- Han, G.J.; Zhang, C.Y.; Liu, T.Q.; Shu, L. A multi-anchor nodes collaborative localization algorithm for underwater acoustic sensor networks. Wirel. Commun. Mob. Comput. 2016, 16, 682–702. [Google Scholar] [CrossRef]
- Zhou, R.; Chen, J.; Tan, W.; Cai, C. Sensor Selection for Optimal Target localization with 3-D Angle of Arrival Estimation in Underwater Wireless Sensor Networks. J. Mar. Sci. Eng. 2022, 10, 245. [Google Scholar] [CrossRef]
- Li, D.; Du, J.; Liu, L. A data forwarding algorithm based on Markov thought in underwater wireless sensor networks. Int. J. Distrib. Sens. Netw. 2017, 13, 377–389. [Google Scholar] [CrossRef]
- Sathish, K.; Anbazhagan, R.; Venkata, R.C.; Arena, F.; Pau, G. Investigation and Numerical Simulation of the Acoustic Target Strength of the Underwater Submarine Vehicle. Inventions 2022, 7, 111. [Google Scholar] [CrossRef]
- Li, S.; Sun, H.; Esmaiel, H. Underwater TDOA Acoustical Location Based on Majorization-Minimization Optimization. Sensors 2020, 20, 4457. [Google Scholar] [CrossRef] [PubMed]
- Arbula, D.; Ljubic, S. Indoor Localization Based on Infrared Angle of Arrival Sensor Network. Sensors 2020, 20, 6278. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Liu, Y.; Su, X.; Kim, P. Efficient and accurate target localization in underwater environment. IEEE Access 2019, 7, 101415–101426. [Google Scholar] [CrossRef]
- Sahota, H.; Kumar, R. Sensor Localization Using Time of Arrival Measurements in a Multi-Media and Multi-Path Application of In-Situ Wireless Soil Sensing. Inventions 2021, 6, 16. [Google Scholar] [CrossRef]
- Dubrovinskaya, E.; Kebkal, V.; Kebkal, O.; Kebkal, K.; Casari, P. Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape. Sensors 2020, 20, 3862. [Google Scholar] [CrossRef] [PubMed]
- Hayder, I.A.; Khan, S.N.; Althobiani, F.; Irfan, M.; Idrees, M.; Ullah, S.; Alsaaq, F.; Glowacz, A.; Goldasz, I.; Tomczyk, M.; et al. Towards Controlled Transmission: A Novel Power-Based Sparsity-Aware and Energy-Efficient Clustering for Underwater Sensor Networks in Marine Transport Safety. Electronics 2021, 10, 854. [Google Scholar] [CrossRef]
- Qin, Q.; Tian, Y.; Wang, X. Three-Dimensional UWSN Positioning Algorithm Based on Modified RSSI Values. Mob. Inf. Syst. 2021, 2021, 5554791. [Google Scholar] [CrossRef]
- Haque, K.F.; Kabir, K.H.; Abdelgawad, A. Advancement of Routing Protocols and Applications of Underwater Wireless Sensor Network (UWSN)—A Survey. J. Sens. Actuator Netw. 2020, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- Kaveripakam, S.; Chinthaginjala, R. Energy balanced reliable and effective clustering for underwater wireless sensor networks. Alex. Eng. J. 2023, 77, 41–62. [Google Scholar] [CrossRef]
- Jan, S.; Yafi, E.; Hafeez, A.; Khatana, H.W.; Hussain, S.; Akhtar, R.; Wadud, Z. Investigating Master–Slave Architecture for Underwater Wireless Sensor Network. Sensors 2021, 21, 3000. [Google Scholar] [CrossRef]
- Yan, L.; He, Y.; Huangfu, Z. An Uneven Node Self-Deployment Optimization Algorithm for Maximized Coverage and Energy Balance in Underwater Wireless Sensor Networks. Sensors 2021, 21, 1368. [Google Scholar] [CrossRef] [PubMed]


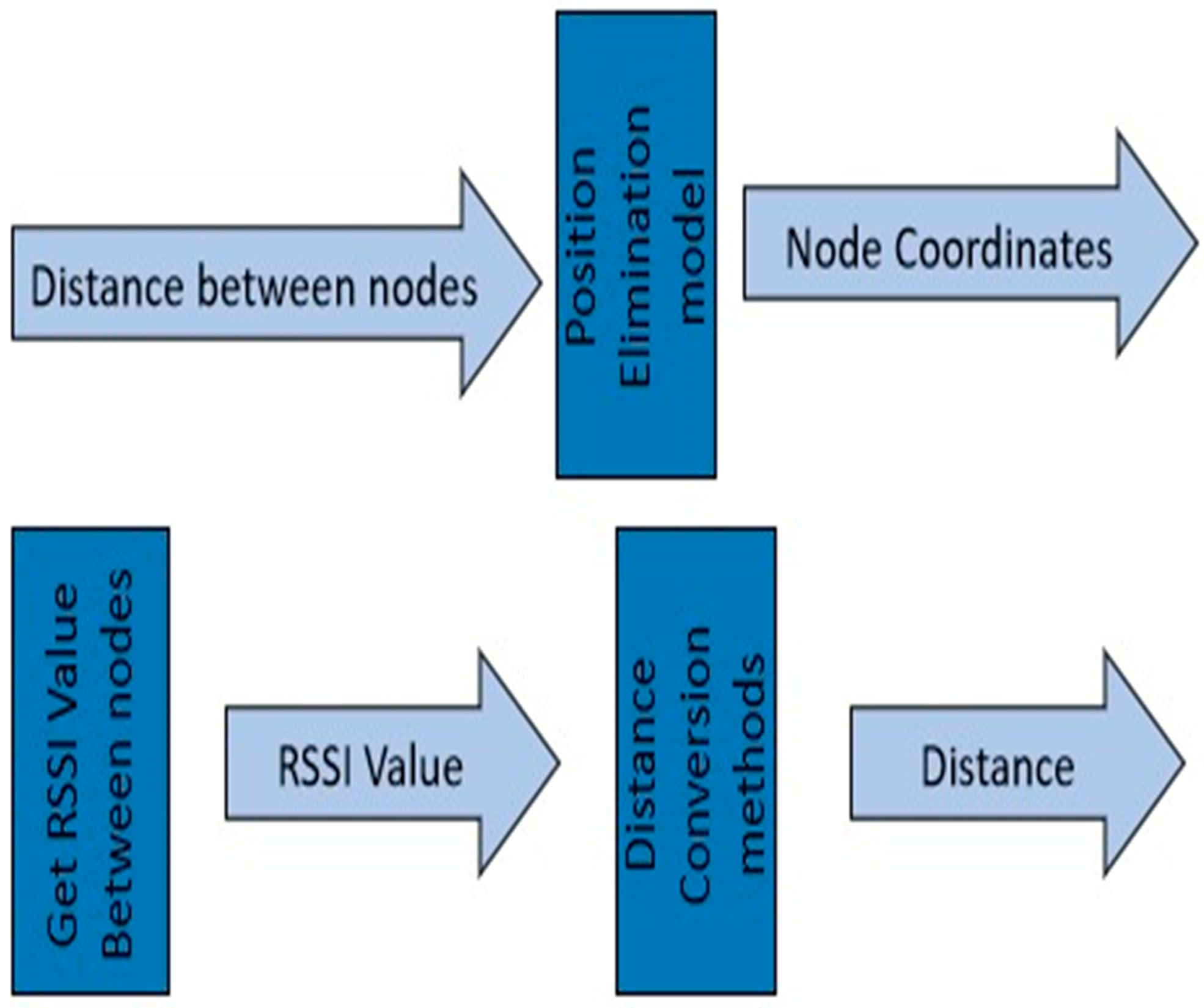
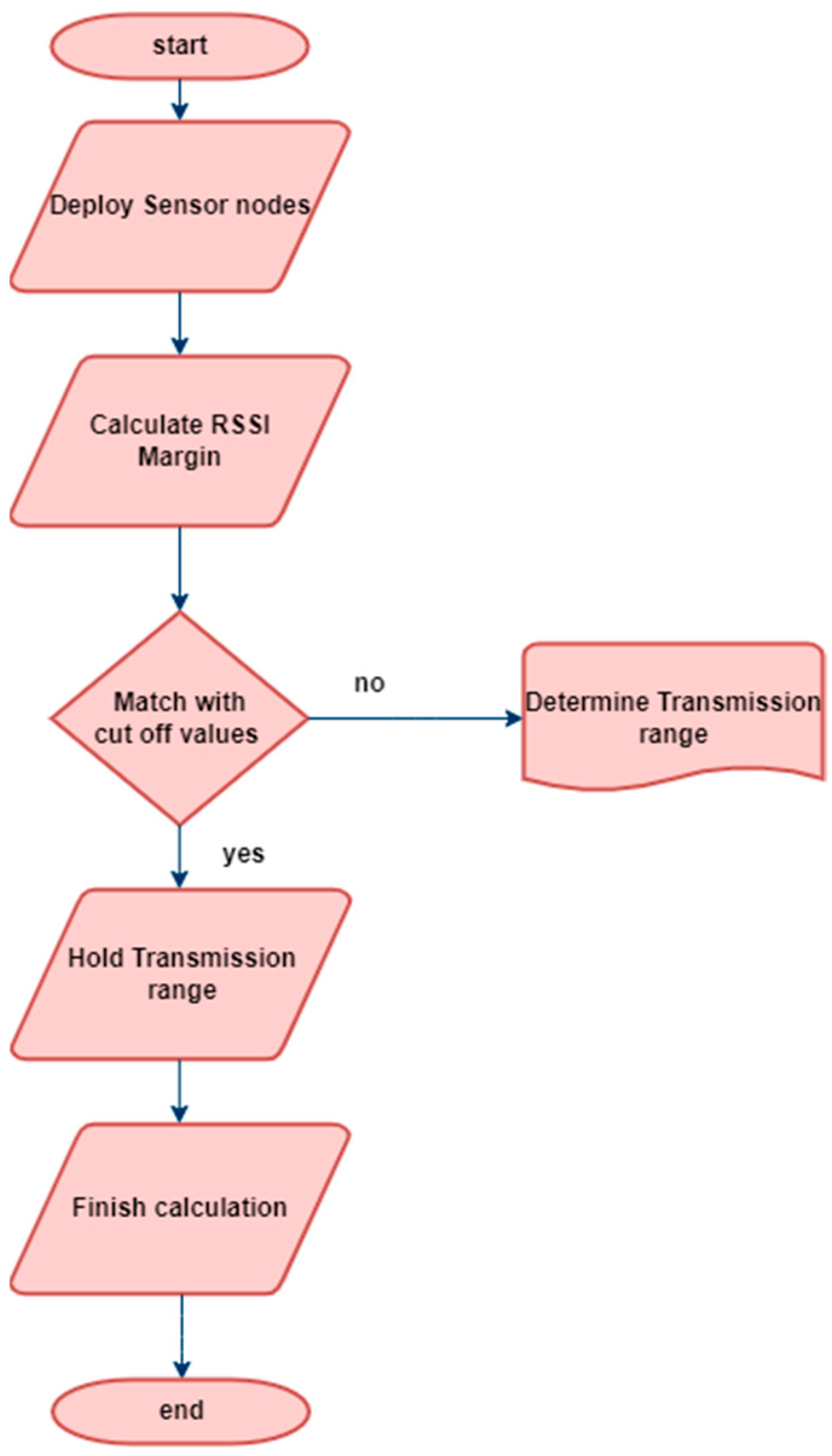




| Trial | Distance (m) |
|---|---|
| 1 | 51.3579 |
| 2 | 52.2380 |
| 3 | 53.3379 |
| 4 | 53.9192 |
| 5 | 54.1750 |
| 6 | 55.2470 |
| Trial | Distance (m) |
|---|---|
| 1 | 2.1474 |
| 2 | 2.9743 |
| 3 | 3.0234 |
| 4 | 3.1299 |
| 5 | 3.3555 |
| 6 | 3.6079 |
| Trial | Distance (m) |
|---|---|
| 1 | 0.12213 |
| 2 | 0.17615 |
| 3 | 0.18138 |
| 4 | 0.19792 |
| 5 | 0.24921 |
| 6 | 0.48601 |
| Trial | Distance (m) | ||
|---|---|---|---|
| AOA | TDOA | RSSI | |
| 1 | 51.3579 | 2.1474 | 0.12213 |
| 2 | 52.2380 | 2.9743 | 0.17615 |
| 3 | 53.3379 | 3.0234 | 0.18138 |
| 4 | 53.9192 | 3.1299 | 0.19792 |
| 5 | 54.1750 | 3.3555 | 0.24921 |
| 6 | 55.2470 | 3.6079 | 0.48601 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sathish, K.; Chinthaginjala, R.; Kim, W.; Rajesh, A.; Corchado, J.M.; Abbas, M. Underwater Wireless Sensor Networks with RSSI-Based Advanced Efficiency-Driven Localization and Unprecedented Accuracy. Sensors 2023, 23, 6973. https://doi.org/10.3390/s23156973
Sathish K, Chinthaginjala R, Kim W, Rajesh A, Corchado JM, Abbas M. Underwater Wireless Sensor Networks with RSSI-Based Advanced Efficiency-Driven Localization and Unprecedented Accuracy. Sensors. 2023; 23(15):6973. https://doi.org/10.3390/s23156973
Chicago/Turabian StyleSathish, Kaveripakam, Ravikumar Chinthaginjala, Wooseong Kim, Anbazhagan Rajesh, Juan M. Corchado, and Mohamed Abbas. 2023. "Underwater Wireless Sensor Networks with RSSI-Based Advanced Efficiency-Driven Localization and Unprecedented Accuracy" Sensors 23, no. 15: 6973. https://doi.org/10.3390/s23156973
APA StyleSathish, K., Chinthaginjala, R., Kim, W., Rajesh, A., Corchado, J. M., & Abbas, M. (2023). Underwater Wireless Sensor Networks with RSSI-Based Advanced Efficiency-Driven Localization and Unprecedented Accuracy. Sensors, 23(15), 6973. https://doi.org/10.3390/s23156973








